扩展功能
文章信息
- 韩霜, 傅惠
- HAN Shuang, FU Hui
- 即时响应式定制公交调度优化
- Optimization of Real-time Responsive Customized Bus Dispatch
- 公路交通科技, 2020, 37(6): 120-127, 158
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 120-127, 158
- 10.3969/j.issn.1002-0268.2020.06.015
-
文章历史
- 收稿日期: 2018-07-23
2. 广东工业大学 机电工程学院, 广东 广州 510006
2. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou Guangdong 510006, China
当前公交出行需求正向个性化、品质化方向发展,国内各大城市正大力发展定制公交以满足这一需求。定制公交作为多元化公共交通的重要组成部分,是指通过集中整合个体的交通出行需求,为出行起终点、出行时间、服务需求相同或相似的人群提供专门定制的公共交通服务方式。定制公交为乘客提供“快捷、准时、舒适”的高品质公交体验,根据响应模式上的差异,可以分为静态预约式和即时响应式定制公交。目前国内已经开通的定制公交服务多属于静态预约模式,主要以通勤人员为服务对象,其面对的出行需求在时空上相对集中并且往往呈现出方向上的不均衡性。在静态预约模式中,运营企业多采用大容量公交车并根据提前征集得到的乘车需求生成线路,乘客按月、周或单次预订已开通的线路并乘车,其线路生成的提前期较长且在较长时间内保持固定,车辆运行途中一般不进行路线调整。即时响应式定制公交既可为通勤人员也可为临时出行者提供服务,它多采用中小容量公交车,通过实时信息交换系统整合接收到的乘车请求,综合考虑车辆行驶中的多种限制条件,迅速规划并开行定制公交线路,系统在车辆行驶过程中持续接收新的乘车请求并判断可响应的请求,然后调整行车路线并实时调度车辆完成被响应乘客的运送。即时响应式定制公交具有较大的灵活性和广泛的适应性,对私家车出行者具有较大的吸引力,有利于充分发挥定制公交在替代私家车出行、缓解拥堵和降噪减排等方面的积极作用。
定制公交属于需求响应式公交,对于需求响应式公交系统的理论研究可以追溯到20世纪60年代末[1]。Nourbakhsh等对无固定路线和站点的需求响应式公交系统进行了研究,在理想化的正方形城市中,以运营和乘客成本最小为目标,探讨了线网最优布局、车辆最优服务区域和发车间隔[2]。Bakas等研究了带时间窗并且具有固定车队规模情况下的需求响应式公交系统的调度方法[3]。Kim等分析了乘客需求对传统公交与需求响应式公交系统最优性的影响,对两种公交系统的车辆规格、发车间隔和车队规模,传统公交的线路间距以及柔性公交的服务区域进行了优化[4]。Boyer等基于司机休息时间、连续工作时间、加班时间等限制条件研究了灵活公交系统的车辆及司机调度方案[5]。近年来,专门针对定制公交的研究开始兴起,主要集中在定制公交的评价[6]、票价制度[7]及线网规划[8-12]等方面。为提高定制公交线路的适应性,王健等根据前1天乘客向公交企业提交的出行需求优化第2天定制公交车辆的调度[13]。针对动态出行需求,Bruni等考虑车辆运行过程中需求的变化,提出了需求响应式公交系统的鲁棒优化,在前期线路规划中同时考虑已知需求及后续未知需求可能引起的路线偏离的影响,减少车辆的绕行成本[14]。邱丰等研究了可变线路式公交的调度,将实时需求插入到根据预约需求规划的行车计划中[15]。郭晓俊针对多起点单终点的定制公交线路,分别建立了发车前根据预约需求进行线路规划、发车后对线路周边实时需求进行响应的优化模型[16]。
综上所述,目前对即时响应模式下的定制公交调度研究比较少,并且针对动态需求的相关研究大多直接采用实时需求进行车辆调度决策。由于单次提交的乘车需求随机性较大,以此为依据进行的调度难以实现系统整体最优,同时也可能出现线路数量和线路行车方向波动较大的情形,影响公交系统的稳定运营,也增加了运营企业在运营资源管理上的复杂度。鉴于此,针对即时响应模式下的定制调度,本研究采用两阶段优化模型对其调度进行优化:首先根据区域内分时段的高概率出行OD点对(可根据历史乘车需求提取出或通过交通大数据分析提取)的地理分布,从整体上对定制公交车辆的初始线路进行优化;其次,以初始线路为基础、根据实时乘车请求对车辆的行驶路线和停靠时间等进行灵活调度,以实现车辆对实时出行请求的及时响应。该两阶段调度方法的优势在于:(1)根据分时段的高概率出行点对定制公交车辆的初始线路进行整体优化,在减少营运车辆(线路)的同时维持高覆盖率;(2)以初始线路为基础并根据实时出行需求对车辆进行调度,综合考虑了实时出行需求以及出行规律对定制公交车辆调度决策的影响,有利于提高车辆与乘客的匹配率,增加服务的乘客数量并提高服务水平。
1 即时响应式定制公交调度决策过程即时响应式定制公交调度决策是行驶线路预规划与车辆实时调度的综合体。由于即时响应式定制公交需要整合高度分散和随机的乘客出行需求,基于提高定制公交系统效益和服务水平的考虑,本研究提出在调度中首先根据区域内分时段的高概率出行OD点对(如商业中心、大型社区等)预先优化定制公交车辆的初始路线;当某条线路接收到的实时出行请求达到一定数量时,则启动该线路的运营,以初始线路为基础,根据可响应的实时出行请求调整车辆行驶路径并调度车辆按照决策的时间点运送乘客。即时响应式定制公交调度决策过程如图 1所示。

|
| 图 1 即时响应式定制公交调度决策过程 Fig. 1 Decision procedure of real-time responsive customized bus dispatch |
| |
在车辆初始线路规划阶段,根据区域内分时段的高概率出行点的地理位置、OD关系以及上/下车站点顺序预先规划车辆初始线路,对该时段内需要的定制公交车辆数量(线路数量)、车辆初始经停站点和停靠顺序等进行决策。车辆初始线路规划有利于运输企业以最少的车辆(线路)覆盖服务区域内的主要出行点,提高运营线路与出行需求的适应度。在车辆实时调度阶段,以初始线路作为参考路径,可选择初始线路中的全部或部分站点作为车辆行驶过程中的必经站点;在此基础上,结合实时乘车请求的时间和空间分布、上/下车站点关系、上/下车时间点、车辆容量等限制条件进行序贯决策,判断是否能够将某个乘车请求加入到行车计划中;最后,根据可响应的乘车请求调整车辆行驶路径并调度车辆按决策的到站时间运送乘客。在定制公交调度中,往往需要平衡运输企业的经济效益(利润或运营成本)和乘客出行品质(服务水平)。
上述两阶段调度方法,从整体(全区域车辆规划)和局部(单车调度)两个层面去平衡运输企业和乘客利益,既保持了即时响应式定制公交的灵活性,也使得其线路方案能够在时空维度上整体把握需求规律,有利于定制公交系统以较少的线路覆盖区域内的主要出行需求,并且其调度方案兼顾了实时需求与后续最可能需求,规避了仅依靠实时需求进行决策带来的弊端。
2 即时响应式定制公交调度优化建模 2.1 问题描述本研究的即时响应式定制公交调度可以描述为:乘客通过实时信息交换平台提交上/下车站点、上/下车时间点(即服务的时间窗)及乘车人数等乘车请求;定制公交系统根据实际限制条件分析得出可以响应的乘车请求,允许车辆晚于乘客要求的上/下车时间点到达,但晚于下车时间到达将产生延误成本;定制公交系统信息平台向乘客反馈决策结果,然后按照决策获得的时间和地点调整车辆的行驶路线,调度车辆及时运送乘客。
为便于建模,做出如下假设:
(1) 乘客均通过定制公交信息平台提交乘车请求,包括上/下车位置、上/下车时间点和乘车人数。
(2) 各个站点都仅有一个上车或下车请求,若一个站点同时具有多个上车或下车请求,在模型中将其拆分为地理位置相同的多个站点。
(3) 任意站点间的行驶距离已知,站点间的距离为路网中各站点间的最短行驶距离。
(4) 除车辆启动和停车阶段外,定制公交车辆以匀速行驶。
(5) 定制公交票价为按次收费的均价。
2.2 车辆初始线路优化模型为方便模型的表达,定义集合及参数如下:N为规划区域内分时段的高概率出行点集合,N={1, …, n1},N=N+∪N-,N+为上车点集合,N-为下车点集合;{0}为车辆的虚拟车场;L为定制公交车辆集合,L={1, …, l1};dij为路网中站点i与站点j之间的最短行驶距离;dmax为定制公交车辆初始线路的最大长度限值;M为每辆车初始线路中的最大站点数;alij为0-1变量,车辆l从站点i开往站点j时取值为1,否则取值为0。
定制公交车辆初始线路优化模型如下:
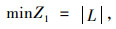
|
(1) |
s. t.
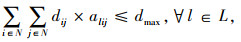
|
(2) |

|
(3) |

|
(4) |
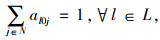
|
(5) |
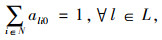
|
(6) |
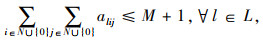
|
(7) |
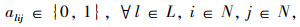
|
(8) |
公式(1)表示定制公交系统的运营车辆数量最小,|L|为集合L中元素的个数;公式(2)表示定制公交车辆的初始行驶距离不超过最大值;公式(3)表示每个高概率出行点都必须被定制公交车辆覆盖;公式(4)表示驶入与驶离中间站点的定制公交车辆数量相等;公式(5)和公式(6)表示车辆需要从虚拟车场出发并且最终回到虚拟车场,公式(7)表示除虚拟车场外,车辆经停的初始站点数量不超过M;公式(8)是决策变量的取值约束。
2.3 车辆实时调度决策模型在车辆实时调度阶段,每辆车可以响应初始线路及其周边的实时乘车请求。定制公交系统通常基于较短的固定时间间隔或基于站点对车辆调度方案进行序贯更新,以确保车辆能够对实时乘车请求进行快速响应。为建立车辆实时调决策模型,定义集合及参数如下:Q为定制公交车辆的最大载客量;Nm为定制公交车辆的必经站点,Nm=Nm+∪Nm-∪N1∪{0},其中Nm+为已响应的上车站点,Nm-为已响应的下车站点,N1为位于车辆初始线路中但没有产生乘车请求或没有被响应的站点,{0}为虚拟车场;Ns为定制公交车辆的可选站点,Ns=Ns+∪Ns-,其中Ns+为可选上车站点,Ns-为可选下车站点,若乘客请求被响应,则其上/下车位置转变为车辆的必经站点;σ1为晚于时间窗送达乘客而产生的延误成本的折算系数;σ2为车辆未响应某个乘客而产生的惩罚成本的折算系数;cv为车辆的单位时间变动成本;cf为车辆单次出车的固定成本;ts为车辆的启动/停车时间;tg为单个乘客上/下车时间;tjk为车辆从站点j到站点k的行驶时间;tj为车辆进入站点j的时间;talj乘客要求车辆到达站点j的时间;quj为站点j的上客数;qdj为站点j的下客数;q0j为车辆到达站点j之前的在车乘客数;p为票价;xjk为0-1决策变量,当定制公交车辆由站点j驶向站点k时取值为1,否则为0。
定制公交车辆实时调度决策模型如下:
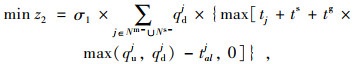
|
(9) |
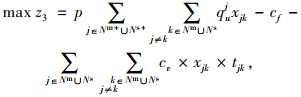
|
(10) |

|
(11) |
s.t.
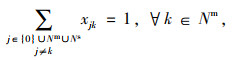
|
(12) |
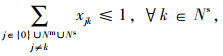
|
(13) |

|
(14) |

|
(15) |
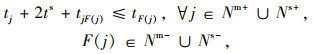
|
(16) |
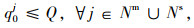
|
(17) |
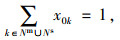
|
(18) |
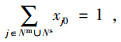
|
(19) |

|
(20) |
公式(9)表示使定制公交车辆晚于乘客要求的时间送达造成的延误成本最小;公式(10)表示定制公交车辆的利润最大化;公式(11)表示因未响应乘客而导致的惩罚成本最小;公式(12)表示车辆必须访问必经站点;公式(13)表示车辆可以访问或者不访问可选站点;公式(14)表示车辆访问中间站点以后必须离开;公式(15)表示定制公交车辆若访问了上车站点j,则必须访问其对应的下车站点,F(j)为上车站点j对应的下车站点;公式(16)表示车辆必须先访问上车站点才能访问其对应的下车站点;公式(17)表示车辆在车乘客总数不超过车辆最大载客量;公式(18)和(19)表示车辆从虚拟车场驶出并最终回到虚拟车场;公式(20)为决策变量的取值约束。
3 模型求解算法 3.1 车辆初始线路优化模型的遗传算法设计定制公交车辆初始线路优化模型是一个线性整数规划模型,本文采用遗传算法进行求解。遗传算法的主体框架与基本遗传算法类似,故在此仅对遗传算法的编码、初始种群以及遗传算子进行简要说明。
(1) 编码
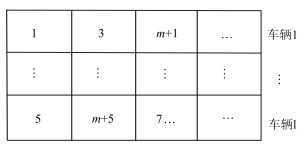
定制公交车辆的初始线路是由多个站点按照一定顺序排列形成的序列,本文采用自然数1,2,…,m表示服务区域内的高概率上车站点,其对应的下车站点则采用m+1,m+2,…,2m进行编号。在遗传算法中,染色体采用实数编码并用二维矩阵存储,矩阵的每一行代表一辆车的初始线路,如图 2所示。
|
| 图 2 车辆初始线路优化模型的编码 Fig. 2 Coding of vehicle initial route optimization model |
| |
(2) 初始种群
初始种群的质量将影响遗传算法的搜索效率,为提高初始种群中的染色体质量并保证种群多样性,采用以下方法生成初始种群中的染色体:
① 随机扰乱高概率出行点对的排列顺序;
② 选择第一对高概率出行点,构成第1辆车的第一对经停站点;
③ 选择下一对高概率出行点,以插入后行驶距离增加值最小为原则将其插入第l(l=1, 2, …, l1)辆车的经停路径,判断是否满足所有约束,如果满足则调整该车辆的初始路径,否则将该高概率出行点对插入下一辆车的经停路径, 不断重复上述过程,直至找到满足约束的最佳插入位置;
④ 依次选择余下的高概率出行点对,重复步骤③,直至将所有高概率出行点对都插入车辆的初始路径中。
(3) 交叉算子
为了加强遗传算法的全局搜索性能,扩大算法的搜索范围,交叉算子采用整条路径交换的形式:首先随机选取两个父代染色体,随机在两个父代染色体中各选一条车辆初始路径,然后进行交换;最后对子代染色体进行修整,使得子代染色体满足约束条件。
(4) 变异算子
变异算子主要用于小范围调整站点顺序:首先随机挑选出进行变异的父代染色体,然后在该染色体中随机选择一对高概率出行点作为变异点,将该高概率出行点对重新插入其他车辆的路径,并对变异后的子代染色体进行修整,以保证染色体满足约束条件。
3.2 车辆实时调度决策模型的NSGA-Ⅱ算法设计定制公交车辆实时调度决策模型是一个多目标的非线性整数规划模型,采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)进行求解。本研究NSGA-Ⅱ算法的基本框架以及快速非支配排序、虚拟适应度计算以及精英保留策略与文献[17]~[18]相似,以下仅对编码和遗传算子进行简要说明。
(1) 编码
车辆实时调度形成的最终行驶路径是由已确定的必经站点和新一轮决策中加入的可响应站点组成的序列。在每一轮优化中,都只需确定乘客新提交的乘车请求中哪些乘车请求可以被响应,即哪些OD对能够加入到原有的行车计划中。采用二进制编码对车辆实时调度决策模型的染色体进行编码,1代表相应的OD对被响应,0则反之。
(2) 遗传算子
车辆实时调度模型的交叉算子为二进制编码规则下的两点交叉,变异算子为二进制编码规则下的单点变异。
4 案例分析选取广州市内的50个高概率出行点(主要为学校、住宅小区、商业设施、公共服务设施等)及其OD关系进行实时响应式定制公交调度决策的模拟,OD点对及经纬度如表 1所示。
| O点编号 | O点经纬度 |
| 1 | (113.330 15, 23.155 507) |
| 2 | (113.338 074, 23.157 742) |
| 3 | (113.351 692, 23.161 264) |
| 4 | (113.352 051, 23.146 112) |
| 5 | (113.327 546, 23.140 961) |
| 6 | (113.335 307, 23.147 900) |
| 7 | (113.315 688, 23.132 919) |
| 8 | (113.326 719, 23.130 858) |
| 9 | (113.326 396, 23.122 715) |
| 10 | (113.304 405, 23.094 611) |
| 11 | (113.296 141, 23.102 456) |
| 12 | (113.293 985, 23.089 824) |
| 13 | (113.283 311, 23.081 316) |
| 14 | (113.349 392, 23.108 307) |
| 15 | (113.285 880, 23.085 025) |
| 16 | (113.292 763, 23.073 999) |
| 17 | (113.360 819, 23.097 005) |
| 18 | (113.390 140, 23.129 446) |
| 19 | (113.303 599, 23.126 833) |
| 20 | (113.341 687, 23.119 355) |
| 21 | (113.317 485, 23.071 938) |
| 22 | (113.343 735, 23.122 812) |
| 23 | (113.346 215, 23.120 352) |
| 24 | (113.359 617, 23.127 265) |
| 25 | (113.396 735, 23.122 014) |
| 26 | (113.319 892, 23.154 485) |
| 27 | (113.311 612, 23.146 208) |
| 28 | (113.352 051, 23.146 112) |
| 29 | (113.320 072, 23.148 172) |
| 30 | (113.307 028, 23.130 559) |
| 31 | (113.329 917, 23.126 803) |
| 32 | (113.315 005, 23.120 987) |
| 33 | (113.349 392, 23.108 307) |
| 34 | (113.285 433, 23.116 683) |
| 35 | (113.326 396, 23.122 715) |
| 36 | (113.279 253, 23.108 174) |
| 37 | (113.345 009, 23.112 96) |
| 38 | (113.340 05, 23.110 035) |
| 39 | (113.293 985, 23.089 824) |
| 40 | (113.290 032, 23.077 457) |
| 41 | (113.360 819, 23.097 005) |
| 42 | (113.399 698, 23.095 661) |
| 43 | (113.292 735, 23.141 558) |
| 44 | (113.343 428, 23.072 869) |
| 45 | (113.308 070, 23.064 423) |
| 46 | (113.348 586, 23.120 153) |
| 47 | (113.329 926, 23.112 242) |
| 48 | (113.414 702, 23.127 598) |
| 49 | (113.435 776, 23.120 535) |
| 50 | (113.310 175, 23.117 693) |
各出行点间的路网最短距离采用百度API计算获得。车辆初始线路优化模型的参数设置如下:车辆初始线路径长度不超过35 km,初始站点数量不超过12个。通过试算,确定遗传算法参数如下:种群规模为50,交叉概率0.6,变异概率为0.4,进化代数为500。经过计算,需要6辆车(6条线路)覆盖所有的高概率出行点,每条线路的经停站点如表 2所示。
| 车辆 | 站点 | 行驶距离/km | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 1 | 23 | 24 | 49 | 48 | — | — | — | — | — | — | — | — | 16.89 |
| 2 | 10 | 12 | 13 | 15 | 40 | 16 | 21 | 35 | 46 | 37 | 38 | 41 | 34.74 |
| 3 | 25 | 18 | 3 | 28 | 5 | 43 | 30 | 7 | 32 | 50 | - | — | 34.40 |
| 4 | 14 | 20 | 9 | 19 | 34 | 11 | 36 | 39 | 45 | 44 | — | — | 32.88 |
| 5 | 4 | 6 | 1 | 26 | 29 | 8 | 31 | 22 | 47 | 33 | 17 | 42 | 31.68 |
| 6 | 2 | 27 | — | — | — | — | — | — | — | — | — | — | 7.46 |
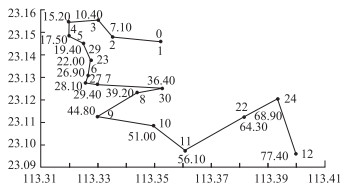
当线路接收到一定数量的出行请求时,该线路即开始运营,其车辆的调度决策基于站点进行序贯更新。因篇幅有限,本研究仅列出车辆5(线路5)的实时调度结果。模型中相关参数设定如下:车辆行驶速度为35 km/h,车辆启/停时间为2 s/次,车辆有效座位数为26,车辆变动成本为80元/时,固定成本折合到单位车时为40元;每个乘客上/下车时间为1 s/人;σ1为5 000,σ2为200;票价为10元/次。NSGA-Ⅱ算法参数如下:种群规模为20,迭代次数为100,交叉概率0.9,变异概率为0.1。随机产生3批乘车请求,如表 3所示。为方便计算,将车辆5初始线路中的实际经停站点按照访问顺序重新用1-12编号,实时响应的乘车请求从13开始依次编号,奇数为上车点,偶数为下车点。经计算,车辆5的路线调整方案如表 4所示,车辆到达各个站点的时间如图 3所示(单位:分)。进一步对数据进行分析可知:车辆5共搭载乘客29人,未响应乘客数为17人;由于在响应时间上采用柔性匹配,车辆在部分站点出现送达延误,最大延误发生在站点24,延误时间为12.6 min,平均延误时间为5.2 min,在非紧急出行中,该延误在可接受范围之内。案例分析的结果说明采用所提出的两阶段调度方法能够取得较好的调度效果。
| 批次 | O点经纬度 | D点经纬度 | 人数 | 上/下车时间 | 是否响应 |
| 1 | (113.352 051, 23.146 112) | (113.320 072, 23.148 172) | 5 | [0.00, 20.12] | 是 |
| (113.330 150, 23.155 507) | (113.319 890, 23.154 485) | 3 | [10.40, 15.54] | 是 | |
| (113.343 735, 23.122 812) | (113.329 926, 23.112 242) | 1 | [32.43, 43.54] | 是 | |
| (113.346 925, 23.133 664) | (113.378 974, 23.121 657) | 2 | [6.76, 28.55] | 否 | |
| (113.360 819,23.097 005) | (113.399 698, 23.095 661) | 4 | [50.01, 65.43] | 否 | |
| (113.335 307,23.147 900) | (113.329 917, 23.126 803) | 2 | [7.10, 25.22] | 是 | |
| 2 | (113.326 719,23.130 858) | (113.381 293, 23.112 352) | 4 | [26.86, 56.03] | 是 |
| (113.327 553,23.137 360) | (113.393 417, 23.120 349) | 4 | [16.03, 56.27] | 是 | |
| (113.330 098,23.142 858) | (113.368 821, 23.126 602) | 5 | [17.58, 49.53] | 否 | |
| (113.319 892,23.154 485) | (113.349 392, 23.108 307) | 5 | [15.21, 42.40] | 是 | |
| (113.320 646,23.152 305) | (113.399 698, 23.095 661) | 3 | [17.13, 68.05] | 是 | |
| 3 | (113.325 941,23.127 422) | (113.399 698, 23.095 661) | 1 | [24.69, 65.13] | 是 |
| (113.325 058,23.144 863) | (113.352 590, 23.124 994) | 4 | [14.85, 36.79] | 是 | |
| (113.326 434,23.153 915) | (113.393 417, 23.120 349) | 2 | [21.95, 57.33] | 否 | |
| (113.320 266,23.129 105) | (113.343 735, 23.122 812) | 1 | [20.66, 35.39] | 否 |
| 序号 | 行驶路线 |
| 初始行驶路径 | 1—2—3—4—5—6—7—8—9—10—11—12 |
| 第1次调整 | 1(13)—2(19)—3(15)—4(16)—5(14)—6—7(20)—8(17)—9(18)—10—11—12 |
| 第2次调整 | 1(13)—2(19)—3(15)—4(16)—5(14)—23—6(21)—7(20)—8(17)—9(18)—10(26)—11—21—24—12 |
| 第3次调整 | 1 (13)—2(19)—3(15)—4(16)—5(14)—29—23—6(21)—27—7(20)—30—8(17)—9(18)—10(26)—11—21—24—12(28) |
| 注:圆括号内的数字表示编号不同但地理位置相同的站点。 | |
|
| 图 3 车辆5到达站点的时间(单位:分钟) Fig. 3 Arrival time of vehicle 5(unit:min) |
| |
5 结论
调度是影响即时响应式定制公交运营的关键技术,本研究兼顾运输企业和乘客利益,综合考虑定制公交出行需求规律及实时出行请求对调度决策的影响,建立了即时响应式定制公交两阶段调度模型,即初始线路优化模型和车辆实时调度决策模型:首先以运营车辆数最小为目标对定制公交系统的初始线路进行整体优化。在此基础上根据实时出行请求,以乘客延误成本最小、运输企业利润最大以及未服务乘客造成的损失最小为目标进行车辆实时调度。该方法具有以下特点:以较少的车辆(线路)覆盖区域内的主要出行点;同时考虑实时出行请求以及需求规律对车辆进行实时调度,调度方案既满足了当前的实时需求也兼顾了后续最可能出现的出行需求,提高车辆与出行需求的匹配率。根据模型的特点,分别设计了求解模型的遗传算法和NSGA-Ⅱ算法。最后,选取广州市内的部分高概率出行点进行了案例分析,计算结果表明本文提出的两阶段调度模型以及设计的算法能够提供合理的实时调度方案。即时响应式定制公交调度是一个复杂的技术问题,本文的车辆实时调度决策模型仅针对各线路进行单独的调度决策,没有考虑线路交叉情况下的乘客需求响应问题,并且在调度中也未能考虑车辆行驶速度的动态性,这将是下一步研究的方向。
| [1] |
WILSON H, WEISSBERG H. Advanced Dial-a-ride Algorithms Research Project: Final Report r76-20[R]. Cambridge: MIT, 1967.
|
| [2] |
NOURBAKHSH S M, OUYANG Y. A Structured Flexible Transit System for Low Demand Areas[J]. Transportation Research Part B:Methodological, 2012, 46(1): 204-216. |
| [3] |
BAKAS I, DRAKOULIS R, FLOUDAS N, et al. A Flexible Transportation Service for the Optimization of a Fixed-route Public Transport Network[J]. Transportation Research Procedia, 2016, 14: 1689-1698. |
| [4] |
KIM M, SCHONFELD P. Maximizing Net Benefits for Conventional and Flexible Bus Services[J]. Transportation Research Part A:Policy and Practice, 2015, 80: 116-133. |
| [5] |
BOYER V, IBARRA-ROJAS J O, Ríos-Solís Á Y. Vehicle and Crew Scheduling for Flexible Bus Transportation Systems[J]. Transportation Research Part B:Methodological, 2018, 112: 216-229. |
| [6] |
卢小林, 张娴, 俞洁, 等. 灵活型定制公交系统综合评价方法研究[J]. 公路交通科技, 2015, 32(5): 135-140. LU Xiao-lin, ZHANG Xian, YU Jie, et al. Research of a Comprehensive Evaluation Method for Customized Flexible Transit System[J]. Journal of Highway and Transportation Research and Development, 2015, 32(5): 135-140. |
| [7] |
杨得婷.定制公交票价制定与运营相关问题研究[D].西安: 长安大学, 2015. YANG De-ting. Study on Issues Related to Customized City Bus Fare and Operation[D]. Xi'an: Chang'an University, 2015. |
| [8] |
胡郁葱, 陈栩, 罗嘉陵. 多起终点多车型混载的定制公交线路规划模型[J]. 广西师范大学学报:自然科学版, 2018, 36(4): 1-11. HU Yu-cong, CHEN Xu, LUO Jia-ling. Network Design Model of Customized Bus in Diversified Operation of Multi-origin-destination and Multi-type Vehicle Mixed Load[J]. Journal of Guangxi Normal University:National Science Edition, 2018, 36(4): 1-11. |
| [9] |
柳伍生, 周向栋, 贺剑, 等. 基于多需求响应的定制公交绿色线网优化[J]. 公路交通科技, 2018, 35(3): 132-142. LIU Wu-sheng, ZHOU Xiang-dong, HE Jian, et al. Optimization of Green Customized Public Transport Network Based on Multiple Demand Response[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 132-142. |
| [10] |
TONG L, ZHOU L S, LIU J T, et al. Customized Bus Service Design for Jointly Optimizing Passenger-to-vehicle Assignment and Vehicle Routing[J]. Transportation Research Part C:Emerging Technologies, 2017, 85: 451-475. |
| [11] |
GUO R G, GUAN W, ZHANG W Y, et al. Customized Bus Routing Problem with Time Window Restrictions:Model and Case Study[J]. Transportmetrica A:Transport Science, 2019, 15(2): 1804-1824. |
| [12] |
LYU Y, CHOW C Y, LEE C S V, et al. CB-Planner:A Bus Line Planning Framework for Customized Bus Systems[J]. Transportation Research Part C:Emerging Technologies, 2019, 101: 233-253. |
| [13] |
王健, 曹阳, 王运豪. 考虑出行时间窗的定制公交线路车辆调度方法[J]. 中国公路学报, 2018, 31(5): 143-150. WANG Jian, CAO Yang, WANG Yun-hao. Customized Bus Route Vehicle Schedule Method Considering Travel Time Windows[J]. China Journal of Highway and Transport, 2018, 31(5): 143-150. |
| [14] |
BRUNI M E, GUERRIERO F, BERALDI P. Designing Robust Routes for Demand-responsive Transport Systems[J]. Transportation Research Part E:Logistics and Transportation Review, 2014, 70: 1-16. |
| [15] |
邱丰, 李文权, 沈金星. 可变线路式公交的两阶段车辆调度模型[J]. 东南大学学报:自然科学版, 2014, 44(5): 1078-1084. QIU Feng, LI Wen-quan, SHEN Jin-xing. Two-stage Model for Flex-route Transit Scheduling[J]. Journal of Southeast University:Natural Science Edition, 2014, 44(5): 1078-1084. |
| [16] |
郭晓俊.基于需求响应的实时定制公交系统研究[D].北京: 北京交通大学, 2016. GUO Xiao-jun. Research of Real-time Custom Bus System Based on Demand Response[D]. Beijing: Beijing Jiaotong University, 2016. |
| [17] |
韩霜, 周芳娟, 谭智华, 等. 动态竞争环境下基于客户价值的物流终端设施优化模型[J]. 公路交通科技, 2013, 30(11): 144-151. HAN Shuang, ZHOU Fang-juan, TAN Zhi-hua, et al. An Optimization Model of Logistics Terminal Facility Based on Customer Value in Dynamic Competitive Environment[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 144-151. |
| [18] |
韩霜, 张邻. 考虑客户价值的动态竞争性物流网络优化[J]. 计算机集成制造系统, 2014, 20(9): 2320-2328. HAN Shuang, ZHANG Lin. Optimization of Logistics Network in Dynamic Competitive Environment Considering Customer Value[J]. Computer Integrated Manufacturing Systems, 2014, 20(9): 2320-2328. |
 2020, Vol. 37
2020, Vol. 37
