扩展功能
文章信息
- 裴玉龙, 潘恒彦, 郭明鹏, 张枭
- PEI Yu-long, PAN Heng-yan, GUO Ming-peng, ZHANG Xiao
- 轨道交通对城市公共交通网络可达性的影响——以哈尔滨市为例
- Influence of Rail Transit on Accessibility of Urban Transit Network —A Case Study of Harbin City
- 公路交通科技, 2020, 37(6): 104-111
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 104-111
- 10.3969/j.issn.1002-0268.2020.06.013
-
文章历史
- 收稿日期: 2019-09-17
2. 济南市政工程设计研究院(集团)有限责任公司, 山东 济南 250002;
3. 上海市城市建设设计研究总院(集团)有限公司, 上海 200125
2. Jinan Municipal Engineering Design & Research Institute Co., Ltd., Jinan Shandong 250002, China;
3. Shanghai Urban Construction Design & Research Institute(Group) Co., Ltd., Shanghai 200125, China
轨道交通能够弥补城市公共交通网络系统运能的不足,北京、上海等城市已形成了庞大的轨道交通网络。公共交通网络中轨道交通的加入,使得多模式公共交通网络变得复杂化。近些年来,可达性被应用到公共交通网络的功能评价上,研究轨道交通线路的开通对城市公共交通网络空间可达性的影响,能够为轨道交通的建设提供理论支持,并改善多模式公共交通网络的空间可达性,使多模式公交系统更加便于居民出行。
可达性的概念由Hansen[1]于1959年提出。可达性考虑出行时间、出行距离及人口规模等指标,用以衡量节点之间联系的难易程度。Bertolini等[2]对可达性进行了如下阐述:在限定的时间或费用下,出行者能够到达目的地的总数数量越多,则可达性越好。Karner等[3]以公交站点辐射范围为基础,对常规公交的区域可达性和布局情况进行了评价。盖春英等[4]从节点层次及驾驶员抉择等方面,以节点最短线路长度、最短出行时间及节点主要度为变量,对公路网络的可达性展开了研究。余伟等[5]以南京市为例,基于Space L模型与Space P模型,就地铁对城市公共交通网络可达性的影响展开研究,发现地铁站点的可达性明显提升。蒋阳升等[6]对公交线网的空间可达性的优化方法展开了研究,为公共交通网络的服务水平的提高提供理论支持;郭建科等[7]基于城市公交网络可达性测度,对大连市医疗服务的空间分异展开了研究。陈少沛等[8]结合GIS技术,分析了广州市的地铁网络的时空演化及空间形态,为可达性的研究及地铁发展提供了实践经验与理论参考。
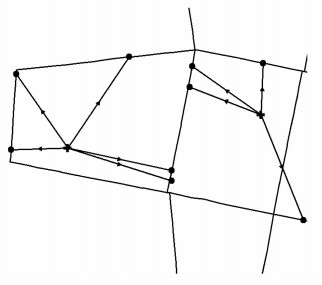
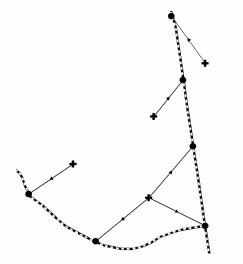
1 可达性度量模型 1.1 站点可达性度量模型本研究将站点可达性分为常规公交站点可达性与地铁站点可达性,分别用于度量常规公交站点与地铁站点的可达程度。不同常规公交站点经停的公交线路不同,出行者选择公交出行时,会根据所乘坐的线路对公交站点进行抉择,将每个居民出行点最近的n个公交站点到出行点的平均距离作为该出行点的常规公交站点可达距离,具体如式(1)与图 1所示。地铁站点间距越大,单个地铁站点辐射范围就越大。某地铁站点服务于某区域的居民出行,因此将距离居民出行点最短地铁站点的距离定义为该出行点的地铁站点可达距离,如式(2)与图 2所示。将出行点i的常规公交站点可达距离与出行点i的地铁站点可达距离分别归一化,则得到出行点i的常规公交站点可达性与地铁站点的可达性,具体如式(3)与式(4)所示。
|
| 图 1 常规公交站点可达距离 Fig. 1 Accessible distances of normal bus stops |
| |
|
| 图 2 地铁站点可达距离 Fig. 2 Accessible distances of subway stations |
| |
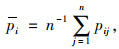
|
(1) |
式中,pi为出行点i的常规公交站点可达距离;n为选择集合中的站点个数;pij为距离出行点到最近的n个公交站点中公交站点j的距离。
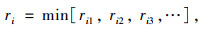
|
(2) |
式中,ri为出行点i的地铁站点可达距离;rij分别为地铁站点j到出行点i的距离。
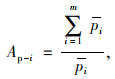
|
(3) |
式中,Ap-i为出行点i的常规公交站点可达性;pi为出行点i的常规公交站点可达距离;m为居民出行点个数。
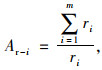
|
(4) |
式中,Ar-i为出行点i的地铁站点可达性;ri为出行点i的地铁站点可达距离;m为居民出行点个数。
1.2 基于平均出行时间的可达性度量模型将某个出行点i到达另一个出行点j的最短时耗定义为此OD点对ij的最短可达时间Tij,则对于出行点i,将从其位置出发,到达区域其他所有出行点最短可达时间Tij的均值定义为出行点i的全局平均可达时间,其公式为:

|
(5) |
式中,At-i为出行点i的全局平均可达时间;n为区域出行点数量;Tij为OD点对ij的最短可达时间,其公式为:
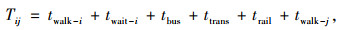
|
(6) |
式中,Tij为OD点对ij的最短可达时间;twalk-i为从出发点i到达公交或地铁站点的步行时间;twait-i为出行者在公交站点的候车时间;tbus和trail分别为出行者乘坐公交与地铁的时间;ttrans为换乘时间,包括公交线路间、地铁线路间、地铁与公交站点的换乘时间;twalk-j为从公交或地铁站点到达目的地j的步行时间。
1.2.1 全局平均可达时间将区域中所有出行点的全局平均可达时间的均值定义为此区域的全局平均可达时间,用于衡量区域内部出行点之间的连通程度,其公式为:
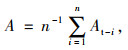
|
(7) |
式中,A为研究区域的全局平均可达时间;At-i为出行点i的全局平均可达时间;n为区域出行点数量。
1.2.2 局部平均可达时间假定某研究区域由n个局部区域构成,每个局部区域分别包含ni个出行点。将局部区域w内所有出行点的全局平均可达时间求均值,将其定义为局部区域w的局部平均可达时间。用于衡量某区域在全局中的连通程度,其公式为:
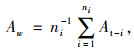
|
(8) |
式中,Aw为局部区域w的局部平均可达时间;At-i为出行点i的全局平均可达时间;ni为局部区域w内部包含的出行点数量。
1.3 基于加权出行时间的可达性度量模型加权出行时间[9-10]是对可达性进行度量的重要方法[11-12]。公交网络的构建,离不开社会经济因素的影响,经济活动在很大程度上决定了区域间居民的出行活动[13]。本研究引入加权平均可达时间的可达性计算方法,将区域间实际的出行活动考虑其中,对区域的可达性进行度量,其公式为:
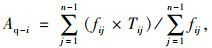
|
(9) |
式中,Aq-i为出行点i的加权平均可达时间;n为区域出行点数量;fij为OD点对ij间的出行权重,本研究将OD点对ij间的居民出行频次近似看做出行权重;Tij为OD点对ij的最短可达时间。
区域加权平均可达时间为某区域内所有出行点加权平均可达时间的均值,其公式为:
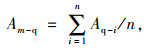
|
(10) |
式中,Am-q为区域m加权平均可达时间;Aq-i为出行点i的加权平均可达时间;n为区域m内的出行点数量。
区域加权平均可达时间能够衡量区域内部居民的实际出行时间。区域加权平均可达时间越小,说明区域内部居民完成出行所消耗的实际时间越短。
1.4 基于出行范围的可达性度量模型图 3(a)~(c)分别表示居民出行点在10,15,20 min的出行阈值范围内的最大可达范围。

|
| 图 3 不同出行阈值内最大可达范围 Fig. 3 Maximum accessible ranges within different trip thresholds |
| |
将从出行点i出发,在给定的出行时间T内所能到达的最大范围定义为出行点i在出行阈值T内的最大可达范围Si-T(如图 3所示),则出行点i基于出行范围的可达性度量模型为:
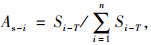
|
(11) |
式中,As-i为出行点i基于出行范围的可达性;Si-T为出行点i在出行阈值T内最大可达范围的面积;n为区域出行点数量。
引入人均可达面积的概念,用于衡量区域内部居民获得出行机会的大小。将某区域内部各出行点i的最大可达范围的面积Si-T求和,并与区域内部出行次数求比值,区域的人均可达面积越大,居民获得出行机会越大,进而该区域的可达性越高。其公式为:
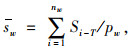
|
(12) |
式中,sw为区域w的人均可达面积;Si-T为出行点i在出行阈值T内最大可达范围的面积;nw为区域w内出行点个数;pw为区域w内的出行次数。
1.5 可达性区位度引入可达性区位度的概念,用以度量某出行点或区域相对于全局的可达性优势,其公式为:
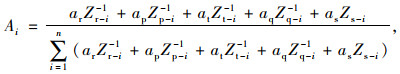
|
(13) |
式中,Ai为出行点i的可达性区位度;Zr-i,Zp-i,Zt-i,Zq-i,Zs-i分别为出行点i的地铁站点可达性Ar-i、常规公交站点可达性Ap-i、全局平均可达时间At-i、加权平均可达时间Aq-i及基于出行范围的可达性As-i归一化后的值;ar,ap,at,aq,as分别为各可达性度量指标的权重,均大于0,其他参数同上。本研究将ar,ap,at,aq,as取等值。
2 案例分析本研究选取哈尔滨市主城区作为研究对象。通过百度地图的API接口对全市的公交站点与线路位置及道路数据进行爬取,并将“全市居民出行普查数据”作为研究辅助数据。将上述数据导入Arcgis10.2地理信息处理软件中,对上述指标进行计算,分析其5条地铁线路开通前后的公交网络空间可达性变化情况。对试验区域每隔300 m插入1个数据采集点(共计3 533个),视为居民出行点。根据行政管理与居民生活习惯进行小区划分,共计31个街道。
2.1 试验假设(1) 公交网络为有向网络,分上行线路与下行线路。
(2) 同名公交站点不视为同一站点,应区别对待。
(3) 不考虑线路的运营情况,如发车频次等。
(4) 对于实际线路调整时网络获取数据不一致的,不予考虑。
(5) 地铁线路运营速度取43.0 km/h,公交线路运营速度取18.0 km/h,步行速度取3.6 km/h。
(6) 哈尔滨市地铁线路建成顺序为1号线、3号线、2号线、4号线、5号线,建成时间分别为2013年、2022年、2024年、2027年、2030年。
(7) 由于忽略线路运营情况,因此换乘时间只考虑不同换乘点之间的步行时间,不考虑同站点换乘线路及不同换乘站点的等待时间。
(8) 试验区域内,各街道的人口比例假设不变,即仅考虑地铁线路开通对可达性的影响,对人口、经济等因素不予过多考虑。即研究区域内各OD点对ij的出行权重相对不变。
2.2 试验结果分析 2.2.1 可达性区位度分析地铁线路建成运行后,各街道的可达性区位度随之变化,具体如表 1所示。可以得出,地铁线路建成运行后,地铁站点周围区域的可达性区位度随之提高,距离地铁站点越近,可达性区位度的变化越明显。
| 交通小区 | 2012年 | 2019年 | 2023年 | 2025年 | 2028年 | 2031年 |
| 松北街道 | 2.83 | 2.17 | 1.82 | 2.16 | 2.06 | 3.12 |
| 松浦街道 | 2.15 | 2.10 | 2.60 | 2.85 | 2.63 | 3.40 |
| 哈西街道 | 4.06 | 4.69 | 4.63 | 3.91 | 3.42 | 3.48 |
| 燎原街道 | 4.68 | 4.38 | 3.40 | 3.40 | 4.77 | 3.61 |
| 松浦镇 | 1.90 | 2.13 | 2.24 | 1.90 | 2.97 | 2.54 |
| 兆麟街道 | 7.17 | 4.20 | 4.21 | 5.37 | 4.38 | 3.57 |
| 安乐街道 | 3.95 | 3.00 | 3.09 | 3.56 | 4.03 | 3.93 |
| 新华街道 | 5.30 | 3.31 | 8.19 | 7.74 | 6.14 | 6.67 |
| 保健路街道 | 2.48 | 3.36 | 2.46 | 2.08 | 2.09 | 1.72 |
| 黎明街道 | 2.38 | 1.88 | 3.37 | 2.93 | 3.10 | 3.57 |
| 新一街道 | 1.87 | 1.45 | 2.04 | 1.76 | 1.41 | 1.06 |
| 世茂街道 | 3.62 | 2.86 | 4.21 | 4.58 | 4.19 | 5.43 |
| 新发街道 | 2.95 | 2.71 | 2.04 | 1.74 | 1.37 | 2.40 |
| 东原街道 | 2.21 | 3.52 | 5.54 | 4.73 | 5.37 | 4.05 |
| 铁东街道 | 1.40 | 1.14 | 0.62 | 0.78 | 0.62 | 0.45 |
| 新疆街道 | 1.53 | 1.70 | 2.25 | 1.89 | 1.93 | 1.93 |
| 奋斗路街道 | 5.67 | 6.05 | 2.54 | 3.53 | 4.52 | 3.51 |
| 文政街道 | 2.98 | 4.87 | 2.69 | 2.30 | 2.59 | 2.94 |
| 太阳岛街道 | 2.62 | 2.51 | 5.65 | 6.71 | 7.34 | 6.99 |
| 新伟街道 | 1.71 | 3.04 | 1.16 | 0.98 | 0.80 | 0.61 |
| 靖宇街道 | 5.64 | 4.36 | 3.53 | 3.87 | 4.78 | 3.56 |
| 新香坊街道 | 1.71 | 1.00 | 4.02 | 3.41 | 2.75 | 2.51 |
| 花园街道 | 4.14 | 5.50 | 2.32 | 2.85 | 3.71 | 3.88 |
| 王岗街道 | 1.57 | 0.98 | 1.46 | 1.24 | 1.02 | 0.74 |
| 松祥街道 | 2.78 | 2.75 | 2.99 | 2.52 | 2.28 | 4.03 |
| 新城街道 | 2.93 | 4.20 | 3.07 | 2.95 | 2.83 | 2.17 |
| 铁顺街道 | 4.32 | 4.55 | 4.86 | 4.12 | 3.36 | 3.82 |
| 跃进街道 | 2.35 | 3.69 | 3.20 | 2.72 | 2.41 | 1.83 |
| 通天街道 | 2.32 | 2.38 | 3.07 | 3.37 | 2.76 | 3.09 |
| 工农街道 | 2.46 | 3.69 | 0.93 | 0.79 | 0.59 | 2.22 |
| 抚顺街道 | 6.42 | 5.69 | 5.76 | 7.31 | 7.90 | 7.12 |
2.2.2 基于平均与加权出行时间的可达性分析
各阶段的全局平均可达时间A与各交通小区的加权出行时间如表 2所示。
| 阶段 | A/h | 方差 | 变化率/% |
| 无地铁线路 | 2.06 | 0.17 | — |
| 1号线开通 | 1.84 | 0.34 | -10.67 |
| 3号线开通 | 1.63 | 0.28 | -11.41 |
| 2号线开通 | 1.52 | 0.25 | -6.75 |
| 4号线开通 | 1.42 | 0.20 | -6.57 |
| 5号线开通 | 1.35 | 0.18 | -4.93 |
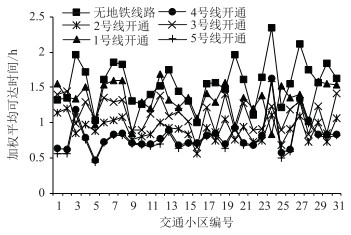
由表 2可知,随着1号线的开通,全局的平均可达时间A从2.06 h降低到1.84 h,但各出行点之间的方差从0.17增加到0.34,区域间差异增大。随着更多地铁线路的开通,全局平均可达时间A不断降低,不同地铁线路的开通缩短了其所在位置的局部平均可达时间Aw,进而使得全局出行点可达时间的方差不断减少。全局平均可达时间变化率逐渐降低,方差也逐渐接近于未开通地铁线路时的水平,各区域间可达性的差异减小。将各阶段每个行政区域的加权出行时间进行计算,并根据降序进行排列,具体如图 4与表 3所示。
|
| 图 4 各阶段交通小区加权平均可达时间 Fig. 4 Weighted average accessible time of traffic districts in each stage |
| |
| 排序 | 无轨道线路 | 1号线 | 3号线 | 2号线 | 4号线 | 5号线 |
| 1 | 道里区(1.43) | 南岗区(1.37)↑ | 道外区(0.82)↑ | 香坊区(0.77) | 香坊区(0.65) | 香坊区(0.64) |
| 2 | 道外区(1.62) | 道里区(1.40) | 香坊区(1.01)↑ | 道外区(0.79) | 道外区(0.68) | 松北区(0.65)↑ |
| 3 | 南岗区(1.71) | 道外区(1.59) | 道里区(1.27) | 松北区(1.00)↑ | 松北区(0.87) | 道外区(0.67) |
| 4 | 香坊区(1.77) | 香坊区(1.75) | 南岗区(1.33) | 道里区(1.19) | 道里区(1.15) | 道里区(1.12) |
| 5 | 松北区(1.82) | 松北区(1.81) | 松北区(1.80) | 南岗区(1.30) | 南岗区(1.27) | 南岗区(1.25) |
| 全局平均加权可达时间 | 1.72 | 1.41 | 1.13 | 0.92 | 0.73 | 0.72 |
| 注:表 3中的↑表示相比上一时期排名上升。 | ||||||
未开通地铁线路前,道里区加权平均可达时间最小,区域内部居民实际完成出行的时间最短,其次是道外区、南岗区以及香坊区,由于松北区位置相对隔离,居民需要通过长时间的出行进行经济活动。随着1号线的开通,南岗区的加权可达时间相对减少,3号线缩短了道外区与香坊区的加权可达时间Am-q,2号线使位于松北区居民到达其他区域的时间缩短;4号线并未使各区域的排序发生变化,只是缩短了全局的加权可达时间;5号线的开通进一步使松北区的加权平均可达时间降低,促进了松北区与其他区域的联系。
2.2.3 基于出行范围的可达性分析洛伦茨曲线[14-15]常用于比较与分析社会收入与分配的公平性程度,近些年逐渐应用于交通公平性的评价中[16],其公式为:
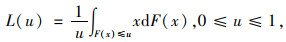
|
(14) |
式中,L(u)为[0, 1]区间内的单调递增函数,且为凸函数;F(x)为累计分布函数。
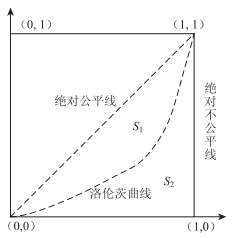
基尼系数G是根据洛伦茨曲线所定义的判断公平程度的指标,G∈[0, 1],具体评价标准[17]如表 4所示。基尼系数常由洛伦茨曲线和绝对公平线围成图形的面积与绝对公平线和绝对不公平线围成图形面积的比值得到[18],具体如图 5与式(15)所示。
| < 0.2 | (0.2, 0.3] | (0.3, 0.4] | (0.4, 0.5] | < 0.5 |
| 绝对公平 | 比较公平 | 相对合理 | 差距较大 | 差距悬殊 |
|
| 图 5 洛伦茨曲线 Fig. 5 Lorentz curve |
| |
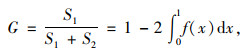
|
(15) |
式中,S1为洛伦茨曲线与绝对公平线围成图形的面积;S2绝对公平线与绝对不公平线围成图形的面积。
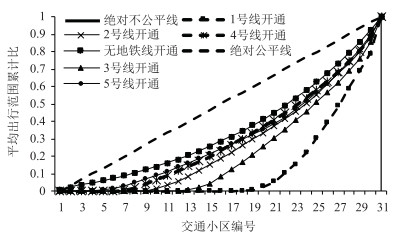
在假定各OD点对ij的出行权重相对不变的情况下,根据式(12)求得试验区域各街道的人均可达面积,并根据式(14)绘制如图 6所示的洛伦茨曲线,进而求得表 5中各阶段街道的基尼系数G。
|
| 图 6 平均出行范围洛伦茨曲线 Fig. 6 Lorentz curves of average travel range |
| |
| 阶段 | 基尼系数G | 解释 |
| 无地铁线 | 0.314 | 相对合理 |
| 1号线开通 | 0.686 | 差距悬殊 |
| 3号线开通 | 0.534 | 差距悬殊 |
| 2号线开通 | 0.451 | 差距较大 |
| 4号线开通 | 0.392 | 相对合理 |
| 5号线开通 | 0.371 | 相对合理 |
可以看出,在无地铁线路开通时,哈尔滨中心城区各街道间,在人均可达范围方面的可达性差异上,公交线路布局相对合理。随着1号线的开通,部分区域可达性优势开始明显,3号线的开通弥补了部分区域的可达性劣势,但整体而言,全局各小区间的可达性仍然差距悬殊,随着2号线、4号线、5号线的开通,全局各小区间的可达性变得相对合理。
3 结论(1) 地铁线路的开通引起了哈尔滨中心城区各区域可达性区位度的变化,地铁站点周围区域的可达性区位度得到有效提高。
(2) 随着地铁线路的逐条开通,哈尔滨中心城区的平均可达时间逐渐缩短,平均可达时间的变化率逐渐降低。在第1条线路建成初期,区域间的平均可达时间方差变大,区域间的差异性增大。随着线路条数的增多和部分地区可达性的改善,全局平均可达时间方差逐渐减小,区域间的可达性差异降低。
(3) 地铁线路的开通降低了哈尔滨中心城区5大行政分区的加权可达时间。不同线路对各行政分区加权平均可达时间的降低程度不同。其中:1号线提高了南岗区居民的出行效率;3号线改善了香坊区与道外区的居民出行效率;2号线与5号线有效改善了松北区居民的出行效率。
(4) 无地铁线路时,哈尔滨中心城区居民的出行机会相对公平合理,基尼系数G为0.314;随着1号线的开通,地铁线路周围获得了较大的出行机会,使得全局的出行机会差距悬殊,基尼系数G增大到0.686;随着地铁线路的逐条开通,地铁辐射范围的增大,哈尔滨中心城区居民获得的出行机会变得相对均衡合理。
| [1] |
HANSEN W G. How Accessibility Shapes Land Use[J]. Journal of the American Institute of Planners, 1959, 25(25): 73-76. |
| [2] |
BERTOLINI L, CLERCQ F L, KAPOEN L L. Sustainable Accessibility:A Conceptual Framework to Integrate Transport and Land Use Plan-making:Two Test-applications in the Netherlands and a Reflection on the Way Forward[J]. Transport Policy, 2008, 12(3): 207-220. |
| [3] |
KARNER A. Assessing Public Transit Service Equity Using Route-level Accessibility Measures and Public Data[J]. Journal of Transport Geography, 2018, 67: 24-32. |
| [4] |
盖春英, 裴玉龙. 公路网络可达性研究[J]. 公路交通科技, 2006, 23(6): 104-107. GAI Chun-ying, PEI Yu-long. Study on Accessibility of Highway Network[J]. Journal of Highway and Transportation Research and Development, 2006, 23(6): 104-107. |
| [5] |
余伟, 马健霄, 张永辉. 地铁对城市公交网可达性的改善研究[J]. 交通运输系统工程与信息, 2011, 11(1): 121-125. YU Wei, MA Jian-xiao, ZHANG Yong-hui. Research on Accessibility Improvement of Urban Public Transport Network Based on Metro[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(1): 121-125. |
| [6] |
蒋阳升, 罗孝羚, 刘媛, 等. 公交线网空间可达性优化研究[J]. 公路交通科技, 2016, 33(4): 102-107. JIANG Yang-sheng, LUO Xiao-ling, LIU Yuan, et al. Study of Optimizing Transit Network Spatial Accessibility[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 102-107. |
| [7] |
郭建科, 邱煜焜, 王方雄, 等. 基于城市公共交通可达性的医疗服务空间分异及均等化:以大连市为例[J]. 公路交通科技, 2019, 36(4): 135-143. GUO Jian-ke, QIU Yu-kun, WANG Fang-xiong, et al. Spatial Differentiation and Equalization of Medical Service Based on Accessibility of Urban Public Transport:A Case Study of Dalian[J]. Journal of Highway and Transportation Research and Development, 2019, 36(4): 135-143. |
| [8] |
陈少沛, 李勇, 庄大昌, 等. 地铁网络可达性时空演化及空间形态分析[J]. 测绘科学, 2018, 43(3): 123-130, 147. CHEN Shao-pei, LI Yong, ZHUANG Da-chang, et al. Spatio-temporal Evolution and Spatial Pattern Analysis of Metro Network Accessibility[J]. Science of Survey and Mapping, 2018, 43(3): 123-130, 147. |
| [9] |
张亦汉, 乔纪纲, 李建程, 等. 广州地铁网络的可达性分析[J]. 测绘与空间地理信息, 2014, 37(2): 9-11. ZHANG Yi-han, QIAO Ji-gang, LI Jian-cheng, et al. Analysis of the Accessibility for Guangzhou Metro Network[J]. Geomatics & Spatial Information Technology, 2014, 37(2): 9-11. |
| [10] |
聂灿权. 广州地铁的可达性变化研究[J]. 北京测绘, 2017(2): 50-55, 59. NIE Can-quan. Accessibility Changes of Metro Network in Guangzhou[J]. Beijing Surveying and Mapping, 2017(2): 50-55, 59. |
| [11] |
陈洁, 陆锋, 程昌秀. 可达性度量方法及应用研究进展评述[J]. 地理科学进展, 2007(5): 100-110. CHEN Jie, LU Feng, CHENG Chang-xiu. Advance in Accessibility Evaluation Approaches and Applications[J]. Progress in Geography, 2007(5): 100-110. |
| [12] |
SALONEN M, TOIVONEN T, COHALAN J M, et al. Critical Distances:Comparing Measures of Spatial Accessibility in the Riverine Landscapes of Peruvian Amazonia[J]. Applied Geography, 2012, 32(2): 501-513. |
| [13] |
肖京格, 周廷刚, 姚林虎, 等. 重庆市交通网络的可达性时空特征及其演化规律[J]. 地球信息科学学报, 2015, 17(1): 54-61. XIAO Jing-ge, ZHOU Ting-gang, YAO Lin-hu, et al. Spatial-temporal Characteristics of Chongqing Transport Network Accessibility and Its Evolution Pattern[J]. Journal of Geo-information Science, 2015, 17(1): 54-61. |
| [14] |
TANAK A K, BORZADARAN G R M, AHMADI J. New Functional Forms of Lorenz Curves by Maximizing Tsallis Entropy of Income Share Function under the Constraint on Generalized Gini Index[J]. Physica A:Statistical Mechanics and Its Applications, 2018, 511: 280-288. |
| [15] |
匡兵, 卢新海, 周敏, 等. 武汉城市群城市用地结构时空演变特征及其机理[J]. 经济地理, 2016, 36(5): 71-78. KUANG Bing, LU Xin-hai, ZHOU Min, et al. Spatio-Temporal Features of Urban Land Structure Change in Wuhan City Group and Underlying Causes[J]. Economy Geography, 2016, 36(5): 71-78. |
| [16] |
吴茂林, 曹凯. 基于基尼系数的交通公平性定量评价[J]. 交通科技与经济, 2011, 13(1): 86-89. WU Mao-lin, CAO Kai. Quantitative Evaluation Method of Traffic Fairness Based on Gini Coefficient[J]. Technology & Economy in Areas of Communications, 2011, 13(1): 86-89. |
| [17] |
房晋源. 基于基尼系数的公交线网评价均衡性研究[J]. 交通运输系统工程与信息, 2012, 12(4): 178-183. FANG Jin-yuan. Evaluation of Urban Public Transportation Network Equilibrium Based on Gini Coefficient[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(4): 178-183. |
| [18] |
DADON-GOLAN Z, DAVID-HADAR I B, KLEIN J. Revisiting Educational (in) Equity:Measuring Educational Gini Coefficients for Israeli High Schools during the Years 2001-2011[J]. International Journal of Educational Development, 2019, 70: 102091. |
 2020, Vol. 37
2020, Vol. 37
