扩展功能
文章信息
- 阮永芬, 余东晓, 杨均, 吴龙, 谭桂平
- RUAN Yong-fen, YU Dong-xiao, YANG Jun, WU Long, TAN Gui-ping
- PSO-SVM反演隧道周围加固软土的力学参数
- Inversion of Mechanical Parameters of Reinforced Soft Soil around Tunnel Based on PSO-SVM
- 公路交通科技, 2020, 37(6): 87-96
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 87-96
- 10.3969/j.issn.1002-0268.2020.06.011
-
文章历史
- 收稿日期: 2019-04-23
2. 中铁四院集团西南勘察设计有限公司, 云南 昆明 650031;
3. 中铁十一局集团城市轨道工程有限公司, 湖北 武汉 430074
2. CRSSDG Southwest Survey and Design Co., Ltd., Kunming Yunnan 650031, China;
3. China Railway 11 th Bureau Group Urban Rail Engineering Co. Ltd., Wuhan Hubei 430074, China
城市地铁具有运量大、能耗小、污染轻、安全度高、占地少等特点而在城市化发展建设中得到快速发展。地铁施工普遍采取盾构法。土层物理力学参数的选择影响着整个盾构施工中管片设计、同步注浆及二次注浆需要量、是否需二次注浆等参数确定,也是路段是否需加固处理、盾构机参数设置及预见可能出现工程事故的依据[1],故土层参数的准确性对盾构施工十分重要。
自1971年Kavanagh和Clough发表了“反演弹性固体弹性模量的有限元法”后[2],在Cercighani、Gioda、Sukurai[3-5]等学者的努力下反分析法取得极大发展,如今已成为解决复杂岩土工程问题的一种主流方法。Pichler[6]通过遗传算法(GA)优化人工神经网络来反演出最佳模型参数估计值。S.Levasseur[7]通过遗传算法的优化算法验证了优化算法可以改进反分析参数精度。高玮[8]将粒子群算法与参数反分析融合,在解空间中寻找系统变量值与目标函数值适应度最小的粒子,从而得到最优反演参数值。赵洪波[9]在弹塑性位移反分析中率先使用支持向量机方法,发现支持向量机具有良好的学习能力。
使用搜索效率高、准确性强的优化算法及找到更优计算方法是提高反演参数精度的有效途径。早期使用的优化法有单纯形法[10]、变量替换法[11]、Powell法[12]及Rosenbrok法[13]等,虽然它们的局部搜索能力突出,但得到的结果通常是局部最优,不是全局最优解,且计算量大,结果也不稳定。在反分析算法上,普遍使用神经网络与遗传算法,但两者都需要大量的样本数据,且学习时间长,训练效果不够理想,所以得出的结果可信度往往不高。
现将全局搜索能力突出的PSO寻优算法与学习能力强的SVM结合起来[14],形成高效准确的反演模型,对土的力学参数反演进行研究。PSO寻优算法先后应用于SVM模型参数的优化选取和反演模量参数的智能搜索,其中SVM模型的核函数形式对反演结果影响大,且目前普遍采用径向基(RBF)核函数,因缺乏平移正交性,使得相应支持向量机模型的逼近能力受到限制,影响参数精度,为此引入morlet核函数作为SVM的核函数,进一步优化SVM模型的计算性能,通过morlrt核函数降低样本空间维度,在样本数量少,空间维度高且非线性的情况下,得到可靠结果。并与RBF核函数SVM模型在适应度、收敛速度、精确度上进行对比,以此验证morlet核函数性能的优越性。
本研究结合昆明地铁5号线穿越滇池湖相沉积软土地层,区间盾构施工地表沉降监测数据,联合PSO算法和Morlet核函数SVM模型对隧道周围分布的不良土层(主要为泥炭质土与黏土)加固后的模量参数进行反演[15]。根据试验参数及专家经验预设反演参数范围,并结合正态分布及均匀试验,设计大量学习和测试样本[16],对支持向量机模型进行训练,最终反演出加固土体模量参数。将反演的力学参数输入到有限元模型中进行沉降计算,并与实际监测沉降值、Peck公式计算值进行对比,分析其差异性,验证反演参数的准确性。
1 反分析方法原理 1.1 粒子群寻优算法(PSO)PSO由Eberhart和Kennedy[17-18]提出,一种模拟鸟群觅食时的协作过程,个体发现食物并将位置信息传递给附近个体,形成一个局部最优位置信息,然后再是局部与局部间传递位置信息,形成一个全局最优位置信息,这样能够快速高效的寻找出最优结果。现将PSO算法运用于函数最优参数选取及SVM模型训练。PSO优化算法流程图如图 1所示。
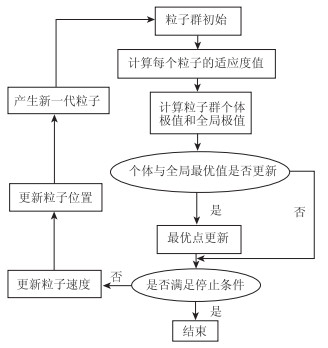
|
| 图 1 PSO算法流程图 Fig. 1 Flowchart of PSO algorithm |
| |
具体步骤如下:
(1) 粒子初始化。每个粒子的初始位置随机分布在空间内,初始速度在-vmax至vmax随机确定,进化代数设置为0。
(2) 训练模型参数进行初始化。
(3) 计算各个粒子速度,公式如下:
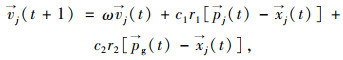
|
(1) |
式中,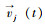
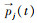
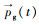
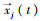
(4) 对粒子速度进行控制,其范围为:
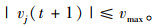
|
(2) |
(5) 计算粒子位置,公式为:
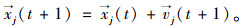
|
(3) |
(6) 计算各粒子适应值。
(7) 计算粒子群与下代各粒子历史最优位置。
(8) 重复计算粒子速度与位置,直到得到满足条件适应度最小的粒子位置。
1.2 支持向量机(SVM)预测系统设非线性约束目标系统含m个变量,Xi为系统中第i个变量。第j组所有变量值的集合为X(j)=(x1(j), x2(j), …, xm(j))T, 对应的目标函数值为y(j)。通过正态分布、均匀试验获得n组系统变量集合X(j)(j∈{1, 2, …, n})与对应的目标函数值y(j)(j∈{1, 2, …, n})。运用其中n-k组系统变量值集合与对应的目标函数值为SVM模型的学习样本,余下的k组为验证SVM模型是否正确的测试样本。为防产生奇异样本增加模型训练时间,对数据进行归一化[19],归一化是采取线性变换的方式将数据值映射到[0, 1]区间内。转换函数如下:
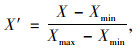
|
(5) |
式中,X′为归一化值,X,Xmax,Xmin分别为样本数据、样本数据的最大值及最小值。
运用归一化后的X(j)′,y(j)′(j∈{1, 2, …, n})分别作为SVM训练的输入向量与输出值。然后需要把输入向量映射至高维特征空间,再构造式(6)完成线性回归:
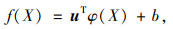
|
(6) |
式中,u为高维权重向量; φ(X)为映射函数; b为偏置项。
回归问题可通过加入不敏感损失函数ε转变成下列求解最优值:
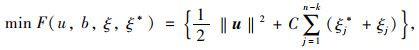
|
(7) |
约束条件:
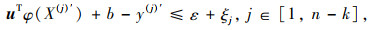
|
(8) |
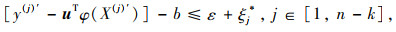
|
(9) |
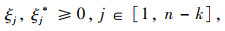
|
(10) |
式中,F(u, b, ξ, ξ*)为回归问题采用ε不敏感损失函数后的待优化目标函数;C为罚参数;ε为损失函数参数;ξj和ξj*为松弛因子。
SVM预测系统采用LIBSVM工具箱进行完成。选取Morlet核函数,采用PSO优化算法选出SVM模型的罚参数C,损失函数p,核宽度g的最优值以及模型的训练,然后基于学习、测试样本,求得最优解。
1.3 Morlet核函数数据维数过高会使搜索性能降低与运算效率下降,Morlet核函数引入高维内积概念,从结构上重新定义了高维特征空间[20],降低了数据维度,使得高维空间线性可分。在SVM模型中选用Morlet核函数,k(x(i), x(j))是x(i)和x(j)的高维内积,公式中出现的x(i)和x(j)都可以用k(x(i), x(j))来替换,使得计算复杂度和空间维度无关,实现了非线性向高维线性的转变,完成SVM模型的建立[21]。
Morlet的母小波是高斯包络线下的单频率复余弦函数:
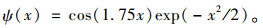
|
(11) |
母小波通过伸缩平移变换形成Morlet核函数,相对应的核函数形式为:
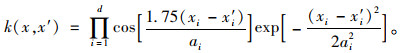
|
(12) |
土体模量参数的反演流程:(1)确定反演参数范围,根据正态分布、均匀试验设计分别得到学习、测试样本;(2)利用粒子群优化算法结合学习、测试样本选出最优SVM模型参数,并引入morlet核函数优化SVM模型;(3)通过MATLAB软件计算出参数反演值;(4)将反演值输入有限元模型计算沉降值并与实际沉降值、Peck公式计算值进行对比验算,分析反演值的准确性。具体反演流程如图 2所示。
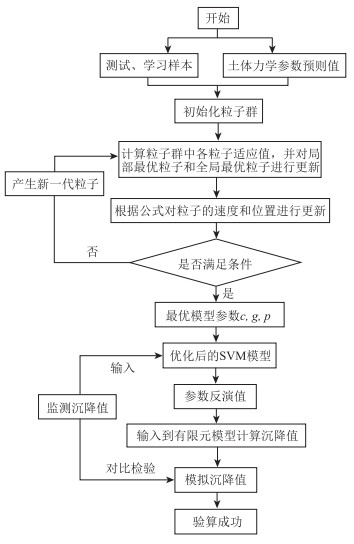
|
| 图 2 反演流程图 Fig. 2 Flowchart of inversion |
| |
2 工程实例 2.1 工程概况
金-福区间隧道里程为DK22+945~ DK23+015分左右线两条隧道,区间埋深约18.9~20.3 m,采用盾构法施工。隧道半径2.75 m;每节衬砌管片长1.2 m,厚0.35 m;注浆加固范围宽3 m,如图 3所示。隧道穿过上下两层泥炭质土及黏土,按规范要求需对穿过不良地质地层隧道周边土体进行注浆加固,加固横断面图如图 4所示。
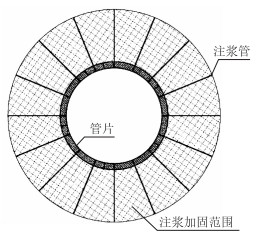
|
| 图 3 不良地质隧道注浆加固横断面图 Fig. 3 Cross-section of poor geological tunnel grouting reinforcement |
| |
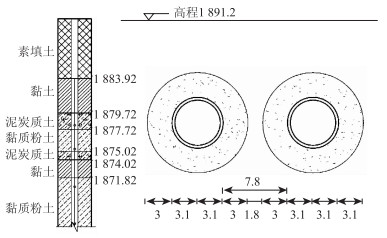
|
| 图 4 隧道与地层分布垂直横断面图(单位:m) Fig. 4 Vertical cross-section of tunnel and stratum distribution(unit:m) |
| |
按施工要求,隧道里程DK22+945~DK23+015区间每20 m设1监测断面,且断面至少布置10个横向地表监测点,水准基点不少于2个,本路段有41, 42两个断面,监测点28个,如图 5所示。
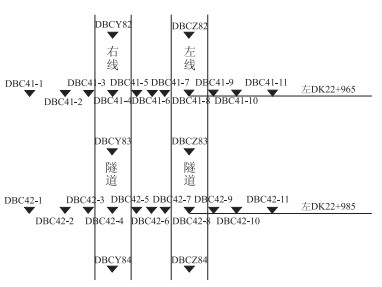
|
| 图 5 监测点布置图 Fig. 5 Layout of monitoring points |
| |
待反演参数为加固泥炭质土及黏土的压缩模量Es1,Es2。根据试验和工程经验,结合规范综合考虑取反演参数初始范围,如表 1所示。
| 土层 | 反演参数/MPa | 范围 |
| 泥炭质土 | Es1 | 1~6 |
| 黏土 | Es2 | 5~30 |
2.2 正态分布、均匀试验设计样本集
学习样本集按照正态分布[22]设计出36组学习样本,测试样本集按照均匀试验[23]均匀表U6(62)设计,需要做6次试验。将每次试验的数据依次输入到有限元软件中作正分析,计算监测点位置处的沉降值,最终得到学习样本集如表 2所示,测试样本集如表 3所示。表中的沉降值对应SVM预测系统中的变化量集合X(j)作为输入值;压缩模量值为目标函数值y(j)作为输出值。
| 序号 | Es1/ MPa |
Es2/ MPa |
DBC41-1/ mm |
DBC41-2/ mm |
… | DBC42-11/ mm |
DBCZ82/ mm |
DBCZ83/ mm |
DBCZ84/ mm |
DBCY82/ mm |
DBCY83/ mm |
DBCY84/ mm |
| 1 | 1.2 | 6.2 | 2.386 2 | 3.154 4 | … | 1.361 1 | 4.158 6 | 2.090 7 | 0.768 3 | 13.445 7 | 6.311 7 | 6.666 2 |
| 2 | 1.2 | 6.1 | 1.916 8 | 2.773 1 | … | 1.365 2 | 4.922 6 | 2.168 0 | 1.061 7 | 16.059 6 | 7.046 8 | 5.047 1 |
| 3 | 1.5 | 7.5 | 2.743 8 | 2.571 9 | … | 2.225 6 | 2.888 4 | 2.839 4 | 1.037 0 | 14.518 0 | 6.668 7 | 7.715 6 |
| 4 | 1.6 | 8.0 | 1.917 0 | 2.915 6 | … | 2.294 1 | 3.285 3 | 2.120 9 | 1.210 5 | 12.931 9 | 5.816 5 | 5.949 4 |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| 15 | 3.3 | 16.7 | 2.124 0 | 2.946 1 | … | 1.614 6 | 3.482 6 | 3.490 9 | 0.866 9 | 16.133 1 | 6.005 5 | 7.379 9 |
| 16 | 3.4 | 17.2 | 2.666 8 | 2.291 2 | … | 1.845 7 | 4.037 8 | 2.569 0 | 1.147 9 | 13.889 3 | 6.148 2 | 5.418 2 |
| 17 | 3.3 | 16.4 | 2.485 6 | 3.015 8 | … | 1.739 7 | 5.220 6 | 3.201 2 | 1.247 6 | 15.690 3 | 6.045 7 | 5.964 0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| 35 | 5.7 | 28.6 | 2.224 8 | 2.417 3 | … | 1.661 1 | 3.180 6 | 3.041 1 | 0.897 7 | 15.941 3 | 5.670 2 | 6.690 5 |
| 36 | 5.4 | 27.2 | 2.012 6 | 3.827 3 | … | 2.156 1 | 2.757 7 | 2.392 8 | 0.633 3 | 13.404 7 | 6.043 8 | 5.818 6 |
| 序号 | Es1/ MPa |
Es2/ MPa |
DBC41-1/ mm |
DBC41-2/ mm |
… | DBC42-11/ mm |
DBCZ82/ mm |
DBCZ83/ mm |
DBCZ84/ mm |
DBCY82/ mm |
DBCY83/ mm |
DBCY84/ mm |
| 37 | 1 | 5 | 2.692 9 | 3.875 | … | 1.965 7 | 5.023 8 | 3.431 | 1.142 2 | 16.358 1 | 7.469 8 | 7.569 6 |
| 38 | 2 | 10 | 2.537 9 | 3.871 5 | … | 1.885 5 | 4.809 3 | 3.356 9 | 1.122 8 | 14.488 1 | 7.186 9 | 7.513 3 |
| 39 | 3 | 15 | 2.453 3 | 3.695 1 | … | 1.860 4 | 4.326 2 | 3.000 4 | 0.994 | 14.253 8 | 7.145 5 | 7.436 7 |
| 40 | 4 | 20 | 2.281 | 3.507 9 | … | 1.725 9 | 3.706 2 | 2.884 | 0.960 9 | 12.084 6 | 6.343 4 | 6.268 1 |
| 41 | 5 | 25 | 2.160 6 | 3.022 1 | … | 1.464 6 | 3.081 | 2.408 7 | 0.828 4 | 11.88 | 6.291 6 | 5.935 2 |
| 42 | 6 | 30 | 2.105 1 | 2.424 | … | 1.309 | 2.716 4 | 2.010 5 | 0.754 4 | 11.280 2 | 5.611 3 | 4.838 6 |
2.3 RBF核函数与Morlet核函数对比
RBF核函数[24]输出的结果相对稳定,运算速度快,是一种常用SVM的核函数,算法相对成熟,认可度高,Matlab软件都内置有RBF算法。通过编译Matlab程序,将RBF核函数与SVM结合[25],与本研究使用的Morlet小波核函数SVM程序进行反演参数精度对比。两种SVM模型都是先通过PSO粒子群算法进行模型参数的寻优及模型优化,然后以测试样本作为源数据,将沉降值作为输入值,输出模量值与测试样本的原始模量值进行比较。通过标准差S来评判两种核函数计算结果:

|
(13) |
利用PSO算法优化Morlet核函数与RBF核函数的SVM模型,对加固后的泥炭质土及黏土的压缩模量Es1及Es2进行参数寻优,寻优过程的适应度值变化趋势如图 6、图 7所示,Morlet核函数的适应度在两种模量的计算中均优于RBF核函数,平均适应度越接近最佳适应度则计算稳定性更高。依据程序计算原理及专著资料[25-26]设定符合该模型的参数与范围,罚参数C的范围设为[0.1, 100],核宽度g为[0.01, 1 000],损失函数p为[0.1, 100]。得到模型最优参数如表 4所示。
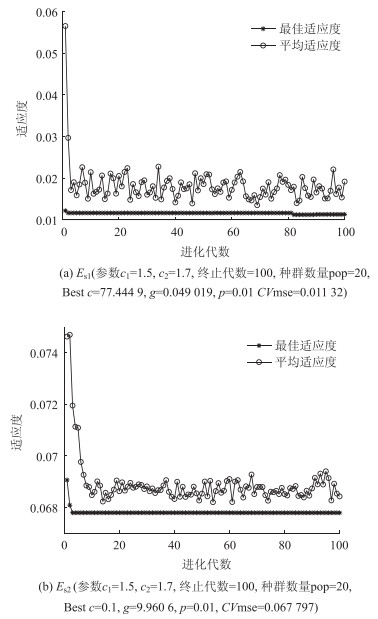
|
| 图 6 Morlet小波支持向量机优化模型适应度趋势 Fig. 6 Morlet wavelet SVM optimization model fitness trends |
| |
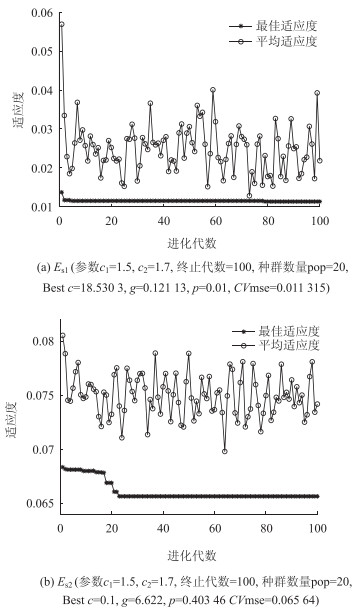
|
| 图 7 RBF支持向量机优化模型适应度趋势图 Fig. 7 RBF SVM optimization model fitness trends |
| |
| 核函数 | 模量 | C | g | p | 模量 | C | g | p |
| Morlet | Es1 | 77.444 9 | 0.049 02 | 0.011 32 | Es2 | 0.1 | 9.960 6 | 0.067 797 |
| RBF | Es1 | 18.530 3 | 0.121 13 | 0.0113 15 | Es2 | 0.1 | 6.622 | 0.065 64 |
将最优参数C,g,p代入训练后的两种核函数SVM模型中,得到模量反演值与原始模量对比结果见表 5。
| 编号 | 原始数据 | Morlet | 标准差 | RBF | 标准差 | |||||||||
| Es1/MPa | Es2/MPa | Es1/MPa | Es2/MPa | Es1 | Es2 | Es1/MPa | Es2/MPa | Es1 | Es2 | |||||
| 1 | 1 | 5 | 1.008 11 | 5.007 23 | 0.008 11 | 0.007 23 | 1.013 2 | 5.014 25 | 0.013 2 | 0.014 25 | ||||
| 2 | 2 | 10 | 2.013 2 | 10.008 6 | 0.013 2 | 0.008 6 | 2.023 6 | 10.012 7 | 0.023 6 | 0.012 71 | ||||
| 3 | 3 | 15 | 3.010 23 | 15.003 5 | 0.010 23 | 0.003 5 | 3.014 2 | 15.007 7 | 0.014 23 | 0.007 73 | ||||
| 4 | 4 | 20 | 4.004 1 | 20.001 2 | 0.004 1 | 0.001 2 | 4.006 1 | 20.006 5 | 0.006 135 | 0.006 54 | ||||
| 5 | 5 | 25 | 5.001 02 | 25.006 3 | 0.001 02 | 0.006 33 | 5.002 0 | 25.007 5 | 0.002 02 | 0.007 48 | ||||
| 6 | 6 | 30 | 6.006 96 | 30.001 6 | 0.006 96 | 0.0016 | 6.018 8 | 30.001 3 | 0.018 84 | 0.001 273 | ||||
| 平均标准差 | 1.881 3E-05 | 1.197 98E-05 | 6.314 14E-05 | 2.166 37E-05 | ||||||||||
由表 5可看出Morlet反演Es1标准差1.881 3E-05小于RBF反演Es1的标准差6.314 14E-05;Morlet反演Es2的标准差1.197 98E-05小于RBF反演Es2的标准差2.166 37E-05。标准差越小则数据越精确,由此表明Morlet小波的反演精度要高于RBF核函数。
最后采用PSO优化后的Morlet核函数SVM模型计算出的泥炭质土及黏土加固土压缩模量反演值如表 6所示。
| 土层 | 反演参数/MPa | 范围 |
| 泥炭质土 | Es1 | 3.972 6 |
| 黏土 | Es2 | 19.757 2 |
2.4 模型及模拟沉降计算结果
采用Midas GTX有限元软件建立隧道里程DK22+945~DK23+015的弹塑性模型,模型长50 m,宽110 m,高38 m,由上至下分别是素填土层、黏质粉土层、泥炭质土层、黏土层,其中隧道主要穿过泥炭质土层与黏土层,按衬砌管片尺寸及加固要求对隧道建模。管片及盾构壳体钢材弹性模量取值分别为3.45×104 MPa及2.5×105 MPa。模型有限元单元网格134 902个。三维有限元模型如图 8所示。

|
| 图 8 有限元模型网格图 Fig. 8 Gridding of FE model |
| |
模型土层参数取值见表 7,其中加固泥炭质土及黏土的压缩模量是采用反演值进行赋值。Midas软件模拟施工阶段进行逐级动态计算。模型计算结果如图 9所示。
| 土类 | c/kPa | φ/(°) | Es/MPa | γ/(kN·m-3) | μ |
| 素填土 | 10 | 5 | 5 | 17.0 | 0.42 |
| 黏质粉土 | 16 | 7 | 10 | 19.4 | 0.30 |
| 泥炭质土 | 21 | 10 | 4.7 | 12.8 | 0.39 |
| 黏土 | 30 | 11 | 6.2 | 17.8 | 0.36 |
| 加固泥炭质土 | 43 | 12 | 3.973 | 17.0 | 0.30 |
| 加固黏土 | 46 | 12.5 | 19.757 | 20 | 0.32 |

|
| 图 9 有限元模型计算结果云图(单位:m) Fig. 9 Nephogram of FE model calculated result(unit:m) |
| |
2.5 计算结果对比分析 2.5.1 Peck公式
Peck[25]假设隧道上方地面沉陷满足正态分布,从而提出隧道开挖诱发地表沉降的计算公式。
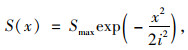
|
(14) |
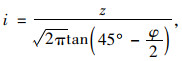
|
(15) |
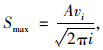
|
(16) |
式中,S(x)为距离隧道中线x处的沉降值;Smax为隧道中线上地面最大沉降值;i为变曲点到隧道中线的距离;Z为隧道埋深;φ为土层内摩擦角;Vi为地层损失率;A为隧道截面面积。
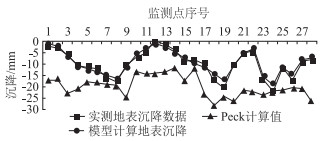
2.5.2 数据对比结果实际监测、有限元模型模拟计算及Peck公式计算沉降值如表 8所示。相应的对比图如图 10所示。图 10中的监测点序号1~11分别对应的是41断面监测点DBC41-1~11;序号12~22分别对应42断面监测点DBC42-1~11;序号23~25对应隧道左线监测点DBCZ82~84;序号26~28对应隧道右线监测点DBCY82~84。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 监测点 | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC |
| 41-1 | 41-2 | 41-3 | 41-4 | 41-5 | 41-6 | 41-7 | 41-8 | 41-9 | 41-10 | 41-11 | 42-1 | 42-2 | 42-3 | |
| 实测数据/mm | -1.97 | -2.8 | -6.27 | -10.77 | -11.58 | -12.46 | -15.89 | -17.64 | -10.78 | -6.75 | -5.03 | -0.21 | -1.47 | -4.19 |
| 模拟数据/mm | -1.16 | -2.28 | -6.74 | -10.84 | -12.25 | -13.38 | -15.12 | -16.5 | -11.61 | -5.79 | -3.13 | -0.87 | -2.48 | -4.75 |
| 差异比例/% | 11.5 | 14.8 | 7.9 | 16.0 | 18.2 | 2.9 | 0.6 | 14.2 | 5.5 | 18.8 | 2.7 | 13.7 | 3.7 | 7.9 |
| Peck数据/mm | -17.19 | -16.95 | -22.87 | -21.16 | -17.89 | -18.33 | -18.88 | -19.24 | -24.57 | -13.29 | -14.5 | -14.06 | -13.52 | -11.52 |
| 差异比例/% | 773 | 505 | 265 | 96 | 54 | 47 | 19 | 9 | 128 | 97 | 188 | 6 595 | 820 | 175 |
| 序号 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 监测点 | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBC | DBCZ | DBCZ | DBCZ | DBCY | DBCY | DBCY |
| 42-4 | 42-5 | 42-6 | 42-7 | 42-8 | 42-9 | 42-10 | 42-11 | 82 | 83 | 84 | 82 | 83 | 84 | |
| 实测数据/mm | -8.51 | -8.47 | -10.31 | -17.19 | -20.34 | -10.54 | -5.15 | -3.87 | -16.42 | -22.17 | -11.54 | -17.14 | -8.54 | -7.95 |
| 模拟数据/mm | -7.53 | -9.72 | -11.12 | -14.44 | -17.32 | -10.85 | -5.12 | -3.32 | -15.52 | -19.6 | -11.23 | -14.79 | -8.22 | -7.32 |
| 差异比例/% | 11.5 | 14.8 | 7.9 | 16.0 | 18.2 | 2.9 | 0.6 | 14.2 | 5.5 | 18.8 | 2.7 | 13.7 | 3.7 | 7.9 |
| Peck数据/mm | -17.35 | -12.02 | -23.17 | -27.91 | -24.47 | -26.32 | -21.61 | -22.27 | -23.85 | -21.79 | -21.48 | -20.38 | -20.81 | -26.54 |
| 差异比例/% | 104 | 42 | 125 | 62 | 20 | 150 | 320 | 475 | 45 | 2 | 86 | 19 | 144 | 234 |
|
| 图 10 沉降结果对比 Fig. 10 Comparison of settlement results |
| |
从表 8中可看出,28个点中实际监测及模拟计算结果有一半的点数值差异小于10%,仅有4个点的超过18%,最大18.8%,这4个点都在左线隧道顶部。由于实际工程场地位于市区,地面建筑物情况复杂,虽盾构机采取同步注浆的方式,但由于土层分布变化大,如图 8所示,对应左线洞顶处泥炭质土及黏土层分布要厚一些,所以注浆时对周围土层施加的压力以及注浆体硬化的过程对沉降产生影响是有区别的,左右相邻两条隧道同时掘进过程中,对周围土体扰动因土质不同影响也是不一致的,所以有4个监测点计算值与实际监测结果差异大了一点,但两者沉降规律是吻合的。而由Peck公式计算出的沉降值则显示出较大差异,大部分都偏大,具体如表 8所示。由此认证了反演参数的科学性和准确性。
3 结论(1) 利用PSO寻优算法对SVM模型基于正态分布、均匀试验设计的学习样本和测试样本进行训练,选出最优SVM模型参数,通过地面沉降监测数据来反演隧道加固土的压缩模量,并进行反分析,可获得较为精准的岩土力学参数值。
(2) 引入Morlet核函数优化SVM模型,降低了数据维度,提升了运算效率和精度,与RBF核函数SVM模型的反演参数的标准差对比,表明Morlet核函数的反演精度比RBF核函数的更高,Morlet核函数比广泛使用的RBF核函数更具优越性。
(3) 合理确定隧道周边不良地质土层加固后的力学指标,对盾构的设计及施工都非常重要。泥炭质土是一种区域性特殊软土,其加固土介质成分复杂,差异性大,传统的力学参数确定方法不能达到满意的效果,由PSO算法与SVM模型通过MATLAB编程与岩土力学交叉融合发展的智能力学参数计算方法,为其提供了一种新的分析方法。实例表明PSO-SVM联合反演效率高、准确性好,是一种有效确定复杂土层力学参数的科学方法。
| [1] |
陈江, 陈思明, 傅金阳, 等. 盾构侧穿邻近桥桩施工影响及加固措施研究[J]. 公路交通科技, 2016, 33(7): 97-102. CHEN Jiang, CHEN Si-ming, FU Jin-yang, et al. Study on Effect of Shield Tunneling Side-crossing Adjacent Piles and Reinforcement Measures[J]. Journal of Highway and Transportation, 2016, 33(7): 97-102. |
| [2] |
KAVANAGH K T, CLOUGH R W. Finite Element Applications in the Characterization of Elastic Solids[J]. International Journal of Solids & Structures, 1971, 7(1): 11-23. |
| [3] |
CERCIGNANI C, MAIER G. Teaching Mechanics in Italy[J]. Mechanics Research Communications, 1978, 5(2): 105-112. |
| [4] |
GIODA G, MAIER G. Direct Search Solution of an Inverse Problem in Elasto-plasticity, Identification of Cohesion, Frication Angle and In-situ Stress by Pressure Tunnel Tests[J]. International Journal for Numerical Methods in Engineering, 1980, 8(15): 1823-1834. |
| [5] |
SAKURAI S, TAKEUCHI K. Back Analysis of Measured Displacement of Tune[J]. Rock Mechanics & Rock Engineering, 1983, 16(3): 173-180. |
| [6] |
PICHLER B, LACKNER R, MANG H A. Back Analysis of Model Parameters in Geotechnical Engineering by Means of Soft Computing[J]. International Journal for Numerical Methods in Engineering, 2003, 57(14): 1943-1978. |
| [7] |
LEVASSEUR S, MALECOT Y, BOULON M, et al. Statistical Inverse Analysis Based on Genetic Algorithm and Principal Component Analysis:Method and Developments Using Synthetic Data[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2009, 33(12): 1485-1511. |
| [8] |
高玮. 基于粒子群优化的岩土工程反分析研究[J]. 岩土力学, 2006, 27(5): 795-798. GAO Wei. Back Analysis Algorithm in Geotechnical Engineering Based on Particle Swarm Optimization[J]. Rock and Soil Mechanics, 2006, 27(5): 795-798. |
| [9] |
赵洪波, 冯夏庭. 位移反分析的进化支持向量机研究[J]. 岩石力学与工程学报, 2003, 22(10): 1618-1622. ZHAO Hong-bo, FENG Xia-ting. Study on Genetic-support Vector Machine in Displacement Back Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1618-1622. |
| [10] |
NELDER J, MEAD R. A Simplex Method for Function Minimization[J]. The Computer Journal, 1965, 7(4): 308-313. |
| [11] |
冯紫良, 杨志法. 关于弹塑性位移反分析的若干研究[M]. 北京: 地震出版社, 1990: 87-102.
|
| [12] |
GIODA G, SAKURAI S. Back Analysis Procedures for the Interpretation of Field Measurements in Geomechanics[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 1987, 11(6): 555-583. |
| [13] |
GIODA G, PANDOLFI A, CIVIDINI A. A Comparative Evolution of Some Back Analysis Algorithms and Their Application to in Situ Load Tests[C]//Proceedings of 2nd International Symposium on Field Measurements in Geomechanics. Rotterdam: A A Balkema, 1988.
|
| [14] |
晏班夫, 陈文兵, 孙雁峰, 等. 基于动力刚度法与粒子群优化算法的拉索参数识别[J]. 公路交通科技, 2017, 34(5): 86-94. ZHAI Ban-fu, CHEN Wen-bing, SUN Yan-feng, et al. Parameter Identification of Cables Based on Dynamic Stiffness Method and Particle Swarm Optimization[J]. Journal of Highway and Transportation, 2017, 34(5): 86-94. |
| [15] |
ZHAO H B, RU Z L, CHANG X, et al. Reliability Analysis of Tunnel Using Least Square Support Vector Machine[J]. Tunnel Undergo Space Technol, 2014, 41: 14. |
| [16] |
曹净, 孙长宁, 宋志刚, 等. 上下接近盾构隧道周围土层参数反分析[J]. 昆明理工大学学报:自然科学版, 2017, 42(1): 105-111. CAO Jing, SUN Chang-ning, SONG Zhi-gang, et al. Back Analysis of Soil Parameters Around Adjacent Shield Tunnel[J]. Journal of Kunming University of Science and Technology:Natural Science Edition, 2017, 42(1): 105-111. |
| [17] |
EBERHART R C, SHI Y H. Particle Swarm Optimization: Developments, Applications and Resources[C]//Proceedings of the 2001 Congress on Evolutionary Computation. Seoul: IEEE, 2002: 81-86.
|
| [18] |
KENNEDY J, EBERHART R C. Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth: IEEE, 1995.
|
| [19] |
侯公羽, 许哲东, 刘欣, 等. 无数学模型的非线性约束单目标系统优化方法改进[J]. 工程科学学报, 2018, 40(11): 1402-1411. HOU Gong-yu, XU Zhe-dong, LIU Xin, et al. Optimization Method Improvement for Nonlinear Constrained Single Objective System without Mathematical Models[J]. Chinese Journal of Engineering, 2018, 40(11): 1402-1411. |
| [20] |
武方方, 赵银亮. 一种基于Morlet小波核的约简支持向量机[J]. 控制与决策, 2006, 21(8): 848-852, 856. WU Fang-fang, ZHAO Yin-liang. Novel Reduced Support Vector Machine on Morlet Wavelet Kernel Function[J]. Control and Decision, 2006, 21(8): 848-852, 856. |
| [21] |
阮永芬, 高春钦, 刘克文, 等. 基于粒子群算法优化小波支持向量机的岩土力学参数反演[J]. 岩土力学, 2019, 40(9): 3662-3669. RUAN Yong-fen, GAO Chun-qin, LIU Ke-wen, et al. Inversion of Rock and Soil Mechanics Parameters Based on Particle Swarm Optimization Wavelet Support Vector Machine[J]. Rock and Soil Mechanics, 2019, 40(9): 3662-3669. |
| [22] |
方开泰. 正交与均匀试验设计[M]. 北京: 科学出版社, 2001. FANG Kai-tai. Orthogonal and Uniform Experimental Design[M]. Beijing: Science Press, 2001. |
| [23] |
王正帅, 邓喀中. 概率积分法参数辨识的多尺度核偏最小二乘回归方法[J]. 岩石力学与工程学报, 2011, 30. WANG Zheng-shuai, DENG Ka-zhong. Parameters Identification of Probability-integral Method Based on Multi-scale Kernel Partial Least-squares Regression Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3863-3870. |
| [24] |
邓乃扬, 田英杰. 支持向量机:理论、算法与拓展[M]. 北京: 科学出版社, 2009. DENG Nai-yang, TIAN Ying-jie. Support Vector Machine:Theory, Algorithm and Extension[M]. Beijing: Science Press, 2009. |
| [25] |
纪震. 粒子群算法及应用[M]. 北京: 科学出版社, 2009. JI Zhen. Particle Swarm Optimization Algorithm and Application[M]. Beijing: Science Press, 2009. |
| [26] |
韩煊, 李宁, STANDINGJ R. Peck公式在我国隧道施工地面变形预测中的适用性分析[J]. 岩土力学, 2007(1): 23-28, 35. HAN Xuan, LI Ning, STANDING J R. An Adaptability Study of Gaussian Equation Applied to Predicting Ground Settlements Induced by Tunneling in China[J]. Rock and Soil Mechanics, 2007(1): 23-28, 35. |
 2020, Vol. 37
2020, Vol. 37
