扩展功能
文章信息
- 刘文博, 张树光, 赵恩禄
- LIU Wen-bo, ZHANG Shu-guang, ZHAO En-lu
- 基于最小耗能原理的海棠山隧道围岩蠕变损伤模型
- Creep Damage Model of Haitang Tunnel Surrounding Rock Based on Principle of Minimum Energy Dissipation
- 公路交通科技, 2020, 37(6): 79-86
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 79-86
- 10.3969/j.issn.1002-0268.2020.06.010
-
文章历史
- 收稿日期: 2018-10-18
2. 广西岩土力学与工程重点实验室, 广西 桂林 541004;
3. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004
2. Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering, Guilin Guangxi 541004, China;
3. School of Civil and Architectural Engineering, Guilin University of Technology, Guilin Guangxi 541004, China
当地下工程的基础向着深部不断推进时,基础所处区域内的深部围岩遭遇的地质条件也更加复杂多变,深部围岩在高围压、高温、高地应力以及强扰动条件下,表现出了复杂的流变特性,而岩石蠕变变形特性以及蠕变变形破坏机理是怎样变化发展的,对于研究材料蠕变破坏机理具有重要的意义。故需要通过对岩石室内进行蠕变试验研究,分析岩石在不同力学状态下蠕变特性,建立一种合适的蠕变本构模型来描述岩石的流变性质,对建立数值力学模型及解决工程实际问题都具有重大的影响[1-4]。
近些年,学者们对于岩石流变性质、变形破坏机理以及如何构建一个合适的蠕变模型做了大量研究[5],主要表现在以下几个方面:张楚旋等[6]发现围压可以有效地提升能量的耗散,且卸载试验的能量耗散要远远大于加载试验中岩石的能量耗散量。王凯等[7]通过试验得到在巷道开挖过程中围岩的变形规律,结合数值计算软件对煤岩开采过程中变形特性进行模拟,最终围岩的耗能随卸载速率逐渐增大,且导致围岩进一步变形破坏。雷涛等[8]通过外部手段对岩石进行不同初始损伤试验,进一步对含有初始损伤的岩石进行卸载试验研究,得出岩石能量耗散与孔隙度均随初始损伤程度的增大而增大。上述试验研究中对于岩石在加载、卸载过程中能量耗散规律进行了深入的研究,验证了通过能量耗散理论可以有效地描述岩石的变形破坏特性。为了进一步研究和预测岩石在不同条件下的变形规律,将结合岩石在蠕变过程中的能量耗散规律,反映岩石在蠕变变形过程中内部结构的劣化情况,从而更好地反映岩石的变形破坏行为。
因此,本研究对取自海棠山隧道围岩进行三轴蠕变试验,研究岩石在不同围压条件下变形劣化特性,然后结合现有最小能量耗散理论推导损伤演化模型,建立一个基于能量耗散理论的岩石非线性损伤蠕变方程,最后通过三轴蠕变试验数据验证模型的正确性与合理性。
1 三轴蠕变试验研究本研究选取的砂岩取自海棠山隧道围岩,为减小试样的差异性,确保试验的可对比性,挑选的岩块均来自同一断面,海棠山隧道所在地区为低山丘陵地貌,山势陡峭为深埋隧道。本研究设定围压为20 MPa和30 MPa,试验每个轴向应力水平分成4级,采用分级加载的方式以达到逐级加载偏差应力。本次试验采用偏差应力加载方法见表 1。
| 应力水平级数 | σ3=20 | σ3=30 |
| 1 | 70 | 80 |
| 2 | 80 | 90 |
| 3 | 90 | 100 |
| 4 | 100 | 110 |
试样的加工精度按照《岩石试验方法标准》(GB50218—94)[8]进行,制备成形状为标准圆柱体,直径50 mm,高度100 mm。本次试验采用MTS812.02岩石试验机如图 1所示。

|
| 图 1 试验系统 Fig. 1 Test system |
| |
试验方案:首先,在试件两端面均匀涂抹凡士林,最大限度地消除端部效应;在加载时设定位移上限值,保证岩石变形不受外界干扰;加载方式采用荷载控制方式,以0.5 MPa/s的速率均匀施加轴向应力和围压,轴向应力水平每次加载10 MPa直至岩石失稳破坏为止,采样间隔设置为5 s;最终通过输出的试验数据绘制出轴径应变-时间历时曲线。
1.1 蠕变历时曲线分析根据上述试验方法和试验方案,对海棠山隧道围岩进行不同围压的常规三轴压缩蠕变试验,σ3=20 MPa和σ3=30 MPa作用下的分级加载轴向历时蠕变曲线如图 2所示。
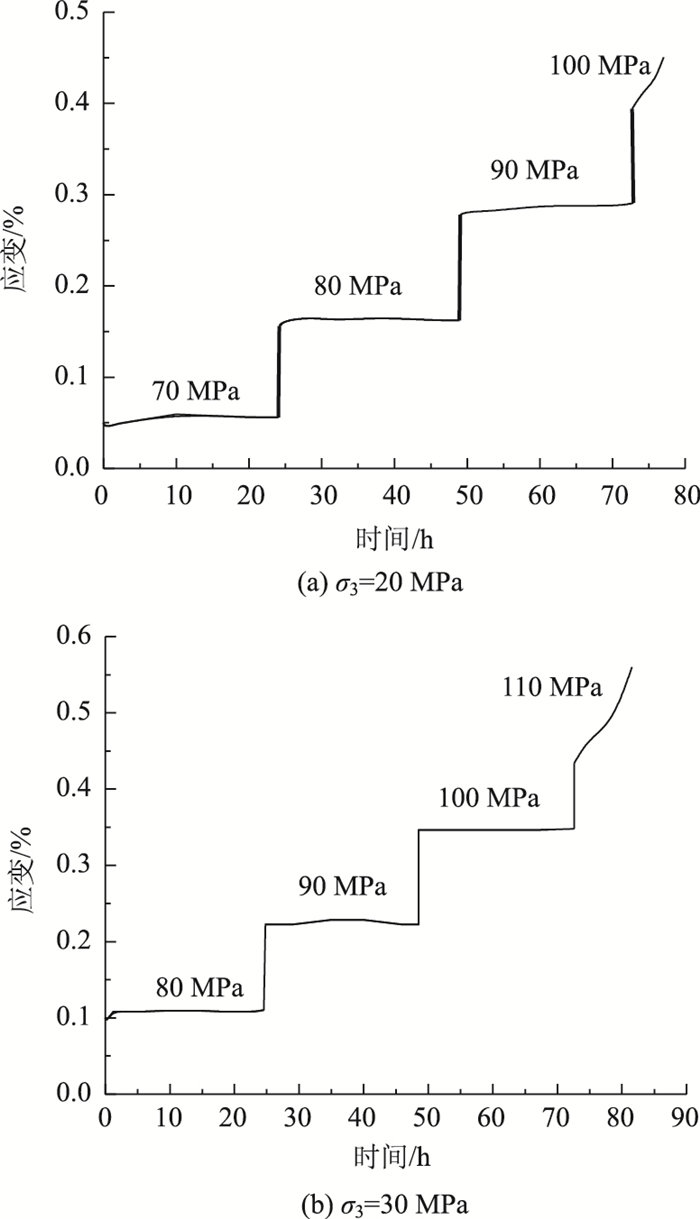
|
| 图 2 轴向蠕变历时曲线 Fig. 2 Axial creep duration curves |
| |
由图 2可知,在围压20 MPa作用下,荷载作用4级后发生失稳变形破坏,在围压30 MPa作用下,荷载作用也经历5级后发生失稳变形破坏;瞬时应变和蠕变应变都随着应力水平增大不断增大,且瞬时应变占总应变比例的变化规律呈现先减小后增大趋势。
1.2 轴向蠕变曲线分析将不同围压条件下所得蠕变试验数据运用Boltzmann叠加原理[9]进行处理,得到各级轴向蠕变曲线如图 3所示。
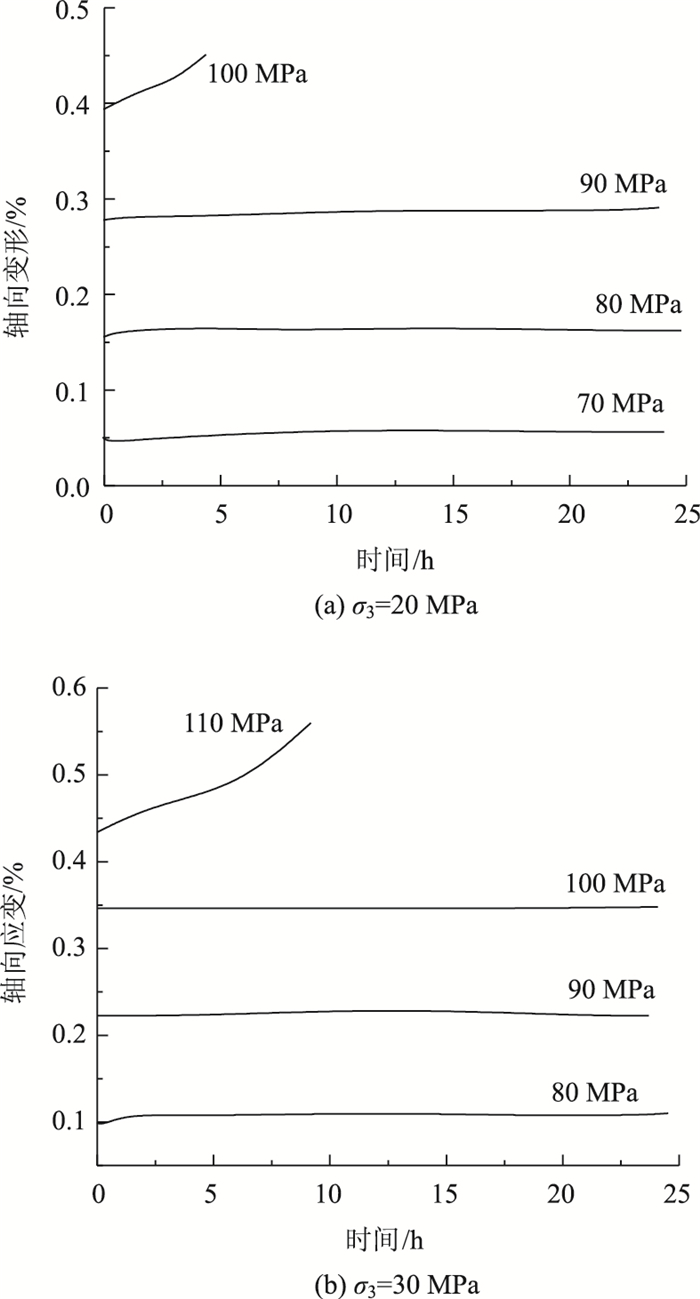
|
| 图 3 轴向分阶段蠕变曲线 Fig. 3 Axial phased creep curves |
| |
由图 3可知,只有当施加在岩石的应力水平较高时,才会出现稳定蠕变和加速蠕变现象,否则蠕变变形只有衰减蠕变变形;以围压30 MPa为例,在σ1=80 MPa时,蠕变速率从初始值衰减至零,最终的蠕变变形为0.110 2%(全部为衰减蠕变);在90 MPa和100 MPa作用下,衰减蠕变变形时间大约为8 h左右,岩石的蠕变变形便转变为稳定蠕变变形,蠕变速率从初始值衰减至一个稳定值;在最后一级应力水平110 MPa作用下,蠕变变形出现加速蠕变变形,变形与时间之间的规律呈现出明显的非线性变化趋势。同时,围压的增高不仅增大了试样的破坏应力水平,同时延缓了轴向蠕变变形。
1.3 蠕变试验瞬时变形分析根据试验数据绘制不同围压下砂岩瞬时变形量与应力水平关系如图 4所示。
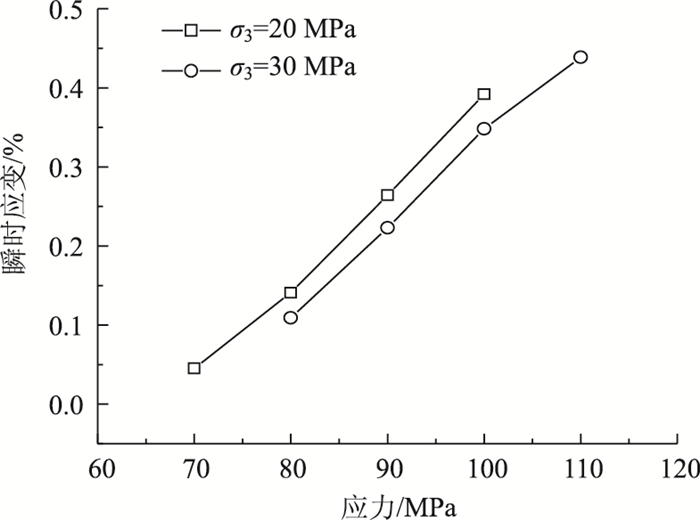
|
| 图 4 瞬时变形曲线 Fig. 4 Instantaneous deformation curves |
| |
岩石在低应力作用下,不考虑岩石初始损伤[10-12],瞬时应变阶段的变形可以当做弹性应变,此时岩石内部空隙开始闭合,在施加较大应力水平后,瞬时应变不仅包含了弹性应变,也包含了塑性应变,此时岩石内部空隙在完全闭合后,会产生一定裂隙使得岩石体积由压缩状态转化为膨胀状态,瞬时应变非线性特性更加明显。
2 非线性损伤蠕变方程 2.1 损伤变量通过引入开关元件来改进西原模型[13],则改进后的西原模型,如图 5所示。
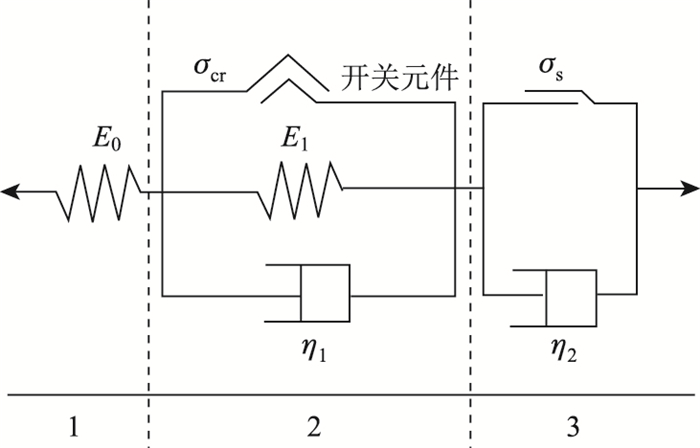
|
| 图 5 改进后的西原模型 Fig. 5 Improved Nishihara model |
| |
当 σ<σcr时
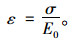
|
(1) |
当σcr≤σ < σs时,
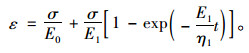
|
(2) |
当σs≤σ时,
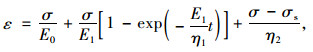
|
(3) |
式中,E0,E1为弹性模量;η1,η2为黏滞性系数;σs为长期强度;σcr为开关元件启动应力;ε为应变;σ为应力。
根据应变等效原理[18-19]将改进后的西原体一维蠕变方程表示如下
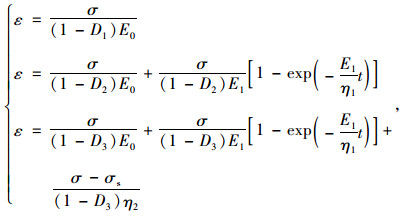
|
(4) |
式中,D1为弹性体劣化的损伤变量;D2为弹性体和黏弹性体劣化的损伤变量;D3为改进后整个西原体劣化的损伤变量。
假设不考虑对时间t求导所得应变速率,分别对上式关于时间t求导数得:
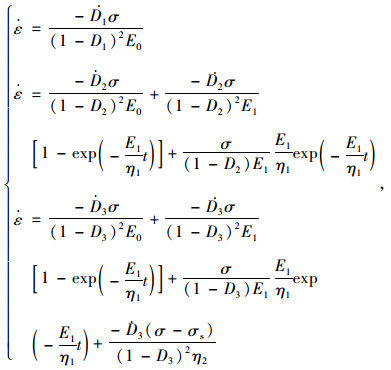
|
(5) |
式中,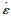
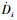
根据材料内变量理论和最小耗能原理[20],在不考虑材料热耗散能时,其耗能率φ (t)为:
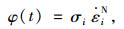
|
(6) |
式中,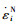
本研究蠕变试验在常温条件下进行假三轴试验(σ1>σ2=σ3),屈服函数选取以下形式,即[21]:
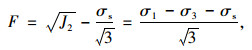
|
(7) |
式中J2为应力偏量第二不变量。
根据最小耗能原理知材料在损伤破坏过程中,岩石任意时刻在约束条件(屈服函数)下耗能最小,即
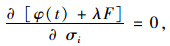
|
(8) |
式中λ为拉格朗日比例常数。
联立式(5)~ (8)式可得:
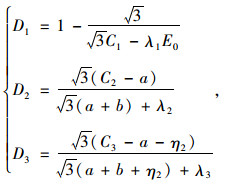
|
(9) |
式中,λi为拉格朗日比例常数,i=1,2,3;C1,C2和C3为材料常数,可拟合得到; a=1/E0+1/E1× [1-exp(-E1×t/η1)];b=exp (-E1×t/η1)/η1。
根据文献[22]知,在不考虑体积变化的前提下,令S=σ1-σ3,将式(1)~ (3)转化为西原体三维状态下的非线性损伤方程,得出岩石的轴向蠕变损伤方程为:
当σ < σcr时,
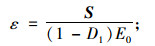
|
(10) |
当σcr≤σ < σs时,
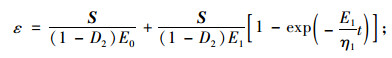
|
(11) |
当σs≤σ时,
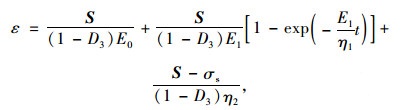
|
(12) |
式中 S为应力偏张量。
2.2 损伤蠕变参数确定根据文献[23-24]可知, 通过等时应力-应变曲线(如图 6所示)可以得出围压30 MPa下砂岩的长期强度为σs=90 MPa。
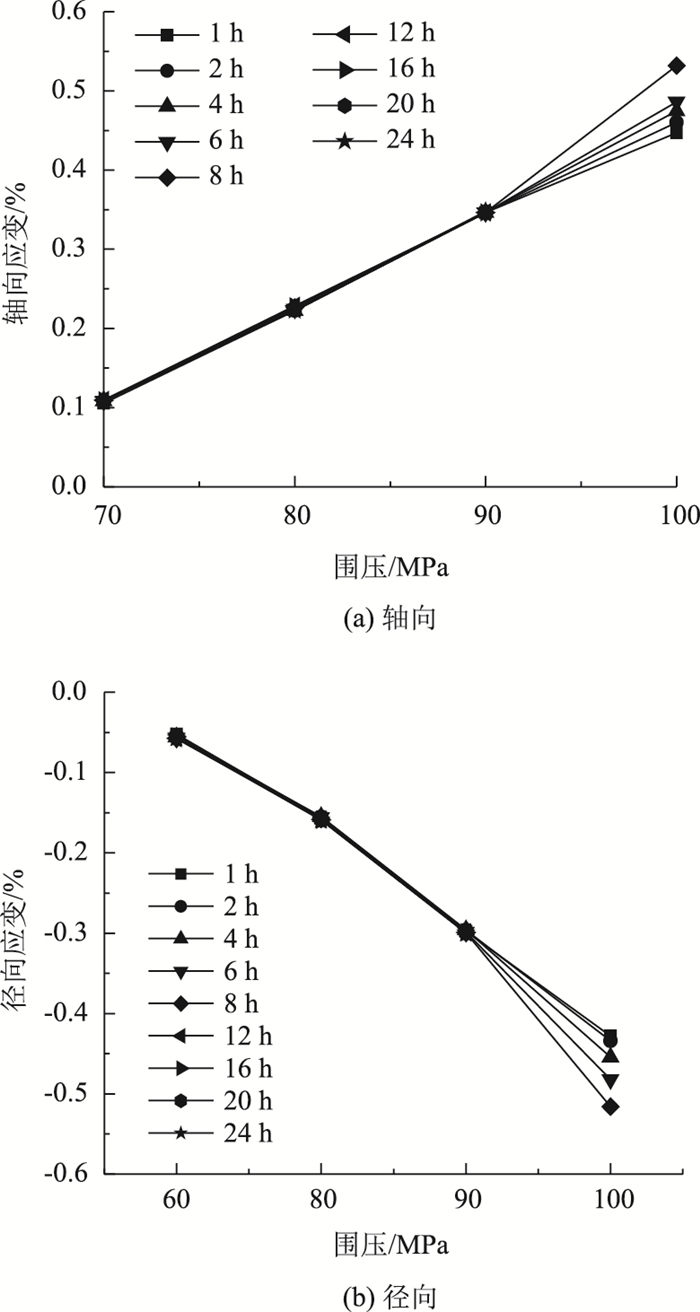
|
| 图 6 等时应力-应变曲线 Fig. 6 Isochronous stress-strain curves |
| |
本研究采用Origin软件对试验曲线进行参数辨识(参数见表 2)。由于所施加应力水平较大,远远超过蠕变起始应力门槛值σcr,不会存在只有瞬时应变且不产生蠕变变形的情况,故只考虑其他两种情况下的蠕变损伤模型与试验数据的对比。
| σ1/MPa | E0/GPa | E1/GPa | η1/GPa | η2/GPa | C2 | λ2 | C3 | λ3 |
| 70 | 139.1 | 2 971.1 | 17 548.3 | — | 21.4 | 41.9 | — | — |
| 80 | 147.4 | 6 060.8 | 36 438.3 | — | 19.0 | 31.6 | — | — |
| 90 | 153.9 | 18 100.4 | 25 714.7 | 1 103.5 | — | — | 18.2 | 27.0 |
| 100 | 59.8 | 122.8 | 1 233.5 | 1 744.3 | — | — | 14.4 | 21.7 |
将表中不同应力水平作用下的蠕变参数值代入到改进后的模型中,得到岩石在不同应力水平作用下模型曲线与试验数据对比如图 7(b)所示。同理,可得围压20 MPa蠕变损伤变量与时间关系的曲线如图 7(a)所示。从试验数据与模型曲线对比可知,结合能量原理和最小能耗原理确定内变量D,可以较好地反映岩石内部变形变化状态,并可以将岩石损伤演化规律以能量变化方式呈现出来,进一步说明岩石损伤贯穿于整个加载试验过程中,也可以通过损伤演化规律来描述岩石能量耗散规律。
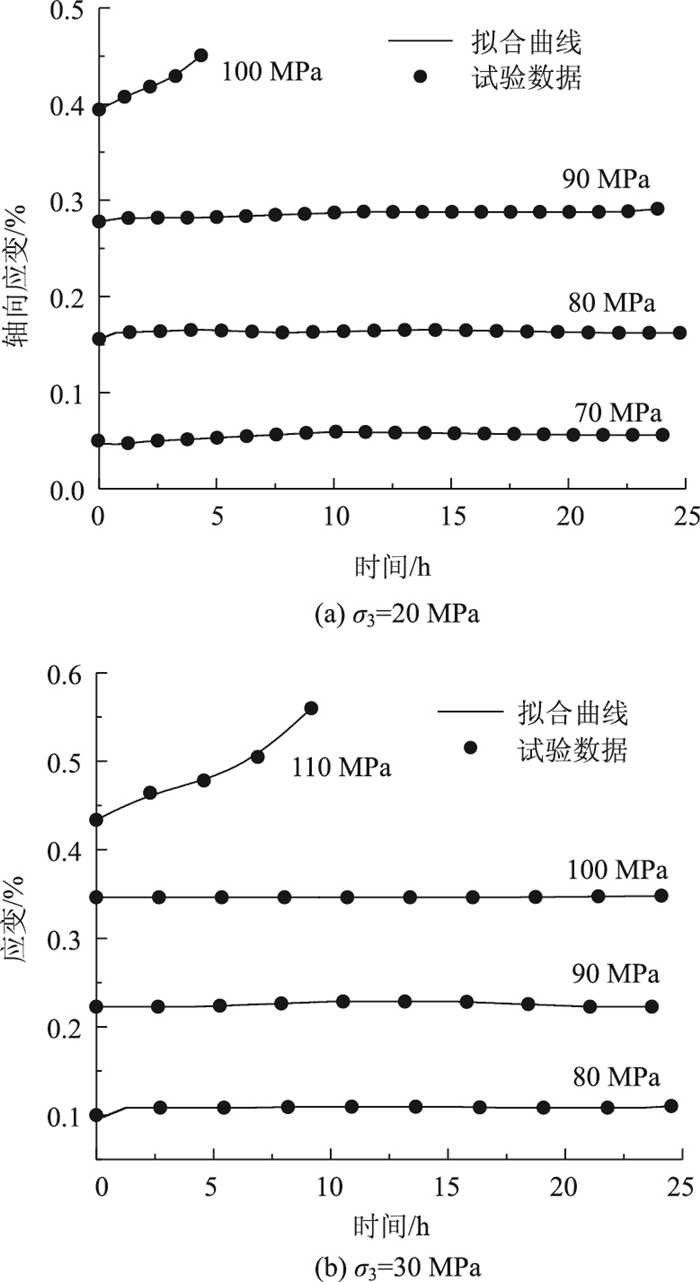
|
| 图 7 对比曲线 Fig. 7 Contrast curves |
| |
将表 2中确定的蠕变参数代入式(9)中,绘制出不同围压条件下,砂岩试样最后一级损伤变量D3与时间t的变化关系如图 8所示。
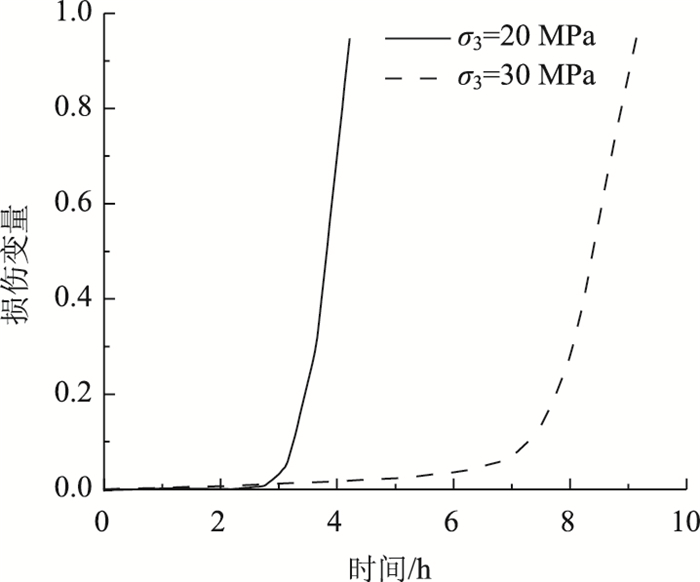
|
| 图 8 损伤变量与时间 Fig. 8 Damage variable vs. time |
| |
由图 8可知,损伤变量随着时间的增加,先呈现出近水平、小幅度增长,在蠕变变形进入加速蠕变后,损伤变量开始急剧增大,数值逐渐趋近于1,这说明了在变形进入加速蠕变变形阶段后,岩石内部空隙首先在软弱区积聚,使得岩石损伤程度进一步加大,内部空隙和裂隙逐渐贯通为宏观裂缝,最终岩石产生失稳破坏。
为了进一步验证本研究建立蠕变损伤模型的适用性,引用文献[25]中花岗岩蠕变试验数据,基于最小二乘法获得蠕变模型参数,然后将计算模型曲线与试验数据对比如图 9所示。
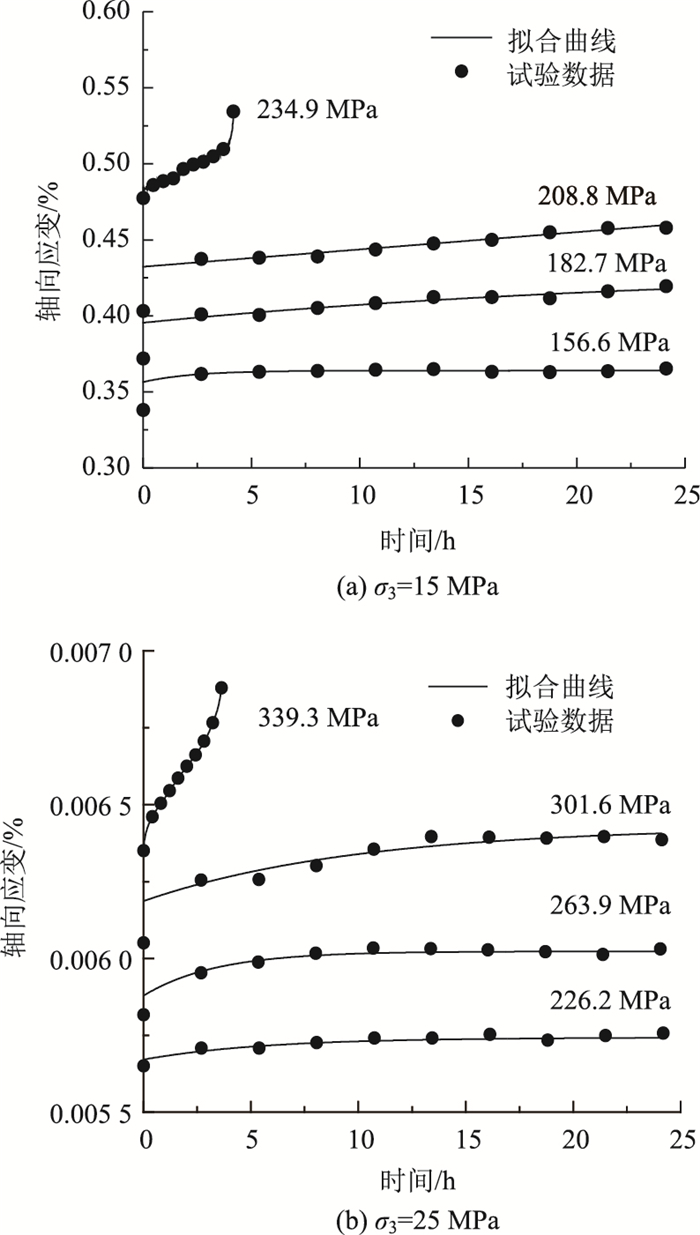
|
| 图 9 计算值与实验值拟合(花岗岩) Fig. 9 Calculated values fit with experimental values (granite) |
| |
由图 9可知,本研究建立的蠕变损伤模型,对于不同围压作用下花岗岩蠕变特性也有较好地描述,计算曲线和试验数据拟合度较高,说明了该损伤模型不仅适用于描述砂岩的蠕变特性,也适用于描述花岗岩的蠕变特性。这是由于建立的损伤模型是考虑岩石耗散机制的基础上,而能量的耗散机制存在于任何一个自然作用中,故本研究建立的损伤模型可以适用于任何岩石的蠕变变形情况。
3 结论以阜新海棠山隧道围岩(砂岩)为研究对象,对三轴蠕变作用机制展开研究,构建了一个新型的能量耗散蠕变模型。得出以下主要结论:
(1) 在施加较大应力水平后,瞬时应变不仅包含了弹性应变,也包含了塑性应变,此时岩石内部空隙在完全闭合后,会产生一定裂隙使得岩石体积由压缩状态转化为膨胀状态,瞬时应变非线性特性更加明显,且瞬时变形逐渐由线性转变为非线性,具有较为明显的转折点。
(2) 在相同围压、不同应力下砂岩蠕变试验曲线与模型曲线拟合度较高,说明了基于最小耗能原理来建立非线性蠕变损伤模型,对砂岩蠕变全过程演化规律描述是合适可行的,也充分地说明将岩石作为耗散结构来确定岩石损伤程度以及反映岩石蠕变全过程变形规律是正确的。
(3) 通过能量原理引入内变量D,可以较好地反映岩石内部应力-应变变化状态,也较好地呈现出岩石内部能量耗散具体过程,且该模型对于不同围压作用下花岗岩蠕变特性也有较好地描述,计算曲线和试验数据拟合度较高,说明了该损伤模型的适用性广泛。
| [1] |
张树光, 刘文博, 张印, 等. 基于最小能耗原理的花岗岩蠕变损伤分析[J]. 应用基础与工程科学学报, 2019, 27(1): 205-215. ZHANG Shu-guang, LIU Wen-bo, ZHANG Yin, et al. Analysis of Creep Damage of Granite Based on the Principle of Minimum Dissipative Energy[J]. Journal of Basic Science and Engineering, 2019, 27(1): 205-215. |
| [2] |
刘文博.砂岩卸荷蠕变特性研究及能量演化分析[D].阜新: 辽宁工程技术大学, 2017. LIU Wen-bo. Study on Unloading Creep Characteristics and Analysis on Energy Evolution of Sandstone[D].Fuxin: Liaoning Technical University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10147-1018255662.htm |
| [3] |
张嘉威, 章杨松, 李晓昭. 考虑渐进性破坏的岩石损伤本构模型研究[J]. 地下空间与工程学报, 2015, 11(6): 1528-1532. ZHANG Jia-wei, ZHANG Yang-song, LI Xiao-zhao. Study on Damage Constitutive Model of Rock Considering Progressive Failure[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(6): 1528-1532. |
| [4] |
张玉, 王亚玲, 张晓东, 等. 高埋深储层膏质泥岩蠕变力学特性试验研究[J]. 岩土力学, 2017, 38(11): 3179-3186. ZHANG Yu, WANG Ya-ling, ZHANG Xiao-dong, et al. Experimental Study of Creep Behaviour of Gypsum Mudstone in a Deep Reservoir[J]. Rock and Soil Mechanics, 2017, 38(11): 3179-3186. |
| [5] |
ZHOU X P, HA Q L. Analysis of Deformation Localization and the Complete Stress-strain Relation for Brittle Rock Subjected to Dynamic Compressive Loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 311-319. |
| [6] |
张楚旋, 戴兵, 吴秋红. 不同应力路径下岩石卸荷破坏过程的变形特性与能量耗散分析[J]. 中国安全生产科学技术, 2014, 10(10): 35-40. ZHANG Chu-xuan, DAI Bing, WU Qiu-hong. Analysis on Deformation Properties and Energy Dissipation of Rock Unloading Failure Process under Different Stress Path[J]. Journal of Safety Science and Technology, 2014, 10(10): 35-40. |
| [7] |
王凯, 郑吉玉, 朱奎胜. 两种应力路径下无烟煤的变形破坏特征及能量分析[J]. 岩土力学, 2015, 36(增2): 259-266. WANG Kai, ZHENG Ji-yu, ZHU Kui-sheng. Analysis of Deformation Failure Characteristics and Energy of Anthracite under Two Kinds of Stress Paths[J]. Rock and Soil Mechanics, 2015, 36(S2): 259-266. |
| [8] |
雷涛, 周科平, 胡建华, 等. 卸荷岩体力学参数劣化规律的细观损伤分析[J]. 中南大学学报:自然科学版, 2013, 44(1): 275-281. LEI Tao, ZHOU Ke-ping, HU Jian-hua, et al. Mechanics Parameters Deterioration Laws of Unloading Rock Mass by Meso-damage Mechanics[J]. Journal of Central South University:Science and Technology Edition, 2013, 44(1): 275-281. |
| [9] |
GB/T 50266-99, 工程岩体试验方法标准[S]. GB/T 50266-99, Standard for Tests Method of Engineering Rock Masses[S]. |
| [10] |
刘文彬.岩石蠕变本构模型的辨识及应用[D].北京: 北京交通大学, 2009. LIU Wen-bin. Identification and Application of Rock Creep Constitutive Model[D]. Beijing: Beijing Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010040859.htm |
| [11] |
余寿文, 冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997. YU Shou-wen, FENG Xi-qiao. Damage Mechanics[M]. Beijing: Tsinghua University, 1997. |
| [12] |
何志磊, 朱珍德, 朱明礼, 等. 基于分数阶导数的非定常蠕变本构模型研究[J]. 岩土力学, 2016, 37(3): 737-744. HE Zhi-lei, ZHU Zhen-de, ZHU Ming-li, et al. An Unsteady Creep Constitutive Model Based on Fractional order Derivatives[J]. Rock and Soil Mechanics, 2016, 37(3): 737-744. |
| [13] |
XU M, JIN D H, SONG E X. A Rheological Model to Simulate the Shear Creep Behavior of Rockfills Considering the Influence of Stress States[J]. Acta Geotechnica, 2018, 13(6): 1313-1327. |
| [14] |
宇晓龙.花岗岩三轴蠕变过程特征分析及本构模型研究[D].阜新: 辽宁工程技术大学, 2013. YU Xiao-long. Analysis of Granite Three-axis Creep Process Characteristics and Research of Constitutive Model[D]. Fuxin: Liaoning University of Engineering and Technology, 2013. |
| [15] |
杨振伟, 金爱兵, 王凯, 等. 基于颗粒流程序的黏弹塑性本构模型开发与应用[J]. 岩土力学, 2015, 36(9): 2708-2715. YANG Zhen-wei, JIN Ai-bing, WANG Kai, et al. Development and Application of a Visco-elastoplastic Constitutive Model in Particle Flow Code[J]. Rock and Soil Mechanics, 2015, 36(9): 2708-2715. |
| [16] |
齐亚静, 姜清辉, 王志俭, 等. 改进西原模型的三维蠕变本构方程及其参数辨识[J]. 岩石力学与工程学报, 2012, 31(2): 347-355. QI Ya-jing, JIANG Qing-hui, WANG Zhi-jian, et al. 3D Creep Constitutive Equation of Modified Nishihara Model and Its Parameters Identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 347-355. |
| [17] |
杨红伟, 许江, 彭守建, 等. 孔隙水压力分级加载砂岩蠕变特性研究[J]. 岩土力学, 2015, 36(增2): 365-370. YANG Hong-wei, XU Jiang, PENG Shou-jian, et al. Study of Sandstone Creep Characteristics under Stepwise Loading Pore Water Pressures[J]. Rock and Soil Mechanics, 2015, 36(S2): 365-370. |
| [18] |
杨超, 黄达, 黄润秋, 等. 断续双裂隙砂岩三轴卸荷蠕变特性试验及损伤蠕变模型[J]. 煤炭学报, 2016, 41(9): 2203-2211. YANG Chao, HUANG Da, HUANG Run-qiu, et al. Experimental Study on the Triaxial Unloading Creep Characteristics of Stone with Two Pre-existing Cracks and Its Damage Creep Model[J]. Journal of China Coal Society, 2016, 41(9): 2203-2211. |
| [19] |
刘开云, 薛永涛, 周辉. 参数非定常的软岩非线性黏弹塑性蠕变模型[J]. 中国矿业大学学报, 2018, 47(4): 921-928. LIU Kai-yun, XUE Yong-tao, ZHOU Hui. A Nonlinear Viscoelastic-plastic Creep Model of Soft Rock with Unsteady Parameters[J]. Journal of China University of Mining & Technology, 2018, 47(4). |
| [20] |
周科平, 苏淑华, 胡振襄, 等. 不同初始损伤下大理岩卸荷的核磁共振试验研究[J]. 岩土力学, 2015, 36(8): 2144-2150. ZHOU Ke-ping, SU Shu-hua, HU Zhen-xiang, et al. Experimental Research into Nuclear Magnetic Resonance in Marble with Different Initial Damages under Unloading Conditions[J]. Rock and Soil Mechanics, 2015, 36(8): 2144-2150. |
| [21] |
张树光, 孙成鑫, 王有涛, 等. 海棠山隧道砂岩变参数蠕变特性研究[J]. 公路交通科技, 2016, 33(10): 104-110. ZHANG Shu-guang, SUN Cheng-xin, WANG You-tao, et al. Study on Variable Parameter Creep Characteristics of Sandstone in Haitangshan Tunnel[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 104-110. |
| [22] |
张龙云, 张强勇, 李术才, 等. 硬脆性岩石卸荷流变试验及长期强度研究[J]. 煤炭学报, 2015, 40(10): 2399-2407. ZHANG Long-yun, ZHANG Qiang-yong, LI Shu-cai, et al. Unloading Rheological Tests of Hard Brittle Rock and Its Long-term Strength Analysis[J]. Journal of China Coal Society, 2015, 40(10): 2399-2407. |
| [23] |
沈明荣, 谌洪菊, 张清照. 基于蠕变试验的结构面长期强度确定方法[J]. 岩石力学与工程学报, 2012, 31(1): 1-7. SHEN Ming-rong, CHEN Hong-ju, ZHANG Qing-zhao. Method for Determining Long-term Strength of Discontinuity Using Shear Creep Test[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 1-7. |
| [24] |
沈明荣, 陈建峰. 岩体力学[M]. 上海: 同济大学出版社, 2006. SHEN Ming-rong, CHEN Jian-feng. Rock Mechanics[M]. Shanghai: Tongji University Press, 2006. |
| [25] |
韩阳, 谭跃虎, 李二兵, 等. 岩石非定常Burgers蠕变模型及其参数识别[J]. 工程力学, 2018, 35(3): 201-217. HAN Yang, TAN Yue-hu, LI Er-bing, et al. Non-stationary Burgers Creep Model of Rock and Its Parameter Identification[J]. Engineering Mechanics, 2018, 35(3): 201-217. |
 2020, Vol. 37
2020, Vol. 37

 ,
,