扩展功能
文章信息
- 王桢, 徐百城, 刘红义, 吴海军, 吴月星
- WANG Zhen, XU Bai-cheng, LIU Hong-yi, WU Hai-jun, WU Yue-xing
- 贝雷片间联系布置对混凝土拱桥拱架稳定性的影响
- Influence of Connective Layout of Bailey Plates on Stability of Arch Centering of Concrete Arch Bridge
- 公路交通科技, 2020, 37(6): 50-58
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 50-58
- 10.3969/j.issn.1002-0268.2020.06.007
-
文章历史
- 收稿日期: 2019-08-23
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075;
3. 中路高科交通检测检验认证有限公司, 北京 100088
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China;
3. China Road Hi-Tech Traffic Inspection & Certification Co., Ltd., Beijing 100088, China
迄今为止,我国建造了许多结构合理、造型美观的大、中跨径箱型截面钢筋混凝土拱桥(通常跨径80~150 m)。与板拱桥、肋拱桥和双曲拱桥相比,箱型拱桥具有施工中稳定性强,成桥后截面抗弯、抗扭刚度大和有效控制工程造价等优势,故大、中跨径钢筋混凝土箱型拱桥成为地势高差较大的不少丘陵、高山深谷地区的优选桥型之一[1-3]。
大、中跨径钢筋混凝土箱型截面拱桥通常采用贝雷拱架分环、分段现浇施工。与落地支架施工和无支架施工相比,贝雷拱架施工具有临时设施投入少、工期短、风险低、桥梁接缝少、整体性能好和贝雷片装拆运输简单、可反复使用等优势。
对大、中跨径钢筋混凝土拱桥的研究,国内外学者将目光更多地放在结构设计、施工工艺和力学特性上。例如朱莉[4]介绍了信阳狮河大桥采用的节段预制、龙门吊机提运、拱架上拼装等施工方法;周水兴[5]介绍了拱架现浇钢筋混凝土拱圈浇注长度;周倩[6]介绍了分界点对混合拱桥受力的影响;王藐民[7]介绍了变截面劲性骨架钢筋混凝土拱桥外包混凝土过程中的线形控制方法;向中富[8]分析了拱架法施工过程中拱桥的力学行为;杜斌[9]研究了上承式钢筋混凝土拱桥的拱架施工工艺;王永宝[10]介绍了循环温度对大跨混凝土拱桥长期变形行为的影响;蒋友宝[11]分析了考虑偏心距的随机特性对箱形截面混凝土拱桥的可靠度;任为东[12]介绍了3跨连续中承式拱桥的结构受力性能。但工程界、学术界对贝雷片间联系布置对箱型拱桥拱架稳定性影响的认识尚显不足,鉴于我国曾发生多起因拱架失稳而造成桥梁垮塌的事故(例如贵州珍珠大桥拱架失稳垮塌事故),且在实际施工中,因为施工工期、便于施工等原因,可能会人为改变原设计的拱架结构(例如取消拱脚上、下弦杆,将无铰拱架变为两铰拱架)[13-17],故在主拱圈浇注阶段,如何合理优化贝雷拱架结构,保证拱架稳定性的前提下最大化兼顾施工进度,值得研究[18]。
基于上述考虑,笔者拟结合贵州某钢筋混凝土拱桥,对贝雷片间上、下弦杆平面联系同步变化布置和不同步变化布置,拱顶、拱脚平面联系布置、竖向联系布置,拱脚上、下弦杆对箱型截面钢筋混凝土拱桥拱架稳定性的影响进行研究。
1 贝雷拱架的稳定性问题贝雷拱架的稳定性理论分为两类:第1类稳定是建立在小位移基础上的理想线弹性有限元理论,与弹性屈曲稳定相关;第2类稳定是建立在大位移基础上的弹塑性非线性有限元理论,通过不断解决结构几何非线性和材料非线性的刚度方程求解极限荷载。
由于考虑了几何非线性和材料非线性,第2类稳定更贴近于实际工程,较第1类稳定而言,其所求的极限荷载较大,稳定安全系数较小。虽然第1类稳定计算过程引入了一定条件的假设,但求解较为简便,可评估结构承载能力,故求解贝雷拱架的第1类稳定具有重要的工程意义。本研究求解的均为第1类弹性稳定安全系数,限值不小于4。现行规范对稳定安全系数限值的规定见表 1。
| 稳定系数和规范 | 《公路桥涵施工技术规范》 (JTG/T F50—2011) |
《公路斜拉桥设计细则》 (JTG/T D65-01—2007) |
《铁路桥涵设计规范》 (TB 10002—2017) |
《空间网格结构技术规程》 (JGJ 7—2010) |
| 第1类稳定 | 拱桥4 | 4 | 拱圈(拱肋)4 | 4.2 |
| 第2类稳定 | — | 混凝土主梁2.5、钢主梁1.75 | — | 2 |
2 工程实例简介
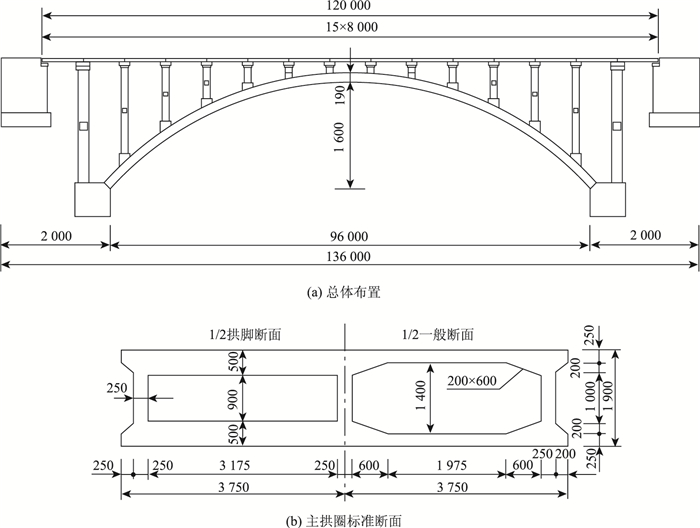
以贵州某大桥为工程实例。桥梁主孔为净跨96 m现浇钢筋混凝土箱形截面拱,矢跨比1/6,拱轴系数1.756,两岸边孔为跨径8 m的预制钢筋混凝土空心板,拱上建筑布置(8+13×8+8)m[1]。主拱圈为单箱双室截面,宽度7.5 m,截面高度1.9 m,采用两铰贝雷拱架作为施工平台,拱圈混凝土分为3层浇注。第1层为底板和下马蹄,第2层为腹板和横隔板,第3层为顶板和上马蹄。大桥总体布置和主拱圈标准断面见图 1。
|
| 图 1 大桥总体布置和主拱圈标准断面(单位:mm) Fig. 1 General layout and standard section of main arch ring of bridge (unit:mm) |
| |
两铰贝雷拱架由贝雷桁架、上下弦杆平面联系、竖向联系、拱脚构件和7类阴阳接头等构件组成。拱架采用2-Φ28的钢丝绳(扣索)悬臂拼装而成,钢丝绳截面面积294 mm2,弹性模量0.75×105 MPa。拱架纵向长度94.96 m,横向宽度7.3 m,横向布置12排贝雷桁架,每排桁架由31个国产标准贝雷片(长度3 m、高度1.5 m、材料16Mn钢)构成。
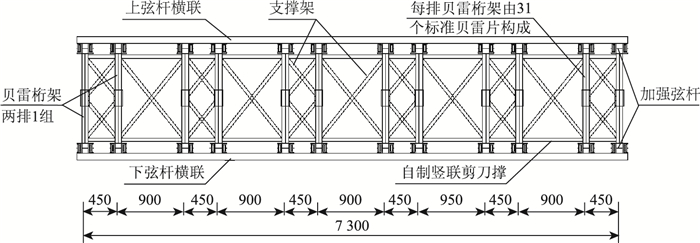
贝雷桁架在横桥向上、下弦杆平面设置支撑架作为上、下弦杆平面联系,在横桥向竖向腹杆上设置支撑架作为竖向联系。大桥贝雷拱架横断面布置见图 2。
|
| 图 2 大桥贝雷拱架横断面布置(单位:mm) Fig. 2 Layout of cross-section of Bailey arch centering of bridge (unit: mm) |
| |
3 有限元计算模型 3.1 计算假定
对大跨径钢筋混凝土拱桥施工阶段的稳定性模拟分析做出如下假定:
(1) 在施工中,始终按照两铰拱架进行考虑。
(2) 对于垫方、模板和施工机械等荷载,均布加载在拱架上。
(3) 尚未考虑山谷风荷载对拱架的影响。
3.2 模型和工况为研究贝雷片间联系布置对拱架稳定性的影响,利用桥梁专用有限元软件MIDAS/Civil建立大桥计算模型,其中贝雷拱架采用梁单元模拟。在拱圈和拱架未形成联合作用时,模拟方法为将垫方、模板、施工机械、底板和下马蹄等重量简化为均布荷载加载在拱架上;在拱圈和拱架形成联合作用后,模拟方法为去除均布荷载,采用实体单元模拟拱圈,拱圈和拱架采用仅受压的弹性连接。因实际桥梁按照两铰拱架施工,故拱脚处拱架和拱座的边界条件模拟为铰接。大桥有限元模型见图 3,有限元模型计算工况见表 2。

|
| 图 3 大桥有限元模型 Fig. 3 FE model of bridge |
| |
| 工况 | 计算内容和结构荷载 |
| 1 | 拱架260 t+垫方、模板165 t+施工机械50 t |
| 2 | 工况1+底板、下马蹄680 t |
| 3 | 工况2+拱圈腹板、横隔板360 t |
| 4 | 拱架预压试验:工况1+1.2×(底板、下马蹄混凝土) |
4 平面联系布置对拱架稳定性的影响 4.1 上、下弦杆平面联系同步变化布置
图 4为贝雷拱架上、下弦杆平面联系同步变化布置方案,图 5为上、下弦杆平面联系同步变化布置的弹性稳定安全系数。

|
| 图 4 贝雷拱架上、下弦杆平面联系同步变化布置方案 Fig. 4 Synchronous change layout schemes of plane connection of upper and lower chords of Bailey arch centering 注:因篇幅有限,对贝雷拱架上、下弦杆平面联系布置分析时,仅示意出1/2的拱架,下同。 |
| |
|
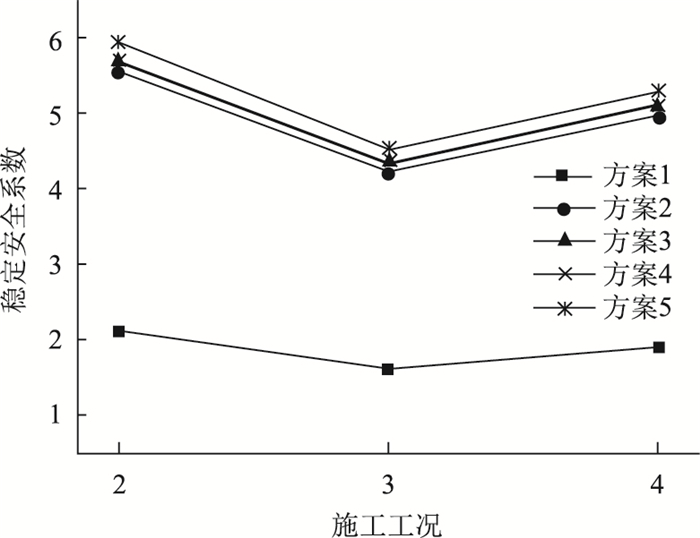
| 图 5 上、下弦杆平面联系同步变化布置的弹性稳定安全系数 Fig. 5 Elastic stability safety coefficient for synchronous change layout of plane connection of upper and lower chords |
| |
由图 5可以看出:
(1) 在工况2~3,随着施工荷载逐渐增大,5种平面联系布置的弹性稳定安全系数逐渐减小。
(2) 在工况2~4,方案1弹性稳定安全系数为1.907~2.314,不能满足《公路桥涵施工技术规范》(JTG/T F50—2011)(以下简称《规范》)中“箱型拱桥单肋横向稳定安全系数应大于4”的规定。这是因为上、下弦杆间无交叉平联,拱架横向刚度小,平面外稳定性差,易发生扭转变形,失稳模态表现为平面外反对称失稳。
(3) 在工况2~4,方案2弹性稳定安全系数为4.237~5.569,满足《规范》要求,且比方案1增大约161%,这是因为方案2增加了标准交叉平联和异形交叉平联,增加的交叉平联对拱架稳定性提高较大,方案2失稳模态发生变化,表现为平面外对称失稳。
(4) 在工况2~4,方案3、方案4的弹性稳定安全系数分别为4.349~5.715和4.340~5.703。方案3、方案4比方案2稳定系数均增大约3%,这是因为方案3、方案4将异形交叉变为满布交叉平联,即标准交叉平联增加约40%,失稳模态表现为平面外对称失稳。
(5) 在工况2~4,方案5弹性稳定安全系数为4.526~5.936,方案5比方案3、方案4稳定系数均增大约4%。虽然方案5将标准交叉平联变为满布交叉平联,即异形交叉平联增加约40%,但稳定系数提高较小,在上、下弦杆均已布置交叉平联时,无论是增加标准交叉平联或异形交叉平联,稳定系数均不会有较大提高,但方案5失稳模态发生变化,表现为平面内反对称失稳。
4.2 上、下弦杆平面联系不同步变化布置4.1节是在上、下弦杆相对应的平面联系同步增减条件下进行分析的,这样无法明确上、下平面联系各自的作用,故在本节进一步分析上、下平面联系各自对拱架稳定性的影响。贝雷拱架上、下弦杆平面联系不同步变化布置方案见图 6,上、下弦杆平面联系不同步变化布置的弹性稳定安全系数见图 7。

|
| 图 6 贝雷拱架上、下弦杆平面联系不同步变化布置方案 Fig. 6 Asynchronous change layout schemes of plane connection of upper and lower chords of Bailey arch centering |
| |
|
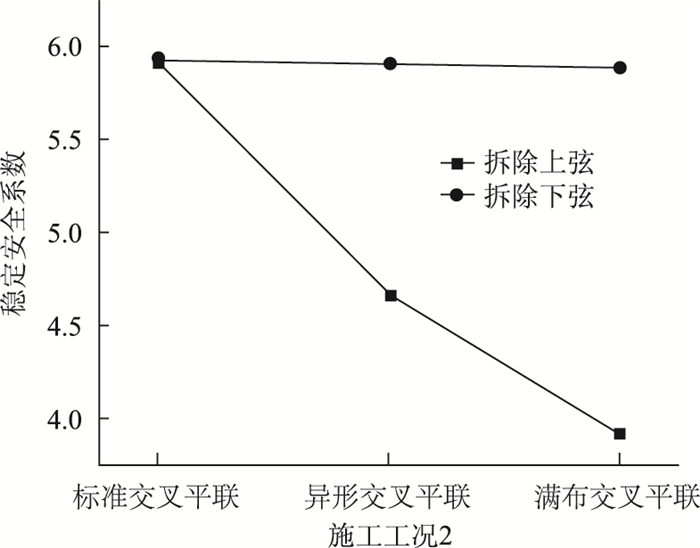
| 图 7 上、下弦杆平面联系不同步变化布置的弹性稳定安全系数 Fig. 7 Elastic stability safety coefficients for asynchronous change layout of plane connection of upper and lower chords |
| |
由图 7可以看出:
(1) 工况2,拆除上、下弦杆满布交叉平联的弹性稳定安全系数分别为3.926和5.89。这表明拆除上弦杆满布交叉平联比拆除下弦杆满布交叉平联对拱架稳定性影响大。
(2) 工况2,拆除上、下弦杆异形交叉平联和标准交叉平联的弹性稳定安全系数分别为4.662~5.904和5.924~5.924。这表明拆除异形交叉平联对拱架稳定性的影响大于拆除标准交叉平联。
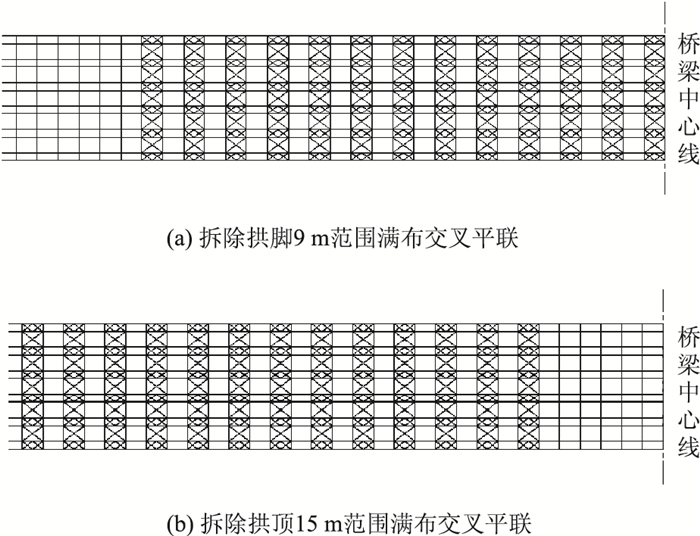
4.3 拱脚、拱顶部位平面联系布置图 8为贝雷拱架拱脚、拱顶部位满布交叉平联布置方案,图 9为拱脚、拱顶部位平面联系布置的弹性稳定安全系数。
|
| 图 8 贝雷拱架拱脚、拱顶部位满布交叉平联布置方案 Fig. 8 Layout schemes of full cross plane connection at foot and crown of Bailey arch centering |
| |

|
| 图 9 拱脚、拱顶部位平面联系布置的弹性稳定安全系数 Fig. 9 Elastic stability safety coefficients for plane connection layout at arch foot and arch crown |
| |
由图 9可以看出:
在工况2~4,拆除拱脚9 m范围平联、拆除拱顶15 m范围平联和不拆除平联的弹性稳定安全系数分别为2.281~2.994,3.415~4.481,4.516~5.936。这说明拆除拱脚部位平面联系对拱架稳定性的影响大于拱顶部位。拆除拱脚9 m范围平联、拆除拱顶15 m范围平联和不拆除平联的失稳模态分别为平面外反对称失稳、平面外对称失稳和平面内反对称失稳。
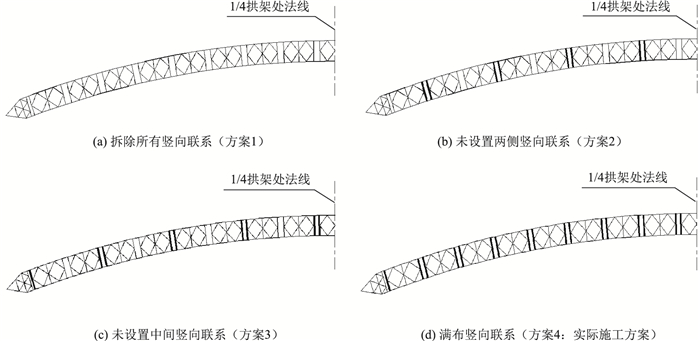
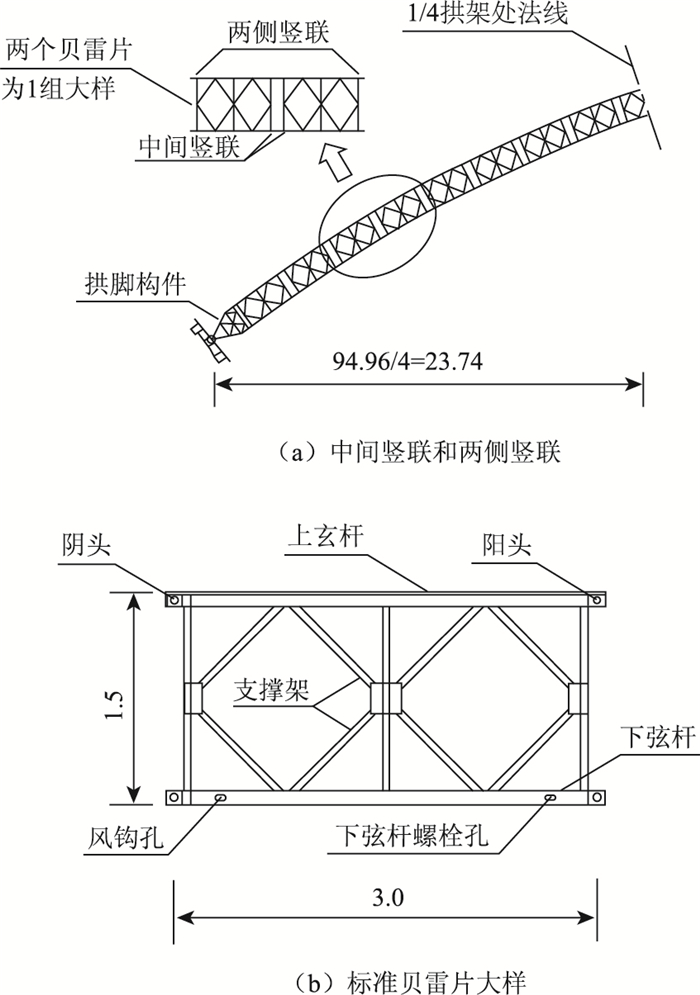
5 竖向联系布置对拱架稳定性的影响图 10为贝雷拱架中间竖联和两侧竖联示意,图 11为贝雷拱架竖向联系布置方案,图 12为竖向联系布置的弹性稳定安全系数。
|
| 图 11 贝雷拱架竖向联系布置方案 Fig. 11 Vertical connection layout of Bailey arch centering 注:1.因篇幅有限,对贝雷拱架竖向联系布置分析时,仅示意出1/4的拱架。2.为使图形清晰紧凑,将拱架适当旋转,图中黑色加粗为布置竖向联系的位置, 黑色淡显为不布置竖向联系的位置。 |
| |
|
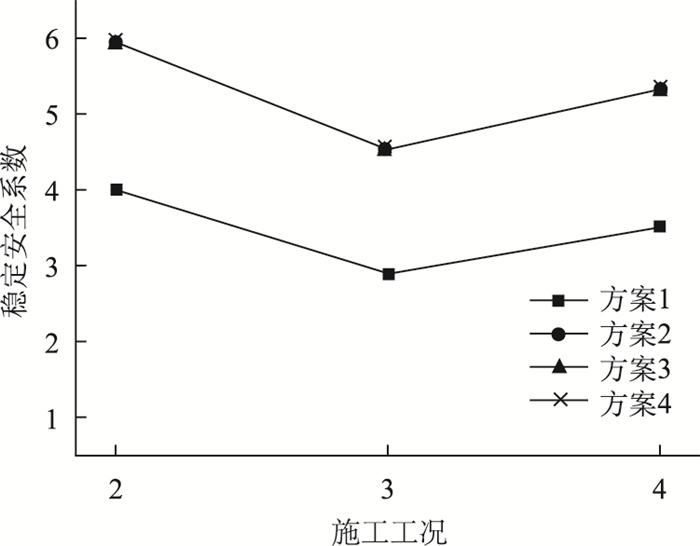
| 图 12 竖向联系布置的弹性稳定安全系数 Fig. 12 Elastic stability safety coefficients for vertical connection layout |
| |
|
| 图 10 贝雷拱架竖联示意(单位: m) Fig. 10 Schematic diagram of vertical connections of Bailey arch centering (unit: m) |
| |
|
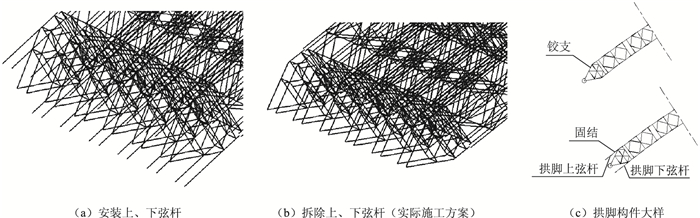
| 图 13 贝雷拱架的拱脚安装和拆除上、下弦杆布置方案 Fig. 13 Layout schemes of installing and removing upper and lower chords at arch foot of Bailey arch centering |
| |
由图 12可以看出:
(1) 在工况2~3,随着施工荷载逐渐增大,4种竖向联系布置的弹性稳定安全系数逐渐减小。
(2) 在工况2~4,方案1弹性稳定安全系数为2.899~4.002,不能满足《规范》要求。这是因为拆除拱架竖向联系后,横向刚度小,拱架平面外的稳定性较差,易发生扭转变形,失稳模态表现为平面外对称失稳。
(3) 在工况2~4,方案2~方案4的弹性稳定安全系数分别为4.521~5.931,4.519~5.921,4.526~5.936。方案2~方案4比方案1稳定系数增大约48%~56%,其均满足《规范》要求,但方案2~方案4之间差值较小。这是因为这3种方案增加了竖向联系,和上、下弦杆平面联系组成桁梁,仅改变拱架部分区域的竖向联系,对整体稳定性影响较小,但对应力均匀分布存在一定影响。
6 拱脚上、下弦杆对拱架稳定的影响由图 14可以看出:

|
| 图 14 拱脚安装和拆除上、下弦杆的弹性稳定安全系数 Fig. 14 Elastic stability safety coefficients for installing and removing upper and lower chords at arch foot |
| |
在工况2~4,拱脚安装上、下弦杆和拱脚拆除上、下弦杆的弹性稳定安全系数分别为6.467~8.495和4.526~5.936。这说明拱脚上、下弦杆对拱架稳定性影响较大,安装上、下弦杆比拆除上、下弦杆的拱架稳定系数增大约40%。
7 结论结合贵州某钢筋混凝土拱桥,对贝雷片间联系布置对箱型拱桥拱架稳定性的影响进行研究,得到如下结论:
(1) 在计算工况中,浇注拱圈底板、拱架预压试验和浇注拱圈腹板的施工荷载逐渐增大,拱架弹性稳定安全系数逐渐减小。
(2) 在浇注拱圈腹板、上下弦杆同步变化时,上、下弦杆未布置交叉平联的拱架弹性稳定系数为1.622。增加交叉平联布置后,弹性稳定安全系数为4.237,提高约161%,失稳模态为平面外对称失稳。在上、下弦杆布置交叉平联后,无论是增加标准交叉平联或异形交叉平联,弹性稳定安全系数为4.34~4.349,提高仅3%~4%,但失稳模态由平面外对称失稳变为平面内反对称失稳。对拱架稳定性的影响,在上、下弦杆均未布置交叉平联时,安装交叉平联影响较大;在上、下弦杆均已布置交叉平联后,增加交叉平联提高较小。
(3) 在浇注拱圈底板,上、下弦杆不同步变化时,仅拆除上弦杆标准、异形、满布交叉平联的弹性稳定安全系数分别为3.926,4.662,5.924;仅拆除下弦杆标准、异形、满布交叉平联的弹性稳定安全系数分别为5.89,5.904,5.924;仅拆除拱脚或拱顶局部范围的满布交叉平联的弹性稳定安全系数分别为2.281,3.451。对拱架稳定性的影响,拆除拱脚部位平面联系大于拆除拱顶部位,拆除上弦杆部位平面联系大于拆除下弦杆部位,拆除满布交叉平联大于拆除异形交叉平联,拆除异形交叉平联大于拆除标准交叉平联,合理优化拱顶部位的下弦杆标准交叉平联,对拱架稳定性影响最小。
(4) 在浇注拱圈腹板时,拱架未布置竖向联系的弹性稳定安全系数为2.899。增加竖向联系布置后,弹性稳定安全系数为4.519~4.526,提高约48%~56%。竖向联系和上、下弦平面联系组成的桁架提高了拱架稳定性。仅改变部分区域的竖向联系布置对拱架稳定性影响较小。
(5) 在浇注拱圈腹板时,拱脚安装上、下弦杆和拆除上、下弦杆的弹性稳定安全系数分别为6.647,4.526,降低约40%。拱脚上、下弦杆对拱架稳定性影响较大,在实际施工中,不建议因为施工工期、方便施工等原因,人为取消拱脚上、下弦杆,将无铰拱架变为两铰拱架,以避免不必要的工程风险。
| [1] |
刘健.拱桥现浇拱架施工过程对结构性能影响研究[D].重庆: 重庆交通大学, 2013. LIU Jian. Study on Effect of Construction Process of Cast-in-situ Arch Center of Arch Bridge on Structure Performance[D]. Chongqing: Chongqing Jiaotong University, 2013. |
| [2] |
FENG M R. Modern Bridges in China[J]. Structure and Infrastructure Engineering, 2014, 10(4): 429-442. |
| [3] |
郑皆连. 我国大跨径混凝土拱桥的发展新趋势[J]. 重庆交通大学学报:自然科学版, 2016, 35(增1): 8-11. ZHENG Jie-lian. New Development Tendency of Large-span Reinforced Concrete Arch Bridges in China[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2016, 35(S1): 8-11. |
| [4] |
朱莉, 卢斌, 张宏杰. 大跨度中承式钢筋混凝土拱桥施工技术[J]. 桥梁建设, 2006(增1): 39-41. ZHU Li, LU Bin, ZHANG Hong-jie. Construction Techniques for Long Span Reinforced Concrete Half-through Arch Bridge[J]. Bridge Construction, 2006(S1): 39-41. |
| [5] |
周水兴, 邓翔. 拱架现浇钢筋混凝土拱圈浇筑长度研究[J]. 重庆交通大学学报:自然科学版, 2013, 32(4): 569-572, 620. ZHOU Shui-xing, DENG Xiang. Casting Length of Cast-in-Place RC Arch Rib in Arch Centering[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2013, 32(4): 569-572, 620. |
| [6] |
周倩, 张策, 周水兴, 等. 分界点对混合拱桥受力影响研究[J]. 重庆交通大学学报:自然科学版, 2019, 38(1): 1-6. ZHOU Qian, ZHANG Ce, ZHOU Shui-xing, et al. Mechanical Influence of Boundary Point on Compound Arch Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2019, 38(1): 1-6. |
| [7] |
王藐民, 吴海军, 钱骥. 变截面劲性骨架钢筋混凝土拱桥外包混凝土过程中的线形控制方法[J]. 公路交通科技, 2017, 34(6): 106-113. WANG Miao-min, WU Hai-jun, QIAN Ji. An Alignment Control Method for CFST Framed Arch Bridge with Variable Cross-section during Pouring Externally Wrapped Concrete[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 106-113. |
| [8] |
向中富, 徐君兰, 王银辉, 等. 拱桥拱架施工过程中的结构行为分析[J]. 重庆交通大学学报:自然科学版, 2001, 20(增1): 17-22. XIANG Zhong-fu, XU Jun-lan, WANG Yin-hui, et al. Structural Analysis during the Course of Construction of Arch Bridge with the Aid of Centring[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2001, 20(S1): 17-22. |
| [9] |
杜斌, 江刚, 王学敏. 上承式钢筋混凝土拱桥拱架施工风险分析研究[J]. 施工技术, 2015, 44(增2): 180-182. DU Bin, JIANG Gang, WANG Xue-min. Analysis of Risk for Reinforced Concrete Deck-through Arch Bridge Falsework during Construction[J]. Construction Technology, 2015, 44(S2): 180-182. |
| [10] |
王永宝, 廖平, 贾毅, 等. 循环温度对大跨混凝土拱桥长期变形行为的影响[J]. 桥梁建设, 2019, 49(3): 57-62. WANG Yong-bao, LIAO Ping, JIA Yi, et al. Effects of Cyclic Temperature on Time-dependent Deformation Behavior of Long-span Concrete Arch Bridge[J]. Bridge Construction, 2019, 49(3): 57-62. |
| [11] |
蒋友宝, 罗军, 张建仁. 考虑偏心距随机特性的矩形和箱形截面混凝土拱桥可靠度分析[J]. 公路交通科技, 2015, 32(4): 78-82, 94. JIANG You-bao, LUO Jun, ZHANG Jian-ren. Analysis of Reliability of Rectangular Sectional and Box Sectional Concrete Arch Bridges Based on Random Eccentricity[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 78-82, 94. |
| [12] |
任为东. 三跨连续中承式拱桥结构受力性能研究[J]. 铁道标准设计, 2018, 62(11): 69-72. REN Wei-dong. Study on Mechanical Properties of Three-span Continuous Half-through Arch Bridge[J]. Railway Standard Design, 2018, 62(11): 69-72. |
| [13] |
刘家奎, 罗浩, 杜斌. 混凝土拱桥拱架法施工风险分析及对策[J]. 重庆交通大学学报:自然科学版, 2018, 37(5): 18-22. LIU Jia-kui, LUO Hao, DU Bin. Concrete Arch Bridge Construction Risk Analysis and Countermeasures[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2018, 37(5): 18-22. |
| [14] |
叶文亚, 卢照辉, 毛雨桥, 等. 基于PDS模块技术的钢筋混凝土拱桥可靠度计算[J]. 公路交通科技, 2014, 31(4): 73-77. YE Wen-ya, LU Zhao-hui, MAO Yu-qiao, et al. Reliability Calculation of RC Arch Bridge Based on PDS Module Technique[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 73-77. |
| [15] |
刘盼, 陈雁云. 钢桁架拱桥主拱提升系统的设计[J]. 公路交通科技, 2018, 35(增1): 110-114. LIU Pan, CHEN Yan-yun. Designing of Lifting System for Main Arch of Steel Truss Arch Bridge[J]. Journal of Highway and Transportation Research and Development, 2018, 35(S1): 110-114. |
| [16] |
秦世强, 李超, 康俊涛. 基于规范的蝶形拱桥试验冲击系数评估[J]. 公路交通科技, 2020, 37(2): 55-62. QIN Shi-qiang, LI Chao, KANG Jun-tao. Evaluation of Experimental Impact Coefficient of Butterfly Arch Bridge Based on Specifications[J]. Journal of Highway and Transportation Research and Development, 2020, 37(2): 55-62. |
| [17] |
李法雄, 聂建国, 王家忠, 等. 钢筋混凝土拱桥罕遇地震响应简化分析方法[J]. 公路交通科技, 2012, 29(3): 109-117. LI Fa-xiong, NIE Jian-guo, WANG Jia-zhong, et al. A Simplified Analysis Method for Reinforced Concrete Arch Bridge under Exceptionally Serious Earthquake[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 109-117. |
| [18] |
王桢, 吴海军, 周志祥, 等. 大跨径自锚式悬索桥吊索索力相邻影响分析[J]. 土木工程学报, 2016, 49(6): 51-60. WANG Zhen, WU Hai-jun, ZHOU Zhi-xiang, et al. Analysis on Near Influence of Cable Force in Large-span Self-anchored Suspension Bridges[J]. China Civil Engineering Journal, 2016, 49(6): 51-60. |
 2020, Vol. 37
2020, Vol. 37

 ,
,