扩展功能
文章信息
- 杨扬, 徐新扬
- YANG Yang, XU Xin-yang
- 基于博弈理论的甩挂运输企业联盟条件与合作演化研究
- Study on Conditions and Cooperative Evolution of Alliance of Trailer Pick-up Transport Enterprises Based on Game Theory
- 公路交通科技, 2020, 37(5): 140-148
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 140-148
- 10.3969/j.issn.1002-0268.2020.05.017
-
文章历史
- 收稿日期: 2019-03-20
甩挂运输是一种结合公路运输与甩挂技术的先进货物运输方式,并因其运输成本低、车辆实载率高以及绿色节能等优点在国际货物运输领域地位日益提高,在西方发达国家70%~80%的货物运输是以甩挂运输形式来进行的[1]。我国自2010年起大力发展甩挂运输,确定了150多家甩挂运输试点企业并对其给予试点补贴,虽然在国家的大力支持下我国甩挂运输方式得到了开展,涌现了一些甩挂运输强势企业[2],但由于我国道路发展的限制;甩挂运输企业组织化程度偏低,管理水平落后的现状;以及挂车所有权难以界定等问题,我国甩挂运输总体发展缓慢。为了解决这一现状,组建甩挂运输企业联盟成为了许多甩挂运输企业的选择,我国近两年来已成立了以武汉为中心的华中甩挂联盟、山东省甩挂联盟、江苏甩挂联盟以及辽鲁甩挂联盟等甩挂运输联盟[3]。但联盟后的收益是否符合预期以及甩挂运输企业选择联盟的条件与联盟后的合作演化趋势还需细致研究与探讨,本研究将通过博弈理论中的古诺模型以及囚徒困境模型对该问题进行研究。
国外发达国家从20世纪60年代便已开始发展甩挂运输,特别是对甩挂运输的路径优化研究颇为全面与深入。E.Zachariadis[4]等建立LDVRP模型并提出了一种局部搜索算法来研究甩挂运输车辆的路径问题。U Derigs[5]等讨论了特定情况下的RVRP问题并利用几种灵活的混合方法计算了甩挂运输中甩挂车与拖车的路线问题。M Drexl[6]通过描述并建立VRPMS模型来解决拖车与转运的车辆路径问题。J.Woxenius[7]等在铁路腹地运输的背景下比较了海运集装箱与半挂车运输,并通过对海德堡港与纳维亚腹地的实证研究得出铁路对于集装箱的腹地运输比半挂车更有竞争力的结论。O.R-Coundert[8]等提出了一种受到严格约束并使用时间窗口的动态路径优化模型,并利用苏格兰龙头运输公司真实数据模拟确定了方法的效率性与可靠性。随着甩挂运输在我国的大力发展,我国学者对甩挂运输的研究也日益深入。如王征宇[9]等利用收益管理的方法,通过分析不同模式的定价方式提出了一种新的挂车租赁定价方式。李红启[10]等通过构建LTDP问题的整数规划模型并通过实例计算得出干线甩挂运输模式具有良好节能减排效果的结论。李维[11]等将甩挂运输任务问题转化为TSP问题并建立数学模型对甩挂运输车辆的路径优化进行研究。梁世斌[12]等通过对甩挂运输企业运输条件的分析,建立了低成本的甩挂运输组织模式组合模型。国内外诸多学者运用博弈论相关知识对联盟进行了研究。P.Frackiewicz[13]等利用Li-Du-Massar量子双寡头研究Stackelberg博弈双头垄断方案,为博弈的均衡提供了完美的子博弈分析。A.Morreale[14]研究在随机和竞争环境中制药和生物技术公司面临的联盟实际权衡,通过实物期权博弈得出联盟时间结果与双方利用净现值评估收益结果相差很大的结论。A.Jakobik[15]等通过建立Stackelberg模型,模拟了典型的云安全场景并提出针对云安全威胁建模的防御方案。Susan L[16]等通过介绍物流联盟中关系量级的概念,并将物流联盟中成员的关系进行分类从而提供给物流联盟管理者启示并对未来研究提供依据。郭晓林[17]等通过建立囚徒困境模型分析了物流联盟稳定条件并提出建议。孙红霞[18]等建立演化博弈模型对新能源汽车补贴时代政府与企业关系进行博弈研究,分4种情景讨论并给出市场健康化建议。朱成娟[19]等构建了三层Stackelberg博弈模型对停车位的分配与定价做了细致研究。何伟[20]等建立合作博弈模型对不确定需求下物流企业的运输合作问题进行了研究。毕晨飞[21]运用古诺模型研究了网络游戏厂商之间竞争关系与联盟优化选择问题。
可以发现目前国外学者针对甩挂运输的研究集中于甩挂运输路径优化研究,国内学者对于甩挂运输路径的研究也有涉猎,更多的是对甩挂运输组织模式的探讨以及甩挂运输设施设备归属与成本优化的研究。同时可以发现国内外学者运用博弈理论针对联盟问题的分析已颇为深入,但对于甩挂运输企业联盟形成的机理和演化特征亟待进一步深入研究。甩挂运输作为一种高效率、低成本、科学有序的新型运输组织方式是我国物流改变现状,健康发展的一个最佳选择。由于国内大部分物流运输企业市场规模小以及甩挂设施设备价格高的现状,通过联盟经营解决发展困难成为了甩挂运输企业们共同的选择。本研究针对甩挂运输企业联盟问题运用博弈理论中古诺模型表达出甩挂运输企业单独经营业务与联盟经营业务的收益,通过对两种情形下收益的差异分析得出甩挂运输企业进行联盟的条件,再运用囚徒困境模型模拟出甩挂运输企业联盟后可能的合作演化趋势。
1 收益模型的假设与建立假设在一双寡头甩挂运输市场竞争区域存在甩挂运输企业A与甩挂运输企业B,两家甩挂运输企业均从个人利益出发坚持选择最优收益,在经营过程中会出现单独经营与联盟经营两种情形。
1.1 基本参数与公式假设单独经营情形:两家甩挂运输企业各自经营自身业务,相互存在竞争关系,我们假设S1为企业A投入市场的甩挂运力,S2为企业B投入市场的甩挂运力,P1为企业A单位运力下的甩挂运输价格,C1为企业A运营成本,C2为企业B运营成本,d1与d2为两企业单位运力对甩挂设施设备的维护费用,e1与e2为两企业各自运力下购置甩挂运输设施设备的费用。其中C=d+e。P1为企业A单位运力下的甩挂运输价格,P2为企业B单位运力下的甩挂运输价格。由于此时两企业存在竞争,为了方便分析,我们采用常用的线性反需求函数[22]作为甩挂运输企业单位运力下的甩挂运输价格表达式:
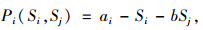
|
(1) |
式中,ai为两家甩挂运输企业潜在的市场规模;b为两家甩挂运输企业之间甩挂运输业务的替代程度,0 < b < 1。
联盟经营情形:当两家甩挂运输企业联盟经营业务后,假设联盟总投入市场运力为S3,P3为两甩挂运输企业联盟后单位运力甩挂运输价格。联盟后企业A获得的利润分配比例为λa,企业B获得的利润分配比例为λb。C3联盟运营成本。在我国大力发展甩挂运输的背景下以及已有联盟的经营可知当企业组成甩挂联盟时可获得政府补贴f,同时也需要对甩挂运输企业联盟进行投资g。由于在双寡头竞争区域内两寡头选择合作联盟,因此我们使用典型市场反需求函数作为联盟后单位运力甩挂运输价格表达式:
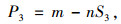
|
(2) |
式中m, n为单位运力甩挂运输价格与需求运力之间逆需求反函数的两个参数,m>0, n>0。
1.2 单独经营时收益模型根据前文假设,结合古诺博弈模型,我们可以构建出两个甩挂运输企业单独经营时的收益模型:
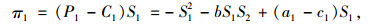
|
(3) |
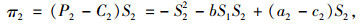
|
(4) |
式中π1,π2分别为甩挂运输企业A与甩挂运输企业B在单独经营业务下的利润。
式(1)对S1求一阶导得:
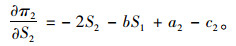
|
(5) |
令式(3)为0得:
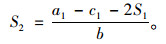
|
(6) |
对(1)式求二阶导得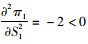
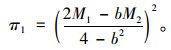
|
(7) |
式(4)对S2求一阶导得:
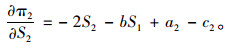
|
(8) |
将式(6)代入式(8)并令其为0可得:
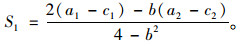
|
(9) |
设M1=a1-c1,M2=a2-c2,并将式(9)代回(6),(7)式可得:
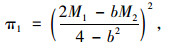
|
(10) |
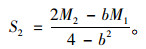
|
(11) |
将式(9),(11)式代回式(3)可得:
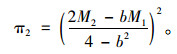
|
(12) |
综上所述可得A,B企业在单独经营业务所获利润最大时的投入运力,单位运力下甩挂运输价格,如表 1所示。
| 最优利润 | 企业A | 企业B |
| 企业投入运力 | 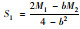 |
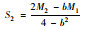 |
| 单位运力甩挂运输价格 | 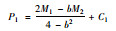 |
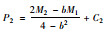 |
| 企业利润 | 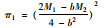 |
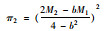 |
1.3 联盟经营时收益模型
当在双寡头市场下甩挂运输企业联盟形成时,由于竞争消失,所以使用典型价格反需求函数P3=m-nS3作为单位运力下甩挂运输价格的表达式,可得联盟后甩挂运输企业联盟总利润:
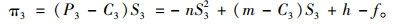
|
(13) |
对式(13)求一阶导,并令其为0可得:
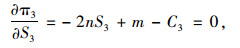
|
(14) |
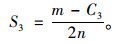
|
(15) |
因为式(13)的二阶导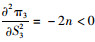
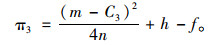
|
(16) |
由两甩挂运输企业形成联盟后的利润分配系数λa,λb可得联盟经营时两企业的各自收益π3A,π3B的值:
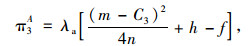
|
(17) |
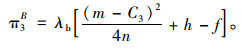
|
(18) |
综上所述可得联盟经营后的各企业所获利润最大时的投入运力,单位运力下甩挂运输价格,如表 2所示。
| 最优利润 | 企业A | 企业B |
| 联盟投入运力 | 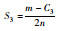 |
|
| 单位运力甩挂运输价格 | 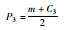 |
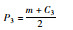 |
| 企业利润 | 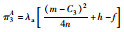 |
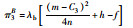 |
1.4 单独经营与联盟经营的比较
本部分将分析甩挂运输企业进行联盟的可行性,若双方都愿意联盟,那么联盟的条件是什么,通过比较甩挂运输企业在单独经营与联盟经营之间的利润差异,分析甩挂运输企业联盟经营的条件。
若企业A倾向于联盟经营,则π3A>π1:
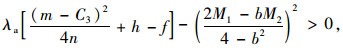
|
(19) |
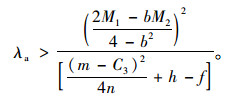
|
(20) |
若企业B倾向于联盟经营,则π3B>π2:
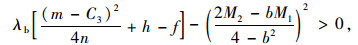
|
(21) |
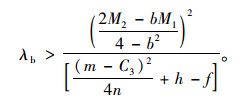
|
(22) |
因此可以得到甩挂运输企业A与企业B选择联盟经营的基本条件是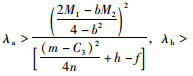
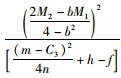
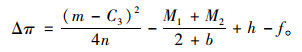
|
(23) |
由式(23)显而易见可知当h增大时,Δπ的值增加,当f增大时Δπ的值减小,即政府对甩挂运输联盟的补贴对联盟的组成具有促进作用,成立联盟所需要的额外投资对甩挂运输企业联盟的成立有抑制作用。
式(23)对b求一阶导得:
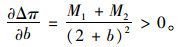
|
(24) |
由式(24)可知参数b与Δπ变化趋势成正比,当b增加时,Δπ增加;b减小时,Δπ减小。这表明当甩挂运输企业A与企业B相互之间甩挂运输替代度越高,相互之间业务竞争越激烈,则两企业越趋向于联盟经营。
式(23)对M1,M2求一阶导得:
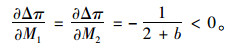
|
(25) |
由式(25)可知M1,M2的值与Δπ变化趋势成反比,当M1,M2增加时,Δπ减小;M1,M2减小时,Δπ增加。因M1=a1-c1,M2=a2-c2。可知当甩挂运输企业独自经营时的潜在市场规模较小,运营成本较大的一方,越主动趋向于联盟经营; 潜在市场规模较大,运营成本较小的的一方更趋向于独自经营。当市场规模悬殊较大的两甩挂运输企业若要联盟,市场规模大的一方往往抗拒联盟,因为联盟后对自己的收益不大但是却令市场规模较小的甩挂运输企业利润剧增。同时由前文假设C=d+e,可知甩挂运输设施设备的维护价格与甩挂设施设备的购置成本压力使得甩挂运输企业倾向于联盟经营业务。
2 甩挂运输企业联盟合作演化趋势上部分研究利用博弈理论中的古诺模型对独自经营与联盟经营甩挂运输企业收益进行了对比,并分析了甩挂运输企业选择联盟经营的基本条件,单纯从收益差对企业是否联盟进行研究,但现实中的联盟往往伴随着风险的存在,联盟内成员为了投机主义而主动破裂联盟对联盟内其他成员造成的损失可能更大。特别是潜在市场规模相差较大的两甩挂运输企业,规模小的企业在窃取了规模大的企业内部机密与技术优势后主动破裂联盟使自己利益剧增,对原本市场规模较大甩挂运输企业造成巨大损失。针对这一问题我们建立囚徒困境模型对联盟内甩挂运输企业成员不同决策造成的合作演化趋势进行研究。
2.1 囚徒困境模型的建立当双寡头市场中的甩挂运输企业A与企业B联盟后,他们拥有继续合作联盟以及主动破裂联盟两种决策。假设当企业A选择合作企业B也选择合作即(合作,合作)时,两企业可获得的收益都为6。当企业A选择合作企业B选择破裂即(合作,破裂)时,企业B因投机主义因而获得比两方合作时更高的收益10,企业A因企业B的投机主义而产生损失只能得到收益2;反之当企业A选择破裂企业B选择合作即(破裂,合作)时,企业A获得的收益为10,企业B获得的收益为2。最后当企业A与企业B均选择破裂联盟即(破裂,破裂)时,双方获得的收益都为4。支付矩阵见表 3。
| A | B | |
| 破裂 | 合作 | |
| 破裂 | 4, 4 | 10, 2 |
| 合作 | 2, 10 | 6, 6 |
观察表中数据我们可以发现,当企业A选择破裂时,企业B要想获得最大收益也需要选择破裂,当企业A选择合作时,企业B为获得更大收益还是会选择破裂。可以发现在单次合作中企业都会因占优战略而放弃合作,因此在单次囚徒困境博弈中合作难以实现,现实中的博弈往往要进行很多次,合作的一个关键特性就是博弈的重复性。我们现在理想的不考虑其他因素令囚徒困境博弈重复n次,并引入“及时止损”策略。“及时止损”策略在首次合作中均会选择合作,若在第一次合作中“及时止损”策略碰到合作策略时,双方会一直合作下去;若在第一次合作中碰到破裂策略时,“及时止损”策略会在接下来(n-1)次合作中一直保持破裂策略。当破裂者与“及时止损”者相遇时,第一次博弈中“及时止损”者选择合作获得收益2,破裂者选择破裂策略获得收益10,之后双方都采取破裂策略,都得到(n-1)×4的收益,因此“及时止损”者的收益为2+(n-1)×4=4n-2,破裂者的收益为10+(n-1)×4=4n+6,如表 4博弈。
| A | B | ||
| 破裂 | 合作 | 及时止损 | |
| 破裂 | 4n,4n | 10n,2n | 4n+6, 4n -2 |
| 合作 | 2 n,10n | 6 n,6n | 6 n,6n |
| 及时止损 | 4 n-2,4 n+6 | 6 n,6 n | 6 n,6 n |
将由两家甩挂运输企业组成的联盟引申为由若干甩挂运输企业所组成的联盟。假设联盟内的若干企业成员有合作、破裂、及时止损3种选择。设在m代中,PAm表示群体中合作者的比例,PBm表示群体中“及时止损”者的比例,PCm=(1-PAm-PBm)表示破裂者的比例。我们可以算出每种策略得到的平均适应值:
合作者的平均适应值:PAm×6n+PBm×6n+PCm×2n;
及时止损者的平均适应值:PAm×6n+PBm×6n+PCm×(4n-2);
破裂者的平均适应值:PAm×10n+PBm×(4n+6)+PCm×4n。
将PCm替换为(1-PAm-PBm)并简化表达式,得到:
合作者的平均适应值:PAm×4n+PBm×4n+2n;
及时止损者的平均适应值:PAm×(2n+2)+PBm×(2n+2)+4n-2;
破裂者的平均适应值:PAm×6n+PBm×6+4n。
接下来对3种不同的策略进行比较研究,首先令及时止损者的平均适应值大于合作者的平均适应值(n>1):
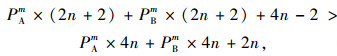
|
(26) |
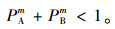
|
(27) |
通过结果PAm+PBm<1可以知道,当合作者的比例与及时止损者的比例小于1时,即群体中存在背叛者的时候,“及时止损”策略优于合作策略,如果不存在背叛者,则“及时止损”策略与合作策略得到的适应值相同。
令及时止损者的平均适应值大于破裂者的平均适应值(n>2):
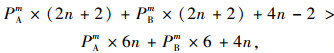
|
(28) |
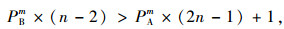
|
(29) |
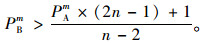
|
(30) |
通过结果可知当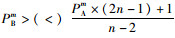
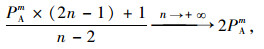
|
(31) |
即PBm>2PAm。
因此可以得到结论:当联盟内合作一直持续下去趋向无限次时,要想让“及时止损”策略收益大于破裂策略收益,及时止损者的比例需大于合作者比例的两倍,不同的数据可能会导致具体计算倍数不同,但总的趋势可以发现“及时止损”策略收益大于破裂策略收益的条件是“及时止损”策略不能太小,需多于合作者的数量。同时不能有太多合作者,尽管及时止损者与合作者合作,但合作者为破裂者得到更高的适应值提供了机会。
令合作者的平均适应值大于破裂者的平均适应值:
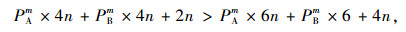
|
(32) |
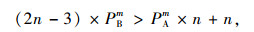
|
(33) |
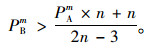
|
(34) |
通过结果可知当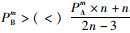
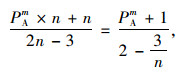
|
(35) |
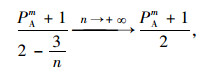
|
(36) |
即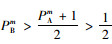
因此可以得出结论:当甩挂运输企业联盟内合作一直持续下去趋向无限次时,要想让合作者收益大于破裂者的收益,合作者的比例要很小,同时破裂者的比例需高于总比例的一半。同样的,由于不同数据得出的结果不同,但我们可以总结出联盟内部关系趋势。要想让合作者收益大于破裂者的收益,及时止损者的比例不能太少,因为当遇到及时止损者时,合作者得到的适应值要高于破裂者得到的适应值,合作者的比例要非常小,因为合作者为背叛者得到更高的适应值提供了机会。
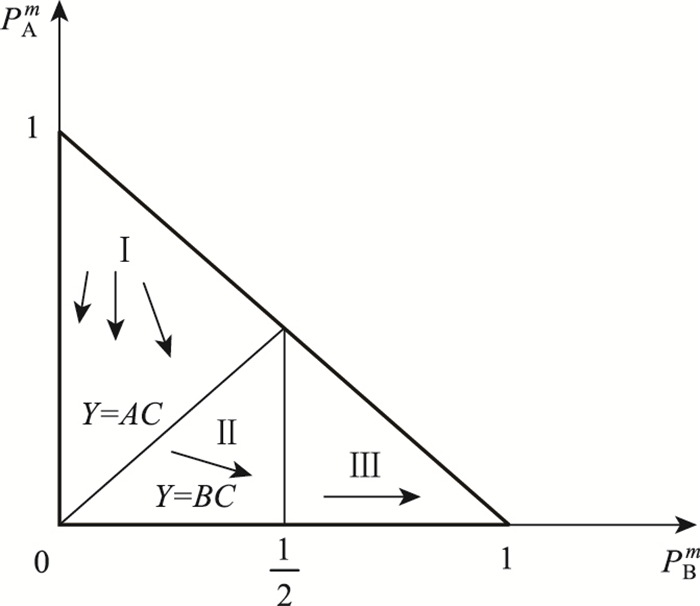
2.2 甩挂运输企业联盟内合作演化趋势分析通过运用囚徒困境模型对甩挂运输企业联盟内成员间相互合作的重复博弈研究,我们可以发现要想让联盟稳定,最完美的情况就是联盟内不存在破裂者。若在破裂者存在的情况下,那么及时止损者与合作者的平均适应值需大于破裂者的平均适应值,这时就要求在甩挂运输企业联盟内的成员选择“及时止损”策略的数量不能太小,需要比选择合作策略的成员数量多,同时不能有太多合作者,因为尽管及时止损者与合作者合作,但是合作者为破裂者得到更高的适应值提供了机会。又或者在甩挂运输企业联盟内的成员选择“及时止损”策略的比例不能太少,因为当遇到及时止损者时,合作者得到的适应值要高于破裂者所得到的适应值,同时合作者的比例不能太大,因为背叛者可以在合作者那里得到更高的适应值。可做出图 1相图来描述上述分析。
|
| 图 1 甩挂运输企业联盟内重复合作博弈趋势 Fig. 1 Repeated cooperative game trend in trailer pick-up transport enterprise alliance |
| |
如图 1所示,PBm横轴上的截距1表示联盟中都是及时止损策略者;PAm竖轴上的截距1表示联盟中都是合作策略者,因此原点0就表示联盟中都是破裂策略者。经过上文推导可知当合作者的平均适应值大于破裂者的平均适应值时,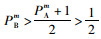
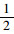
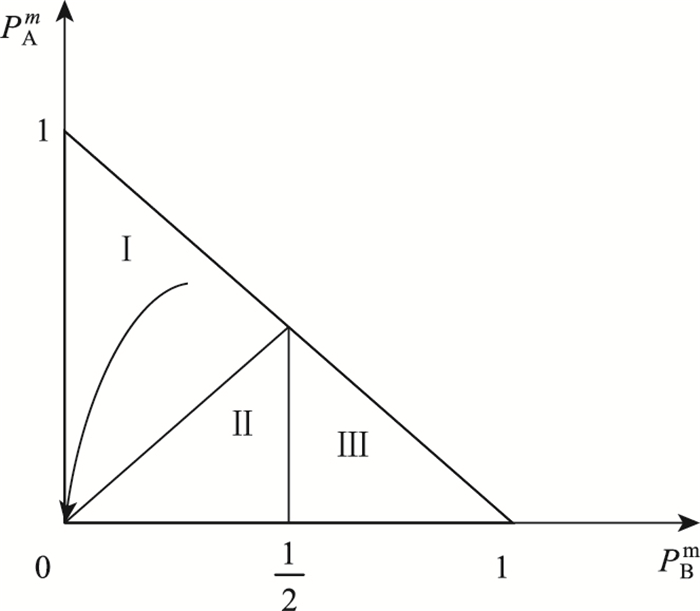
假设在甩挂运输企业联盟刚开始时只有少数成员被赋予了及时止损策略,那么破裂者将会获得最高的平均适应值,因为无论是在与合作者还是与破裂者的博弈当中,及时止损者的平均适应值都低于破裂者的平均适应值;只有在与及时止损者的博弈中,及时止损者的平均适应值高于破裂者的平均适应值,但由于此时联盟内只有少数及时止损者,因此联盟内合作者与及时止损者都将会被破裂者所淘汰,联盟也将破裂。通过图 2相位图可以描述此结论。
|
| 图 2 联盟中较少企业选择及时止损策略时合作趋势 Fig. 2 Cooperation trend when fewer enterprises choosing stop-loss strategy timely in alliance |
| |
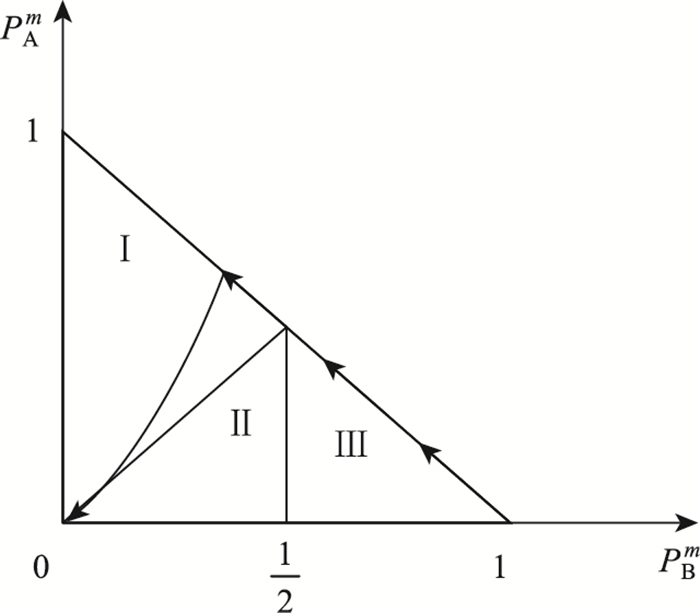
假设甩挂运输企业联盟内有很多合作者,那么合作者将会被破裂者所淘汰。假设联盟内有很多及时止损者,合作者很少时,因为及时止损者与及时止损者之间的博弈为合作博弈,此时合作者便会出现,随着合作者的增加,当增加到一定程度时,即增加到相图的第Ⅰ象限中时,联盟内有一定几率出现投机主义的破裂者,突变出破裂策略,这时的破裂者便会淘汰所有合作者,从而成为联盟内主导策略,联盟也将走向破裂。通过图 3相位图我们可以直观看出此结论。
|
| 图 3 联盟中大部分企业选择及时止损策略时合作趋势 Fig. 3 Cooperation trend when most enterprises choosing stop-loss strategy timely in alliance |
| |
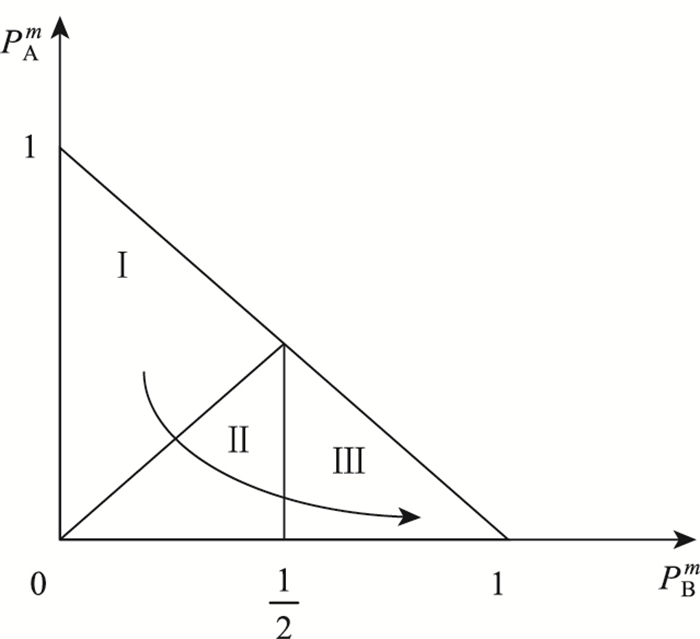
假设在甩挂运输企业联盟内有足够采取及时止损策略的成员,只有极少部分成员采取合作策略,及时止损者有足够可以合作的成员,可以继续采取及时止损策略,及时止损者在增加,极少数的合作者被破裂者欺负数量越来越少,联盟内环境越来越适合及时止损者,对破裂者越来越不适宜。当进入相图第Ⅱ象限后,及时止损者的平均适应值最大,合作者继续减少;当进入第Ⅲ象限时,及时止损者的平均适应值最大,破裂者的适应值最低,因为合作者越来越少了,这时的联盟也逐渐趋于稳定。通过图 4相位图可以描述此结论。
|
| 图 4 联盟中足够企业及时止损且极少部分企业选择合作策略的合作趋势 Fig. 4 Cooperation trend when enough enterprises stopping loss timely and few enterprises choosing cooperation strategy |
| |
通过对甩挂运输企业联盟内成员不同选择的囚徒困境重复博弈研究,发现选择合作策略永远得不到最高的平均适应值,这里需要注意的是只有在与背叛者博弈时,才能区分出合作者与及时止损者,因为及时止损者在与合作者博弈时也呈现合作策略,合作只有在一定条件下才可以稳定。要想达到联盟向稳定趋势发展,则需要在联盟时有足够成员被赋予及时止损策略,但当联盟趋于及时止损占多数的稳定时,又会出现如第2种假设中所分析的爆发合作突变策略,导致合作者增多,也会出现投机主义的破裂者再次分裂联盟。
3 结论针对甩挂运输企业联盟问题进行了博弈研究,运用了古诺博弈模型分析了影响甩挂运输企业进行联盟经营的因素,并得出甩挂运输企业联盟成立的基本利润分配比例。再运用囚徒困境模型对于联盟后存在的背叛风险而导致的联盟内不同合作演化趋势进行了分析。从研究结果来看,当甩挂运输企业之间甩挂运输业务替代度越大,即竞争越激烈时,甩挂运输企业倾向于联盟经营业务,同时甩挂运输的运营成本也影响着甩挂运输企业的经营决策。如果成立联盟后能减轻甩挂运输设施设备购置与维护成本,将会促进甩挂运输企业成立联盟经营业务。独自经营业务时潜在市场规模的大小也决定着甩挂运输企业是否联盟的决策,研究表明独自经营时潜在市场规模的大小与甩挂运输企业成立联盟的意愿成反比,市场规模越大越不愿意联盟,规模越小的企业越趋向于联盟,这是由于联盟对于市场规模大的企业利润增加并不明显,反而扶持了市场规模小的企业,令自己的寡头优势消失。成立联盟后由于投机风险的存在,特别是市场规模差异较大的企业间联盟时会导致联盟稳定性不足,运用囚徒困境对甩挂运输联盟内各企业不同抉择进行博弈,并分析出合作演化趋势,可知要想让联盟趋于稳定,则需要及时止损者的数量足够多,同时还要存在少数合作者,同时还要对合作者增多时的突变破裂策略进行提防。
通过本研究可知在组成甩挂运输企业联盟时要尽量寻找甩挂运输与企业规模相差不大的对象进行联盟,当市场规模相差较大时市场规模较大的企业往往抗拒联盟。同时组成联盟后联盟应采取措施降低甩挂运输设施设备的购置与维护成本,如寻求购车折扣,联盟内建立甩挂设施设备循环使用系统,建立联盟甩挂运输站场等。成立联盟后各甩挂运输企业应相互信任,共同受益,避免因信任危机产生的联盟破裂情形,同时要具备一定的防范意识,在联盟内某一成员为了更高的投机收益而选择破裂联盟时,要及时终止合作,及时止损以避免后续更大的损失。
| [1] |
LYRIDIS D V, FYRVIK T, KAPETANIS G N. Optimizing Shipping Company Operations using Business Process Modelling[J]. Maritime Policy & Management, 2005, 32(4): 403-420. |
| [2] |
白璟, 陈方建. 甩挂运输-绿色高效的运输方式[J]. 物流技术, 2011(2): 37-38. BAI Jing, CHEN Fang-jian. Drop-and-pull Transport:Green and Efficient Transport[J]. Logistics Technology, 2011(2): 37-38. |
| [3] |
刘光琦. 联盟-甩挂运输的中国式发展[J]. 中国储运, 2015(2): 52-56. LIU Guang-qi. Alliance:Chinese-style Development of Drop-and-pull Transport[J]. China Storage and Transport, 2015(2): 52-56. |
| [4] |
ZACHARIADIS E E, TARANTILIS C D, KIRANOUDIS C T. The Load-dependent Vehicle Routing Problem and Its Pick-up and Delivery Extension[J]. Transportation Research Part B:Methodological, 2015, 71: 158-181. |
| [5] |
DERIGS U, PULLMANN M, VOGEL U. Truck and Trailer Routing:Problems, Heuristics and Computational Experience[J]. Computers & Operations Research, 2013, 40(2): 536-546. |
| [6] |
DREXL M. Applications of the Vehicle Routing Problem with Trailers and Transshipments[J]. European Journal of Operational Research, 2013, 227(2): 275-283. |
| [7] |
WOXENIUS J, BERGQVIST R. Comparing Maritime Containers and Semi-trailers in the Context of Hinterland Transport by Rail[J]. Journal of Transport Geography, 2011, 19(4): 680-688. |
| [8] |
REGNIER-COUDERT O, MCCALL J, AYODELE M. Truck and Trailer Scheduling in a Real World, Dynamic and Heterogeneous Context[J]. Transportation Research Part E:Logistics & Transportation Review, 2016, 93: 389-408. |
| [9] |
王征宇, 任建伟. 租赁式甩挂运输挂车租赁价格定价机制研究[J]. 公路交通科技, 2018, 35(1): 142-148. WANG Zheng-yu, REN Jian-wei. Study on Trailer Rent Pricing Mechanism for a Rental Mode of Trailer Pick-up Transport[J]. Journal of Highway and Transportation Research and Development, 2018, 35(1): 142-148. |
| [10] |
李红启, 常馨玉, 朱晓宁. 城际干线甩挂运输的公路牵引车调度问题及其求解[J]. 公路交通科技, 2016, 33(2): 151-158. LI Hong-qi, CHANG Xin-yu, ZHU Xiao-ning. Intercity Line-haul Tractor Dispatching Problem in Trailer Pick-up Transport and Its Solving Method[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 151-158. |
| [11] |
李维, 成耀荣, 吴百珂. 基于甩挂运输组织的车辆路径优化[J]. 物流科技, 2017, 40(3): 77-80. LI Wei, CHENG Yao-rong, WU Bai-ke. Optimization for Vehicle Routing Based on Truck-trailer Transportation[J]. Logistics Sci-Tech, 2017, 40(3): 77-80. |
| [12] |
梁世斌, 胡景福. 基于最低成本的甩挂运输组织方式优化分析[J]. 内蒙古公路与运输, 2018(4): 53-56. LIANG Shi-bin, HU Jing-fu. Optimization Analysis of Drop-and-Hook Transportation Organization Mode Based on Lowest Cost[J]. Highways & Transportation in Inner Mongolia, 2018(4): 53-56. |
| [13] |
FRCKIEWICZ P, PYKACZ J. On Subgame Perfect Equilibria in Quantum Stackelberg Duopoly[J]. Physics Letters A, 2018, 382(8): 561-565. |
| [14] |
MORREALE A, ROBBA S, LO NIGRO G. A Real Options Game of Alliance Timing Decisions in Biopharmaceutical Research and Development[J]. European Journal of Operational Research, 2017, 261: 1189-1202. |
| [15] |
JAKOBIK A, PALMIERI F, KOŁODZIEJ J. Stackelberg Games for Modeling Defense Scenarios Against Cloud Security Threats[J]. Journal of Network and Computer Applications, 2018, 110: 99-107. |
| [16] |
GOLICIC S L, FOGGIN J H, MENTZER J T. Relationship Magnitude and Its Role in Interorganizational Relationship Structure[J]. Journal of Business Logistics, 2003, 24(1): 57-75. |
| [17] |
郭晓林, 贺盛瑜. 囚徒困境情形下物流联盟的稳定性分析[J]. 软科学, 2005, 19(1): 34-35. GUO Xiao-lin, HE Sheng-yu. The Analyses on the Stability of logistic Alliance under the Condition of Prisoners Dilemma[J]. Soft Science, 2005, 19(1): 34-35. |
| [18] |
孙红霞, 吕慧荣. 新能源汽车后补贴时代政府与企业的演化博弈分析[J]. 软科学, 2018, 32(2): 24-29. SUN Hong-xia, LÜ Hui-rong. Evolutionary Game Analysis between Government and Enterprise in New Energy Vehicles Market under New Subsidy Policy[J]. Soft Science, 2018, 32(2): 24-29. |
| [19] |
朱成娟, 贾斌, 韩凌辉. 基于Stackelberg博弈的停车位分配与定价[J]. 交通运输系统工程与信息, 2015, 15(3): 19-24. ZHU Cheng-juan, JIA Bin, HAN Ling-hui. Parking Space Allocation and Pricing Based on Stackelberg Game[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(3): 19-24. |
| [20] |
何伟, 徐福缘. 不确定需求下物流企业运输合作博弈模型研究[J]. 交通运输系统工程与信息, 2013, 13(5): 22-29. HE Wei, XU Fu-yuan. Game Model of Enterprises' Logistics and Transport Cooperation with Uncertain Demands[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(5): 22-29. |
| [21] |
毕晨飞. 基于古诺模型的我国网络游戏厂商横向兼并与联盟优化选择[J]. 哈尔滨商业大学学报:社会科学版, 2008(4): 123-126. BI Chen-fei. The Optimal Choose between the Mergers and Allies of Our Online Game Firms Based on Cournot Model[J]. Journal of Harbin University of Commerce:Social Science Edition, 2008(4): 123-126. |
| [22] |
TREMBLAY C H, TREMBLAY V J. The Cournot-Bertrand Model and the Degree of Product Differentiation[J]. Economics Letters, 2011, 111(3): 233-235. |
 2020, Vol. 37
2020, Vol. 37
