扩展功能
文章信息
- 周建, 杨新安, 蔡键, 杨帆
- ZHOU Jian, YANG Xin-an, CAI Jian, YANG Fan
- 深埋复合式衬砌隧道二衬分担比研究
- Study on Secondary Lining Sharing Ratio for Deep-buried Composite Lining Tunnel
- 公路交通科技, 2020, 37(5): 92-99
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 92-99
- 10.3969/j.issn.1002-0268.2020.05.011
-
文章历史
- 收稿日期: 2019-03-20
2. 浙江温州沈海高速公路有限公司, 浙江 温州 325000
2. Zhejiang Wenzhou Shenhai Expressway Co., Ltd., Wenzhou Zhejiang 325000, China
复合式衬砌是矿山法施工隧道主要采用的支护方式,初期支护(简称初支)和二次衬砌(简称二衬)是复合式衬砌的主要组成部分[1-3]。一般情况下,初支基本稳定后施加二衬,当初支具备一定强度后,初支将一部分围岩压力转移至二衬,形成“围岩+初支+二衬”的复合式承载结构。然而,关于二衬承担围岩压力的比例(二衬分担比)至今存在诸多疑惑。
在隧道设计过程中,二衬分担比对隧道支护参数的选择具有直接影响,长期以来二衬分担比均通过实测数据确定,如房倩等[4]通过对铁路隧道6个不同断面初支、二衬间接触压力的监测,得到在一定条件下初支和围岩承担全部荷载、二衬作为安全储备的结论;孙毅等[5]将监测结果与数值模拟结果进行对比分析,发现实测的铁路隧道二次衬砌受载量远小于其承载极限能力;何本国等[6]对深埋铁路隧道现场支护结构荷载量测试验,得出二衬作为重要支护形式平均分担50.1%荷载的结论;Prof[7]指出:喷射混凝土与二衬复合体视为承受全部荷载的永久支护;刘善琪[8]采集齐岳山隧道3个断面的围岩与初支、初支与二衬之间的压力,得到二衬最大承受30%左右的压力;田鹏[9]依托兰新铁路第二双线大梁隧道,得到二次衬砌围岩压力分担比例平均值在45.0%~70.3%的结论。上述学者根据依托工程实例监测数据,得到各自的二衬分担比,然而监测数据仅对所建工程服务,故不能作为指导工程实践的依据。刘学增等[10]基于山岭公路隧道围岩压力的监测数据,得到不同级别围岩二衬分担比,但研究内容仅限于山岭公路隧道,存在局限性;李鹏飞等[11]根据围岩压力监测数据,得到围岩压力的分布规律,但难以预测隧道二衬分担围岩压力的比值;所以,关于能够指导工程实践的隧道二衬分担比的建议值有待进一步研究。
2010版《公路隧道设计细则》(JTG/T D70—2010)[12]和2016版《铁路隧道设计规范》(TB1003—2016)[13]均认为Ⅰ~Ⅲ级围岩二衬可作为安全储备,而Ⅳ级及以上等级围岩《公路隧道设计细则》(JTG/T D70—2010)仅给出双车道二衬分担比建议值,《铁路隧道设计规范》(TB1003—2016)提出二衬根据地质情况宜按荷载结构设计,两种主流隧道规范未能明确给出Ⅳ级及以上软弱围岩二衬分担比建议值。本研究认为在隧道工程建设所处地质条件越来越复杂的新形势下,Ⅳ级及以上软弱围岩二衬分担比建议值有待完善。
本研究根据深埋隧道围岩与初支、初支与二衬的监测数据,列出了不同围岩级别隧道断面围岩压力随埋深、跨度变化的分布散点,并与经验公式计算值对比,探究经验公式的适用性;另外,探讨了不同围岩级别隧道的二衬分担比分布区间,运用“叠合梁”理论与实测数据的二衬分担比进行对比分析,并对“叠合梁”理论的适用性作出评价。
1 初支与二衬荷载的传递机理现阶段,关于二衬分担比理论方面研究十分有限,仅有“叠合梁”理论来分析初支与二衬荷载之间的关系,部分研究成果均有提及[14-16],但尚未通过大量实测数据来证明该理论的适用性。
文献[17]研究根据复合式衬砌特点,初支结构几乎通过径向传力于二衬结构,从而使得初支与二衬组成“叠合梁”式结构,提出了初支荷载传递至二衬的理论方法,并作出如下假定:(1)初支与二衬为圆形梁单元并紧密贴合;(2)复合式衬砌所受外力为均布压力。“叠合梁”力学模型如图 1所示,图中r0,r1和r2分别为隧道、初支内边缘和二衬内边缘的等效半径。
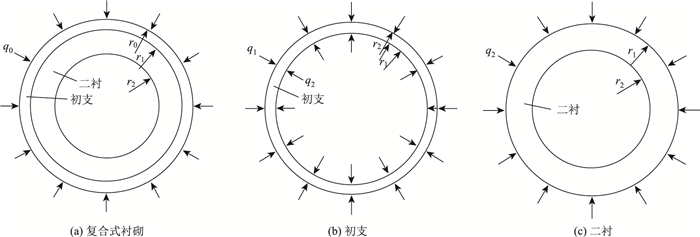
|
| 图 1 “叠合梁”结构力学模型 Fig. 1 Structural mechanical model of "composite beam" |
| |
在大多数情况下,隧道洞室断面为非圆形,本研究整理的隧道断面形状为马蹄形或直墙拱形,在计算洞室塑性区半径时通常将非圆形断面按某种标准等效成圆形断面,对于马蹄形和直墙拱形断面常采用外接圆半径法,如图 2所示。图中实线为断面真实的形状,虚线为等效圆的形状。
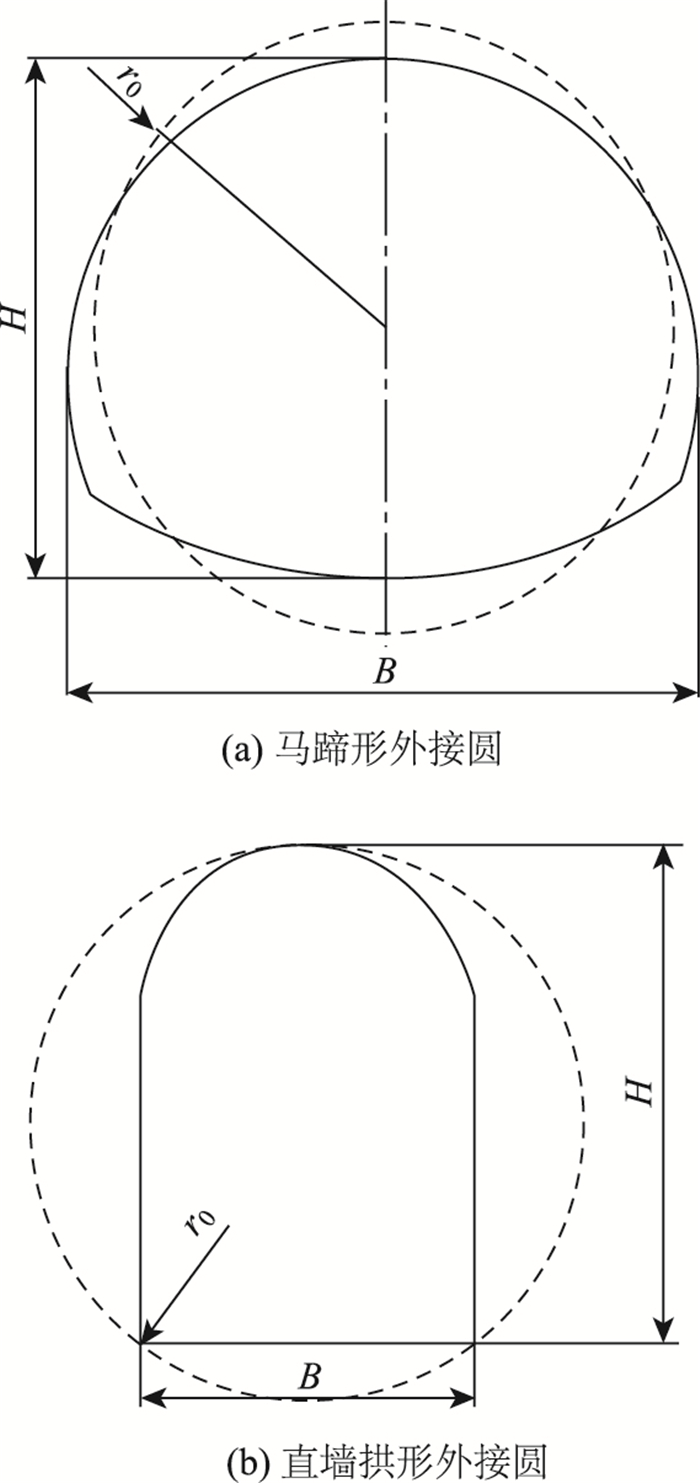
|
| 图 2 外接圆半径法示意图 Fig. 2 Schematic diagram of circumscribed radius method |
| |
文献[18]指出:高跨比在0.8~1.25之间的隧道其等效圆计算半径可以参考以下公式:
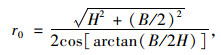
|
(1) |
式中,H,B分别为隧道断面高度、宽度。
对于大跨度或高边墙的隧道断面,通过典型类比法得到此类隧道的半径公式为:
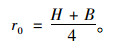
|
(2) |
根据“叠合梁”理论,初支结构在作用力q1和q2作用下,其内边缘位移U1为:
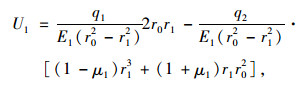
|
(3) |
式中,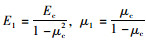
二衬外边缘位移U2为:
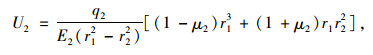
|
(4) |
式中,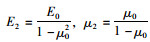
根据初支与二衬接触面位移变形协调条件: U1= U2,可求得q2,定义二衬荷载分担比G0为:
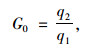
|
(5) |
则二衬荷载分担比的表达式为:
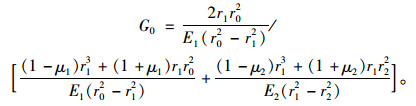
|
(6) |
初支与围岩间的接触压力是计算深埋隧道二衬分担比的重要组成部分,一般情况下,通过计算洞壁所受围岩压力q1来等效初支与围岩间的接触压力,所以,工程实践十分重视围岩压力的监测与计算,设计人员常依据《公路隧道设计规范》(JTG/T D70—2010)、太沙基公式、普氏理论等围岩松弛压力经验公式预测围岩压力,虽然计算结果常与实测值存在差距,但目前尚未建立符合客观实际情况的围岩压力理论方法,李鹏飞等[19]给出了埋深、跨度等参数不同时经验公式的适用范围,但没有给出监测数据的验证;因此,经验公式是否适用于深埋岩质隧道仍值得探究。本节以深埋隧道初支与围岩监测数据为基础,对隧道断面主要受力部位(左拱脚、左边墙、左拱腰、拱顶、右拱腰、右边墙和右拱脚)围岩压力监测数据进行整理,共统计31座隧道120个断面,统计样本如表 1所示。断面分布按围岩级别分类如下:Ⅲ级围岩43个,Ⅳ级围岩34个,Ⅴ和Ⅵ级围岩43个(其中Ⅵ级围岩6个)。由于本研究的隧道范围为深埋隧道,因此,将断面各测点围岩压力的平均值作为统计数据。最后,将围岩压力实测值与《公路隧道设计细则》(JTG/T D70—2010)、太沙基理论、普氏理论经验公式的计算值对比分析,试图寻找围岩压力实测值与经验公式计算值的某种联系。
| 隧道名称 | 围岩级别 | 监测断面/个 | 隧道跨/m | 隧道高度/m | 埋深/m | 围岩与初支间压力/kPa | 初支与二衬间压力/kPa |
| 明月山隧道 | Ⅲ | 33 | 12.37 | 10.52 | 281.0 | 55.88 | 11.3 |
| Ⅳ | 4 | 12.37 | 10.52 | 120.8 | 95.4 | 30.5 | |
| 铜锣山隧道 | Ⅲ | 5 | 10.25 | 8.32 | 204.8 | 55.76 | 11.1 |
| Ⅳ | 15 | 10.25 | 8.32 | 109.7 | 106.4 | 26.6 | |
| Ⅴ | 7 | 10.25 | 8.32 | 125 | 210.5 | 74.1 | |
| 阳宗隧道 | Ⅲ | 1 | 14.8 | 8.9 | 141 | 36.9 | 45.4 |
| 麦积山隧道 | Ⅲ | 1 | 12.64 | 8.0 | 274 | 74.9 | 6.9 |
| Ⅳ | 1 | 12.64 | 8.0 | 156 | 26.2 | 1.5 | |
| Ⅴ | 1 | 12.64 | 8.0 | 268 | 46.9 | 12.7 | |
| 马鞍山隧道 | Ⅲ | 2 | 15.36 | 8.07 | 136 | 49.4 | 37.6 |
| Ⅴ | 2 | 15.36 | 8.07 | 70 | 61.7 | 60.13 | |
| 瑶寨隧道 | Ⅴ | 1 | 12.26 | 8.4 | 270 | 85.31 | 11.1 |
| 安远隧道 | Ⅴ | 1 | 12.38 | 10.35 | 80 | 62.1 | 33 |
| 麻崖子隧道 | Ⅳ | 1 | 12.8 | 8.5 | 568 | 126.1 | 56.4 |
| Ⅴ | 1 | 12.8 | 8.5 | 431 | 173.6 | 31.3 | |
| 终南山隧道 | Ⅳ | 1 | 12.5 | 5.0 | 1 200 | 244.5 | 104.7 |
| 朱家山隧道 | Ⅳ | 1 | 8.24 | 12.58 | 179 | 49.4 | 75.1 |
| Ⅴ | 1 | 8.24 | 12.58 | 206 | 103.7 | 118 | |
| 大梁隧道 | Ⅳ | 3 | 14.86 | 12.54 | 465 | 490.9 | 261.2 |
| 黄草隧道 | Ⅲ | 1 | 6.73 | 8.97 | 736 | 538.0 | 358 |
| 乌鞘岭隧道 | Ⅴ | 3 | 12.38 | 10.35 | 445 | 272.0 | 100.0 |
| 关山隧道 | Ⅳ | 2 | 7.0 | 9.0 | 650 | 83.78 | 32.49 |
| 齐岳山隧道 | Ⅴ~Ⅵ | 3 | 8.52 | 10.17 | 670 | 145.42 | 42.2 |
| 木寨岭隧道 | Ⅴ | 2 | 10.58 | 12.08 | 629.1 | 1 546.2 | 508.8 |
| 包家山隧道 | Ⅳ | 2 | 10.5 | 8.03 | 680 | 26.7 | 6.4 |
| 明垭子隧道 | Ⅴ | 1 | 13.8 | 11.4 | 90 | 196.4 | 65.4 |
| 岭脚隧道 | Ⅴ | 2 | 13.6 | 9.5 | 110 | 55.4 | 8.6 |
| 武都西隧道 | Ⅳ | 2 | 11.86 | 11.86 | 1 000 | 469.2 | 482.9 |
| 大有山隧道 | Ⅴ | 2 | 11.8 | 9.6 | 95 | 349.6 | 55.7 |
| 北二十里铺隧道 | Ⅳ | 1 | 12.2 | 8.5 | 75 | 114.2 | 74.6 |
| 唐家塬隧道 | Ⅴ | 5 | 16.73 | 10.39 | 75 | 252.1 | 151.3 |
| 太行山隧道 | Ⅴ | 4 | 8.6 | 10.0 | 241 | 98.5 | 142.5 |
| 两水隧道 | Ⅴ | 1 | 14.0 | 17.0 | 346 | 286.6 | 596.2 |
| 胡麻岭隧道 | Ⅴ | 1 | 13.2 | 11.5 | 295 | 61.2 | 40.0 |
| 兴源隧道 | Ⅵ | 1 | 15.0 | 14.3 | 123 | 743.6 | 669.6 |
| 刘家坪3号隧道 | Ⅳ | 1 | 11.8 | 12.5 | 40 | 155.65 | 66.86 |
| 卓克基隧道 | Ⅴ | 1 | 10.25 | 5.0 | 118 | 623.1 | 220.7 |
| 魏家嘴隧道 | Ⅴ | 1 | 12.6 | 10.2 | 156 | 372.5 | 48.5 |
| 安定隧道 | Ⅵ | 2 | 12.2 | 8.68 | 170 | 228.1 | 104.5 |
从表 1不难看出,深埋复合式衬砌隧道支护结构接触压力总体随着围岩级别或隧道埋深的增加而增加,而与隧道跨度﹑高度无明显联系。
为简化理论计算,作如下假设:(1)对于深埋隧道,将隧道中心的埋深记为隧道埋深;(2)统计的围岩压力是各断面监测部位围岩压力的平均值。围岩的物理力学参数可参考隧规,各参数均设定为均值,如表 2所示。
| 围岩级别 | 重度/(kN·m-3) | 弹性模量/GPa | 泊松比 | 内摩擦角/(°) | 黏聚力/MPa |
| Ⅲ | 23~25 | 7~20 | 0.25~0.3 | 39~50 | 0.7~1.5 |
| Ⅳ | 20~23 | 1.3~7 | 0.3~0.35 | 27~39 | 0.2~0.7 |
| Ⅴ | 17~20 | 1~2 | 0.35~0.45 | 20~27 | 0.05~0.2 |
| Ⅵ | 15~17 | < 1 | 0.4~0.5 | < 20 | < 0.2 |
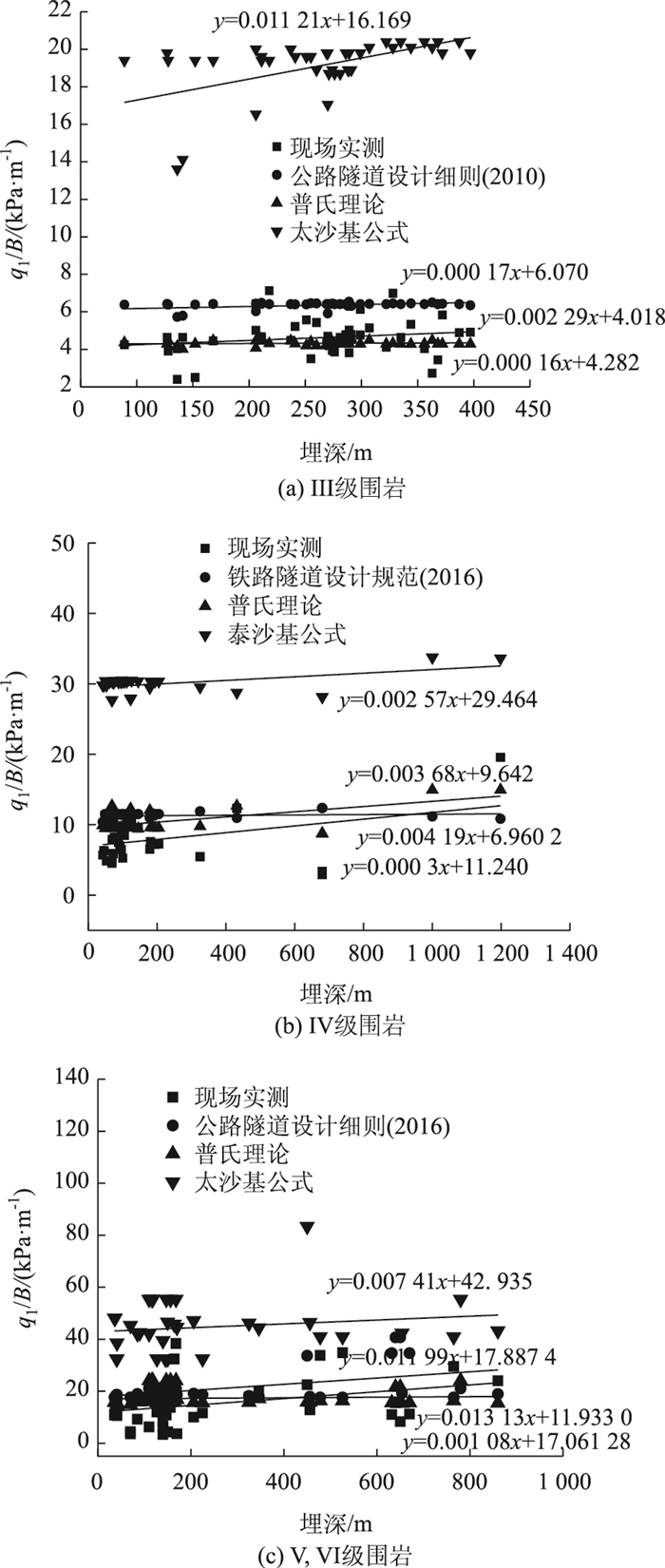
通过侧向压力q1/B(单位:kPa/m)来间接反应围岩压力的变化,如图 3所示。图 3中(a)、(b)和(c)依次为Ⅲ,Ⅳ,Ⅴ和Ⅵ级侧向围岩压力q1/B与埋深H之间的关系图(为了保持较好的拟合度,剔除少数坏点)。
|
| 图 3 围岩侧向压力q1/B与埋深H之间的关系 Fig. 3 Relationships between lateral pressure q1/B and buried depth H of surrounding rock |
| |
对围岩压力的数据分析可得出:随着埋深的增加,围岩压力总体呈增大的趋势,不过增大幅度不大。少数断面(图 3未列出)在埋深不大情况下围岩压力却较类似断面大很多,其原因是受高地应力的影响。从图 3中不难看出,经验公式计算值与实测值接近程度从优到劣依次为:普氏理论、《公路隧道设计细则》(JTG/T D70—2010)、太沙基公式。普氏理论计算值虽然较接近实测值,但在埋深部分区段甚至低于实测值,不利于工程实践预测。对于Ⅲ,Ⅳ级围岩,太沙基公式计算值是实测值的4倍左右,Ⅴ,Ⅵ级围岩太沙基公式计算值是实测值的2~3倍,其若作为指导工程实践的依据,则极不经济。至于太沙基公式为何与实测相去甚远,隧规认为:Ⅰ~Ⅳ级围岩中的深埋隧道,围岩压力为主要形变压力,而Ⅳ~Ⅵ级围岩中深埋隧道的围岩压力为松散荷载,太沙基公式将围岩视为松散体,主要考虑重力作用,所以,岩石越完整,沙基公式计算值与实测值相差越大。在埋深800 m以内,《公路隧道设计细则》(JTG/T D70—2010)计算值一般是实测值的1.3~1.5倍,埋深超过1 000 m,此规范难以适用,因此,满足埋深小于800 m时,《公路隧道设计细则》(JTG/T D70—2010)预测围岩压力较为合适。
为了提高从初支到二衬荷载传递理论的精确性,现在上述经验公式中选取合适的计算公式,根据图 3线性拟合变化的特点,将普氏理论计算值修正为:

|
(7) |
q1将代替q1代入“叠合梁”理论计算。
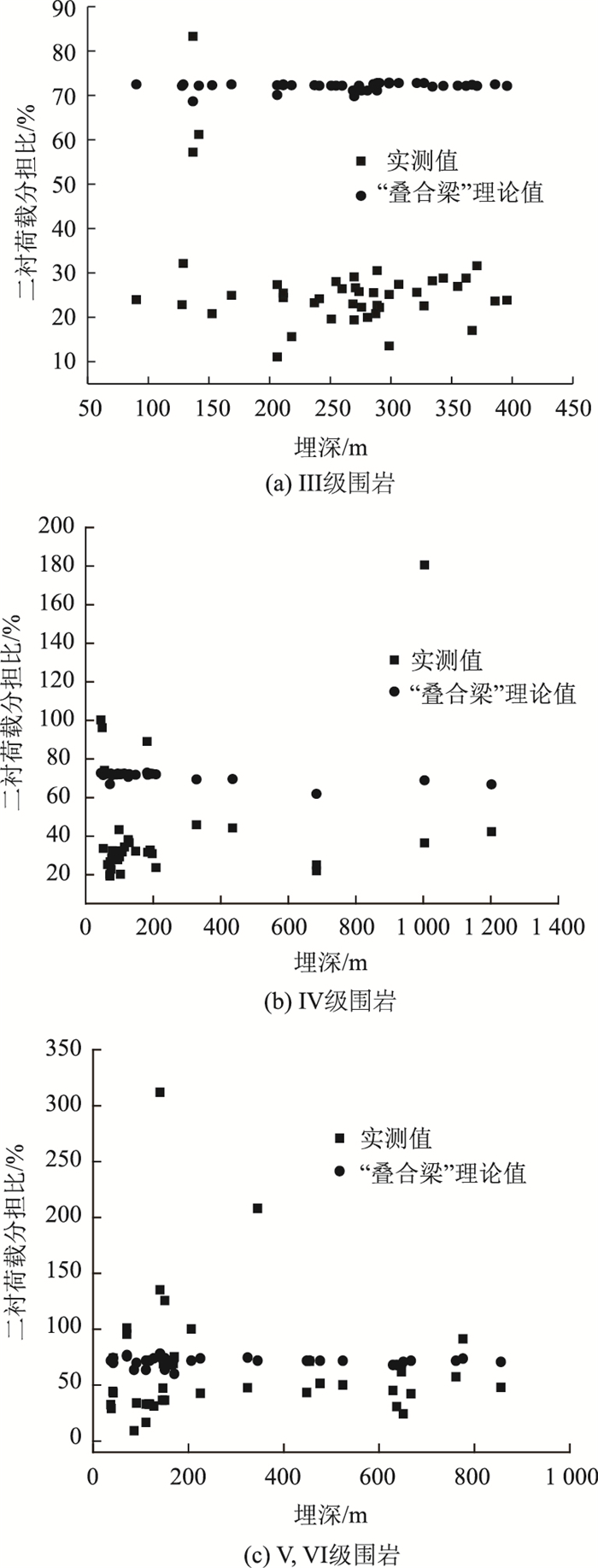
2.2 二衬分担比数据分析关于“叠合梁”理论部分文献多有提及,但对该理论的适用性尚未作出系统评价,通过对深埋隧道不同围岩级别二衬分担比的实测数据与“叠合梁”理论对比分析,试图验证“叠合梁”理论的适用性,数据对比如图 4所示。
|
| 图 4 “叠合梁”理论和现场实测的二衬分担比散点分布图 Fig. 4 Scatter diagrams of secondary lining sharing ratio obtained by"composite beam" theory and field measurement |
| |
根据图 4实测值与“叠合梁”理论计算值散点分布可知:
(1) 从实测数据可以看出,随着围岩级别的增大,二衬分担比G0越大,Ⅲ,Ⅳ,Ⅴ和Ⅵ级围岩的G0多集中于20%~30%,30%~45%,40%~70%;虽然Ⅲ级围岩二衬结构承受荷载相对不大,且隧规认为“ Ⅲ级围岩二衬结构可看作安全储备”,图 4(a)中数据验证了这一说法的普遍性,但根据监测数据,仍有极少数断面二衬分担比因高地应力超过50%,个别断面甚至达到83.7%的现象。因此,对于高地应力Ⅲ级围岩隧道,二衬结构设计需谨慎对待。Ⅳ,Ⅴ和Ⅵ级围岩少数断面二衬分担比超过100%,这是因为该部分隧道地应力高、围岩条件差,初支未及时施作而导致二衬承担较大荷载,超过了隧规提出的二衬分担比建议值。以上从侧面反映了分析二衬分担比对支护设计有重要的指导作用。
(2) 从“叠合梁”理论计算值与实测值对比可以看出:从数据总体反映来看,“叠合梁”理论计算值比实测值大,围岩级别越小,G0差距更明显,Ⅲ,Ⅳ,Ⅴ和Ⅵ级围岩二衬分担比“叠合梁”理论计算值是实测值的4倍、3倍和1.5倍左右。显然,“叠合梁”理论不适用于计算Ⅲ,Ⅳ级围岩二衬分担比;在没有高估初支结构承担荷载能力的前提下,Ⅴ和Ⅵ级二衬分担比的预测可由“叠合梁”理论计算值乘以0.7来实现。
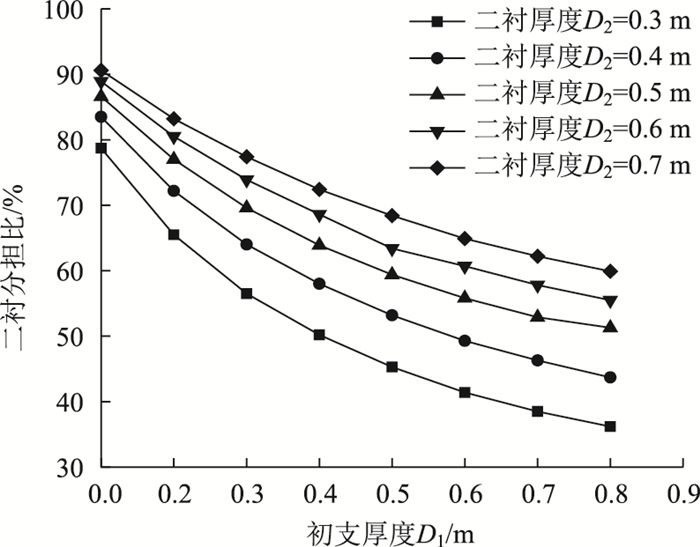
2.3 “叠合梁”理论的问题分析在运用“叠合梁”理论计算二衬分担比时发现,二衬分担比受支护材料物理力学参数的影响甚微,而受初支厚度D1与二衬厚度D2的影响颇大,在此,设计支护材料基本物理力学参数如表 3所示,来探究二衬分担比与D1,D2之间的关系,如图 5所示。
| 等效半径/m | 初支弹性模量/GPa | 初支泊松比 | 二衬弹性模量/GPa | 二衬泊松比 |
| 6 | 25 | 0.25 | 28.5 | 0.2 |
|
| 图 5 二衬分担比与初支、二衬厚度的关系曲线 Fig. 5 Curves of secondary lining sharing ratio vs. thicknesses of primary support and secondary lining |
| |
从图 5表面上看,在D1一定的条件下,D2越大,二衬分担比G0越大;D2不变时,G0随D1增大呈现减小的趋势。进一步分析图 5数据,可得到“叠合梁”理论存在以下两方面缺陷:(1)对于岩性较完整的围岩,初支足够承担围岩荷载,增加二衬厚度并不能提高G0,而“叠合梁”理论G0却有一定的增大幅度,与事实相悖。(2)根据2010版《公路隧道设计细则》有关隧道复合式衬砌厚度设计分析,二衬混凝土厚度是初支混凝土厚度的2~4倍,其中对于Ⅲ级以上的围岩,D1在0.08~0.28 m之间,D2在0.35~0.60 m之间,对应到图 5中,G0应在60%以上,而Ⅲ,Ⅳ级围岩G0基本在45%以下,图 5要想降低G0至Ⅲ,Ⅳ级围岩水平,则需使得D2 < 0.3 m,D1>0.6 m,这与隧规严重不符。因此,可断定“叠合梁”理论不适用于Ⅳ级及以下围岩隧道二衬分担比计算。
3 结论本研究基于围岩与初支、初支与二衬间接触压力的监测数据,获得以下几方面成果:
(1) 通过经验公式计算值与实测值的对比,经验公式计算值与实测值接近程度从优到劣依次为:普氏理论、2010版《公路隧道设计细则》、太沙基公式;满足埋深小于800 m时,2016版《铁路隧道设计规范》预测围岩压力较为合适;计算复合式衬砌隧道二衬分担比,围岩与初支的接触压力可根据修正的普氏理论计算。
(2) 通过对Ⅲ级以上围岩二衬分担比分析,Ⅲ,Ⅳ,Ⅴ和Ⅵ级围岩的二衬分担比多集中于20%~30%,30%~45%,40%~70%;在地应力较高或围岩条件太差的情况下,二衬承担主要荷载,因此,在隧道支护设计时应引起重视。
(3) 将“叠合梁”理论计算值与实测数据的二衬分担比进行对比,得出了岩性越完整的围岩“叠合梁”理论计算误差越大的结论。另外,“叠合梁”理论受支护厚度D1,D2的影响甚大,难以适用于Ⅳ级及以下围岩二衬分担比的计算,对于Ⅴ和Ⅵ级围岩二衬分担比的预测可由“叠合梁”理论计算值的70%来实现。
| [1] |
肖明清. 复合式衬砌隧道的总安全系数设计方法探讨[J]. 铁道工程学报, 2018, 35(1): 84-88. XIAO Ming-qing. Discussion on Design Method of General Safety Factor of Composite Lining Tunnel[J]. Journal of Railway Engineering Society, 2018, 35(1): 84-88. |
| [2] |
冯冀蒙, 仇文革, 王航. 隧道复合式衬砌初期支护极限状态模型试验研究[J]. 岩土力学, 2012, 33(11): 3345-3351. FENG Ji-meng, QIU Wen-ge, WANG Hang. Model Testing Research on Limit State of Primary Support in Composite Lining Tunnels[J]. Rock and Soil Mechanics, 2012, 33(11): 3345-3351. |
| [3] |
陈建勋, 欧阳院平, 王明年. 公路隧道复合式衬砌结构数值计算及分析[J]. 中国公路学报, 2006, 19(2): 74-79. CHEN Jian-xun, OUYANG Yuan-ping, WANG Ming-nian. Numerical Computing and Analysis of Highway Tunnel Composite Lining Structure[J]. China Journal of Highway and Transport, 2006, 19(2): 74-79. |
| [4] |
房倩, 张顶立, 王毅远, 等. 高速铁路隧道初支、二衬间接触压力研究[J]. 岩石力学与工程学报, 2011, 30(增2): 3377-3385. FANG Qian, ZHANG Ding-li, WANG Yi-yuan, et al. Study of Contact Pressure between Primary Lining and Secondary Lining for Tunnels of Passenger Dedicated Lines[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3377-3385. |
| [5] |
孙毅.隧道支护体系的承载特性及协同作用原理[D].北京: 北京交通大学, 2016. SUN Yi. Bearing Characteristics and Cooperative Action Principle of Tunnel Support System[D].Beijing: Beijing Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10004-1017058674.htm |
| [6] |
何本国, 朱永全, 孙明磊, 等. 高速铁路膏溶角砾岩深埋隧道支护荷载确定方法[J]. 岩土力学, 2013, 34(3): 827-832. HE Ben-guo, ZHU Yong-quan, SUN Ming-lei, et al. Method for Determining Supporting Load of Deep Tunnel on High-speed Railway in Gypsum Breccia Stratum[J]. Rock and Soil Mechanics, 2013, 34(3): 827-832. |
| [7] |
DUDDECK H, MEISTER D, WERNER E. Road Tunnel in Very Soft Soil in Terrace Deposits in the Harz Mountains[C]//Proceedings of the 2nd International Symposium. London: IMM, 1979.
|
| [8] |
刘善琪.基于结构健康长期监测的岩溶隧道结构受力分析研究[D].武汉: 华中科技大学, 2016. LIU Shan-qi. Structure Stress Analysis of Karst Tunnel Based on Long-term Structural Safety Monitoring[D].Wuhan: Huazhong University of Science and Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10487-1016779992.htm |
| [9] |
田鹏. 高地应力软岩隧道围岩压力及二衬受力特征研究[J]. 铁道标准设计, 2016, 60(8): 108-112. TIAN Peng. Study on Surrounding Rock Pressure and Mechanical Characteristics of Secondary Lining in Weak Rock Tunnel with High Geo-stress[J]. Railway Standard Design, 2016, 60(8): 108-112. |
| [10] |
刘学增, 叶康. 山岭公路隧道围岩压力统计规律分析[J]. 岩土工程学报, 2011, 33(6): 890-895. LIU Xue-zeng, YE Kang. Statistical Analysis of Surrounding Rock Pressure of Mountain Road Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 890-895. |
| [11] |
李鹏飞, 赵勇, 张顶立, 等. 基于现场实测数据统计的隧道围岩压力分布规律研究[J]. 岩石力学与工程学报, 2013, 32(7): 1392-1399. LI Peng-fei, ZHAO Yong, ZHANG Ding-li, et al. Study of Distribution Laws of Tunnel Surrounding Rock Pressure Based on Field Measured Data Statistics[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(7): 1392-1399. |
| [12] |
JTG/T D70-2010, 公路隧道设计细则[S]. JTG/T D70-2010, Guidelines for Design of Highway Tunnel[S]. |
| [13] |
TB10003-2016, 铁路隧道设计规范[S]. TB10003-2016, Code for Design of Railway Tunnel[S]. |
| [14] |
彭信.隧道复合式衬砌计算模型及力学机理研究[D].石家庄: 石家庄铁道大学, 2013. PENG Xin. Research on Calculation Model and Mechanical Mechanism in Composite Lining of Tunnels[D].Shijiazhuang: Shijiazhuang Tiedao University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10107-1013310976.htm |
| [15] |
杨昌贤.公路隧道二次衬砌承载能力与优化设计研究[D].成都: 西南交通大学, 2010. YANG Chang-xian. Study on Bearing Capacity and Optimization Design of Secondary Linings in Highway Tunnel[D].Chengdu: Southwest Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10613-2010122592.htm |
| [16] |
王长辉.公路隧道二次衬砌受力及结构优化设计研究[D].西安: 长安大学, 2012. WANG Chang-hui. Study on Stress and Optimization of Secondary Linings in Highway Tunnel[D]. Xi'an: Chang'an University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017745.htm |
| [17] |
王后裕, 陈上明, 言志信. 地下工程动态设计原理[M]. 北京: 化学工业出版社, 2008. WANG Hou-yu, CHEN Shang-ming, YAN Zhi-xin. Dynamic Design Principle of Underground Engineering[M]. Beijing: Chemical Industry Press, 2008. |
| [18] |
傅鹤林, 韩汝才. 隧道衬砌荷载计算理论及岩溶处治技术[M]. 长沙: 中南大学出版社, 2005. FU He-lin, HAN Ru-cai. Tunnel Lining Load Calculation Theory and Karst Treatment Technology[M]. Changsha: Central South University Press, 2005. |
| [19] |
李鹏飞, 周烨, 伍冬. 隧道围岩压力计算方法及其适用范围[J]. 中国铁道科学, 2013, 34(6): 55-60. LI Peng-fei, ZHOU Ye, WU Dong. Calculation Methods for Surrounding Rock Pressure and Application Scopes[J]. China Railway Science, 2013, 34(6): 55-60. |
 2020, Vol. 37
2020, Vol. 37
