扩展功能
文章信息
- 王向阳, 吴琼, 张林凯
- WANG Xiang-yang, WU Qiong, ZHANG Lin-kai
- 基于LS-DYNA的车-桥墩碰撞及可靠度研究
- Study on Vehicle-pier Collision and Reliability Based on LS-DYNA
- 公路交通科技, 2020, 37(5): 64-72
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 64-72
- 10.3969/j.issn.1002-0268.2020.05.008
-
文章历史
- 收稿日期: 2018-06-22
2. 湖北省交通规划设计院股份有限公司, 湖北 武汉 430051
2. Hubei Transportation Planning and Design Institute Co., Ltd., Wuhan Hubei 430051, China
在日常生活中,有时会发生车撞桥墩事故。桥梁的可靠度和使用年限是衡量桥梁安全的两个重要因素,车-桥墩碰撞事故发生后会不同程度地影响这些因素。因此,分析桥梁碰撞产生的影响,并采用可靠度理论研究桥墩碰撞后不同位置的受力特征和破坏模式及其可靠度十分必要,将为桥梁防撞研究和设计等提供依据。
本研究采用ANSYS/LS-DYNA软件建立车-桥墩碰撞有限元模型,以某双柱式桥墩为背景,根据现有规范对车辆撞击力进行研究。利用ANSYS参数化建模的便利及可靠度理论,分析桥墩被车辆碰撞后的可靠性和敏感效应。
1 工程概况以某两跨60 m连续梁桥为工程背景,连续梁桥的上部结构截面尺寸如图 1所示,混凝土强度为C50。因为是研究车辆与桥墩的碰撞,所以上部结构对桥墩主要是重力和惯性力作用,在不影响模型准确性的前提下,将上部结构截面简化为图 2,模型截面对应尺寸见表 1。下部构造盖梁尺寸为11.14 m×2.20 m×1.50 m,双柱式桥墩混凝土强度为C30,直径1.60 m,高7.00 m,纵筋为HRB400钢筋。

|
| 图 1 桥梁截面(单位:mm) Fig. 1 Bridge section (unit:mm) |
| |

|
| 图 2 简化后桥梁截面(单位:mm) Fig. 2 Simplified bridge section(unit:mm) |
| |
| 截面类型 | 原始截面 | 模型截面 |
| 面积/m2 | 4.5 | 4.5 |
| 竖向惯性矩/m4 | 5.5 | 5.6 |
| 横向惯性矩/m4 | 2.2 | 1.8 |
2 车-桥墩碰撞模型 2.1 材料参数和本构关系
采用弹塑性本构关系建模,采用常用卡车作为撞击车辆,卡车材料为钢材。
2.1.1 车辆模型选取某中型自卸卡车为碰撞车辆,该车重量约为8 t。建立车辆有限元模型,由于主要研究对象为桥墩的受力特征,因此将车辆模型简化为由驾驶室(包含保险杠)、车身、货箱等组成[1]。车辆各部位名称及其本构关系等参数见表 2。
| 模型部位 | 材料本构关系 | 弹性模量/MPa | 泊松比 |
| 驾驶室 | 塑性随动模型 | 1.7×105 | 0.30 |
| 保险杠 | 塑性随动模型 | 1.7×105 | 0.30 |
| 车身 | 双线性各向同性模型 | 2.0×105 | 0.30 |
| 货箱 | 刚体模型 | 2.0×105 | 0.30 |
碰撞发生时,车辆驾驶室变形一般很大,因此需要考虑驾驶室组成材料的应变率和屈服应力,计算式为[2]:
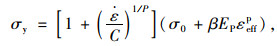
|
(1) |
式中,σy为应力;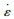
有限元仿真时,将货厢看作为刚体,通过改变车厢钢板厚度调节车辆质量。
2.1.2 桥梁模型建模时没有考虑主梁结构的钢筋(包括普通钢筋和预应力筋),这基本不影响有限元模型分析结果的准确性。主梁混凝土强度C50,材料参数见表 3。
| 模型部位 | 材料本构关系 | 弹性模量/MPa | 泊松比 |
| 主梁 | 双线性各向同性模型 | 3.45×103 | 0.20 |
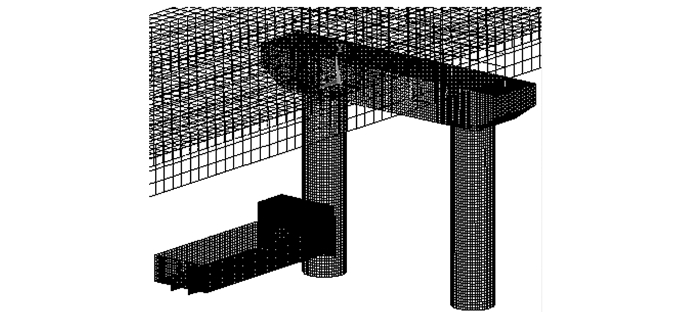
车-桥墩碰撞有限元模型见图 3。
|
| 图 3 有限元模型 Fig. 3 Finite element model |
| |
2.2 车-桥墩碰撞过程仿真
用车辆以某速度沿着桥梁纵向与桥墩发生正面碰撞来研究桥墩在碰撞过程中的应力规律。本节中设定车辆总重为16 t,以80 km/h的速度与桥墩发生碰撞。
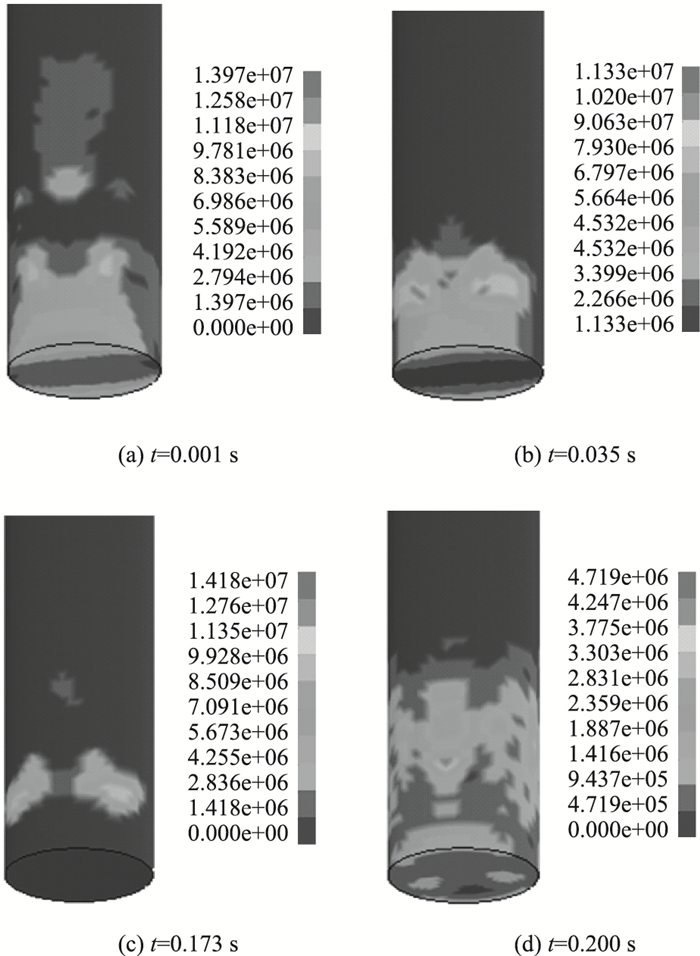
经过有限元计算得到如图 4所示的桥墩剪应力云图。可以看到,碰撞区域附近的剪应力比其他区域较大, 且刚开始碰撞过程中剪应力较大,而后剪应力减小,再上升,但此时剪应力分布较开始时密集。
|
| 图 4 车-桥墩碰撞剪应力云图(单位:Pa) Fig. 4 Nephograms of shear stress of vehicle-pier collision(unit:Pa) |
| |
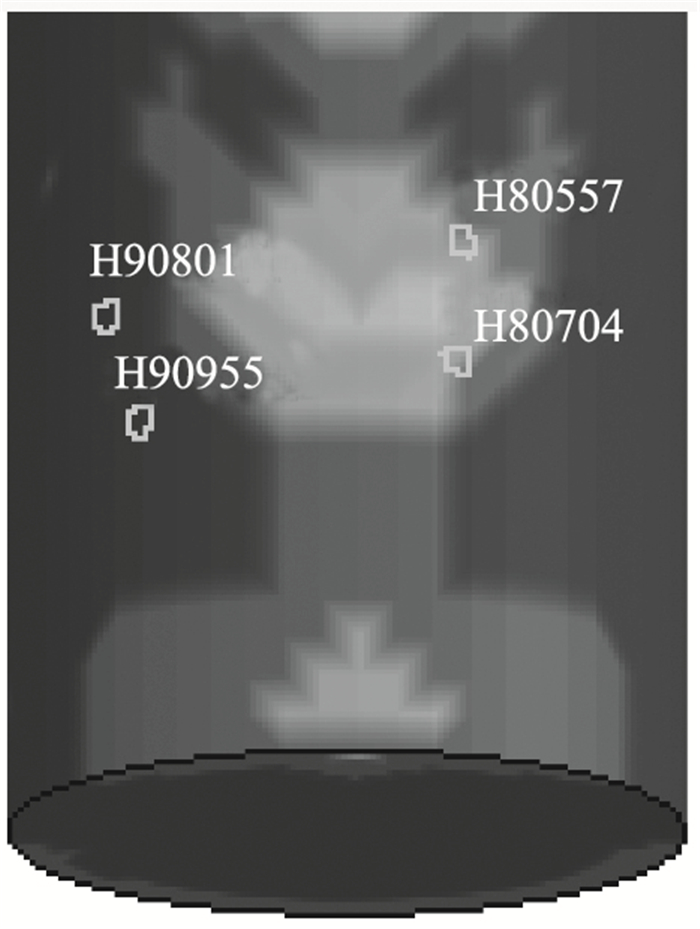
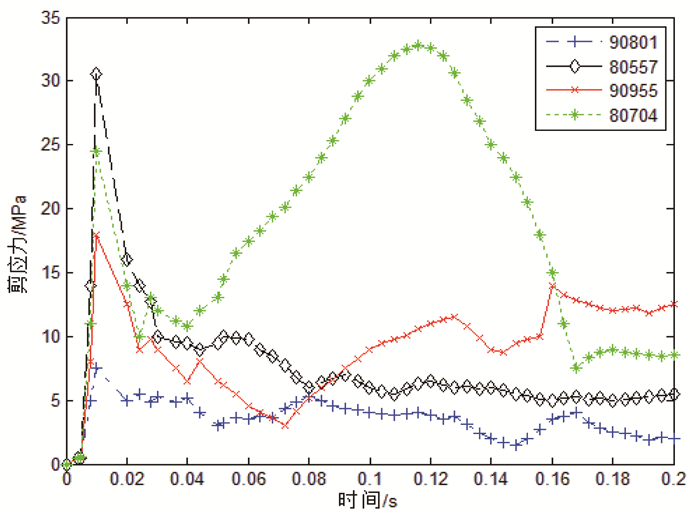
为了具体分析剪应力的变化特征,在桥墩上随机选择4个单元(图 5),分析结果见图 6。可以得到其剪应力最大值为32.8 MPa,最小值约为7.3 MPa,均超过C30混凝土土抗剪强度标准值2.9 MPa。
|
| 图 5 所选单元位置图 Fig. 5 Selected unit location |
| |
|
| 图 6 车-桥墩碰撞剪应力时程 Fig. 6 Shear stress time history of vehicle-pier collision |
| |
图 4和图 6表明在车-桥墩碰撞区域,部分混凝土结构有可能会发生由于剪应力过大造成的损坏。因此在车辆与桥墩发生撞击之后,桥墩碰撞区域易发生剪切破坏。
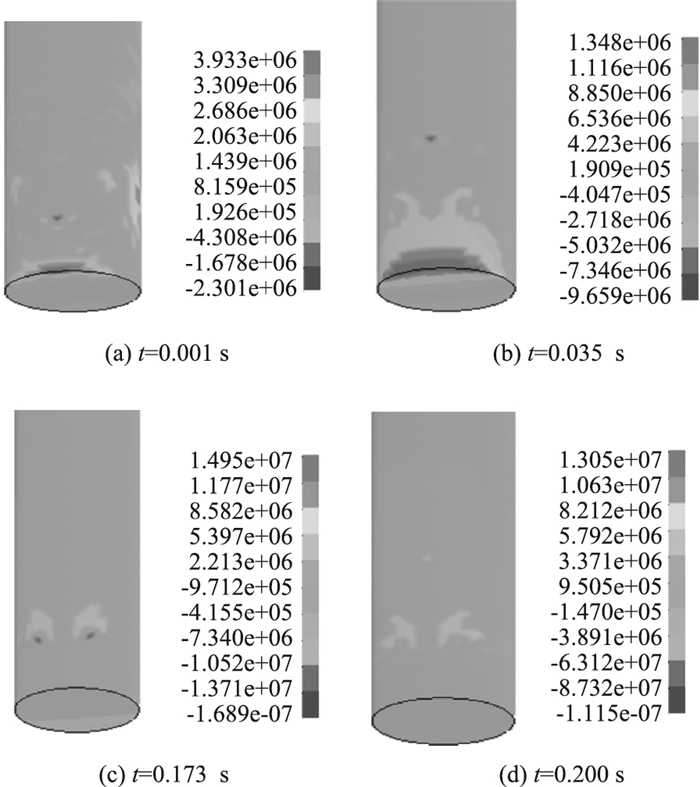
通过计算得到图 7的桥墩最大主应力云图。可以看到,在碰撞过程中最大主应力开始时较大,然后减小,再增大,不断上升下降直到归于一个稳定值。
|
| 图 7 车-桥墩碰撞最大主应力云图(单位:Pa) Fig. 7 Nephograms of maximum principal stress of vehicle-pier collision(unit:Pa) |
| |
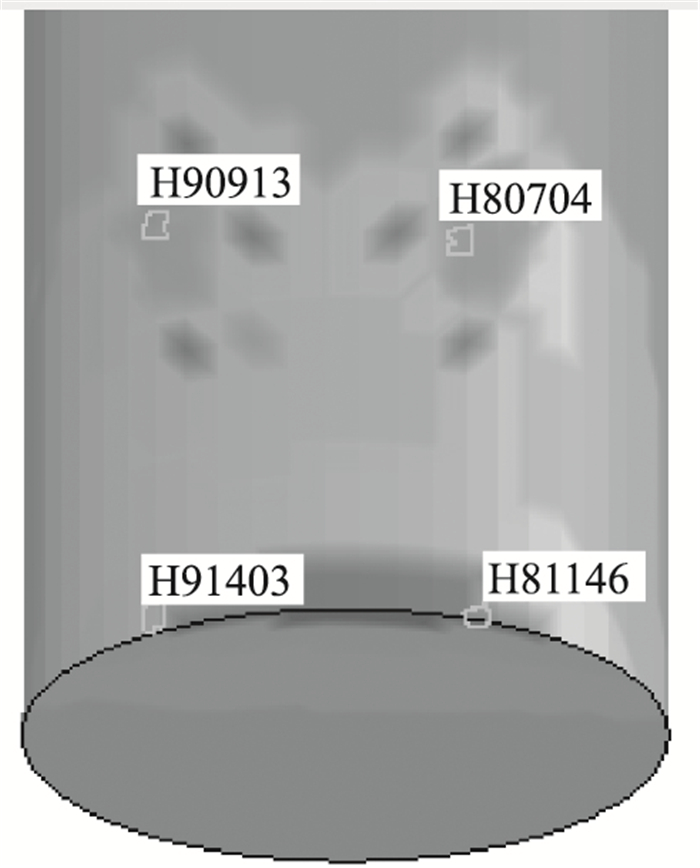
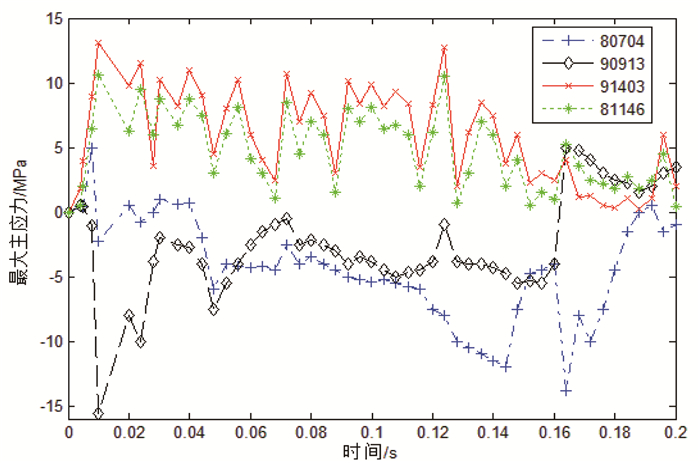
在桥墩和墩底各选两个单元来分析剪应力的变化特征(图 8),分析结果见图 9。可以看到,墩底区域始终表现为主拉应力,最大值为13.1 MPa,远大于C30抗拉强度标准值2.0 MPa。碰撞区域主拉应力和主压应力都存在,其主压应力最大值为15.6 MPa,满足C30混凝土抗压标准,主拉应力最大值均大于C30混凝土轴心抗拉强度标准值2.0 MPa。
|
| 图 8 所选单元位置图 Fig. 8 Selected units location |
| |
|
| 图 9 车-桥墩碰撞最大主应力时程图 Fig. 9 Maximum principal stress time relationship of vehicle-pier collision |
| |
上述车-桥墩碰撞研究分析表明,被车辆撞击后桥墩不同区域的破坏模式不同,碰撞区域易发生剪切破坏,墩底区域易发生弯曲破坏。
3 拟合车-桥墩撞击力计算公式车辆与桥墩碰撞是一个瞬时动态过程,它们之间的撞击力不是一个定值,而是不断变化的,与撞击时车辆的速度、质量和接触面积等有关系。分析中直接考虑这一动态撞击过程是非常复杂的,所以往往需要将这过程等效为一个静力荷载作用。采用文献[7]推荐的方法计算撞击力的等效静力荷载,时间取0.05 s。
参照车辆撞击力的有关研究成果,本研究仅考虑影响车辆撞击力最大的3个因素:车-桥墩碰撞的偏心距参数α、车辆速度V、车辆质量M。α影响较大,所以在数据样本中多取值进行分析,分别取0.20,0.40,0.60,0.80,1.00;V分别取20,40,60,80 km/h;M分别取8,30,55 t,模拟不同情况下的车辆。根据前面的研究,建立60组车-桥墩碰撞模型,得到60组数据样本,经过试算和调整,拟合出车撞力F的公式为:
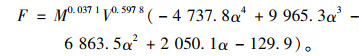
|
(2) |
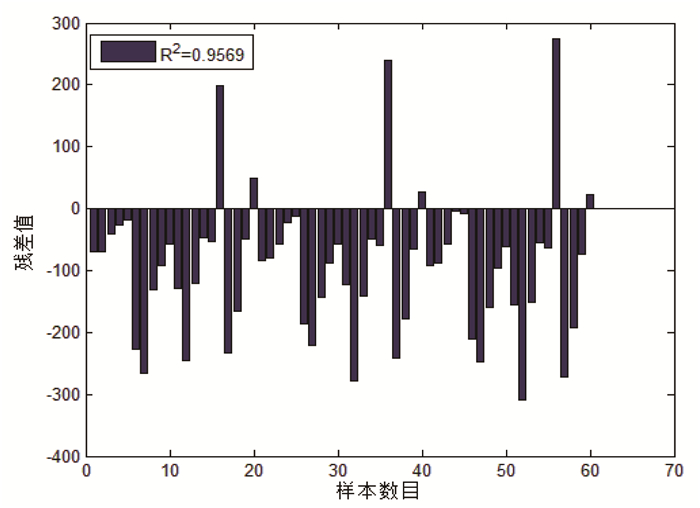
根据式(2)计算出车撞力,与上述60组数值仿真结果进行残差分析,结果见图 10。两种计算方法其残差分析的相关系数R2基本接近于1.0,相关度非常大,拟合度非常好。因此,式(2)运用于车撞力的计算是合适的。
|
| 图 10 残差分析直方图 Fig. 10 Residual analysis histogram |
| |
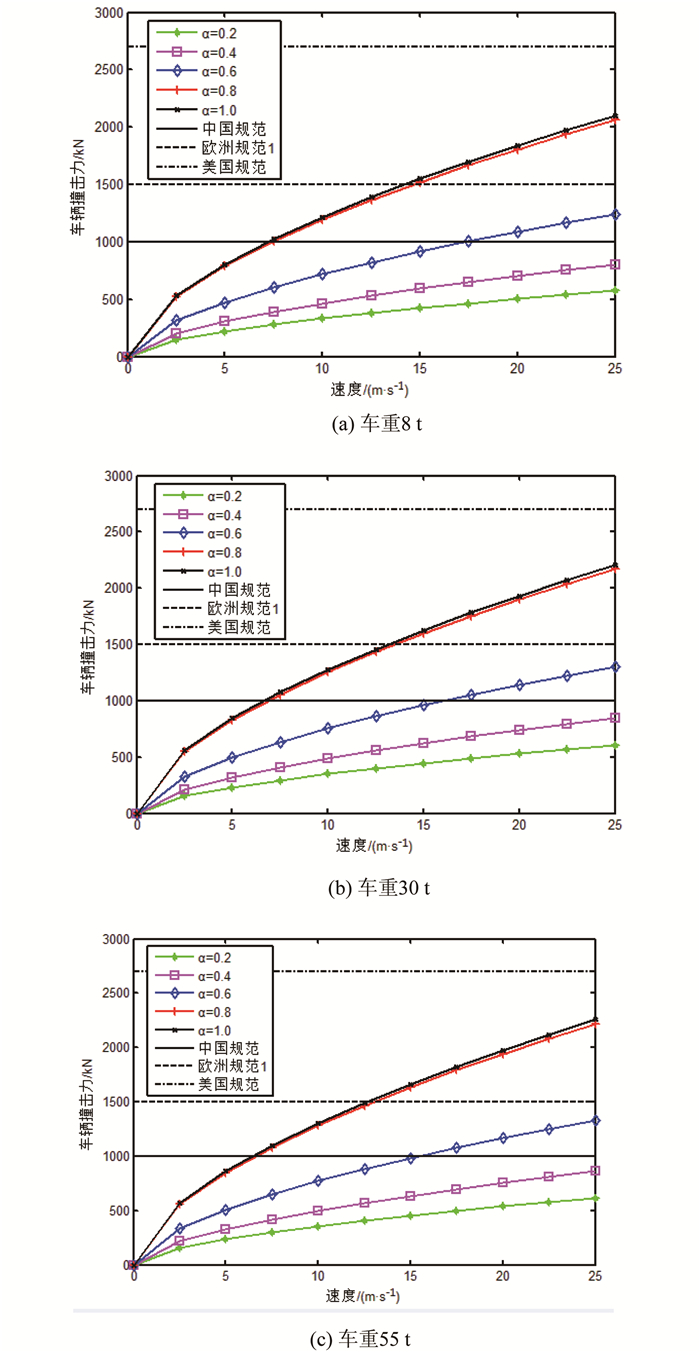
将式(2)计算得到的车撞力与规范[8-13]计算结果进行比较,见图 11。计算时取用5个不同的偏心距参数α,车辆速度V取值范围为2.5~25 m/s,其间隔为2.5 m/s。可以看出,美国规范计算得到的限值最大,欧洲规范其次,我国规范最小。式(2)计算得到的数值始终小于美国规范限值;只有当α大于0.6时,得到的数值才与欧洲规范得到的限值有可能重合;而只有当α大于0.4时,得到数值才与我国规范得到的限值有可能重合。另外,考虑不同车辆重量时,我国规范得到的车撞力计算结果与实际情况相比可能偏小。
|
| 图 11 不同α参数和规范时撞击力对比 Fig. 11 Comparison of impact forces in different α parameters and specifications |
| |
4 车撞桥墩可靠度研究 4.1 桥墩被车辆撞击的概率模型 4.1.1 车辆撞击力的概率模型
根据前面拟合出的车辆撞击力式(2),建立车撞力概率模型,其中车辆质量M在8~55 t之间服从均匀分布;车速V为正态分布,其均值15.07 m/s,均方差0.93 m/s。
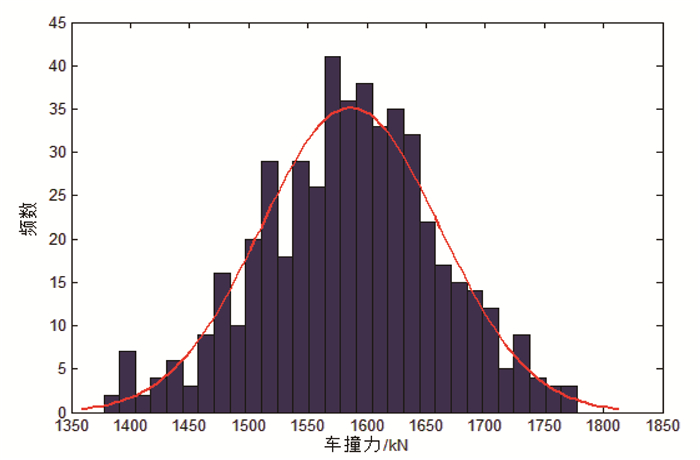
计算车-桥墩碰撞后桥墩可靠度和下部结构体系的失效概率。通过随机模拟车-桥墩碰撞的车撞力样本来得到车撞力的概率分布特点,如图 12所示,该直方图呈凸形的趋势。由此考虑建立检验假设H0[14-15]:总体上车撞力服从某正态分布N(μ, σ2),均值μ和均方差σ均为未知量。采用自编程序对上述假设进行χ2拟合优度检验,表明在显著性水平α=0.1下,保留原假设H0,χ2拟合优度检验认为车撞力F服从正态分布,均值1 586 kN,均方差75.7 kN,具有很高的置信水平。因此,可以认为在横桥向和纵桥向车辆撞击力F均服从正态分布F~N(1 586,75.72)。
|
| 图 12 车辆撞击力概率分布直方图 Fig. 12 Probability distribution histogram of vehicle impact force |
| |
4.1.2 被撞桥墩的概率模型
建立桥梁碰撞模型时,进行合理简化,其中桥墩几何形状的改变忽略不计,把混凝土的弹性模量作为随机变量。
文献[12]指出混凝土的弹性模量Ec服从正态分布,计算公式如下:
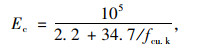
|
(3) |
式中, fcu.k为抗压强度标准值,在fcu.k均值μfcu.k处进行泰勒展开并取前两项:
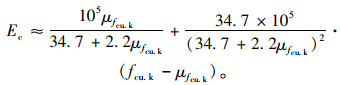
|
(4) |
若对Ec求均值μEc和变异系数δEc,可得:
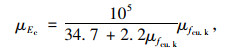
|
(5) |
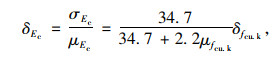
|
(6) |
式中,σEc为Ec的标准差;δfcu.k为fcu.k的变异系数。取C30混凝土强度标准值,另外μfcu, k,δfcu, k分别取20.1 MPa和0.14,代入式(5)、(6)得到Ec的均值为2.54×1011 Pa,标准差为3.53×1010 Pa。
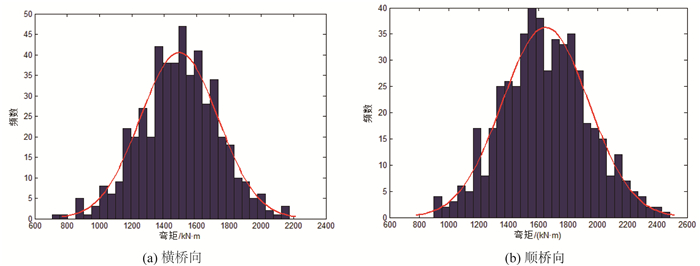
4.2 桥墩响应随机分布特性在不影响计算准确性前提下,按文献[13]相同的处理方法,在墩顶支座处施加上部结构重力。由4.1节建立的车-桥墩碰撞有限元模型,给予桥墩车撞力,距底面高度为车辆重心高度,在位于桥墩底部以上1.4 m处模拟实际车辆撞击桥墩事故。采用拉丁超立方抽样法随机抽出500组非线性车-桥墩碰撞模型样本,根据确定性的分析方法在ANSYS中的概率设计模块进行编程,得到图 13和图 14所示的桥墩墩底截面弯矩随机分布直方图和碰撞点剪力随机分布直方图。
|
| 图 13 墩底截面弯矩随机分布图 Fig. 13 Bending moment random distributions of pier bottom section |
| |
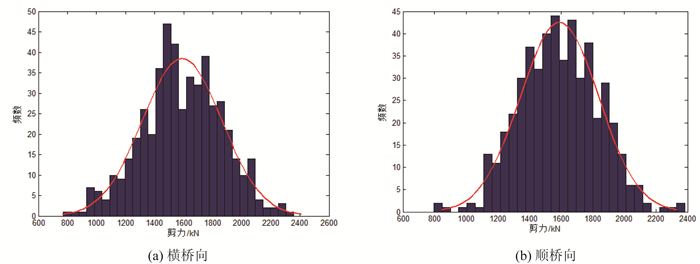
|
| 图 14 碰撞点剪力随机分布图 Fig. 14 Shear force random distributions at impact point |
| |
采用MATLAB进行χ2拟合优度检验,得到表 4结果。
| 弯矩 | 分布 | 均值/ (kN·m) |
标准差/ (kN·m) |
变异系数 | 置信水平 |
| 横向 | 正态 | 1 495 | 260 | 0.170 | 0.983 |
| 顺向 | 正态 | 1 640 | 280 | 0.170 | 0.983 |
| 剪力 | 分布 | 均值/ kN |
标准差/ kN |
变异系数 | 置信水平 |
| 横向 | 正态 | 1 587 | 267 | 0.170 | 0.983 |
| 顺向 | 正态 | 1 598 | 258 | 0.160 | 0.983 |
由表 4可知,在车撞力作用下,对于桥墩关键截面的内力响应,无论是在横桥向还是在顺桥向,χ2拟合优度检验认为其服从正态分布置信水平能达到0.982以上。因此,可以认为在横桥向和纵桥向,桥墩关键截面的内力响应服从正态分布。
4.3 车-桥墩碰撞模型的可靠度计算 4.3.1 车-桥墩碰撞模型的可靠性分析选用的车-桥墩碰撞模型的下部构造由3个双柱式桥墩组成,其中任何一个桥墩破坏意味着整个桥梁下部结构破坏;双柱桥墩中两个墩柱视为串联体系,即一个失效则全部失效。失效模式见图 15。

|
| 图 15 桥梁墩柱关系图 Fig. 15 Relationship between bridge piers |
| |
车-桥碰撞后,结构体系可靠度计算步骤为:
假设每根墩柱的可靠指标βi(i=1, 2, …, n)都相等,则应满足:β1=β2=, …, =βn=β0;双柱式墩的左右两个墩柱是串联体系,则双柱式墩的可靠指标:
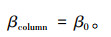
|
(7) |
根据串联体系分析方法,整个体系的失效概率:
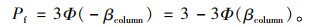
|
(8) |
首先计算独墩在剪切或者弯曲破坏模式下的失效概率;然后将整个下部结构视为串联体系,再由式(8)计算桥梁下部结构体系的可靠度。
4.3.2 桥梁下构体系可靠性分析利用4.2节结论,将桥墩在车撞力作用下关键截面的内力响应与可靠度(失效概率)进行计算,结果见表 5、表 6。
| 车撞力 | 内力 | 承载能力 | 可靠性指标 | 失效概率 | |||
| 均值 | 标准差 | 均值 | 标准差 | ||||
| 弯矩 | 1 495 | 260 | 6 648 | 1 200 | 4.20 | 4.08×10-5 | |
| 剪力 | 1 587 | 267 | 5 469 | 1 011 | 3.71 | 3.06×10-4 | |
| 注:表中弯矩单位为kN·m, 剪力单位为kN。 | |||||||
| 车撞力 | 内力 | 承载能力 | 可靠性指标 | 失效概率 | ||
| 均值 | 标准差 | 均值 | 标准差 | |||
| 弯矩 | 1 640 | 280 | 6 648 | 1 200 | 4.06 | 7.26×10-5 |
| 剪力 | 1 598 | 258 | 5 469 | 1 011 | 3.71 | 3.10×10-4 |
| 注:表中弯矩单位为kN·m, 剪力单位为kN。 | ||||||
从表 5、表 6可得,剪力作用下桥墩的失效概率比弯矩作用下高出一个数量级,因此,车-桥墩碰撞后桥墩更容易发生剪切破坏。假定两个方向上的破坏模式互不影响,则模型的失效概率为:
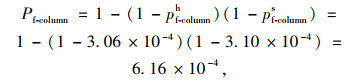
|
(9) |
式中,pf-columnh为横桥向墩柱的失效概率;pf-columns为表示顺桥向墩柱的失效概率。
由式(9)可知,本算例的桥墩失效概率几乎为0,可靠性较高。车-桥墩碰撞有限元模型计算结果表明,本研究的桥墩满足车辆防撞击的要求。
4.4 桥墩相关参数敏感性分析计算在对车-桥墩碰撞模型进行可靠度研究时,我们发现不同参数的取值会对结果产生不同程度的影响。因此,对这些参数进行敏感性分析很有必要。从上节可以看出,在车辆冲击力作用下,桥墩更容易发生剪切破坏。为了简化而不失通用性,本节研究剪切破坏的参数敏感性问题。
4.4.1 分析方法本研究选用单墩抗剪可靠性指标作为控制目标,通过对某变量选取不同的值来研究抗剪可靠性指标的变化[16-18]。当变量发生改变时,其抗剪可靠性指标为:
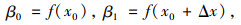
|
(10) |
式中,x0为基准值;Δx为变化量;β0为可靠度基准值;β1为改变后可靠度。
参数敏感性指标β为:
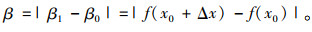
|
(11) |
本节研究随机变量均值和标准差改变对桥墩抗剪性能可靠度的影响。通过改变随机变量的均值和标准差来研究,结果见表 7和表 8。
| 变化率/% | 混凝土 | 箍筋 | ||||
| 强度/ MPa |
重度/ (kN·m-3) |
强度/ MPa |
直径/ cm |
间距/ cm |
||
| -20 | 3.51 | 3.6 | 3.58 | 3.6 | 3.8 | |
| -15 | 3.53 | 3.7 | 3.60 | 3.6 | 3.8 | |
| -10 | 3.58 | 3.7 | 3.63 | 3.7 | 3.8 | |
| -5 | 3.65 | 3.7 | 3.66 | 3.7 | 3.8 | |
| 0 | 3.71 | 3.7 | 3.71 | 3.7 | 3.7 | |
| 5 | 3.75 | 3.7 | 3.74 | — | 3.7 | |
| 10 | 3.80 | 3.8 | 3.76 | — | 3.7 | |
| 15 | 3.84 | 3.8 | 3.78 | — | 3.7 | |
| 20 | 3.85 | 3.8 | 3.79 | — | 3.7 | |
| 变化率/% | 混凝土 | 箍筋 | ||||
| 强度/ MPa |
重度/ (kN·m-3) |
强度/ MPa |
直径/ cm |
间距/ cm |
||
| -20 | 3.75 | 3.7 | 3.73 | 3.7 | 3.7 | |
| -15 | 3.75 | 3.7 | 3.73 | 3.7 | 3.7 | |
| -10 | 3.74 | 3.7 | 3.73 | 3.7 | 3.7 | |
| -5 | 3.73 | 3.7 | 3.72 | 3.7 | 3.7 | |
| 0 | 3.71 | 3.7 | 3.71 | 3.7 | 3.7 | |
| 5 | 3.69 | 3.7 | 3.70 | 3.7 | 3.7 | |
| 10 | 3.66 | 3.7 | 3.69 | 3.7 | 3.7 | |
| 15 | 3.64 | 3.7 | 3.68 | 3.7 | 3.7 | |
| 20 | 3.63 | 3.7 | 3.67 | 3.7 | 3.7 | |
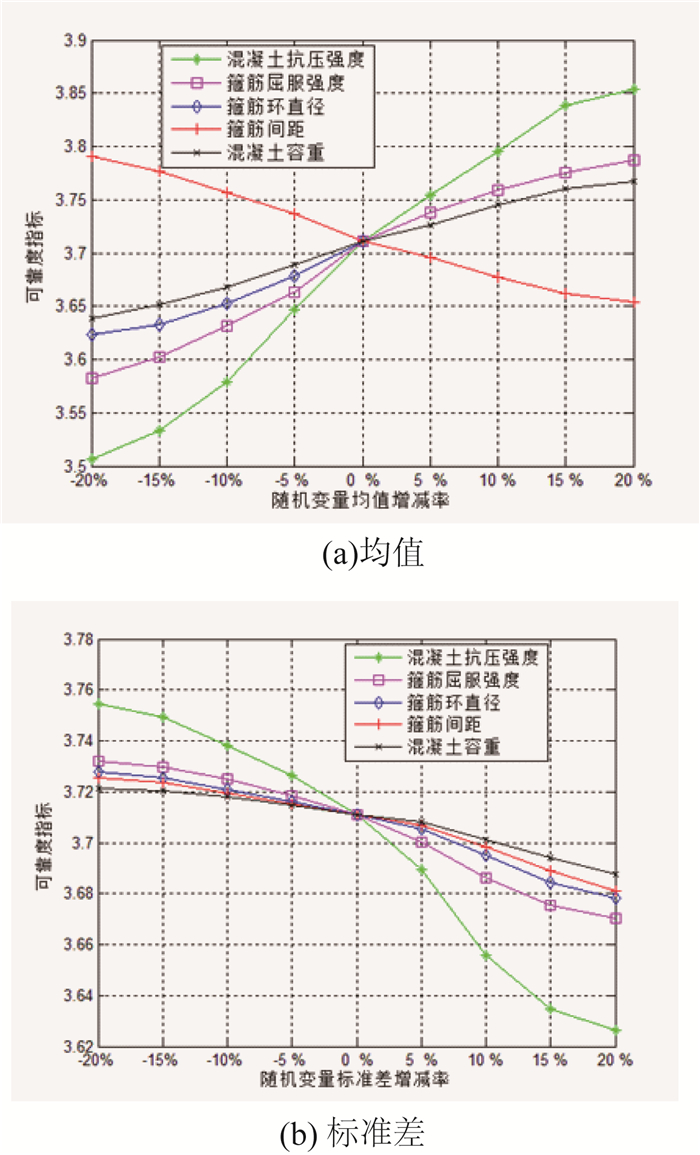
图 16为可靠度指标与随机变量变化主的关系。可以看出,各随机变量曲线在均值变化时,除箍筋间距之外,其他的变化趋势都相同;在标准差变化时,各随机变量曲线的变化趋势都相同,但增减幅度不同。
|
| 图 16 可靠度指标与随机变量变化率的关系 Fig. 16 Relationship between reliability indicator and random variable change rate |
| |
为了更好地研究各随机变量的敏感性,取均值和标准差各自变化-5%,得到相应的抗剪性能可靠性指标。β0为原可靠度,β1为变化后的可靠度,β为可靠度之差,结果见表 9和表 10。
| 均值 -5% |
混凝土 | 箍筋 | ||||
| 强度/ MPa |
重度/ (kN·m-3) |
强度/ MPa |
直径/ cm |
间距/ cm |
||
| β0 | 3.71 | 3.71 | 3.71 | 3.7 | 3.7 | |
| β1 | 3.65 | 3.69 | 3.66 | 3.7 | 3.7 | |
| β | 0.06 | 0.02 | 0.05 | 0.03 | 0.03 | |
| 标准差 -5% |
混凝土 | 箍筋 | ||||
| 强度/ MPa |
重度/ (kN·m-3) |
强度/ MPa |
直径/ cm |
间距/ cm |
||
| β0 | 3.71 | 3.71 | 3.71 | 3.71 | 3.71 | |
| β1 | 3.73 | 3.72 | 3.72 | 3.72 | 3.72 | |
| β | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | |
可以看出,当随机变量之一的混凝土强度均值减小5%时,体系可靠性指标的变化比较明显。因此,混凝土强度对桥墩抗剪承载力可靠度的影响最大。当标准差变化时,其对可靠性指标的影响没有均值变化时那么大。混凝土强度变异系数对抗剪承载力可靠性指标的敏感性也较小。因此,混凝土的强度对桥墩抗剪性能影响最大,在实际的施工过程中,由于温度、施工实际等不确定因素会使其与设计值有所差别,所以在桥梁施工和后期养护过程中需要重点关注。
5 结论(1) 通过建立车-桥墩碰撞有限元模型,研究碰撞后桥墩各区域的应力特征,进行仿真分析计算,结果表明,被车辆撞击后桥墩不同区域的破坏模式不同,桥墩碰撞区域更易发生剪切破坏,而桥墩墩底更易发生弯曲破坏。
(2) 根据有限元模型,模拟一系列车撞桥墩工况,得到样本数据,拟合出车撞力的计算公式。在不同的车速下,采用我国规范得到的车撞力计算值偏低。
(3) 通过建立车撞力和被撞桥墩的概率模型来研究桥墩弯矩和剪力响应分布特征。结果表明,桥墩墩底内力响应服从正态分布,具有很高的置信水平,且无论是横桥向还是顺桥向,桥墩在车撞力作用下更易发生剪切破坏。
(4) 桥墩的参数敏感性分析结果表明,混凝土强度对墩柱抗剪承载力可靠性指标影响最大。
| [1] |
徐林枫.车辆撞击下桥墩的撞击力和墩身的应变研究[D].北京: 北京交通大学, 2014. XU Lin-feng. Research on Impact Force and Strain of Pier under Vehicle Impact[D]. Beijing: Beijing Jiaotong University, 2014. |
| [2] |
王泽鹏, 胡仁喜, 康士廷, 等. ANSYS13.0/LS-DYNA非线性有限元分析实例指导教程[M]. 北京: 机械工业出版社, 2011: 44-47. WANG Ze-peng, HU Ren-xi, KANG Shi-ting, et al. Case Guidance Course for ANSYS13.0/LS-DYNA Nonlinear Finite Element Analysis[M]. Beijing: China Machine Press, 2011: 44-47. |
| [3] |
吴琼, 基于LS-DYNA的车-桥墩碰撞分析及可靠度研究[D].武汉: 武汉理工大学, 2018. WU Qiong. Analysis of Vehicle-pier Collision and Pier and Reliability Research Based on LS-DYNA[D].Wuhan: Wuhan University of Technology, 2018. |
| [4] |
陆新征, 何水涛, 黄盛楠. 超高车辆撞击桥梁上部结构研究:破坏机理、设计方法和防护对策[M]. 北京: 中国建筑工业出版社, 2014. LU Xin-zheng, HE Shui-tao, HUANG Sheng-nan. Collision between Over-height Vehicles and Bridge Superstructure:Failure Mechanism, Design Method and Protective Measures[M]. Beijing: China Architecture & Building Press, 2014. |
| [5] |
POLANCO-LORIA M, HOPPERSTAD O S, BØRVIK T, et al. Numerical Predictions of Ballistic Limits for Concrete Slabs Using a Modified Version of the HJC Concrete Model[J]. International Journal of Impact Engineering, 2008, 35(5): 290-303. |
| [6] |
陈诚.桥梁设计船撞力及损伤状态仿真研究[D].上海: 同济大学, 2006. CHEN Cheng. Simulation Study on Ship Collision Force and Damage State for Bridge Design[D]. Shanghai: Tongji University, 2006. |
| [7] |
崔堃鹏, 夏禾, 夏超逸, 等. 汽车撞击桥墩瞬态撞击力的等效静力计算[J]. 振动与冲击, 2014, 33(4): 48-53. CUI Kui-peng, XIA he, XIA Chao-yi, et al. Equivalent Static Force Calculation Methods for Transient Impact Force of a Vehicle in Collision with Piers[J]. Journal of Vibration and Shock, 2014, 33(4): 48-53. |
| [8] |
EL-TAWIL S, SEVERINO E, FONSECA P. Vehicle Collision with Bridge Piers[J]. Journal of Bridge Engineering, 2005, 10(3): 345-353. |
| [9] |
AASHTO. AASHTO LRFD Bridge Design Specifications[S]. Washington, D.C.: AASHTO, 2013.
|
| [10] |
JTG D60-2004, 公路桥涵设计通用规范[S]. JTG D60-2004, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [11] |
TB10002.1-2005, 铁路桥涵设计基本规范[S]. TB10002.1-2005, Fundamental Code for Design on Railway Bridge and Culvert[S]. |
| [12] |
BS EN 1991-1-7 Eurocode 1, Actions on Structures-Part 1-7: General Actions-Accidental Actions[S].
|
| [13] |
GB50010-2010, 混凝土结构设计规范[S]. GB50010-2010, Code for Design of Concrete Structures[S]. |
| [14] |
JOSHI A S, GUPTA L M. A Simulation Study on Quantifying Damage in Bridge Piers Subjected to Vehicle Collisions[J]. International Journal of Advanced Structural Engineering, 2012, 4(1): 8. |
| [15] |
程海根, 邹江娜. 用LS-DYNA仿真车-桥墩碰撞时角度对桥梁的影响[J]. 华东交通大学学报, 2013, 30(6): 19-24. CHENG Hai-gen, ZOU Jiang-na. Influence of Angle on Bridge in Vehicle-pier Collision Based on LS-DYNA Simulation[J]. Journal of East China Jiaotong University, 2013, 30(6): 19-24. |
| [16] |
BERTRAND D, KASSEM F, DELHOMME F, et al. Reliability Analysis of an RC Member Impacted by a Rockfall Using a Nonlinear SDOF Model[J]. Engineering Structures, 2015, 89(15): 93-102. |
| [17] |
DAVIDSON M T, CONSOLAZIO G R, GETTER D J, et al. Probability of Collapse Expression for Bridges Subject to Barge Collision[J]. Journal of Bridge Engineering, 2012, 18(4): 287-296. |
| [18] |
BUTH C E, BRACKIN M S, WILLIAMS W F, et al. Analysis of Large Truck Collisions with Bridge Piers[R]. College Station: Texas Transportation Institute, 2010.
|
 2020, Vol. 37
2020, Vol. 37
