扩展功能
文章信息
- 李传习, 冯峥, 郭立成, 柯红军, 刘科强
- LI Chuan-xi, FENG Zheng, GUO Li-cheng, KE Hong-jun, LIU Ke-qiang
- 密集横隔板UHPC箱梁锚固区局部效应分析及配筋设计
- Local Effect Analysis and Reinforcement Design for Anchorage Zone of UHPC Box Girder with Densely Distributed Diaphragms
- 公路交通科技, 2020, 37(5): 53-63
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 53-63
- 10.3969/j.issn.1002-0268.2020.05.007
-
文章历史
- 收稿日期: 2019-04-02
2. 佛山市路桥建设有限公司, 广东 佛山 528303
2. Foshan Road & Bridge Construction Co., Ltd., Foshan Guangdong 528303, China
后张预应力混凝土梁桥的锚固区受到预应力集中锚固张拉力的作用、钢束局部弯曲引起的径向力作用,存在局部承压和应力扩散等问题,被认为是混凝土结构中的典型应力扰动区(D区)[1]。锚固区的局部承压强度及抗裂性能会影响到整个桥梁结构的安全性、耐久性。文献[1-4]利用有限元及拉压杆模型对普通混凝土箱梁锚固区进行了系统的受力分析研究,相关研究成果被采纳于《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[5](后文简称为JTG—2018)中。普通混凝土箱梁锚固区在受力分析及配筋设计上已较为明确。但由于普通混凝土材料强度较低,预应力锚固区开裂现象较为普遍。且现有已建大跨度预应力混凝土梁桥在运营过程中普遍出现了主跨过度下挠和梁体开裂的问题[6],而采用高性能水泥基材料被认为是解决此类问题的最有效方式,也是桥梁建设未来的发展方向。
随着超高性能混凝土(UHPC[7-9])的快速发展,UHPC已被广泛用于桥梁结构中[10-11]。文献[12-13]提出了密集横隔板UHPC连续箱梁桥的概念,该桥型使得桥梁上部结构的自重可减轻约50%,具有良好的综合经济性。采用UHPC建造大跨度桥梁的理念正逐渐深入人心[6]。相应地,UHPC桥梁中预应力锚固区的局压性能成为了人们关注的重点。虽可以参考普通混凝土局压区的设计经验,但UHPC从微观结构到宏观力学性能与普通混凝土相比均有较大差异,其内部微裂纹发展、外部开裂直至破坏的整个非线性过程也有其自身特点。并且由于UHPC薄壁箱梁桥顶板、腹板和底板厚度均较薄,预应力钢束需要采用体外束,大量的体外预应力束通过尺寸较小的转向块或齿块锚固在壁板上。因此,过于薄壁化的结构将会导致预应力UHPC箱梁桥锚固块、锚固处的顶底板和锚固隔板成为关键的受力部位,而国内外相关的技术研究还不够充分。
文献[14]对UHPC连续箱梁锚固区进行了线弹性有限元分析,研究了锚固区的4种典型局部效应,并得到了壁板厚度对锚固区局部弯曲效应的影响规律,且经计算发现了将齿块锚固于相邻横隔板之间具有最优的锚固效果,但未对该锚固方式下锚固区的局部效应开展更深入的参数研究,例如未关注锚固处隔板宽度、隔板间距及多齿块锚固作用对锚固区受力性能的影响,尚需进一步的研究。
拉压杆模型法是解决锚固区应力复杂问题的一种有效方法,因而确定拉压杆模型的几何构形是进行隔板连通式齿块(齿块置于横隔板与横肋之间或相邻横隔板之间)配筋设计的重要手段。但因隔板的存在,隔板连通式齿块锚固区的应力分布特征和力流传递规律与传统齿块锚固区[2-4](包括独立矩形齿块、独立三角齿块、角隅矩形齿块等)明显不同。理解这一应力分布特征所抽象的几种典型局部作用效应及相应的拉压杆模型应有所区别,但目前针对此方面的研究还较为缺乏。
本研究以某拟建UHPC连续箱梁桥为工程背景,利用ABAQUS对隔板连通式齿块的局部作用效应进行了多种参数研究,分析了隔板设置情况、隔板宽度、隔板间间距以及多齿块锚固对隔板连通式齿块受力性能的影响,并在此基础上提出了隔板连通式齿块锚固区拉压杆模型的构建方法,且给出了配筋设计实例。
1 工程背景与简化的分析对象以某拟建UHPC连续梁桥为基本原型进行锚固区的局部效应分析。该桥为三跨(56+103+56) m变截面UHPC连续箱梁桥,梁宽16.75 m,顶板处采用带肋板,肋板最厚处为25 cm。横隔板板厚12 cm,横隔板间距为3 m。在相邻横隔板的中间部位设置横肋,肋板厚为20 cm,肋板高度为60 cm。箱梁腹板厚度为18~25 cm。顶板束齿块锚固端面高47 cm,宽40 cm。钢绞线为19束布置,均采用直径为15.2 mm、标准强度为1 860 MPa的普通无黏结成品索,波纹管的孔径为12 cm。普通钢筋采用HRB400级钢筋。箱梁钢束锚固示意参见图 1。

|
| 图 1 箱梁钢束锚固体系示意图(单位:cm) Fig. 1 Schematic diagram of steel stand anchoring system for box girder (unit: cm) |
| |
为获得隔板连通式齿块锚固区的应力分布特征以及隔板等参数变化下的主应力变化情况,仅取出背景工程中顶板三角齿块锚固区的基本尺寸进行研究,而箱梁桥锚固区真实的受力情况另文研究。基于此,为便于参数分析,在箱梁原设计的基础上保持锚固区的基本尺寸不变对结构进行简化,简化的分析模型详细设计尺寸如图 2所示。该模型顶板部位简化为平板,顶板和底板的厚度分别为220 mm和180 mm;腹板厚度取最小值180 mm;模型高度为2.5 m,长度为4 S(S为横隔板与横肋之间的距离,无特别说明时取1.5 m),模型宽度为(L+360) mm(L为相邻腹板内侧面间的距离,即横隔板宽度);锚固齿块设置在简化模型的正中间(有特别说明时除外);齿块、横隔板和横肋尺寸与原设计一致;预应力仍按19束钢绞线设计,计算时荷载按70%的标准强度取值。

|
| 图 2 简化的分析模型设计尺寸(单位:mm) Fig. 2 Dimensional design of simplified analytical model (unit: mm) |
| |
利用ABAQUS对简化的分析模型锚固区进行线弹性分析,UHPC箱梁采用八节点六面体缩减积分单元C3D8R模拟,UHPC材料参数按该桥拟采用的UHPC材性试验结果取值,弹性模量E取44.0 GPa,泊松比υ取0.2。根据文献[15]的研究成果,有限元模型考虑了预应力孔道对锚固区受力性能的削弱作用。为对后续拉压杆模型的构建提供有利的参考,模型未考虑普通钢筋及锚垫板等对锚固区受力性能的影响。锚固张拉力等效简化为均布荷载施加于锚板上,作用范围与锚垫板的受力面积保持一致,钢束转向产生的径向力亦采用均布力施加于转向位置处。边界条件设置为约束梁段两端X,Y,Z,这3个方向上的自由度。对模型锚固区合理密布网格,关注部位网格细化至10 mm,保证各部位的计算结果收敛良好。本研究的各有限元模型均基于该方法建立,由于有限元模型数较多,故后续不再赘述。
2 应力分布特征 2.1 拉应力分布特征根据有限元结果可知,隔板连通式齿块与常规独立三角齿块在受力效应上大体相同,但由于锚固隔板的受力介入,隔板连通式齿块受力要更为复杂。去除拉应力量值较小的部分,将锚固区拉应力的集中分布特征归因于6种典型局部效应,参见图 3。除常规独立三角齿块中的锚下劈裂效应、锚后牵拉效应、局部弯曲效应、径向力效应、悬臂效应外[4-5],还包括横隔板部位的隔板弯曲效应。

|
| 图 3 隔板连通式齿块典型局部效应 Fig. 3 Typical local effect of DABIAS |
| |
前5种局部效应文献[4]及规范[5]针对常规独立三角齿块已做了详细的论述,此处不再细述。而隔板连通式齿块特有的隔板弯曲效应主要体现在横隔板内侧面与齿块交接区域的横向拉应力以及竖向拉应力值较大,存在较为明显的应力集中现象。这是由于锚固处横隔板在周边壁板的约束下形成一个三边固结一边自由的受力板,在齿块预应力的作用下产生了局部弯曲,使得该部位面外应力较为显著。
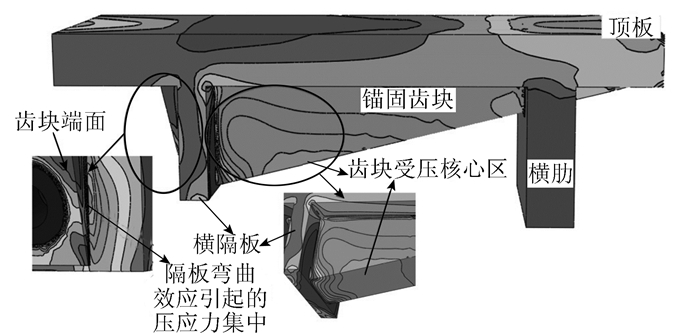
2.2 压应力分布特征图 4为锚固区的压应力等值线图,从图中可以看出锚固区中齿块体的压应力值较大。横隔板与横肋之间的齿块部位存在核心受压区,即压应力沿纵桥向先增大后减小,并呈拱状分布,位于距离横隔板中心线S/4~S/2的一定区域内。这是由于齿块体在两端受压的状态下会局部压缩变形并上拱,在顶板区形成局部弯曲效应并在齿块体形成核心受压区。此外,横隔板与齿块锚固端交界处由于隔板弯曲效应产生了压应力集中,由此亦反映出横隔板提供给齿块一个较大的反向支承力。
|
| 图 4 锚固区压应力分布特征 Fig. 4 Distribution characteristics of compressive stress in anchorage zone |
| |
3 隔板参数分析与讨论
隔板连通式齿块与常规独立三角齿块最大的不同在于齿块前后隔板提供的锚固支承作用,而已有研究仅分析了壁板厚度、钢束转向方式以及是否设锚前隔板(本研究中的横肋)对锚固区受力效应的影响,但忽略了是否设锚端隔板(本研究中的横隔板)、横隔板宽度、横隔板间距对锚固区受力效应的影响。以简化的分析模型为基础对隔板连通式齿块的隔板参数进行分析。
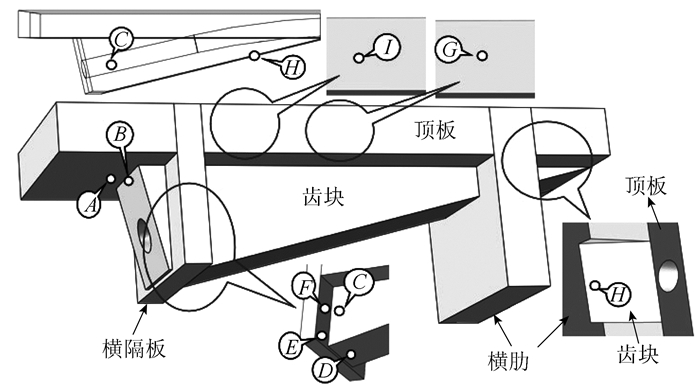
考虑到UHPC的抗压强度在150 MPa以上,而有限元中非锚垫板区的压应力值不足70 MPa,未达到其抗压强度的1/2,因此参数分析中不再考虑隔板参数对锚固区受压性能的影响,仅分析锚固区的拉应力情况。根据锚固区的几种典型局部效应确定拉应力分布的不利点(见图 5)。其中A,B,D,I,G点以及H点均位于齿块纵向中心线上,I点距横隔板中线250 mm,G点位于横隔板与横肋的正中间,距离横隔板中线750 mm(该值的确定以横隔板与横肋之间的间距S=1.5 m时为基础,当S变化时,I,G点的位置根据比例类推)。考虑锚固区的应力集中区域有一定的范围(取值原则为取小区域的最大值),限于篇幅各关注点详细的位置情况未逐点解释说明,可根据图 5中所示位置获知。
|
| 图 5 “隔板连通式齿块”关注点位示意图 Fig. 5 Schematic diagram of key points for DABIAS |
| |
3.1 隔板设置情况的影响
以简化的分析模型为基础,保持横隔板与横肋之间的间距S=1.5 m不变,横隔板宽度L取1.2 m。设置了4种锚固方案进行对比分析:方案1为设计中隔板连通式齿块锚固方案,方案2在方案1的基础上取消了锚固处的横肋(保留横隔板),方案3在方案1的基础上取消了锚固处的横隔板(保留横肋),方案4在方案1的基础上取消了锚固处横隔板与横肋。
根据有限元分析(FEA)结果,将各隔板设置情况下齿块锚固区关注点的应力值列入表 1中(表中纵向应力(Longitudinal Stress)由L.S表示;横向应力(Transversal Stress)由T.S表示;竖向应力(Vertical Stress)由V.S表示,下同),表中只列出了与局部效应有关方向上的应力值。
| A点 | B点 | D点 | E点 | G点 | H点 | I点 | |
| (L.S) | (V.S) | (T.S) | (T.S) | (T.S) | (T.S) | (L.S) | |
| 方案1 | 26.7 | 20.2 | 9.5 | 18.8 | 6.4 | 5.8 | 6.6 |
| 方案2 | 29.5 | 26.5 | 9.5 | 18.9 | 9.2 | 17.8 | 6.6 |
| 方案3 | 32.4 | 23.4 | 7.5 | — | 7.3 | 6.5 | 7.7 |
| 方案4 | 33.4 | 31.6 | 7.6 | — | 11.6 | 18.0 | 7.6 |
根据表 1可知,方案1(隔板连通式齿块)与方案4(常规独立三角齿块)相比,A点的纵向拉应力值减小了20.1%,B点的竖向拉应力值减小了36.1%,G点的横向拉应力值减小了44.8%,H点的横向拉应力值减小了67.8%,I点的纵向拉应力值减小了13.2%。因此将齿块锚固在横隔板与横肋上可降低锚固区的锚后牵拉效应、悬臂效应、局部弯曲效应和径向力效应,且大大降低了锚固区的最大主拉应力值。方案2与方案4相比,A点的纵向拉应力值减小了11.7%,B点的竖向拉应力值减小了16.1%,D点的横向拉应力值增加了25.0%,G点的横向拉应力值减小了20.7%,H点的横向拉应力值基本无变化。因此仅将齿块锚固在横隔板上可以降低锚固区的锚后牵拉效应、悬臂效应、局部弯曲效应,但对径向力效应影响不大,且会增强锚下劈裂效应。方案3与方案4相比,无锚固横隔板对锚固区的锚后牵拉效应、锚下劈裂效应的影响不大,但由于横肋的作用能显著降低锚固区的悬臂效应、局部弯曲效应和径向力效应。综上可述,隔板连通式齿块相较于常规的独立三角齿块锚固性能更优,大大减小了锚固区的局部效应。
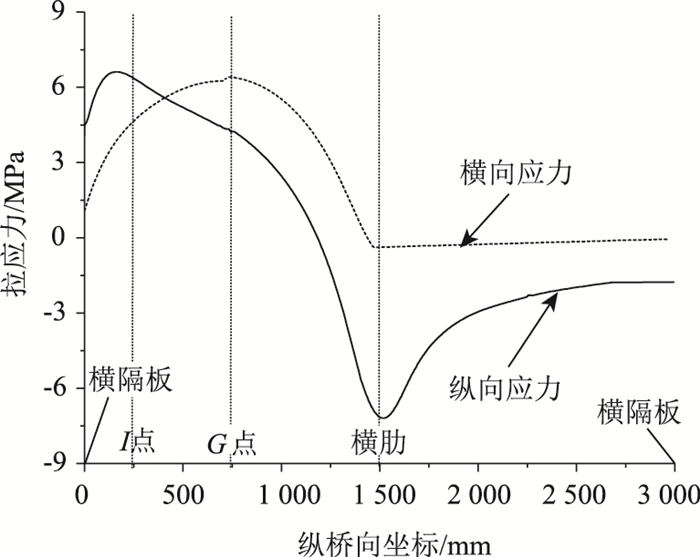
由于顶板中线部位的G, I点在纵桥向和横桥向的应力值变化趋势存在差异,为此,将方案1锚固区中顶板中心线位置上缘各点的横向、纵向拉应力情况列如图 6中,以便更好地获知隔板连通式齿块锚固区的局部弯曲效应。图中横坐标轴0点对应锚固处横隔板的中线位置,1 500 mm坐标对应横肋的中线位置,3 000 mm坐标对应锚固后端横隔板的中线位置。
|
| 图 6 齿块中心线位置顶板上缘各点的横向、纵向应力 Fig. 6 Transversal and longitudinal stresses at each point on top edge of top plate in center-line position of anchor block |
| |
由图 6可知,锚固区横隔板与横肋之间顶板区域各点的横桥向、纵桥向拉应力成波形分布(应力值先增大后减小,在横肋位置达到最小值)。但G, I点的应力峰值点并未处于同一点,由此说明局部弯曲效应不只体现在一个方向的应力,但以往的研究往往只关注了顶板区域的纵桥向应力[1-5],而横桥向的局部弯曲效应应引起同样的重视。此外,顶板锚固区的拉应力集中部位仅分布于横肋坐标轴以左,由此说明顶板锚固区的钢筋布置仅需考虑横肋中心线以左的部位。
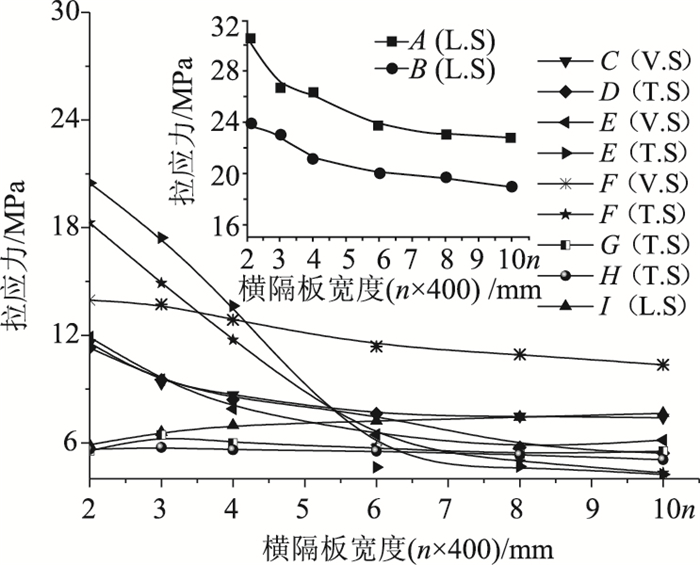
3.2 隔板宽度的影响保持横隔板与横肋之间的间距S=1.5 m不变,横隔板宽度L取为(n×b)mm(b为锚固齿块的宽度,取值为400 mm,n依次取值为2,3,4,6,8,10),横隔板宽度的增加也意味着箱梁宽度的增加。根据FEA结果将各关注点的主拉应力值随横隔板宽度的变化情况列如图 7中,图中均只列出了关注点应力较大方向上的主拉应力值,下同。
|
| 图 7 拉应力值随横隔板宽度的变化情况 Fig. 7 Tensile stress varying with diaphragm width |
| |
由图 7可知,A点~F点的应力均随横隔板宽度的增加而下降明显,由此说明增大横隔板宽度可以有效降低锚固区的锚后牵拉效应、悬臂效应、锚下劈裂效应以及隔板弯曲效应。但当横隔板宽度达到齿块宽度的6倍以上时,下降幅度则不再明显。H点应力值随横隔板宽度的增加而变化幅度不大,即横隔板宽度对锚固区径向力效应的影响不大。I点应力随横隔板宽度的增加而增加,因此增加横隔板的宽度会略微增加锚固区局部弯曲效应。
综合上述分析,设计时保证横隔板宽度在6b以上能大大降低锚固区的局部效应,特别是对于锚后牵拉效应、锚下劈裂效应以及隔板弯曲效应。
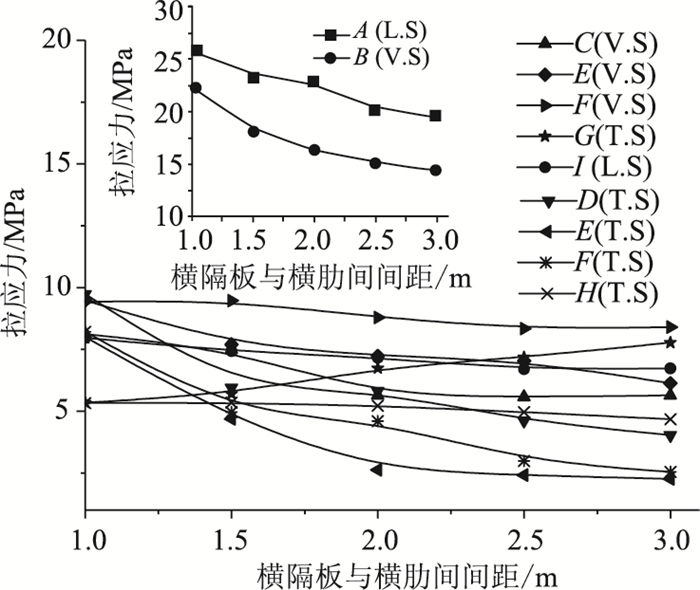
3.3 隔板间距的影响在图 2的基础上保持横隔板宽度L=8b (3.2 m)不变,横隔板与横肋之间的间距S取1,1.5,2.0,2.5,3 m。各关注点拉应力值随间距S的变化情况如图 8所示。
|
| 图 8 拉应力值随横隔板与横肋间间距的变化情况 Fig. 8 Tensile stress varying with spacing between diaphragm and transverse rib |
| |
由图 8可知,A,B点的拉应力值随隔板间距的增加而下降显著,由此说明增大隔板间距可以有效降低锚固区的锚后牵拉效应、悬臂效应。C~F点的拉应力值随隔板间距的增加而下降,但当隔板间距达到2 m以上时,应力变化幅度不明显,由此说明当隔板间距较小时,劈裂效应和隔板弯曲效应才与隔板间距密切相关。G点的拉应力值随隔板间距的增大而增大,说明隔板间距的增加会增大锚固区的局部弯曲效应。H点的应力值随隔板间距的增加而变化不大,隔板间距对径向力效应基本无影响。
基于上述分析,设计时横隔板与横肋间的间距不宜太小,综合考虑横隔板在整个箱梁中的作用(如抵抗扭转、畸变等)[10],间距S宜控制在1.5~2.5 m为宜。或者当箱梁不设置横肋时齿块仅锚固在横隔板上,则锚固处相邻横隔板可替代横肋,此时,相邻横隔板之间的间距宜控制在3.0~5.0 m。
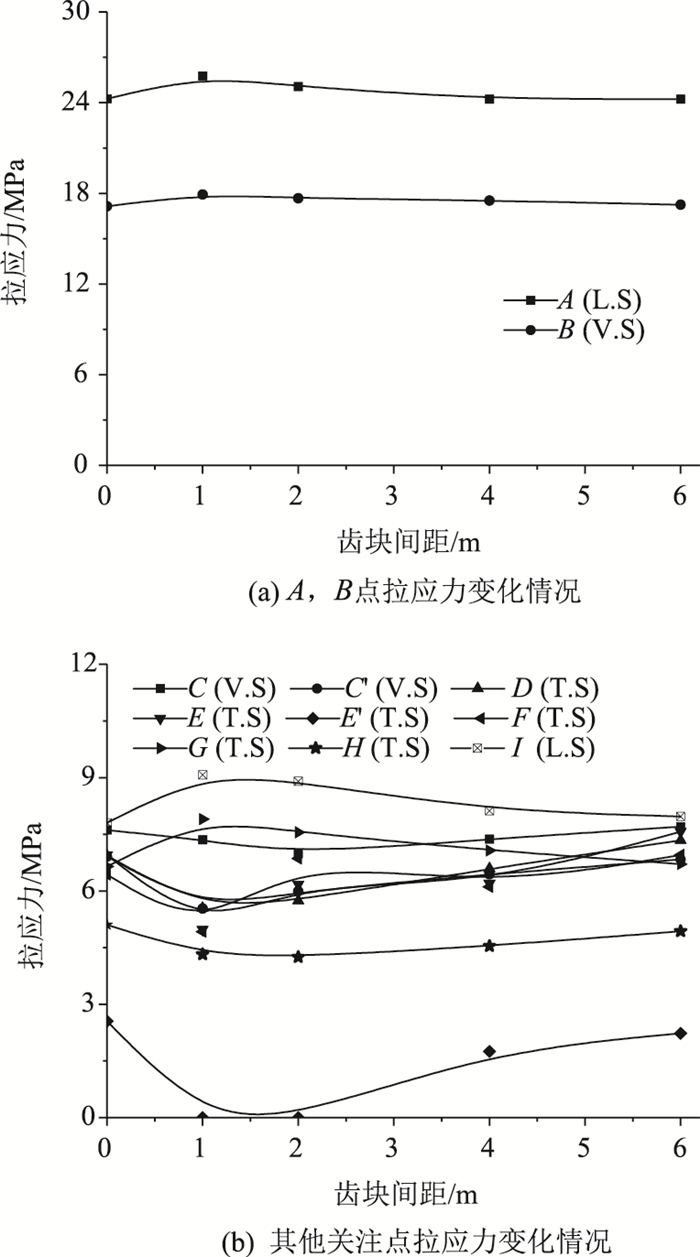
4 多齿块锚固对局部效应的影响进一步地,开展同一横隔板处多齿块锚固及齿块间距对锚固区局部效应的影响研究。基于图 2模型,设计了5种齿块间距,分别为0,1,2,4,6 m。横隔板与横肋之间的间距S取1.5 m,横隔板宽度L取8.96 m。为便于与对称单齿块锚固进行对比分析(例如图 8中横隔板宽度等于6b时),将该模型中关注齿块纵向中心线距腹板内边缘的距离定为1.2 m(3b),参数分析中该齿块位置不加以改变,仅变化另一齿块的位置,间距为0时即为非对称单齿块锚固。
根据FEA结果将各关注点应力值随相邻齿块间间距的变化情况列如图 9中,图中C,E点位于关注齿块中近腹板侧,C′,E′与C,E点关于齿块中心线对称。
|
| 图 9 拉应力值随相邻齿块间间距的变化情况 Fig. 9 Tensile stress varying with spacing between adjacent anchor blocks |
| |
由图 9可知,同一锚固隔板上双齿块锚固对锚固区的最大拉应力值影响不大(增幅6.2%)。同时,设置双齿块会降低横隔板和齿块部位的拉应力值,特别是当齿块相距为1 m时,齿块相邻侧的横隔板部位的拉应力值接近于0。这是由于在双齿块的协同作用下齿块间的横隔板与齿块变形协调,导致隔板弯曲效应大大降低。当齿块间距逐渐增大时,齿块间的变形协调效应变得不明显,逐渐转变为单齿块作用。此外,E点的应力值要显著大于E′点的应力值(绝对值均较小),说明在同一锚固体系中隔板弯曲效应与齿块所处位置息息相关,越靠近腹板,作用效应越显著。但设置双齿块会增加顶板上缘的拉应力值(增加了18.8%),而当齿块间距逐渐增大时,对局部弯曲效应的影响程度会有所下降,特别是当间距S达到6 m时,其影响基本为0。
综上可知,对于隔板连通式齿块,同一横隔板上采用多齿块锚固对锚固区的整体受力产生的负面影响较小。
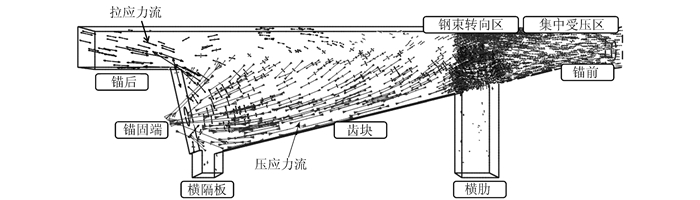
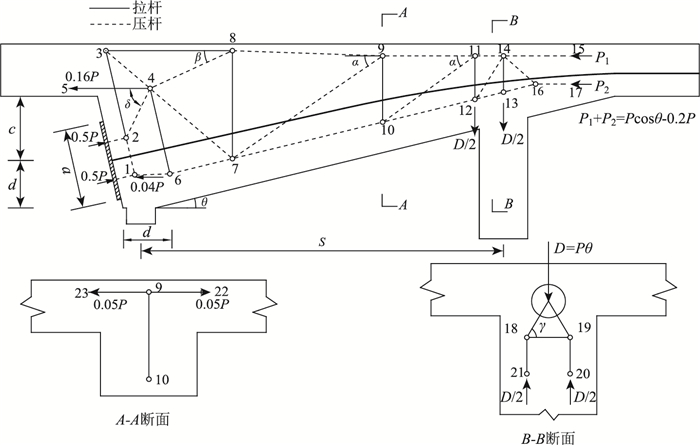
5 拉压杆模型及配筋设计 5.1 拉压杆模型考虑到目前国际上尚无针对UHPC箱梁桥隔板连通式齿块拉压杆模型的相关设计规定,以及隔板连通式齿块5种典型局部效应与独立三角齿块较为接近,因此可参考独立三角齿块的部分规定[5, 16-18]、已有案例[4, 19]以及本锚固方式下的应力等值线(图 3、图 4)及应力迹线分布特征(图 10)构建拉压杆模型,如图 11所示。
|
| 图 10 锚固区应力迹线分布图 Fig. 10 Distribution of stress traces in anchorage zone |
| |
|
| 图 11 锚固区拉压杆模型 Fig. 11 Strut-and-tie model for anchorage zone |
| |
局压锚固区拉压杆模型的基本构形及设计符合以下规定:
(1) 根据JTG—2018[5]的规定将1~2压杆至锚固区的距离取为0.25倍锚垫板宽度,1,2号节点的间距取0.5倍锚垫板宽度,由此可确定1,2号节点的位置。
(2) 力筋轴线与齿块纵向边缘之间均匀分布的压应力场通过平行于齿块纵向边缘的压杆来模拟,将压杆边距取为0.25倍齿块高度。根据规范[5]锚下劈裂效应作用位置至锚固端面的水平距离d与锚固张拉力中心至齿块下边缘的垂直距离相等的原则可确定6号节点位置。
(3) 根据应力等值线图 3,7号节点处于距离横隔板中心线S/4~S/2的核心受压区内,由此可确定7号节点。4~6号拉杆表示锚下劈裂应力区,已有的研究认为[20]锚下拉杆位置与劈裂应力合力点位置一致时可实现对劈裂开裂的有效控制。基于此并考虑与抵抗锚后牵拉效应的4~5节点重合可确定4号节点位置(4号节点为弥散型节点,必定位于顶板内且靠近与齿块的交界处部位,起到主应力转向作用)。
(4) 根据规范[18]的建议,规定4~8压杆与水平向拉杆的倾角β在25°~65°范围内取值可避免压杆在压力作用下强度过于软化,建议取下限值25°(可确定7,8号节点),由此可得到该区域竖向拉杆抵抗纵向剪力的最小配筋量。此处竖向拉杆7~8之所以能抵抗齿块与壁板交界区域的纵向剪切破坏是由于竖向拉杆与斜压杆之间组成了协同作用机制。
(5) 为避免预应力荷载传递过程中锚固齿块与顶板的交界面产生剪切破坏,界面剪力Vu与竖向压力N需满足Vu≤μN的关系式,其中Vu,N分别表示(混凝土)斜压杆内力的水平与竖直分力。根据AASHTO规范[17]壁板与齿块交界面的摩擦系数取1.4,因此斜压杆倾角α不应小于arctan(1/μ)。在36°附近取值,可得到锚固区抗剪所需的最小钢筋计算量。进一步地,根据力流传递规律可得到9~12号节点。
(6) 考虑横肋对径向力的支承作用,因此将13,14号节点布置于横肋的中心线上。压杆12~14,14~16仅起到对拉杆13~14的锚固作用,而不影响拉杆本身内力的计算,因此16号节点位置可根据P2受力情况微调。
(7) 径向力按JTG—2018[5]中预应力钢筋转向前后的切线夹角(rad)与锚固张拉力的乘积取值,即D=Pθ。横肋提供的竖向反力根据表 1计算结果偏保守地取值为径向力的50%,因此径向区的箍筋配置量也可大大减少。径向力传递过程中斜压杆与横向拉杆之间的夹角γ应尽可能大,以发挥齿块中预应力孔道下缘横向受拉钢筋的抗裂作用。
(8) 根据JTG—2018[5]独立三角齿块锚后牵拉力设计值取锚固力设计值大小的20%,但隔板连通式齿块由于横隔板以及横肋提供的水平向支承力可分担部分锚后牵拉力。根据参数分析结果(表 1)近似取锚后牵拉力的20%。因此,本模型锚后牵拉力设计值取锚固力设计值大小的16%,横隔板以及横肋提供一个4%锚固力设计值大小的水平向支反力,锚前顶板部分则分担剩余的水平向支反力。
(9) 根据应力等值线图 3以及顶板上缘各点的横向、纵向应力图 6,局部弯曲效应作用区域位于横隔板与横肋中间部位。本模型中局部弯曲效应横向拉力特征通过9~22杆和9~23杆模拟,横向拉力值根据参数分析结果(图 7、图 8)偏保守地取锚后牵拉力的1/3,即0.05P。
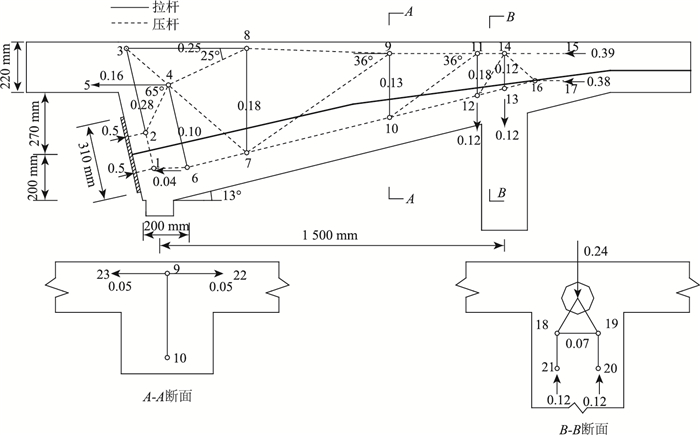
5.2 配筋设计——算例以背景工程为例进行配筋设计,抗裂钢筋的配筋量取值由上述拉压杆模型中拉杆内力控制。参照规范JTG—2018[5]的建议按照极限状态法进行锚固区的配筋设计,所需配筋量为:
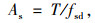
|
(1) |
式中,As为配筋面积;T为拉杆内力设计值;fsd为普通钢筋抗拉强度设计值(HRB400钢筋按规范[5]取330 MPa)。
由于已有的规范中锚固区配筋设计均未考虑混凝土抗拉强度的贡献,因此本算例配筋设计亦仅将UHPC的抗拉强度作为一种安全储备(UHPC的直接拉伸强度一般超过7 MPa,抗折强度超过30 MPa),但也不再对钢筋强度进行折减。由于UHPC具有超高的抗压强度(一般超过150 MPa),因此对压杆不再加以验算。背景工程中预应力钢束采用19束1860型ϕ15.2 mm钢绞线,按70%的控制张拉力计算,则预应力设计值为3 463 kN。锚固力设计值为1.2倍的预应力设计值,则锚固力设计值P为4 156 kN。
以上述拉压杆模型(图 11)为基础,利用桁架计算理论计算各拉杆内力,可得到背景工程中隔板连通式齿块的拉压杆模型,如图 12所示。
|
| 图 12 背景工程中齿块锚固区拉压杆模型 Fig. 12 Strut-and-tie model for anchorage zone in background project |
| |
结合规范[5, 17]对齿板锚固区关键受力部位进行配筋设计,如图 13所示,锚固区配筋量计算情况如表 2所示。配筋设计简述如下:(1)齿块锚下配置抵抗劈裂效应的闭合式箍筋,间距为100 mm,纵向范围取1.2倍齿块高度,并将箍筋插入到顶板区域与顶板纵筋形成钢筋网;(2)悬臂效应的拉应力方向以及受力范围与锚下劈裂效应基本一致,因此设计为同类钢筋共同受力,视为整体进行配筋;(3)锚后牵拉效应在横向上以锚固点为中心向两侧不断衰减,其配筋设计的横向分布范围取预应力钢筋轴线两侧各1.5倍齿块宽度范围内,钢筋间距为100 mm,为充分发挥锚后钢筋的抗裂作用,锚固钢筋长度取2.5 m;(4)根据前文计算结果(图 7~图 9),实际上局部弯曲效应拉应力值较小,远小于锚后牵拉效应,且应力迹线图 10也表明两种局部效应在顶板区域的界限不明显,因此配筋设计时将两种效应视为整体进行配筋;(5)在顶板横向部位布置2层钢筋与顶板纵向钢筋形成钢筋网络,亦用于抵抗局部弯曲作用的横向拉力,横向分布范围取力筋轴线两侧各1.5倍齿块宽度范围内;(6)预应力钢束转向区配置少量闭合式箍筋,分担部分竖向力及横向拉应力。
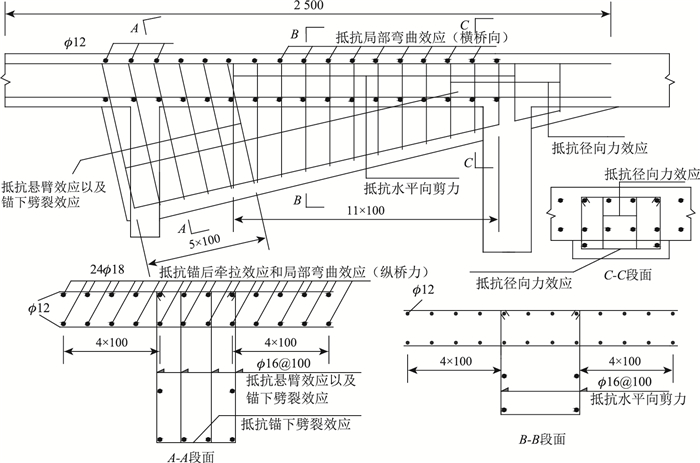
|
| 图 13 锚固区的配筋设计(单位:mm) Fig. 13 Reinforcement design for anchorage zone (unit: mm) |
| |
| 锚后牵拉力 | 悬臂效应拉力 | 局部弯曲效应拉力 | 径向力效应拉力 | 劈裂效应拉力 | 抗剪钢筋承担拉力 | ||||
| 横向 | 纵向 | 横向 | 竖向 | ||||||
| 对应拉杆内力 | T4-5 | T2-3 | T9-22 | T3-8 | T18-19 | T19-20 | T4-6 | T7-8+T9-10+T11-12-0.12P | |
| 拉杆内力大小/kN | 664.7 | 1 163.7 | 207.8 | 1 039 | 290.9 | 498.7 | 415.6 | 1 537.7 | |
| 钢筋抗拉强度设计值/MPa | 330 | 330 | 330 | 330 | 330 | 330 | 330 | 330 | |
| 需配钢筋量/mm2 | 2 014 | 3 526 | 630 | 3 148 | 882 | 1 511 | 1 259 | 4 660 | |
| 实配钢筋量/mm2 | 6 108 | 4 826 | 1 018 | — | 1 006 | 1 609 | — | 5 229 | |
6 结论
(1) 通过应力等值线分析,揭示了隔板连通式齿块锚固区的6种典型局部效应,即锚下劈裂效应、锚后牵拉效应、局部弯曲效应、径向力效应和悬臂效应以及横隔板部位的隔板弯曲效应,其中局部弯曲效应在纵桥向和横桥向的拉应力集中均较为明显。
(2) 横隔板与横肋之间的齿块压应力沿纵桥向先逐渐增大随后逐渐减小,存在核心受压区,位于距离横隔板中心线S/4~S/2的范围内(S为横隔板与横肋之间的距离)。
(3) 相比于常规独立三角齿块,隔板连通式齿块可大大降低锚固区的拉应力集中情况。增大横隔板宽度及隔板间间距能有效降低锚固区的局部效应,但当隔板宽度超过6倍齿块宽度时、隔板间距超过2 m时,下降趋势变得不明显。同一横隔板在多齿块锚固下对锚固区的负面影响较小,特别地,当齿块间距逐渐增大到6 m时,双齿块锚固效应逐渐转变为单齿块锚固效应。
(4) 基于局部效应分析结果、力流特征以及力流平衡关系提出了UHPC箱梁隔板连通式齿块锚固区拉压杆模型的基本构建方法,并通过算例展示了密集横隔板UHPC箱梁锚固区配筋设计过程,适用于该类锚固方式的工程设计。
| [1] |
LIU Z, LU Z T, HUI Z, et al. Review of Application and Research on Strut-and-tie Models for Concrete Bridges[J]. Engineering Sciences, 2008(10): 14-21. |
| [2] |
林波, 刘钊, 吕志涛. 体外预应力独立矩形齿块锚固区的拉压杆模型及配筋设计[J]. 工程力学, 2011, 28(12): 59-64. LIN Bo, LIU Zhao, LÜ Zhi-tao. Strut-and-tie Model and Reinforcement Design Method for Isolated Rectangular Anchor Block for External Tendons[J]. Engineering Mechanics, 2011, 28(12): 59-64. |
| [3] |
林波, 刘钊. 体外预应力角隅矩形齿块锚固区的拉压杆模型及配筋设计[J]. 工程力学, 2012, 29(4): 155-160, 167. LIN Bo, LIU Zhao. Strut-and-tie Model and Reinforcement Design for Corner Rectangular Anchor Block of External Tendons[J]. Engineering Mechanics, 2012, 29(4): 155-160, 167. |
| [4] |
林波, 刘钊. 预应力齿板锚固区拉压杆模型及配筋设计[J]. 公路交通科技, 2011, 28(6): 91-96. LIN Bo, LIU Zhao. S Strut-and-tie Models and Reinforcement Design for Prestressed Anchorage Plates[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 91-96. |
| [5] |
JTG 3362-2018, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG 3362-2018, Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [6] |
刘勇, 邵旭东, 詹豪. 主跨400 m的UHPC连续梁桥优化设计[J]. 公路交通科技, 2014, 31(8): 83-90. LIU Yong, SHAO Xu-dong, ZHAN Hao. Optimal Design for UHPC Continuous Box Girder Bridge with 400 m Main Span[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 83-90. |
| [7] |
徐强, 杜进生, 张劲泉. 活性粉末混凝土受压力学性能试验[J]. 公路交通科技, 2011, 28(7): 8-13. XU Qiang, DU Jin-sheng, ZHANG Jin-quan. Experiment of Mechanical Properties of Reactive Powder Concrete in Compression[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 8-13. |
| [8] |
LI C X, FENG Z, K L, et al. Experimental Study on Shear Performance of Cast-in-place Ultra-high Performance Concrete Structures[J]. Materials, 2019, 12(19): 3254. |
| [9] |
WILLE K, EI-TAWIL S, NAAMAN A E. Properties of Strain Hardening Ultra High Performance Fibre Reinforced Concrete (UHPFRC) under Direct Tensile Loading[J]. Cement and Concrete Composites, 2014, 48: 53-66. |
| [10] |
ZHOU M, LU W, SONG J W, et al. Application of Ultra-high Performance Concrete in Bridge Engineering[J]. Construction and Building Materials, 2018, 186: 1257-1266. |
| [11] |
VOO Y L, FOSTER S J, VOO C C. Ultrahigh Performance Concrete Segmental Bridge Technology:Toward Sustainable Bridge Construction[J]. Journal of Bridge Engineering, 2015, 20(8): 1-12. |
| [12] |
邵旭东, 詹豪, 雷薇, 等. 超大跨径单向预应力UHPC连续箱梁桥概念设计与初步实验[J]. 土木工程学报, 2013, 46(8): 83-89. SHAO Xu-dong, ZHAN Hao, LEI Wei, et al. Conceptual Design and Preliminary Experiment of Super-long-span Continuous Box-girder Bridge Composed of One-way Prestressed UHPC[J]. China Civil Engineering Journal, 2013, 46(8): 83-89. |
| [13] |
邱明红, 邵旭东, 甘屹东, 等. 单向预应力UHPC连续箱梁桥面体系优化设计研究[J]. 土木工程学报, 2017, 50(11): 87-97. QIU Ming-hong, SHAO Xu-dong, GAN Yi-dong, et al. Research on Optimal Design of Deck System in Longitudinal Prestressed UHPC Continuous Box Girder Bridge[J]. China Civil Engineering Journal, 2017, 50(11): 87-97. |
| [14] |
邵旭东, 张良, 张松涛, 等. 新型UHPC连续箱梁桥的体外预应力锚固构造形式研究[J]. 湖南大学学报:自然科学版, 2016, 43(3): 1-7. SHAO Xu-dong, ZHANG Liang, ZHANG Song-tao, et al. Study on Structural Forms of External Prestressing Anchorage for a Novel Continuous UHPC Box-girder Bridge[J]. Journal of Hunan University:Natural Sciences Edition, 2016, 43(3): 1-7. |
| [15] |
周威, 胡海波. 预留孔道活性粉末混凝土局压性能与承载力分析[J]. 工程力学, 2014, 31(7): 119-128. ZHOU Wei, HU Hai-bo. Analysis on Bearing Capacity and Behavior of Reactive Powder Concrete with Empty Concentric Duct under Local Pressure[J]. Engineering Mechanics, 2014, 31(7): 119-128. |
| [16] |
Euro International Committee for Concrete and International Federation for Prestressing. Practical Design of Structural Concrete[M]. London: SETO Ltd, 1999: 92-101.
|
| [17] |
AASHTO. AASHTO LRFD Bridge Design Specification[M]. Washington, D.C.: AASHTO, 2017.
|
| [18] |
ACI 318M-08, Building Code Requirements for Structural Concrete and Commentary[S].
|
| [19] |
HOU D W, ZHAO J L, SHEN J S L, et al. Investigation and Improvement of Strut-and-tie Model for Design of End Anchorage Zone in Post-tensioned Concrete Structure[J]. Construction and Building Materials, 2017(136): 482-494. |
| [20] |
BREEN J E, BURDET O, ROBERTS C, et al. Anchorage Zone Reinforcement for Post-tensioned Concrete Girders (Report 365)[R]. Washington, D. C.: Transportation Research Board, 1994.
|
 2020, Vol. 37
2020, Vol. 37
