扩展功能
文章信息
- 杨涛, 滕世权, 李国维, 李航
- YANG Tao, TENG Shi-quan, LI Guo-wei, LI Hang
- 动载下桩承式路堤中平面土拱形态演化的数值模拟
- Numerical Simulation of Evolution of 2D Soil Arch Shape in Pile Supported Embankment under Dynamic Load
- 公路交通科技, 2020, 37(5): 25-32
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 25-32
- 10.3969/j.issn.1002-0268.2020.05.004
-
文章历史
- 收稿日期: 2018-11-15
2. 中梁控股集团, 上海 200062;
3. 河海大学 道路与铁道工程研究所, 江苏 南京 210098
2. Zhongliang Holdings Group, Shanghai 200062, China;
3. Research Institute of Road and Railway Engineering, Hohai University, Nanjing Jiangsu 210098, China
桩承式路堤是近年来软土地区新型的路堤施工技术,它施工速度快,稳定性高,施工期沉降和工后沉降小,已在国内外公(铁)路建设中得到广泛应用。
桩承式路堤分为桩承式加筋路堤和无筋桩承式路堤两种类型。土拱效应计算是桩承式路堤设计的核心内容,而土拱形态是建立土拱效应计算模型的基础。Carlsson[1]和Guido等[2]分别提出平面三角形和空间金字塔形刚塑性土拱形态模型。Hewlett等[3]和Low等[4]分别提出了空间半球形和平面半圆形土拱形态模型。Zaeske等[5]提出了多拱形态模型。Van Eekelen等[6]根据加筋上倒三角形竖向应力分布特征,提出了空间同心球土拱形态模型。杨涛等[7]通过数值模拟方法获得了平面半椭圆形土拱形态模型。芮瑞、房营光和付海平等[8-10]通过室内模型试验和离散元数值方法,研究了平面土拱形态随路堤填筑的演化过程。一些国家依据不同土拱形态模型制定了桩承式路堤设计规范或手册[11-13]。
桩承式路堤竣工后承受交通动载作用。近年来动载下的土拱效应问题开始受到学者们的关注。叶阳升等[14]进行了低矮铁路桩承式加筋路堤原位动载试验,发现550万次动载下路堤中原有静力土拱处于稳定状态,动应力的传递受土拱影响不明显。韩高孝等[15]和许朝阳等[16]分别进行了动载下无筋和加筋桩承式路堤三维模型试验,发现动应力的传递仍受土拱影响,但土拱效应发生了退化,加筋减小了土拱效应削弱的程度,加筋层数的增加使动载的影响减弱。陈仁朋等[17]通过动载下铁路桩承式加筋路堤足尺模型试验证实了动载下土拱效应的存在,发现只有在动载作用次数较大时动力土拱效应才会减弱。Zhuang等[18]采用三维有限元法,研究了汽车移动荷载下桩承式加筋路堤中的动力土拱效应,并对现有的土拱效应模型进行了修正。
目前,国内外学者关于静载下桩承式路堤土拱形态、效应及其演化规律的研究取得了大量成果,行车动力荷载下土拱效应的研究也开始展开。尽管如此,目前交通荷载下土拱形态及其演化规律的研究尚未有研究成果报道。有鉴于此,并考虑到通过室内外试验研究土拱形态较为困难,本研究采用弹塑性有限元方法,对交通循环荷载下的公路无筋桩承式路堤中平面土拱形态以及相关因素的影响进行模拟分析,为建立公路桩承式路堤动力土拱形态模型提供参考。
1 平面土拱有限元模型 1.1 几何模型与边界条件地基土总厚度20 m,从上至下分别为2 m硬壳层、18 m淤泥质黏土和基岩。公路无筋桩承式路堤大面积填筑,路堤高度H=5 m,其上的沥青混凝土路面用0.4 m厚的半刚性材料近似模拟。由于研究平面土拱,假设路堤受到纵向连续分布的桩帽梁支撑。桩帽宽度a=1 m,厚度0.3 m。桩墙厚度0.4 m,间距s=2.6 m。由于桩帽梁加固的对称性,单个桩帽梁+桩间土+路堤+路面组成了“典型单元体”,如图 1所示。利用对称性,取二分之一典型单元体KJGE建立土拱静、动力分析的有限元模型。图 2给出了土拱动力分析有限元模型。模型左边界为桩帽梁的中心线,右边界为桩间土中心线。在土拱形态的有限元静力分析中,模型左、右侧边界水平向约束,竖向自由。顶部为路堤顶面,水平向和竖向都自由。

|
| 图 1 典型单元体 Fig. 1 Typical unit cell |
| |
|
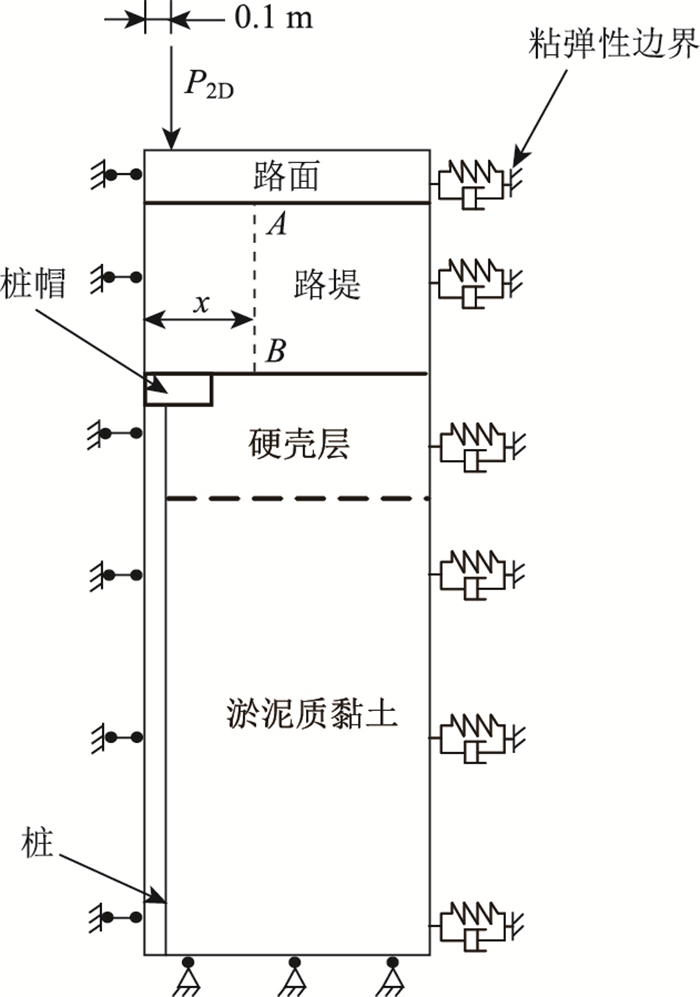
| 图 2 交通动载下有限元模型 Fig. 2 FE model under traffic dynamic load |
| |
模型底面为基岩,水平向与竖向都约束。交通动力荷载下进行土拱形态有限元分析时,考虑右侧边界上反射波的吸收和截断边界外侧土体的弹性恢复力,在模型右侧边界采用人工黏弹性边界。路面顶面水平和竖向自由,其他边界的边界条件与有限元静力分析时相同。
1.2 材料的本构模型及参数Satibi[19]调查了路堤填土本构模型的选择对土拱效应数值计算结果的影响,发现采用简单的摩尔-库伦弹塑性模型获得的桩荷载分担比与采用复杂的硬化土模型和小应变硬化土模型的数值近乎相同。基于此,本研究中无黏性路堤填土、硬壳层和淤泥质黏土采用摩尔-库伦理想弹塑性模型,桩帽、桩墙以及路面材料采用线弹性模型。各材料模型参数如表 1所示。
| 材料 | 重度/ (kN·m-3) |
弹性模量/ MPa |
泊松比 μ |
凝聚力/ kPa |
内摩擦角/ (°) |
动弹模量/ MPa |
阻尼系数/ (kN·s·m-1) |
刚度系数/ (kN·m-1) |
| 路堤 | 17 | 25 | 0.30 | 1 | 30 | 75 | 239 | 369 |
| 硬壳层 | 17 | 15.56 | 0.31 | 33.7 | 21.17 | 46.68 | 197 | 228 |
| 桩帽 | 24 | 25 500 | 0.15 | — | — | 76 500 | — | — |
| 桩墙 | 24 | 22 000 | 0.20 | — | — | 66 000 | — | — |
| 路面 | 17.5 | 4 134 | 0.30 | — | — | 12 402 | 3 121 | 61 153 |
| 淤泥质黏土 | 16.8 | 1.7 | 0.35 | 18.0 | 10.3 | 5.1 | 68 | 24 |
人工黏弹性边界中弹簧-阻尼单元的刚度系数kb和阻尼系数cb按下式计算[20]:
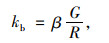
|
(1) |
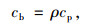
|
(2) |
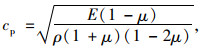
|
(3) |
式中,G,E和ρ分别为剪切模量、弹性模量和质量密度;μ和cp分别为泊松比和纵波波速;R为散射波源至人工黏弹性边界的距离,本研究取为动载作用点到竖向黏弹性边界的平均距离,R=13 m。β为修正系数,参考Han等人[21]的研究,本研究取β=0.5。各材料阻尼系数和刚度系数的计算结果也列于表 1中。
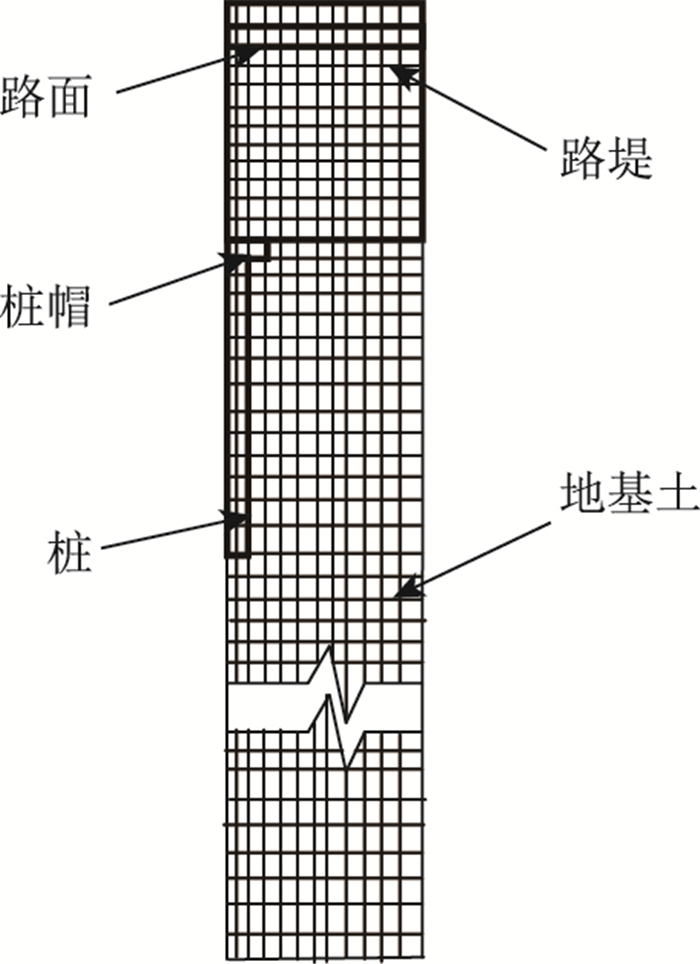
采用大型有限元软件ADAIN进行静动力荷载下土拱形态的数值模拟分析。各材料均采用四边形4结点单元进行离散。由于动、静荷载下端承刚性带帽桩-土间的差异沉降较小,此时桩帽-土界面性质对土拱的影响不大[21],故桩帽-路堤填土之间和桩墙-地基土之间未设置接触单元。单元总数3 432个,节点总数3 710个。图 3给出有限元网格示意图。为近似模拟路堤分级填筑,每级填筑0.25 m。
|
| 图 3 有限元网格 Fig. 3 FE mesh |
| |
1.3 交通荷载
将行驶在公路上的车辆产生的交通循环荷载采用正弦波振动来模拟。三维情况下交通行车载P3D可按式(4)计算[18]:
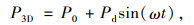
|
(4) |
式中,P0为车辆轮载,是车辆总荷载的静载部分。Pdsin(ωt)为车辆总荷载的动载部分;ω为振动圆频率。动载幅值Pd按下式计算:
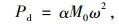
|
(5) |
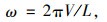
|
(6) |
式中,M0为车辆簧下质量; α为路面不平顺情况下的矢高; L为车辆长度; V为车辆速度; t为加荷时间。参照文献[18],本研究取P0=50 kN,M0=250 N·s2/m,α=2 mm,L=6 m。
沿公路纵向取1 m,车辆轮胎宽度取0.2 m,则平面应变条件下交通行车均布荷载p2D分布在0.2 m×1 m范围内,数值按式(7)计算[22]:
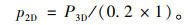
|
(7) |
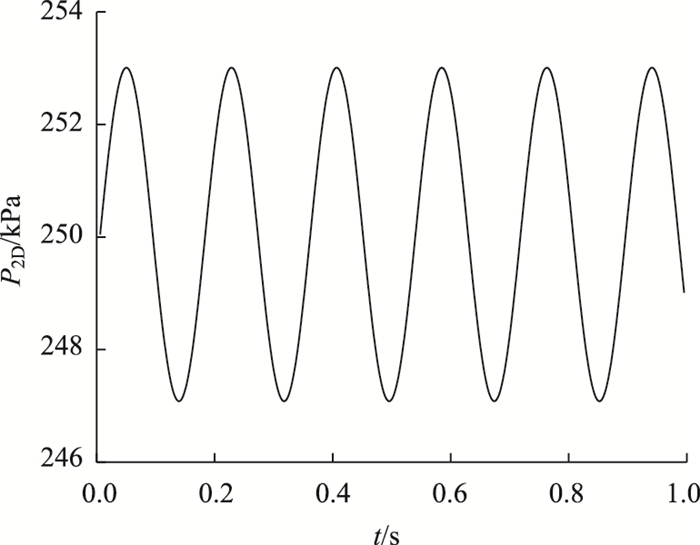
取车辆轮距2.4 m,将车辆的中轴线与桩间土中心线重合,由于对称性,在有限元模型中p2D的合力P2D作用线距桩帽中心线0.1 m,如图 2所示。图 4给出车速V=120 km/h时p2D随时间变化曲线。
|
| 图 4 p2D-t曲线 Fig. 4 p2D-t curve |
| |
2 循环动载下的土拱现象
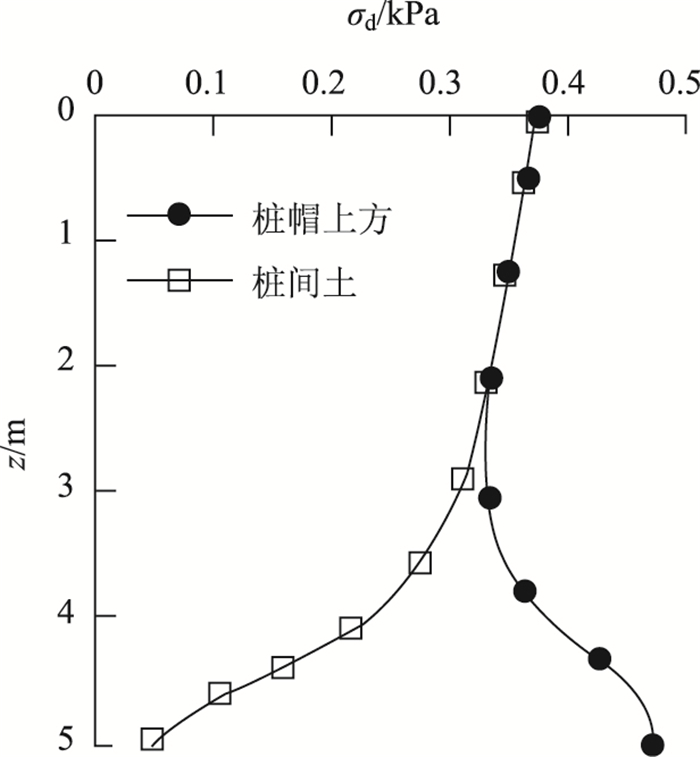
为研究循环动力荷载引起的动应力在桩帽-土间的分担与传递特性,考虑路基路面仅受到车辆荷载中的循环动载Pdsin(ωt)作用,车速V=120 km/h。用有限元法计算出H=5 m路堤中第500周期波峰时刻桩帽中心线和桩间土中心线处的竖向动应力σd沿路堤深度z分布曲线,如图 5所示。从图 5中可见,经过刚度较大的路面后路堤表面动应力有较大的衰减。在路堤一定深度范围内,桩帽上方和桩间土上方竖向动应力线完全重合,且沿路堤深度线性减小。超过该深度后两条动应力线彼此分离,桩帽上方路堤中的动应力要大于桩间土上方的动应力。桩帽上方路堤中的动应力随着深度的增加逐渐增大,靠近基底时又开始略微变小。桩间土上方路堤中的动应力随深度逐渐减小,桩帽-土动应力比nd=10。有限元计算表明,车辆荷载引起的动应力在桩帽和桩间土之间传递仍然受土拱效应控制,这种动力土拱效应必然会影响路堤中已有的静力土拱形态。
|
| 图 5 桩帽与桩间土上方竖向动应力分布曲线 Fig. 5 Curves of vertical dynamic stress distribution above pile cap and pile-soil |
| |
3 交通荷载下的土拱形态 3.1 土拱形态曲线的确定
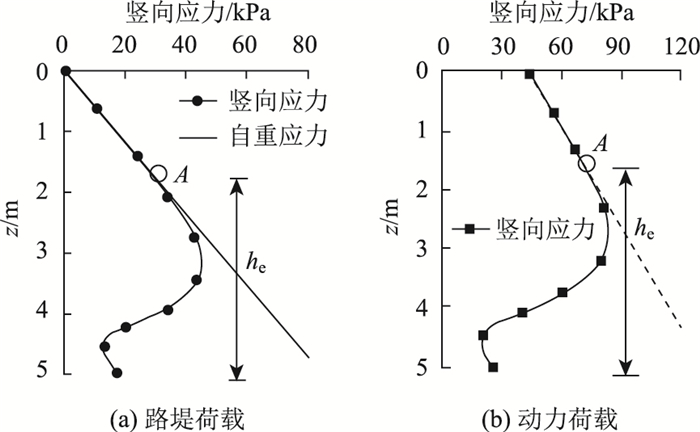
考虑静载(路堤荷载)和路堤+路面+交通动力荷载(简称动载)二种荷载情况,图 6给出桩间土上方路堤中距离桩帽中心x的任一竖直截面AB上的竖向应力沿路堤深度分布曲线示意图。若仅受路堤自重荷载作用(图 6(a)),当路堤填筑到给定高度时,由于存在土拱效应,该截面上某一深度以上竖向应力线与自重应力线重合,而在该深度以下的路堤中出现剪应力,路堤竖向应力小于相应的自重应力,偏离点A一定在静载下的土拱(静力土拱)上。室内试验和数值模拟发现[16, 18],当路面受到车辆交通动力荷载后,桩间土上方路堤中任一截面的上竖向应力分布曲线由直线段和曲线段两部分组成,如图 6(b)所示。参考魏静等[23]的方法,可根据竖向应力分布线偏离直线段的点A确定交通动力荷载作用下的土拱(动力土拱)曲线坐标。设A点距基底的距离为he,在桩间土表面取一系列点xi,计算过xi点的路堤竖直截面上土拱形态曲线坐标(xi,hei),然后选择适当的曲线进行拟合,即可得到静力土拱或动力土拱的形态曲线方程。
|
| 图 6 静、动载下土拱坐标的确定 Fig. 6 Determination of coordinates of soil arch under static and dynamic loads |
| |
3.2 交通动载下既有土拱形态的演化
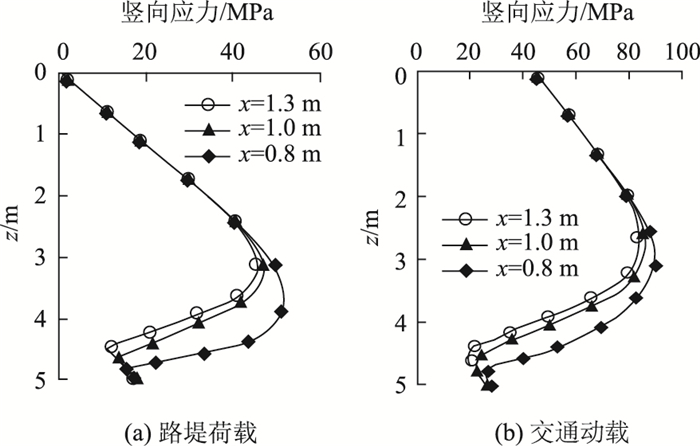
桩间距一定时完整土拱的形成需要路堤达到足够的高度。本研究有限元计算发现,路堤高度H超过3.5 m后可形成完整土拱。此外,如图 5所示,路堤中的动应力沿深度逐渐衰减。基于这两点,路堤高度取较低的H=3.5 m和较高的H=5 m两种情况进行分析。交通动力荷载作用时取车速V=120 km/h。在桩间土上方路堤中选择了x分别为0.7,0.8,0.9,1.0,1.1,1.2 m和1.3 m共7个竖直截面,通过有限元法分别计算出路堤静力荷载和交通动力荷载作用到第N=500个周期波峰时这些截面上的竖向应力,部分竖向应力分布曲线如图 7所示。按前述方法计算出静、动荷载下土拱形态曲线坐标(xi,hei),在x-y坐标系下用不同的曲线对这两个不同高度路堤中的土拱曲线点进行拟合,发现用椭圆曲线拟合效果最好,相关系数的平方(R2)数值都超过了0.95,拟合方程如下:
|
| 图 7 静、动荷载下竖向应力分布曲线 Fig. 7 Vertical stress distribution curves under static and dynamic loads |
| |
(1) H=3.5 m
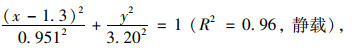
|
(8) |
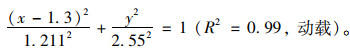
|
(9) |
(2) H=5 m
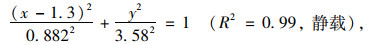
|
(10) |
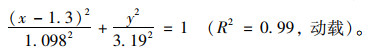
|
(11) |
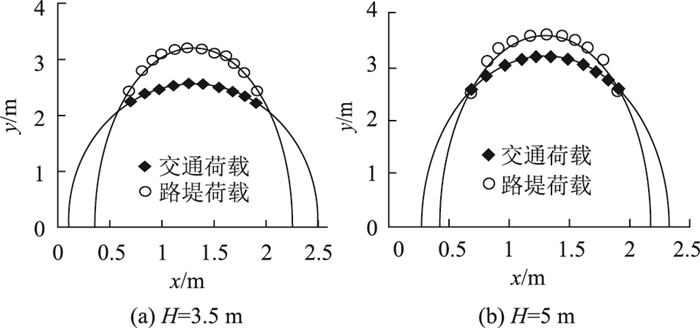
图 8给出有限元计算获得的不同高度路堤中静、动力土拱坐标点和相应的土拱形态曲线。由图 8和式(8)~(11)可以发现:(1)路堤荷载下静力土拱的形态是半个椭圆,H=3.5 m和H=5 m时静力土拱的高度分别为3.2 m和3.58 m,跨度分别为1.9 m和1.76 m。路堤较高时静力土拱的高度较大,但跨度较小,拱跨均大于桩帽净距s-a=1.5 m,说明静力土拱的拱脚落在桩帽上。(2)交通动力荷载施加后,路堤中的动力土拱形态仍然是半个椭圆,H=3.5 m和H=5 m时动力土拱的高度分别为2.55 m和3.19 m,跨度分别为2.42 m和2.20 m。动力土拱的高度也随路堤高度的增加而增大,其跨度随路堤高度的增加而减小,动力土拱也坐落在桩帽上。(3)与静力土拱相比,动力土拱的高度变小,跨度增大。路堤高度H=3.5 m和5 m时,交通动载作用下土拱高度分别下降了20.3%和10.9%。有限元计算表明,交通动载施加后路堤中原有土拱的半椭圆形态并没有变化,但土拱的高度降低了,拱跨变大了。静、动力土拱都坐落在桩帽上。
|
| 图 8 静、动荷载下土拱形态的比较 Fig. 8 Comparison of soil arch shapes under static and dynamic loads |
| |
4 动力土拱形态影响因素分析
土拱高度是土拱的重要形态参数。下面通过参数分析,研究行车车速V、动载作用周期N、路堤高度H和路堤填料内摩擦角φ的变化对动力土拱高度H0的影响。基准参数如下:H=5 m,a=1 m,s=2.6 m,φ=30°,V=120 km/h。每次计算变化一个参数,其他参数保持不变。计算的土拱高度是相应周期中波峰时刻的值。
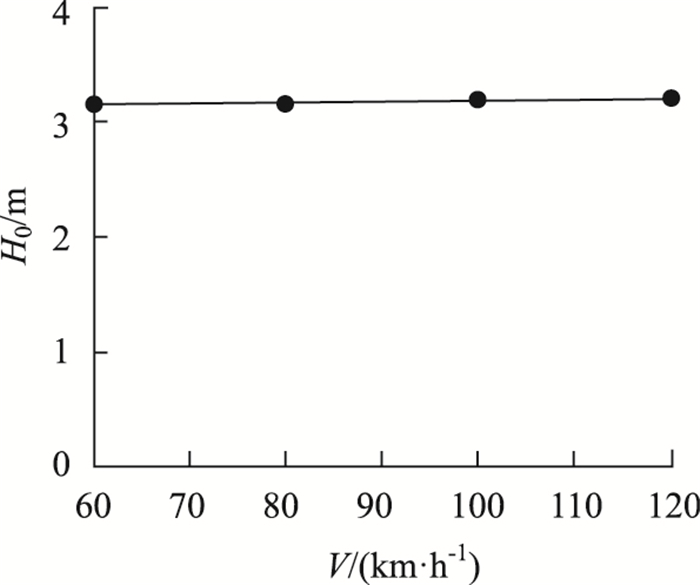
图 9给出行车荷载作用到N=500时动力土拱高度H0随车速V的变化曲线。从图 9中可见,路堤中动力土拱高度随车速的增加而增大,但增幅非常小,车速从60 km/h增加到120 km/h,土拱高度由3.14 m增加到3.19 m,增幅仅1.6%。计算表明,车速对动载下土拱高度的影响很小。
|
| 图 9 动力土拱高度随车速变化曲线 Fig. 9 Curve of H0 varying with V |
| |
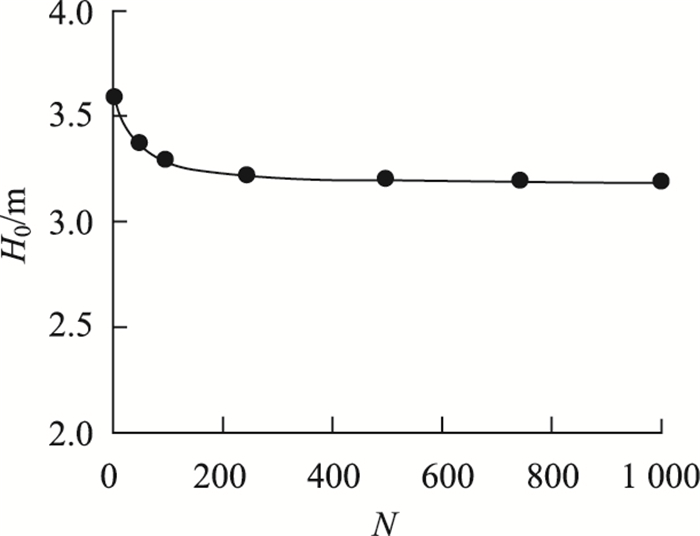
图 10给出动力土拱高度H0随动载作用周期N的变化曲线,N=0时的土拱高度是静力土拱的高度。图 10清楚地表明,动力土拱高度随动载作用周期的增加逐渐减小,前100周期中动力土拱高度下降幅度较大,拱高由静力土拱时3.58 m下降到N=100时的3.29 m,降幅占拱高总降幅的74%。动载作用周期N超过250后动力土拱高度稳定不变,稳定的动力土拱高度H0=3.19 m。
|
| 图 10 动力土拱高度随动载作用周期变化曲线 Fig. 10 Curve of H0 varying with N |
| |
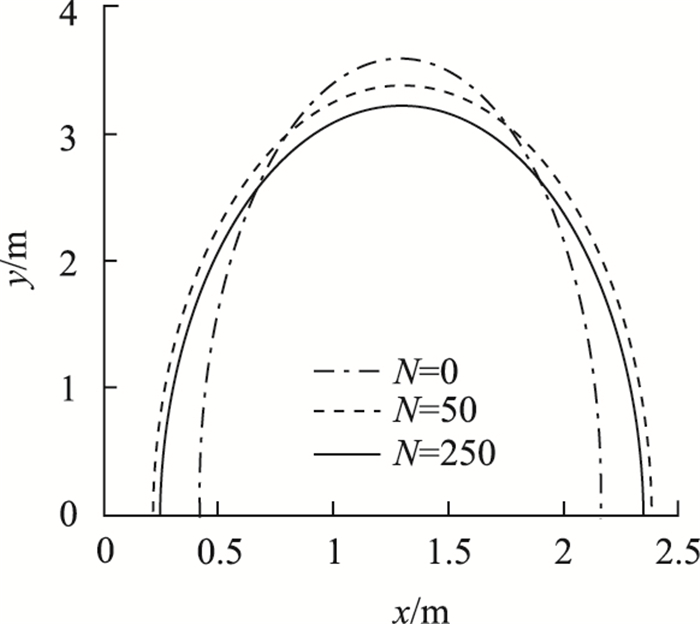
为分析交通动载作用周期对动力土拱形态的影响,有限元法计算并拟合出N=50,100,250和500时动力土拱形态曲线。由于各曲线彼此靠得较近,为便于观察和比较,图 11仅给出N=0,50和250时的动力土拱形态曲线。有限元计算再一次表明,动力土拱的高度小于静力土拱,动力土拱的跨度大于静力土拱。N=50,100和250时动力土拱的高度分别为3.36,3.29 m和3.20 m,相应的土拱跨度分别为2.17,2.13 m和2.12 m,N>250后动力土拱形态曲线几乎不再随N变化。图 10和图 11表明,随着动载作用周期N的增加,椭圆形动力土拱的高度逐渐降低然后趋于稳定,但其跨度仅略微减小。
|
| 图 11 动力土拱形态曲线随动载周期的变化 Fig. 11 Curves of dynamic soil arch shape varying with N |
| |
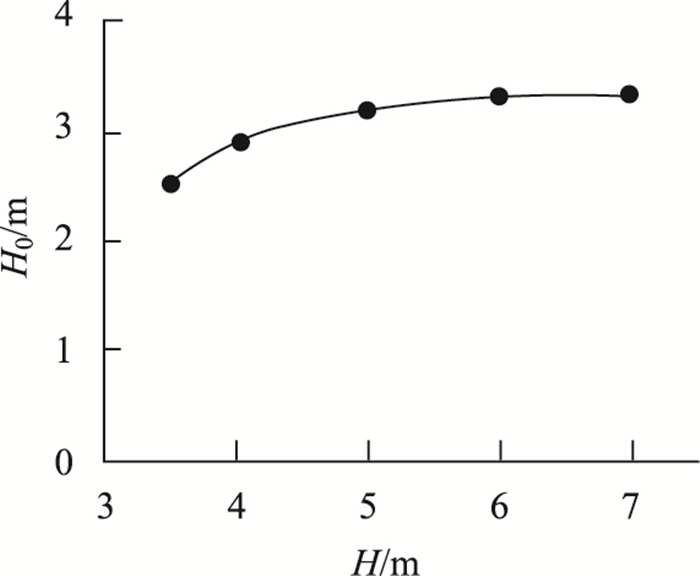
图 12给出N=500时动力土拱高度H0随路堤高度H变化曲线。由图 12可知,交通动载作用下桩承式路堤中动力土拱高度随路堤高度的增加先增加后稳定不变。对于所研究的工况,路堤高度超过6 m后动力土拱的高度稳定在H0=3.32 m不再随路堤高度的增加而变化。计算中还发现,伴随着土拱高度的逐渐增大土拱跨度逐渐减小,稳定的土拱跨度约为2.13 m。
|
| 图 12 动力土拱高度随路堤高度变化曲线 Fig. 12 Curve of H0 varying with H |
| |
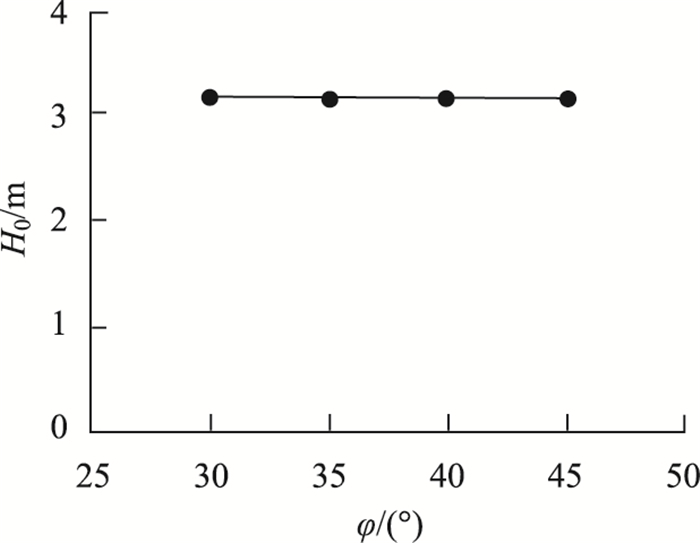
图 13给出N=500时动力土拱高度H0随路堤填土内摩擦角φ的变化曲线。从图 13中可以发现,土拱高度约稳定在3.19 m,路堤填土内摩擦角的变化对动力土拱高度几乎没有影响。
|
| 图 13 动力土拱高度随路堤内摩擦角变化曲线 Fig. 13 Curve of H0 varying with φ |
| |
5 结论
采用数值模拟方法研究公路桩承式无筋路堤在交通循环荷载作用下平面土拱的形态及演化规律,分析了各因素对动力土拱高度的影响,主要结论如下:
(1) 纯动应力在桩帽和桩间土中的传递受到动力土拱效应的控制。公路通车运营后路堤中既有的静力土拱形态曲线在交通动载作用下会发生变化。
(2) 桩承式无筋路堤中的静力土拱呈半椭圆形。交通循环动荷载的施加使静力土拱的高度降低,跨度增大,动力土拱仍为半椭圆形。
(3) 桩承式无筋路堤中动力土拱的高度随路堤高度的增加而增大,其跨度随之逐渐减小。路堤高度超过一定值以后动力土拱形态曲线稳定不变。
(4) 动力土拱高度随动载作用周期的增加逐渐降低,其跨度仅略微减小。动载作用周期超过一定数值后动力土拱形态曲线稳定不变。
(5) 行车速度和路堤内摩擦角的变化对动力土拱形态的影响很小。
| [1] |
CARLSSON B O. Reinforced Soil, Principles for Calculation[M]. Linköping: Terratema AB, 1987.
|
| [2] |
GUIDO V A, KNUEPPEL J D, SWEENY M A. Plate Loading Tests on Geogrid-reinforced Earth Slabs[C]//Proceedings of the Geosynthetics'87, New Orleans: IFAI, 1987: 216-225.
|
| [3] |
HEWLETT W J, RANDOLPH M F. Analysis of Piled Embankments[J]. Ground Engineering, 1988, 21(3): 12-18. |
| [4] |
LOW B K, TANG S K, CHOA V. Arching in Piled Embankments[J]. Journal of Geotechnical Engineering, 1994, 120(11): 1917-1938. |
| [5] |
ZAESKE D, KEMPFERT H G. Calculation and Behavior of Unreinforced and Reinforced Bearing Layers over Point-or Line shaped Searing Elements[J]. Bauingenieur, 2002, 77(2): 80-86. |
| [6] |
VAN EEKELEN S J M, BEZUIJEN A, VAN TOL A F. An Analytical Model for Arching in Piled Embankments[J]. Geotextiles and Geomembranes, 2013, 39: 78-102. |
| [7] |
杨涛, 王刚刚, 闫业强, 等. 桩承式路堤中土拱形态与成拱过程中土拱效应研究[J]. 岩土工程学报, 2014, 36(4): 731-735. YANG Tao, WANG Gang-gang, YAN Ye-qiang, et al. Shape of Soil Arching and Development of Its Effect in a Piled Embankment[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 731-735. |
| [8] |
芮瑞, 胡港, 夏元友, 等. 砂填料桩承式路堤宏观土拱形态与演化模型[J]. 岩石力学与工程学报, 2014, 33(2): 396-404. RUI Rui, HU Gang, XIA Yuan-you, et al. Macroscopic Soil Arch Shape and Evolution Model of Sand Filling Piled Embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 396-404. |
| [9] |
房营光, 侯明勋, 谷任国, 等. 桩承式路堤中土拱效应产生过程可视化分析[J]. 岩土工程学报, 2015, 37(9): 1678-1684. FANG Ying-guang, HOU Ming-xun, GU Ren-guo, et al. Visual Analysis of Initiation of Soil Arching Effect in Piled Embankments[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1678-1684. |
| [10] |
付海平, 郑俊杰, 赖汉江. 桩承式路堤"土拱结构"形成演化规律离散元分析[J]. 岩土工程学报, 2017, 39(11): 2050-2057. FU Hai-ping, ZHENG Jun-jie, LAI Han-jiang. Discrete Element Analysis of the Development and Evolution of "Soil Arching" within a Piled Embankment[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2050-2057. |
| [11] |
BS8006-2010. Code of Practice for Strengthened/Reinforced Soils and Other Fills[S].
|
| [12] |
EBGEO. Recommendations for Design and Analysis of Earth Structures Using Geosynthetic Reinforcements, English Version[S]. Berlin: Wilhelm Ernst & Sohn, 2011.
|
| [13] |
Nordic Geotechnical Society. Nordic and Book-reinforced Soils and Fills[S].Stockholm: Nordic Geotechnical Society, 2004.
|
| [14] |
叶阳升, 张千里, 蔡德钩, 等. 高速铁路桩网复合地基低矮路基动静荷载传递特性研究[J]. 高速铁路技术, 2010, 1(1): 10-15. YE Yang-sheng, ZHANG Qian-li, CAI De-gou, et al. On Static and Dynamic Load Transfer Peculiarity of Low Embankment for High Speed Railway Pile-net Composite Foundation[J]. High Speed Railway Technology, 2010, 1(1): 10-15. |
| [15] |
韩高孝, 宫全美, 周顺华. 列车动荷载下桩网结构路基土拱效应试验研究[J]. 岩土力学, 2014, 35(6): 1600-1606. HAN Gao-xiao, GONG Quan-mei, ZHOU Shun-hua. Experimental Study of Soil Arching Effect in Geogrid Reinforced Pile Supported Embankment under Train Dynamic Load[J]. Rock and Soil Mechanics, 2014, 35(6): 1600-1606. |
| [16] |
许朝阳, 周峰, 吕惠, 等. 动荷载下桩承式路堤的承载特性及机制研究[J]. 岩土力学, 2014, 35(11): 3231-3239. XU Chao-yang, ZHOU Feng, LÜ Hui, et al. Bearing Behavior and Mechanism of Pile-supported Embankment under Dynamic Load[J]. Rock and Soil Mechanics, 2014, 35(11): 3231-3239. |
| [17] |
陈仁朋, 汪焱卫, 陈金苗, 等. 大振次列车动荷载作用下桩网加筋路堤土拱效应模型试验研究[J]. 铁道学报, 2015, 37(9): 107-113. CHEN Ren-peng, WANG Yan-wei, CHEN Jin-miao, et al. Experimental Study on Soil Arching Effect in Pile-supported Reinforced Embankment under Dynamic Train Loads with Large Number of Vibration Cycles[J]. Journal of the China Railway Society, 2015, 37(9): 107-113. |
| [18] |
ZHUANG Y, WANG K Y. Finite-Element Analysis of Arching in Highway Piled Embankments Subjected to Moving Vehicle Loads[J]. Géotechnique, 2018, 68(10): 857-868. |
| [19] |
SATIBI S. Numerical Analysis and Design Criteria of Embankment on Floating Piles[D]. Stuttgart: University of Stuttgart, 2009.
|
| [20] |
张燎军, 张慧星, 王大胜, 等. 黏弹性人工边界在ADINA中的应用[J]. 世界地震工程, 2008, 24(1): 12-16. ZHANG Liao-jun, ZHANG Hui-xing, WANG Da-sheng, et al. The Application of Artificial Viscous-spring Boundary in ADINA[J]. World Earthquake Engineering, 2008, 24(1): 12-16. |
| [21] |
HAN G X, GONG Q M, ZHOU S H. Soil Arching in a Piled Embankment under Dynamic Load[J]. International Journal of Geomechanics, 2015, 15(6): 04014094. |
| [22] |
田飞, 褚进晶. 交通荷载特性及其模拟方法研究[J]. 水利与建筑工程学报, 2014, 12(4): 66-71, 161. TIAN Fei, CHU Jin-jing. Research on Traffic Load Characteristics and Simulation Methods[J]. Journal of Water Resources and Architectural Engineering, 2014, 12(4): 66-71, 161. |
| [23] |
魏静, 魏平, 杨松林, 等. 列车荷载下的桩网结构低路基土拱效应[J]. 交通运输工程学报, 2015, 15(6): 35-44. WEI Jing, WEI Ping, YANG Song-lin, et al. Soil Arching Effect of Low Subgrade with Pile-net Structure under Train Load[J]. Journal of Traffic and Transportation Engineering, 2015, 15(6): 35-44. |
 2020, Vol. 37
2020, Vol. 37
