扩展功能
文章信息
- 易富, 葛丽娜, 赵琪琪
- YI Fu, GE Li-na, ZHAO Qi-qi
- 基于颗粒离散元的沥青混合料尺寸效应及影响因素
- Study on Size Effect and Influence Factors of Asphalt Mixture Based on Particle Discrete Element
- 公路交通科技, 2020, 37(5): 1-10
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(5): 1-10
- 10.3969/j.issn.1002-0268.2020.05.001
-
文章历史
- 收稿日期: 2018-12-18
尺寸效应是岩石、混凝土等脆性材料存在的普遍现象,主要表现为材料力学性能的离散性和体积效应。沥青混合料与混凝土材料类似,具有非均质特性,沥青混合料的宏观破坏是其内部微结构的扩展, 成核, 演化至最终贯通的结果,而沥青混合料内部微结构的扩展演化过程主要受其颗粒级配、尺寸等影响。为准确描述尺寸影响下的不同级配沥青混合料力学性能上的差异,系统研究沥青混合料的尺寸效应现象显得尤为重要。
近年来,国内外诸多学者从试验、理论和数值模拟等方面对于岩石、混凝土等脆性材料的尺寸效应现象进行了研究,并取得了丰富的成果。王青元、朱万成等[1]通过建模、室内试验和数值模拟等手段研究岩石长期强度的尺寸效应。苏捷[2]通过抗压试验,系统研究了不同强度等级普通混凝土和高强混凝土试件立方体抗压强度的尺寸效应。刘建友等[3]通过分析不同结构围岩的变形机制,研究了隧道围岩变形的尺寸效应与围岩的变形机制存在密切的关系。梁正召等[4]基于物理力学试验与细观参数统计分布和统计宏观节理分布理论,提出一种从细观层次、宏观层次的多尺度岩体工程计算方法,并建立2种尺度效应的联系。李冬等[5]采用数值模拟手段,从混凝土材料本身的非均质性和钢筋混凝土相互作用力学行为的高度复杂性两个方面探究了钢筋混凝土构件的尺寸效应行为的根源。Syroka-Korol E[6]等对具有纵向钢筋且没有抗剪钢筋的混凝土梁进行了试验,表明在混凝土梁中存在明显的尺寸效应。除了常规的抗压、抗拉、抗剪等性能外,对于材料其他性能的尺寸效应研究逐渐增多。程志诚等[7]研究了水泥砂浆立方体试件劈拉强度的尺寸效应,探索试件劈拉面上的水平拉应力分布规律以及试件的劈拉破坏机理。屈彦玲等[8]利用有限元方法进行碾压混凝土的细观损伤断裂和劈裂抗拉数值模拟,对其劈裂抗拉强度及其尺寸效应进行了研究。Wang Y[9]等研究了尺寸对峰值轴向应力、峰值轴向应变、复合弹性模量和延性系数的影响。Li D等[10]通过轴向压缩试验对几何相似的钢筋混凝土(RC)柱进行了尺寸效应研究,结果表明具有较高长细比、较低配筋率和较高混凝土强度等级的RC柱具有较强的尺寸效应。Barbhuiya S等[11]通过考虑具有一些特定缺陷的3种类型的梁柱连接进行试验,并对每种类型的3种不同尺寸的试样进行评估,观察到每单位体积的试样能量耗散以及应力随相对挠度的变化,表明存在尺寸效应。Reddy D V等[12]对钢筋混凝土构件耐火性的尺寸效应现象进行了深入的研究,结果表明,在相似载荷比下的耐火性随着构件横截面尺寸和混凝土保护层厚度的增加而增加。
目前,国内外学者关于脆性材料的尺寸效应开展了大量研究,并取得了丰硕成果。但关于试样尺寸对沥青混合料力学特性的影响鲜见报道。因此,利用颗粒流数值模拟软件(PFC2D)开展了不同级配、不同尺寸对沥青混合料强度特性的尺寸效应及其影响因素研究,并基于此进行了沥青混合料抗压强度临界尺寸和临界强度的计算。研究成果对于基础研究中试样的制备、工程中路面结构的施工指导及沥青混合料耐久性的提高具有重要意义。
1 数值模型构建及细观参数设定 1.1 试验分组沥青混合料内部结构不均匀性的主要影响因素为最大公称粒径和级配组成,在沥青混合料中,粗集料占比较大,发生破坏的主要原因是低强度单元或缺陷主要集中于粗集料和沥青砂浆的界面处,而沥青砂浆内部含有的缺陷较少,可将其看作均质材料,因此可以认为粗集料对沥青混合料的尺寸效应影响较大[13-14]。为避免单一级配模拟结果的偶然性,以SMA-16试件为例,研究了5组不同级配情况下的尺寸效应,各组级配曲线见图 1。

|
| 图 1 级配曲线图 Fig. 1 Gradation curves |
| |
粗集料比CA用于评价矿料中粗集料的含量和分析空隙特征,其计算公式如下:

|
(1) |
式中,PD/2为粒径为D/2(D为公称最大粒径)的通过率;PPCS为第一控制筛孔的通过率。
将5组级配计算得到CA值如表 1所示。根据工程实践,考虑最佳压实特性的CA范围为0.4~0.8,级配A,B,C,D的CA值均在0.4~0.8之间,满足级配良好条件值,能形成较好的骨架结构,而级配E的粗集料比CA值略小于0.4,结构不良。
| 级配 | 合成级配 A |
合成级配 B |
合成级配 C |
合成级配 D |
合成级配 E |
| 粗集料比CA | 0.444 8 | 0.461 7 | 0.501 1 | 0.559 6 | 0.329 4 |
1.2 模型建立
表征单元体是材料力学性质尺寸效应的反映,细观上包含着混合料应具备的内部结构性质,宏观上能够代表整体性能的最小尺寸。为表征沥青混合料的整体性能,采用直观确定法[15]将沥青混合料的微细观结构力学效应进行均一化以表征单元体的宏观性质。采用PFC2D建立数值计算模型,建模时改变以往利用球体代替集料的粗糙建模方式。首先由所设定的最小直径单元颗粒粘结组成不规则集料颗粒,在指定尺寸的矩形空间内随机生成具有级配特征的集料。用规则排列颗粒填充矩形空间的孔隙部分,形成沥青砂浆模型。最后在砂浆单元部分随机删除一定数量的单元作为空隙,形成具有一定孔隙率的沥青混合料数值计算模型。考虑SMA的最大公称粒径、标准马歇尔试验试件尺寸以及路面常用结构层厚度等因素,拟定划分试件尺寸高宽比均为1:2,共建立5种尺寸大小模型,分别为20 mm×40 mm,40 mm×80 mm,60 mm×120 mm,80 mm×160 mm,100 mm×200 mm,如图 2所示。

|
| 图 2 沥青混合料试件尺寸划分方式(单位:mm2) Fig. 2 Size division of asphalt mixture samples(unit:mm2) |
| |
1.3 细观参数设定
颗粒流数值计算时微观参数的标定普遍利用“试错法”,先研究单个或组合无量纲参数的影响,同时保持其他变量不变,然后将模拟获取的宏观力学参数与试样室内试验结果对比,反复对细观力学参数进行调试[16]。本研究利用40 mm×80 mm,60 mm×120 mm两种尺寸试样进行细观参数标定,最终获取理想的数值模型细观力学参数,如表 2所示。
| PFC模型参数 | PFC命令 | 砂浆内部参数 | 砂浆与集料参数 |
| 开尔文单元法向刚度Kkn/ (MPa·mm·s) |
bur_knk | 187.4 | 374.81 |
| 开尔文单元法向黏度Ckn/ (MPa·mm) |
bur_cnk | 3 467.4 | 6 934.8 |
| 麦克斯韦单元法向刚度Kmn/ (MPa·mm·s) |
bur_knm | 164.2 | 82.4 |
| 麦克斯韦单元法向黏度Cmn/ (MPa·mm) |
bur_cnm | 36 767.7 | 73 523.5 |
| 开尔文单元切向刚度Kks/ (MPa·mm·s) |
bur_ksk | 74.9 | 149.9 |
| 开尔文单元切向黏度Cks/ (MPa·mm) |
bur_csk | 1 386.9 | 2 773.9 |
| 麦克斯韦单元切向刚度Kms/ (MPa·mm·s) |
bur_ksm | 65.7 | 32.9 |
| 麦克斯韦单元切向黏度Cms/ (MPa·mm) |
bur_csm | 14 704.7 | 29 409.4 |
结果表明,虚拟试验应力应变曲线变化趋势同室内试验[17]基本一致(图 3),二者的差别主要在峰值强度方面,考虑到研究沥青混合料试件尺寸效应现象旨在寻找沥青混合料的抗压强度与试件尺寸之间存在的规律,因此标定的细观参数满足数值试验要求。

|
| 图 3 室内试验与虚拟试验对比 Fig. 3 Comparison of indoor test and virtual test |
| |
2 尺寸效应分析及参数计算 2.1 应力-应变曲线特征
对不同级配类型下各尺寸试样开展单轴压缩数值试验[18],获得不同级配下沥青混合料的应力-应变曲线,且曲线变化规律相同。由于篇幅有限,本研究以B、C两组级配为例,分析沥青混合料在单轴压缩过程的应力应变特征。B、C组应力应变曲线如图 4、图 5所示。

|
| 图 4 B组级配应力-应变曲线 Fig. 4 Stress-strain curves of gradations of group B |
| |

|
| 图 5 C组级配应力-应变曲线 Fig. 5 Stress-strain curves of gradations of group C |
| |
数值试验结果表明,不同级配、相同级配不同尺度条件下沥青混合料的应力-应变曲线类似,可分为压密阶段、弹性阶段和向塑性变形过渡直至破坏阶段。由图 4、图 5可知,沥青混合料的压密阶段并不明显,试样受力后很快进入弹性阶段,这是因为内部的孔隙、裂隙较为均匀且孔隙裂隙非常细小,导致其在压力作用下产生非常小的变形后即完成了试件的压密。沥青混合料的线弹性阶段维持时间较长且线性较好,该阶段主要发生新裂隙的产生和原有裂隙的稳定扩展。沥青混合料应力-应变曲线存在明显的屈服阶段,即存在一点使试件由弹性转变为塑性,此点应力值接近峰值强度,经过此点后试样内部新生产的孔隙、裂隙不断扩展,演化,贯通,形成宏观裂纹。当达到峰值强度后,宏观裂纹贯穿试样,试样发生破坏。
由图 4、图 5知,级配相同时,试件尺寸越小其峰值强度越大,且随着尺寸的增大,试件峰值强度的差距逐渐减小;同时,尺寸越小,试件的峰值强度所对应的应变较大,且随着尺寸的增大,峰值强度所对应的应变差距逐渐减小。不同级配情况下,试样的应力-应变曲线随尺寸的变化表现出相同的规律,说明沥青混合料是否具备尺寸效应现象不会因级配组成的变化而改变。
2.2 抗压强度的尺寸效应分析单轴压缩试验得到的5种级配条件下不同尺寸试件的单轴抗压强度值如表 3所示。
| 试件尺寸/ (mm×mm) |
单轴抗压强度/MPa | ||||
| 级配A | 级配B | 级配C | 级配D | 级配E | |
| 20×40 | 5.183 0 | 5.188 9 | 5.007 8 | 4.993 2 | 5.209 5 |
| 40×80 | 4.635 8 | 4.441 0 | 4.570 2 | 4.508 4 | 4.891 2 |
| 60×120 | 4.306 5 | 4.323 9 | 4.431 3 | 4.303 2 | 4.586 3 |
| 80×160 | 4.203 2 | 4.280 8 | 4.339 0 | 4.231 7 | 4.234 5 |
| 100×200 | 4.150 4 | 4.262 3 | 4.316 5 | 4.209 1 | 4.204 0 |
根据表 3中数据,绘制不同级配条件下的沥青混合料的单轴抗压强度与试样尺寸关系图,如图 6所示。

|
| 图 6 沥青混合料试件单轴抗压强度折线图 Fig. 6 Fold lines of uniaxial compressive strength of asphalt mixture samples |
| |
以表 3中级配A为例进行分析计算,20 mm×40 mm的试件所对应的单轴抗压强度为5.183 0 MPa,40 mm×80 mm试件的抗压强度为4.635 8 MPa,下降幅度为10.6%,试件由40 mm×80 mm增大到60 mm×120 mm抗压强度下降幅度为7.1%,试件由60 mm×120 mm增大到80 mm×160 mm抗压强度下降幅度为2.4%,试件由80 mm×160 mm增大到100 mm×200 mm抗压强度下降幅度为1.3%,下降幅度逐渐减小。由图 6可知,其余各级配试样单轴抗压强度也均随着试样尺寸的增加逐渐降低,且下降幅度逐渐减小。级配E的抗压强度变化与其他级配不同,出现较大幅度的波动,拐点也发生右移,因为SMA型沥青混合料的特点是粗集料含量多,在70%~80%之间,它们互相嵌挤形成骨架结构,级配E是达到级配上限的试件结构,粗集料含量多,该级配的粗集料比CA值小于0.4,不在工程中的最优级配范围内,粗集料过多可能导致内部结构不均匀,易出现离析情况,因此将需要达到更大的尺寸时才能保证性能达到稳定。
2.3 尺寸效应的理论参数专家学者对于岩体、混凝土等准脆性材料的尺寸效应已做大量的试验研究及理论探讨,分别总结出了统计尺寸效应理论(Weibull理论)[19]、能量释放尺寸效应理论(Bazant理论)[20-21]、分形特征引起的尺寸效应理论(Carpinteri理论)[22],利用数值模拟结果综合评论适用于沥青混合料的尺寸效应理论。
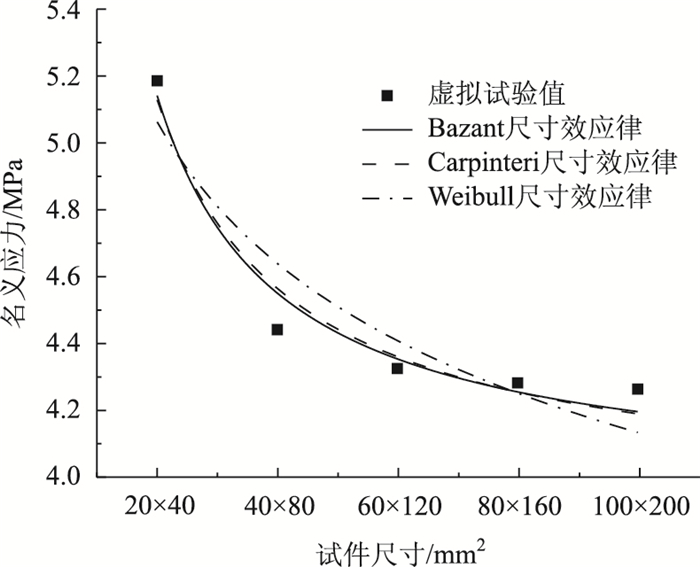
将各级配条件下不同尺寸试件的单轴抗压强度通过Bazant, Carpinteri和Weibull尺寸效应律公式进行拟合,拟合结果如图 7所示,并以粗集料含量为75%的级配B为例,绘制上述3种尺寸效应律下的拟合曲线与虚拟试验值的对比图,如图 8所示。

|
| 图 7 不同尺寸效应理论拟合曲线 Fig. 7 Fitting curves of different size effect theories |
| |
|
| 图 8 粗集料含量为75%时各尺寸效应理论拟合结果 Fig. 8 Fitting result of each size effect theory with 75% coarse aggregate content |
| |
图 7和图 8可知:(1)由拟合优度分析,通过Bazant、Carpinteri尺寸效应公式拟合得到的每条曲线的可决系数较高,而通过Weibull公式拟合的可决系数较低;(2)Bazant、Carpinteri拟合得到的各曲线的残差平方和在0.01~0.02之间,而Weibull拟合的残差平方和数值较大,试验值与拟合值之间存在较大误差。从图 8中可以明显看出Bazant和Carpinteri尺寸效应律拟合到的曲线彼此非常接近,且与散点较好拟合,而Weibull尺寸效应律拟合到的结果存在较大偏离,因此,Weibull尺寸效应理论对于研究沥青混合料的尺寸效应适用性不强。
将拟合得到的尺寸效应律参数值汇总,得到表 4。
| 级配 (粗集料含量/%) |
Bazant参数 | Carpinteri参数 | |||
| fr∞ | Db | A | B | ||
| 级配A(77) | 3.897 | 6.730 | 14.716 | 247.081 | |
| 级配B(75) | 3.957 | 6.001 | 15.342 | 219.854 | |
| 级配C(73) | 4.133 | 4.227 | 16.889 | 163.031 | |
| 级配D(70) | 3.991 | 5.033 | 15.662 | 184.710 | |
| 级配E(80) | 4.058 | 6.120 | 15.962 | 243.57 | |
为探讨参数与粗集料含量之间的关系,拟合整理得到粗集料含量与尺寸效应律参数之间的关系式如下。
Bazant公式:
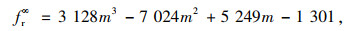
|
(2) |
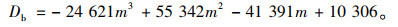
|
(3) |
Carpinteri公式:

|
(4) |

|
(5) |
式中,fr∞为试件尺寸为无穷大时的名义应力;Db为有效厚度,均为常数;A、B为几何参数;m为粗集料含量百分比(m=0.7~0.8)。
虽然不同级配的沥青混合料试件的尺寸效应具有相同的变化规律及趋势,但通过上述公式可知,不同粗集料含量的尺寸效应律的参数存在差异,图 9为不同尺寸下的抗压强度与粗集料含量之间的关系曲线,可知:(1)尺寸小的试件抗压强度明显高于尺寸大的试件,且尺寸越小,抗压强度增长幅度越大;(2)因本研究针对SMA-16,其粗集料含量范围在70%~80%,同一尺寸试件的抗压强度也在一定的范围内波动,随着粗集料含量的增加,抗压强度呈上升趋势,这正说明粗集料的含量影响着混合料名义应力值,决定着沥青混合料的整体性能。

|
| 图 9 粗集料含量对抗压强度的影响 Fig. 9 Influence of coarse aggregate content on compressive strength |
| |
2.4 临界尺寸和临界强度
从沥青混合料的应力应变曲线分析和抗压强度分析能够确定沥青混合料具备尺寸效应现象,其性质随着尺寸的增大逐渐稳定,但不同粗集料含量的混合料性质存在差异,且在图中并不能准确确定各类级配组成条件下的临界尺寸和临界强度值。苏婕[2]在论文中曾给出确定临界尺寸和临界强度的条件,即随着沥青混合料试件尺寸不断增大,通过尺寸效应律计算得到该尺寸所对应的抗压强度值,若随着应力的增加抗压强度值的变化率低于0.01,则认为该尺寸为临界尺寸,所对应的抗压强度值为临界强度,通过计算得到两种尺寸效应律下的临界尺寸和临界强度如表 5所示。
| 级配 (粗集料含量/%) |
Bazant | Carpinteri | |||
| 临界尺寸 Dcr/mm |
临界强度 fcr/MPa |
临界尺寸 Dcr/mm |
临界强度 fcr/MPa |
||
| 级配A(77) | 49.82 | 4.42 | 52.97 | 4.40 | |
| 级配B(75) | 48.72 | 4.44 | 49.73 | 4.45 | |
| 级配C(73) | 41.80 | 4.55 | 47.16 | 4.51 | |
| 级配D(70) | 44.69 | 4.44 | 45.61 | 4.44 | |
| 级配E(80) | 49.83 | 4.56 | 51.76 | 4.55 | |
粗集料含量与CA值和粗集料临界尺寸、临界强度之间的关系分别如图 10和图 11所示。

|
| 图 10 不同粗集料含量下临界尺寸值 Fig. 10 Critical size values with different coarse aggregate contents |
| |

|
| 图 11 不同粗集料含量下的临界强度值 Fig. 11 Critical strength values with different coarse aggregate contents |
| |
由图 10可以看出,CA比随着粗集料含量的增加呈下降状态,临界尺寸随着粗集料含量的变化在一定范围内波动,且波动幅度较大,但两种尺寸效应律得到的结果相近,临界尺寸和粗集料比CA值均呈反向变化,且随着粗集料含量的增加临界尺寸值将变大,通过计算得到Bazant和Carpinteri尺寸效应律对应的临界尺寸与最大公称粒径的比值S分别为2.61~3.11倍和2.85~3.31倍,说明粗集料含量对虽然临界尺寸影响较大,但S值波动很小。从图 11中可以看出,粗集料含量和对SMA的临界强度影响较小,临界强度保持在小范围内波动。
3 尺寸效应影响因素分析 3.1 粗集料性能对尺寸效应的影响为验证粗集料性能是否会影响沥青混合料的尺寸效应,将玄武岩弹性模量分别设定为40,55,75 GPa和90 GPa进行单轴压缩虚拟试验,不同粗集料含量下的抗压强度值如图 12所示。

|
| 图 12 不同粗集料弹性模量下的抗压强度值 Fig. 12 Compressive strength values with elastic moduli of different coarse aggregate materials |
| |
由图 12可知,相同尺寸条件下试样弹性模量越大,试样单轴抗压强度越大。不同弹性模量试样的单轴抗压强度随着试样尺寸的增加均逐渐减小,且试样弹性模量越大,随着试样尺寸的增加,其抗压强度降低的幅度变小,即弹性模量越大的试样受尺寸效应的影响越小。
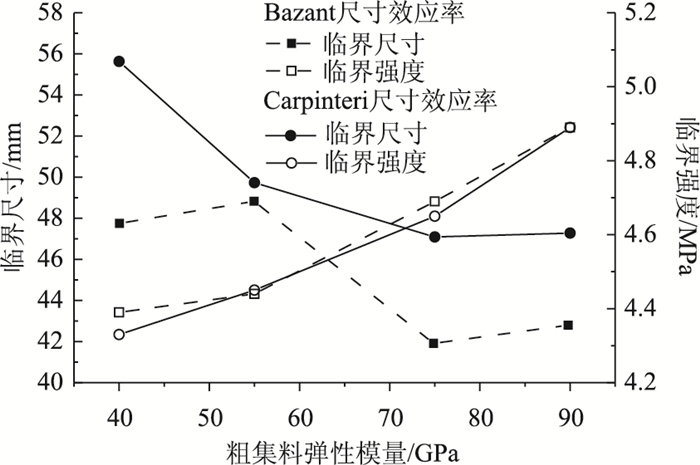
根据2.4节方法,得到不同粗集料弹性模量条件下的临界尺寸和临界强度值,并绘制临界尺寸和临界强度与粗集料特性之间的关系图,如图 13所示。
|
| 图 13 临界尺寸和临界强度与粗集料特性之间的关系 Fig. 13 Relationship between critical size and critical strength with properties of coarse aggregate |
| |
由图 13可知,两种尺寸效应律得到的规律相同,随着粗集料弹性模量的增大,临界强度值不断增大,而临界尺寸呈下降趋势,但整体在一定的范围内波动。通过Bazant和Carpinteri尺寸效应律计算得到的临界尺寸分别为最大粒径的2.6~3.0倍和2.9~3.5倍,可知粗集料性能的不同将改变临界强度的大小,但对临界尺寸的影响较小。
3.2 最大公称粒径对尺寸效应的影响为研究最大公称粒径对尺寸效应现象和临界尺寸、临界强度的影响,分别对SMA10, SMA13和SMA16共3种粒径进行模拟计算,3种试样的级配曲线如图 14所示。

|
| 图 14 级配曲线 Fig. 14 Gradation curves |
| |
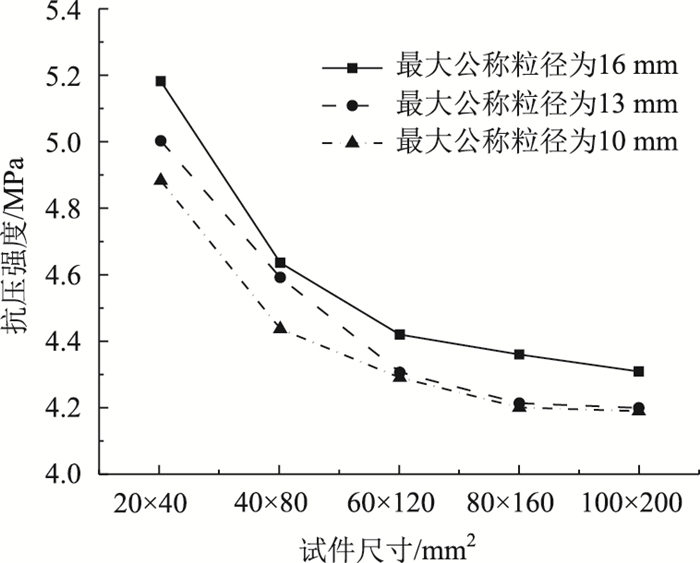
根据数值试验得到不同公称粒径下各尺寸试件的单轴抗压强度值,不同最大公称粒径下的抗压强度值如图 15所示。
|
| 图 15 不同最大公称粒径下的抗压强度值 Fig. 15 Compressive strengths with different maximum nominal particle sizes |
| |
不同的最大公称粒径的沥青混合料均具备尺寸效应现象。粒径大小会影响抗压强度,粒径越小,抗压强度越小,但抗压强度随试件尺寸的增大变化趋势相同。
根据2.4节方法,得到不同公称粒径条件下的临界尺寸和临界强度值,并绘制临界尺寸和临界强度与最大公称粒径之间的关系如图 16所示。

|
| 图 16 临界尺寸和临界强度与最大公称粒径之间关系 Fig. 16 Relationship between critical size and critical strength with maximum nominal particle size |
| |
由图 16可知,不同尺寸效应律计算的结果存在偏差,但整体变化规律相同,随着粒径增大临界尺寸和临界强度都逐渐增大,其中Carpinteri尺寸效应律得到的结果变化幅度大于Bazant尺寸效应律的结果,原因是Carpinteri和Bazant尺寸效应律的适用条件不同,Carpinteri适用于非稳定开裂的情况,而Bazant适用于稳定开裂情况。若以临界尺寸与最大公称粒径之间的比值S来分析,当最大公称粒径分别为16,13 mm和10 mm时,两种尺寸效应律下的临界尺寸分别为最大公称粒径的2.94,3.51,4.20倍和3.41,3.59,4.27倍,与之前得到的结果相近。
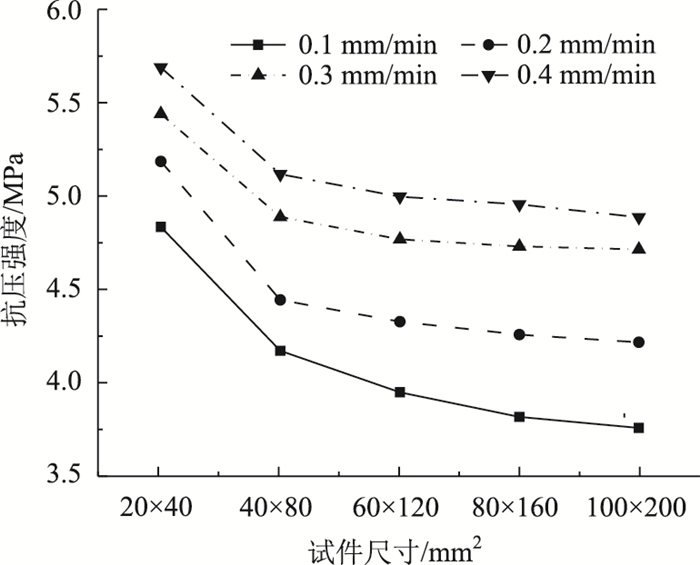
3.3 加载速率对尺寸效应的影响为研究加载速率对试样尺寸效应的影响,进行加载速率为1,2,3,4 mm/min的单轴压缩数值试验。所得不同加载速率下的单轴抗压强度与试样尺寸的关系如图 17所示。
|
| 图 17 不同加载速率下的单轴抗压强度值 Fig. 17 Uniaxial compressive strengths at different loading rates |
| |
由图 17可知,尺寸相同情况下,试样单轴抗压强度随着加载速率的增加而逐渐增大。不同加载速率情况下,试样的单轴抗压强度均随着试样尺寸的增加而逐渐减小,并且试样尺寸越小时降低幅度越大,试样尺寸超过40 mm×80 mm后,单轴抗压强度下降幅度很小。
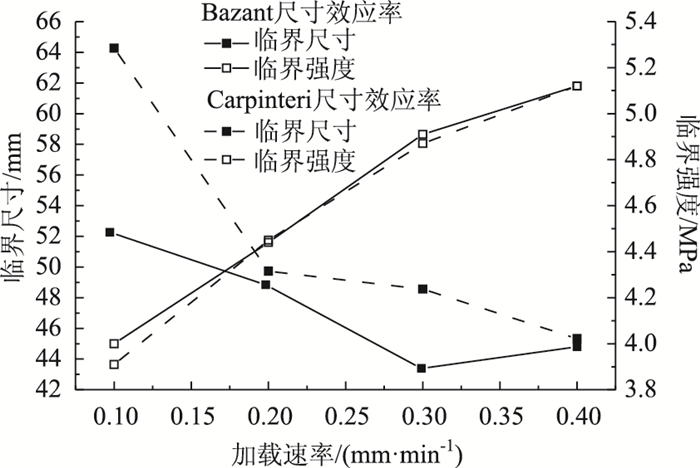
计算并分析临界尺寸和临界强度与加载速率之间的关系如图 18所示。
|
| 图 18 临界尺寸和临界强度与加载速率之间的关系 Fig. 18 Relationship between critical size and critical strength with loading rate |
| |
由图 18同样可以看出随着加载速率增大,临界强度不断增大,临界尺寸逐渐降低,若以临界尺寸与最大公称粒径之间的倍数关系来分析,Bazant尺寸效应律下的临界尺寸范围是最大公称粒径的2.71~3.26倍,Carpinteri尺寸效应律下的临界尺寸范围是最大公称粒径的2.83~4.02倍,变化幅度较小。
4 结论(1) 采用颗粒离散元研究了不同级配下沥青混合料的单轴抗压强度,结果表明不同级配、不同尺寸的沥青混合料试样单轴压缩试验所得应力-应变曲线具有较好的阶段性特征,表现为压密阶段、弹性阶段和向塑性变形过渡直至破坏阶段,验证了沥青混合料具有尺寸效应特征。
(2) 评价了3种尺寸效应理论的适用程度并计算了与之对应的尺寸效应律参数,得到Bazant、Carpinteri尺寸效应律在分析沥青混合料的尺寸效应现象时更为适用,利用虚拟试验结果与尺寸效应律公式进行拟合,得到粗集料含量与效应律公式参数之间的表达式和粗集料含量对临界尺寸及临界强度的影响。对于SMA16,粗集料含量在70%~80%之间时,临界尺寸约为最大公称粒径的2.61~3.31倍。
(3) 确定了各级配情况下沥青混合料试件的临界尺寸和临界强度值,分析了粗集料性能、最大公称粒径、加载速率3种因素对沥青混合料尺寸效应的影响。结果表明:3种因素对沥青混合料抗压强度均存在影响。
(4) SMA在用作路面结构层时,其厚度设计可以根据结构层厚度与最大公称粒径的比值S来确定,Bazant尺寸效应律计算得到的S范围是2.6~3.5,Carpinteri尺寸效应律计算得到的S范围是2.6~4.0。
(5) 本研究仅研究了沥青混合料的单轴抗压性能,得到其具备尺寸效应现象,对于抗拉、抗剪等性能的尺寸效应分析仍需讨论。且研究对象是沥青玛蹄脂碎石混合料,根据尺寸效应律在给出了适用于结构层厚度设计的参考范围,对于其他结构类型的沥青混合料的适用范围也需要试验或模拟来确定。
| [1] |
王青元, 朱万成, 刘洪磊, 等. 单轴压缩下绿砂岩长期强度的尺寸效应研究[J]. 岩土力学, 2016, 37(4): 981-990. WANG Qing-yuan, ZHU Wan-cheng, LIU Hong-lei, et al. Size Effect of Long-term Strength of Sandstone under Uniaxial Compression[J]. Rock and Soil Mechanics, 2016, 37(4): 981-990. |
| [2] |
苏捷, 方志. 普通混凝土与高强混凝土抗压强度的尺寸效应[J]. 建筑结构学报, 2013, 16(6): 1078-1086. SU Jie, FANG Zhi. Scale Effect on Cubic Compressive Strength of Ordinary Concrete and High-strength Concrete[J]. Journal of Building Materials, 2013, 16(6): 1078-1086. |
| [3] |
刘建友, 赵勇, 李鹏飞. 隧道围岩变形的尺寸效应研究[J]. 岩土力学, 2013, 34(8): 2165-2173. LIU Jian-you, ZHAO Yong, LI Peng-fei. Study of Size Effect of Deformation of Rockmass Surrounding Tunnel[J]. Rock and Soil Mechanics, 2013, 34(8): 2165-2173. |
| [4] |
梁正召, 张永彬, 唐世斌, 等. 岩体尺寸效应及其特征参数计算[J]. 岩石力学与工程学报, 2013, 32(6): 1157-1166. LIANG Zheng-zhao, ZHANG Yong-bin, TANG Shi-bin, et al. Size Effect of Rock Masses and Associated Representative Element Properties[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1157-1166. |
| [5] |
李冬, 金浏, 杜修力. 钢筋混凝土柱轴心受压性能及尺寸效应的细观数值研究[J]. 水利学报, 2016, 47(2): 209-218. LI Dong, JIN Liu, DU Xiu-li. Mesoscopic Simulation of the Mechanical Properties and the Size Effect of Reinforced Concrete Column Subjected to Axial Compressive Loading[J]. Journal of Hydraulic Engineering, 2016, 47(2): 209-218. |
| [6] |
SYROKA-KOROL E, TEJCHMAN J. Experimental Investigations of Size Effect in Reinforced Concrete Beams Failing by Shear[J]. Engineering Structures, 2014, 58(7): 63-78. |
| [7] |
程志诚, 徐青, 徐轶. 水泥砂浆立方体试件劈拉强度尺寸效应研究[J]. 武汉大学学报, 2018, 51(9): 772-777. CHENG Zhi-cheng, XU Qing, XU Yi. Size Effect Study of Splitting Tensile Strength of Cement Mortar Cubic Specimen[J]. Engineering Journal of Wuhan University, 2018, 51(9): 772-777. |
| [8] |
屈彦玲, 杨茜, 张相龙. 碾压混凝土劈裂抗拉强度及其尺寸效应的细观数值研究[J]. 公路交通科技, 2008, 25(12): 80-83. QU Yan-ling, YANG Qian, ZHANG Xiang-long. Numerical Study of Split-tensile Strength and Size Effect of Rolled Compacted Concrete on Meso-level[J]. Journal of Highway and Transportation Research and Development, 2008, 25(12): 80-83. |
| [9] |
WANG Y, CHEN P, LIU C, et al. Size Effect of Circular Concrete-filled Steel Tubular Short Columns Subjected to Axial Compression[J]. Thin-Walled Structures, 2017, 120: 397-407. |
| [10] |
LI D, JIN L, DU X, et al. Size Effect Tests of Normal-strength and High-strength RC Columns Subjected to Axial Compressive Loading[J]. Engineering Structures, 2016, 109: 43-60. |
| [11] |
BARBHUIYA S, CHOUDHURY A M. A Study on the Size Effect of RC Beam-column Connections under Cyclic Loading[J]. Engineering Structures, 2015, 95: 1-7. |
| [12] |
REDDY D V, SOBHAN K, LIU L, et al. Size Effect on Fire Resistance of Structural Concrete[J]. Engineering Structures, 2015, 99: 468-478. |
| [13] |
罗代松, 田春林, 郭猛, 等. 改性再生沥青混合料配合比设计及性能验证[J]. 公路交通科技, 2018, 35(12): 7-13. LUO Dai-song, TIAN Chun-lin, GUO Meng, et al. Mix Design and Performance Verification of Modified Recycled Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2018, 35(12): 7-13. |
| [14] |
郭金星, 张书华. 沥青种类对SMA-13级配的影响[J]. 公路交通科技, 2018, 35(9): 9-14. GUO Jin-xing, ZHANG Shu-hua. Influence of Asphalt Types on SMA-13 Gradation[J]. Journal of Highway and Transportation Research and Development, 2018, 35(9): 9-14. |
| [15] |
王晓明, 郑银河. 裂隙岩体表征单元体及尺寸效应研究进展[J]. 岩土力学, 2015, 36(12): 3456-3464. WANG Xiao-ming, ZHENG Yin-he. Review of Advances in Investigation of Representative Elementary Volume and Scale Effect of Fractured Rock Masses[J]. Rock and Soil Mechanics, 2015, 36(12): 3456-3464. |
| [16] |
李坤蒙, 李元辉, 徐帅, 等. PFC~(2D)数值计算模型微观参数确定方法[J]. 东北大学学报:自然科学版, 2016, 37(4): 563-567. LI Kun-meng, LI Yuan-hui, XU Shuai, et al. Method to Determine Microscopic Parameters of PFC2D Numerical Model[J]. Journal of Northeastern University:Natural Science Edition, 2016, 37(4): 563-567. |
| [17] |
李明, 彭伟, 王彦伟. 沥青混合料单轴压缩试验的细观分析[J]. 山东交通学院学报, 2016, 24(1): 64-69. LI Ming, PENG Wei, WANG Yan-wei. Microscopic Analysis for Uniaxial Compression Test of Asphalt Mixtures[J]. Journal of Shandong Jiaotong University, 2016, 24(1): 64-69. |
| [18] |
杨军, 焦丽亚, 王克利, 等. 基于离散元方法的沥青混合料虚拟三轴剪切试验三维模拟[J]. 东南大学学报:自然科学版, 2014, 44(5): 1057-1061. YANG Jun, JIAO Li-ya, WANG Ke-li, et al. Three Dimensional Simulation of Virtual Triaxial Shear Test for Asphalt Mixture Based on Discrete Element Method[J]. Journal of Southeast University:Natural Science Edition, 2014, 44(5): 1057-1061. |
| [19] |
WEIBULL W. A Statistical Distribution Function of Wide Applicability[J]. Journal of Applied Mechanics, 1951, 18(2): 293-297. |
| [20] |
李勇, 郑建军, 金贤玉. Bazant尺寸效应律分析及其应用[J]. 混凝土, 2003, 41(2): 33-34, 41. LI Yong, ZHENG Jian-jun, JIN Xian-yu. Analysis and Application of Bazant's Size Effect Laws[J]. Concrete, 2003, 41(2): 33-34, 41. |
| [21] |
BAŽANT Z P. Size Effect in Blunt Fracture:Concrete, Rock, Metal[J]. Journal of Engineering Mechanics, 1984, 110(4): 518-535. |
| [22] |
CARPINTERI A. Fractal Nature of Material Microstructure and Size Effects on Apparent Mechanical Properties[J]. Mechanics of Materials, 1994, 18(2): 89-101. |
 2020, Vol. 37
2020, Vol. 37
