扩展功能
文章信息
- 蒋劲羽, 杨忠振
- JIANG Jin-yu, YANG Zhong-zhen
- 基于移动治超模式的农村公路治超站选址
- Location for Overloaded Truck Control Station on Rural Highway Based on Mobile Enforcement Mode
- 公路交通科技, 2020, 37(4): 125-132
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 125-132
- 10.3969/j.issn.1002-0268.2020.04.017
-
文章历史
- 收稿日期: 2018-11-19
2. 宁波大学 海运学院, 浙江 宁波 315800
2. School of Maritime and Transportation, Ningbo University, Ningbo Zhejiang 315800, China
货车超载运输问题在我国普遍存在,超载车辆恶化了公路的技术条件,缩短了公路的使用年限。因此,国家一直在加大货车超载的治理力度,2004年以来持续开展超载运输治理工作[1],针对农村公路常用的治超方式是在超载严重的地方设置治超站,检测超载车辆,进行相应的处罚。但是,由于农村公路等级低,路网结构复杂,货车走行路径多变,绕行成本低,超载车辆会绕行躲避治超站。因此,针对农村公路,固定治超难以有效截获超载车辆,治超效果和效率不理想。在这种情况下,如何创新农村公路超载治理模式,提高治超效果和效率是急需解决的问题。
在国内外关于超载治理的研究中,Bagui[2]给出了超载运输的定义,提出通过惩罚超载运输业者来补偿超载对路面造成的损害;Quintero[3]基于运输业者的最小运输成本和超载治理者的最小运营成本,建立了双层规划模型来描述运输业者对执法密度和罚款变化的响应,得到了均衡状态下超载管理站的设置方案,但并未研究管理站的具体选址和执法车队的执法路径。国内学者则从宏观层面的对策和策略研究出发,提出了治理超载运输的方案和具体的政策建议[4-7],但并未涉及具体的治超方案优化问题。
本研究提出依托治超站实施移动治超,即治超车携带设备对路网内的车辆进行巡查,然后在给定治超站数量和治超车数量的情况下,优化治超站的空间分布与治超车的巡游路径。目前,有很多文献涉及此类设施选址和路径联合优化问题。Nagy[8]把选址-路径问题定义为在已知候选配送中心和客户地点的前提下,同时确定了配送中心的数量和位置及车辆的运输路线,以使总成本(包括配送中心建设成本和配送成本)最小;孙青伟[9]同时考虑配送车辆的取货和送货等,研究了配送中心的选址及多车型的路径问题;为使配送系统中多个目标同时达到最优,Caballero,Zhao,Liu等[10-12]都采用了多目标选址-路径模型对设施的选址和车辆的路径进行了优化;曾庆成等[13]建立了上层为配送中心选址问题,下层为车辆路径优化问题的双层规划模型,以优化配送系统的总成本和整体效率;罗耀波等[14]考虑仓库和车辆的容量约束,对多仓库的选址-路径问题进行了研究。这些研究多围绕物流领域的配送中心/仓库选址和配送车辆路径优化开展研究,但根据巡游路径上超载车辆密度同时优化设施选址和巡游路径的有关研究较少。相关公路设施选址文献中,程学庆[15]研究了干线公路管理站选址和物资运输车队路径优化的有关问题。在上述基础上,本研究有望在实施农村公路移动治超时,为决策者提供理论依据和技术方法。
1 治超站选址候选点集合确定首先,把超载严重的路段离散为点组成治超站选址的初始候选集U0=(1, 2, 3, …, n),由于治超车需移动治超,因此需按其最大巡游时间确定每个初始候选点的责任路段,即确定治超车在最大巡游时间内所能经过的路段,也称覆盖路段。然后,建立表 1所示的选址候选点评价体系,用层次分析法对初始候选点进行综合评价。
| 1级 指标 | 指标体系 | ||||
| 环境 因素 | 基础设施 因素 | 经济 因素 | 不可抗 因素 | 运输 需求 | |
| 2级 指标 | 地质条件 | 交通便利性 | 拆迁费用 | 军事基地 | 覆盖路段货车交通量 |
| 气象条件 | 通讯便利性 | 建设费用 | 规划用地 | 站点处货车交通量 | |
| 地形条件 | 电力便利性 | ||||
为得到各层指标的权重,把指标间的相对重要程度分为1~9级(见表 2,其中A1和A2表示任意两个指标)。通过专家问卷调查到这些得分,再整理得到各级指标的判断矩阵,然后计算各判断矩阵的最大特征根所对应的特征向量。如果判断矩阵满足一致性,则把特征向量作为各层指标的权重向量。
| 等级 | 含义 |
| 1 | A1与A2同样重要 |
| 3 | A1比A2稍微重要 |
| 5 | A1比A2明显重要 |
| 7 | A1比A2非常重要 |
| 9 | A1比A2强烈重要 |
| 2,4,6,8 | 表示重要性在奇数标度之间 |
| 倒数 | A1与A2比较的值和A2与A1比较的值呈倒数 |
最后,通过各层级的权重向量计算得到初始候选点的综合权重,方法如式(1)所示:
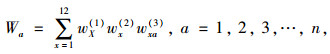
|
(1) |
式中,Wa为初始候选点a的综合权重;wX(1)为包含二级指标x的一级指标X的权重;wx(2)为二级指标x的权重;w(3)xa为二级指标x下初始候选点a的权重。
为压缩初始候选集规模,减轻筛选工作量,需对覆盖相似路段的初始候选点进行聚类,用类中最适候选点代替同类中的其他候选点。聚类时,先把每个初始候选点看作是1个类,即开始时1个类中只有1个初始候选点。这样会得到n个初始类:va0∈V0, a=1, 2, 3, …, n(其中va0为含有候选点a的初始类;V0为所有初始类的集合)。然后,基于类中候选点的覆盖路段,分别计算当前类与其他类覆盖路段的相似度。此时,把当前类中的候选点作为参照候选点,其他类中的候选点作为比较候选点,相似度用参照候选点和比较候选点重复覆盖的路段长度与参照候选点覆盖路段长度的比值表示,计算方法见式(2),其中a为参照候选点,b为比较候选点。
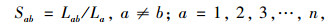
|
(2) |
式中,Sab为参照候选点a与比较候选点b的相似度;Lab为参照候选点a和比较候选点b重复覆盖的路段长度;La为参照候选点a的覆盖路段长度。
计算得到相似度后,把与a相似度大的b放到a所在的类中,得到1个包含多个初始候选点的类,然后只保留其中权重最高的候选点,删除其他候选点,最后得到1个只包含1个初始候选点的类va1。据此分别对参照候选点a=1, 2, 3, …, n进行操作,得到n个新类,即va1∈V1, a=1, 2, 3, …, n(其中V1为所有新类的集合)。把这n类中的初始候选点组成具有n个元素的集合U1,删除U1中重合的候选点,得到最终的实用候选点集J。
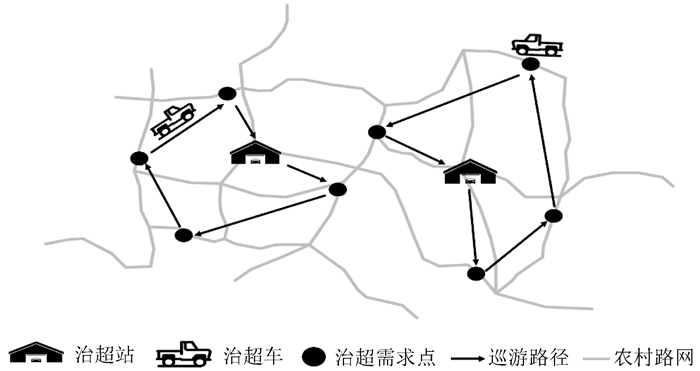
2 选址-路径模型 2.1 问题描述把超载严重路段离散为点,组成治超需求点集合。假设为治理超载,各治超站需至少配备1辆治超车,所有治超车的车型都相同,且为每辆治超车配备相等数量的移动治超人员和移动式称重设备。治超车从各自的治超站出发,行驶到需求点时,移动治超人员停车对经过的货车进行拦截,并使用移动式称重设备对拦截的货车进行超载检测。巡游过程中,每个需求点的停车检测时间相等,且每辆治超车都要返回治超站。移动治超流程示意图如图 1所示。
|
| 图 1 移动治超示意图 Fig. 1 Schematic diagram of overloading control by enforcement vehicle |
| |
研究的问题是在治超站数量和治超车数量给定的情况下,从最终的实用候选点集J中筛选出治超站,并确定治超车的巡游路径。优化的目的在于使治超车能够截获最多的超载车辆,约束条件是每个需求点最多被检测1次,而每辆治超车的单次巡游时间不超过其最大能够的巡游时间。
2.2 选址-路径模型建立假设路段的超载概率相同,且超载货车在时间上均匀分布,则货车流量大的路段的超载货车多。由此可知,当治超站和治超车数量给定时,可以以治超车巡游路径上的货车流量最多为目标,建立治超站选址-治超车路径优化模型。
2.2.1 变量及参数设置模型的集合:J为治超站候选点集合,j为J中的任意一个候选点,即j∈J;C为需求点集合,c为C中的任意一个需求点,即c∈C;K为移动治超车集合,k为K中的任意一辆治超车,即k∈K。
模型的已知参数:m为治超站数;v为治超车行驶速度;t为治超车在需求点的停车检测时间;tmax为治超车单次最大巡游时间;qc和q′c分别为需求点c和c′上的货车流量;qj为治超站j上的货车流量。
模型的中间变量:D为治超车巡游时经过的需求点数;Lk为治超车k单次巡游的路径里程。
模型的决策变量:zj为是否在候选点j设置治超站,是为1,反之为0;xcc′k为治超车辆k是否从需求点c到另一个需求点c′,是为1,反之为0;xjck为治超车辆k是否从治超站j到需求点c,是为1,反之为0。
2.2.2 模型公式
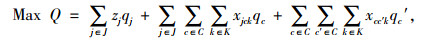
|
(3) |

|
(4) |
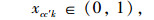
|
(5) |
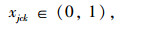
|
(6) |
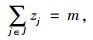
|
(7) |
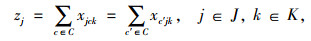
|
(8) |
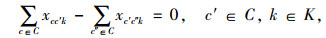
|
(9) |

|
(10) |
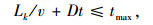
|
(11) |

|
(12) |
式(3)是目标函数,其中Q为经过治超站的货车流量和所有治超车巡游路径上的货车流量总和;式(4)~(6)表示决策变量zj, xcc′k, xjck是0-1变量;式(7)是治超站数量约束,表示设置的治超站数量为m;式(8)表示当在j点建设治超站时,保证至少有1辆治超车从治超站j出发,并最终返回到治超站j;式(9)保证治超车k的巡游路径是闭合的;式(10)保证需求点c′最多只被1辆治超车访问;式(11)确保每辆治超车巡游时间不大于最大巡游时间tmax;式(12)保证治超车不会从一个治超站j到另一个治超站j′。
3 模型求解算法上述模型是由选址问题(Location Allocation Problem,LAP)和路径选择问题(Vehicle Routing Problem,VRP)组合成的非线性规划问题,即LRP问题,属于NP-hard难题,这类问题通常采用启发式算法求解[16-18]。
蚁群算法是一种寻找优化路径的机率型启发式算法,根据求解的问题自定义节点之间的信息素增量(启发式因子),可有效缩小可行解的范围,并快速找到满足目标函数的最优路径,非常适合大规模的路径优化计算。
本研究的求解思路是先对所有可能的选址组合都采用蚁群算法进行治超车的路径优化,得到与各选址组合对应的治超车能截获最多超载货车的路径集合,然后选取集合中车辆最多的路径及相应的选址方案作为优化的选址-巡游路径方案。在具体求解过程中,由于多基地-多车辆路径优化问题求解复杂,这里把其转化为单基地-多车辆路径优化问题。做法是用1个虚拟治超站代替治超站选址组合,并认为所有治超车都以虚拟治超站为始终点,所有需求点都是虚拟治超站需要覆盖的对象。把需求点i到组合内所有治超站的最短距离di作为需求点i与虚拟治超站之间的距离,这样利用虚拟治超站可把多基地-多车辆路径问题转化为单基地-多车辆路径问题[19]。最后利用改进的蚁群算法求解治超站选址-治超车路径优化模型,具体步骤如下:
Step 1:输入参数
输入需建设的治超站数m、配备的治超车数N、治超车在各需求点停车检测的时间t、治超车的最大巡游时间tmax、最大迭代次数NIT。
Step 2:选址组合
在候选集中组合得到所有可能的选址组合,并把组合编号为1, 2, 3, …, A。
Step 3:输入组合编号G(从G=1开始)
Step 4:初始化
设蚂蚁数等于需求点数,且所有蚂蚁都从组合G的虚拟治超站出发,需求点之间的初始信息素设为1,治超车的初始数量n=0,初始迭代次数nIT=0。
Step 5:确定期望值
用ηij表示边(i, j)的期望值,即蚂蚁在i点选择j点作为下一节点的期望值,取j点货车流量值和i, j两点间距离的商表示,即qj/lij。
Step 6:计算选择下一节点的概率
根据信息素浓度和期望值,求由i点出发选择j点的概率为:
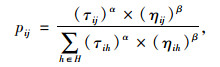
|
(13) |
式中,pij为蚂蚁由i点出发选择j点的概率;τij为边(i, j)上路径信息素的数量;ηij为边(i, j)上的期望值;α和β分别为路径信息素和能见度启发式因子;H为可行节点集合;h为其中的任意一个可行节点;τih为边(i, h)上路径信息素的数量;ηih为边(i, h)上的期望值。
Step 7:确定实际治超站
蚂蚁从虚拟治超站出发,先按式(13)计算每个可行节点的选择概率。为跳出局部最优,用轮盘赌选择法增加选择下一节点的随机性[20],具体过程为:取随机数ε, ε∈(0, 1),按节点编号顺序依次累加可行节点的选择概率pij,当加至某可行节点j的累加概率值≥ε时,则取j点为下一节点,假设距离j点最近的一个治超站为O,则将O看作是蚂蚁出发的实际治超站,最后蚂蚁将返回治超站O。
Step 8:确定下一节点
按式(13)和轮盘赌选择法选择下一个节点,同时还需判断如果将下一节点j′纳入行程中,是否符合最大巡游时间约束,即判断蚂蚁从治超站O行走到j′点的巡游时间与j′点直接到治超站O的时间之和是否小于最大巡游时间。如果小于,则取j′点作为下一节点,同时将该点加入到禁忌表,蚂蚁继续从j′点按照式(13)和轮盘赌选择法选择下一个节点;否则,放弃j′点,蚂蚁结束行程,从当前节点返回治超站O,蚂蚁巡游时间归零,治超车数量n=n+1。重新将蚂蚁看作是从虚拟治超站出发,继续按照Step 7确定实际治超站后,前往下一节点。当治超车数量n=N时,则前往Step 9。
Step 9:更新信息素
在完成1次迭代后,首先需更新蚂蚁走过路径上的信息素浓度,方法如式(14)所示,同时更新迭代次数nIT=nIT+1,然后返回Step 4进行下一轮迭代。当nIT=NIT时,前往Step 10。

|
(14) |
式中,τijold, τijnew分别为边(i, j)上更新前后的信息素量;ρ为信息素挥发系数;bij是0-1变量,边(i, j)在第b只蚂蚁行进的路径上时为1,不是为0;Δτijb为第b只蚂蚁在边(i, j)上留下的信息素,即信息素增量,用第b只蚂蚁行进路径上路径总流量Qb表示;B为所有的蚂蚁。
Step 10:优化下一选址组合的巡游路径
更新治超站组合编号G=G+1,如果G≤A,返回Step 3。反之,结束计算。
4 案例分析调查得知贵阳市农村公路有50处超载严重的路段,这里把它们作为初始候选点,同时也是治超需求点(简称需求点),各点的货车流量如表 3所示。假设需建设3个治超站,用6辆车型相同的治超车实施移动治超,治超车的行驶速度为40 km/h,在1个需求点停车检测需0.5 h,最大巡游时间为4 h。
| 需求点 | 流量/ (pcu·d-1) |
| 1 | 603 |
| 2 | 1 355 |
| 3 | 589 |
| 4 | 707 |
| 5 | 1 055 |
| 6 | 590 |
| 7 | 667 |
| 8 | 687 |
| 9 | 1 098 |
| 10 | 598 |
| 11 | 1 227 |
| 12 | 1 058 |
| 13 | 1 189 |
| 14 | 913 |
| 15 | 909 |
| 16 | 998 |
| 17 | 509 |
| 18 | 1 069 |
| 19 | 534 |
| 20 | 1 170 |
| 21 | 1 381 |
| 22 | 577 |
| 23 | 1 290 |
| 24 | 593 |
| 25 | 1 005 |
| 26 | 985 |
| 27 | 1 002 |
| 28 | 1 279 |
| 29 | 554 |
| 30 | 1 065 |
| 31 | 621 |
| 32 | 1 577 |
| 33 | 1 380 |
| 34 | 601 |
| 35 | 1 201 |
| 36 | 569 |
| 37 | 592 |
| 38 | 1 211 |
| 39 | 1 110 |
| 40 | 1 159 |
| 41 | 1 264 |
| 42 | 545 |
| 43 | 1 192 |
| 44 | 1 312 |
| 45 | 679 |
| 46 | 701 |
| 47 | 655 |
| 48 | 664 |
| 49 | 595 |
| 50 | 609 |
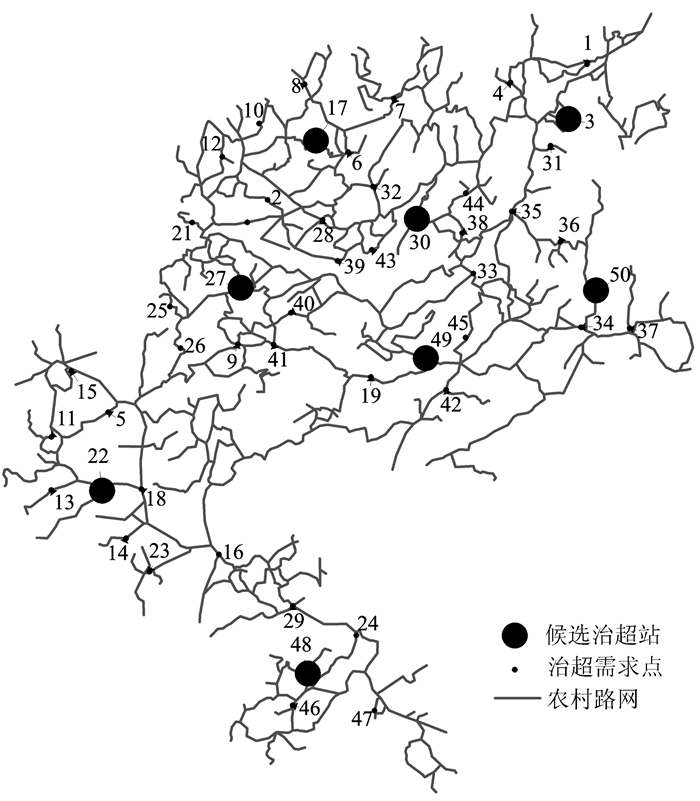
计算时,先用MapInfo平台数字化贵阳市农村公路网,再根据治超车的最大巡游时间(4 h),计算得到初始候选点覆盖的路段集合。然后,按第2章的方法以参照点和比较点间覆盖路段的相似程度大于60%为标准,聚类初始候选点,并按初始候选点的综合权重筛选得到的候选点集为J=(3,17,22,27,30,48,49,50),其空间位置如图 2所示。
|
| 图 2 候选点的空间分布 Fig. 2 Spatial distribution of candidate locations |
| |
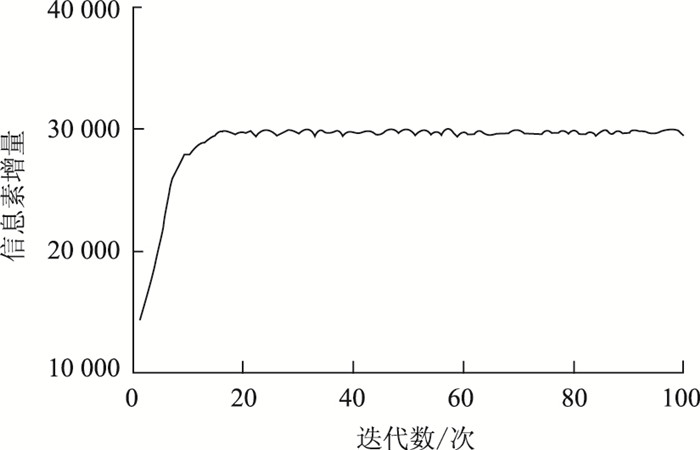
基于8个候选点建设3个治超站,共有56种可能的选址组合,用改进的蚁群算法求解每个组合。计算时设蚂蚁数为50,启发因子为1,期望因子为2,信息素挥发系数为0.50,用巡游路径上的货车总流量表示信息素增量,每只蚂蚁的迭代次数为100次。在Excel 2016编制的程序环境中,求解计算时间为56 s,其中1种选址组合下蚂蚁信息素增量和蚂蚁迭代次数的变化关系如图 3所示。
|
| 图 3 信息素增量-迭代次数关系 Fig. 3 Relationship between pheromone increment and iteration number |
| |
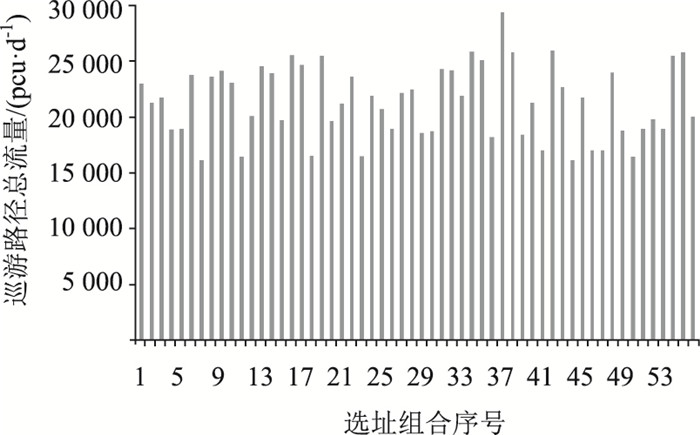
由图 3可知,在迭代初期,蚂蚁的信息素增量随迭代次数的增加而增加,但增速逐渐变小。当迭代计算20次时,信息素增量收敛,表明此时所有蚂蚁的行走路径已确定,即该种组合下的最优巡游路径确定。各选址组合下,最优巡游路径上的货车总流量如图 4所示。
|
| 图 4 不同选址组合下巡游路径上的货车流量 Fig. 4 On-route truck volumes under different location combinations |
| |
由图 4可知,选址组合37号的巡游路径上的货车总流量最大,此时3个治超站分别选址在标号为22,27,30的候选地点,即选址决策变量z22=1,z27=1和z30=1,相应的巡游路径如图 5所示。

|
| 图 5 选址-路径方案 Fig. 5 Scheme of location-routing |
| |
22号、27号、30号治超站周边矿产资源丰富,矿运卡车数量多,超载严重。其中22号治超站的巡游路径1经过3个城镇和多个煤矿开采地,主要覆盖道路是城镇主要的连接通道,道路等级较高,货车流量大(3 912 pcu/d);巡游路径2经过2个城镇、3个风景区、多个煤矿及水泥厂,覆盖的农村公路等级较高,货车流量大(4 850 pcu/d)。
由图 5可知,最优选址-路径方案下,移动治超可覆盖28个超载严重的路段,路段覆盖率为56%(28/50);50条超载严重的农村公路的货车总流量为45 493 pcu/d,每天巡游路径上的货车总流量值为29 387 pcu,车辆覆盖率为64.6%。即移动治超覆盖56%的超载路段,就可截获64.6%的车辆。用车辆覆盖率与路段覆盖率的比值表示移动治超效率,其公式如式(15)所示,其值越大说明在巡游路径上可截获检测的车辆越多,移动治超效率越高,反之则越低。

|
(15) |
式中,W为移动治超效率;S1为车辆覆盖率;S2为路段覆盖率。
最优选址-路径方案下,移动治超效率为1.15(64.6%/56%)。以车辆覆盖率和路段覆盖率相等时(即S1=S2时)的工作效率作为移动治超的标准工作效率,由式(15)可知,标准工作效率等于1。最优方案下,移动治超效率大于标准工作效率,治超车的治超效率较为理想。
5 结论针对依托固定治超站,实施移动治超的治超模式,用聚类分析法和层次分析法确定了治超站候选选址点集合,协同优化了治超站的选址分布及其治超车的巡游路径。优化的方案有助于在拟建治超站数量和治超车数量确定的情况,发挥最大的治超功效。基于贵阳市农村公路实际数据的实例研究表明,最优方案下,治超站覆盖多条高等级农村公路和货车流量大的路段,治超效率高,验证了模型和算法的可行性,有助于管理者实施治超站的选址决策和治超车路径选择。
本研究从规划层面出发,研究治超站选址-治超车路径选择的宏观和中观问题,模型对治超车的巡游过程进行了相应的简化。如:在超载路段上的停车检测时间不随交通量的变化(而将其设为定值),未考虑移动治超工作人员在停车检测过程中具体的拦车规则和检测活动。这些问题是后续执法层面的微观问题,难以与选址-路径优化这样的宏观/中观问题一起处理,而需要在治超站建成和配备巡游车辆后,再根据即时的数据和情况予以具体决策。
| [1] |
李丽, 吴群琪. 基于各方主体经济利益实现的长效治理超限超载对策研究[J]. 公路交通科技, 2008, 25(3): 153-158. LI Li, WU Qun-qi. Research on Countermeasures of Long-tem Oversize and Overload Controlling Base on Relational Interest Factors[J]. Journal of Highway and Transportation Research and Development, 2008, 25(3): 153-158. |
| [2] |
BAGUI S, DAS A, BAPANAPALLI C. Controlling Vehicle Overloading in BOT Projects[J]. Procedia-Social and Behavioral Sciences, 2013, 104: 962-971. |
| [3] |
MORENO-QUINTERO E, FOWKES T, WATLING D. Modelling Planner-carrier Interactions in Road Freight Transport:Optimisation of Road Maintenance Costs via Overloading Control[J]. Transportation Research Part E:Logistics & Transportation Review, 2013, 50: 68-83. |
| [4] |
李忠奎, 荣朝和. 治理公路超载超限运输的长效机制和对策研究[J]. 中国公路学报, 2005, 18(4): 96-99. LI Zhong-kui, RONG Zhao-he. Research on Long-term Solution Mechanism and Counter-measure to Overload and Oversize Transportation of Highway[J]. China Journal of Highway and Transport, 2005, 18(4): 96-99. |
| [5] |
陈荫三. 运用经济杠杆长效治理超载超限运输[J]. 中国公路学报, 2004, 17(2): 94-99. CHEN Yin-san. Long-term Effective Solution to the Overload Transportation with Economic Lever[J]. China Journal of Highway and Transport, 2004, 17(2): 94-99. |
| [6] |
李丁, 麻丽娅. 计重收费政策对治理超限超载运输的成效分析[J]. 公路交通科技, 2012, 29(增1): 109-112. LI Ding, MA Li-ya. Analysis of Influence of Weight Charge Policy on Overload Transportation[J]. Journal of Highway and Transportation Research and Development, 2012, 29(S1): 109-112. |
| [7] |
耿莉萍. 公路超载的理论分析与治理措施的探讨[J]. 北京交通大学学报:社会科学版, 2013, 12(1): 67-71. GENG Li-ping. A Survey on Overload Transportation of Highway and Its Counter Measures[J]. Journal of Beijing Jiaotong University:Social Sciences Edition, 2013, 12(1): 67-71. |
| [8] |
NAGY G, SALHI S. Location-routing:Issues, Models and Methods[J]. European Journal of Operational Research, 2007, 177(2): 649-672. |
| [9] |
孙青伟, 张杨. 带同时取送货的选址-多车型路径问题研究[J]. 交通运输工程与信息学报, 2017, 15(2): 100-104, 118. SUN Qing-wei, ZHANG Yang. Study on Location-routing Problem with Simultaneous Pickup and Delivery[J]. Journal of Transportation Engineering and Information, 2017, 15(2): 100-104, 118. |
| [10] |
CABALLERO R, GONZÁLEZ M, GUERRERO F M, et al. Solving a Multiobjective Location Routing Problem with a Metaheuristic Based on Tabu Search:Application to a Real Case in Andalusia[J]. European Journal of Operational Research, 2007, 177(3): 1751-1763. |
| [11] |
ZHAO J, VERTER V. A Bi-objective Model for the Used Oil Location-routing Problem[J]. Computers & Operations Research, 2015, 62: 157-168. |
| [12] |
LIU H, WANG W, ZHANG Q. Multi-objective Location-Routing Problem of Reverse Logistics Based on GRA with Entropy Weight[C]//Proceedings of 2011 IEEE International Conference on Grey Systems and Intelligent Services. IEEE: Nanjing, 2011.
|
| [13] |
曾庆成, 杨忠振, 蒋永雷. 配送中心选址与车辆路径一体优化模型与算法[J]. 武汉理工大学学报:交通科学与工程版, 2009, 33(2): 267-270. ZENG Qing-cheng, YANG Zhong-zhen, JIANG Yong-lei. Optimization Model and Algorithm of Coordinated Distribution Center Location and Vehicle Routing[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2009, 33(2): 267-270. |
| [14] |
罗耀波, 孙延明, 廖鹏. 带退货和软时间窗的多仓库选址-路径问题研究[J]. 运筹与管理, 2014, 23(5): 78-85. LUO Yao-bo, SUN Yan-ming, LIAO Peng. Research on Multi-depot Location Routing Problem with Backhauls and Soft Time Windows[J]. Operations Research and Management Science, 2014, 23(5): 78-85. |
| [15] |
程学庆, 贾江涛, 李月, 等. 干线公路管理站选址双层规划模型与算法[J]. 交通运输系统工程与信息, 2016, 16(3): 207-213. CHENG Xue-qing, JIA Jiang-tao, LI Yue, et al. Bi-level Programming and Algorithm on the Location of Arterial Highway Management Station[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(3): 207-213. |
| [16] |
于滨, 靳鹏欢, 杨忠振. 两阶段启发式算法求解带时间窗的多中心车辆路径问题[J]. 系统工程理论与实践, 2012, 32(8): 1793-1800. YU Bin, JIN Peng-huan, YANG Zhong-zhen. Two-stage Heuristic Algorithm for Multi-depot Vehicle Routing Problem with Time Windows[J]. Systems Engineering-Theory & Practice, 2012, 32(8): 1793-1800. |
| [17] |
贺政纲, 邹晔, 杨晓. 报废汽车物流网络选址-路径问题建模与求解算法研究[J]. 公路交通科技, 2016, 33(3): 138-145. HE Zheng-gang, ZOU Ye, YANG Xiao. Research of Modeling and Algorithm for ELV Logistics Network Location-routing Problem[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 138-145. |
| [18] |
NADIZADEH A, HOSSEINI-NASAB H. Solving the Dynamic Capacitated Location-routing Problem with Fuzzy Demands by Hybrid Heuristic Algorithm[J]. European Journal of Operational Research, 2014, 238(2): 458-470. |
| [19] |
马建华, 房勇, 袁杰. 多车场多车型最快完成车辆路径问题的变异蚁群算法[J]. 系统工程理论与实践, 2011, 31(8): 1508-1516. MA Jian-hua, FANG Yong, YUAN Jie. Mutation Ant Colony Algorithm for Multiple-depot Multiple-types Vehicle Routing Problems with Shortest Finish Time[J]. Systems Engineering-Theory and Practice, 2011, 31(8): 1508-1516. |
| [20] |
贺韵竹, 杨忠振. 自营货车与公交车协同快件配送优化[J]. 交通运输工程学报, 2017, 17(6): 97-103. HE Yun-zhu, YANG Zhong-zhen. Optimization of Express Distribution by Cooperatively Using Private Trucks and Buses[J]. Journal of Traffic and Transportation Engineering, 2017, 17(6): 97-103. |
 2020, Vol. 37
2020, Vol. 37
