扩展功能
文章信息
- 卢锦川
- LU Jin-chuan
- 基于扰动收缩粒子群算法的物联网配送车辆调度
- Scheduling Distribution Vehicles in Internet of Things Based on Perturbation Contraction Particle Swarm Optimization
- 公路交通科技, 2020, 37(4): 111-117
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 111-117
- 10.3969/j.issn.1002-0268.2020.04.015
-
文章历史
- 收稿日期: 2019-02-19
目前物流行业对智能化的要求越来越高,通过物联网融入可避免传统车辆模式缺陷,物联网配送车辆能够记录跟踪车辆到达时间以及地理偏差等重要信息[1-2],使得服务质量提高,减少运输工程成本的增加[3]。
物联网配送车辆调度要求运输成本最优,解决方法主要有列生成法、集分割法、动态规划法等,但是由于其计算复杂度与规模之间呈几何级数变化关系,根本无法求得问题的最优解,不能满足现代物联网实际应用要求[4-5]。当前,智能优化算法具有求解效率高等优点,如遗传算法(Genetic Algorithms, GA)[6]、蚁群算法(Ant Colony, AC)[7]、粒子群算法(Particle Swarm Optimization, PSO)等越来越受到研究者的关注[8-9]。但是在实际应用中也存在着局部搜索能力差、收敛时间过长、易陷于局部最优等问题,遗传算法对初始种群产生十分敏感,蚁群算法易受参数影响,计算量大,粒子群算法收敛后期易陷入局部最优解。混沌量子粒子群算法(Chaotic Quantum Particle Swarm Optimization, CQPSO)应用于车辆调度问题[10],取得了较好的效果;模拟退火粒子群算法(Simulated Annealing Particle Swarm Optimization, SAPSO)[11],快速求得带时间窗车辆路径问题的优化解;柯西变异粒子群算法(Cauchy Mutation Particle Swarm Optimization, CMPSO)可应用在多车场多车型车辆路径调度问题[12],但是算法后期效率也比较低。
为了获得更加理想的物联网配送车辆调度方案,针对标准粒子群算法的不足,采用扰动收缩粒子群算法(Perturbation Contraction Particle Swarm Optimization, PCPSO),扰动过程通过非线性控制,收缩通过加权系数进行,并完成相关仿真内容,以验证算法的有效性。
1 物联网配送车辆优化调度问题的数学模型每辆车上装载电子标签,当经过读写器时,存储在电子标签芯片中的车牌号信息被获取,为后续对该车信息管理提供了保障;GPS定位对车辆定位与跟踪;管理系统对实现本地、外地的交通路线、车辆位置和轨迹等信息的可视化,实现实时获取物流配送车辆的位置、速度、载货量、到达及离开各配送节点的时间,使得车辆信息管理系统查看智能化;GPRS网络实现完成车辆和各种数据网之间的数据传送和格式转换。物联网配送车辆调度系统如图 1所示。

|
| 图 1 物联网配送车辆调度系统 Fig. 1 Internet of Things distribution vehicle scheduling system |
| |
将无线数字传输模块植入交通信号系统及联网车辆,实现相互之间的信息传输,实现车辆与道路基础设施、车辆之间的信息交换,汽车的显示终端可作为城市道路交通导航系统使用,车辆之间可以相互提供数字化信号灯信息、位置、车速等信息,以此作为接受信息车辆安全行驶的依据。在执行配送任务过程中,基于反映顾客需求、车辆及道路等变化情况的实时信息,对车辆运行路重新进行设计和优化,形成新的调度方案并安排执行, 考虑到货物品种及数量、需求时间和地点、运输线路以及运输时间的不确定性,因此从运输成本、时间惩罚成本、固定成本3个方面建立数学模型。
1.1 运输成本假设在物联网配送中心存在M个客户,每个客户的位置固定[13],送货物的重量分别为qi(i=1, 2, …, M);配送车辆数量共有K个, 每辆车的载重量分别为Qk(k=1, 2, …, K);单次配送车辆里程数为Dk(k=1, 2, …, K);配送车辆单次配送客户数为Ck(k=1, 2, …, K);第k辆车进行配送服务的用户数控制为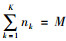
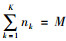
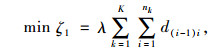
|
(1) |
式中,λ为单位里程费用;d(i-1)i为客户(i-1)到客户i的距离。
1.2 时间惩罚成本由于顾客对配送时效的要求越来越高,物联网配送车辆在实际配送过程需要接受顾客的接收时间[14-15],因此增设惩罚成本ζ2:
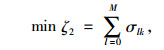
|
(2) |
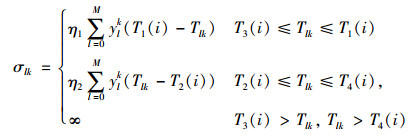
|
(3) |
式中,σlk为第k辆车服务于第i个客户时产生的惩罚成本;η1为物联网配送车辆提前到达客户接受时间段,产生等待成本;η2为物联网配送车辆晚到客户接受时间段,产生赔偿成本;Tlk为第k辆车到达第i个客户的时间点,[T1(i), T2(i)]为指定时间段,[T3(i), T4(i)]为可接受时间段,ylk=1为第k辆车送达到第i个客户。
1.3 固定成本物联网配送车辆的固定成本ζ3与派遣车辆数量有关,使用较少的车辆数减少企业的固定成本。
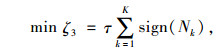
|
(4) |
式中,τ为单个物流配送车辆完成单次配送任务的固定费用,包括物联网器材以及使用费、车辆保养费、司机费等;Nk为车辆k在配送过程中的客户节点数量,sign(Nk)=1为车辆k被使用。
根据优化目标要求配送车辆总里程数为最短,并且固定成本、惩罚成本最少,则总成本最小化数学模型为:
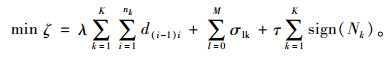
|
(5) |
基本粒子群算法参数比较简单[16],涉及到学习因子c1和c2及惯性权重ω,粒子更新自己的速度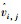
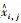

|
(6) |
式中,t为迭代次数;

尽管传统的粒子群算法可以解决非线性优化问题,为避免算法运行后期易出现局部最优解误认为全局最优解现象发生,增设扰动收缩操作。
2.2.1 扰动操作对基本粒子群算法增设扰动因子δ用来平衡粒子的全局和局部搜索[17],则粒子更新速度和位置为:

|
(7) |
δ为一个随机数,主要作用是控制随机扰动的振幅。δ值越大,粒子越具有强大的能力逃离当前位置,而δ值越小,越可以提高粒子的局部搜索能力。
对δ操作控制如图 2所示。

|
| 图 2 δ控制过程 Fig. 2 δ Control process |
| |
在迭代前期δ值设置比较小,让粒子主要进行局部搜索,而在后期δ值设置逐渐变大,让粒子逃离当前位置,进行全局搜索。
2.2.2 收缩操作为了加速粒子的收缩性,增设收缩算子gcenterĝ, ĵ,这样增强局部搜索能力,避免粒子的过度振荡。假设粒子处在被具有m个最佳位置包围的区域,即(gĝ, ĵ)1、(gĝ, ĵ)2, …, (gĝ, ĵ)m,它们之中包含最佳位置,定义为:
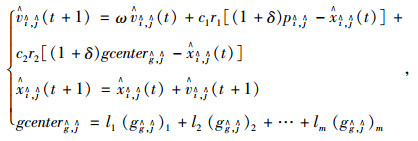
|
(8) |
式中,gcenterĝ, ĵ为第t次迭代时的m个最佳加权位置;lm为加权系数,l1>l2>…>lm,l1+l2+…+lm=1。
2.3 粒子编码方式由于配送涉及到3个变量,即收货点、物流配送车、行驶线路[18-19],因此粒子编码如表 1所示。
2.4 粒子解码方式
(1) 对粒子第2行的元素aij进行取整操作int(aij),收货点j得到分配的车辆i。
(2) 对于车辆i的行驶路径,先完成收货点j的配送任务,然后按照收货点j对第3行元素bij从小到大排序确定车辆i行驶路线。
把ζ作为所研究问题的目标函数,ζ越低越好,而粒子的适应度值是越高越好,适应度函数采用ζ的倒数表示。
算法流程:
① 初始化粒子的参数及迭代次数;
② 计算粒子适应度,找出个体最优和全局最优值;
③ 对粒子群进行扰动收缩;
④ 更新粒子的速度和位置,并更新历史全局最优值;
⑤ 满足迭代次数,输出寻优结果,否则进行步骤③。
3 试验仿真 3.1 数据来源试验设置粒子群个数为80个,最大迭代次数为200,采用Matlab进行仿真试验。假设某企业有物联网配送车辆3辆,需要配送客户9个,车辆额定载质量为5 t,单位里程费用为3元,车辆的行驶时间与距离成正比,每个任务点的需求量、装卸货的时间以及任务点的时间窗要求如表 2所示。比如任务序号1,其货运量为3 t,配送时间为1.3 h,最早到达时间为1 h,最晚到达时间为2.5 h。
| 任务序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 货运量/t | 3 | 2.5 | 4.5 | 3 | 3.5 | 4 | 2 | 1.5 | 3 |
| 配送时间/h | 1.3 | 2.1 | 2.1 | 1.1 | 2.1 | 2.2 | 3.1 | 1.2 | 1.2 |
| 时间窗/h | 1, 2.5 | 2, 4 | 1, 1.5 | 3, 5 | 3, 6 | 4, 6 | 1, 3 | 2, 5 | 1.2, 2 |
仓库与任务点以及各任务点之间的距离如表 3所示。
| 任务点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0 | 35 | 40 | 68 | 90 | 120 | 160 | 90 | 75 |
| 2 | 35 | 0 | 50 | 75 | 80 | 90 | 130 | 180 | 150 |
| 3 | 40 | 50 | 0 | 60 | 55 | 80 | 90 | 105 | 120 |
| 4 | 68 | 75 | 60 | 0 | 50 | 35 | 60 | 90 | 150 |
| 5 | 90 | 80 | 55 | 50 | 0 | 40 | 80 | 60 | 100 |
| 6 | 120 | 90 | 80 | 35 | 40 | 0 | 55 | 150 | 100 |
| 7 | 160 | 130 | 90 | 60 | 80 | 55 | 0 | 120 | 60 |
| 8 | 90 | 180 | 105 | 90 | 60 | 150 | 120 | 0 | 35 |
| 9 | 75 | 150 | 120 | 150 | 100 | 00 | 60 | 35 | 0 |
3.2 结果与分析 3.2.1 目标函数优化分析
物联网配送车辆总成本是评价分析算法性能的重要指标,对本研究涉及到的GA,AC,PSO,CQPSO,SAPSO,CMPSO以及PCPSO算法对比分析,目标函数总成本优化的迭代曲线如图 3(a)所示,任务目标点寻优地理位置偏差如图 3(b)所示。

|
| 图 3 目标函数优化分析 Fig. 3 Analysis of objective function optimization |
| |
从图 3(a)可以看出,各种算法都随进化迭代次数的增加而目标函数总成本呈递减趋势,但是本研究PCPSO算法前期递减速率较快,在第60次迭代时,总成本值逐渐趋于稳定,其他算法需要较多的迭代次数才能够趋于稳定;从图 3(b)可以看出,本研究PCPSO算法对任务目标点寻优地理位置偏差值最小,避免了总成本增加。
各种算法获得目标函数总成本最优时消耗时间结果对比如表 4所示。
| 耗时 | 算法 | ||||||
| GA | AC | PSO | CQPSO | SAPSO | CMPSO | PCPSO | |
| 时间/s | 25.5 | 23.2 | 20.1 | 16.4 | 15.2 | 13.5 | 8.2 |
从表 4可以看出,本研究PCPSO算法消耗时间少于其他算法,在处理时间上都有着明显的提高,说明本研究PCPSO算法可以在较少的时间内获得总成本最优化,主要是PCPSO算法通过非线性控制δ值,迭代前期让粒子主要进行局部搜索,后期进行全局搜索,从而获得最优结果。
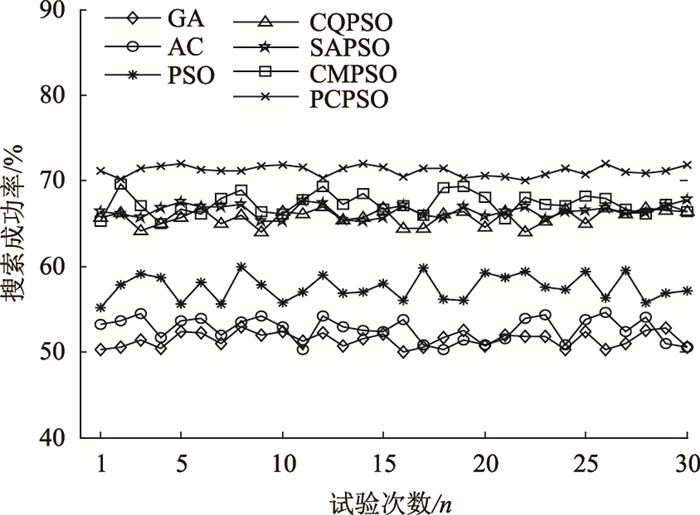
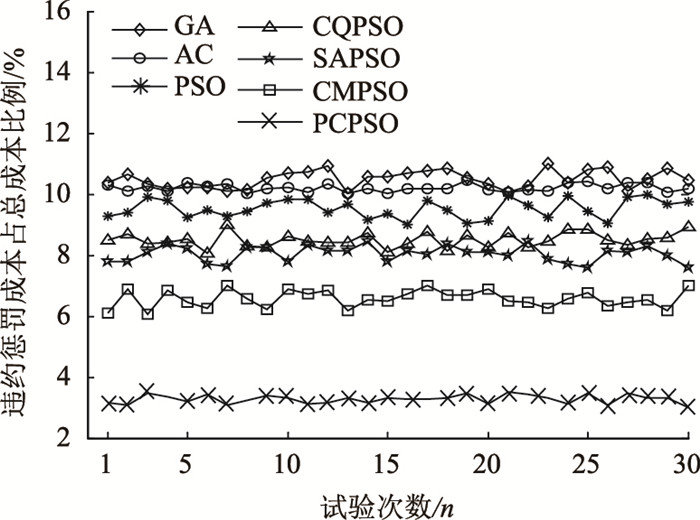
3.2.2 算法其他性能对比分析涉及到的对比算法有GA,AC,PSO,CQPSO,SAPSO,CMPSO以及本研究PCPSO算法,对每种算法均进行30次蒙特卡罗试验。搜索成功率、违约惩罚成本占总成本比例如图 4、图 5所示。
|
| 图 4 搜索成功率 Fig. 4 Search success rate |
| |
|
| 图 5 违约惩罚成本占总成本比例 Fig. 5 Proportion of default penalty cost to total cost |
| |
从图 4可以看出,本研究PCPSO算法每次试验的搜索成功率最高为70%,同时从图 5可以看出,本研究PCPSO算法每次试验的违约惩罚成本占总成本比例最低为3%,说明本研究PCPSO算法具有较好的搜索成功率以及控制违约惩罚成本,主要是PCPSO算法可通过较少的迭代次数找到最优解,增强算法搜索功能,从而获得更优的车辆配送方案。
4 结论针对物联网配送车辆调度过程中的效率问题,提出了扰动收缩粒子群算法,对成本最小化模型寻优使得配送成本最优,避免了运输成本的增加。试验仿真显示本研究算法对目标函数总成本优化中使用最少的迭代次数即可获得最优值,每次试验的搜索成功率最低为70%,每次试验的违约惩罚成本占总成本比例最高为3%,是一种高效的优化方法,为物联网配送车辆调度提供了一种新方法。
| [1] |
曹琦, 曹阳. 应急物资配送车辆调度模型与优化综述[J]. 计算机应用, 2018, 38(8): 2416-2422, 2430. CAO Qi, CAO Yang. Review of Model and Optimization of Vehicle Scheduling for Emergency Material Distribution[J]. Journal of Computer Applications, 2018, 38(8): 2416-2422, 2430. |
| [2] |
FIGLIOZZI M A. The Time Dependent Vehicle Routing Problem with Time Windows:Benchmark Problems, an Efficient Solution Algorithm, and Solution Characteristics[J]. Transportation Research Part E:Logistics and Transportation Review, 2012, 48(3): 616-636. |
| [3] |
赵建峰, 袁细国, 梁伯栋, 等. 基于车联网及云计算的电动物流车智能调度算法[J]. 公路交通科技, 2019, 36(6): 112-124. ZHAO Jian-feng, YUAN Xi-guo, LIANG Bo-dong, et al. An Electric Logistics Vehicle Intelligent Scheduling Algorithm Based on Internet of Vehicles and Cloud Computing[J]. Journal of Highway and Transportation Research and Development, 2019, 36(6): 112-124. |
| [4] |
LEE C G, EPELMAN M A, WHITE III C C, et al. A Shortest Path Approach to the Multiple-vehicle Routing Problem with Split Pick-ups[J]. Transportation Research Part B:Methodological, 2006, 40(4): 265-284. |
| [5] |
珠兰, 胡大伟. 不确定情形下的绿色物流网络和库存问题研究[J]. 公路交通科技, 2018, 35(6): 121-130. ZHU Lan, HU Da-wei. Study on Green Logistic Network and Inventory Problem under Uncertain Condition[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 121-130. |
| [6] |
申艳光, 张玲玉, 刘永红. 基于混合遗传算法的物流路径优化方法研究[J]. 计算机技术与发展, 2018, 28(3): 192-196. SHEN Yan-guang, ZHANG Ling-yu, LIU Yong-hong. Study on Optimizing of Physical Routing Method Based on Hybrid Genetic Algorithm[J]. Computer Technology and Development, 2018, 28(3): 192-196. |
| [7] |
张庆华, 吕小丹. 电商退换货车辆路径问题及蚁群算法研究[J]. 计算机工程与应用, 2018, 54(22): 239-245. ZHANG Qing-hua, LÜ Xiao-dan. Research on Vehicle Routing Problem with Return and Replacement in E-commerce Environment and Its Solution to Ant Colony Algorithm[J]. Computer Engineering and Applications, 2018, 54(22): 239-245. |
| [8] |
张利娟, 仇建伟, 杜登崇, 等. 基于Spark和PSO算法的军事物流配送路径优化问题研究[J]. 计算机与现代化, 2018(11): 65-68, 76. ZHANG Li-juan, QIU Jian-wei, DU Deng-chong, et al. Research on Military Logistics Distribution Routing Optimization Problem Based on Spark and PSO Algorithm[J]. Computer and Modernization, 2018(11): 65-68, 76. |
| [9] |
杜明洋, 程琳, 李雪峰. 基于自适应粒子群小波网络的公共自行车出行需求预测[J]. 公路交通科技, 2019, 36(6): 94-102. DU Ming-yang, CHENG Lin, LI Xue-feng. Prediction of Public Bike Trip Demand Based on APSO-WNN[J]. Journal of Highway and Transportation Research and Development, 2019, 36(6): 94-102. |
| [10] |
王雷震, 汪定伟, 王素欣. 多起讫点货物转运配送车辆调度模型及其粒子群、蚁群算法混合求解[J]. 信息与控制, 2018, 47(5): 564-572. WANG Lei-zhen, WANG Ding-wei, WANG Su-xin. Study of Multi-depots Goods Transhipment Vehicle Scheduling Problem Model and Its Particle Swarm and Ant Colony Optimization Hybrid Arithmetic[J]. Information and Control, 2018, 47(5): 564-572. |
| [11] |
程倩. 基于改进粒子群算法的烟草物流优化方案[J]. 兰州工业学院学报, 2018, 25(1): 73-77. CHENG Qian. Tobacco Logistics Network Information Optimization Based on Improved Particle Swarm Algorithm[J]. Journal of Lanzhou Institute of Technology, 2018, 25(1): 73-77. |
| [12] |
吕立国, 季伟东. 结合质心思想和柯西变异策略的粒子群优化算法[J]. 计算机应用, 2017, 37(5): 1369-1375, 1418. LÜ Li-guo, JI Wei-dong. Improved Particle Swarm Optimization Algorithm Combined Centroid and Cauchy Mutation[J]. Journal of Computer Applications, 2017, 37(5): 1369-1375, 1418. |
| [13] |
郭键. 大型物流车辆配送线路自适应调度方法[J]. 计算机测量与控制, 2017, 25(11): 166-169. GUO Jian. Adaptive Scheduling Method for Large-scale Logistics Distribution Vehicle Lines[J]. Computer Measurement & Control, 2017, 25(11): 166-169. |
| [14] |
张占云.多智能体冷链物流车辆路径优化问题研究[D].保定: 河北大学, 2018. ZHANG Zhan-yun.Research on Vehicle Routing Optimization of Multi-agent Cold Chain Logistics[D]. Baoding: Hebei University, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10075-1018958281.htm |
| [15] |
邹旭辉.基于改进粒子群算法的家电物流配送车辆调度优化问题研究[D].重庆: 重庆交通大学, 2018. ZOU Xu-hui.Research on Vehicle Scheduling Optimization of Electrical Appliances Logistics Distribution Based on Improved Particle Swarm Optimization[D].Chongqing: Chongqing Jiaotong University, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10618-1018174540.htm |
| [16] |
万玉龙, 李新春, 周红标. 基于WPD-PSO-ESN的短期交通流预测[J]. 公路交通科技, 2019, 36(8): 144-151. WAN Yu-long, LI Xin-chun, ZHOU Hong-biao. Prediction of Short-term Traffic Flow Based on WPD-PSO-ESN[J]. Journal of Highway and Transportation Research and Development, 2019, 36(8): 144-151. |
| [17] |
OUYANG Z Y, LIU Y, RUAN S J, et al. An Improved Particle Swarm Optimization Algorithm for Reliability Redundancy Allocation Problem with Mixed Redundancy Strategy and Heterogeneous Components[J]. Reliability Engineering and System Safety, 2019, 181(6): 62-74. |
| [18] |
吴聪, 杨建辉. 基于改进粒子群算法的物流配送车辆调度优化[J]. 计算机工程与应用, 2015, 51(13): 259-262, 270. WU Cong, YANG Jian-hui. Vehicle Routing Problem of Logistics Distribution Based on Improved Particle Swarm Optimization Algorithm[J]. Computer Engineering and Applications, 2015, 51(13): 259-262, 270. |
| [19] |
WANG Y, HU D W, LI H F. Solution of Emergency Supply Model under Multi-supply Subjects Using an Immune Algorithm-based Particle Swarm Optimization[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 130-138. |
 2020, Vol. 37
2020, Vol. 37
