扩展功能
文章信息
- 黄华, 郭朋, 吴先兵, 张凡涛
- HUANG Hua, GUO Peng, WU Xian-bing, ZHANG Fan-tao
- 断索对双钢拱塔斜拉桥力学性能的影响
- Influence of Cable Breaking on Mechanical Properties of Double-steel-arch-pylon Cable-stayed Bridge
- 公路交通科技, 2020, 37(4): 62-71, 117
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 62-71, 117
- 10.3969/j.issn.1002-0268.2020.04.009
-
文章历史
- 收稿日期: 2019-01-04
斜拉桥在200 m到800 m的跨度范围内显示出较大的优越性,是大跨度桥梁的最主要桥型[1]。拉索作为斜拉桥的主要受力构件,直接布置在主梁和索塔的外部,尺寸小、应力大,且与空气直接接触,车辆冲击、疲劳和腐蚀等均可对拉索造成严重的损伤。此外,一些极端情况,如火灾、暴风情况下,拉索容易出现破损,甚至断裂。1979年委内瑞拉Maracaibo Lake大桥拉索突然断裂,造成桥梁局部坍塌;2001年四川南门大桥拉索振动,进而导致吊索断裂,最终致使桥梁主体断裂;2014年湖南郴州在建赤石特大桥6号桥墩左幅塔顶突发大火,导致9根斜拉索断裂,断索侧桥面下降约2.15 m;2018年夏,受台风影响,苏通大桥一根斜拉索和其连接固定的支架发生分离,在大风中发生强烈的摇晃。
目前,拉索系统出现损伤甚至断裂的问题受到了国内外专家学者的广泛关注。D Janjic[2]、WANG Yang-Cheng[3]等人采用刚度矩阵法,分析了斜拉索的数量、斜拉索之间的间距等因素对斜拉桥静、动力特性和承载力的影响;B Shekastehband等[4]对张拉整体结构进行了断索理论分析和试验研究,指出不同区域的拉索破断对结构产生的影响完全不同,严重时甚至会引起张拉整体结构的连续性倒塌;M Wolff等[5]考虑拉索垂度、横向振动、结构阻尼等因素的影响,进而确定了动力响应放大系数;R Das等[6]通过非线性动态过程演示了典型斜拉桥的建模与分析,讨论了多种类型关键斜拉索损耗情况下斜拉桥模型的响应,指出当故障斜拉索位置靠近索塔时,模型失效的可能性降低,在此过程中确定了斜拉桥的渐进式倒塌模式;C Kao等[7]研究了拉索断裂对大跨度斜拉桥结构性能的影响,认为外侧拉索断裂对结构内力、位移和极限承载力影响较为明显;S Kim等[8]基于结构形态的变化和内力的分布研究了单根拉索失效后结构的静力特性,发现尽管只有一根拉索失效,结构静力性能和极限承载力仍会发生显著的变化;BAI Zhi-zhou等[9]在不考虑拉索断裂和考虑拉索断裂情况下,分别提出了斜拉桥达到极限承载力时的破坏机理,认为不考虑拉索断裂情况下结构失效时延展性较好,考虑斜拉索断裂情况下结构失效时表现出明显的脆性;JIN Xiao-Long等[10]建立了巴东长江大桥有限元模型并进行试验研究,得出拉索断裂对索力影响程度大于对主梁位移和固有频率的影响程度。罗晓峰[11]等提出了修正的弹性支撑法,可在弹性范围内较准确地对桥塔刚度较大、索距较小的双塔双索面斜拉桥桥塔做稳定性分析;于刚等[12]以主梁最小屈曲安全系数和最大应力安全系数作为结构性能参数,对不同位置拉索断裂的损伤场景进行了易损性分析,明确了结构对不同位置拉索断裂的敏感性,为结构健康监测中监测内容的选取以及传感器的布设提供了参考依据;郑小博等[13]通过反向加载模拟斜拉索断裂的作用效应,分析了斜拉索在不同断裂时间下桥梁的动力响应特征,提出如果考虑两根以上斜拉索同时失效,根据2.0的动力放大系数进行安全储备设计是不足的;闫冬[14]等以实例分析识别了桥梁的倒塌模式,提出的简化计算方法计算精度高、运算速度快,为桥梁抗倒塌设计和加固提供了科学依据;宗钟凌等[15]对一直径6 m的葵花型索穹顶进行了简单的模型试验研究,指出单根拉索瞬间破断会引起结构的微幅振动,不同位置断索对结构的影响程度不同;王霄翔等[16]对某弦支穹顶结构进行了局部环索断索动力冲击效应试验,指出断索点附近的杆件受到断索的影响而发生一定的震荡以及内力变化,且索力越大、节点约束越弱,波动幅度越大;汪永兰[17]、赵翔[18]先后对润扬长江公路大桥对称拉索、非对称拉索及拉索不同程度损伤下斜拉桥的静动力结构性能进行了分析。
然而,当前对带有水平索的V型双钢拱塔斜拉桥的研究较少,且在施工控制方面国内现行规范只对常规斜拉桥做了相关要求,而未涉及本文所研究的V型双钢拱塔斜拉桥。因此为保证局部拉索突然断裂时剩余结构的安全性,对V型双拱斜拉桥拉索断裂后的力学性能进行研究很有必要。本研究以西安市某双钢拱塔斜拉桥为工程背景,进行V型双拱斜拉桥的拉索断裂性能分析,研究主梁线形变化和索力分配规律,为此类桥梁设计、施工以及运营监控提供参考。
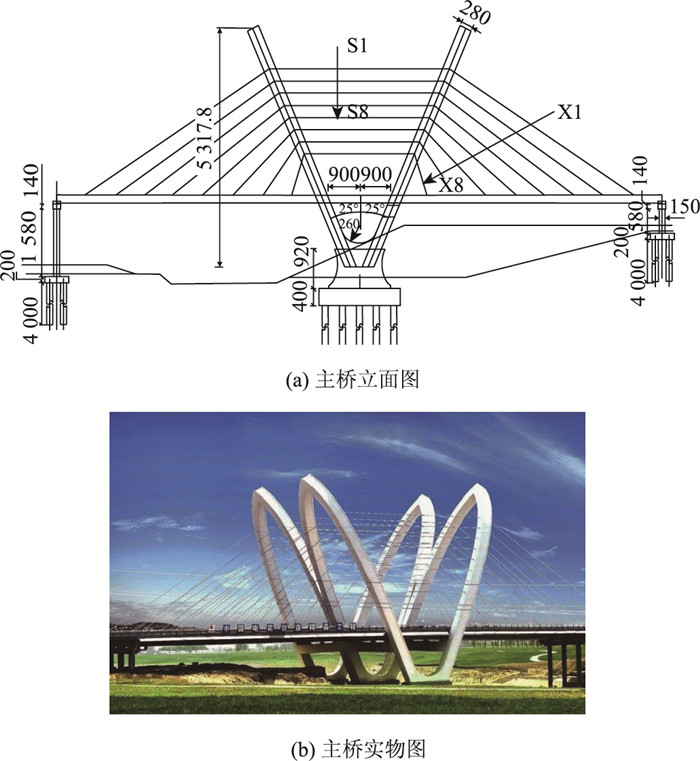
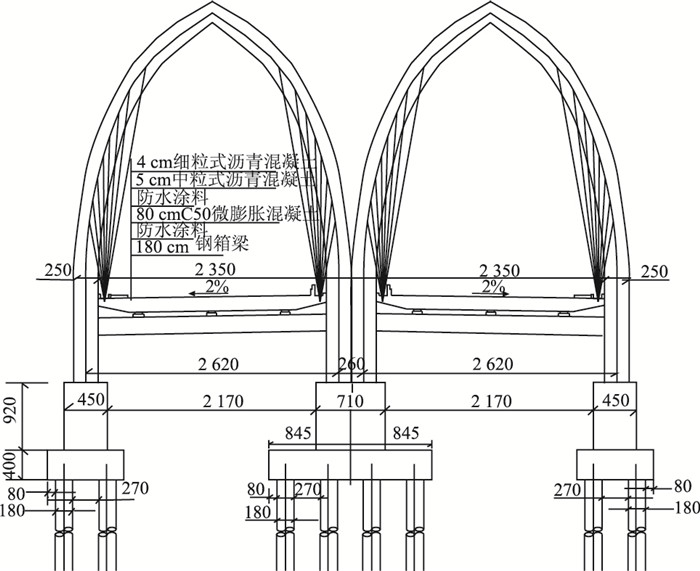
1 工程概况西安市某大桥主桥为V型双钢拱塔斜拉桥,半漂浮体系,塔墩固结,塔梁分离。桥梁跨度为(80+80)m,宽度为23.5×2=47.0 m。本桥主塔采用“花瓣式”钢双拱塔,钢拱塔外观立体图呈花瓣式,正视图呈倾斜的双网球拍形,与竖直方向立面约呈1:2.5的倾斜角,塔身净高约53.2 m,其中桥面距离塔顶39.0 m。主塔采用钢箱截面,截面纵桥向2.8 m,横桥向2.5 m,主塔内高出桥面3 m范围内灌充C40混凝土。主梁采用钢箱梁结构形式,梁高1.8 m,单箱多室结构,在非锚固区顶板厚度16 mm,底板厚度12 mm,在锚固区将顶板、底板均加厚至20 mm,腹板厚度16 mm,U形肋厚6,8 mm,间距60~70 cm,横隔板间距2 m,厚12 mm[19]。拉索采用空间密索体系,包括水平索和斜拉索,并沿顺桥向及横桥向对称布置,双拱塔间采用8对水平索通过两端张拉连接,主梁跟主塔之间通过8对斜拉索连接,并在主梁上张拉,这两套索构成了空间索体系。全桥共48根索,拉索在主塔上的索距为竖向2.8 m,在主梁上顺桥向标准间距为8 m。二期恒载包括桥面铺装以及其他桥面附属设施,按72.3 kN/m计,汽车荷载采用公路一级,单幅横向按5车道考虑。该桥立面图及实物图如图 1所示,侧视图如图 2所示。
|
| 图 1 某斜拉桥(单位:cm) Fig. 1 A cable-stayed bridge (unit: cm) |
| |
|
| 图 2 大桥侧面图(单位:cm) Fig. 2 Side view of bridge (unit: cm) |
| |
2 结构模型
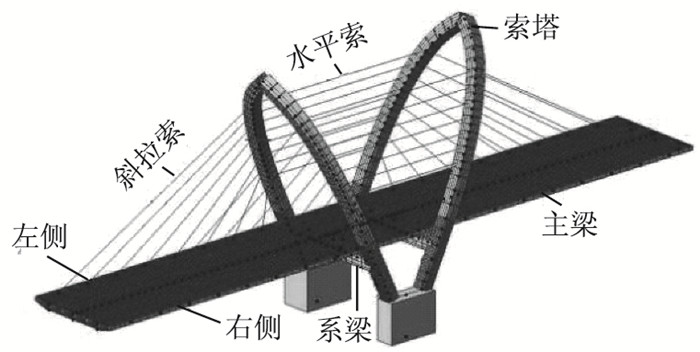
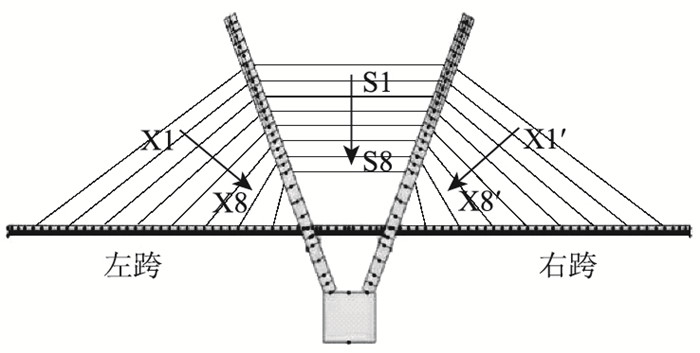
采用Midas/Civil 2015软件,建立双拱独塔斜拉桥空间结构计算模型,全桥共划分为281个节点,316个单元,其中主梁88个单元。索塔和主梁采用空间梁单元模拟;水平索和斜拉索采用Ernst公式修正后的桁架单元进行模拟,以消除拉索垂度对结构非线性的影响。由于钢拱塔基础为群桩基础,且桩的长度较大,故塔底边界条件采用固结进行模拟;塔墩固结处通过共用节点进行模拟;斜拉索节点和主梁节点间采用刚性连接进行模拟,全桥共划分为38个施工段。由于该大桥左右幅对称,故仅对单幅结构进行分析,并将水平索从上到下依次编号为S1~S8,左跨斜拉索从左到右依次编号为X1~X8,右跨斜拉索从右到左依次编号为X1′~X8′。单幅模型图如图 3所示,拉索编号如图 4所示,该模型钢材、钢绞线以及混凝土的材料特性如表 1所示。
|
| 图 3 大桥单幅模型图 Fig. 3 Single deck model of bridge |
| |
|
| 图 4 拉索编号 Fig. 4 Cable numbers |
| |
| 材料名称 | 类别 | 构件 | 特性 | |||
| 弹性模量/MPa | 泊松比 | 线膨胀系数 | 密度/(kN·m-3) | |||
| 混凝土 | C40 | 主塔塔座 | 3.25×104 | 0.2 | 1.0×10-5 | 26.0 |
| C30 | 基础 | 3.00×104 | 0.2 | 1.0×10-5 | 26.0 | |
| 钢绞线 | fpk=1 860 MPa | 斜拉索 | 2.05×105 | 0.3 | 1.2×10-5 | 78.5 |
| 钢材 | Q345 | 主梁/索塔 | 2.10×105 | 0.3 | 1.2×10-5 | 78.5 |
3 断索对结构性能的影响分析
将正装成桥索力与设计成桥索力对比如表 2所示。根据上表索力情况可以看出,(正装成桥索力-设计成桥索力)/设计成桥索力(%)的最大值为1.1%,最小为-4.0%,正装成桥索力与设计成桥索力基本保持一致。在运营状态下拉索最大应力为700.5 MPa,小于0.4fpk=0.4×1 860=744 MPa的限值,主梁跨中向上、向下挠度分别为12.86,-46.58 mm,总计59.44 mm,挠跨比为1/1 345,小于1/500,满足JTG/TD65-01—2007规范[20]要求。说明该方法可以比较有效地对模型各阶段进行模拟。
| 编号 | 设计成桥索力/kN | 正装成桥索力/kN | (正装-设计)/设计/% | |
| 水平索 | S1 | 1 763.2 | 1 705.3 | -3.3 |
| S2 | 1 882.8 | 1 844.1 | -2.1 | |
| S3 | 1 726.2 | 1 724.6 | -0.1 | |
| S4 | 1 717.2 | 1 690.1 | -1.6 | |
| S5 | 1 590.3 | 1 549.0 | -2.6 | |
| S6 | 1 125.1 | 1 080.1 | -4.0 | |
| S7 | 1 056.0 | 1 015.0 | -3.9 | |
| S8 | 1 950.0 | 1 941.7 | -0.4 | |
| 斜拉索 | X1 | 1 170.9 | 1 133.1 | -3.2 |
| X2 | 1 880.1 | 1 886.6 | 0.3 | |
| X3 | 1 552.5 | 1 562.2 | 0.6 | |
| X4 | 1 508.4 | 1 509.4 | 0.1 | |
| X5 | 1 410.3 | 1 411.7 | 0.1 | |
| X6 | 1 210.5 | 1 220.2 | 0.8 | |
| X7 | 1 134.0 | 1 146.1 | 1.1 | |
| X8 | 956.7 | 963.6 | 0.7 |
本研究利用Midas/Civil中的钝化功能,结合施工阶段来模拟斜拉桥的拉索断裂现象,即先将要断裂的拉索定义为一个结构组,然后在完好模型的基础上,添加一个施工阶段,通过在该施工阶段中钝化已定义的结构组来模拟拉索的断裂。本研究仅分析正常运营条件下,即恒载+公路一级车道荷载作用下,当断索的数量和位置不同时,主梁的位移变化以及剩余索力分配规律。
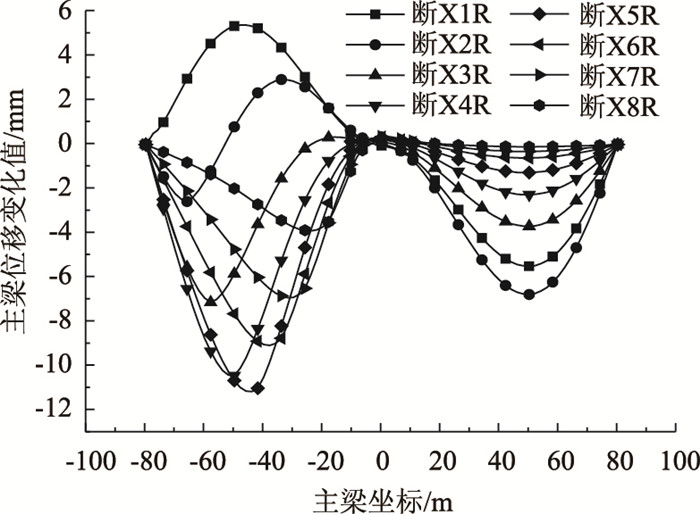
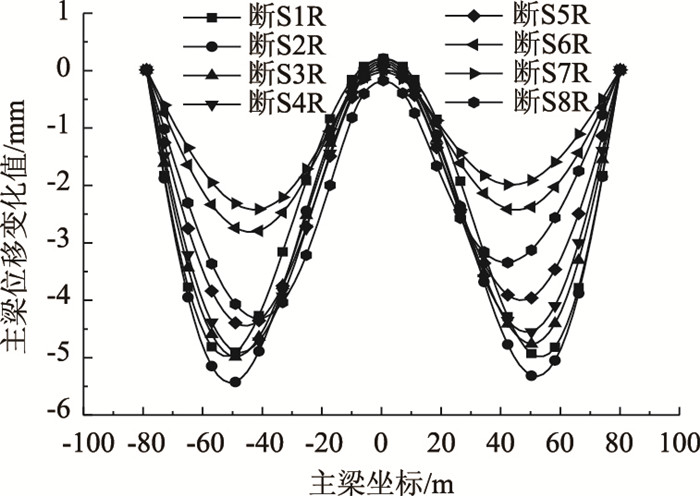
3.1 斜拉桥单索断裂对主梁线形的影响由于该桥为对称结构,故仅需模拟X1R~X8R以及S1R~S8R分别断裂时主梁位移的变化即可,X1R~X8R分别断裂时主梁位移变化曲线如图 5所示,S1R~S8R分别断裂时主梁位移的变化曲线如图 6所示(其中,R代表右侧拉索,主梁跨中节点横坐标为0 m,正值表示主梁断索后相对断索前发生上挠,负值表示主梁断索后相对断索前发生下挠)。
|
| 图 5 X1R~X8R分别断裂时主梁挠度变化值 Fig. 5 Changes of deflection of main girder when X1R-X8R fractured separately |
| |
|
| 图 6 S1R~S8R分别断裂时主梁挠度变化值 Fig. 6 Changes of deflection of main girder when S1R-S8R fractured separately |
| |
由图 5可知:
(1) 斜拉索断裂对断裂跨主梁线形的影响大于非断裂跨。其中,最外侧斜拉索的断裂会导致断裂跨梁体上挠,次外侧斜拉索的断裂会导致断裂跨梁体部分上挠,部分下挠,其余斜拉索的断裂会导致断裂跨梁体下挠,下挠峰值均出现在锚固点附近。
(2) 任意一根斜拉索断裂均会导致非断裂跨梁体下挠,下挠峰值出现在非断裂跨跨中附近,随断索位置向索塔靠近,拉索断裂对非断裂跨主梁下挠的影响逐渐减小。
(3) 中间索X5R断裂对主梁位移变化值的影响最大,最大值为-11.18 mm,较未断索时增大25%。
(4) X1R~X8R单索断裂对两系梁之间主梁段的位移基本没有影响,X7R断裂时,主梁坐标0 m处位移变化值最大,为0.36 mm,较未断裂时减小5.4%。
由图 6可知:
(1) 相对于斜拉索,水平索断裂对梁体位移的影响较小,每一根水平索的断裂都会导致主塔两侧梁体下挠,且下挠值基本相同,断索后两跨跨中附近梁体位移变化最大,其中S2R断裂时主梁位移变化量最大,为5.5 mm,较未断裂时增大12.0%。
(2) 水平索断裂对两系梁之间主梁段线形的影响也很小,但比斜拉索断裂影响大。外侧水平索S1R断裂时,主梁坐标-9 m处梁体位移变化最大,最大值为-0.71 mm,较未断裂时增大11%,但由于两系梁之间主梁段的位移在断索前就很小,所以基本可以忽略拉索断裂后两系梁间主梁段线形的变化。
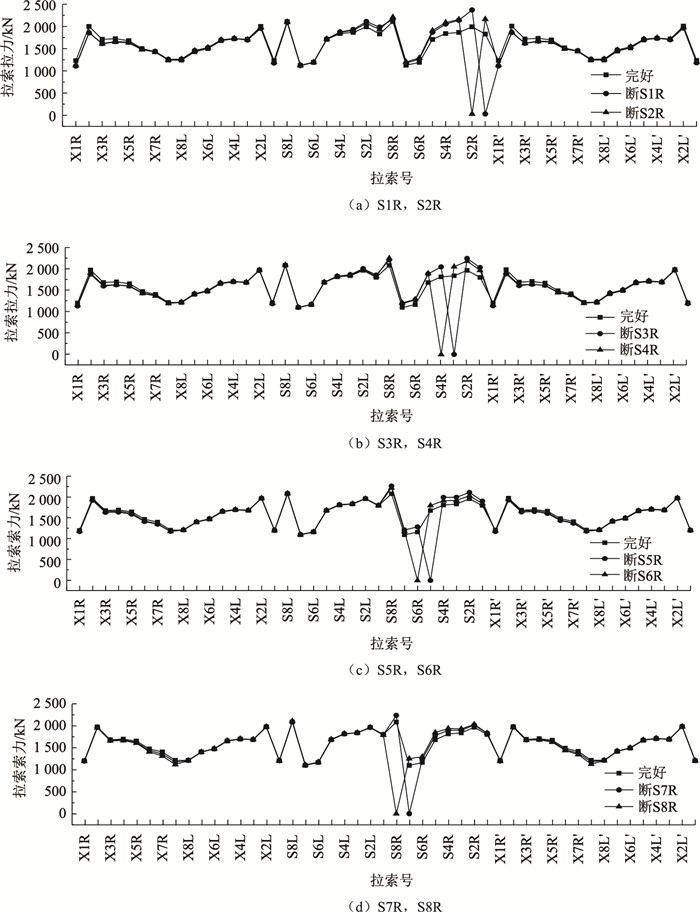
3.2 单索断裂对剩余拉索索力的影响列出X1R~X8R分别断裂时剩余拉索索力变化曲线如图 7所示,S1R~S8R分别断裂时剩余拉索索力变化曲线如图 8所示(横坐标从左到右依次是X1R~X8R,X1L~X8L,S8L~S1L,S8R~S1R,X1R′~X8R′,X1L′~X8L′)。

|
| 图 7 X1R~X8R单索断裂时剩余索力的变化情况 Fig. 7 Changes of residual cable forces when X1R-X8R fractured separately |
| |
|
| 图 8 S1R~S8R单索断裂时剩余索力的变化情况 Fig. 8 Changes of residual cable forces when X1R-X8R fractured separately |
| |
从图 7可知:
(1) 单根斜拉索断裂对本侧拉索索力的影响明显大于对另一侧拉索索力的影响。任意一根斜拉索断裂时,其同跨同侧和同跨异侧附近几根索的索力增大,与该断索相连的水平索以及该水平索附近几根索的索力变小,与该断索关于跨中对称的斜拉索以及该斜拉索附近的几根索索力也会变小。
(2) 断索位置越靠近索塔,断索处附近拉索的索力增量越大,但受到影响的拉索数量越少,当内侧索X7R断裂时,除X7R同侧附近的几根拉索索力增大,其余拉索的索力基本没有变化,此时X8R的索力变化值最大,为328.18 kN,较未断裂时增大27.1%,表明外侧索所承受的拉力可以均匀分配给附近的拉索,而内侧索所受拉力仅可集中分配给与其相邻的少量拉索[21]。
由图 8可知:
(1) 任意一根水平索断裂时,该侧水平索的索力均会增大,与该断索纵向对称的另一侧水平索以及该水平索附近几根索的索力也会增大,与该断索相连的两根斜拉索以及斜拉索附近的几根拉索索力降低,且降低值基本相同,一侧水平索断裂对另一侧斜拉索的索力基本没有影响。
(2) 与斜拉索不同,外侧水平索断裂时,其附近拉索索力增量较大,当外侧索S1R断裂时,S2R索力变化值最大,为381.04 kN,较未断裂时增大19.4%。
3.3 斜拉桥双索断裂对主梁线形的影响考虑到斜拉桥双索断裂的组合较多,本研究基于单索中的分析结果,将对主梁线形影响较大的单索X1R,X5R,S1R进行组合。
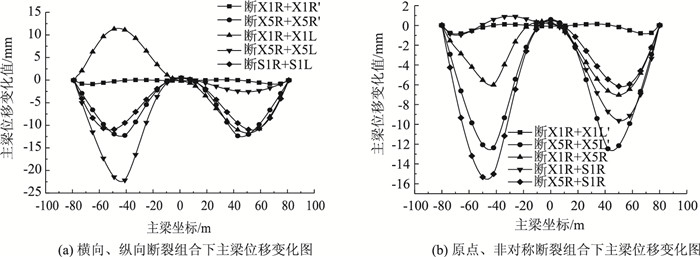
按照以下4种情况进行分析:(1)横向对称断裂;(2)纵向对称断裂;(3)原点对称断裂;(4)非对称断裂。列出断裂组合如表 3所示。各种断裂组合下主梁的位移变化如图 9所示:
| 横向对称断裂 | 纵向对称断裂 | 原点对称断裂 | 非对称断裂 |
| X1R+X1R′ | X1R+X1L | X1R+X1L′ | X1R+X5R |
| — | X5R+X5L | — | X1R+S1R |
| X5R+X5R′ | S1R+S1L | X5R+X5L′ | X5R+S1R |
|
| 图 9 几种断裂组合下主梁位移变化情况 Fig. 9 Changes of displacement of main girder under several fracture combinations |
| |
(1) 拉索发生横向对称断裂和原点对称断裂时,主梁线形对称变化,相对于横向对称断裂和原点对称断裂,纵向对称断裂和非对称断裂对主梁线形的影响较大,尤其是纵向对称拉索X5R+X5L断裂时,断裂跨的最大位移为-68.34 mm,相比于未断裂时增加了50.2%,但仍满足1/500挠跨比的要求。
(2) 任意两根索断裂引起的主梁位移变化值约为这两根索单独断裂时主梁位移变化值之和,即符合叠加原理。如同时断裂X5R+X5L时,-48 m处主梁的挠度变化值为22.1 mm,单独断裂X5R时,该处挠度变化值为10.99 mm,单独断裂X5L时,该处挠度变化值为11.0 mm。
(3) 由3.1分析可知最外侧斜拉索断裂时,会导致断裂跨上挠,非断裂跨下挠,而且上挠值与下挠值基本相同,因此同时断裂X1R+X1R′或者同时断裂X1R+X1L′时,主梁线形基本没有变化。同理,同时断裂X1R+X1L时会使断裂跨主梁上挠最明显。
3.4 斜拉索双索断裂时对剩余拉索索力的影响由前面分析可知,从影响程度和范围来看,拉索X1,X7,S1断裂时对附近拉索索力的影响较大。但是,为了研究该类桥梁双索断裂后剩余索力的变化是否具有叠加性,本研究对多种断索组合下剩余拉索索力的变化进行分析,限于篇幅,仅列出组合X1R+X1L,X7R+X7L,S1R+S1L,S8R+S8L分别断裂时剩余拉索索力的变化曲线如图 10所示:

|
| 图 10 几种断裂组合下剩余索力的变化情况 Fig. 10 Changes of residual cable forces under several fracture combinations |
| |
分别列出图 10各断索工况下剩余索力的变化最大值如表 4所示。
| 断索号 | 剩余索力/kN | 断索号 | 剩余索力/kN | 断索号 | 剩余索力/kN | 断索号 | 剩余索力/kN | |||
| X2R | X8R | S2R | S7R | |||||||
| X1R | 205.88 | X7R | 328.48 | S1R | 381.04 | S8R | 154.62 | |||
| X1L | 75.63 | X7L | 13.34 | S1L | 119.29 | S8L | 10.18 | |||
| X1R+X1L | 299.59 | X7R+X7L | 336.48 | S1R+S1L | 547.88 | S8R+S8L | 166.50 |
由表 4可知:单独断裂X1R时,X2R索力增大205.88 kN,单独断裂X1L时,X2R索力增大75.63 kN,同时断裂X1R和X1L时,X2R索力增大299.59 kN,较未断裂时增大15.2%,此时所有拉索中X2R索力最大,为753 MPa。
单独断裂X7R时,X8R索力增大328.48 kN,单独断裂X7L时,X8R索力增大13.34 kN,同时断裂X7R和X7L时,X8R索力增大336.48 kN,较未断裂时增大27.8%,此时所有拉索中X6R索力最大,为724.7 MPa。
单独断裂S1R时,S2R索力增大381.04 kN,单独断裂S1L时,S2R索力增大119.29 kN,同时断裂S1R和S1L时,S2R索力增大547.88 kN,较未断裂时增大27.9%,此时所有拉索中S3R索力最大,为836 MPa。
单独断裂S8R时,S7R索力增大154.62 kN,单独断裂S8L时,S7R索力增大10.18 kN,同时断裂S8R和S8L时,S7R的索力增大166.50 kN,较未断裂时增大15.2%,此时所有拉索中S6R索力最大,为784.5 MPa。
由以上分析可知,最外侧两根斜拉索或者最外侧两根水平索同时断裂时,相比于单根索断裂后的叠加有一些放大效应,但随着斜拉索断索位置向索塔靠近、水平索断索位置向主梁靠近,这种放大效应逐渐减弱,整体而言,双索断裂基本符合叠加原理,通过断索分析和叠加原理容易得知,纵向对称断索较横向对称和原点对称断索危险;双索断裂时,剩余拉索索力最大为836.1 MPa,相比于其极限抗拉强度1 860 MPa,安全系数仍然达到2.2。
3.5 主梁及索塔应力分析根据计算结果,得出不同断索工况下主梁及索塔的最大应力见表 5,最不利工况下主梁及索塔的应力云图见图 11~图 12。
| 工况 | 最大应力/MPa |
| 完整 | 49.2 |
| 断S1R | 58.9 |
| 断S2R | 57.8 |
| 断S3R | 54.9 |
| 断S4R | 52.2 |
| 断S5R | 48.9 |
| 断S6R | 48.7 |
| 断S7R | 48.7 |
| 断S8R | 52.8 |
| 断X1R | 56.1 |
| 断X2R | 60.4 |
| 断X3R | 55.7 |
| 断X4R | 53.7 |
| 断X5R | 51.6 |
| 断X6R | 49.5 |
| 断X7R | 51.8 |
| 断X8R | 54.1 |
| 断X1R+X1R′ | 49.6 |
| 断X5R+X5R′ | 49.5 |
| 断X1R+X1L | 58.9 |
| 断X5R+X5L | 51.0 |
| 断S1R+S1L | 63.7 |
| 断X1R+X1L′ | 53.4 |
| 断X5R+X5L′ | 52.2 |
| 断X1R+X5R | 62.1 |
| 断X1R+S1R | 60.0 |
| 断X5R+S1R | 58.7 |
|
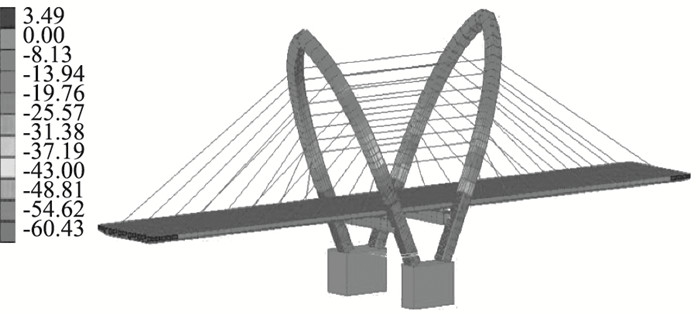
| 图 11 X2R断裂时主梁及索塔应力(单位:MPa) Fig. 11 Stresses of main girder and pylon when X2R fractured(unit:MPa) |
| |
|
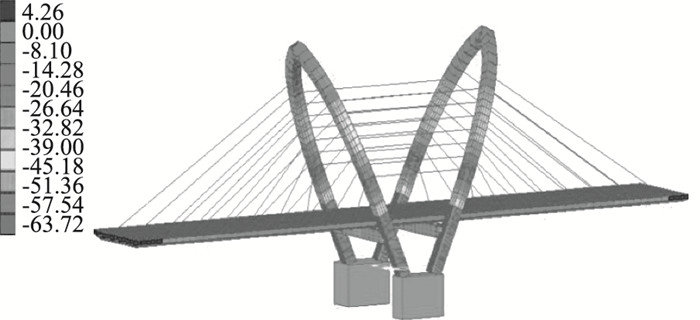
| 图 12 S1R+S1L断裂时主梁及索塔应力(单位:MPa) Fig. 12 Stresses of main girder and pylon when S1R+S1L fractured(unit:MPa) |
| |
从上述图表可以看出,各种断裂工况下最大应力出现在索塔单元,主梁应力相对较小,单索断裂工况下,X2R断裂时主梁及索塔应力达到最大,最大值为60.4 MPa,双索断裂工况下,S1R+S1L断裂时主梁及索塔应力达到最大,最大值为63.7 MPa,较未断索时增大29.5%,但相对于Q345钢材的屈服强度而言,仍然有较大的富余度。综合前面分析得知,断索对剩余拉索承载力的影响要高于对主梁和索塔的影响。
4 结论本研究以西安市富裕路某大桥为工程背景,进行V型双拱斜拉桥的拉索断裂性能分析,研究正常运营条件下主梁线形变化和索力分配规律,具体结论如下:
(1) 拉索断裂的数量、位置不同对主梁线形影响不同,双索断裂后,主梁位移最大增加50.2%,但仍满足1/500挠跨比的要求。
(2) 单索断裂和双索断裂对两系梁之间主梁段的位移影响基本可以忽略,任意两根索断裂引起主梁位移的变化值约为这两根索单独断裂时主梁位移变化值之和,即符合叠加原理,纵向对称断索较横向对称和原点对称断索危险。
(3) 外侧斜拉索断裂会导致与其相邻的水平索和另一侧斜拉索索力明显降低,内侧斜拉索的断裂会明显增大其附近斜拉索的索力,但水平索和另一跨斜拉索索力的降低不太明显;左侧水平索的断裂对右侧斜拉索基本没有影响,某根水平索的断裂导致与其相连的两根斜拉索索力降低值基本相同。
(4) 双索断裂对剩余拉索索力的影响基本符合叠加原理,少量拉索的断裂不会引起结构达到极承载能力,即使两根危险索同时断裂,断索后剩余拉索索力最大为836 MPa,安全系数达到2.2。
本研究主要分析正常运营条件下双钢拱塔斜拉桥断索后的主梁线形变化和索力分配规律,未涉及地震、台风等极端条件下结构的力学响应,下一步有必要针对此类极端条件进行分析,以贴近工程实际。
| [1] |
项海帆. 21世纪世界桥梁工程的展望[J]. 土木工程学报, 2000, 33(3): 1-6. XIANG Hai-fan. Prospect of World's Bridge Projects in 21st Century[J]. China Civil Engineering Journal, 2000, 33(3): 1-6. |
| [2] |
JANJIC D, PIRCHER M, PIRCHER H. Optimization of Cable Tensioning in Cable-stayed Bridges[J]. Journal of Bridge Engineering, 2003, 8(3): 131-137. |
| [3] |
WANG Y C. Number of Cable Effects on Buckling Analysis of Cable-stayed Bridges[J]. Journal of Bridge Engineering, 1999, 4(4): 242-248. |
| [4] |
SHEKASTEHBAND B, ABEDI K, DIANAT N, et al. Experimental and Numerical Studies on the Collapse Behavior of Tensegrity Systems Considering Cable Rupture and Strut Collapse with Snap-through[J]. International Journal of Non-Linear Mechanics, 2012, 47(7): 751-768. |
| [5] |
WOLFF M, STAROSSEK U. Cable Loss and Progressive Collapse in Cable-stayed Bridges[J]. Bridge Structures, 2009, 5(1): 17-28. |
| [6] |
DAS R, PANDEY A D, MAHESH M J, et al. Progressive Collapse of a Cable Stayed Bridge[J]. Procedia Engineering, 2016, 144: 132-139. |
| [7] |
KAO C, KOU C. The Influence of Broken Cables on the Structural Behavior of Long-span Cable-stayed Bridges[J]. Journal of Marine Science and Technology, 2010, 18(3): 395-404. |
| [8] |
KIM S, KANG Y. Structural Behavior of Cable-stayed Bridges after Cable Failure[J]. Structural Engineering and Mechanics, 2016, 59(6): 1095-1120. |
| [9] |
BAI Z Z, ZHU B Z. Study of Ultimate Load Bearing Capacity of Very Long Span Hybrid Girder Cable-stayed Bridges[J]. Bridge Construction, 2017, 47(5): 36-40. |
| [10] |
JIN X L, YAN Y, QIAN K. Research on Force Performance of Cable Breaking on Cable-stayed Bridges[J]. Applied Mechanics and Materials, 2014, 644-650: 5061-5064. |
| [11] |
罗晓峰, 项贻强, 颜东煌, 等. 斜拉桥桥塔稳定性实用计算方法[J]. 公路交通科技, 2011, 28(9): 60-65. LUO Xiao-feng, XIANG Yi-qiang, YAN Dong-huang, et al. A Practical Calculation Method of Stability for Pylon of Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(9): 60-65. |
| [12] |
于刚, 孙利民. 断索导致的斜拉桥结构易损性分析[J]. 同济大学学报:自然科学版, 2010, 38(3): 323-328. YU Gang, SUN Li-min. Vulnerability Analysis of Cable-stayed Bridge due to Cable Failures[J]. Journal of Tongji University:Natural Science Section, 2010, 38(3): 323-328. |
| [13] |
郑小博, 张岗, 宋一凡. 双塔钢桁斜拉桥斜拉索破坏动态响应[J]. 长安大学学报:自然科学版, 2017, 37(6): 70-77. ZHENG Xiao-bo, ZHANG Gang, SONG Yi-fan. Dynamic Response of Cable Breakage in Double-tower Cable-stayed Bridge With Steel Truss Girder[J]. Journal of Chang'an University:Natural Science Edition, 2017, 37(6): 70-77. |
| [14] |
闫冬, 任胜健, 何勇. 桥梁倒塌模式识别方法:实例分析[J]. 公路交通科技, 2011, 28(9): 77-80, 111. YAN Dong, REN Sheng-jian, HE Yong. Identification Method of Bridge Collapse Pattern:Analysis of Cases[J]. Journal of Highway and Transportation Research and Development, 2011, 28(9): 77-80, 111. |
| [15] |
宗钟凌, 郭正兴. 葵花型索穹顶结构力学性能及拉索破断试验研究[J]. 工程力学, 2013, 30(1): 271-276. ZONG Zhong-ling, GUO Zheng-xing. Experimental Research on Mechanical Properties and Cable Broken of Levy Cable Dome[J]. Engineering Mechanics, 2013, 30(1): 271-276. |
| [16] |
王霄翔, 陈志华, 刘红波, 等. 弦支穹顶局部环索断索动力冲击效应试验[J]. 天津大学学报:自然科学与工程技术版, 2017, 50(11): 1210-1220. WANG Xiao-xiang, CHEN Zhi-hua, LIU Hong-bo, et al. Dynamic Impact Effect Experiment on a Suspendome Subjected to Local Hoop Cable Rupture[J]. Journal of Tianjin University:Science and Technology Edition, 2017, 50(11): 1210-1220. |
| [17] |
汪永兰.拉索损伤对斜拉桥结构性能影响研究[D].南京: 东南大学, 2004. WANG Yong-lan. Study on Effect of Cable Damage on Structural Performance of Cable-stayed Bridges[D]. Nanjing: Southeast University, 2004. |
| [18] |
赵翔.拉索损伤对斜拉桥结构性能影响的研究[D].南京: 东南大学, 2005. ZHAO Xiang. Study on Effect of Cable Damage on Structural Performance of Cable-stayed Bridges[D]. Nanjing: Southeast University, 2005. |
| [19] |
殷任宏. V形双拱独塔斜拉桥结构参数研究[D].西安: 长安大学, 2017. YIN Ren-hong. Study on Structural Parameters of V-shaped Double-arch Single-tower Cable-stayed Bridge[D]. Xi'an: Chang'an University, 2017. |
| [20] |
JTG D65-01-2007, 公路斜拉桥设计细则[S]. JTG D65-01-2007, Guidelines for Design of Highway Cable-stayed Bridge[S] |
| [21] |
王今朝.大跨斜拉桥断索危险性理论分析及健康监测方法研究[D].哈尔滨: 东北林业大学, 2010. WANG Jin-chao. Theoretical Analysis on Cable Breakage Risk of Long-span Cable-stayed Bridges and Research on Health Monitoring Method[D]. Harbin: Northeast Forestry University, 2010. |
 2020, Vol. 37
2020, Vol. 37
