扩展功能
文章信息
- 王民, 肖丽, 王滔, 兰超
- WANG Min, XIAO Li, WANG Tao, LAN Chao
- 钢桥面沥青铺装材料模量参数取值方法
- A Method for Determining Modulus Parameter of Steel Deck Asphalt Pavement Material
- 公路交通科技, 2020, 37(4): 47-52
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 47-52
- 10.3969/j.issn.1002-0268.2020.04.007
-
文章历史
- 收稿日期: 2018-04-09
2. 重庆市桥面铺装工程技术研究中心, 重庆 401336
2. Chongqing Bridge Deck Pavement Technology Research Center, Chongqing 401336, China
我国公路沥青路面设计规范已经发布了7版,规范中的路面结构设计方法均以压缩弹性体系模型为基础,在使用11年之久的《公路沥青路面设计规范》(JTG D50—2006)中,以15 ℃的静态抗压回弹模量作为沥青路面设计的主要参数。在现行的《公路沥青路面设计规范》(JTG D50—2017)中,以20 ℃的动态压缩模量作为沥青路面设计的主要参数[1-2]。沥青路面力学分析时,一般采用抗压回弹模量、动态模量或弯拉劲度模量[3-5]。对于钢桥面铺装而言,受其支撑体系(正交异性钢桥面板)结构特性的影响,铺装体系内部应力应变分布状态较为复杂,与一般沥青路面受力状况有较大区别[6-8]。
目前,钢桥面铺装力学分析同样以静力弹性模型为基础,关于钢桥面铺装材料模量参数,虽已有不少科研院校进行了一些探索,但还没有形成普遍认可的取值方法或范围[9]。部分学者对钢桥面进行分析时采用静态模量,模量取值为500~2 000 MPa[10-12];另有部分学者采用压缩动态模量进行分析,模量取值高达7 000~12 000 MPa[13-14]。由此可见,采用静态或者动态材料模量参数进行钢桥面铺装力学分析时,计算结果存在较大的差异。因此,有必要针对钢桥面铺装的特性,确定其模量参数取值方法及范围。
根据测试方法的不同,弹性模量通常有抗压弹性模量和弯拉弹性模量两种。在行车过程中,钢桥面沥青铺装呈现弯拉受力特征,这也是引发桥面铺装开裂的主要因素,因此弯拉弹性模量更能真实反映钢桥面铺装受力过程中的材料力学特性。本研究根据钢桥面铺装的受力特点,采用复合梁五点加载模型,建立考虑铺装结构因素的钢桥面铺装材料弯拉模量的数值分析模型及解析法计算公式[15]。对高弹改性沥青SMA10和浇注式沥青混合料GA10进行不同温度条件下逐级加载测试和数据分析,确定了两种典型铺装材料弯拉模量取值方法及通用值范围。
1 复合梁五点加载试验 1.1 试验模型在进行钢桥面铺装沥青混合料模量测试时,为了更好地模拟包括正交异性板在内的铺装结构体系的受力特性[16],本研究借鉴德国钢桥面铺装层复合梁性能测试体系,以五点加载复合梁(见图 1)作为研究对象进行相关的室内试验和理论分析[17]。

|
| 图 1 五点加载复合梁 Fig. 1 Five-point loading composite beam |
| |
五点加载复合梁由钢板和铺装层组成,铺装厚度、钢板厚度、加劲肋厚度等可采用约定尺寸,也可采用与实桥一致的参数。本研究钢板尺寸为700 mm×200 mm×12 mm,铺装层尺寸为700 mm×150 mm×70 mm。试件支承于直径为50 mm的3个钢制辊轴支座上,支承间距为300 mm,加载点通过四脚施力架直接导向钢板的4个加载点[18]。
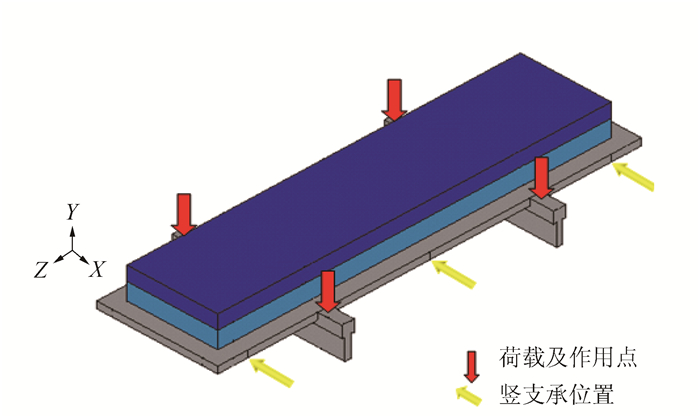
1.2 试验方法按照设计铺装结构,首先依次进行钢板喷砂除锈、涂刷防腐层、涂刷防水黏结层、铺筑沥青混合料层,制得复合梁试件,然后采用沥青混合料动态疲劳试验系统对试件进行分级加载、卸载,测试4个加载点的变形,加载速率为50 mm/min,相邻两级荷载间隔时间为30 s,如图 2所示。
|
| 图 2 复合梁五点加载测试 Fig. 2 Composite beam five-point loading test |
| |
加载级别的确定:首先,确定最大荷载P,即钢板裸板加载点变形达到0.8 mm时的力值,经测试P为27.1 kN;然后,取0.1P,0.2P,0.3P,…,0.9P,1.0P作为10级试验荷载。
试验过程:动态疲劳试验系统自动记录试验荷载值,用千分表测试加载点变形值,加载过程中竖向位移值取4个加载点变形的平均值。
弯拉模量的确定:将各级荷载下的竖向位移曲线绘制成平滑的曲线,并进行原点修正,得到各级荷载下的竖向位移,然后采用有限元数值分析方法或者2.1节提出的解析公式法进行弯拉模量的计算。
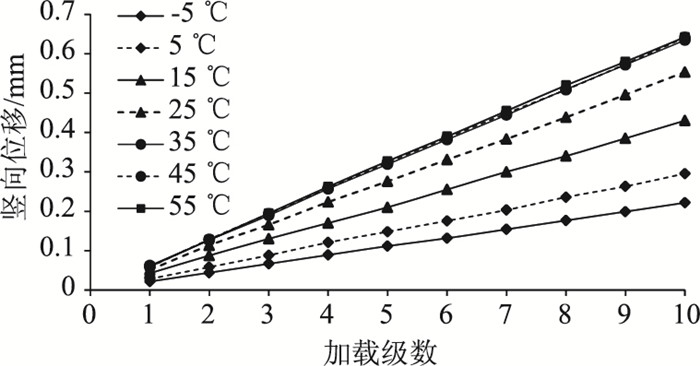
1.3 复合梁试验测试结果实验室制作两种结构的试件:浇注式沥青混合料GA10复合梁(3.5 cm GA10+3.5 cm GA10)和高弹改性沥青SMA10复合梁(3.5 cm SMA10+3.5 cm SMA10),并采用10级试验荷载对复合梁进行分级加载,测试每级荷载下加载点的竖向位移,试验温度从-5~55 ℃(间隔10 ℃取1个温度),每个温度下进行2次平行试验,取其平均值,试验结果见图 3和图 4。
|
| 图 3 GA10分级加载试验竖向位移 Fig. 3 Vertical displacement for GA10 in stepwise loading |
| |
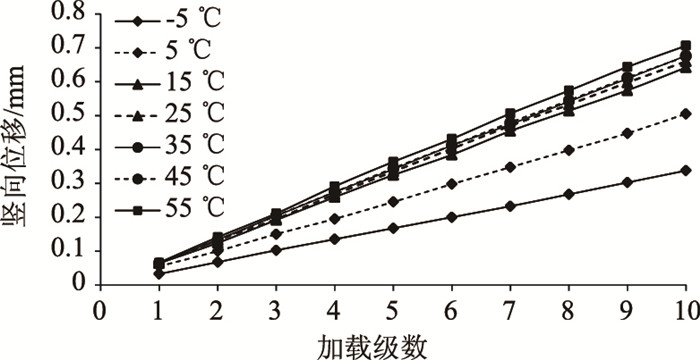
|
| 图 4 SMA10分级加载试验竖向位移 Fig. 4 Vertical displacement for SMA10 in stepwise loading |
| |
从图 3和图 4可以看出,在试验温度和加载力范围内,复合梁加载点变形与荷载呈较好的线性关系;当荷载较小时,温度对两种复合梁的变形影响差别不大,随着荷载的增加,温度影响越来越大。在较低的温度下,浇注式沥青混合料GA10复合梁的变形明显小于高弹沥青SMA10复合梁,在较高的温度下,二者相差不明显。
2 弯拉模量取值方法 2.1 弯拉模量解析公式法根据五点加载复合梁结构尺寸及加载模式,通过理论推导可得到用于确定五点加载复合梁铺装层材料弯拉模量的计算公式如式(1)所示,采用该公式确定铺装层材料弯拉模量的过程分为两步。
(1) 按1.2节中复合梁五点加载试验方法实测加载点的竖向位移Δ;
(2) 通过迭代方法求出可以满足式(1)的铺装层材料弯拉模量。
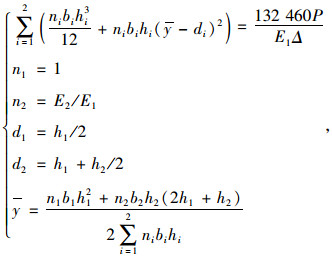
|
(1) |
式中,P为施加在复合梁上的荷载;Δ为荷载作用下加载点竖向位移;n1,n2分别为复合梁中铺装层弯拉模量、钢板弹性模量与铺装层弯拉模量的比值;h1,h2分别为复合梁中铺装层厚度、钢板厚度;b1,b2分别为复合梁中铺装层宽度、钢板宽度;E1,E2分别为铺装层材料弯拉模量、钢板弹性模量;d1为试件表面距铺装上层中心的距离;d2为试件表面距离铺装下层中心的距离;y为试件表面距铺装层形心的距离。
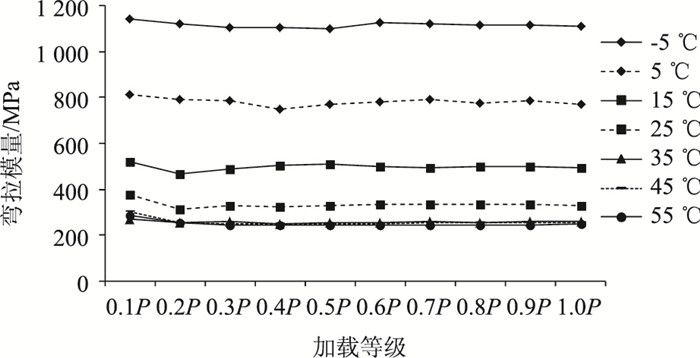
根据两种材料五点加载复合梁分级加载试验的实测数据,按式(1)计算浇注式沥青混合料GA10和高弹改性沥青SMA10在不同温度和不同加载等级下的弯拉模量,见图 5和图 6。
|
| 图 5 GA10分级加载弯拉模量 Fig. 5 Flexural-tensile modulus of GA10 in stepwise loading |
| |
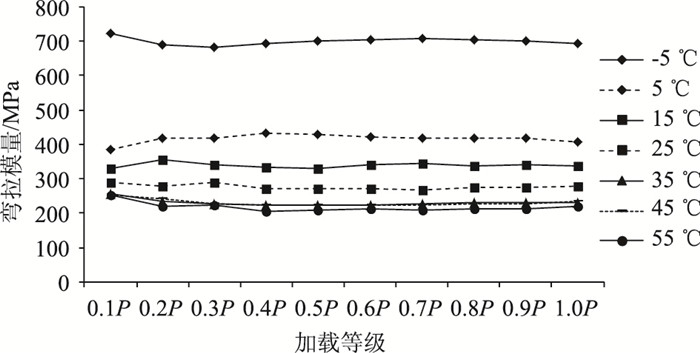
|
| 图 6 SMA10分级加载弯拉模量 Fig. 6 Flexural-tensile modulus of SMA10 in stepwise loading |
| |
从图 5和图 6可以看出,除第1级加载外,浇注式沥青混合料GA10和高弹改性沥青SMA10的弯拉模量随荷载大小的变化曲线接近水平,相对极差小于6.15%,因此荷载大小变化对弯拉模量影响较小。
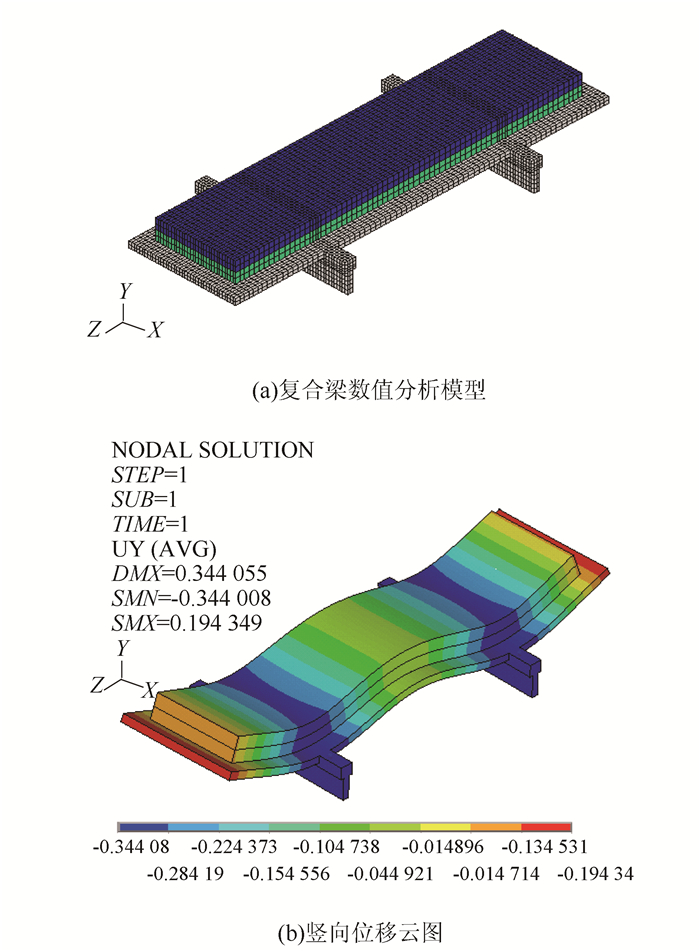
2.2 弯拉模量数值分析方法采用Ansys软件建立五点加载复合梁数值分析模型,如图 7所示。以15 ℃时高弹改性沥青SMA10复合梁和浇注式沥青混合料GA10复合梁测试数据为例,以第4级和第5级加载对应的实测竖向位移为目标,调整铺装层材料模量数值,使其与实测竖向位移接近,得到铺装材料弯拉模量,并与解析公式法确定的结果进行对比,见表 1。
|
| 图 7 复合梁五点加载数值模拟图 Fig. 7 Numerical simulation nephograms of five-point loading on composite beam |
| |
| 混合料类型 | 加载等级 | 实测竖向位移/mm | 弯拉模量/MPa | 2种方法差异率/% | |
| 解析公式法 | 数值分析法 | ||||
| SMA10 | 第4级 | 0.182 | 307 | 300 | 2.33 |
| 第5级 | 0.222 | 310 | 300 | 3.33 | |
| GA10 | 第4级 | 0.128 | 495 | 480 | 3.13 |
| 第5级 | 0.158 | 508 | 500 | 1.60 | |
对比表 1中两种方法所确定的计算结果,可以看出,采用解析公式法确定的结果与数值分析法计算的结果具有较好的一致性,当竖向位移达到同样值时,两种方法计算得到的弯拉模量差异率均在4%以内。因此,为了实用和方便,本研究提出以复合梁五点加载试验和式(1)作为确定钢桥面铺装材料弯拉模量的取值方法。由此可见,采用此方法可以确定钢桥面铺装结构中的材料弯拉模量,且和传统静力学计算所采用的弹性模型参数值存在较大差异。
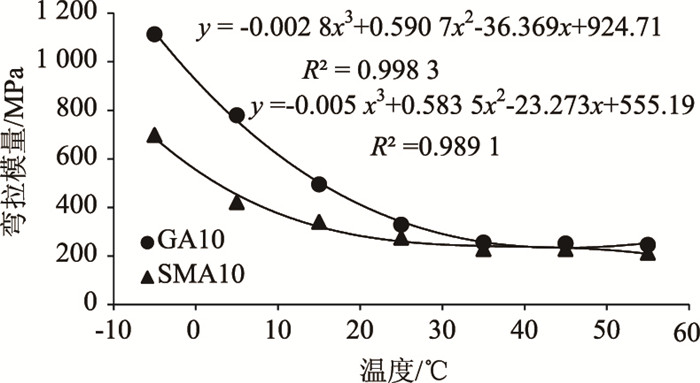
3 铺装材料弯拉模量确定从图 5和图 6可知,除第1级加载外,浇注式沥青混合料GA10和高弹改性沥青SMA10的弯拉模量随荷载大小变化较小。考虑到试验开始和结束时加载的瞬时性,剔除第1级和第10级加载数据,各温度下的弯拉模量取第2~第9级的平均值,结果见图 8。
|
| 图 8 不同温度下GA10和SMA10的弯拉模量 Fig. 8 Flexural-tensile moduli of GA10 and SMA10 at different temperatures |
| |
从图 8可以看出,用3次多项式对不同温度下浇注式沥青混合料GA10和高弹改性沥青SMA10的弯拉模量进行拟合,相关度R2大于0.98。因此浇注式沥青混合料GA10和高弹改性沥青SMA10在温度为T时的弯拉模量可以用式(2)和式(3)近似计算。
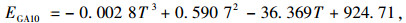
|
(2) |
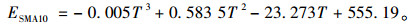
|
(3) |
从图 8还可以看出,浇注式沥青混合料GA10和高弹改性沥青SMA10的弯拉模量随温度的升高而逐渐降低,当温度较低时,模量下降较快,浇注式沥青混合料GA10从-5~35 ℃弯拉模量下降了77.09%,高弹改性沥青SMA10从-5~35 ℃弯拉模量下降了66.77%。两种沥青混合料从35~55 ℃,模量降低小于10 MPa,因此,建议力学分析时-5~55 ℃各温度区间弯拉模量参数按照表 2取值。
| 温度范围/℃ | -5~5 | 5~15 | 15~25 | 25~35 | 35~55 |
| GA10弯拉模量/MPa | 1 100~700 | 800~500 | 500~300 | 350~250 | 250~200 |
| SMA10弯拉模量/MPa | 700~400 | 450~300 | 350~250 | 300~200 | 250~200 |
4 结论
(1) 在试验温度和加载力范围内,复合梁加载点变形与荷载大小成较好的线性关系,并且在较低的温度下,浇注式沥青混合料GA10复合梁的变形明显小于高弹改性沥青SMA10复合梁,在较高温度下,二者相差不大。
(2) 建立了钢桥面铺装材料弯拉模量的解析法计算公式及数值分析模型,测试及分析结果表明,采用解析公式法确定的弯拉模量与数值分析法计算的结果具有较好的一致性,当竖向位移达到同样值时,两种方法计算得到的弯拉模量差异率在4%以内。
(3) 通过计算及分析,确定了不同温度下浇注式沥青混合料GA10和高弹改性沥青SMA10的弯拉模量计算式,并提出了不同温度范围下弯拉模量的取值范围,可为钢桥面铺装层结构设计及力学分析提供参数支撑。
| [1] |
JTG D50-2006, 公路沥青路面设计规范[S]. JTG D50-2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [2] |
JTG D50-2017, 公路沥青路面设计规范[S]. JTG D50-2017, Specifications for Design of Highway Asphalt Pavement[S]. |
| [3] |
王刚, 刘黎萍, 孙立军. 沥青混凝土抗剪强度及抗压回弹模量试验研究[J]. 建筑材料学报, 2012, 15(2): 279-282. WANG Gang, LIU Li-ping, SUN Li-jun. Research on Shearing Strength and Compressive Resilient Modulus Experiment of Asphalt Concrete[J]. Journal of Building Materials, 2012, 15(2): 279-282. |
| [4] |
FAKHRI M, GHANIZADEH A R. An Experimental Study on the Effect of Loading History Parameters on the Resilient Modulus of Conventional and SBS-modified Asphalt Mixes[J]. Construction and Building Materials, 2014, 53(53): 284-293. |
| [5] |
刘亚敏, 韩森, 徐鸥明, 等. 疲劳试验中沥青混合料的弯拉劲度模量[J]. 广西大学学报:自然科学版, 2010, 35(1): 127-130. LIU Ya-min, HAN Sen, XU Ou-ming, et al. Stiffness Modulus of Hot-mix Asphalt Mixtures in Fatigue Test[J]. Journal of Guangxi University:Natural Science Edition, 2010, 35(1): 127-130. |
| [6] |
王民, 胡德勇.钢桥面铺装病害成因多因素分析[C]//2012年全国桥梁学术会议论文集.北京: 人民交通出版社, 2012. WANG Min, HU De-yong. Multi-factor Analysis on Diseases of Steel Bridge Deck Pavement[C]//Proceedings of 2012 National Bridge Academic Conference. Beijing: China Communications Press, 2012. |
| [7] |
余涛.大路径连续刚构桥桥面铺装受力分析与合理结构研究[D].重庆: 重庆交通大学, 2012. YU Tao. Stress Analysis and Reasonable Structure Study on Deck Pavement of Large Span Continuous Rigid Frame Bridge[D]: Chongqing: Chongqing Jiaotong University, 2012. |
| [8] |
刘云, 钱振东. 立转式开启桥钢桥面铺装结构的应力状态分析[J]. 公路交通科技, 2014, 31(1): 55-60, 66. LIU Yun, QIAN Zhen-dong. Analysis of Stress of Steel Deck Pavement Structure on Bascule Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(1): 55-60, 66. |
| [9] |
黄卫. 大跨径桥梁钢桥面铺装设计理论与方法[M]. 北京: 中国建筑工业出版社, 2006. HUANG Wei. Research on Theory and Method of Long-span Steel Deck Pavement Design[M]. Beijing: China Architecture & Building Press, 2006. |
| [10] |
李兴海, 黄卫, 钱振东, 等. 基于Overlay Tester的钢桥面铺装力学特征的数值分析[J]. 公路交通科技, 2013, 30(10): 33-38. LI Xing-hai, HUANG Wei, QIAN Zhen-dong, et al. Numerical Analysis on Mechanical Characteristics of Steel Deck Pavement Based on Overlay Tester[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 33-38. |
| [11] |
顾兴宇, 吴一鸣. 钢桥桥面铺装层间剪应力影响因素及简化计算[J]. 交通运输工程学报, 2007, 7(3): 70-75. GU Xing-yu, WU Yi-ming. Influence Factors and Simplified Calculation of Interbedded Shear Stress of Asphalt Paving on Steel Bridge[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 70-75. |
| [12] |
陈艳金, 程鹏, 兰超, 等. 钢箱梁桥面铺装弯拉应变分布规律[J]. 交通标准化, 2013(2): 64-68. CHEN Yan-jin, CHENG Peng, LAN Chao, et al. Distribution Laws of Flexure Tensile Strain of Steel Box Girder Deck Pavement[J]. Transportation Standardization, 2013(2): 64-68. |
| [13] |
张顺先.基于使用性能的钢桥面铺装环氧沥青混合料设计研究与疲劳寿命预测[D].广州: 华南理工大学, 2013. ZHANG Shun-xian. Design of Epoxy Asphalt Mixture for Steel Bridge Deck Pavement Based on Applying Performance and Fatigue Life Prediction[D].Guangzhou: South China University of Technology, 2013. |
| [14] |
ZHAO Y Q, TANG J M, LIU H. Construction of Triaxial Dynamic Modulus Master Curve for Asphalt Mixtures[J]. Construction and Building Materials, 2012, 37(12): 21-26. |
| [15] |
张华, 王民, 兰超, 等.基于复杂应力状态下钢桥面铺装关键技术研究[R].重庆: 重庆市智翔铺道技术工程有限公司, 2013. ZHANG Hua, WANG Min, LAN Chao, et al. Research on Key Technology of Steel Bridge Deck Pavement Based on Complicated Stress[R]Chongqing: Chongqing Zhixiang Paving Technology Engineering Co., Ltd., 2013. |
| [16] |
KIM H, BUTTLAR W G. Discrete Fracture Modeling of Asphalt Concrete[J]. International Journal of Solids and Structures, 2009, 46(13): 2594-2600. |
| [17] |
LEONARD D, VANELSTRAETE A, PAREWYCK S. Structural Design of Flexible Pavements Using Steel Netting as Base Reinforcement[J]. International Journal of Geomechanics, 2002, 2(3): 291-303. |
| [18] |
BILIGIRI K P, KALOUSH K E. Effect of Specimen Geometries on Asphalt Mixtures' Phase Angle Characteristics[J]. Construction and Building Materials, 2014, 67: 249-257. |
 2020, Vol. 37
2020, Vol. 37
