扩展功能
文章信息
- 罗伟, 荣耀, 刘安, 耿大新, 曾润忠
- LUO Wei, RONG Yao, LIU An, GENG Da-xin, ZENG Run-zhong
- 基于非线性Barton-Bandis准则的岩质边坡可靠度研究
- Study on Reliability of Rock Slope Based on Nonlinear Barton-Bandis Criterion
- 公路交通科技, 2020, 37(4): 32-36
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 32-36
- 10.3969/j.issn.1002-0268.2020.04.005
-
文章历史
- 收稿日期: 2018-08-03
2. 江西省交通科学研究院, 江西 南昌 330200;
3. 江西交通咨询有限公司, 江西 南昌 330008
2. Jiangxi Transportation Institute, Nanchang Jiangxi 330200, China;
3. Jiangxi Transportation Consulting Co., Ltd., Nanchang Jiangxi 330008, China
边坡稳定性分析一直是岩土工程中的一个热点问题,以往岩质边坡稳定性分析大多采用线性Mohr-Coulomb (M-C)破坏准则。然而,大量的试验及研究表明,在岩质边坡中往往存在结构面,且岩体结构面上的破坏特征大都不满足线性M-C准则。因此,越来越多的研究将Hoek-Brown、Barton-Bandis等非线性破坏准则应用于岩质边坡稳定性分析[1-4]。此外,目前在进行边坡稳定性分析时,大多采用传统的确定性分析方法,无法体现岩土工程参数不确定性的影响。为更好地评估边坡稳定性,国内外学者将可靠度理论拓展运用到边坡稳定性分析之中[5-12],取得了良好效果。基于上述考虑,本研究采用可较好地表征岩体非线性力学性质的Barton-Bandis破坏准则,并结合可靠度理论,开展岩质边坡稳定性研究及参数分析,以期为岩质边坡稳定性分析提供有益参考。
1 基于非线性Barton-Bandis准则的稳定性分析模型 1.1 非线性Barton-Bandis准则非线性Barton-Bandis准则最早是由Barton和Bandis通过分析大量天然结构面的岩体剪切试验结果后提出的一种破坏模式[13],其破坏准则为:
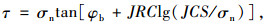
|
(1) |
式中,τ和σn分别为结构面上的剪应力和正应力;JRC为结构面粗糙系数;JCS为结构面有效抗压强度;φb为结构面基本摩擦角。
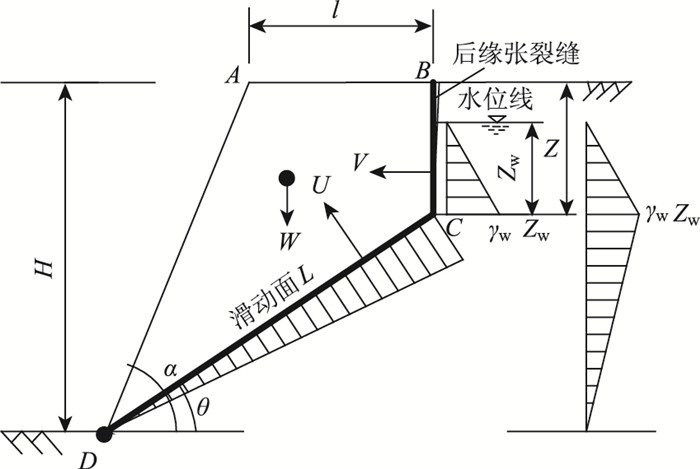
1.2 稳定性分析模型的构建本研究参照Hoek和Bray提出的典型平面滑动岩质边坡的破坏模式[14],构建基于非线性Barton-Bandis破坏准则的稳定性分析模型(图 1)。图 1中的H为边坡高度;θ为滑动面倾角;α为滑坡面坡角;l为后缘张裂缝距坡顶的水平距离;Z和Zw分别为张裂缝深度及水位线高度;V为坡顶裂缝底部的静水压力;U为坡体滑面的静水压力;γw为水的容重;L为滑动面长度。
|
| 图 1 平面滑动岩质边坡破坏模型 Fig. 1 Plane sliding rock slope failure model |
| |
本研究采用如图 1所示的水力分布形态,分析地下水对边坡稳定性的影响,其静水压力的计算表达式为:
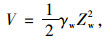
|
(2) |
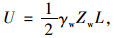
|
(3) |
经推导,得到结构面上的正应力为:
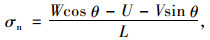
|
(4) |
式中,W为滑动体ABCD的重力。
在仅考虑岩质边坡滑动过程中的抗滑力和下滑力之间的静力平衡条件下,可以得到基于非线性Barton-Bandis破坏准则的岩质边坡安全系数表达式:
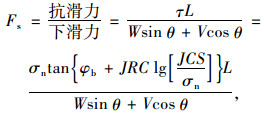
|
(5) |
式中σn由式(4)求得。
2 可靠度理论可靠度理论是一门迅速发展的新科学,可靠度分析方法被誉为近代工程技术的重要发展。边坡的可靠度是指边坡在规定的条件、时间内完成预定功能的概率,即边坡保持稳定性的概率。边坡工程中常用安全系数Fs来判定边坡的稳定情况,基于已有研究结果,本研究采用Fs≤1的失效概率Pf作为边坡可靠度的评价指标[15]:
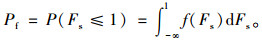
|
(6) |
此外,失效概率与可靠度指标β之间存在如下关系:
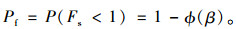
|
(7) |
为了计算边坡的可靠度指标,本研究采用一阶可靠度方法进行求解,其表达式为[16]:
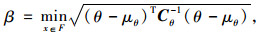
|
(8) |
式中,θ为不确定的随机变量;μθ为随机变量θ的均值;Cθ为协方差矩阵。
利用一阶可靠度方法计算可靠度指标时,以Fs=1为约束,运用MATLAB强大的优化处理功能,通过编程可快速有效地获取边坡的可靠度指标。
3 算例分析某石灰石矿区位于横阳山盆地之南部边缘,周围群山环绕[17]。根据实地测量、理论分析确定该露天边坡稳定性分析模型如图 1所示,其基本几何参数为:H=15 m,Z=5 m,θ=37°,α=70°。边坡可靠度分析采用非线性Barton-Bandis破坏准则,相关参数取值参考文献[1]:γ=25 kN/m3,φb=32°,JCS=24.4 MPa,JRC=9。分析过程中将JCS,JRC和φb视作随机变量,服从正态分布,并考虑其不确定性对边坡稳定性分析的影响。
| 随机变量 | 分布类型 | 均值 | 变异系数(COV) |
| JCS/MPa | 正态分布 | 24.4 | 0.3 |
| JRC | 正态分布 | 9 | 0.2 |
| φb/(°) | 正态分布 | 32 | 0.2 |
根据上述数据,采用MATLAB编制一阶可靠度求解程序计算得到可靠度指标β=2.10, 失效概率Pf=0.018。由此可得,该岩质边坡失效概率较小,具有足够的稳定性。
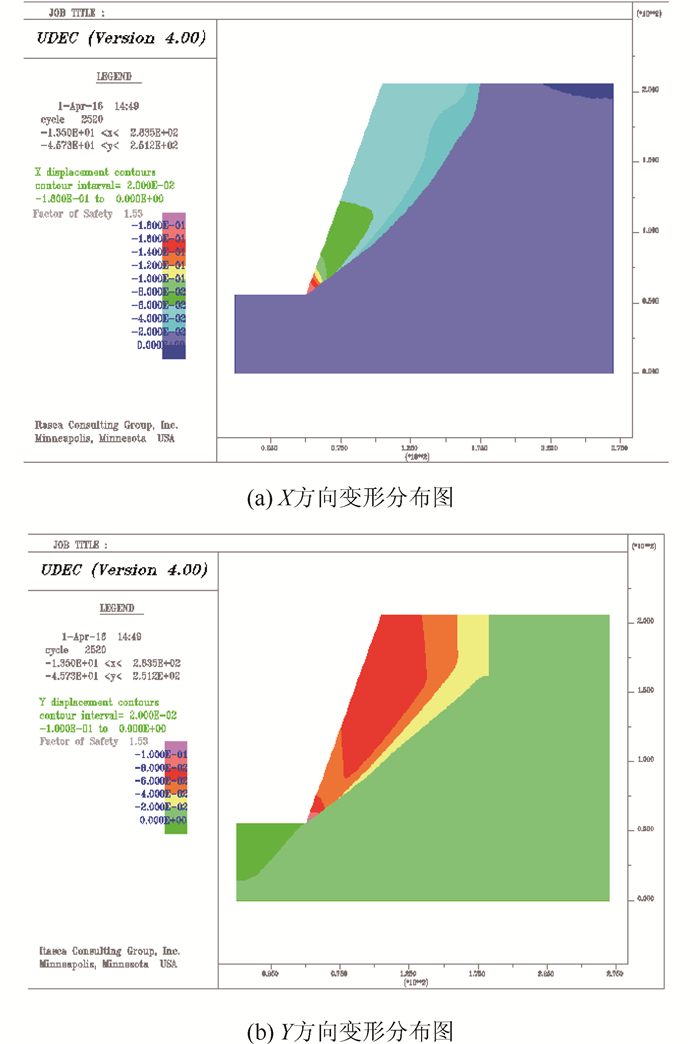
同时,为验证计算结果的准确性,采用内含Barton-Bandis破坏准则计算程序的软件UDEC[18]对该岩质边坡进行模拟计算。模型建立过程中,左右边界固定水平位移,底部边界固定竖向位移。通过分析计算,得到其位移变化如图 2所示,坡趾变形大于坡顶变形。其中,采用UDEC计算得到的基于Barton-Bandis破坏准则边坡安全系数Fs=1.53,采用本研究式(5)计算得到的边坡安全系数Fs=1.537 8,二者吻合良好,验证了本研究计算方法的可行性和有效性。
|
| 图 2 边坡变形分布(单位:m) Fig. 2 Distribution of slope deformation(unit:m) |
| |
3.1 随机变量对边坡稳定性的影响
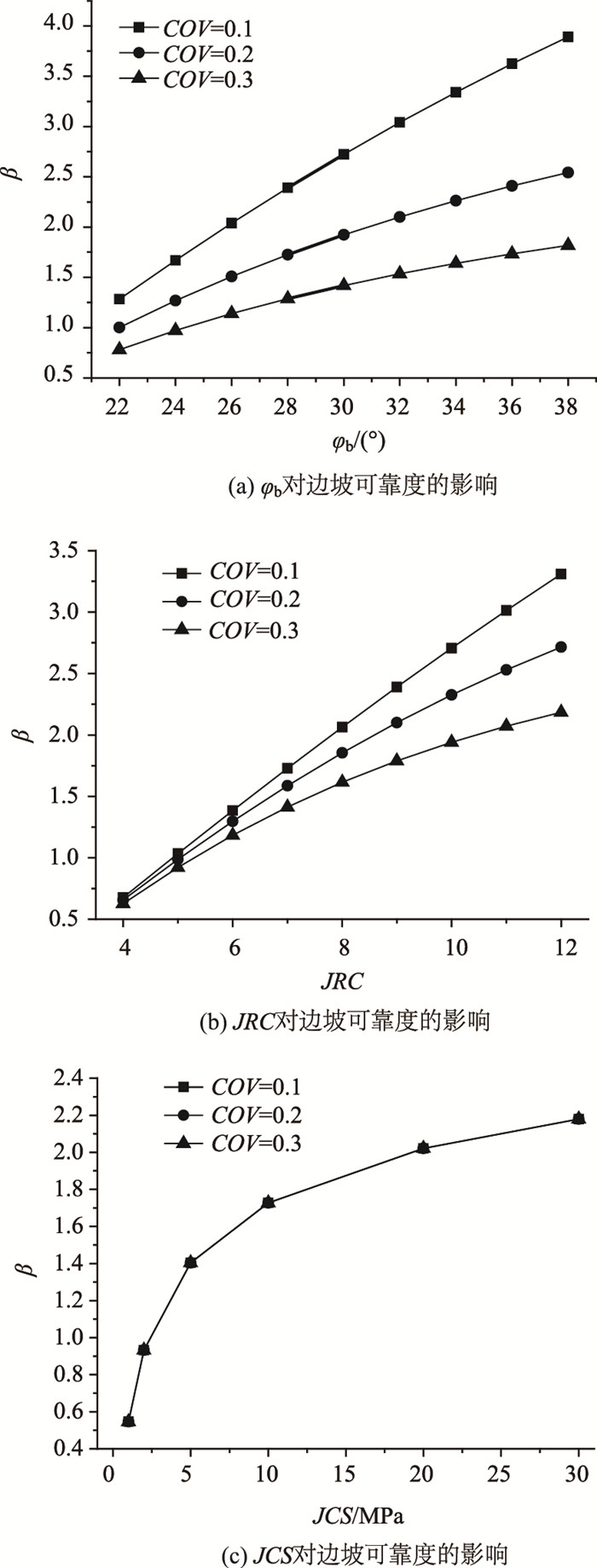
为分析各个随机变量对岩质边坡稳定性的影响,通过改变各个随机变量取值计算相应的可靠度指标。同时,分别将各随机变量的变异系数COV取值设为0.1,0.2,0.3,分析随机变量参数的不确定性对边坡稳定性的影响。经计算,其可靠度指标β如图 3所示。
|
| 图 3 随机变量对边坡可靠度的影响 Fig. 3 Influence of variables on reliability of slope |
| |
从图 3可以看出,φb,JRC和JCS的增加,均会导致边坡可靠度指标β的增加,表明增大φb, JRC和JCS可使岩质边坡趋于稳定。同时,随着变异系数的增加,可靠度指标β呈现不同程度的降低,即变量不确定性对边坡稳定性影响的敏感性不一,其中φb和JRC不确定性对边坡稳定性的影响显著,JCS影响相对较小。
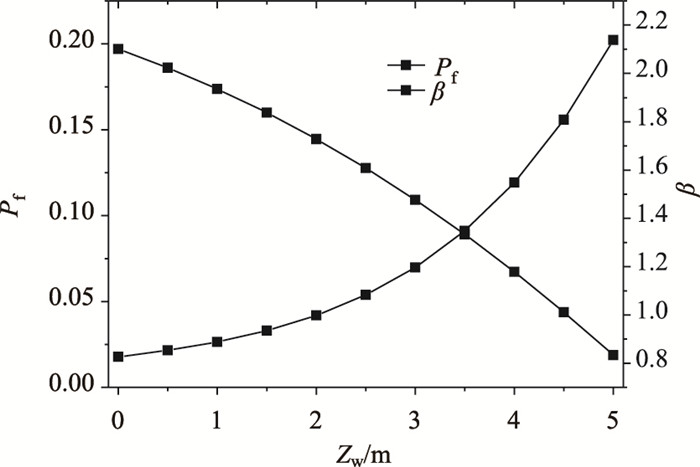
3.2 地下水位对边坡稳定性的影响为分析地下水水位变化对该岩质边坡稳定性的影响,本研究通过改变图 1所示的张裂缝中地下水位高度Zw,其他参数的取值不变,计算结果见图 4。
|
| 图 4 地下水对边坡可靠度的影响 Fig. 4 Influence of groundwater on reliability of slope |
| |
由图 4可知,地下水位的增加会导致边坡的可靠度指标显著降低,当后缘张裂缝中地下水位高度从1 m增加到5 m时,失效概率增加了7倍多,可见地下水水位的升高将大幅降低边坡的稳定性。
4 结论本研究基于典型平面滑动岩质边坡破坏模型,结合可靠度理论与Barton-Bandis非线性破坏准则,开展了岩质边坡可靠度分析研究,得到以下结论:
(1) 非线性Barton-Bandis破坏准则的主要变量φb,JRC和JCS对岩质边坡稳定性有着显著影响,且岩质边坡稳定性随着φb,JRC和JCS的增加而提升。
(2) 随着随机变量参数φb,JRC和JCS变异系数的增加,岩质边坡稳定性有所降低,各参数敏感性差异较大,其中φb和JRC的影响较为显著,JCS的影响较弱。
(3) 地下水变化对边坡稳定性的影响较大,随着后缘裂缝地下水位的升高,岩质边坡的失效概率成倍增大,有必要设置完善的坡体内部排水系统。
| [1] |
罗强, 赵炼恒, 李亮, 等. 基于Barton-Bandis准则的锚固边坡稳定性分析[J]. 岩土力学, 2013, 34(5): 1351-1359. LUO Qiang, ZHAO Lian-heng, LI Liang, et al. Stability Analysis of Anchored Rock Slope Based on Barton-Bandis Failure Criterion[J]. Rock and Soil Mechanics, 2013, 34(5): 1351-1359. |
| [2] |
ZUO J P, LIU H H, LI H T. A Theoretical Derivation of the Hoek-Brown Failure Criterion for Rock Materials[J]. Journal of Rock Mechanics & Geotechnical Engineering, 2015, 42(4): 361-366. |
| [3] |
罗伟, 李亮, 赵炼恒, 等. 临河岩石边坡抗滑稳定性分析[J]. 公路交通科技, 2013, 30(8): 23-28, 42. LUO Wei, LI Liang, ZHAO Lian-heng, et al. Study on Anti-slide Stability of Rock Slope along River[J]. Journal of Highway and Transportation Research and Development, 2013, 30(8): 23-28, 42. |
| [4] |
李永红, 彭振斌, 钟正强, 等. 基于Barton-Bandis非线性破坏准则的岩体强度预测[J]. 中南大学学报:自然科学版, 2009, 40(5): 1388-1391. LI Yong-hong, PENG Zhen-bin, ZHONG Zheng-qiang, et al. Strength Prediction for Rock Mass Based on Barton-Bandis Nonlinear Failure Criterion[J]. Journal of Central South University:Science and Technology Edition, 2009, 40(5): 1388-1391. |
| [5] |
孙超伟, 柴军瑞, 许增光, 等. 基于Hoek-Brown强度折减法的边坡稳定性图表法研究[J]. 岩石力学与工程学报, 2018, 37(4): 838-851. SUN Chao-wei, CHAI Jun-rui, XU Zeng-guang, et al. Stability Charts for Rock Slopes Based on the Method of Reduction of Hoek-Brown Strength[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 838-851. |
| [6] |
唐高朋, 李亮, 赵炼恒, 等. 非线性破坏准则下边坡稳定性极限分析斜条分法[J]. 岩土力学, 2015, 36(7): 2063-2072. TANG Gao-peng, LI Liang, ZHAO Lian-heng, et al. Inclined Slices Method for Limit Analysis of Slope Stability with Nonlinear Failure Criterion[J]. Rock and Soil Mechanics, 2015, 36(7): 2063-2072. |
| [7] |
周建普, 李献民, 王永和. 粘土边坡可靠性分析方法研究[J]. 湖南大学学报:自然科学版, 2002, 29(5): 92-97, 103. ZHOU Jian-pu, LI Xian-min, WANG Yong-he. Research for Method of Reliability Analysis for Clayey Soil Slope[J]. Journal of Hunan University:Natural Science Edition, 2002, 29(5): 92-97, 103. |
| [8] |
BARTON N, CHOUBEY V. The Shear Strength of Rock Joints in Theory and Practice[J]. Rock Mechanics, 1977, 10(1): 1-54. |
| [9] |
罗正东, 苏永华, 付雄, 等. 基于逆可靠度方法的边坡稳定性分析[J]. 公路交通科技, 2014, 31(3): 43-48. LUO Zheng-dong, SU Yong-hua, FU Xiong, et al. Analysis of Slope Stability Based on Inverse Reliability Method[J]. Journal of Highway and Transportation Research and Development, 2014, 31(3): 43-48. |
| [10] |
李早, 赵树德. 基于可靠性理论的岩土工程反分析设计[J]. 西安建筑科技大学学报:自然科学版, 2006, 38(2): 159-162, 177. LI Zao, ZHAO Shu-de. Inverse Analysis Design in Geotechnical Engineering Based on the Reliability Theory[J]. Journal of Xi'an University of Architecture & Technology:Natural Science Edition, 2006, 38(2): 159-162, 177. |
| [11] |
李典庆, 周创兵, 胡冉. 基于n维等效方法的岩质边坡楔体稳定体系可靠度分析[J]. 岩石力学与工程学报, 2009, 28(7): 1415-1424. LI Dian-qing, ZHOU Chuang-bing, HU Ran. System Reliability Analysis of Rock Slope Wedge Stability Based on N-dimensional Equivalent Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1415-1424. |
| [12] |
LI D Q, JIANG S H, CHEN Y F, et al. System Reliability Analysis of Rock Slope Stability Involving Correlated Failure Modes[J]. KSCE Journal of Civil Engineering, 2011, 15(8): 1349-1359. |
| [13] |
BARTON N, BANDIS S, BAKHTAR K. Strength, Deformation and Conductivity Coupling of Rock Joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1985, 22(3): 121-140. |
| [14] |
HOEK E, BRAY J W. Rock Slope Engineering[M]. 3rd ed. London: Institution of Mining and Metallurgy, 1981.
|
| [15] |
孙立川, 王红贤, 周念清, 等. 可靠度理论在岩质边坡楔形体破坏反分析中的应用[J]. 岩石力学与工程学报, 2012, 31(增1): 2660-2667. SUN Li-chuan, WANG Hong-xian, ZHOU Nian-qing, et al. Application of Reliability Theory to Back Analysis of Rocky Slope Wedge Failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 2660-2667. |
| [16] |
LOW B K. Reliability Analysis of Rock Slopes Involving Correlated Nonnormals[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 922-935. |
| [17] |
曾晟.平面破坏型岩质边坡稳定可靠度研究及其应用[D].衡阳: 南华大学, 2005. ZENG Sheng. Reliability Analysis of Plane-failure Rock Slope and Application[D]. Hengyang: University of South China, 2005. |
| [18] |
CHOI S O, CHUNG S K. Stability Analysis of Jointed Rock Slopes with the Barton-Bandis Constitutive Model in UDEC[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(S1): 581-586. |
 2020, Vol. 37
2020, Vol. 37
