扩展功能
文章信息
- 冯锦艳, Thant Yee Mon SAN
- FENG Jin-yan, Thant Yee Mon SAN
- 一种考虑损伤的沥青路面本构关系在冲击载荷作用下的应用
- Application of a Constitutive Relation of Asphalt Pavement Considering Damage under Impact Load
- 公路交通科技, 2020, 37(4): 9-14, 61
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(4): 9-14, 61
- 10.3969/j.issn.1002-0268.2020.04.002
-
文章历史
- 收稿日期: 2018-08-08
沥青路面作为一种主要的高等级路面结构形式,广泛应用于公路工程和机场工程。随着军事需要,一些道路常需满足战备使用要求,因此开展大冲击载荷作用下的沥青道面损伤性能和弯沉规律研究势在必行。
沥青路面具有明显的黏弹性特征[1-3],且随着载荷形式和温度的变化发生疲劳损伤,因此建立一种能够描述冲击载荷作用下的沥青路面本构关系[4-6]成为服务沥青路面在满足战备需要后养护的首要问题。Burgers元器件模型由于和材料自身性质无关,通过拟合应力-应变关系完成参数确定,成为描述材料黏弹性特征的最佳模型之一。许多学者基于Burgers模型对沥青路开展了研究,取得了丰硕的研究成果。黄永强[7]使用FLAC3D程序中的经典Burgers模型对路基的长期沉降进行计算,通过实测数据验证了Burgers模型的合理性。魏贤奎[8]等推导了由Burgers模型参数转化为Prony级数的计算公式,通过水泥乳化沥青砂浆试验结果验证了公式的合理性。邵勇等[9]将Burgers模型转化为经验模型,依据工程经验可确定计算参数并进行工程计算。
Burgers模型可以合理描述沥青路面的黏弹性特性,但存在局限性,即无法描述沥青路面的加速破坏阶段和疲劳损伤,不利于合理评估沥青路面的力学性能和剩余使用寿命,无法服务于沥青路面的养护工作。许多学者从岩石损伤入手开展了相关研究[10]。袁海平[11]将摩尔-库伦塑性元件与经典Burgers模型串联,使其能够描述材料的加速破坏阶段。Cheng等[12]将Burgers模型中的串联黏滞体时间参数非线性化为时间的二次函数,建立了改进的Burgers模型,并通过沥青动态间接拉伸试验进行了验证。杨文东等[13]在经典Burgers模型上加入了损伤变量与时间的指数函数,完成了在FLAC3D程序中的二次开发。
从损伤的定义来讲,基于Lemaitre[14]等效应变原理的损伤变量定义是描述材料微单元名义应力与有效应力的关系,实质是材料的微观结构破坏,直接变化材料宏观物理力学指标的方法有待商榷。金磊等[15]对直接将损伤变量D作用于经典模型参数进行了研究,得出的结论为:采用指数形式增长的损伤函数,与目前试验研究公认的损伤变量与应变的关系相矛盾,指数关系曲线的凹凸形式与试验结果曲线的形式相反。
本研究将在经典Burgers模型中引入与应变和材料参数相关的损伤变量D,建立损伤Burgers模型。在一定假设基础上,对冲击载荷作用下的损伤Burgers模型进行求解和试验验证,实现其在FLAC3D程序中的二次开发和应用,使其能够计算沥青路面弯沉变形和损伤程度,为大载荷作用后的沥青路面养护提供一种理论支撑。
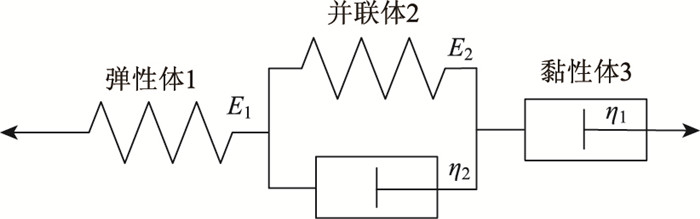
1 基本理论 1.1 经典Burgers模型经典Burgers模型由Maxwell体和Kelvin体串联而成,如图 1所示。
|
| 图 1 经典Burgers模型 Fig. 1 Classic Burgers model |
| |
弹性体1的应力-应变关系为:
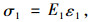
|
(1) |
式中,σ1为弹性体1的应力;E1为弹性体1的弹性模量;ε1为弹性体1的应变。
并联体2(Kelvin体)的应力-应变关系为:
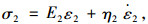
|
(2) |
式中,σ2为并联体2中的弹性体应力;E2为并联体2中的弹性体弹性模量;ε2为并联体2中的弹性体应变;η2为并联体2中的黏壶黏滞系数。
黏性体3的应力-应变关系为:
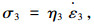
|
(3) |
式中,σ3为黏性体3的应力;ε3为黏性体3的应变;η3为黏性体3的黏壶黏滞系数。
Burgers模型中各元件满足如下应力-应变关系:
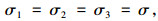
|
(4) |
式中σ为Burgers模型的总应力。
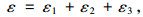
|
(5) |
式中ε为Burgers模型的总应变。
由式(4)和(5)可得经典Burgers模型的应力-应变方程为:
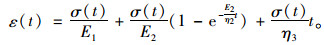
|
(6) |
1996年Lemaitre提出了应变等价原理,假设物体在应力σ作用下引起的受损材料应变与在有效应力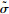
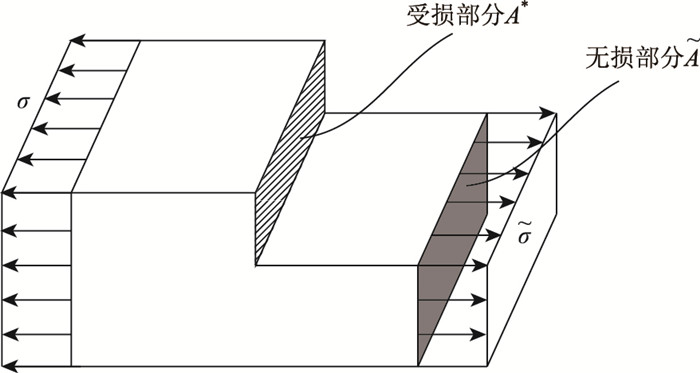
定义损伤变量D。如图 2所示,在物体内部取一小面,假设该面受到力的作用产生一定程度的均匀损伤。该面的总面积为A,损伤面积为A*,则该面的净面积或有效面积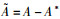
|
| 图 2 Lemaitre等效应变原理 Fig. 2 Lemaitre equivalent strain principle |
| |
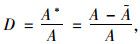
|
(7) |
式中,当D=0时,对应无损伤状态;当D=1时,为完全损伤(断裂)状态;当0<D<1时,对应于不同程度的损伤状态。
1.3 冲击载荷下损伤Burgers模型的近似求解沥青混合料的应力-应变关系曲线包括应力峰值前和应力峰值后两个阶段。以往研究常假设沥青混合料的损伤从应力峰值后才开始发展,而试验发现,沥青混合料在应力峰值前甚至是起始阶段已经开始出现损伤。
杨大勇等[16-18]基于最小耗能原理和内变量的概念,提出了一种材料损伤本构关系模型。该模型认为材料损伤阈值为损伤变量D=0时的应变值,根据材料的应变可计算其损伤程度D:
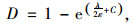
|
(8) |
式中,D为损伤变量;ε为应变;λ和C为材料参数,可通过式(9)~(10)求得:
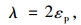
|
(9) |
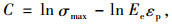
|
(10) |
式中,εp和σmax分别为材料应力-应变曲线峰值对应的应变和应力值;Ee为材料的弹性模量。
将式(8)引入经典Burgers模型,假设所有元件均发生同一程度损伤,则损伤Burgers模型的应力-应变方程可写为:
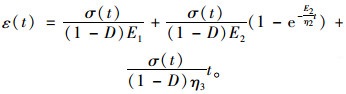
|
(11) |
求得损伤变量D为:
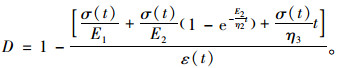
|
(12) |
假设时间增量Δt足够小时,应力σ不变,损伤变量D不变,则应变增量可写为:
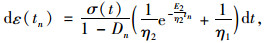
|
(13) |
式中,tn为第n个时刻;Dn为第n个时刻的损伤变量。
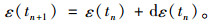
|
(14) |
在已知冲击载荷随时间的关系前提下,由式(12)和式(13)可求得沥青材料在受力方向的损伤程度D与应变及时间的关系曲线。
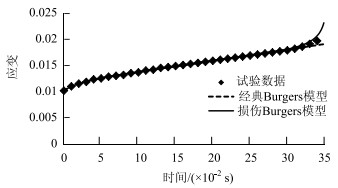
2 损伤Burgers模型的试验验证本研究将损伤Burgers模型计算结果与参考文献[19]进行的沥青混合料非线性黏弹性蠕变试验(20 ℃)结果进行了对比。图 3给出了试验结果、经典Burgers模型计算结果及损伤Burgers模型计算结果的对比曲线,3种方法在材料的前两个变形阶段,即初始蠕变阶段和稳定蠕变阶段吻合良好,损伤Burgers模型的优点在于可以描述材料的加速破坏阶段,这对于评估沥青路面小养护时间具有重要意义。
|
| 图 3 不同方法得到的沥青混合料蠕变曲线 Fig. 3 Creep curves of asphalt mixture obtained by different methods |
| |
由图 3可得到沥青混合料的材料参数λ=0.046,C=-1.67。表 1给出了由最小二乘法得到的模型其他参数,其中σ为应力值。
| σ/MPa | E1/MPa | η2/(MPa·s) | E2/MPa | η3/(MPa·s) |
| 0.7 | 162 | 3.566 | 22.64 | 1.1 |
3 损伤Burgers模型在FLAC3D程序中的二次开发
三维快速拉格朗日差分分析法(Fast Lagrangian Analysis of Continua in 3 Dimensions, FLAC3D)是University of Minnesota和Itasca Consulting Group Inc.联合开发的三维有限差分计算程序。自定义本构模型的开发需要编写或修改头文件(.h)、源文件(.cpp)和版本信息文档,然后通过visio studio软件(2010以上版本)编译生成动态链接库(.dll),并将编译生成的文件放在FLAC3D安装文件的EXE文件夹下的plugin文件夹中,即可实现在FLAC3D中程序的使用。
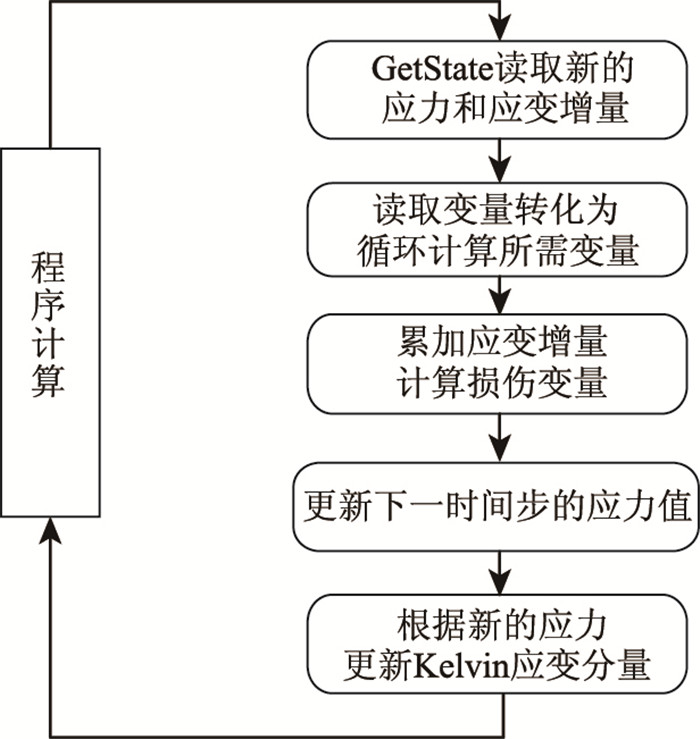
损伤Burgers模型的基本算法如图 4所示。
|
| 图 4 损伤Burgers模型算法 Fig. 4 Algorithm of damage Burgers model |
| |
4 损伤Burgers模型的应用 4.1 路面结构
取某典型路面结构形式,道路土基为夯实的黄土,压实度为0.97,高为2.62 m,土基层上为18 cm厚的石灰稳定土土底基层,石灰稳定土上设20 cm厚的水泥稳定碎石基层,基层上为5 cm厚的沥青混凝土面层,材料为AC-10。
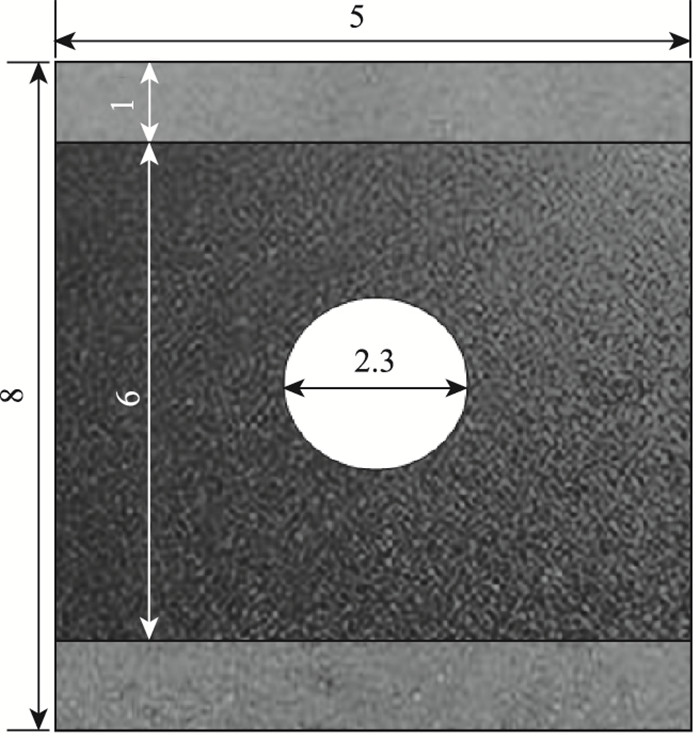
同时对路面结构进行数值模拟计算和现场试验。试槽长8 m,宽5 m,除沥青路面外,均满尺寸铺筑。沥青路面层长6 m,宽5 m,如图 5所示。
|
| 图 5 路面平面尺寸(单位:m) Fig. 5 Plane dimensions of pavement (unit: m) |
| |
4.2 冲击载荷形式
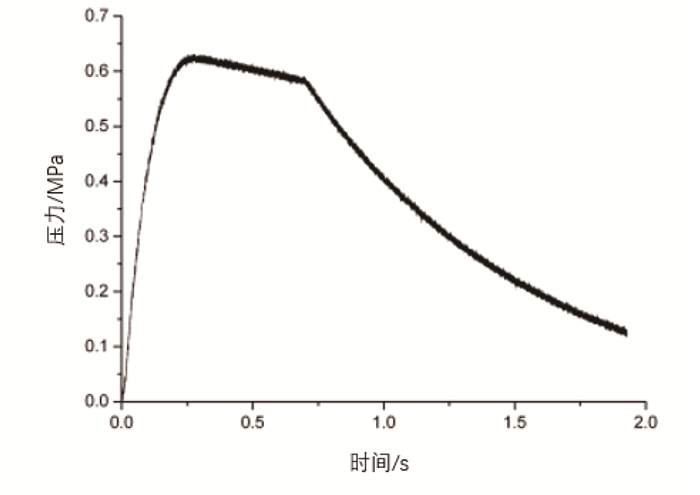
冲击荷载为军事载荷,作用于道路的中心位置,作用区域为直径2.3 m的圆(图 5),荷载作用时间为2 s,峰值为0.65 MPa,如图 6所示。
|
| 图 6 冲击载荷曲线 Fig. 6 Curve of impact load |
| |
4.3 计算参数
计算中采用的结构层力学参数来源于试验,数值如表 2所示,沥青面层黏弹性参数如表 1所示。
| 结构层 | 材料 | 弹性模量/ MPa | 密度/(kg·m-3) | 泊松比 | 黏聚力/kPa | 内摩擦角/(°) | 剪胀角/(°) |
| 面层 | AC-10 | 1 200 | 1 200 | 0.35 | — | — | — |
| 基层 | 水泥稳定碎石基层(5%) | 900 | 2 300 | 0.25 | — | — | — |
| 底基层 | 石灰稳定土 | 550 | 1 750 | 0.35 | 25.6 | 20 | — |
| 土基 | 黄土 | 40 | 1 900 | 0.4 | 10 | 30 | 45 |
沥青面层采用损伤Burgers模型,水泥稳定碎石基层采用弹性模型,石灰土底基层采用摩尔-库伦模型,土基采用D-P模型。
4.4 沥青路面破坏分析数值计算结果显示,在大冲击载荷作用下,沥青路面的水泥稳定碎石基层发生了剪切拉伸复合破坏,会造成道路结构层之间的脱空,道路两侧的边坡出现了滑移线,严重影响了道路的使用性能。
数值计算结果(图 7)与现场试验结果吻合良好,现场试验显示基层(剥离面层后)出现了不同程度的断裂裂缝。这说明本研究中的损伤Burgers模型对于描述大冲击载荷作用下的沥青路面性能具有很好的精度。

|
| 图 7 数值计算得到的沥青路面破坏场分布 Fig. 7 Distribution of failure field of asphalt pavement obtained by numerical calculation |
| |
4.5 沥青路面弯沉分析
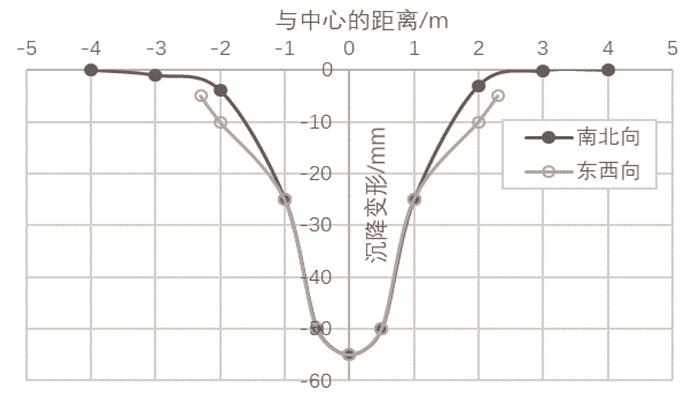
图 8给出了数值计算得到的冲击载荷作用下的沥青路面弯沉曲线。可以看出,最大弯沉区域出现在载荷作用区,最大弯沉值达到了55 mm左右,与现场试验结果基本吻合,极易形成影响安全驾驶的车辙或塌陷坑,建议大载荷作用后立即对道路进行填补维护。对于已经使用且存在损伤的道路,其弯沉量会加剧,严重时可影响军事应用的准确性,建议实施必要的缓冲措施。
|
| 图 8 数值计算得到的沥青路面弯沉曲线 Fig. 8 Curves of asphalt pavement deflection obtained by numerical calculation |
| |
4.6 沥青路面损伤分析
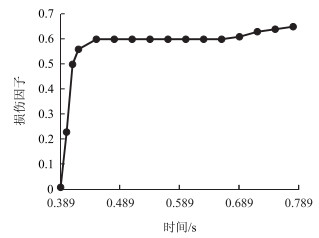
通过对计算结果进行后处理,得到图 9所示的损伤因子和时间的关系曲线。随着大冲击载荷数值的增加,沥青路面的损伤程度急剧上升到了0.6左右。随着冲击载荷的减小直至消失,路面损伤程度基本保持恒定。沥青路面的大程度损伤与基层出现断裂相吻合,路面的使用性能急剧下降,需采取必要的修补措施。
|
| 图 9 数值计算计算得到的沥青路面损伤因子 Fig. 9 Damage factor of asphalt pavement obtained by numerical calculation |
| |
因此对于等级较低的公路用于战备使用时,需考虑必要措施减小压力,如提前铺设橡胶片进行缓冲等,或在载荷作用后及时进行修补维护。
5 结论基于有效应力的定义,在经典Burgers模型的基础上引入损伤因子D,建立了可以描述冲击载荷作用下的沥青路面损伤Burgers模型。改进的Burgers模型可以较为完整地描述沥青路面在大冲击载荷作用下的流变特性,较好地预测沥青路面的流变破坏,对路面后期维护和使用具有重要意义。
运用C++语言,完成了该损伤模型在FLAC3D程序中的二次开发及对某道路在冲击载荷作用下的计算。通过对比道路结构破坏、弯沉盆及损伤因子可知,数值计算结果与现场试验结果吻合良好,进一步说明了损伤Burgers模型用于计算大冲击载荷作用下路面性能的合理性。
现场试验和数值计算结果显示,低等级公路用于战备使用时,应充分考虑使用前的降压措施及使用后的快速修补和维护措施。在可选的情况下,应尽可能避免低等级公路段,如三级及以下的公路。
| [1] |
张肖宁. 沥青与沥青混合料的黏弹力学原理及应用[M]. 北京: 人民交通出版社, 2006. ZHANG Xiao-ning. Viscoelastic Mechanics Principle and Application of Asphalt and Asphalt Mixture[M]. Beijing: China Communications Press, 2006. |
| [2] |
黄明奎. 公路工程材料流变学[M]. 成都: 西南交通大学出版社, 2010. HUANG Ming-kui. Rheology of Highway Engineering Materials[M]. Chengdu: Southwest Jiaotong University Press, 2010. |
| [3] |
AIREY G D, RAHIMZADEH B, COLLOP A C. Linear Rheological Behavior of Bituminous Paving Materials[J]. Journal of Materials in Civil Engineering, 2004, 16(3): 212-220. |
| [4] |
WU J, YANG X H, BAI F. A Micromechanical Framework with Aggregate-mastic Interface Effect for Predicting Uniaxial Compression Creep of Asphalt Mixture[J]. Acta Mechanica Solida Sinica, 2014, 27(3): 306-314. |
| [5] |
LEWANDOWSKI R, CHORAŻYCZEWSKI B. Identification of the Parameters of the Kelvin-Voigt and the Maxwell Fractional Models, Used to Modeling of Viscoelastic Dampers[J]. Computers & Structures, 2010, 88(1/2): 1-17. |
| [6] |
CELAURO C, FECAROTTI C, PIRROTTA A, et al. Experimental Validation of a Fractional Model for Creep/Recovery Testing of Asphalt Mixtures[J]. Construction and Building Materials, 2012, 36: 458-466. |
| [7] |
黄永强.高速公路路基沉降及路面动力特性研究[D].长沙: 中南大学, 2010. HUANG Yong-qiang. Research on Settlement of Embankment and Mechanics of Pavement for Freeway[D]. Changsha: Central South University, 2010. |
| [8] |
魏贤奎, 刘浩, 徐浩, 等. 水泥乳化沥青砂浆蠕变试验数据处理及其数值仿真[J]. 铁道科学与工程学报, 2015, 12(5): 1084-1087. WEI Xian-kui, LIU Hao, XU Hao, et al. Data Processing and Numerical Simulation for Creep Test of Cement Emulsified Asphalt Mortar[J]. Journal of Railway Science and Engineering, 2015, 12(5): 1084-1087. |
| [9] |
邵勇, 闫长虹, 许宝田. 基于BURGERS模型的大型堆山工程沉降预测[J]. 长江科学院院报, 2014, 31(8): 73-81. SHAO Yong, YAN Chang-hong, XU Bao-tian. Settlement Prediction for Large Heap Mountain Project Based on Burgers Model[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(8): 73-81. |
| [10] |
孙亚军.基于能量耗散原理的类岩石材料损伤演化试验研究和数值模拟[D].大连: 大连理工大学, 2013. SUN Ya-jun. Experimental Study and Numerical Simulation of Damage Evolution in Rock-like Materials Based Energy Dissipation Principle[D]. Dalian: Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198351.htm |
| [11] |
袁海平, 曹平, 许万忠, 等. 岩石粘弹塑性本构关系及改进的BURGERS蠕变模型[J]. 岩土工程学报, 2006, 28(6): 796-799. YUAN Hai-ping, CAO Ping, XU Wan-zhong, et al. Visco-elastop-lastic Constitutive Relationship of Rock and Modified Burgers Creep Model[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 796-799. |
| [12] |
CHENG Y, GUO Q, TAN G. Creep Characteristic Analysis of Asphalt Concrete Based on the Modified Burgers Model[C]//2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE). Changchun: IEEE, 2011: 2248-2251.
|
| [13] |
杨文东, 张强勇, 张建国, 等. 基于FLAC3D的改进BURGERS蠕变损伤模型的二次开发研究[J]. 岩土力学, 2010, 31(6): 1956-1964. YANG Wen-dong, ZHANG Qiang-yong, ZHANG Jian-guo, et al. Second Development of Improved Burgers Creep Damage Constitutive Model of Rock Based on FLAC3D[J]. Rock and Soil Mechanics, 2010, 31(6): 1956-1964. |
| [14] |
勒迈特J.损伤力学教程[M].倪金刚, 陶春虎, 译.北京: 科学出版社, 1996. LEMAITRE J. Damage Mechanics Course[M]. NI Jin-gang, TAO Chun-hu, translated. Beijing: Science Press, 1996. |
| [15] |
金磊, 夏才初. 理论流变力学模型中蠕变损伤的研究方法与问题[J]. 岩石力学与工程学报, 2011, 30(增1): 3006-3013. JIN Lei, XIA Cai-chu. Study Methods for Creep Damage in Theoretical Rheological Models and Some Problems[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S1): 3006-3013. |
| [16] |
高玮, 汪磊, 杨大勇. 基于能量原理的岩石损伤研究[J]. 地下空间与工程学报, 2010, 6(增2): 1672-1677. GAO Wei, WANG Lei, YANG Da-yong. Study on the Rock Damage Evolution Based on Energy Principle[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(S2): 1672-1677. |
| [17] |
杨大勇.基于能量原理的岩石损伤研究[D].武汉: 武汉工业学院, 2008. YANG Da-yong. Research on Rock Damage Based on Energy Theory[D]. Wuhan: Wuhan University of Technology, 2008. |
| [18] |
高玮, 汪磊, 杨大勇. 岩石损伤演化的能量方法研究[J]. 岩石力学与工程学报, 2011, 30(增2): 4087-4092. GAO Wei, WANG Lei, YANG Da-yong. Rock Damage Evolution Based on Energy Principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 4087-4092. |
| [19] |
高东东.沥青混合料的非线性粘弹性蠕变分析[D].湘潭: 湘潭大学, 2015. GAO Dong-dong. Analysis of Nonlinear Viscoelastic Creep Behavior of Hot-mix Asphalt[J]. Xiangtan: Xiangtan University, 2015. |
 2020, Vol. 37
2020, Vol. 37
