扩展功能
文章信息
- 万远航, 邵毅明, 胡广雪, 徐进
- WAN Yuan-hang, SHAO Yi-ming, HU Guang-xue, XU Jin
- 重载货车长下坡挂挡决策行驶安全仿真
- Simulation of Driving Safety of Heavy-duty Truck Driver's Gear Shifting Decision on Long Downhill Section
- 公路交通科技, 2020, 37(3): 130-136, 144
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(3): 130-136, 144
- 10.3969/j.issn.1002-0268.2020.03.016
-
文章历史
- 收稿日期: 2018-11-29
2. 重庆交通大学 机电与车辆工程学院, 重庆 400074
2. School of Mechanical & Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China
公路运输是交通运输的重要组成部分,在西部地区承担干线运输的任务。据统计,我国货运车辆逐步呈现大型化趋势[1]。不同于乘用车,大型车辆在长大下坡路段存在换档困难、制动器易失效等问题,是引发交通事故的主要车辆。现有研究多关注于长大下坡制动器温升变化[2-5]、速度预测模型[6-8]和事故路段特征[9],缺乏对驾驶人驾驶行为与行车安全耦合特性的研究。然而驾驶人作为车辆操纵主体,其操纵行为与行车安全存在高度相关性,尤其在重载货车长下坡行驶过程中,合理的档位决策不但能够减少制动器使用频率、缓解制动器工作负荷,还能最大程度地保证运输经济性[10]。
由于驾驶人在真实长下坡驾驶过程中难以长时间感知细小的坡度变化,故可采用车辆动力学软件进行先期道路安全仿真,通过道路警示标识、人机交互层面来降低长下坡对驾驶人的驾驶要求,保障行车安全。近年来,TruckSim软件、Adams软件的逐步完善使实现人-车-路协同仿真成为可能。不少学者[11-12]在驾驶人预瞄模型基础上通过设置期望车速对车辆临界或危险工况开展研究,在评价道路平面线形安全等方面取得了一定成果,但这并不能反映驾驶人长下坡挂挡决策对行车安全的影响,进而难以为长下坡道路安全措施改进提供有效依据。
本研究通过构建重载货车整车模型、转向控制器和踏板控制器,基于TruckSim软件和Matlab软件,联合设计驾驶人挂挡决策对行车安全的控制策略,最后引入1条真实长下坡路段验证该控制策略有效性,并研究车辆长下坡不同档位的挂挡行车安全。
1 车-路仿真系统构建 1.1 整车动力学模型车辆数据源于国内某款重载货车,整车模型建模均在TruckSim车辆模型库完成。动力系统采用8×4驱动,各轮间轴距分别为1.95,4.55,1.35 m,整备质量为11 t,额定载重为19 t,车辆其他主要技术参数见表 1。
| 参数 | 数值 | 参数 | 数值 |
| 质心高度/mm | 1 175 | 车轮半径/mm | 510 |
| 驱动形式 | 8×4 | 轮距/mm | 2 030 |
| 发动机功率/kW | 225 | 单轮最大载荷/N | 1.0×106 |
| 后桥速比 | 4.4 | 手动档位数 | 10 |
| 传动比(VII-IX) | 8.2,6.06,4.49,3.32 | ||
1.2 道路模型
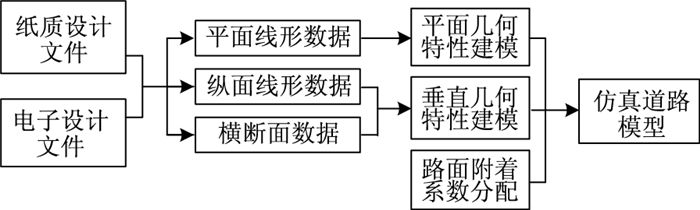
实例路段数据来源于四川省某长下坡路段。道路建模流程见图 1,其步骤如下:
|
| 图 1 道路建模流程 Fig. 1 Road modeling process |
| |
(1) 首先通过设计文件和CAD电子文件获取道路水平特征参数参数,通过空间三维软件求解道路平面线形、纵面线形、横断面数据。
(2) 利用平面线形数据在x,y坐标平面中规划出1条渐变连续性的水平线,采用毕达哥拉斯原理计算行驶里程s,按行驶里程等距分割道路,并赋予每个路段单元车道宽度L。
(3) 构造平面垂直高度函数z (L, s)完成对长大纵坡和倾斜路面的设计,为保证各路段单元间的平顺性,采用样条插值方法进行过渡。
(4) 分别赋予各路段单元附着系数,以此模拟不同路面环境。
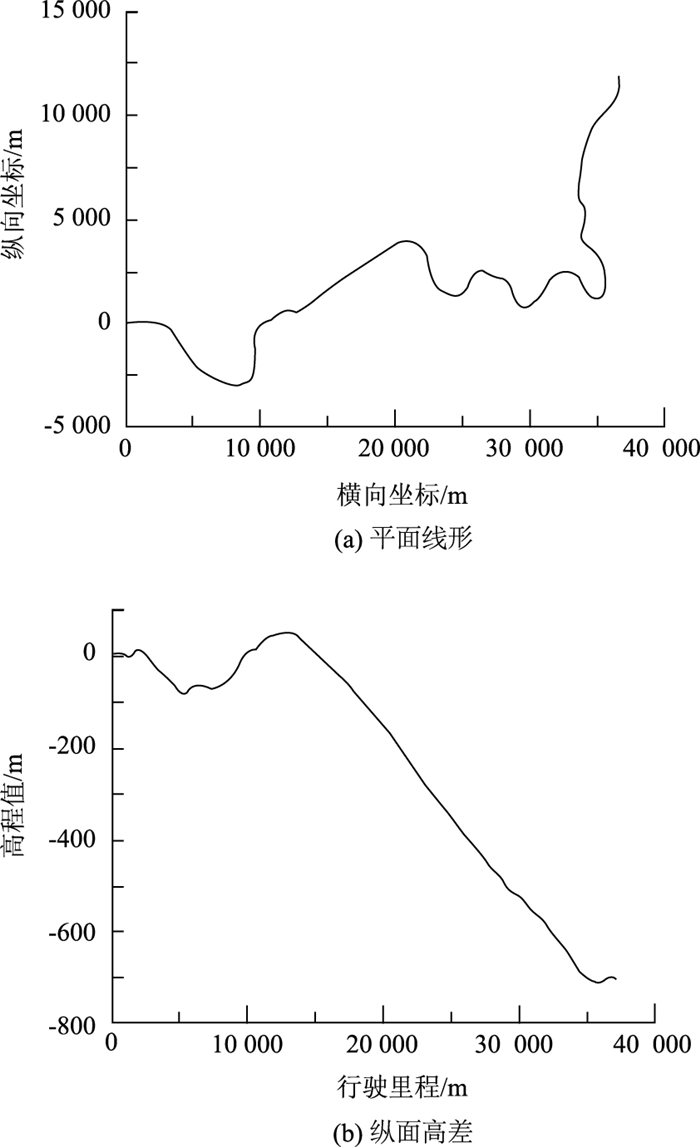
长下坡实际道路平纵面线形见图 2,路段行驶里程全程长为56 km,前半段21 km里程为长上下坡交替路段,21~52 km里程路段属于典型长下坡路段,最小转弯半径为383 m,平均坡度为3%,其高低起伏差大,有利于开展重载货车长下坡路段仿真。
|
| 图 2 仿真路段平纵面线性 Fig. 2 Horizontal/vertical alignment of simulation road |
| |
1.3 发动机仿真模型
车辆长大下坡挂档自行过程中,利用发动机内部摩擦和空气泵气损失产生的反拖力矩来钳制驱动轮速增长。为获取各时刻驱动轮力矩的变化,需给出发动机各转速下对应的制动扭矩。本研究车辆发动机功率为225 kW,最大转速为2 200 r/min,其各转速下的制动扭矩见表 2。
| 发动机转速/ (r·min-1) |
制动扭矩/ (N·m) |
发动机转速/ (r·min-1) |
制动扭矩/ (N·m) |
| 800 | 0 | 1 700 | -75 |
| 1 100 | -34.1 | 1 800 | -81.8 |
| 1 200 | -40.9 | 1 900 | -88.6 |
| 1 300 | -47.7 | 2 000 | -95.5 |
| 1 400 | -54.5 | 2 100 | -102.3 |
| 1 500 | -61.4 | 2 150 | -102.3 |
| 1 600 | -68.2 | 2 200 | -136.4 |
2 驾驶人仿真系统构建
驾驶人操纵行为是对道路条件的具体响应,当相邻路段之间道路线形或坡度发生改变时,会采取不同的响应措施,体现为驾驶人方向盘转向特性和油门/制动踏板操纵幅频特性。为准确模拟重载货车的长下坡行驶特性,依次建立转向控制器、踏板控制器并定义驾驶人边界约束。
2.1 驾驶人转向控制器根据车辆实际路径与所建道路中心线的偏差,采用最优控制理论求解方向盘转角控制量[13]。控制方程为:
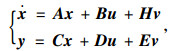
|
(1) |
式中,x为状态变量;u为控制输入;v为车辆行驶过程中的干扰;y为输出变量;A,B,C,D,E,H为带常系数矩阵。
设置仿真步长为0.001 s,由于仿真步长小,单位周期内可假设控制量和外界干扰恒定,故方程可忽略矩阵D和E:
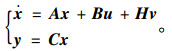
|
(2) |
采用车辆二自由度模型表征车辆运动状态变化,该模型能够较好地表征驾驶人期望行驶特性,结构简单,运算量小,能保证控制的实时性要求[14-16]。依次选取侧向位移、航向角、侧向速度、横摆角速度作为状态变量,其各状态矩阵为:
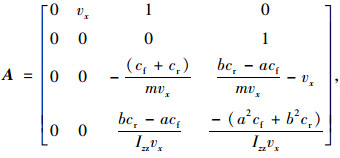
|
(3) |
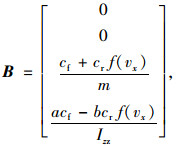
|
(4) |
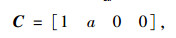
|
(5) |
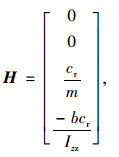
|
(6) |
式中,cf为前轴轮胎刚度系数;cr为后轴轮胎刚度系数;m为整车质量;vx为纵向速度;f (vx)为后轮转向到前轮转向角比的函数;Izz车辆绕质心z轴的转动惯量;a为车辆质心到前轴的距离;b为车辆质心到后轴的距离。
2.2 驾驶人踏板控制器基于期望速度差,采用PI模型控制踏板控制器,并在其基础上引入非线性立方反馈,以实现驾驶人油门加速、制动减速踏板操纵间的相互转换,其期望加速度计算式为:
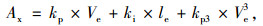
|
(7) |
式中,Ax为期望加速度;kp为比例增益系数;Ve为期望速度与实际速度间的误差;ki为积分增益系数;le为期望速度与实际速度间误差的积分;kp3为立方增益系数。
2.3 驾驶人边界约束车辆加速度是车辆面对不同道路线形的具体表现参数[17-18]。与国外货车不同,国内重载货车比功率低,整体动力性能较弱,故采用国外重载货车加速度数值标定并不适用于国内重载货车行驶安全仿真。本研究依托重载货车驾驶人自然驾驶数据[19],采用所测数据中加速度最大值的95th分位值作为驾驶人边界约束进行求解,即纵向加速度区间设置为-0.5~ 0.4 m/s2,侧向加速度区间设置为-0.5~0.5 m/s2。
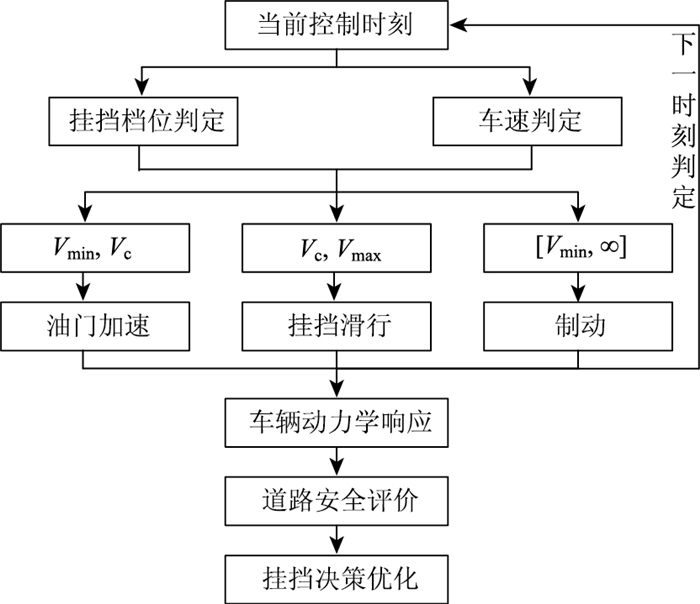
3 挂档下坡行驶控制策略真实长下坡驾驶过程中,道路坡度并不是固定不变的,驾驶人难以长时间感知细小的道路坡度变化,仅根据仪表盘和主观感受信息决策操纵存在相对滞后性。其次,为减少制动器使用频率,缓解制动器工作负荷,驾驶人会在一定车速下采取挂挡滑行措施,车辆期望车速不再符合单一固定值,而是呈现区间波动的特点。因此,本研究在TruckSim现有驾驶人模型基础上,通过联合Simulink软件中的Stateflow控制循环对驾驶人模型进行扩展。通过油门踏板触发车速Vmin、空档滑行触发车速Vc、制动踏板触发车速Vmax对挂挡下坡行驶控制策略展开设计,具体控制流程见图 3。
|
| 图 3 控制流程图 Fig. 3 Flowchart of control |
| |
当重载货车进入长下坡路段时,在各控制时刻根据不同的挂挡档位确定对应的加速区间[Vmin,Vc]、挂挡滑行区间[Vc,Vmax]、制动区间[Vmax,+∞],并结合车速判定情况进行相应的控制操作。随后,在下一控制时刻重复该流程,最后通过对输出的车辆动力学响应仿真结果进行分析,判断车辆行车安全,进而为该路段同类货车挂挡决策优化提供依据。
4 典型驾驶模式仿真及结果分析为验证挡下坡行驶控制策略的有效性,引入实际长下坡道路进行仿真,并与通用预瞄定速仿真模式进行对比,研究不同挂挡决策下车辆行车安全。
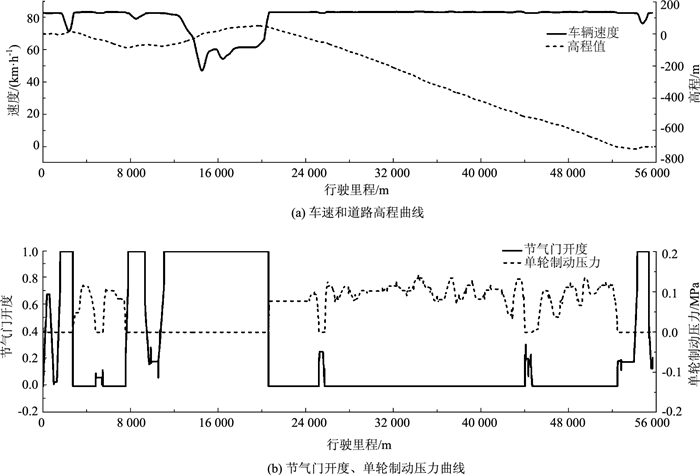
4.1 预瞄定速模式仿真及结果分析期望车速设定为80 km/h (道路设计车速),车辆居中行驶,挂挡档位不固定。图 4示出预瞄定速模型长下坡仿真结果,包括车辆速度、道路高程值、发动机节气门开度、车轮制动压力变化曲线。
|
| 图 4 预瞄定速模式仿真结果 Fig. 4 Simulation result of preview and fixed speed mode |
| |
从图 4(a)中可以看出,重载货车在进入长下坡路段(21~52 km)后, 车辆行驶车速逐步稳定在80 km/h,如果仅从车辆速度幅频特性变化层面来评价当前道路车辆行车安全,重载货车能够保证在该路段安全通行。
然而从图 5(b)示出的车辆节气门、制动压力仿真结果可以看出,重载货车单轮制动压力随路段变化呈现出不同幅度波动且数值长期处于零刻度线以上,说明定速巡航模式并未考虑车辆制动器长时间制动所产生的热衰退影响。其次,车辆节气门开度和单轮制动压力曲线呈现相互交替的态势,与驾驶人真实长下坡驾驶过程操纵不符,故难以为驾驶人挂挡决策优化及道路后设计提供有效判定依据。
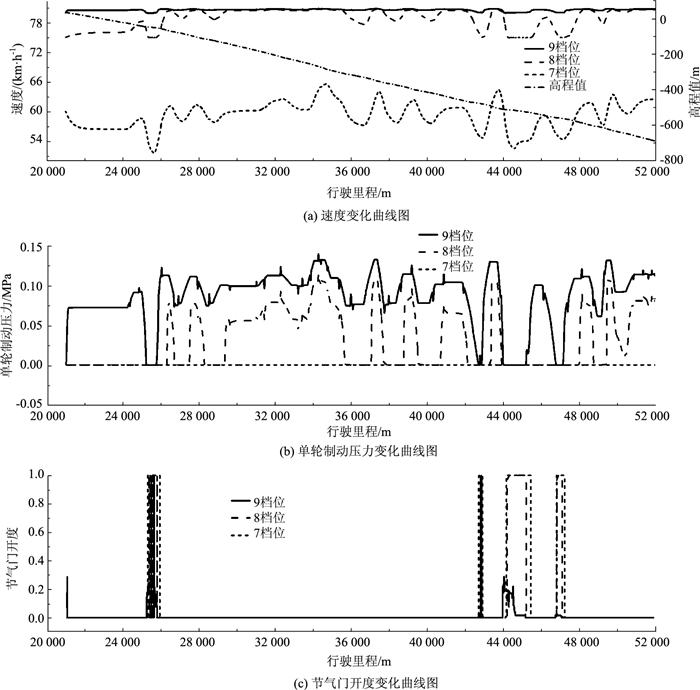
|
| 图 5 挂档控制模式仿真结果 Fig. 5 Simulation result of gear shift control mode |
| |
4.2 挂档下坡控制模式仿真及结果分析 4.2.1 驾驶人挂档档位选取
根据汽车理论及车辆动力传递原理,车辆长大下坡挂低档位行驶时,低档位下行虽然缓解了车辆制动器的工作负荷,但会造成车速下降,一定程度上牺牲了运输经济效益。真实驾驶过程中,驾驶人为追求更高的运输经济效益,多拉快跑已成常态。该路段重载货车驾驶人问卷调查显示,类似重载货车挂档下坡时,驾驶人选取7~8档位挂档下行。因此本研究仿真将对重载货车7~9档位挂档下行工况进行研究。
4.2.2 期望速度区间设置根据重载货车不同档位匹配的动力性能,设置对应期望速度区间,详细参数见表 3。
| 档位数 | Vmin/(km·h-1) | Vc/(km·h-1) | Vmax/(km·h-1) |
| 7 | 52 | 62 | 80 |
| 8 | 75 | 79 | 80 |
| 9 | 75 | 79 | 80 |
4.2.3 挂挡控制模式结果分析
图 5为驾驶人不同档位挂档下坡行驶仿真结果,包括车辆速度、单轮制动压力、节气门开度变化曲线。可以看出,车辆节气门开度和车轮制动压力呈现互不交替的特点,能够在设立的速度区间完成加速、挂挡滑行、制动操作,较好地表征了驾驶人长下坡行驶过程中的操纵行为。
为进一步分析车辆行驶安全,实现该路段重载货车驾驶人挂挡决策优化,分别对各类仿真结果进行分析。
从图 5(a)可以看出,车辆7档位挂挡车速波动于52~66 km/h,8档位波动于75~80 km/h,9档位稳定于80 km/h,说明该路段9档位运输效率最优,8档位次优,7档位最差。
从图 5(b)可以看出,9档位车辆车轮制动压力几乎全程处于零刻度线以上,频繁的制动势必会导致制动器产生热衰退现象,进而引发车辆失控;8档位所对应的单轮制动压力幅度较小,其制动波动频率也呈现出较好的分隔性,为制动器预留了足够的散热时间,一定程度保证了行车安全;而7档位挂档下行所对应的单轮制动压力曲线全程停留在零刻度线,说明车辆制动踏板处于闲置状态,重载货车仅凭发动机制动就能保证车辆安全下行,行驶安全性最优。
从图 5(c)可以看出,相较于其他两个档位,7档位节气门开度无论幅值还是频域,其波动变化最为剧烈,说明该档位燃油经济性最差。因此,在保证行驶安全性的前提下,同时兼顾车辆运输时效及燃油经济性,该路段同类重载货车挂挡下行时8档位最优、7档位次优。
此外,现有避险车道位置设计缺乏统一量化指标。制动器失效是导致交通事故的主要诱因,而频繁制动是导致制动器失效的关键因素,因此从驾驶人制动幅值变化和波动频域层面来为避险车道位置参数设计提供依据显然更具意义。图 5(b)中,车辆8档位挂档下行过程中,重载货车在行驶里程28.3~35.5 km路段单轮制动压力呈现了较高的频域及幅值波动。故可认为车辆在该路段最易发生车辆失控,道路设计者和管理部门应在此路段根据相应情况添设避险车道。
5 结论(1) 在TruckSim环境下联合Simulink软件设计了挂档下坡行驶控制仿真模式,相较于传统预瞄定速模式,其仿真结果更加切合重载货车驾驶人长下坡操纵过程,能够反映不同挂挡决策对长下坡车辆行车安全的影响。
(2) 不论是拟建造道路设计方案,还是在建和已运行的长大复杂下坡路段,在生成三维道路模型后都可采用本研究模式进行仿真,通过分析不同档位下的车辆行驶速度、单轮制动压力幅值变化和波动频域特性,以此优化该路段驾驶人挂档决策,进行避险车道设计,进而提升车辆长大复杂下坡路段的行驶安全。
(3) 由于本研究目前尚未考虑制动性能衰减作用,但提供了能够反映驾驶人挂档决策对车辆长下坡路段行驶安全影响的一种仿真新思路,进一步的研究拟结合制动器温升模型进行,以期更真实地反映长大下坡重载货车的行驶特性。
| [1] |
徐进, 罗骁, 张凯, 等. 基于自然驾驶试验的山区公路汽车行驶轨迹特性研究[J]. 中国公路学报, 2016, 29(7): 38-51. XU Jin, LUO Xiao, ZHANG Kai, et al. Investigation on Characteristics of Vehicle Travelling Tracks on Mountain Highways Based on Natural Driving Tests[J]. China Journal of Highway and Transport, 2016, 29(7): 38-51. |
| [2] |
YAN M, XU J. Prediction Model for Brake-drum Temperature of Large Trucks on Consecutive Mountain Downgrade Routes Based on Energy Conservation Law[J]. Mathematical Problems in Engineering, 2018, 2018: 1-10. |
| [3] |
GUO Y S, WANG C. Temperature Rise Model of Drum Brake[J]. Applied Mechanics and Materials, 2013, 419: 701-705. |
| [4] |
YEVTUSHENKO A A, KUCIEJ M, OCH E. Temperature in Thermally Nonlinear Pad-disk Brake System[J]. International Communications in Heat and Mass Transfer, 2014, 57: 274-281. |
| [5] |
胡立伟, 李林育, 王淼, 等. 基于台架试验的长下坡路段满载中型货车制动风险阈值研究[J]. 公路交通科技, 2017, 57(7): 135-144. HU Li-wei, LI Lin-yu, WANG Miao, et al. Study on Braking Risk Threshold Value for Full-loaded Medium Trucks on Continuous Long and Steep Downhill Sections Based on Bench Test[J]. Journal of Highway and Transportation Research and Development, 2017, 57: 135-144. |
| [6] |
郭应时, 付锐, 袁伟. 山区公路事故率与平面线形的关系[J]. 交通运输工程学报, 2012, 12(1): 63-71. GUO Ying-shi, FU Rui, YUAN Wei, et al. Relation between Accident Rate and Horizontal Alignment for Mountain Highway[J]. Journal of Traffic & Transportation Engineering, 2012, 12(1): 63-71. |
| [7] |
徐进, 罗庆, 毛嘉川, 等. 考虑弯道几何要素和交通量影响的汽车行驶速度预测模型[J]. 中国公路学报, 2012, 25(5): 47-57. XU Jin, LUO Qing, MAO Jia-chuan, et al. Speed Prediction Model of Car/Truck Considering the Effect of Curve Geometric Features and Traffic Volume[J]. China Journal of Highway and Transport, 2012, 25(5): 47-57. |
| [8] |
王志新, 余强, 赵轩, 等. 长大下坡路段载货汽车行驶速度预测研究[J]. 公路交通科技, 2017, 34(7): 130-134. WANG Zhi-xin, YU Qiang, ZHAO Xuan, et al. Study on Truck Speed Prediction in Long and Steep Downhill Sections[J]. Journal of Highway and Transportation Research and Development, 2017, 34(7): 67-74. |
| [9] |
陈斌, 袁伟, 付锐, 等. 连续长大下坡路段交通事故特征分析[J]. 交通运输工程学报, 2009(4): 75-78. CHEN Bin, YUAN Wei, FU Rui, et al. Analysis of Traffic Accident Characteristic on Continuous Long Downgrade Section[J]. Journal of Traffic and Transportation Engineering, 2009(4): 75-78. |
| [10] |
丰明洁, 王婷, 王雪松, 等. 山区高速公路平纵组合路段设计安全评估[J]. 北京工业大学学报, 2018, 44(6): 124-130. FENG Ming-jie, WANG Ting, WANG Xue-song, et al. Safety Evaluation of Combined Horizontal and Vertical Alignments on Mountainous Freeways[J]. Journal of Beijing University of Technology, 2018, 44(6): 124-130. |
| [11] |
徐进, 邵毅明, 杨奎, 等. 基于人-车-路协同仿真的山区道路大型车辆行驶适应性分析[J]. 中国公路学报, 2015, 28(2): 14-25. XU Jin, SHAO Yi-ming, YANG Kui, et al. Analysis of Adaptability of Large Vehicles on Mountainous Highways Based on Driver-vehicle-road Collaborative Simulation[J]. China Journal of Highway and Transport, 2015, 28(2): 14-25. |
| [12] |
徐进, 赵军, 罗庆, 等. 基于轨迹-速度耦合策略的复杂道路汽车行驶速度决策[J]. 西南交通大学学报, 2015, 50(4): 577-589. XU Jin, ZHAO Jun, LUO Qing, et al. Driving Speed Decision-Making on Complex Highways Based on Strategy of Trajectory-speed Coupling[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 577-589. |
| [13] |
ABE M. Vehicle Handling Dynamics:Theory and Application[M]. Amsterdam: Elsevier Science, 2015: 180-192.
|
| [14] |
MACADAM C C. Application of an Optimal Preview Control for Simulation of Closed-loop Automobile Driving[J]. IEEE Transactions on Systems, Man and Cybernetics, 1981, 11(6): 393-399. |
| [15] |
GHONEIM Y A, LIN W C, SIDLOSKY D M, et al. Integrated Chassis Control System to Enhance Vehicle Stability[J]. International Journal of Vehicle Design, 2000, 23(1): 124-144. |
| [16] |
丁海涛.轮胎附着极限下汽车稳定性控制的仿真研究[D].长春: 吉林大学, 2003. DING Hai-tao. Simulating Study on Vehicle Stability Control under Tire Adhesion Limit[D]. Changchun: Jinlin University, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y530761 |
| [17] |
徐进, 彭其渊, 罗庆, 等. 单曲线弯道几何参数对小客车转向行为的影响[J]. 西南交通大学学报, 2013, 48(4): 678-687. XU Jin, PENG Qi-yuan, LUO Qing, et al. Effect of Geometric Features of Simple Curves on Steering Behavior of Passenger Car[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 678-687. |
| [18] |
RICHL L, SAYED T. Effect of Speed Prediction Models and Perceived Radius on Design Consistency[J]. Canadian Journal of Civil Engineering, 2005, 32(2): 388-399. |
| [19] |
徐进, 杨奎, 罗骁, 等. 山区双车道公路运行速度预测模型的加速度标定[J]. 哈尔滨工业大学学报, 2017, 49(3): 181-188. XU Jin, YANG Kui, LUO Xiao, et al. Calibrating of Acceleration and Deceleration Rate for the Operating Speed Prediction Models of Two-lane Roads in a Mountainous Area[J]. Journal of Harbin in Statute of Technology, 2017, 49(3): 181-188. |
 2020, Vol. 37
2020, Vol. 37

 ,
,