扩展功能
文章信息
- 许斐
- XU Fei
- 曲线梁桥合理水平约束体系研究
- Study on Reasonable Horizontal Constraint System of Curved Girder Bridge
- 公路交通科技, 2020, 37(3): 80-87
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(3): 80-87
- 10.3969/j.issn.1002-0268.2020.03.010
-
文章历史
- 收稿日期: 2019-04-02
曲线梁桥以其线形优美流畅且适应能力强的特点,越来越广泛地应用于现代高等级公路、城市高架快速路、立交匝道桥以及山区公路中。由于曲线梁桥受力复杂,设计难度高,其设计理论和技术仍不够充分成熟,曲线梁桥的相关研究尚不完善[1-4],目前我国仍未形成统一的标准和规范用于指导曲线梁桥的设计。
随着已建曲线梁桥服役年限的增长,其设计上的一些缺陷也逐渐显现出来。调查发现,滞后的理论研究已导致大量曲线梁桥出现了不同程度的病害,主要表现为:梁体径向偏位、梁体翻转翘曲、支座脱空、墩梁固结处开裂、限位抗震挡块压溃等[5-6],已经危及到桥梁的正常使用,甚至导致严重的工程事故,造成人员伤亡和社会经济损失。
引起曲线梁桥病害发生的具体原因可能是多方面的[7-9],但是对曲线梁桥空间受力及变形特性认识不足,设计中沿用和参照直线梁桥的方法和规则,从而造成曲线梁桥支承约束体系设计不合理是导致此类桥梁普遍存在质量问题和安全隐患的主要原因。
曲线梁桥的支承约束体系分为竖向支承体系和水平约束体系。很多学者对曲线梁桥的竖向支承体系进行了大量的研究工作[10-13],得出可以通过设置支座预偏心以及合理布置抗扭支承的方法来解决曲线梁桥支座脱空和梁体扭转等问题。
在曲线梁桥的水平约束体系方面也有学者进行了相关的研究,王新定等[14]提出设计中可以在梁体与防震挡块之间设置弹性支座来限制梁体的侧向位移。但目前对由于水平约束体系设计不合理导致的梁体侧移病害还没有得到很好的解决,侧移病害仍时有发生,曲线梁桥的爬移问题依然是工程界的一个难题。
目前我国经济正处在由快速发展时期转变为提高质量和效益的时期,为了提高公路和城市道路网的通行效率,曲线梁桥的建设不可避免并将会越来越广泛。因此,有必要对曲线梁桥的设计理论和方法开展系统的研究,并尽快制定出相应的规范标准用于规范和指导曲线梁桥的设计。
本研究主要针对曲线梁桥的水平约束体系问题,选择一座典型的小半径大跨径曲线梁桥作为研究依托工程,通过有限元数值方法分析了曲线梁桥传统水平约束体系的局限性,然后基于曲线梁桥的温度变形特点,提出了曲线梁桥的“温度自适应”约束体系设置形式及相应的限位约束措施,并证明了该约束体系的合理性、有效性及可行性,同时探讨了限位销槽安装角度的影响。
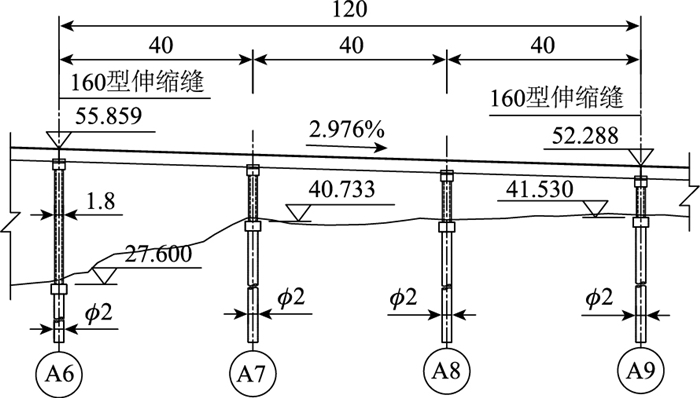
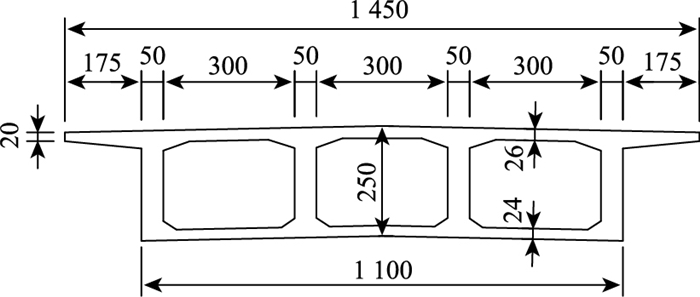
1 依托工程项目概况某桥梁工程A匝道第三联桥属于典型的小半径大跨径预应力混凝土连续曲线梁桥,桥跨位于半径60 m的圆曲线上,跨径布置为3×40 m,该联桥的平面和立面布置如图 1和图 2所示。主梁为单箱三室截面,采用C50混凝土,梁高2.5 m,顶板宽14.5 m,标准截面顶板厚26 cm,底板厚24 cm,腹板厚50 cm,标准断面如图 3所示;下部桥墩采用钢筋混凝土墙式实体墩,墩高6.4~17.4 m,横桥向设置两个支座。桥梁设计时速30 km/h,双向两车道。
|
| 图 1 桥梁立面布置(单位:m) Fig. 1 Elevation arrangement of bridge (unit:m) |
| |
|
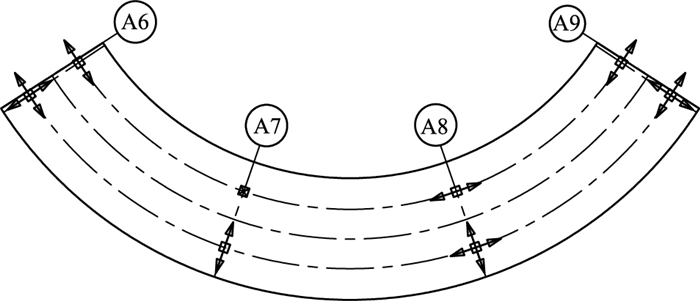
| 图 2 桥梁平面布置(单位:m) Fig. 2 Plane arrangement of bridge (unit:m) |
| |
|
| 图 3 箱梁标准横断面(单位:cm) Fig. 3 Standard cross-section of box girder (unit:cm) |
| |
2 传统约束体系下曲线梁桥支座径向力分析
支座剪切破坏、梁体径向偏位和挡块开裂压溃是曲线梁桥在传统约束体系下的典型病害,这一系列病害均是由于支座承受的水平径向力过大引起的,下面结合本研究依托工程进行具体分析。
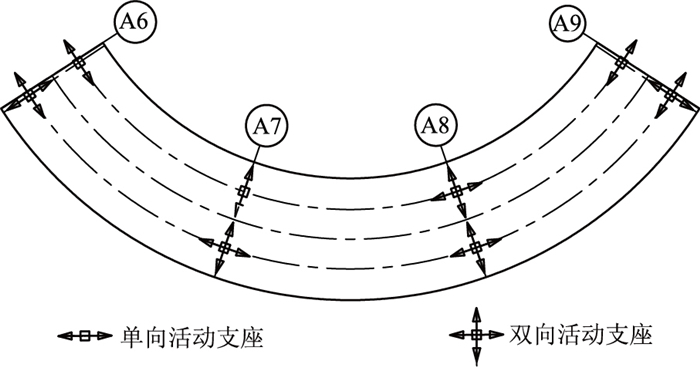
2.1 曲线梁桥的传统水平约束体系目前国内曲线梁桥普遍采用板式橡胶支座联合钢筋混凝土挡块的约束体系形式,在靠近桥跨中心的一个桥墩上设置限制切向位移的支座;同时为防止结构在水平面内发生整体侧移,各桥墩一侧采用限制径向位移的支座,另一侧采用允许径向位移的支座,其约束体系布置形式如图 4所示。
|
| 图 4 曲线梁桥传统约束体系布置图 Fig. 4 Traditional constraint system of curved girder bridge |
| |
2.2 有限元模型
采用Midas/civil有限元软件建立本研究依托工程在传统约束体系下的单梁模型,主梁和桥墩采用空间梁单元模拟,支座采用弹性连接模拟,墩底固结。设计体系温度为升温24 ℃,降温20 ℃,横向温度梯度按规范取6.75 ℃,竖向温度梯度作用按规范建议取值,混凝土收缩徐变按10 a计,汽车荷载为公路-Ⅰ级,双向两车道。汽车荷载离心力按照公路桥涵设计通用规范(JTG D60—2015)计算取值,设计时速30 km/h,曲线半径60 m,则离心力系数为302÷127÷60=0.118,离心力为550×2×0.118=129.8 kN。有限元分析模型如图 5所示。

|
| 图 5 有限元模型 Fig. 5 Finite element model |
| |
2.3 计算结果分析
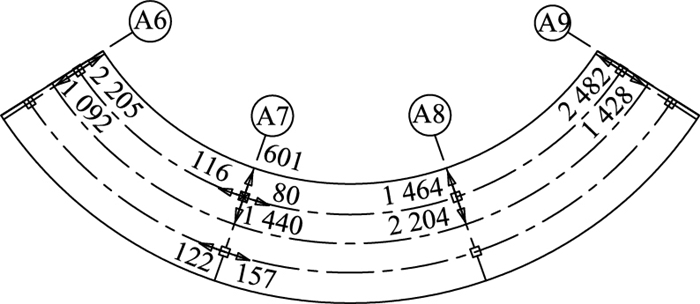
所有荷载组合工况下桥梁支座水平受力如图 6所示。
|
| 图 6 荷载组合工况下桥梁支座的水平受力(单位:kN) Fig. 6 Horizontal forces of bridge bearings under combined loads (unit: kN) |
| |
曲线梁桥的传统水平约束体系属于一种径向全限位体系,从图 6计算结果可以看出,支座径向水平力较大,边支座最大径向水平力达2 482 kN,本依托工程边支座竖向设计承载力为8 000 kN,可见支座水平剪力已经超过其竖向承载力的30%,支座无法满足水平抗剪承载要求;而钢筋混凝土挡块按当前配筋习惯设计,其强度普遍偏弱,无法完全限制梁体的横向位移,从而导致曲线梁桥一系列病害的发生。
为了找出对曲线梁桥支座径向水平力起主要作用的因素,下面列出各荷载单独作用下支座的径向水平力如表 1所示。表 1计算结果可以看出,引起曲线梁桥水平径向力的主要因素是横向温度梯度和整体升降温作用,其次是预应力和混凝土收缩作用。
| 荷载工况 | 6#内侧 | 7#内侧 | 8#内侧 | 9#内侧 | |||||||
| 最大 | 最小 | 最大 | 最小 | 最大 | 最小 | 最大 | 最小 | ||||
| 恒载 | 131.09 | — | — | -165.63 | 65.94 | — | 40.00 | — | |||
| 预应力 | 332.99 | — | — | -130.38 | — | -294.17 | 395.48 | — | |||
| 收缩 | 267.48 | — | — | -108.60 | — | -230.80 | 315.86 | — | |||
| 徐变 | — | -72.30 | 19.81 | — | 77.63 | — | — | -95.24 | |||
| 整体升降温包络 | 483.29 | -579.95 | 225.36 | -187.80 | 516.49 | -430.41 | 579.23 | -695.07 | |||
| 竖向温度梯度包络 | 25.11 | -50.25 | 13.40 | -6.70 | 54.57 | -27.27 | 33.33 | -66.70 | |||
| 横向温度梯度包络 | 878.99 | -878.99 | 323.90 | -323.90 | 810.90 | -810.90 | 1 071.35 | -1 071.35 | |||
| 风荷载包络 | 40.76 | -40.76 | 243.25 | -243.25 | 236.80 | -236.80 | 43.24 | -43.24 | |||
| 离心力包络 | 6.62 | -104.53 | 4.59 | -107.90 | 23.10 | -109.28 | 9.80 | -126.04 | |||
| 制动力包络 | 39.70 | -39.70 | 67.67 | -67.67 | 115.01 | -115.01 | 46.66 | -46.66 | |||
| 汽车包络 | 60.78 | -48.97 | 87.54 | -95.36 | 68.75 | -74.12 | 33.19 | -26.60 | |||
| 人群包络 | 11.33 | -9.05 | 20.09 | -22.88 | 20.51 | -19.51 | 9.22 | -8.43 | |||
| 组合工况 | 2 205.83 | -1 092.95 | 601.00 | -1 440.26 | 1 464.73 | -2 204.70 | 2 482.12 | -1 428.00 | |||
| 注:表中正值表示支座受力沿径向指向曲线内侧,负值表示支座受力沿径向指向曲线外侧。 | |||||||||||
横向温度梯度引起的径向力很大,公路桥涵设计通用规范(JTG D60—2004)未对横向温度梯度做出明确规定[15],新的公路桥涵设计通用规范(JTG D60—2015)建议对无悬臂的宽幅箱梁,宜考虑横向温度梯度引起的效应[16],可见横向温度梯度效应已经引起重视。虽然规范是针对无悬臂宽幅箱梁提出了考虑横向温度梯度效应的建议,但是谭万忠等[17]对某带悬臂箱型曲线梁桥进行了温度监测,实测箱梁横向温度差最大达11.2 ℃,因此,曲线梁桥的横向温度梯度效应须格外引起重视,对荷载因素考虑不周也是曲线梁桥病害的主要原因之一。
3 曲线梁桥“温度自适应”水平约束体系的提出对曲线梁桥传统水平约束体系的分析可以看出,温度作用是引起曲线梁桥径向力的主要因素。想要通过合理设置曲线梁桥的水平约束体系,以减小曲线梁桥在温度作用下的径向力,首先要准确掌握曲线梁桥温度作用下的变形特点。
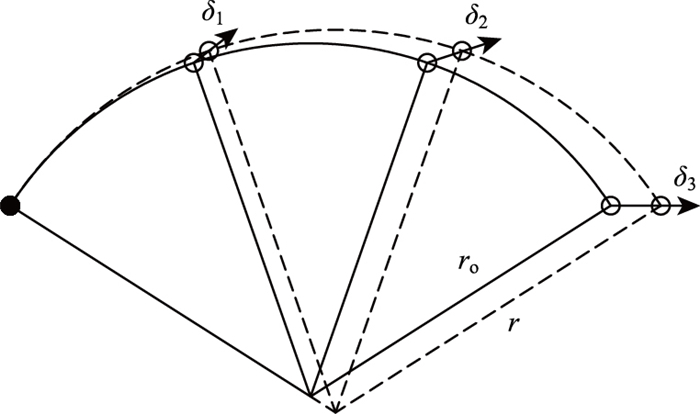
3.1 曲线梁桥的温度变形特点曲线梁桥由温度变化引起的变形属于弧段膨胀或收缩性质的变形,变形前后弧段圆心角不变,曲率半径增大或减小。图 7表示整体升温作用下一端采用固定支座其余采用多向活动支座的曲线梁变形图。
|
| 图 7 曲线梁温度作用下的变形图 Fig. 7 Deformation diagram of curved girder under temperature effect |
| |
图 7可以看出,整体升温作用下,曲线梁不仅发生了切向位移,同时还产生了径向位移。除整体升降温外,横向温度梯度和混凝土收缩等也能引起曲线梁的径向位移。
3.2 “温度自适应”约束体系的设计思路温度和混凝土收缩等作用使曲线梁桥不可避免地产生径向位移,传统设计往往采用限制径向位移的措施来保证曲线梁桥的运营安全,位移受到支座的约束将使主梁在水平面内产生很大的次内力,特别是墩高较矮的小半径曲线梁桥,次内力更大。支座在长期反复较大的水平剪力作用下容易发生剪切破坏,最终导致主梁一系列的侧移病害。
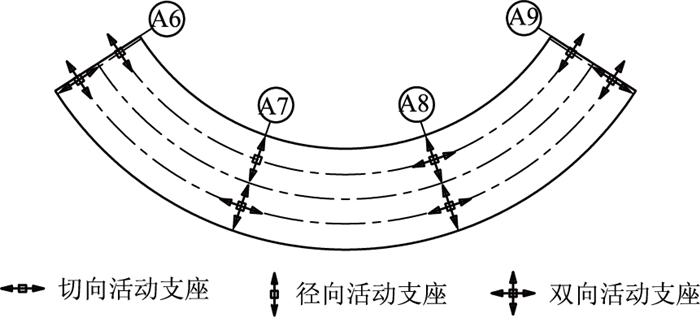
想要减小曲线梁桥的水平约束力,就要尽可能地释放梁体的变形。基于此,在充分认识曲线梁桥平面内变形特点的基础上,提出了一种曲线梁桥的“温度自适应”约束体系形式。该约束体系在梁端内侧(或外侧)采用约束径向位移允许切向位移的单向支座;中间靠近桥跨中心的一个桥墩内侧(或外侧)采用限制切向位移允许径向位移的单向支座;其余支座均为多向活动支座,所有支座均为能够释放水平转角的类型。“温度自适应”约束体系能够释放曲线梁桥外力作用引起的次内力,同时防止梁端错位导致的伸缩缝活动困难,且结构体系受力简单明确。“温度自适应”约束体系布置形式如图 8所示。
|
| 图 8 曲线梁桥“温度自适应”约束体系布置图 Fig. 8 Arrangement of "temperature adaptive" constraint system of curved girder bridge |
| |
3.3 计算分析
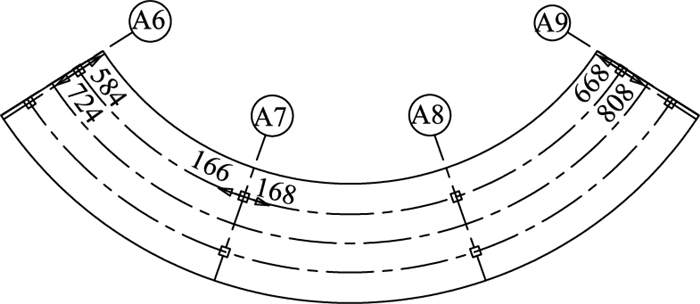
对本研究依托工程项目采用“温度自适应”约束体系进行受力分析,得到所有荷载组合工况下桥梁支座的水平受力如图 9所示,梁体的横向位移曲线如图 10所示。
|
| 图 9 “温度自适应”约束体系下桥梁支座的水平受力(单位:kN) Fig. 9 Horizontal forces of bridge bearings using "temperature adaptive" constraint system (unit: kN) |
| |
|
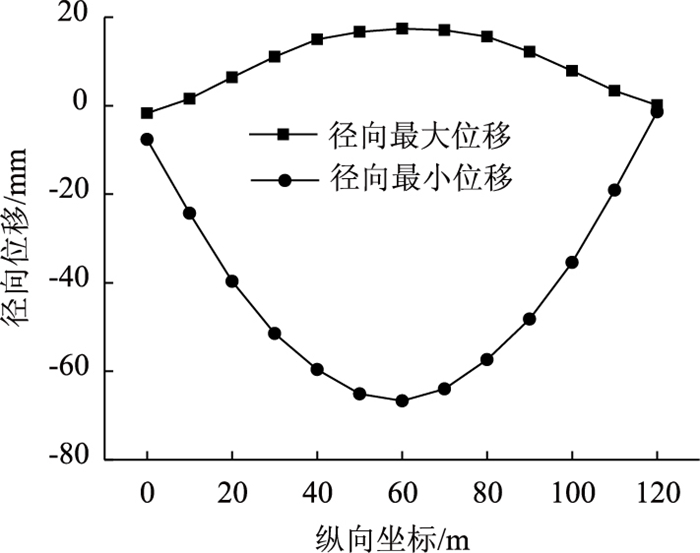
| 图 10 “温度自适应”约束体系下桥梁径向位移曲线 Fig. 10 Radial displacement curves of bridge under "temperature adaptive" constraint system |
| |
图 9可以看出,“温度自适应”约束体系下曲线梁桥由外力引起的次内力被释放,支座水平力显著减小。图 10中径向位移负值表示梁体向曲线外侧偏移,正值表示梁体向曲线内侧偏移,可以看出,梁体的最大径向位移为向曲线外侧偏移6.7 cm,结构的径向位移不会明显改变桥梁的设计线形。因此,曲线梁桥的“温度自适应”约束体系是合理可行的。
根据本研究“温度自适应”约束体系的设计思路和支座布置方法可知,该约束体系属于水平面内的静定结构,可释放温度作用产生的支座水平力,而其他作用产生的支座水平力均较小,因此本研究“温度自适应”约束体系可适用于任何跨数的曲线梁桥。
4 爬移病害分析及限位约束措施曲线梁桥由于自身结构特点和支承形式等原因,梁体在外荷载作用下发生的侧向位移不能完全恢复,随着时间的推移和荷载的长期反复作用,残余位移不断累积的现象称为爬移,爬移累积到一定程度就会导致梁体滑移和倾覆。
4.1 爬移原因分析曲线梁桥的爬移现象是一个长期且复杂的过程,目前对爬移问题的认识还不够深入,爬移现象产生的原因和机理还没有统一的定论。就目前学者们的研究成果[18-20]来看,爬移产生的原因大致有以下几种情况:
(1) 对于采用橡胶支座的曲线梁桥,特别是在传统约束体系下,支座承受较大剪力,支座本身的变形累积和老化问题导致位移无法恢复。
(2) 对于中间墩采用点铰支承的曲线梁桥,伴随径向位移的发生,梁体有向外侧扭转的残余累积,扭转变形所产生的自重分力会使径向位移值进一步增大。
(3) 由于支座摩阻力的存在,汽车离心力和制动力等长期定向荷载会使曲线梁桥的径向位移逐渐累积而不断增大。
对曲线梁桥爬移原因的分析归纳可以看出,若要预防曲线梁桥爬移的产生,在支承形式布置和支座类型选择方面要特别注意,但是支座摩阻力是无法消除的,也就是说爬移问题是无法完全避免的。
4.2 销轴式限位约束措施曲线梁桥的“温度自适应”约束体系允许梁体在中间桥墩位置发生径向位移,但是为了防止爬移累积位移过大致使支座失效甚至梁体的突然整体滑移和翻转,同时为了避免地震作用下的落梁,还必须设置一定的限位措施,为此,提出了一种与曲线梁桥“温度自适应”约束体系相应的销轴式限位约束措施。
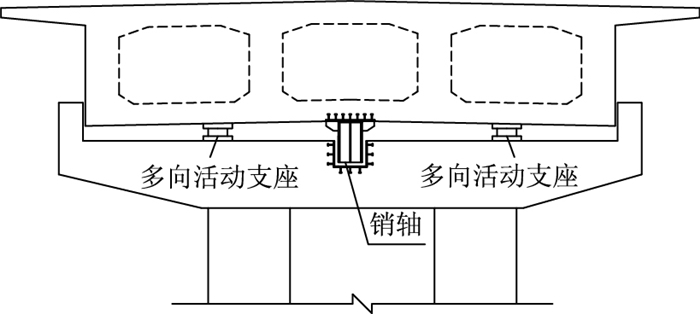
销轴式限位约束措施通过将固定在梁底的销轴插入桥墩盖梁上的销槽来实现对曲线梁桥的水平约束和限位,销槽形状为与桥墩轴线方向一致的长方体。销轴与销槽底部不接触,销轴在销槽中可水平转动并可沿预定的径向或切向移动,销轴式限位约束措施立面图如图 11所示。
|
| 图 11 销轴式限位约束措施立面图 Fig. 11 Elevation diagram of pin-type limit and constraint measure |
| |
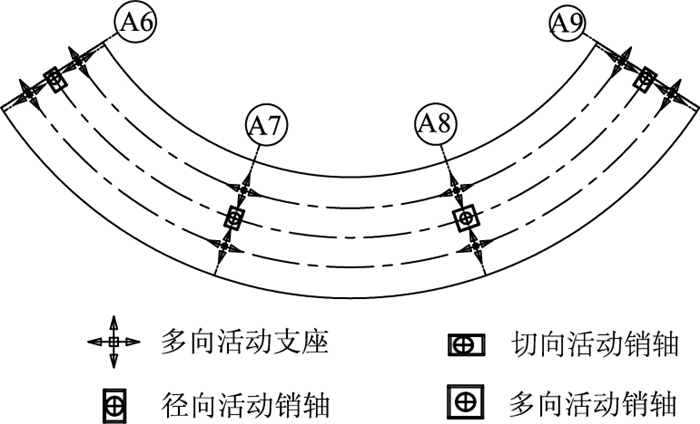
销轴式限位约束措施能够确保梁体在桥墩上按照预设的方向活动且不发生落梁,因此,它既是一种限位措施,同时也是一种曲线梁桥的水平约束措施。采用销轴式限位约束措施时,曲线梁桥的支座可以采用多向活动支座,销轴提供水平约束,支座提供竖向支承。本研究依托工程项目曲线梁桥销轴式限位约束措施平面图如图 12所示。
|
| 图 12 销轴式限位约束措施平面图 Fig. 12 Plane diagram of pin-type limit and constraint measure |
| |
销轴式限位约束措施布置在曲线梁桥的设计轴线上,梁端桥墩设置切向活动销轴,最靠近桥跨中心的一个桥墩上设置径向活动销轴,其余桥墩为多向活动销轴。
5 销槽安装角度偏差影响分析采用销轴式限位约束措施的曲线梁桥,桥墩帽梁上的销槽应该按照设计的位置和角度进行安装,销槽安装角度偏差会使曲线梁桥不能按照预定的方向活动,也会对结构的受力产生影响。
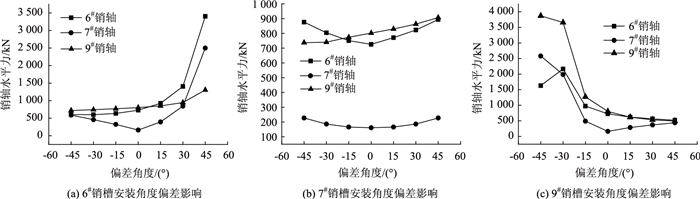
结合本研究依托工程项目对销槽安装角度偏差的影响进行分析,本研究依托工程项目8#墩上设置多向活动销轴,其销槽安装角度偏差不会对结构产生影响,因此仅讨论其余3个桥墩上的销槽安装角度偏差影响,图 13为6#墩、7#墩和9#墩上销槽安装角度偏差对销轴水平力的影响曲线。
|
| 图 13 销槽安装角度偏差对销轴水平力的影响 Fig. 13 Influence of installation angle deviation of pin-channel on horizontal force of pin |
| |
图 13(a)和图 13(c)可以看出,6#墩上销槽顺时针偏差和9#墩上销槽逆时针偏差均会使销轴水平力显著增大;图 13(b)表明中间7#墩上销槽安装角度偏差对销轴水平力的影响相对较小。因此,曲线梁桥采用销轴式限位约束措施时,一定要确保梁端桥墩上销槽的安装精度,其偏差不但对销轴受力影响较大,也会影响伸缩缝的正常工作。
6 梁体径向变位对结构安全性的影响分析曲线梁桥“温度自适应”约束体系允许梁体在中间桥墩位置发生径向偏位,实际运营中,汽车和人群荷载可能作用在已经发生变形的梁体上。通过提取梁体最不利变形后的坐标值,对模型坐标进行更新,对比分析梁体变形前后结构的竖向支反力,来评价梁体径向变位对结构安全性的影响。表 2为梁体在最不利径向偏位时与梁体在设计轴线位置时的竖向支反力比较。
| 荷载工况 | 6#墩 | 7#墩 | 8#墩 | 9#墩 | |||||||
| 内侧 | 外侧 | 内侧 | 外侧 | 内侧 | 外侧 | 内侧 | 外侧 | ||||
| 变形前最小反力/kN | 1 531.23 | 5 069.77 | 6 538.43 | 9 214.72 | 6 725.78 | 9 260.59 | 1 217.00 | 5 061.43 | |||
| 变形后最小反力/kN | 1 483.89 | 5 101.29 | 6 392.58 | 9 391.50 | 6 578.79 | 9 431.24 | 1 157.02 | 5 067.71 | |||
| 反力变化程度/% | -3.09 | 0.62 | -2.23 | 1.92 | -2.19 | 1.84 | -4.93 | 0.12 | |||
| 变形前最大反力/kN | 3 403.25 | 7 278.26 | 10 706.80 | 12 909.88 | 10 605.85 | 12 667.56 | 3 411.44 | 7 618.63 | |||
| 变形后最大反力/kN | 3 353.56 | 7 312.34 | 10 544.59 | 13 093.54 | 10 445.33 | 12 847.86 | 3 349.26 | 7 626.21 | |||
| 反力变化程度/% | -1.46 | 0.47 | -1.52 | 1.42 | -1.51 | 1.42 | -1.82 | 0.10 | |||
表 2计算结果可以看出,梁体发生向曲线外侧最不利径向位移后,梁体内侧支反力减小,外侧支反力增大,径向位移对结构竖向支反力影响不明显,9#墩内侧支反力变化程度最大,反力也仅减小了4.93%,因此,“温度自适应”约束体系下结构是安全的。
7 结论曲线梁桥合理的水平约束体系设计是避免病害发生的关键之一,本研究以一座典型的小半径大跨径曲线梁桥为依托,对曲线梁桥合理水平约束体系的设计进行了分析和探讨,得出以下结论:
(1) 对于小半径大跨径的预应力混凝土曲线梁桥,传统的径向全限位水平约束体系在外力作用下会产生较大的水平次内力,其中横向温度梯度和整体升降温是引起支座水平径向力过大的主要因素。
(2) 基于曲线梁桥的温度变形特点,提出了一种曲线梁桥的“温度自适应”水平约束体系形式,该约束体系能够释放曲线梁桥外力作用下的次内力,显著减小支座承受的水平力,同时能够防止梁端错位导致的伸缩缝活动困难。
(3) 为了防止爬移累积位移过大致使支座失效甚至梁体的突然整体滑移和翻转,同时也为了避免地震时发生落梁,提出了一种与曲线梁桥“温度自适应”约束体系相应的销轴式限位约束措施,该措施既是一种限位措施,也是一种曲线梁桥的水平约束措施。
(4) 采用销轴式限位约束措施的曲线梁桥,一定要确保梁端桥墩帽梁上的销槽安装精度,其偏差不但对销轴受力影响较大,也会影响梁端伸缩缝的正常工作,同时应尽量控制在气温与设计基准温度相近的时间内进行销轴与销槽的安装定位。
(5) 采用“温度自适应”约束体系的曲线梁桥,梁体径向位移不会明显改变桥梁的设计线形,且径向位移也不会明显影响结构的竖向支反力,因此,该约束体系是合理可行的。
| [1] |
李广慧, 余正武, 王用中. 曲线连续梁桥的病害与温度效应[J]. 公路交通科技, 2008, 25(1): 58-63. LI Guang-hui, YU Zheng-wu, WANG Yong-zhong. Diseases of Curved Continuous Bridge and Temperature Effect[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 58-63. |
| [2] |
SENNAH K M, KENNEDY J B. State-of-the-art in Design of Curved Box-girder Bridges[J]. Journal of Bridge Engineering, 2001, 6(3): 159-167. |
| [3] |
SAMAAN M, SENNAH K, KENNEDY J B. Distribution Factors for Curved Continuous Composite Box-girder Bridges[J]. Journal of Bridge Engineering, 2005, 10(6): 678-692. |
| [4] |
NUTT R, VALENTINE D E. Development of Design Specifications and Commentary for Horizontally Curved Concrete Box-girder Bridges, NCHRP REPORT 620[R]. Washington, D.C.: Transportation Research Board, 2008.
|
| [5] |
林丽娟.曲线梁桥的横向"爬移"分析[D].郑州: 郑州大学, 2015. LIN Li-juan. Study on Lateral Deviation of Curved Beam Bridge[D]. Zhengzhou: Zhengzhou University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D646325 |
| [6] |
鲁圣弟, 熊文, 丁旭东, 等. 桥型布置对独柱墩曲线梁桥抗倾覆性能的影响[J]. 公路交通科技, 2017, 34(5): 95-101. LU Sheng-di, XIONG Wen, DING Xu-dong, et al. Influence of Structure Arrangement on Anti-overturn Performance of Curved Beam Bridge with Single-column Piers[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 95-101. |
| [7] |
GOMEZ H C, FANNING P J, FENG M Q, et al. Testing and Long-term Monitoring of a Curved Concrete Box Girder Bridge[J]. Engineering Structures, 2011, 33(10): 2861-2869. |
| [8] |
吕宏奎, 安群慧, 王夷. 某小半径连续曲线梁桥偏位成因分析及纠偏方案研究[J]. 世界桥梁, 2013, 41(2): 80-83. LÜ Hong-kui, AN Qun-hui, WANG Yi. Analysis of Analysis of Offsetting Causes and Study of Offsetting Correction Scheme of a Sharp-radius Continuous Curved Beam Bridge[J]. World Bridges, 2013, 41(2): 80-83. |
| [9] |
徐毅.预应力曲线连续箱梁桥径向偏位影响因素及其对策研究[D].北京: 中国铁道科学研究院, 2014. XU Yi. Research on Influencing Factors and Corresponding Solutions in Lateral Displacement of Curved Continuous Box Girder Bridge[D]. Beijing: China Academy of Railway Sciences, 2014. http://cdmd.cnki.com.cn/article/cdmd-83801-1015500237.htm |
| [10] |
滕军, 胡渝, 郭时安, 等. 高墩小半径曲线梁桥支点预偏心时力学性能分析[J]. 工程抗震与加固改造, 2009, 31(2): 9-15. TENG Jun, HU Yu, GUO Shi-an, et al. Mechanical Characteristics Analysis of Small Radius Curve Beam Bridge with Pivots Pre-eccentricity with High Piers[J]. Earthquake Resistant Engineering and Retrofitting, 2009, 31(2): 9-15. |
| [11] |
汤竞兴.预应力混凝土曲线箱梁桥支座布置效应研究[D].西安: 长安大学, 2009. TANG Jing-xing. Effect of Form of Bearing for Prestressed Concrete Curved Box Girders Bridge[D]. Xi'an: Chang'an University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1526661 |
| [12] |
江婧.超小半径曲线梁桥受力特点和合理约束方式研究[D].长沙: 中南大学, 2010. JIANG Jing. Research on Mechanical Characteristics and Reasonable Restraint Mode of Curved Girder Bridges with Ultra-small Radius[D]. Changsha: Central South University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1915645 |
| [13] |
方诗圣, 肖兵, 张吉烁, 等. 支座布置形式对曲线梁桥力学性能的影响[J]. 世界桥梁, 2011(4): 49-52. FANG Shi-sheng, XIAO Bing, ZHANG Ji-shuo, et al. Impact of Bearing Arrangement on Mechanical Behavior of Curved Girder Bridge[J]. World Bridges, 2011(4): 49-52. |
| [14] |
王新定, 丁汉山, 吉林, 等. 混凝土连续弯梁桥侧向位移分析及对策研究[J]. 公路交通科技, 2006, 23(11): 64-67. WANG Xin-ding, DING Han-shan, JI Lin, et al. Study on Lateral Displacement of Continuous Curved Girder Concrete Bridges[J]. Journal of Highway and Transportation Research and Development, 2006, 23(11): 64-67. |
| [15] |
JTG D60-2004, 公路桥涵设计通用规范[S]. JTG D60-2004, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [16] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [17] |
谭万忠, 张佐汉, 柯在田. 平面曲线梁桥温度变形与支承体系布置探讨[J]. 铁道建筑, 2005(4): 7-9. TAN Wan-zhong, ZHANG Zuo-han, KE Zai-tian. Discussion on Temperature Deformation and Supporting System Arrangement of Curved Girder Bridges[J]. Railway Engineering, 2005(4): 7-9. |
| [18] |
平然.曲线梁桥爬移问题的研究[D].北京: 北京建筑大学, 2014. PING Ran. Research on Lateral Displacement of Curved Girder Bridge[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2014. |
| [19] |
焦驰宇, 刘陆宇, 龙佩恒, 等. 城市曲线梁桥爬移现象及解决措施研究[J]. 工程力学, 2015, 32(增1): 177-183. JIAO Chi-yu, LIU Lu-yu, LONG Pei-heng, et al. Study on "Creeping" Phenomenon of Curved Continuous Girder Bridges[J]. Engineering Mechanics, 2015, 32(S1): 177-183. |
| [20] |
李杰, 冯冠杰, 林丽娟, 等. 温度作用下考虑残余变形累积效应的曲线梁爬移机理分析[J]. 科学技术与工程, 2017, 17(34): 124-129. LI Jie, FENG Guan-jie, LIN Li-juan, et al. Lateral Creep Deformation Mechanism Analysis of Curved Beam Considering the Cumulative Effect of Residual Deformation under Temperature[J]. Science Technology and Engineering, 2017, 17(34): 124-129. |
 2020, Vol. 37
2020, Vol. 37
