扩展功能
文章信息
- 闫林君, 张经伟, 罗奎
- YAN Lin-jun, ZHANG Jing-wei, LUO Kui
- 装配式多主梁钢-混组合梁桥的荷载横向分布研究
- Study on Lateral Load Distribution of Prefabricated Multi-girder Steel-concrete Composite Girder Bridge
- 公路交通科技, 2020, 37(3): 59-69
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(3): 59-69
- 10.3969/j.issn.1002-0268.2020.03.008
-
文章历史
- 收稿日期: 2019-03-20
装配式钢-混组合梁桥以其自重轻、建筑高度小、抗震性能好、预制方便及施工工艺简单等优点,成为目前中小跨径桥梁常用的结构形式[1-2]。它与传统钢筋混凝土梁相比,不仅减轻了自重,而且避免了底板混凝土受拉破坏,在一定程度上优化了桥梁结构受力性能。装配式多主梁桥的多片主梁之间通过横向连接和桥面板联结成整体结构,共同承受外荷载。工程实践中多主梁钢-混组合桥梁由于荷载横向分布考虑不周,造成横向连接系的破坏而变为单根梁受力状态,直接影响了桥梁的承载力,最终导致全桥破坏。目前,公路桥梁设计中,通常引入横向分布系数来评估车辆荷载作用下各主梁的内力分布,将复杂的空间问题合理转化为简单的平面问题[3-4]。
国外对横向分布系数的计算往往是通过改变桥梁的相关参数,计算不同参数影响下的横向分布系数,并通过大量的数据回归得到简化的计算公式[5]。Kim等[6-7]运用有限元法对桥梁跨径、宽度、主梁数等不同设计参数下的桥梁进行建模分析,得出了非标准车作用下的多主梁钢-混组合梁桥的荷载横向分布系数。Tabsh等[8]通过对多种车辆作用下的钢-混组合梁桥荷载横向分布分析,提出了基于非标准车作用下的荷载横向分布计算的修正公式。Goodrich等[9]通过有限元模拟,获得了超重车辆作用下的桥梁荷载横向分布计算公式,并证明用弯矩比值求得的横向分布系数精确度优于剪力比值求得的横向分布系数。Mohseni等[10]通过对160座多主梁混凝土箱梁桥的荷载横向分布进行试验统计分析,得到箱梁横隔板对桥梁荷载横向分布的影响规律。国内横向分布系数计算方法包括杠杆原理法、刚性横梁法、修正的刚性横梁法、铰接梁法、刚接梁法、G-M法6种[11]。这些计算方法大多用于传统T梁和空心板梁桥的荷载横向分布计算,是否适用于钢-混组合梁桥,尚无定论[12]。项贻强等[13]提出修正的G-M法分析加固后桥梁的荷载横向分布;魏志刚等[14]提出考虑桥面铺装的荷载横向分布系数计算的修正刚接梁法;聂瑞锋等[15]通过有限元建模和多元线性回归分析法提出了考虑结构性能退化的横向分布系数计算方法;邬晓光等[16]提出装配式桥梁的横向分布的数值分析方法。李院军等[17]以12座实际桥梁为工程背景,引入主梁折减系数,通过数值拟合得到了考虑主梁损伤的装配式梁桥的荷载横向分布系数计算公式,并通过和有限元值及实测数据的对比分析,研究了该公式的正确性。
虽然国内外学者对桥梁的横向分布的研究已取得了丰硕的成果,但针对主梁为钢板梁的钢-混组合梁桥的横向分布计算尚无精确的计算方法。现有的横向分布系数计算方法是否适用于求解此类桥梁的荷载横向分布,是亟待讨论的问题。因此,对于装配式多主梁钢-混组合梁桥荷载横向分布进行研究,有助于工程界对此类桥梁的荷载横向分布形成更充分全面的认识,对改善桥梁设计、降低桥梁的安全隐患、合理安排桥梁维修周期和维修费用也具有重要意义。本研究选取了6座由不同跨径、主梁数、主梁高度、主梁间距组合下的多梁式钢-混组合梁桥,分别采用6种国内常用横向分布系数计算方法和有限元法求解其横向分布系数,通过对计算结果的比较分析,得出适用于此类桥梁横向分布系数的计算方法,并通过数值回归方法拟合出简化计算公式,可为以后此类桥梁的荷载横向分布系数计算提供一定的参考依据。
1 计算模型的建立与求解 1.1 结构概况为使得计算结果有明确的对比性,本研究选取如表 1所示的6种简支装配式多主梁钢-混组合梁桥作为研究对象。表 1中6种桥的参数变化主要有跨径(12~48 m)、主梁数(4~8)、主梁间距(1.74~4.1 m)、主梁高度(0.5~ 2.05 m),表中12-6表示跨径为12 m,主梁数为6的组合梁。为简化计算和对比方便,6种桥的混凝土桥面板厚均为20.5 cm,宽为14.18 m,I形钢主梁上翼缘板厚15 mm,腹板厚10 mm,下翼缘板厚25 mm,防撞护栏尺寸为38 cm×86.5 cm。所有桥梁的边梁中心至防撞护栏外边缘的距离均为99 cm,主梁高度和跨径按恒定的高跨比设计,约为0.04。主梁横向布置及各桥横截面构造如图 1所示,图中n为主梁数,L为跨径。
| 桥型 | 跨径/m | 主梁高/mm | 主梁间距/m | 主梁数 |
| 12-6 | 12 | 500 | 2.44 | 6 |
| 24-4 | 24 | 1 100 | 4.1(4.0) | 4 |
| 24-6 | 24 | 1 100 | 2.44 | 6 |
| 24-8 | 24 | 1 100 | 1.75(1.74) | 8 |
| 36-6 | 36 | 1 540 | 2.44 | 6 |
| 48-6 | 48 | 2 050 | 2.44 | 6 |
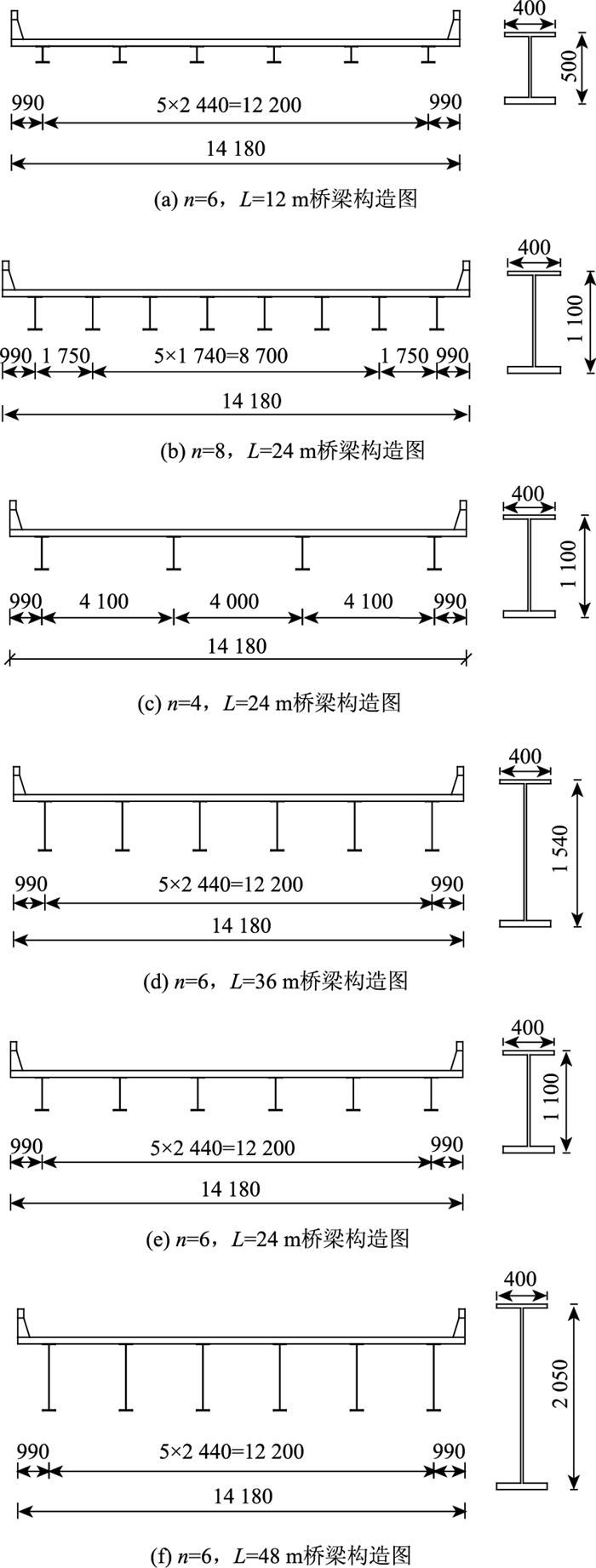
|
| 图 1 组合梁构造图(单位:mm) Fig. 1 Structure of composite girder(unit:mm) |
| |
1.2 有限元模型的建立与求解
采用有限元软件ANSYS18.2建立了6座桥的三维有限元模型。桥面板、主梁和横向联系均采用solid45实体单元,横向联系和钢主梁使用相同的材料,截面形式为I形,分别在跨中和两支点处设置横向联系。由于钢-混组合梁为两种材料组合截面,实际工程中,通过剪力连接件来限制两种材料的相对滑移。本研究为建模方便,采用共节点的方法连接两种材料,不考虑两种不同材料间的相对滑移,主梁横向通过实体单元桥面板和横向联系连接成整体,该建模方法已在文献[6-7]中验证了其正确性。单元网格划分最大尺寸为0.12 mm,这样的网格密度在桥跨长度的0.002 5%~0.01%范围内, 符合一般网格划分的要求。简支体系支座采用支承条件约束模拟,分别定义在跨径两端钢主梁底板节点位置。限于篇幅,本研究中只列出12-6桥的有限元模型与影响线竖标计算值。建立的有限元模型如图 2所示。本研究计算中混凝土和钢材的弹性模量分别取26 GPa和200 GPa,泊松比分别取为0.25和0.3,密度分别取为2 400 kg/m3和7 850 kg/m3。
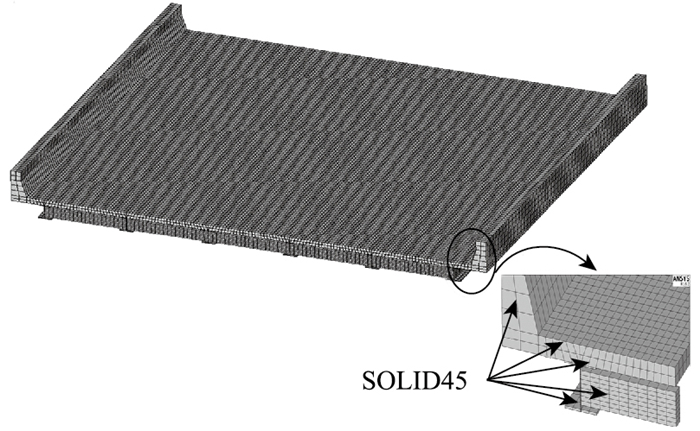
|
| 图 2 有限元模型 Fig. 2 Finite element model |
| |
为验证所建立有限元模型的正确性,采用理论计算的挠度和ANSYS模型求解的挠度进行比较[5]。理论简化计算图如图 3所示。
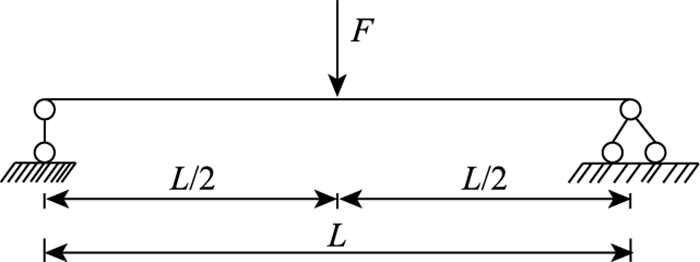
|
| 图 3 初等梁理论加载图 Fig. 3 Theoretical loading diagram of elementary girder |
| |
简支梁作用有跨中集中荷载时,挠度采用式(1)计算:
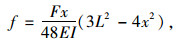
|
(1) |
式中,f为简支梁的挠度;F为跨中集中荷载,本研究中取F=550 kN;x为跨径方向坐标值,如荷载作用于跨中时,x=L/2;EI为换算截面的抗弯刚度,截面换算按文献[18]中11.1.3节第2条计算;L为简支梁的跨径。
对不同的桥,分别用式(1)计算其跨中挠度,再与有限元计算所得的跨中挠度进行对比。比较结果如表 2所示。
| 桥型 | 12-6 | 24-8 | 24-4 | 36-6 | 24-6 | 48-6 |
| 理论值/mm | 7.909 | 8.733 | 8.707 | 9.942 | 8.703 | 10.968 |
| 有限元/mm | 8.282 | 9.125 | 9.032 | 10.378 | 9.056 | 11.509 |
| 误差/% | 4.5 | 4.3 | 3.6 | 4.2 | 3.9 | 4.7 |
通过表 2可以看出,挠度的ANSYS有限元计算值与初等梁理论计算值的最大误差为4.7%,误差均在5%以内,验证了所建立有限元模型的正确性。
为求跨中的荷载横向分布系数,在每片主梁的正上方加载单个集中荷载,通过式(2)求解出各主梁的挠度影响线竖标,然后使用规范规定的标准车在影响线的最不利位置加载,从而计算得到桥梁的横向分布系数。
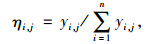
|
(2) |
式中, ηi, j为i号主梁的荷载横向分布影响线在j号主梁轴线下的竖标值;i,j为主梁编号;yi, j为单位力作用于j号主梁时i号主梁的挠度值;n为主梁数。
所求得的各桥的影响线竖标值如表 3所示,加载后的挠度图如图 4所示。
| 桥型 | 梁号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 12-6 | 1 | 0.433 | 0.281 | 0.148 | 0.081 | 0.043 | 0.014 |
| 2 | 0.182 | 0.322 | 0.252 | 0.143 | 0.073 | 0.029 | |
| 3 | 0.085 | 0.215 | 0.306 | 0.227 | 0.121 | 0.047 | |
| 4 | 0.047 | 0.121 | 0.227 | 0.306 | 0.215 | 0.085 | |
| 5 | 0.029 | 0.073 | 0.143 | 0.252 | 0.322 | 0.182 | |
| 6 | 0.014 | 0.043 | 0.081 | 0.148 | 0.281 | 0.433 |
|
| 图 4 加载后的挠度图 Fig. 4 Deflection after loading |
| |
通过ANSYS有限元计算得到的不同桥梁的横向分布系数如图 5所示。
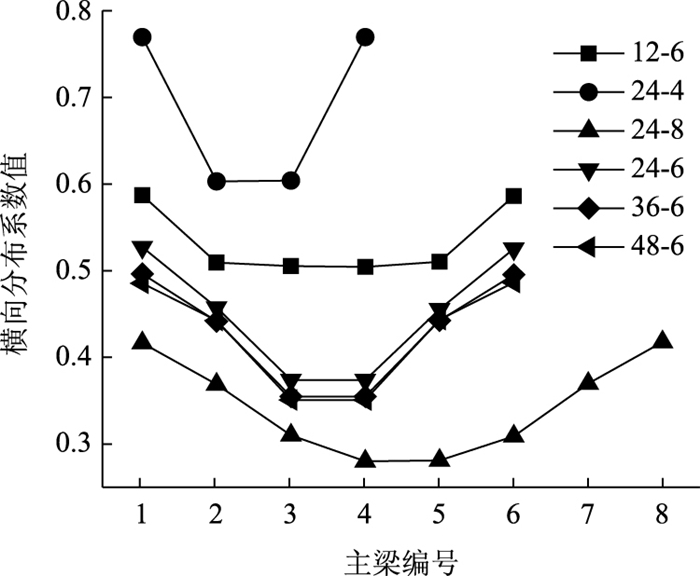
|
| 图 5 有限元模型计算结果 Fig. 5 Calculation result by finite element model |
| |
从图 5中可以看出,当主梁数最少时(4片),求得各主梁的横向分布系数最大,其中边梁最大值为0.769;当主梁数最多时(8片),求得各主梁的横向分布系数最小,其中边梁最大值为0.416,约为4片主梁边梁横向分布系数的54%。当主梁数相同时,跨径越小,求得的横向分布系数值越大。由此可见,跨径、主梁数的变化,会对桥梁的横向分布系数产生较大的影响。
2 已有的横向分布系数计算方法所得结果对钢-混组合梁桥横向分布系数计算时,由于混凝土顶板通过剪力连接装置和钢主梁共同承担荷载作用,截面特性计算时应计入顶板混凝土的影响。本研究中,混凝土顶板的有效宽度根据文献[18]中附录下的第F.0.1条计算取用。各桥组合梁截面特性计算值如表 4所示。
| 桥梁类型 | 抗弯惯性矩/(×10-2m4) | 抗扭惯性矩/(×10-3m4) |
| 12-6 | 0.581 47 | 6.962 45 |
| 24-4 | 2.226 43 | 0.000 01 |
| 24-6 | 2.070 64 | 6.925 33 |
| 24-8 | 1.993 58 | 4.933 59 |
| 36-6 | 4.080 36 | 6.981 24 |
| 48-6 | 7.600 15 | 6.950 92 |
采用杠杆原理法、刚性横梁法、修正的刚性横梁法、铰接梁法、刚接梁法、G-M法分别计算得到各桥的横向分布系数如图 6~图 11所示。因采用理论计算方法计算时,除了截面特性的处理不同于传统T梁外,其他计算步骤和传统T梁横向分布系数计算相同。限于篇幅,此处省略具体计算过程,仅列出计算结果。
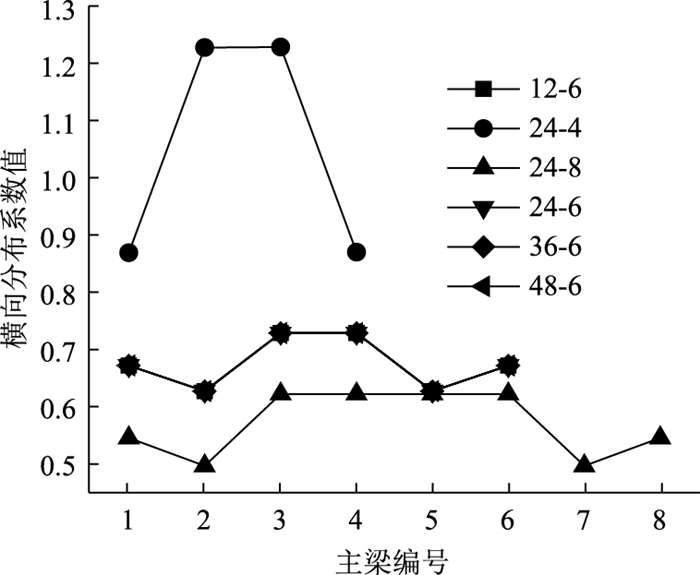
|
| 图 6 杠杆原理法计算结果 Fig. 6 Calculation result by lever principle |
| |
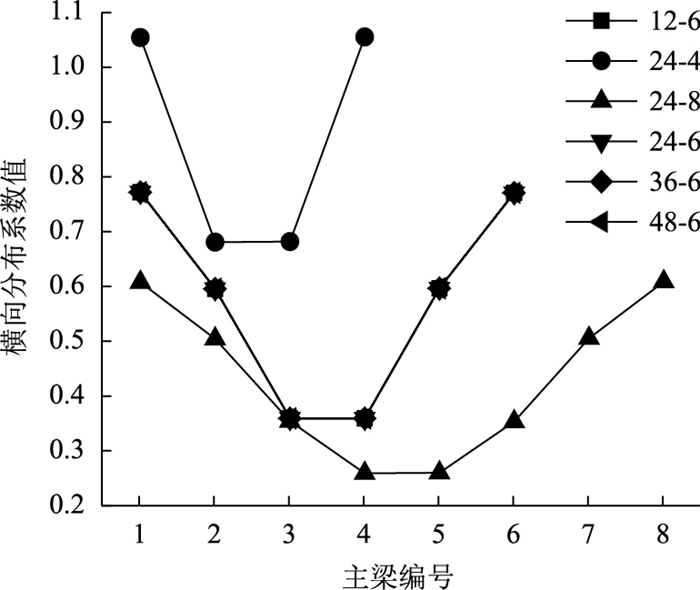
|
| 图 7 刚性横梁法计算结果 Fig. 7 Calculation result by rigid transverse girder method |
| |
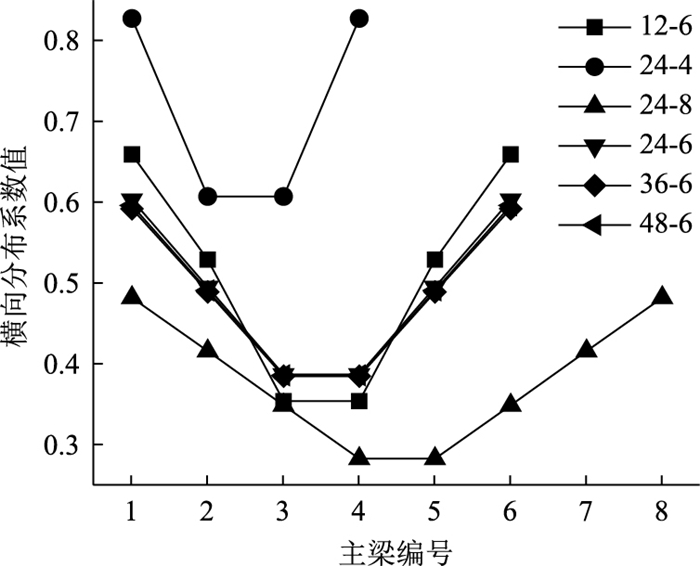
|
| 图 8 修正的刚性横梁法计算结果 Fig. 8 Calculation result by modified rigid transverse girder method |
| |
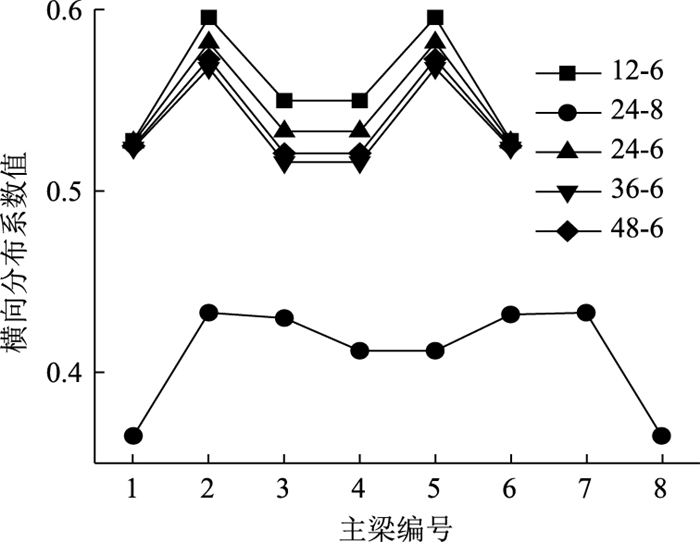
|
| 图 9 铰接梁法计算结果 Fig. 9 Calculation result by hinge-jointed girder method |
| |
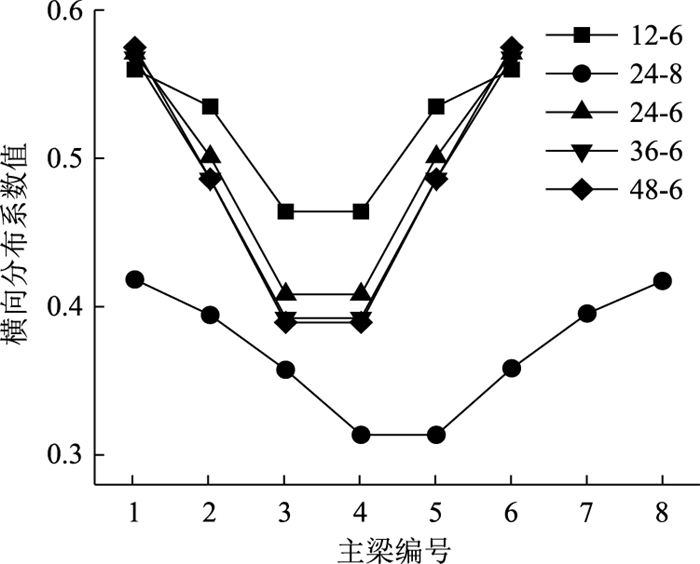
|
| 图 10 刚接梁法计算结果 Fig. 10 Calculation result by rigid-jointed girder method |
| |
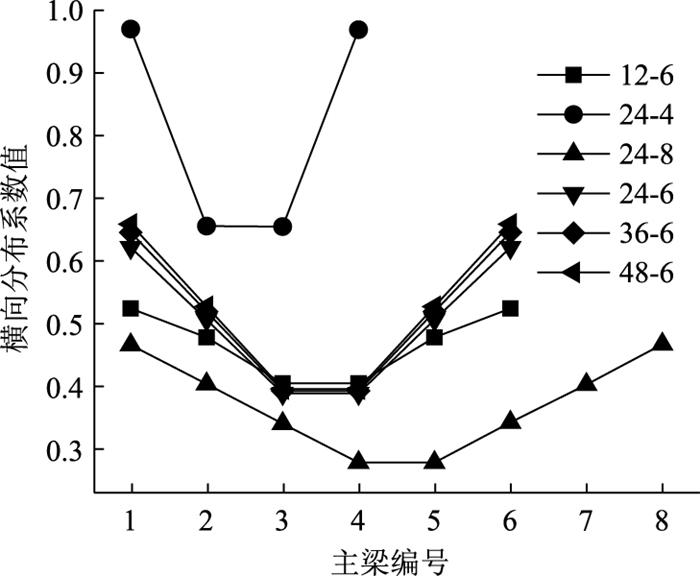
|
| 图 11 G-M法计算结果 Fig. 11 Calculation result by G-M method |
| |
从图 6~图 11中可以看出,采用杠杆原理法和刚性法计算时,由于不涉及主梁截面特性的影响,所以,计算得到的横向分布系数仅与主梁数和主梁间距有关,而与跨径、主梁高度无关。采用修正的刚性横梁法、铰接梁法、刚接梁法、G-M法计算时,随跨径的增大,横向分布系数呈减小趋势;对于24-4桥,由于主梁数少、主梁间距大,换算截面的抗弯惯性矩比抗扭惯性矩大5个数量级,使得采用铰接梁法或刚接梁法计算时,刚度系数求解过大,无法计算。由此可知,铰接梁法和刚接梁法不适用于组合梁换算截面抗扭刚度比抗弯刚度小太多的横向分布系数计算。
3 计算结果对比分析文中6种装配式多主梁钢-混组合梁桥,涉及到的可变参数包括主梁数、主梁间距、跨径、主梁高度;涉及到的计算方法包括杠杆原理法、刚性横梁法、修正的刚性横梁法、铰接梁法、刚接梁法、G-M法等6种理论计算方法和有限元法。为得到该类桥梁横向分布系数计算的一般规律和具体计算公式,本研究将从以下3个方面对计算结果进行比较分析。
3.1 不同计算方法对比相同的桥梁,采用不同的计算方法得到的横向分布系数并不相同,计算结果如图 12~图 17所示。
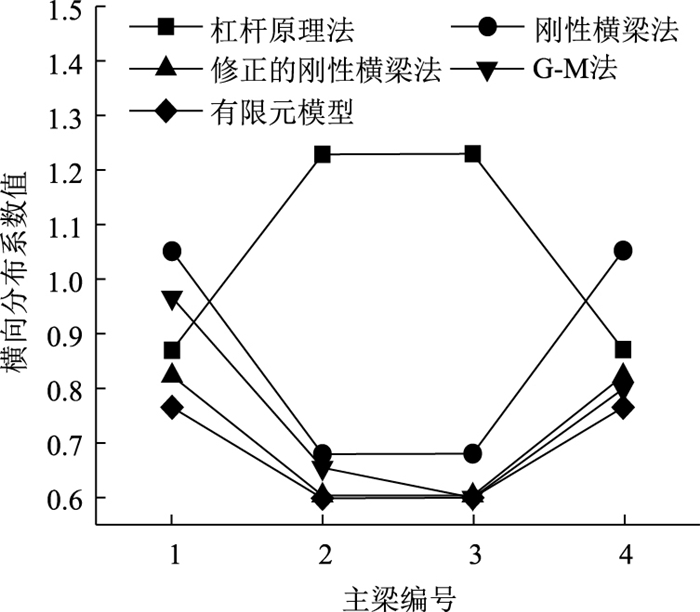
|
| 图 12 24-4计算结果 Fig. 12 Calculation result of type 24-4 |
| |
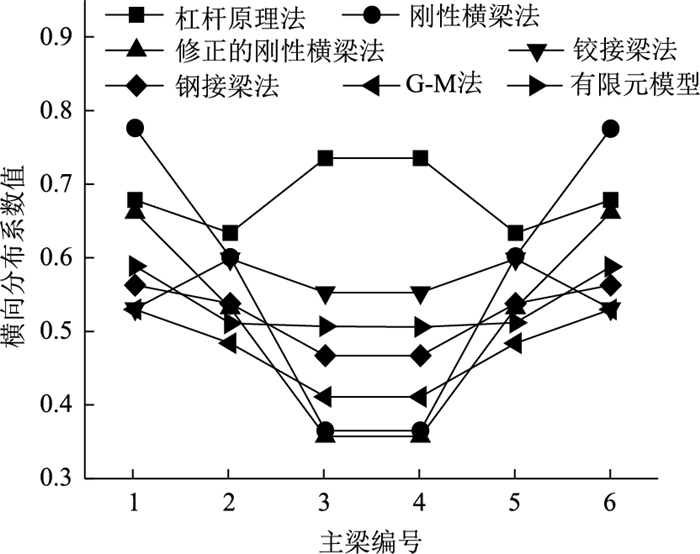
|
| 图 13 12-6计算结果 Fig. 13 Calculation result of type 12-6 |
| |
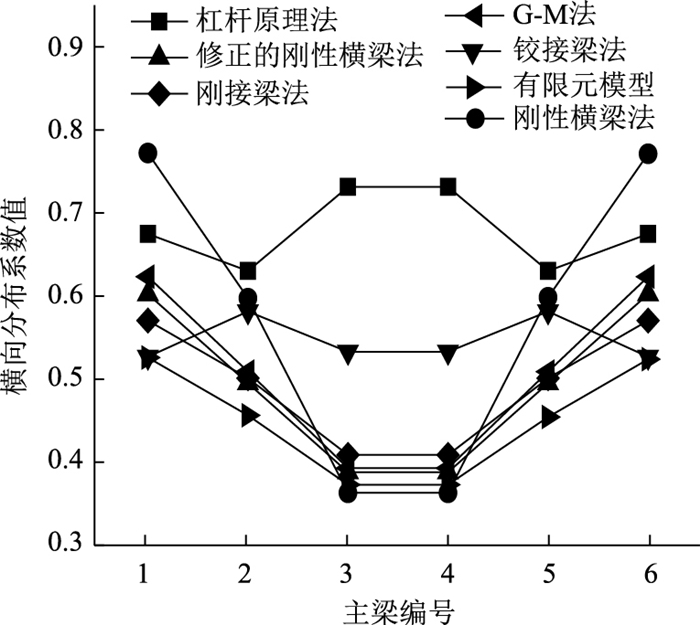
|
| 图 14 24-6计算结果 Fig. 14 Calculation result of type 24-6 |
| |
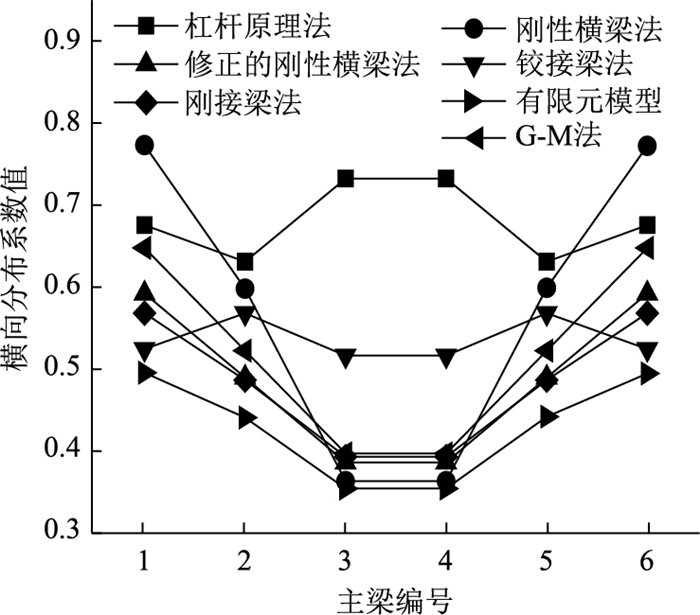
|
| 图 15 36-6计算结果 Fig. 15 Calculation result of type 36-6 |
| |
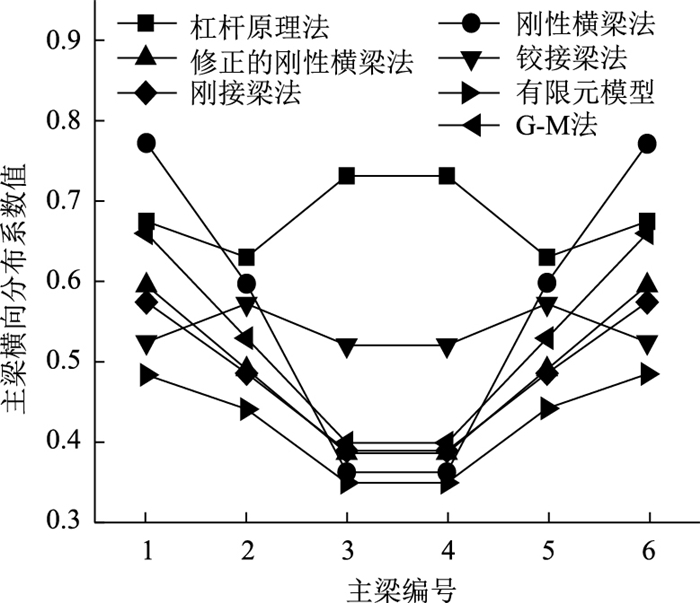
|
| 图 16 48-6计算结果 Fig. 16 Calculation result of type 48-6 |
| |
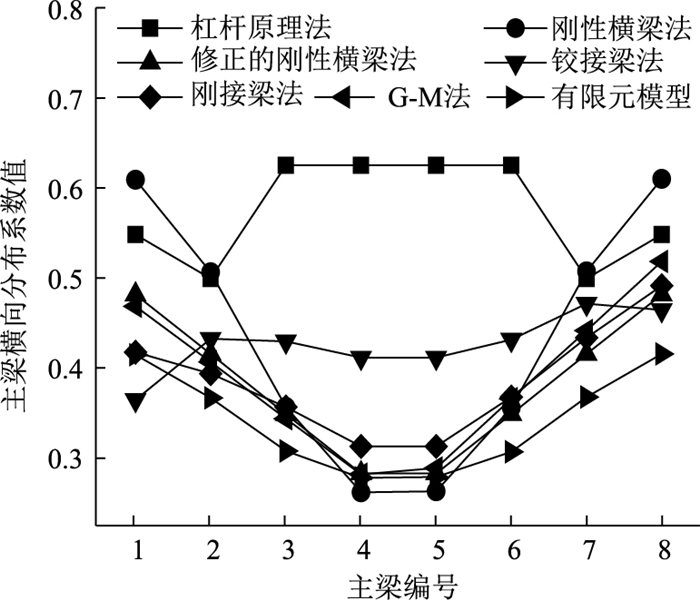
|
| 图 17 24-8计算结果 Fig. 17 Calculation result of type 24-8 |
| |
从图 12~图 17可看出,杠杆原理法和铰接梁法计算得到的横向分布系数不同于其他计算方法计算得到的横向分布系数分布规律,尤其是中梁横向分布系数计算值总是大于其他方法中梁横向分布系数的计算值。由此可见,对于多梁式钢-混组合梁桥的跨中横向分布系数计算,杠杆原理法和铰接梁法不再适用。
刚性横梁法计算得到的边梁横向分布系数总是大于其他方法计算得到的边梁横向分布系数,如48-6桥有限元模型计算值约为刚性横梁法计算值的62.5%,可见,刚性横梁法求解的钢-混组合梁桥的边梁荷载横向分布系数过大,若按此方法进行边梁设计,势必会造成材料的浪费。所以,在装配式多主梁钢-混组合梁桥设计过程中,不建议使用该方法计算荷载横向分布系数。
各计算方法计算得到的横向分布系数,与有限元法计算得到的横向分布系数之间的误差如表 5所示。由于在前面已经证明杠杆原理法和铰接梁法不适用于本研究所述桥型,故表 5对其计算误差不予列出,另外,鉴于横向分布系数的对称性,仅列出横向一半主梁的横向分布系数计算结果。
| 桥型 | 梁号 | ANSYS | 刚性横梁法 | 修正的刚性横梁法 | 刚接梁法 | G-M法 | ||||||||
| 计算值 | 计算值 | 误差/% | 计算值 | 误差/% | 计算值 | 误差/% | 计算值 | 误差/% | ||||||
| 12-6 | 1 | 0.586 | 0.774 | 32 | 0.659 | 12 | 0.560 | 4 | 0.527 | 10 | ||||
| 2 | 0.508 | 0.598 | 18 | 0.529 | 4 | 0.535 | 5 | 0.481 | 5 | |||||
| 3 | 0.504 | 0.362 | 28 | 0.354 | 30 | 0.464 | 8 | 0.408 | 19 | |||||
| 24-8 | 1 | 0.415 | 0.610 | 47 | 0.482 | 16 | 0.418 | 1 | 0.469 | 13 | ||||
| 2 | 0.367 | 0.507 | 38 | 0.416 | 13 | 0.394 | 7 | 0.407 | 11 | |||||
| 3 | 0.308 | 0.357 | 16 | 0.349 | 13 | 0.357 | 16 | 0.344 | 12 | |||||
| 4 | 0.278 | 0.262 | 6 | 0.283 | 2 | 0.313 | 13 | 0.282 | 1 | |||||
| 24-6 | 1 | 0.526 | 0.774 | 47 | 0.603 | 15 | 0.571 | 9 | 0.624 | 19 | ||||
| 2 | 0.456 | 0.598 | 31 | 0.495 | 9 | 0.501 | 10 | 0.509 | 12 | |||||
| 3 | 0.372 | 0.362 | 3 | 0.387 | 4 | 0.408 | 10 | 0.392 | 5 | |||||
| 24-4 | 1 | 0.769 | 1.056 | 37 | 0.827 | 8 | — | — | 0.971 | 26 | ||||
| 2 | 0.602 | 0.683 | 13 | 0.607 | 1 | — | — | 0.658 | 9 | |||||
| 36-6 | 1 | 0.495 | 0.774 | 56 | 0.592 | 20 | 0.568 | 15 | 0.648 | 31 | ||||
| 2 | 0.440 | 0.598 | 36 | 0.489 | 11 | 0.486 | 10 | 0.522 | 19 | |||||
| 3 | 0.353 | 0.362 | 3 | 0.385 | 9 | 0.392 | 11 | 0.396 | 12 | |||||
| 48-6 | 1 | 0.484 | 0.774 | 60 | 0.596 | 23 | 0.575 | 19 | 0.661 | 37 | ||||
| 2 | 0.441 | 0.598 | 36 | 0.491 | 11 | 0.486 | 10 | 0.530 | 20 | |||||
| 3 | 0.349 | 0.362 | 4 | 0.386 | 11 | 0.389 | 11 | 0.399 | 14 | |||||
通过表 5可以看出,12-6桥、24-6桥采用刚接梁法的计算值和有限元法计算值最接近,最大误差分别为-8%和10%;24-8桥、36-6桥和48-6桥采用G-M法计算结果和ANSYS有限元计算值最接近,最大误差分别为13%,15%和19%;24-4桥采用修正的刚性横梁法计算结果和有限元值最接近,最大误差为8%。由此可见,对于多梁式钢-混组合梁桥,当桥梁参数不同时,应该采用不同的横向分布系数计算方法。
建议当宽跨比大于0.5且主梁间距和桥面宽度的比值在0.125~0.28之间时,横向分布系数采用刚接梁法进行计算,尤其当宽跨比大于1时,对计算结果乘以1.08的放大系数;当宽跨比小于0.5或宽跨比大于0.5但主梁间距和桥面宽度的比值小于0.125时,横向分布系数采用G-M法进行计算;当宽跨比大于0.5但主梁间距和桥面宽度的比值大于0.25时,横向分布系数采用修正的刚性横梁法进行计算。
3.2 相同主梁数、不同跨径通过前节的对比分析知,杠杆原理法、铰接梁法和刚性横梁法不适用于文中所述桥梁的横向分布系数计算,故本节只对相同主梁数、不同跨径的桥梁通过修正的刚性横梁法、刚接梁法、G-M法、有限元法计算值进行对比分析,对比结果如图 18~图 21所示。
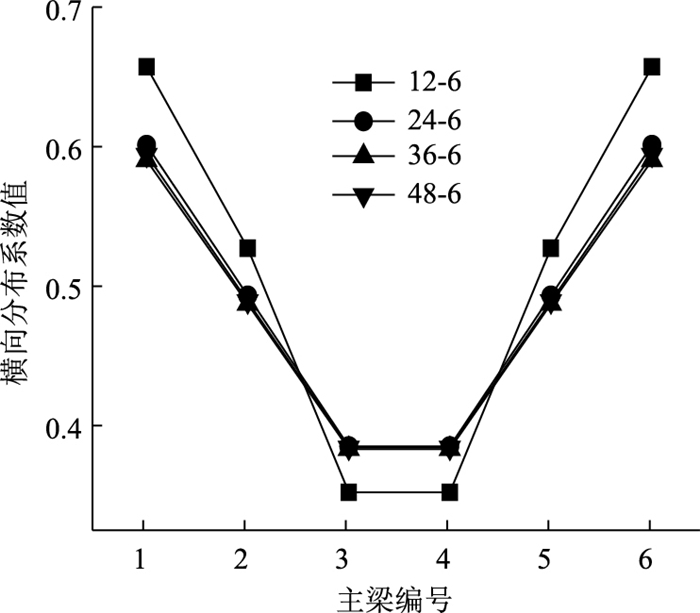
|
| 图 18 修正的刚性横梁法计算结果 Fig. 18 Calculation result by modified rigid transverse girder method |
| |
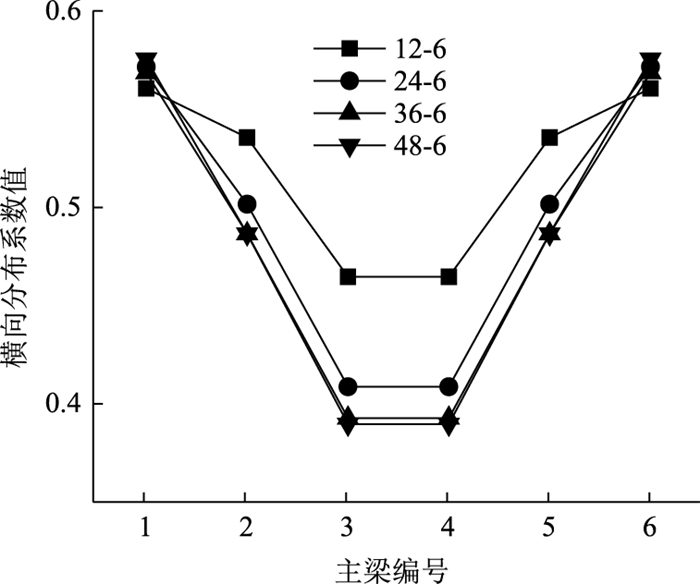
|
| 图 19 刚接梁法计算结果图 Fig. 19 Calculation result by rigid-jointed girder method |
| |
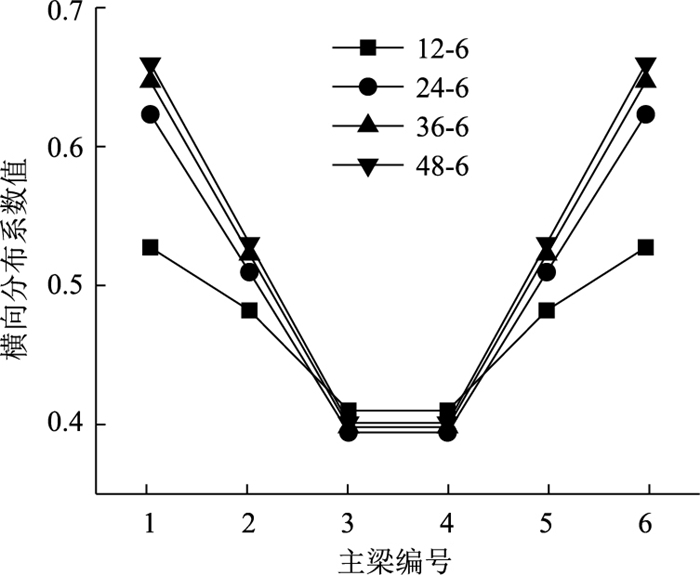
|
| 图 20 G-M法计算结果 Fig. 20 Calculation result by G-M method |
| |
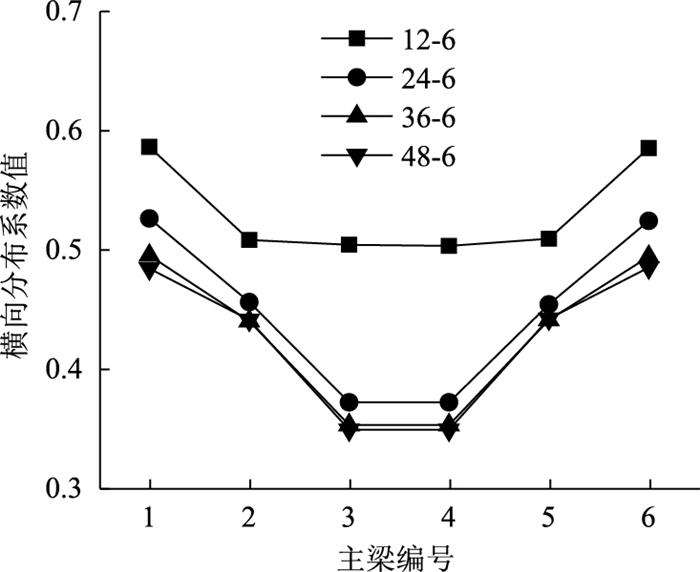
|
| 图 21 有限元模型计算结果图 Fig. 21 Calculation result by finite element model |
| |
从图 18~图 21可以看出,钢-混组合梁桥的宽跨比不同时,采用相同计算方法获得的横向分布系数不同。当宽跨比小于0.5时,对横向分布系数计算结果的影响较小,如12-6桥与48-6桥中梁使用有限元模型计算的结果相差22%,而36-6桥与48-6桥中梁使用有限元模型计算的结果只差0.01%。因此,钢主梁的跨径对多梁式钢-混桥梁的影响取决于宽跨比,当宽跨比越大,计算的各主梁横向分布系数越大。另外,主梁高度的变化也会对计算结果造成很大的影响,故12-6桥与48-6桥的横向分布系数值的差别也是主梁高度变化引起的。
3.3 公式拟合在桥面宽度一定的情况下,跨径、主梁数等对横向分布均有影响,其和横向分布系数的相关性如表 6所示, 其中,相关系数采用式(3)计算。
| 项目 | 跨径L | 主梁数n | I/It | 主梁高h |
| 相关系数 | -0.260 1 | -0.779 6 | 0.694 7 | -0.270 3 |
注:I/It为主梁换算截面抗弯惯性矩和抗扭惯性矩的比值。
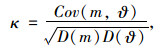
|
(3) |
式中,m为荷载横向分布系数;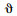
从表 6可以看出,对横向分布系数影响最大的是主梁数,随着主梁数的增多,横向分布系数减小;对横向分布系数影响最小的是跨径,随着跨径的增大,横向分布系数亦呈减小趋势;钢-混组合梁换算截面抗弯和抗扭惯性矩的比值与横向分布系数呈正相关。
通过对本研究中6个有限元模型计算值进行曲线拟合,引入影响钢-混组合梁桥横向分布系数的相关参数,对装配式多主梁钢-混组合梁桥的荷载横向分布系数计算公式使用数值回归的方法进行拟合,得到的简化计算公式如式(4)所示。式(3)计算值与ANSYS计算值误差如表 7所示。
| 桥型 | 梁号 | ANSYS计算值 | 式(3)计算值 | 误差/% |
| 12-6 | 1 | 0.586 | 0.537 | 8 |
| 2 | 0.508 | 0.521 | 3 | |
| 3 | 0.504 | 0.488 | 3 | |
| 24-8 | 1 | 0.415 | 0.403 | 3 |
| 2 | 0.367 | 0.382 | 4 | |
| 3 | 0.308 | 0.353 | 14 | |
| 4 | 0.278 | 0.297 | 7 | |
| 24-6 | 1 | 0.526 | 0.467 | 11 |
| 2 | 0.456 | 0.453 | 1 | |
| 3 | 0.372 | 0.424 | 14 | |
| 24-4 | 1 | 0.769 | 0.742 | 3 |
| 2 | 0.602 | 0.694 | 14 | |
| 36-6 | 1 | 0.495 | 0.439 | 11 |
| 2 | 0.440 | 0.426 | 3 | |
| 3 | 0.353 | 0.399 | 13 | |
| 48-6 | 1 | 0.484 | 0.419 | 13 |
| 2 | 0.441 | 0.406 | 8 | |
| 3 | 0.349 | 0.381 | 9 |
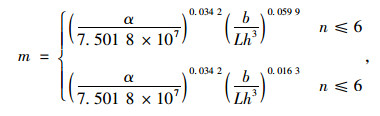
|
(4) |
式中,m为荷载横向分布系数;α为换算截面抗弯惯性矩和抗扭惯性矩的比值;b为主梁到桥面中心的距离;L为桥梁跨径;h为主梁高度;n为主梁数。
从表 7可以看出,式(3)计算值与ANSYS计算值间的最大误差为14%,计算误差均在15%以内。可见,式(3)计算值与ANSYS计算值吻合良好,能够满足主梁为钢板梁的装配式多主梁钢-混组合梁桥的荷载横向分布系数的计算,可为此类桥梁的工程设计提供参考依据。
4 结论(1) 杠杆原理法和铰接梁法计算误差较大,不适用于计算装配式多主梁钢-混组合梁桥的跨中荷载横向分布系数。
(2) 刚性横梁法计算的边梁横向分布系数值偏大(约30%),不适用于计算装配式多主梁钢-混组合梁桥的荷载横向分布系数。
(3) 当宽跨比大于0.5且主梁间距和桥面宽度的比值在0.125~0.28之间时,横向分布系数宜采用刚接梁法进行计算;当宽跨比小于0.5或宽跨比大于0.5且主梁间距和桥面宽度的比值小于0.125时,横向分布系数宜采用G-M法进行计算;当宽跨比大于0.5但主梁间距和桥面宽度的比值大于0.25时,横向分布系数宜采用修正的刚性横梁法进行计算。
(4) 拟合的简化计算公式可用于主梁为钢板梁的装配式多主梁钢-混组合梁桥的荷载横向分布系数计算。
| [1] |
刘永健, 高诣民, 周绪红, 等. 中小跨径钢-混凝土组合梁桥技术经济性分析[J]. 中国公路学报, 2017, 30(3): 1-13. LIU Yong-jian, GAO Yi-min, ZHOU Xu-hong, et al. Technical and Economic Analysis in Steel-concrete Composite Girder Bridges with Small and Medium Span[J]. China Journal of Highway and Transport, 2017, 30(3): 1-13. |
| [2] |
田山坡. 钢混组合梁剪力连接件的计算方法研究[J]. 铁道工程学报, 2014, 31(8): 56-61. TIAN Shan-po. Research on the Calculation of Shear Connector of Steel Concrete Composite Beam[J]. Journal of Railway Engineering Society, 2014, 31(8): 56-61. |
| [3] |
马磊, 章勇, 万水, 等. 单箱多室波形钢腹板PC组合箱梁荷载横向分布[J]. 长安大学学报:自然科学版, 2017, 37(1): 85-92. MA Lei, ZHANG Yong, WAN Shui, et al. Load Transverse Distribution of Single Box Multi-cell PC Composite Girder with Corrugated Steel Webs[J]. Journal of Chang'an University:Natural Science Edition, 2017, 37(1): 85-92. |
| [4] |
战家旺, 高胜星, 闫宇智, 等. 基于模型修正的公路简支板梁桥荷载横向分布系数计算方法[J]. 中国公路学报, 2019, 32(5): 72-79. ZHAN Jia-wang, GAO Sheng-xing, YAN Yu-zhi, et al. A Calculation Method for Transverse Load Distribution Coefficient of Highway Simply-supported Slab-girder Bridges Based on Model Updating[J]. China Journal of Highway and Transport, 2019, 32(5): 72-79. |
| [5] |
聂建国, 张晓光, 樊健生, 等. 钢-混凝土组合梁加宽混凝土梁桥的横向分布系数[J]. 清华大学学报:自然科学版, 2010, 50(6): 805-809. NIE Jian-guo, ZHANG Xiao-guang, FAN Jian-sheng, et al. Transverse Distribution Coefficient of Concrete Bridges Widened with Steel-concrete Composite Beams[J]. Journal of Tsinghua University:Science and Technology Edition, 2010, 50(6): 805-809. |
| [6] |
KIM Y J, TANOVIC R, WIGHT R G. A Parametric Study and Rating of Steel I-girder Bridges Subjected to Military Load Classification Trucks[J]. Engineering Structures, 2013, 56: 709-720. |
| [7] |
KIM Y J, TANOVIC R, WIGHT R G. Load Configuration and Lateral Distribution of NATO Wheeled Military Trucks for Steel I-girder Bridges[J]. Journal of Bridge Engineering, 2010, 15(6): 740-748. |
| [8] |
TABSH S W, TABATABAI M. Live Load Distribution in Girder Bridges Subject to Oversized Trucks[J]. Journal of Bridge Engineering, 2001, 6(1): 9-16. |
| [9] |
GOODRICH B L, PUCKETT A J. Simplified Load Distribution for Vehicles with Nonstandard Axle Gauges[J]. Transportation Research Record, 2000, 1696: 158-170. |
| [10] |
MOHSENI I, RASHID A K A, KANG J. Effect of Intermediate Diaphragm on Lateral Load Distribution Factor of Multicell Box-girder Bridges[J]. KSCE Journal of Civil Engineering, 2014, 18(7): 2128-2137. |
| [11] |
钱若霖, 苏佩, 邬晓光. 考虑畸变变位的多梁式小箱梁桥横向分布计算[J]. 铁道科学与工程学报, 2018, 15(9): 2270-2275. QIAN Ruo-lin, SU Pei, WU Xiao-guang. Calculation Method of Transverse Distribution of Multi-beam Small Box Girder Bridge with Distorted Displacement[J]. Journal of Railway Science and Engineering, 2018, 15(9): 2270-2275. |
| [12] |
李瑞琪, 袁万城, 高康, 等. 装配式简支钢-混组合小箱梁桥荷载向分布系数的研究[J]. 结构工程师, 2015, 31(4): 54-59. LI Rui-qi, YUAN Wan-cheng, GAO Kang, et al. The Analysis of the Transverse Distribution Coefficient of the Simply Supported Fabricated Steel-concrete Composite Girder Bridge[J]. Structural Engineers, 2015, 31(4): 54-59. |
| [13] |
项贻强, 邢骋, 邵林海, 等. 横向加固空心板梁桥荷载横向分布计算方法与试验研究[J]. 中国公路学报, 2013, 26(2): 63-68, 76. XIANG Yi-qiang, XING Cheng, SHAO Lin-hai, et al. Calculating Method and Experimental Research on Lateral Load Distribution of Transversely Strengthened Hollow Slab Bridge[J]. China Journal of Highway and Transport, 2013, 26(2): 63-68, 76. |
| [14] |
魏志刚, 刘寒冰, 时成林, 等. 考虑桥面铺装作用的简支梁桥横向分布系数计算[J]. 吉林大学学报:工学版, 2018, 48(1): 105-112. WEI Zhi-gang, LIU Han-bing, SHI Cheng-lin, et al. Calculation of Transverse Distribution Coefficient of Simply Supported Beam Bridge with Effect of Bridge Deck Pavement[J]. Journal of Jilin University:Engineering and Technology Edition, 2018, 48(1): 105-112. |
| [15] |
聂瑞锋, 石雪飞, 阮欣, 等. 在役多车道空心板梁桥弯矩横向分布系数计算方法研究[J]. 桥梁建设, 2014, 44(2): 56-60. NIE Rui-feng, SHI Xue-fei, RUAN Xin, et al. Research of Calculation Method for Moment Lateral Distribution Factors of Multi-Lane Hollow Slab Beam Bridges in Service[J]. Bridge Construction, 2014, 44(2): 56-60. |
| [16] |
邬晓光, 钱若霖, 苏佩. 考虑刚度损伤的装配式T梁桥横向分布计算[J]. 公路交通科技, 2018, 35(6): 61-66. WU Xiao-guang, QIAN Ruo-lin, SU Pei. Calculation of Transverse Distribution of Assembled T-beam Bridge Considering Stiffness Damage[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 61-66. |
| [17] |
李院军, 邬晓光, 黄成, 等. 考虑主梁损伤的装配式梁桥荷载横向分布系数计算[J]. 铁道科学与工程学报, 2019, 16(6): 1459-1465. LI Yuan-jun, WU Xiao-guang, HUANG Cheng, et al. Calculation of Transverse Load Distribution Coefficient of Assembled Girder Bridge Considering Main Girder Damage[J]. Journal of Railway Science and Engineering, 2019, 16(6): 1459-1465. |
| [18] |
JTG D64-2015, 公路钢结构桥梁设计规范[S]. JTG D64-2015, Specifications for Design of Highway Steel Bridge[S]. |
 2020, Vol. 37
2020, Vol. 37

 ,
,