扩展功能
文章信息
- 郝丽, 郝新军, 胡大伟, 李晨
- HAO Li, HAO Xin-jun, HU Da-wei, LI Chen
- 基于T-JIT理论背景下的双渠道供应链协同风险优化研究
- Study on Cooperative Risk Optimization of Dual-channel Supply Chain Based on Background of T-JIT theory
- 公路交通科技, 2020, 37(2): 146-158
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(2): 146-158
- 10.3969/j.issn.1002-0268.2020.02.019
-
文章历史
- 收稿日期: 2018-01-02
2. 长安大学 汽车学院, 陕西 西安 710064;
3. 山东交通学院 汽车工程学院, 山东 济南 250357
2. School of Automobile, Chang'an University, Xi'an Shaanxi 710064, China;
3. School of Automobile Engineering, Shandong Jiaotong University, Jinan Shandong 250357, China
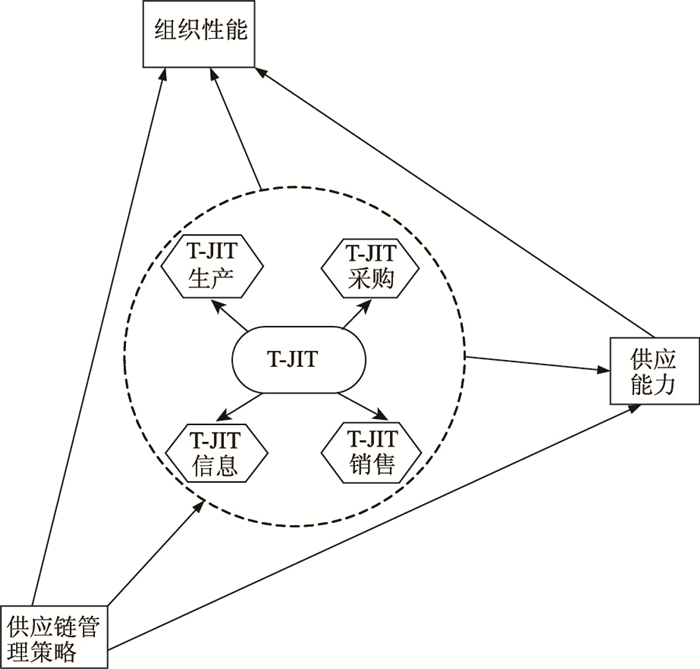
随着“大数据、云计算、区块链、人工智能、互联网+”等先进信息科技的发展,物流行业的发展空前高涨,第三产业的比重也在持续增加,而物流行业也在朝着数字物流方向发展。Kenneth首次提出Total Just In Time(T-JIT)的理论,其概念突显了当代数字化供应链的新领域,T-JIT理论的创新之处在于把传统的3个JIT即JIT生产、JIT采购、JIT销售变成4个JIT的概念,即新增加了JIT信息,主要集成考虑其在上述4个JIT理论融合的过程中对整个供应链管理策略的影响[1],其理论结构如图 1所示。目前双渠道供应链的网络化、信息化是物流4.0时代的新趋势,即传统企业的营销模式与网络直销渠道如何平衡线上、线下协同,同时对双渠道供应链协同机制的研究既是机遇又是挑战。挑战在于双渠道供应链无论哪个环节的信息共享率和风险弹性受到波动,直接造成整个供应链物流、信息流、资金流、人流的动态链接中断的可能,无法实现价值链的增值。风险管理与协同管理的柔和形成了供应链管理的核心,也是其价值增值过程的源泉。考虑T-JIT理论背景下双渠道供应链如何通过有效的合作来降低风险,解决双渠道供应链协同管理的风险评价优化问题已经成为学术界研究的热点,该研究可进一步完善供应链协同风险管理理论体系。为了保证网络化、信息化的双渠道供应链协调发展,首先需对双渠道供应链协同的风险管理进行研究,国内外学者已经做了有意义的探讨。
|
| 图 1 T-JIT理论模型 Fig. 1 T-JIT theoretical model |
| |
20世纪90年代末,B2B、B2C等电子商务的兴起促使国外专家对双渠道供应链的协同风险的研究比较重视,主要表现为Y.Li等提出一个风险预警和实践控制系统的框架结构来研究食品供应链网络中的应用问题[2]。Gang Li等创新性地从一个整体机构和协同视角研究集成的供应链风险管理[3]。Frank Wiengarten等研究了供应链整体集成系统,即考虑风险、风险管理实践来集成整个供应链并进行有效管理[4]。MihalisGiannakis等从绿色供应链独特的视角下研究供应链的可持续发展,研究方法主要是供应链风险管理方法[5]。Tsan-Ming Choi等从中断风险管理、运营中风险控制、灾难和突发事件的管理、物流服务风险分析这几个方面对整个供应链系统风险进行研究,体现整体协同的管理思想[6]。AndraBadea基于供应链管理实践,应用层次分析法研究影响供应链的两个协同概念(水平和垂直)对整个供应链的风险的影响[7]。Fang Zhang等研究了在考虑服务价值的双渠道供应链下灵活的价格策略和协调问题[8]。
国内主要侧重于单独对供应链协同管理、风险管理进行理论和方法的创新研究,但是考虑风险与协同融合概念下整体供应链的协同风险管理研究还比较少。主要代表是李真通过统计方法分析对影响供应链风险预警指标体系进行评估[9]。李艳萍侧重于可持续供应链的角度对广西传统制造业供应链风险管理与对策进行研究[10]。程国平研究了生产-库存系统、库存-分销系统和生产-分销系统的协同,提出了一种合理划分协同利润的方法[11]。方忠民对契约合作与信息共享的供应链协同进行研究[12]。郑庆华研究了林业绿色供应链物流的一体化管理的物流特点[13]。董珊珊等对绿色供应链协同问题进行综述研究,提高整条供应链的效率[14]。温磊主要侧重于供应链协同管理方法上的创新,主要是运筹学和模糊数学理论的结合下进行方法创新[15]。许民利等探讨了在不同风险偏好下双渠道供应链定价决策问题[16]。徐琪等研究了双渠道供应链库存协调合作策略[17]。
综上所述,学者们侧重于对供应链风险评估和控制机制进行研究,还没有学者以T-JIT为背景对双渠道供应链线上、线下如何协同管理进行风险优化研究,着重考虑JIT信息对双渠道供应链各节点企业内部的风险优化,达到整体利益最大化的目的。本研究借助数理统计理论、运筹学和博弈理论对双渠道供应链风险指标进行识别,采用因子分析法(FAM)和逼近理想点排序法(TOPSIS)的同时融入模糊数学理论,建立双渠道供应链协同风险的模糊评价模型;同时考虑广告促销因素和信息服务水平因素对双渠道供应链期望利润决策影响,以双渠道供应链各节点企业利益最大化为目标,建立斯坦克伯格博弈模型并用实例和数值仿真验证了该方法和模型的可行性与有效性,同时与已有研究方法进行比较,为双渠道供应链协同风险机制优化研究提供了理论指导和可行的方法借签。
1 双渠道供应链协同风险指标选择指标选取是双渠道供应链协同风险管理的关键,也是保障供应链各节点顺利运营的前提。双渠道供应链节点企业多、地理位置分布广泛、参与环节多注定了其复杂性、广泛性的特点,再加上双渠道供应链自身混合销售渠道的特殊性,决定了双渠道供应链协同管理风险指标划分的复杂性、多样性、个性化的特点。
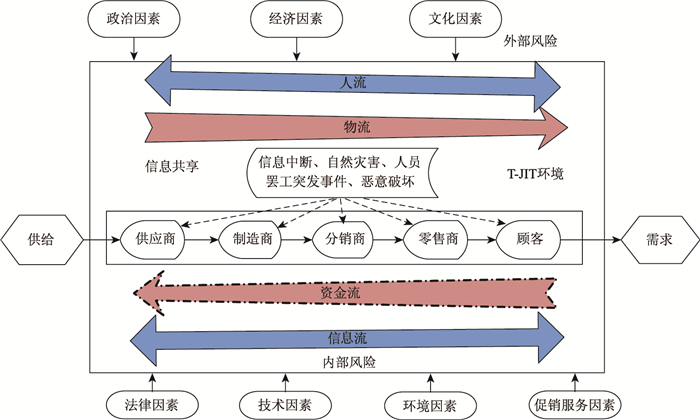
本研究从系统宏观的角度出发,考虑双渠道供应链是一条完整闭合的增值链,其稳定性必然受到供应线上和线下的影响,因此把双渠道供应链链上的协同风险分为内生风险,链下视为外生风险[18-19]。内生风险指供应链系统内部各要素成员之间的交替流动。这类风险主要由缺乏透明性、主导意识淡薄、JIT的不正确应用和预测决策的效率低导致。外生风险指供应链与外部环境的互动风险和人为的促销服务风险,包括信息中断、自然灾害、人员罢工突发事件、恶意破坏广告补贴率降低或中断等造成的损害[1]。上述协同风险影响因素见图 2。
|
| 图 2 双渠道供应链协同风险影响因素 Fig. 2 Influencing factors of collaborative risk in dual-channel supply chain |
| |
根据文献[20-24],得出双渠道供应链协同风险的影响因素如表 1所示:
| 内生风险 | 外生风险 | |||||
| 一级指标 | 二级指标 | 属性 | 一级指标 | 二级指标 | 属性 | |
| 沟通协作风险S1 | 企业间联系渠道拥堵S11 | 定量 | 环境风险S9 | 自热环境S91 | 定性 | |
| 沟通的有效性不足S12 | 定性 | 社会环境S92 | 定性 | |||
| 利益分配风险S2 | 利益分配不均S21 | 定量 | 法律风险S10 | 政治法规符合指数S101 | 定量 | |
| 诚信风险S3 | 供应链人员素质低S31 | 定性 | 法律法规稳定性S102 | 定性 | ||
| 诚信机制不健全S32 | 定性 | 经济风险S11 | 经济体制稳定性S111 | 定性 | ||
| 供应链合同不完备性S33 | 定性 | 行业景气指数S112 | 定量 | |||
| 信息共享风险S4 | 信息真实性S41 | 定性 | GDP增长速度S113 | 定量 | ||
| 信息有效性S42 | 定性 | 市场风险S12 | 供需率S121 | 定量 | ||
| 财务风险S5 | 资金变动风险S51 | 定量 | 汇率波动率S122 | 定量 | ||
| 投融资风险S52 | 定量 | 顾客流失率S123 | 定量 | |||
| 道德风险S6 | 人为破坏风险S61 | 定性 | 市场开发效率S124 | 定量 | ||
| 管理漏洞延迟风险S62 | 定性 | 技术风险S13 | 技术先进性指数S131 | 定量 | ||
| 个人私立主义目标冲突风险S63 | 定性 | 质量合格率S132 | 定量 | |||
| 运营能力风险S7 | 内部资源整合能力S71 | 定量 | 产品替代柔性指数S133 | 定性 | ||
| 总运营成本水平S72 | 定量 | 人文风险S14 | 顾客思想先进性S141 | 定性 | ||
| 最终产品周转率S73 | 定量 | 企业文化差异性S142 | 定性 | |||
| 企业间合作伙伴战略能力S74 | 定性 | 促销服务风险S15 | 制造商广告投入S151 | 定量 | ||
| 管理风险S8 | 交货及时性风险S81 | 定量 | 零售商广告投入S152 | 定量 | ||
| 库存周转率风险S82 | 定量 | |||||
| 人事管理风险S83 | 定性 | |||||
考虑双渠道供应链自身的混合性特征,表 1在前人研究的基础上把原有指标融会贯通并强调人文风险、沟通协作风险、信息共享风险、促销服务风险对双渠道供应链协同的影响,可分15个一级指标和38个二级指标强化双渠道供应链的可靠性和有效性[25],采用梯形直觉模糊数的FAM-TOPSIS法解决双渠道供应链中风险指标优化选择问题,随后对选择的重点指标进行数值模拟分析,对风险管理做出优化决策。
2 梯形直觉模糊数的FAM-TOPSIS多属性评价方法 2.1 梯形直觉模糊数的定义及运算规则定义1 假设X代表某具体运算的一个非空集合,再引入模糊数学的理念,假设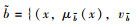

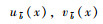
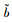
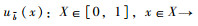
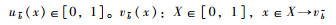
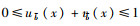
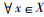
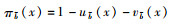
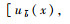
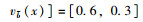
本研究定义梯形模糊数B= < (bm, b1, b2, bn), 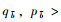
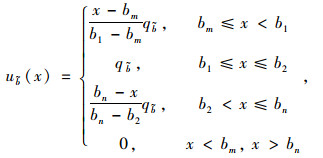
|
(1) |
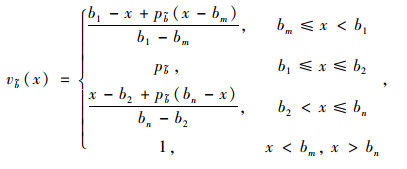
|
(2) |
式中,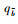
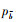
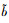
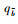
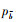
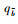
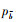
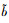
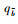
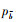
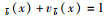
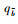
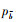
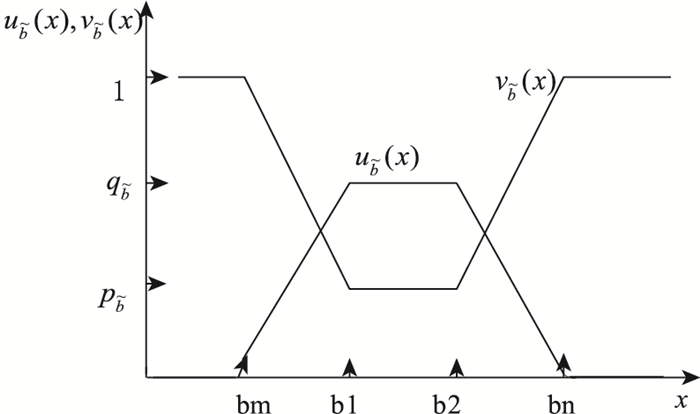
|
| 图 3 梯形直觉模糊数曲线图 Fig. 3 Curves of trapezoidal intuitionistic fuzzy number |
| |
定义2 假设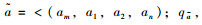
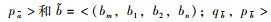
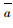
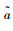
(1) 用梯形直觉模糊数表示的语言值的加法⊕:
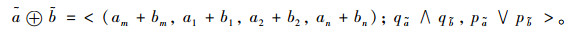
|
(3) |
(2) 用梯形直觉迷糊数表示的语言值的乘法:
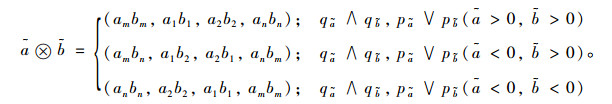
|
(4) |
(3) 用梯形直觉迷糊数表示的语言值的除法÷:
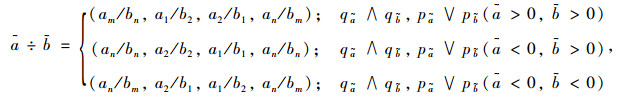
|
(5) |
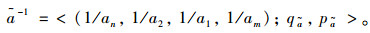
|
(6) |
定义3 [28]假设Ai(i=1, 2, …, n)是一组直觉梯形模糊数集合,w=(w1, w2, …, wn)T是Ai的权重向量,则直觉梯形模糊加权平均算子(TrIFWA)定义为:
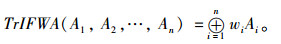
|
(7) |
对于所有i=1, 2, …, n。若wi=1/n,则TrIFWA算子退化为直觉梯形模糊算术平均算子(FrIFA);
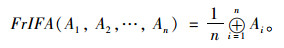
|
(8) |
定义4 梯形直觉模糊数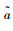
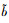
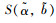
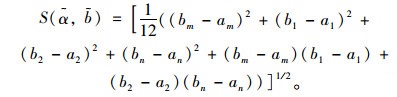
|
(9) |
假设参与评价的方案集为R=[r1, r2, …, rt],有t个评价方案,评价的指标集为U=[u1, u2, …, uk],方案Rt关于属性集Uk的评价值表示为梯形直觉模糊数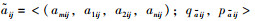
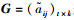
求解步骤如下:
步骤1:对评价指标进行KMO和BARTLETT统计检验,看是否适合做因子分析,确定出主要影响因素和各主导因素的权重Wi[26]。
步骤2:建立梯形直觉模糊数的评价矩阵G。首先需要对决策矩阵G进行规范化的去模糊化处理来消除不同量纲的影响,得到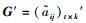
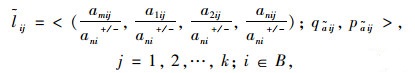
|
(10) |
式中,若B属于效益型属性,anij+=max{anij|j=1, 2, …, k},i属于B;若B属于成本性属性,则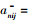
步骤3:按照决策者的偏好信息接近群体的平均偏好程度确定决策者权重,越接近权重越大,反之则越小[30]。假设决策者UK对给出方案Rt上属性Cj的评估值为htj(k)(t=1, 2, …, T; j=1, 2, …, n),则根据(8)求出群体关于方案Rt上属性Cj的偏好均值为h′tj,即
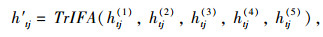
|
(11) |
随后计算h(k)tj与群体平均偏好的相似度:
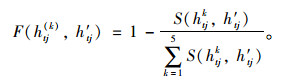
|
(12) |
对每个单属性偏好信息对应的权重计算:
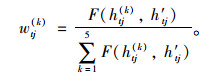
|
(13) |
所有个人决策信息需要集合为群体决策信息,可以采用FrIFWA算子来进行集合
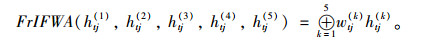
|
(14) |
步骤4:计算加权梯形直觉模糊数的决策矩阵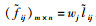
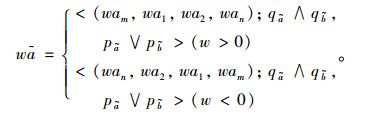
|
(15) |
步骤5:根据规范决策矩阵G定义梯形直觉模糊数的正负理想方案集合为:R+=(f1+, f2+, …, fm+),R-=(f1-, f2-, …, fm-),其中
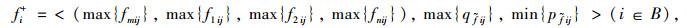
|
(16) |
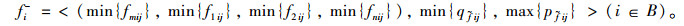
|
(17) |
步骤6:计算各个方案Rt∈R与梯形直觉模糊正负理想方案的相对贴近度如下:
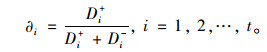
|
(18) |
对各方案进行优劣排序,贴近度越大,得出结果最优。其中,Di+,Di-代表方案Ri与梯形直觉模糊正负理想方案的欧式距离:
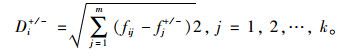
|
(19) |
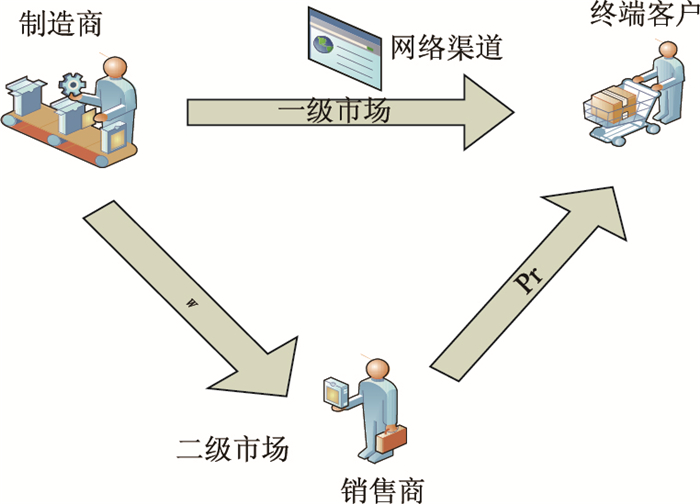
首先本文的研究对象是一个双渠道供应链模式,即随着电子商务、互联网等信息技术支撑的网络直销渠道与传统零售渠道相结合的情况下,采用因子分析法(FAM)和逼近理想点排序法(TOPSIS)的同时融入模糊数学理论,建立了双渠道供应链协同风险的模糊评价模型,对多属性评价指标进行降维处理,解决了双渠道风险协同评价指标融合和评价指标过硬问题;随后把提炼的重要指标选择相关性最高的两个因素来模拟分析其对供应链线上、线下的期望利润的影响;并用算例和仿真验证了该方法和模型的可行性与有效性,为双渠道供应链绩效评价和风险协同优化决策提供了一种可行的方法借签。双渠道供应链运作关系如图 4所示:
|
| 图 4 双渠道供应链运作图 Fig. 4 Operation diagram of dual-channel supply chain |
| |
模型变量符号如下所示:
Em为制造商的期望利润;Er为零售商的期望利润;Esc为协同订货策略下供应链的期望利润;ri、rj分别为网络渠道和销售渠道的单位缺货成本;si、sj分别为网络渠道和销售渠道的单位货品残值;Qj为零售渠道的订货量;di、dj分别为网络渠道和销售渠道的市场需求;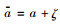
(1) 模型假设
为确保模型构建的意义和现实性,需对模型进行如下假设:
① 假定Em和Er均为正值,这样可以保障双渠道供应链协同管理的定价决策顺利运行。
② 假设网络直销店和传统零售店面对的市场需求为随机变量。
③ 设订货周期的最标准时间为0,同时定义y≤0表示制造商在提前期内按时供货;若y>0表示制造商的延期供货时间。
④ 信息完全共享的及时性与准确性是双渠道供应链整体协同的基本条件。
(2) 模型构建
该模型是在风险规避情况下构建的,为了实现风险协同管理这里主要引入信息共享替代因子c和制造商为零售商承担促销成本比例因子。假设网络渠道的需求比例用θ来表示,则(1-θ)为零售渠道的需求比例;且θ∈(0, 1),c∈(0, 1)。信息共享特征是整个供应链的基本需求,这种情况下提前期重叠产生的风险可以大大降低。为了达到整体供应链共赢的最终目标,渠道之间需要进行合作才能实现最终目标。该模式主要靠引入的两个因子进行调节,即零售商的广告促销的投入的部分成本需要制造商在广告促销中承担,剩余部分补偿给零售商,弥补部分需求转移的损失[17],该损失主要因网络渠道的加入引起的广告促销投入成本分摊比例为f,如若f∈(0, 1)则制造商承担f·k的广告促销费用。供应链双方显示Stackelberg主从博弈,制造商和零售商的利润函数分别为:
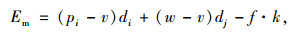
|
(20) |
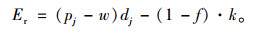
|
(21) |
考虑风险规避态度下的模型构建:
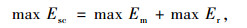
|
(22) |
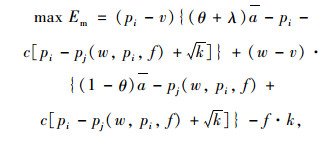
|
(23) |
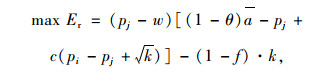
|
(24) |
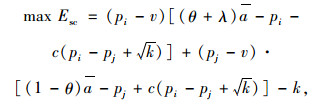
|
(25) |
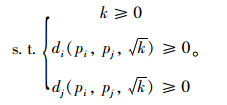
|
(26) |
所有的约束为正,采用逆向归纳法求解,对pi、pj求一阶倒数,令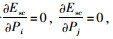
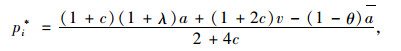
|
(27) |
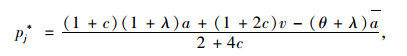
|
(28) |
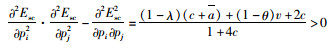
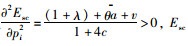
当θ+λ≥1-θ, 即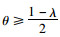
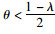
广西某汽车企业从2010年到2017年对网络销售、汽车超市等汽车销售方式不断完善,并开始线上、线下同时销售的情况,以某汽车企业[31]为例,拟定从3个同行企业{H1, H2, H3}中选择一个最佳企业形成供应链协同管理的长期合作联盟。为有效解决评价指标融合问题和指标过硬问题,文章主要聘请了8位专家{M1, M2, M3, M4, M5,M6, M7, M8}组成决策小组,对双渠道供应链的风险指标进行问卷调查。采用梯形直觉模糊数的FAM-TOPSIS法确定双渠道供应链的风险绩效评价指标,并确定出最优合作企业,步骤如下:
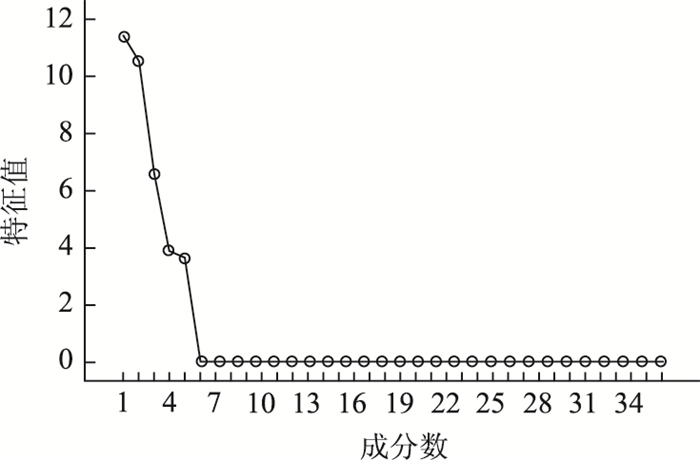
步骤1:采用问卷调查法,分发给8位专家对供应链风险的38个指标进行打分,其中专家团队包括高校学术型专家2位,政府管理型专家2位,企业实际运营型专家2位,供应链典型代表企业专家2位,以10分制为打分原则,对双渠道供应链协同管理影响因素进行分析打分。其中,影响程度很高、较高、一般、较低、低分别代表 9~10分、7~8分、5~6分、3~4分、1~2分;采用FAM法对收集的数据进行分析,首先确定该评价指标适合做因子分析,如表 2和表 3所示;然后提炼出主要影响因素,如图 5所示能提炼出6种主成分。根据因子方差分析运行结果可以得出因子影响程度大到小的顺序排列为K42,K82,K151,K61,K11,K71,且由解释的总方差的相关系数表计算出权重系数W=(0.19,0.174,0.167,0.164,0.17,0.159)。
| 取样足够度的Kaiser-Meyer-Olkin度量 | 0.784 |
| Bartlett的球形度检验近似卡方 | 85.958 |
| df | 17 |
| Sig | 0.005 |
| 成份 | |||||
| 1 | 2 | 3 | 4 | 5 | |
| K42 | 0.963 | 0.023 | 0.157 | 0.258 | -0.083 |
| K82 | 0.939 | -0.122 | 0.213 | -0.243 | 0.130 |
| S81 | 0.913 | 0.107 | 0.045 | 0.413 | 0.114 |
| K151 | 0.911 | 0.074 | 0.145 | 0.175 | 0.111 |
| K92 | 0.891 | -0.373 | -0.192 | -0.075 | 0.116 |
| K61 | 0.875 | -0.207 | 0.106 | -0.432 | 0.025 |
| K91 | 0.874 | -0.282 | 0.061 | 0.391 | -0.133 |
| K71 | 0.849 | 0.375 | 0.340 | -0.018 | -0.045 |
| K113 | 0.806 | -0.339 | -0.074 | 0.061 | 0.494 |
| K152 | 0.790 | -0.302 | -0.005 | -0.095 | 0.275 |
| K112 | 0.783 | -0.205 | 0.021 | -0.196 | -0.536 |
| K41 | 0.725 | 0.553 | 0.230 | 0.247 | 0.230 |
| K51 | 0.676 | 0.615 | -0.328 | 0.280 | -0.050 |
| K111 | 0.647 | -0.189 | -0.582 | -0.141 | -0.416 |
| K102 | -0.339 | -0.856 | -0.162 | 0.182 | -0.279 |
| K62 | -0.023 | 0.869 | -0.132 | -0.056 | 0.498 |
| K11 | -0.519 | 0.856 | -0.036 | 0.079 | 0.153 |
| K32 | 0.021 | 0.816 | -0.416 | -0.162 | -0.363 |
| K133 | 0.035 | 0.789 | 0.092 | 0.428 | -0.449 |
| K123 | 0.027 | -0.757 | 0.126 | -0.488 | 0.395 |
| K122 | -0.226 | -0.739 | 0.131 | 0.425 | 0.464 |
| K74 | 0.494 | 0.757 | -0.177 | 0.114 | 0.413 |
| K12 | 0.580 | 0.675 | 0.434 | -0.220 | 0.043 |
| K83 | 0.385 | 0.671 | 0.279 | -0.555 | -0.166 |
| K63 | 0.263 | 0.076 | -0.890 | 0.285 | 0.226 |
| K33 | -0.033 | 0.521 | 0.822 | 0.221 | -0.176 |
| K132 | 0.080 | 0.637 | -0.733 | -0.047 | 0.226 |
| K21 | 0.510 | 0.307 | -0.725 | 0.267 | -0.224 |
| K142 | -0.138 | -0.087 | 0.713 | 0.698 | -0.072 |
| K101 | 0.374 | -0.522 | -0.669 | 0.186 | -0.275 |
| K52 | 0.131 | -0.610 | 0.686 | 0.157 | -0.322 |
| K72 | 0.401 | 0.622 | 0.633 | 0.274 | 0.065 |
| K121 | 0.592 | -0.526 | 0.599 | 0.134 | 0.026 |
| K73 | 0.548 | -0.357 | -0.531 | 0.427 | 0.362 |
| K31 | 0.233 | 0.602 | 0.160 | -0.695 | -0.271 |
| K141 | -0.304 | 0.612 | 0.138 | 0.712 | -0.178 |
| K124 | -0.569 | 0.451 | 0.044 | 0.012 | 0.694 |
| K131 | 0.575 | -0.159 | 0.393 | -0.184 | 0.694 |
|
| 图 5 碎石图 Fig. 5 Scree plot |
| |
表 2中,KMO值为0.784>0.5,表明变量间的共同因子多,适合做因子分析;Bartlett球体检验显著水平值为0.005 < 0.05,表明变量间存在相关性,适合做因子分析。表 3中可以选择出主要的影响指标K42,K82,K81,K151,K92,K91,K61,K71,而这些二级指标对应一级指标分别为:K4,K8,K15,K9,K6,K7。
步骤2:对选出的主要因素进行梯形直觉模糊数评价,去模糊化结果如表 4所示。
| 专家 | 企业 | 信息风险K42 | 管理风险K82 | 广告促销风险K151 | 道德风险K61 | 沟通协作风险K11 | 运营能力风险K71 |
| H1 | < (2,2,3,4); 0.7,0.2> | < (1,3,4,5); 0.5,0.1> | < (1,4,6,7); 0.6,0.3> | < (1,3,3,5); 0.5,0.3> | < (4,5,7,8); 0.7,0.2> | < (3,5,6,7); 0.7,0.2> | |
| M1 | H2 | < (4,5,6,7); 0.6,0.3> | < (2,3,4,6); 0.6,0.3> | < (3,4,5,9); 0.7,0.2> | < (2,4,6,8); 0.6,0.2> | < (3,5,6,7); 0.8,0.1> | < (3,5,8,9); 0.5,0.4> |
| H3 | < (2,3,6,8); 0.5,0.4> | < (2,3,4,5); 0.8,0.2> | < (2,4,5,7); 0.5,0.4> | < (1,3,5,6); 0.7,0.2> | < (2,4,5,6); 0.6,0.3> | < (2,4,6,8); 0.6,0.1> | |
| H1 | < (3,4,5,8); 0.5,0.4> | < (1,3,4,5); 0.8,0.2> | < (1,2,3,5); 0.6,0.2> | < (1,2,6,7); 0.5,0.4> | < (1,3,6,9); 0.8,0.2> | < (2,5,6,7); 0.7,0.1> | |
| M2 | H2 | < (1,2,2,4); 0.8,0.0> | < (2,4,6,8); 0.5,0.4> | < (2,6,8,9); 0.8,0.1> | < (2,4,6,8); 0.8,0.1> | < (2,3,5,6); 0.7,0.2> | < (3,5,7,8); 0.7,0.2> |
| H3 | < (2,2,5,7); 0.7,0.2> | < (1,2,6,8); 0.6,0.2> | < (3,5,7,8); 0.7,0.2> | < (3,5,6,8); 0.7,0.2> | < (2,4,6,7); 0.8,0.1> | < (1,2,3,7); 0.7,0.2> | |
| H1 | < (4,5,8,9); 0.5,0.2> | < (2,3,6,7); 0.6,0.3> | < (1,2,4,5); 0.7,0.1> | < (2,3,5,7); 0.6,0.3> | < (3,4,5,7); 0.7,0.1> | < (3,5,7,8); 0.8,0.1> | |
| M3 | H2 | < (2,3,3,4); 0.8,0.1> | < (3,5,7,8); 0.7,0.2> | < (3,4,5,7); 0.8,0.1> | < (2,4,6,8); 0.8,0.2> | < (1,3,5,6); 0.8,0.1> | < (2,3,6,7); 0.5,0.4> |
| H3 | < (1,3,4,5); 0.7,0.0> | < (1,4,6,7); 0.5,0.4> | < (2,4,7,8); 0.7,0.2> | < (3,6,7,8); 0.6,0.3> | < (3,4,7,8); 0.8,0.2> | < (3,5,6,9); 0.7,0.2> | |
| H1 | < (3,4,7,8); 0.8,0.1> | < (2,3,6,8); 0.8,0.1> | < (3,6,7,7); 0.6,0.3> | < (2,4,6,7); 0.5,0.3> | < (4,5,7,7); 0.7,0.2> | < (2,4,8,9); 0.6,0.2> | |
| M4 | H2 | < (2,2,3,4); 0.6,0.3> | < (1,2,6,7); 0.6,0.1> | < (4,5,6,9); 0.7,0.2> | < (1,2,5,7); 0.5,0.3> | < (2,4,7,8); 0.8,0.2> | < (4,6,7,9); 0.5,0.3> |
| H3 | < (2,4,6,8); 0.7,0.0> | < (2,6,7,8); 0.7,0.2> | < (1,2,3,5); 0.5,0.3> | < (2,4,6,8); 0.6,0.2 | < (3,4,6,8); 0.7,0.2> | < (3,5,6,7); 0.8,0.1> | |
| H1 | < (5,6,7,8); 0.8,0.1> | < (1,3,4,6); 0.8,0.2> | < (2,4,5,7); 0.7,0.2> | < (2,4,5,6); 0.7,0.1> | < (2,3,7,9); 0.8,0.2> | < (1,3,5,8); 0.5,0.3> | |
| M5 | H2 | < (2,2,3,4); 0.7,0.2> | < (3,5,7,9); 0.5,0.4> | < (3,3,6,7); 0.8,0.2> | < (3,5,7,8); 0.8,0.1> | < (2,4,6,8); 0.7,0.2> | < (2,3,7,8); 0.6,0.3> |
| H3 | < (3,5,6,7); 0.6,0.2> | < (2,4,6,8); 0.7,0.3> | < (3,6,7,8); 0.7,0.2> | < (3,5,7,8); 0.7,0.2> | < (3,6,6,7); 0.8,0.1> | < (3,5,7,8); 0.8,0.2> | |
| H1 | < (2,4,6,7); 0.5,0.4> | < (2,3,5,6); 0.8,0.2> | < (2,3,4,7); 0.6,0.2> | < (2,4,5,7); 0.5,0.4> | < (2,4,7,9); 0.8,0.2> | < (2,4,6,8); 0.7,0.1> | |
| M6 | H2 | < (2,3,3,5); 0.8,0.0> | < (3,5,7,8); 0.5,0.4> | < (3,6,7,9); 0.8,0.1> | < (2,5,7,8); 0.8,0.1> | < (2,5,6,7); 0.7,0.2> | < (3,4,6,9); 0.7,0.2> |
| H3 | < (3,4,5,8); 0.7,0.2> | < (2,3,5,8); 0.6,0.2> | < (3,5,8,9); 0.7,0.2> | < (3,4,7,8); 0.7,0.2> | < (3,5,7,9); 0.8,0.1> | < (2,3,6,8); 0.7,0.2> | |
| H1 | < (4,6,7,9); 0.5,0.2> | < (2,5,8,9); 0.6,0.3> | < (2,4,6,8); 0.7,0.1> | < (2,3,5,7); 0.6,0.3> | < (3,5,7,9); 0.7,0.1> | < (2,5,6,7); 0.8,0.1> | |
| M7 | H2 | < (3,4,5,7); 0.8,0.1> | < (3,5,6,8); 0.7,0.2> | < (3,5,7,9); 0.8,0.1> | < (3,5,7,8); 0.8,0.2> | < (2,5,6,8); 0.8,0.1> | < (3,5,7,8); 0.5,0.4> |
| H3 | < (2,4,6,8); 0.7,0.0> | < (2,4,6,8); 0.5,0.4> | < (3,2,6,7); 0.7,0.2> | < (4,6,8,9); 0.6,0.3> | < (3,5,6,8); 0.8,0.2> | < (3,6,7,9); 0.7,0.2> | |
| H1 | < (3,5,6,7); 0.8,0.1> | < (2,4,7,9); 0.8,0.1> | < (3,5,8,9); 0.6,0.3> | < (2,3,5,7); 0.5,0.3> | < (3,6,8,9); 0.7,0.2> | < (2,5,7,9); 0.6,0.2> | |
| M8 | H2 | < (3,4,5,6); 0.6,0.3> | < (2,3,7,8); 0.6,0.1> | < (4,5,7,9); 0.7,0.2> | < (2,3,4,8); 0.5,0.3> | < (2,3,5,7); 0.8,0.2> | < (4,5,6,8); 0.5,0.3> |
| H3 | < (2,3,7,8); 0.7,0.0> | < (3,5,7,9); 0.7,0.2> | < (3,4,5,7); 0.5,0.3> | < (3,4,5,8); 0.6,0.2 | < (2,4,7,8); 0.7,0.2> | < (3,4,7,8); 0.8,0.1> |
步骤3:计算决策者权重如表 5所示。
| 决策者权重 wk |
指标属性Sj | ||||||
| 企业类型 | 信息风险K42 | 管理风险K82 | 广告促销风险K151 | 道德风险K61 | 沟通协作风险K11 | 运营能力风险K71 | |
| w1 | H1 | 0.165 58 | 0.225 97 | 0.227 01 | 0.204 23 | 0.225 48 | 0.218 05 |
| H2 | 0.145 28 | 0.204 98 | 0.236 35 | 0.229 29 | 0.227 06 | 0.229 01 | |
| H3 | 0.229 52 | 0.185 02 | 0.236 01 | 0.218 93 | 0.179 21 | 0.226 15 | |
| w2 | H1 | 0.288 04 | 0.265 99 | 0.241 04 | 0.264 89 | 0.230 55 | 0.268 32 |
| H2 | 0.251 98 | 0.286 21 | 0.230 21 | 0.210 68 | 0.235 21 | 0.290 52 | |
| H3 | 0.265 42 | 0.231 02 | 0.269 64 | 0.213 12 | 0.267 31 | 0.215 22 | |
| w3 | H1 | 0.271 43 | 0.314 83 | 0.293 03 | 0.333 56 | 0.269 32 | 0.362 45 |
| H2 | 0.292 98 | 0.313 02 | 0.318 34 | 0.318 40 | 0.305 43 | 0.278 53 | |
| H3 | 0.276 02 | 0.341 26 | 0.338 46 | 0.352 05 | 0.251 09 | 0.285 83 | |
| w4 | H1 | 0.394 11 | 0.280 02 | 0.261 00 | 0.414 07 | 0.326 31 | 0.331 25 |
| H2 | 0.344 83 | 0.347 01 | 0.356 21 | 0.337 03 | 0.287 89 | 0.273 21 | |
| H3 | 0.334 33 | 0.287 66 | 0.292 36 | 0.312 05 | 0.369 45 | 0.372 07 | |
| w5 | H1 | 0.321 40 | 0.382 05 | 0.447 12 | 0.263 32 | 0.410 03 | 0.324 21 |
| H2 | 0.400 08 | 0.315 21 | 0.346 98 | 0.373 01 | 0.412 16 | 0.389 57 | |
| H3 | 0.367 06 | 0.417 44 | 0.328 24 | 0.355 68 | 0.398 94 | 0.367 34 | |
| w6 | H1 | 0.321 56 | 0.432 52 | 0.325 46 | 0.367 43 | 0.348 70 | 0.395 45 |
| H2 | 0.345 35 | 0.387 64 | 0.346 78 | 0.325 68 | 0.357 89 | 0.297 65 | |
| H3 | 0.297 84 | 0.313 57 | 0.398 64 | 0.389 32 | 0.297 22 | 0.312 97 | |
| w7 | H1 | 0.493 13 | 0.298 64 | 0.298 63 | 0.434 76 | 0.367 32 | 0.367 83 |
| H2 | 0.365 74 | 0.397 541 | 0.387 53 | 0.359 32 | 0.312 47 | 0.296 23 | |
| H3 | 0.325 67 | 0.382 14 | 0.325 75 | 0.365 42 | 0.396 52 | 0.396 32 | |
| w8 | H1 | 0.388 75 | 0.421 54 | 0.465 75 | 0.374 21 | 0.435 67 | 0.364 32 |
| H2 | 0.487 64 | 0.124 64 | 0.376 53 | 0.423 21 | 0.476 42 | 0.467 32 | |
| H3 | 0.387 95 | 0.367 89 | 0.378 433 | 0.350 14 | 0.401 23 | 0.401 24 | |
步骤4:计算企业之间的加权梯形直觉模糊数的决策矩阵,如表 6所示。
| 企业 | 信息风险K42 | 管理风险K82 | 广告促销风险K151 | 道德风险K61 | 沟通协作风险K11 | 运营能力风险K71 |
| < (H1j | < (5.354, 6.8, 8.8, 12)> | < (2.94, 6, 7.4, 8.10)> | < (2.96, 5.2, 7.3, 9.9)> | < (2.68, 5.6, 8, 9.7)> | < (4.06, 6.5, 8.8, 13)> | < (2.88, 5.4, 8.8, 13)> |
| < (H2j | < (1.92, 3.4, 4.8, 6.3)> | < (3.93, 6.4, 8.4, 12)> | < (4.59, 6.9, 9.3, 14)> | < (2.6, 5.7, 8.5, 14)> | < (2.45, 5.3, 7.2, 14)> | < (3.92, 7.2, 9.3, 15)> |
| < (H3j | < (2.96, 5.3, 7.8, 13)> | < (2.99, 5.4, 7.9, 13)> | < (3.83, 7, 8.4, 13)> | < (3.69, 6.2, 7.6, 9.8)> | < (3.95, 6.4, 7.9, 9.9)> | < (3.6, 5.7, 9, 12)> |
步骤5:得出梯形直觉模糊数的正负理想解如表 7所示。
| R+ | R- |
| < 5.27, 6.91, 9.73, 10.9> | < 1.98, 3.8, 4.85, 6.68> |
| < 3.92, 6.26, 8.28, 15> | < 3.44, 5, 6.3.9, 8.9> |
| < 4.59, 6.77, 9.16, 12.3> | < 2.96, 5.16, 7.07, 8.76> |
| < 3.88, 6.26, 8.48, 16.57> | < 2.60, 5.56, 7.7, 9.68> |
| < 4.06, 6.39, 8.8, 11.9> | < 2.44, 5.3, 7.08, 9.86> |
| < 3.92, 7.2, 9.3, 11.59> | 2.88, 5.32, 7.97, 12.4> |
步骤6:得到备选方案与梯形直觉模糊数的正负理想解的相对贴近度并排序比较如表 8所示。
表 8可以看出H1>H3>H2,则H1是最优的方案。相比已有的多属性决策方法[14],本研究首先应用直觉梯形模糊数表示决策信息,同时采用FAM法对所选指标进行降维处理,选出6个主要一级指标进行计算,减少了计算量;同时在利用模糊数对决策者权重进行确定,把定性的指标定量化处理,在客观刻画决策者权重方面更为精细和准确,减小决策损失;其次利用TOPSIS法比较评价对象与正负理想解的相对贴近程度,对多属性方案进行择优排序,更加真实地反映了决策者对事物的评价和感知。
4.2 期望利润模型求解选择上述两个指标信息共享因素和广告促销服务因素,以双渠道供应链整体利润最大为目标,对上述模型进行仿真计算,得出这两种因素如何影响双渠道供应链线上、线下的协调风险管理。假设该系统是一个由制造商和多个零售商组成的二级市场结构,参考文献[32]各参数为离散数据,其取值范围如下:
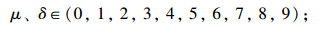
|

|
其中k的值相对选大,能反映促销服务补贴率的重要性。
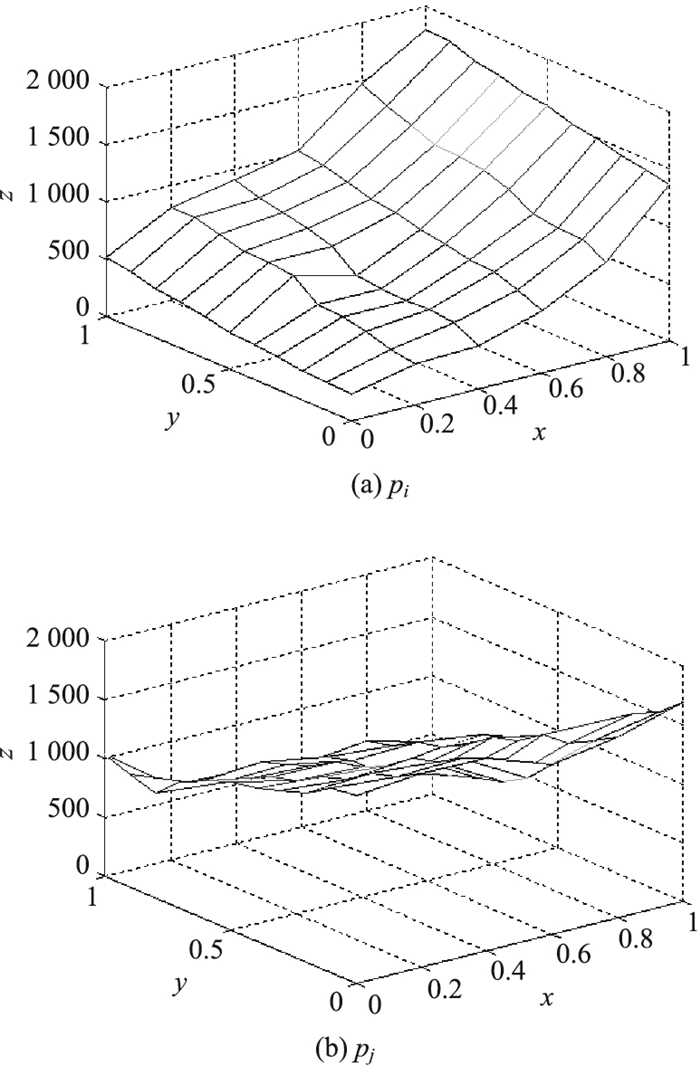
采用Matlab编程对如上期望利润模型进行仿真分析,结果如图 6所示:pi、pj在图(a)、(b)中分别表示z轴,ξ代表图中的y,c代表图中的x。
|
| 图 6 pi和pj随着ξ和c的变化 Fig. 6 pi and pj varying with ξ and c |
| |
pi、pj随着信息共享替代因子c和交货提前期重叠的影响因子ξ的变化而变化,当ξ一定时,pi随着替代因子c的增加而提高,而pj随着ξ和c的增大而降低,并与Pi交会,随着网络渠道客户的增加,零售渠道的客户就是转移到网络渠道,要想实现共赢,零售渠道必须提高售价。相反,pj随着ξ和c的减小而增加。
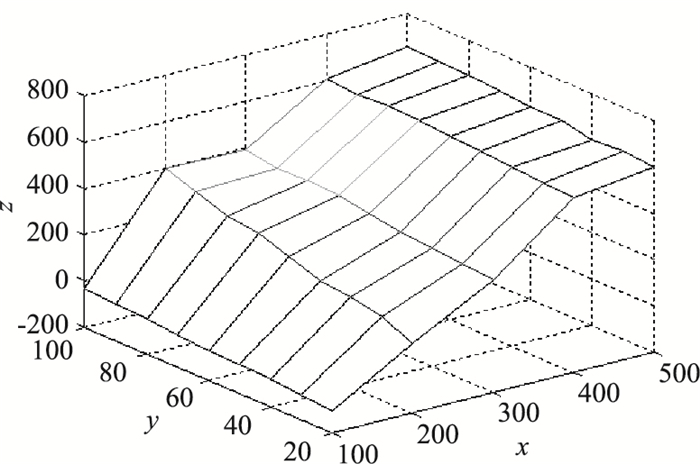
对Qr、g和τ做仿真练习,结果如图 7所示,图中x,y,z轴分别代表τ,g和Qr。
|
| 图 7 Qr随着g和τ的变化 Fig. 7 Qr j varying with g and τ |
| |
图 7可以看出当g不变,Qr随τ的增加而增加;同理当τ不变,Qr随g的增加也在增加,说明可以通过增加订货量来减小波动引起的缺货风险。
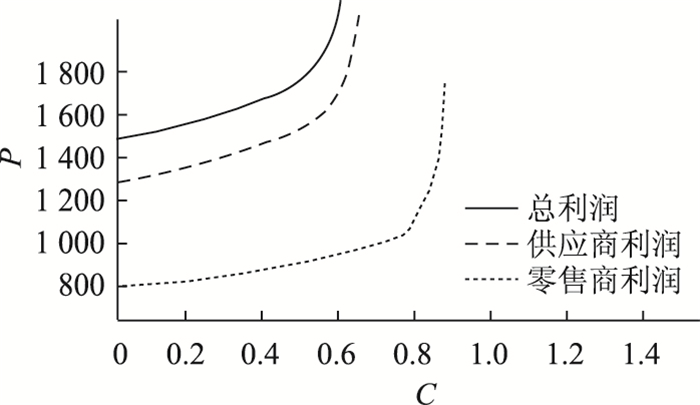
对参数赋值,通过数值仿真来计算出信息共享和广告促销服务因素对零售商、制造商和供应链总利润的影响,如图 8、图 9所示。
|
| 图 8 信息共享因素对供应链利润的影响 Fig. 8 Influence of information sharing factor on supply chain profits |
| |
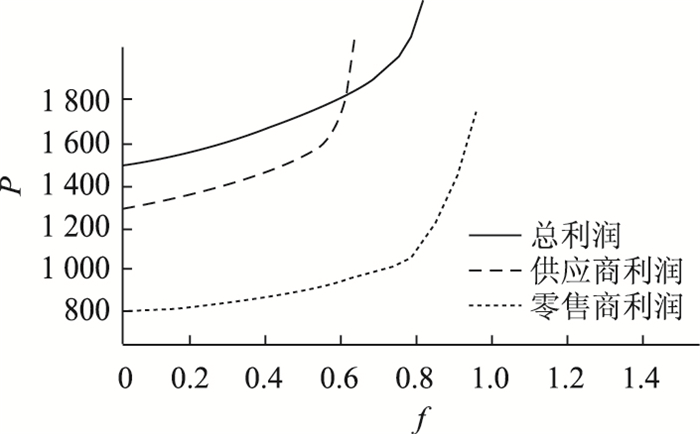
|
| 图 9 广告促销因素对供应链利润的影响 Fig. 9 Influence of advertising promotion factor on supply chain profits |
| |
图 8可以看出随着信息共享替代因子的增加,零售商和制造商的利润会显著增长,且零售商的利润小于制造商的利润;信息共享下的总利润水平都要大于各种的利润。
图 9可以看出随着广告促销投入的增加,零售商、制造商的利润会有所增长,并且零售商的利润总体要小于制造商的利润。因为随着广告投入的增加,产品的批发价格有所减少,制造商的利润就会增加。总体趋势来看,供应商的总利润大于制造商和零售商单独的利润,因此在广告促销投入力度增大时,总的供应链利润水平也会增加。对比图 8可以得出信息共享投入远比广告投入所导致的利润增速快,可见政府部门和各节点企业要增加信息共享投入比例。
5 结论文章对T-JIT环境下双渠道供应链线上、线下的风险协同优化进行研究,首先结合模糊理论提出基于梯形直觉模糊数FAM-TOPSIS的多属性决策评价方法来解决风险评价指标融合困难和权重确定“过硬”问题;同时根据风险评价选出的两个最重要的影响因素,以双渠道整体利益最大化为目标,应用stackelberg博弈理论建立期望利润决策模型,并用仿真与算例分析得出如下结论:
(1) 全面准确地确定出双渠道供应链风险指标影响因素,利用梯形直觉模糊数的FAM法对多属性指标进行降维处理并选择出主要的影响因素和权重,同时用TrIFWA算子和直觉梯形模糊数期望值计算决策者的期望权重。
(2) 引用算例采用TOPSIS法计算梯形直觉模糊正负理想方案的相对贴近度排序,总结出最优的风险控制管理企业,同时可为企业进一步优化风险管理做出正确决策。
(3) 双渠道供应链协同合作整体利润最大化的前提下,信息共享率增强时,制造商和零售商都能提高产品销售量,定价比较透明;当制造商信息共享替代性增强时,制造商会提高定价,零售商会降低售价来吸引顾客,促使利润从制造商流向零售商来达到平衡。
(4) 供应链各主体和政府部门要加强信息共享和广告促销服务的投入比例,才能保证各节点企业整体利润最大化,提高供应链线上、线下物流中断的风险水平。
本研究为不确定风险环境下双渠道供应链企业正确识别、评价和选择供应商提供理论参考和方法借签,在未来研究中,可以综合考虑风险偏好和绿色度偏好程度等因素对供应链风险弹性的影响,进一步研究双渠道绿色供应链的利润和定价决策问题。
| [1] |
郝丽, 胡大伟. 基于BP神经网络和蜂群算法对在T-JIT环境下供应链协同风险的预警研究[J]. 公路交通科技, 2018, 35(6): 112-120. HAO Li, HU Da-wei. Study on Early Warning of Supply Chain Coordination Risk in T-JIT Environment Based on BP Neural Network and Bee Colony Algorithm[J]. Journal of Highway and Transportation Technology, 2018, 35(6): 112-120. |
| [2] |
LI Y, KRAMER M R, BEULENS A J M, et al. A Framework for Early Warning and Proactive Control Systems in Food Supply Chain Network[J]. Computers in Industry, 2010, 61(9): 852-862. |
| [3] |
LI G, FAN H, LEE P K C, et al. Joint Supply Chain Risk Management:An Agency and Collaboration Perspective[J]. International Journal of Production Economics, 2015(164): 83-94. |
| [4] |
WIENGARTEN F, HUMPHREYS P, GIMENEZ C, et al. Risk, Risk Management Practices, and the Success of Supply Chain Integration[J]. International Journal of Production Economics, 2016(171): 361-370. |
| [5] |
GIANNAKIS M, PAPADOPOULOS T. Supply Chain Sustainability:A Risk Management Approach[J]. International Journal of Production Economics, 2016(171): 455-470. |
| [6] |
CHOI T M, CHIU C H, CHAN H K. Risk Management of Logistics Systems[J]. Transportation Research Part E:Logistics and Transportation Review, 2016, 90: 1-6. |
| [7] |
BADEA A, PROSTEAN G, GONCALVES G, et al. Assessing Risk Factors in Collaborative Supply Chain with the Analytic Hierarchy Process[J]. Procedia-Social and Behavioral Sciences, 2014, 124: 114-123. |
| [8] |
ZHANG F, WANG C. Dynamic Pricing Strategy and Coordination in a Dual-channel Supply Chain Considering Service Value[J]. Applied Mathematical Modelling, 2018, 54: 722-742. |
| [9] |
李真.供应链风险预警管理系统研究[D].兰州: 兰州大学, 2008. LI Zhen. Study on Risk Early-warning Management System of Supply Chain[D]. Lanzhou: Lanzhou University, 2008. |
| [10] |
李艳萍.广西传统制造业绿色供应链风险评估与控制对策研究[D].柳州: 广西工学院, 2010. LI Ye-ping. An Analysis on Green Supply Chain Risk's Evaluation and Control Countermeasures of Traditional Manufacturing Industry in Guangxi[D]. Liuzhou: Guangxi Technical College, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10594-2011013033.htm |
| [11] |
程国平.供应链管理中的协同问题研究[D].天津: 天津大学, 2004. CHENG Guo-ping. Research on Coordination Problem in Supply Chain Management[D]. Tianjin: Tianjin University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10056-2004064436.htm |
| [12] |
方忠民.基于契约合作与信息共享的供应链协同研究[D].长沙: 中南大学, 2013. FANG Zhong-min. A Study on Collaborative Supply Chain Based on Contract Cooperation and Information Sharing[D]. Changsha: Central South University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10533-1013358616.htm |
| [13] |
郑庆华.林业绿色供应链的物流一体化管理系统研究[D].南京: 南京林业大学, 2011. ZHEN Qing-hua. Research on Integrated Logistics Management System in Forestry Green Supply Chain[D]. Nanjing: Nanjing Forestry University, 2011. |
| [14] |
董姗姗, 吕律, 陈鑫. 绿色供应链协调问题研究综述[J]. 东方企业文化, 2014(21): 356. DONG Shan-shan, LÜ Lü, CHEN Xin. Research Overview on Coordination of Green Supply Chain[J]. Oriental Enterprise Culture, 2014(21): 356. |
| [15] |
温磊, 赵伟, 王锐. 供应链协同风险评价研究[J]. 物流技术, 2013, 32(1): 218-221. WEN Lei, ZHAO Wei, WANG Rui. Study on Risk Evaluation of Supply Chain Collaboration[J]. Logistics Technology, 2013, 32(1): 218-221. |
| [16] |
许民利, 聂晓哲, 简惠云. 不同风险偏好下双渠道供应链定价决策[J]. 控制与决策, 2016, 31(1): 91-98. XU Min-li, NIE Xiao-zhe, JIAN Hui-yun. Pricing Decision of Dual-channel Supply Chain with Risk Preference[J]. Control and Decision, 2016, 31(1): 91-98. |
| [17] |
刘峥, 徐琪. 考虑风险态度的双渠道供应链协同优化决策[J]. 东华大学学报:自然科学版, 2016, 42(1): 98-103. LIU Zheng, XU Qi. Dual-channel Supply Chain Collaborative Optimal Strategies Based on Risk Attitudes[J]. Journal of Donghua University:Natural Science Edition, 2016, 42(1): 98-103. |
| [18] |
邱洪全. 生鲜农产品双渠道供应链协同创新对物流服务绩效的影响[J]. 中国流通经济, 2017, 31(9): 22-30. QIU Hong-quan. Study on the Effect of Cooperative Innovation on the Performance of Logistics Service in the Double-channel Supply Chain of Fresh Agricultural Products[J]. China Business and Market, 2017, 31(9): 22-30. |
| [19] |
郝丽, 胡大伟, 李晨. T-JIT环境下企业供应链中采购管理供应商选择和订单分配[J]. 公路交通科技, 2018, 35(1): 149-158. HAO Li, HU Da-wei, LI Chen. Supplier Selection and Order Allocation of Purchasing Management for Enterprise Supply Chain in T-JIT Environment[J]. Journal of Highway and Transportation Technology, 2018, 35(1): 149-158. |
| [20] |
张韦唯, 李舒颖. 汽车供应链协同管理绩效评价研究综述[J]. 中国管理信息化, 2017, 20(21): 89-91. ZHANG Wei-wei, LI Shu-ying. Summary of Research on Performance Evaluation of Automobile Supply Chain Collaborative Management[J]. China Management Informationization, 2017, 20(21): 89-91. |
| [21] |
黄晓霞.多主体协同创新项目治理绩效评价研究[D].济南: 山东大学, 2016. HUANG Xiao-xia. Research on Governance Performance Evaluation of Multi-agent Collaborative Innovation Project[D]. Jinan: Shandong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10422-1017001660.htm |
| [22] |
苏乐天, 杜栋. 协同管理研究综述与展望[J]. 科技管理研究, 2015, 35(24): 198-202. SU Le-tian, DU dong. A Review and Prospect on the Research of Collaborative Management[J]. Science and Technology Management Research, 2015, 35(24): 198-202. |
| [23] |
邱建华.企业技术协同创新的运行机制及绩效研究[D].长沙: 中南大学, 2013. QIU Jian-hua. Research on Operation Mechanism and Performance of Enterprise Technology Collaborative Innovation[D]. Changsha: Central South University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10533-1013358662.htm |
| [24] |
孙清华.基于价值网的汽车供应链协同管理研究[D].北京: 北京交通大学, 2010. SUN Qing-hua. Research on Collaborative Management of Automobile Supply Chain Based on Value Network[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10004-2010115595.htm |
| [25] |
郝丽, 李晓霞. 缺陷汽车产品召回管理预警体系研究[J]. 物流科技, 2017, 40(4): 85-90. HAO Li, LI Xiao-xia. Study on Early Warning System of Defective Automobile Product Recall[J]. Logistics Sci-Tech, 2017, 40(4): 85-90. |
| [26] |
周晓辉, 姚俭, 吴天魁. 基于梯形直觉模糊数的TOPSIS多属性决策方法[J]. 上海理工大学学报, 2014, 36(3): 281-286. ZHOU Xiao-hui, YAO Jian, WU Tian-kui. Multi-attribute Decision-making Based on Trapezoidal Intuitionistic Fuzzy Numbers TOPSIS Method[J]. Journal of University of Shanghai for Science and Technology, 2014, 36(3): 281-286. |
| [27] |
刘文生, 吴作启, 崔铁军. 基于三角模糊数的AHP-TOPSIS村庄下开采接续方案优选方法研究[J]. 计算机应用研究, 2016, 33(2): 458-461. LIU Wen-sheng, WU Zuo-qi, CUI Tie-jun. Research on Preferred Method of Connecting Mining Village Based on AHP-TOPSIS of Triangular Fuzzy Numbers[J]. Application Research of Computers, 2016, 33(2): 458-461. |
| [28] |
向隅. 基于三角模糊数的TOPSIS评价方法在新建铁路线路选择中的应用[J]. 石家庄铁道大学学报:自然科学版, 2011, 24(2): 56-60. XIANG Yu. Application of TOPSIS Evaluation Method Based on Triangle Fuzzy Number in New Railway Line Selection[J]. Journal of Shijiazhuang Tiedao University:Natural Science Edition, 2011, 24(2): 56-60. |
| [29] |
LI H, HU D W, LAN Z, et al. Study on the Warning System of the Green Degree Supply Chain Based on the FAM-TOPSIS Method[C]//Proceedings of 16th COTA International Conference of Transportation. Reston: American Society of Civil Engineers, 2016: 13-25.
|
| [30] |
王中兴, 谢海斌. 一种基于优势度的直觉梯形模糊数排序方法[J]. 统计与决策, 2011, 18: 27-30. WANG Zhong-xing, XIE Hai-bin. An Intuitionistic Triangular Fuzzy Number Sorting Method Based on Dominance[J]. Statistics and Decision, 2011, 18: 27-30. |
| [31] |
许民利, 聂晓哲, 简惠云. 不同风险偏好下双渠道供应链定价决策[J]. 控制与决策, 2016, 31(1): 91-98. XU Min-li, NIE Xiao-zhe, JIAN Hui-yun. Pricing Decision of Dual-channel Supply Chain with Risk Preference[J]. Control and Decision, 2016, 31(1): 91-98. |
 2020, Vol. 37
2020, Vol. 37

 ,
,