0 引言

近年来随着世界范围内服务经济快速发展，产品服务化和服务外包的不断增长为服务供应链的形成和发展奠定了基础，服务供应链逐渐成为供应链管理研究的新趋势。作为一类典型的服务供应链，物流服务供应链(Logistics Service Supply Chain, LSSC)是由不同层级利益主体物流集成商和能力提供商构成的以“物流提供商→物流集成商→物流用户”为基本结构，通过提供柔性化的物流服务保证产品供应链物流运作的一种新型供应链(刘伟华，2007)。在物流服务供应链中最主要的两种参与企业是物流集成商(综合物流服务的设计者与提供者)与物流提供商(给予物流集成商提供具体的物流功能服务)。物流服务供应链安全可持续运作是实现物流能力高效协调机制的前提，为有效抵御需求风险集成商必须对风险要素合理分析制定并实施有效的防范与应急措施来保障物流服务供应链正常运转。物流需求是指从下游市场服务需求出发进而逆向传递确定物流容量，并传导影响物流服务供应链上游供给的能力决策。需求风险是因市场需求发生变化影响物流用户短期需求出现大幅波动，造成逆向传递效应，产生需求风险。因此为保障供应链整体系统稳定运作，研究物流服务供应链能力需求降低后集成商如何实现物流提供商与服务客户间的平衡优化具有重要意义。较早对供应链需求风险展开研究的是Qi^[2]在Omega上发表的研究论文“Supply Chain Coordination with Demand Disruptions”。此后Cao^[3]建立收益共享契约机制应对需求和生产成本突变情景；Nooraie^[4]利用多属性决策建模来最大化供应链可见度、最小化风险及成本，提供处理不确定需求的供应链管理模型；Govindan^[5]研究需求随机与高时变情况时两阶段供应链网络风险问题，使用不同风险测量方法与极大极小化目标衡量目标风险均值。国内严建援等^[6]对比分析了需求风险由供应链整体承担和需求风险由提供商直接承担两种不同策略下双方的决策及供应链绩效；童泽平等^[7]研究供应链所面临的需求随机性以及供应方的产能限制各参与主体行为选择机理及协同优化的实现路径；柴文龙等^[8]分析突发事件下需求依赖融资利息的资本供应链应急协调问题；珠兰等^[9]研究了不确定情形下的绿色物流网络和库存问题，提出了考虑网络成本和CO₂排放当量的双目标随机规划模型；杜娟等^[10]基于需求和汇率风险下全球二级供应链，分别建立并求解了制造商对冲/不对冲汇率风险两种情形下的模型均衡。供应链高效运作需要内在因素与外在因素的相互结合共同作用，上述研究针对产品供应链中需求风险问题进行深入探讨，得出需求风险对供应链可持续运作具有重要影响，并给出实现供应链协调决策措施。但由于物流服务供应链自身特性产品供应链的优化协调过程及结论无法简单应用，需要针对物流服务供应链需求风险问题的复杂特点提出有效应对措施。

供应链特别是收益明显的核心企业有必要在需求下降风险阶段针对成员企业给予适当补贴实现供应链短期均衡，保障供应链需求风险阶段安全过渡，强化竞争优势实现供应链可持续运作。国外Kurata^[11]在渠道竞争与品牌竞争的角度下设计出批发价格补贴契约；Ma^[12]基于政府补助下双渠道闭环模型证明回收补贴有益于消费者、制造商及零售商；Zhang^[13]研究企业产能价格补贴模型决策问题，得出价格补贴的正向效应随着补贴数额的增加边际效应递减的结论；Li et al.^[14]从再制造闭环供应链角度讨论政府何时及如何实施碳补贴能够鼓励企业减少碳排放。国内刘珩等^[15]探讨存在缺货损失情况下由损失厌恶型零售商与损失厌恶型供应商组成的供应链价格补贴契约设计；李新然等^[16]构建有无政府补贴集中式与分散式差别定价闭环供应链模型，分析补贴对四种模式的决策影响问题；徐兵等^[17]研究两条供应链相互竞争时决策者实现链内协调的回购加促销补贴契约；鄢飞等^[18]考虑功能商之间存在横向公平偏好心理构建物流服务供应链双重委托代理模型。以上研究可看出供应链运作中补贴策略机制的重要性，实施补贴引导机制是供应链成员企业效率的重要保障。但值得注意的是现有研究对象多是对闭环供应链中某环节或某特定成员的政府补贴展开研究，主要以期望收益或损失最优化作为目标函数，忽略了需求风险阶段补贴策略公平分配问题，同时对价值补偿额度形成机理研究不够深入，未能从整体与共赢角度考察补贴政策引导效果。因此分析物流服务供应链的补贴引导作用以及集成商如何制定补贴政策提高物流服务供应链运作效率是值得深入研究的问题。本研究对物流服务供应链需求降低风险展开研究，分析集成商面对需求风险时为保证物流服务供应链可持续运作设计需求补偿策略，同时探讨集成商物流价格变化能否实现物流提供商与物流客户的帕累托改进，为供应链成员企业采取有效补偿措施、确定合理补偿价值提供科学依据。

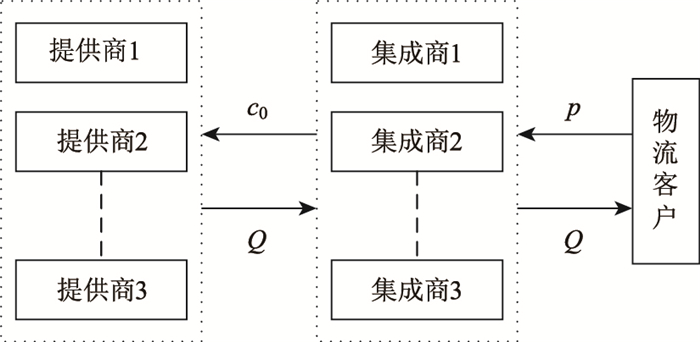
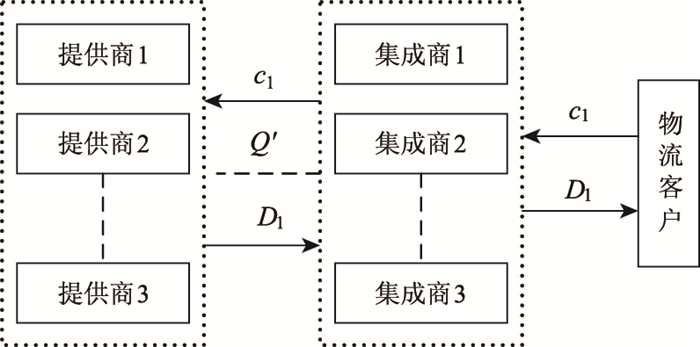
1 问题描述与基本假设 1.1 问题描述

研究以典型两级物流服务供应链结构作为研究对象，其中物流集成商与物流提供商互为独立决策者，集成商根据市场供需情况在合约期内以一定销售价格向客户提供物流服务，同时物流提供商在合约期内将基于自身期望收益最大化原则为集成商确定最优的物流订购价格及供给量。当物流客户与物流提供商在合约运作期内未发生需求风险时提供商物流服务供给量与最优合约产量相同，即提供商在合作服务期内将按照之前所约定最优价格与产量供给，见图 1。然而，考虑到服务过程中受到市场环境变化、客户偏好转移及消费者违约等因素冲击而引发顾客服务需求下降，从而可能导致物流提供商前期成本投资无法收回，致使物流服务供应链合作失败，损害各成员企业利益，本研究针对由物流供应商、物流集成商及物流客户组成的物流服务供应链系统，研究需求风险导致物流服务供应链系统合作期间物流需求下降风险补贴策略。考虑风险事件短时间内可能造成的严重破坏性必须采取非常规方法来处理，不同于正常情况时物流服务供应链交易运作机制，为实现物流服务供应链系统合作稳定，假设需求风险期间集成商暂不考虑自身收益，客户交易价格以提供商服务订购价格为基准，见图 2，同时采用需求风险补贴机制保障物流服务供应链系统可持续运作，即当物流需求下降后集成商将对提供商进行风险补贴，以期实现物流客户剩余与提供商期望收益的帕累托改进。

其中，相关符号含义如下，其中价格单位为元，时限单位为天。

D₀：合约初期物流市场需求；

D₁：需求风险后物流市场需求；

C₀：提供商服务期内固定成本；

C_t：提供商服务期内t时刻运作成本；

p：集成商面向客户的单位能力出售价格；

λ：集成商单位能力价格盈利系数；

c₀：风险事前提供商单位能力订购价格；

c₁：风险事后提供商单位能力订购价格；

c₂：价格上限内集成商补偿后订购价格；

c₃：价格再议后集成商补偿后订购价格；

：正常执行合约情况时提供商单位能力最高订购价格；

：需求风险阶段提供商单位能力最高订购价格；

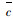
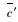
μ：需求函数边际运作价格；

β：服务时间边际运作价格；

T：集成商与提供商签订的合约总时限；

t：提供商未发生风险正常运作的时限；

t₁：客户物流需求风险发生时刻；

t′：需求风险发生后集成商与提供商的谈判时间；

a：需求风险发生前需求函数截距；

b：需求风险发生前需求函数斜率；

a′：需求风险发生后需求函数截距；

b′：需求风险发生后需求函数斜率；

π₀：正常执行合约情况时的物流提供商收益；

π₁：发生需求风险时的物流提供商收益；

π11：需求风险阶段的物流提供商收益；

π₁₂：最高价格固定情景时物流提供商收益；

π₁₃：最高价格再议情景时物流提供商收益；

w₀：正常执行合约情况时客户剩余；

w₁：发生需求风险时客户剩余；

w₁₁：需求风险阶段客户剩余；

w₁₂：最高价格固定情景时客户剩余；

w₁₃：最高价格再议情景时客户剩余；

r₁(t′)：需求风险发生后集成商重新谈判成本；

r₂(t′)：需求风险发生后提供商重新谈判成本；

Q：集成商向提供商的物流服务能力订购量；

Q′：集成商向提供商的物流服务能力补偿量。

1.2 模型假设

为了有效方便解决研究问题，分析过程中提出以下假设：

假设1：需求风险事件前后市场需求与成本结构等均为完全信息；

假设2：根据经济学知识，需求风险事件前后客户物流服务需求均为服务价格的线性函数；

假设3：物流提供商运作成本包括固定成本与变动成本，由于变动成本为支付给各种变动要素的费用，其变动成本为运作时间与合约需求的线性函数；

假设4：需求风险发生后物流集成商与提供商需要重新确定价格的谈判成本为双方谈判时间的函数；

假设5：需求风险期间集成商暂不考虑自身收益，面向客户的能力出售价格以订购价格作为基准；

假设6：集成商对物流提供商的补偿值不超过合约初期物流市场需求最优值。

参数间存在如下关系：a>a′>0，确保需求风险发生后需求为0时的价格水平低于原需求函数；ba>b′a′>0，说明需求风险发生导致物流需求降低；0 < μ < a，需求边际成本低于最低价格水平，确保提供商每时段收益为正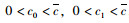；，集成商为保证物流服务供应链系统整体稳定性，最高订购成本为正常情况提供商订购成本上限值；p=(1+λ)c₀，集成商对物流客户销售价格与提供商物流服务订购价格的关系，其中，为保证集成商利润为正，λ>0；0≤Q′≤Q，集成商物流服务能力补偿量限定在能力订购量内部；0 < t₁ < T，物流需求风险发生时刻位于合约期限内部；D₀(c₀)=ba－bc₀，合约初期集成商与提供商根据市场预测每时段线性需求函数；D₁(c₁)=b′a′－b′c₁，需求风险发生后物流服务供应链需求函数；C_t=C₀+βt+μD(c)，第t时段的提供商运作线性成本函数包括固定成本与变动成本两部分。

2 模型构建及求解 2.1 集成商未实施补偿机制的情形

(1) 物流客户正常执行需求合约

首先建立合约期内需求风险未发生，即物流客户正常执行合约情况时物流提供商收益与客户剩余的基准模型。此时物流提供商在整个订货周期内的利润函数与客户剩余模型为：

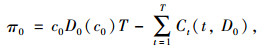
(1)

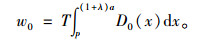
(2)

代入上文D₀与C_t表达式得：

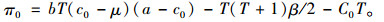
(3)

对式(3)求导，得提供商最优订购价格为c₀^*=(a+μ)/2，即正常情景时提供商执行价格为c₀^*，符号*表示目标函数最优值，下文同。提供商最优利润与客户剩余为π₀^*=bT(a-μ)²/4－T(T+1)β/2－C₀T与。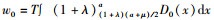

(2) 物流客户发生需求风险合约情形

当合约时限内物流客户发生需求风险时，集成商未对提供商实施补偿的提供商利润函数与客户剩余表示为：

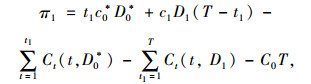
(4)

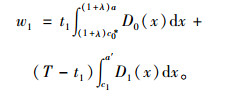
(5)

代入上文D₁与C_t表达式得：

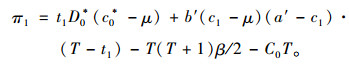
(6)

对式(6)求导，得需求风险发生后提供商最优订购价格为c₁^*=(a′+μ)/2，即正常情景时提供商服务执行价格为c₁^*，显然此时c₁^* < c₀^*。此时提供商最优利润与客户剩余为：

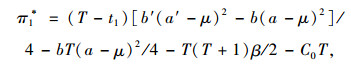
(7)

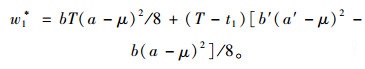
(8)

提供商受到需求风险后为促进销售将物流服务价格降至c₁^*，进而提供商利润与客户剩余差值分别为(π₀^*－π₁^*)与(w₀^*－w₁^*)。考虑到π₀^*－π₁^*>0可知需求风险造成提供商利润发生下降，为保障提供商自身权益，提供商将要求与集成商重新谈判服务价格，同时b′(a′-μ)²－b(a－μ)²≤0使得w₀^*－w₁^*>0，即需求风险也将造成客户消费者剩余值下降。因而，集成商在需求风险发生后为实现提供商利润与客户消费剩余的帕累托改进将实施对提供商服务销售的补偿机制。t₁时刻发生需求风险后造成提供商在(T－t₁)时段内产生损失，若集成商未对提供商实施补偿，该时段内提供商的最优利润函数与客户剩余模型为：

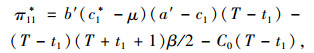
(9)

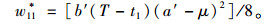
(10)

可将式(9)作为研究集成商实施补偿策略的对比模型。

2.2 集成商实施补偿机制的情形

(1) 集成商规定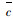不变

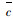
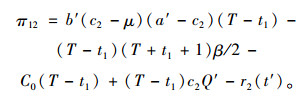
当在合约时限内物流客户发生需求风险情况时，为保障物流服务供应链系统稳定以实现提供商收益与客户剩余的共同改进，集成商需要对提供商实施需求补偿值为Q′，其中0≤Q′≤Q。提供商在集成商所规定的价格上限内根据具体补偿情形制定最优订购价格c₂^*(0≤c₂^*≤ )，并确定最优价格是否能够同时实现客户剩余提升。此时(T－t₁)期限内提供商利润函数表示为：

(11)

对式(11)求导得提供商最优订购价格c₂^*为：

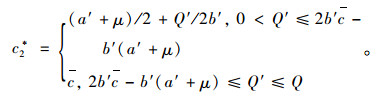
(12)

将最优订购价格c₂^*代入求得需求补偿前后提供商的利润差值为：

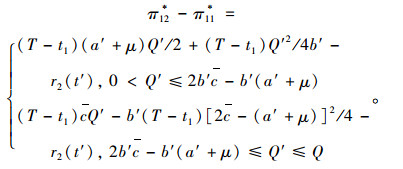
(13)

从利润差值(π₁₂^*－π₁₁^*)可看出，在区间Q′∈(0, Q)内均为增函数。

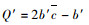
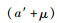
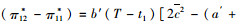
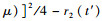
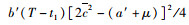
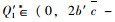
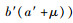
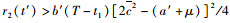
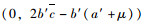
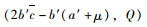
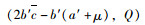
由Q′=0时(π₁₂^*－π₁₁^*) < 0，当时；若(π₁₂^*－π₁₁^*)≥0则r₂(t′)≤ ，在区间Q′∈(0, Q)内为增函数，此时必然存在 使得(π₁₂^*－π₁₁^*)=0，因此在区间(Q′₁^*, Q)内存在提供商的有效补偿Q′。

若时虽然(π₁₂^*－π₁₁^*) < 0，在区间内均小于0。然而在区间内当集成商补偿值Q′=Q时使(π₁₂^*－π₁₁^*)=0，因此区间内存在Q′₂^*使其差值为0，而集成商对提供商的最优补偿Q′定存在于(Q′₂^*, Q)。

风险补偿阶段集成商为保障自身利益能力会将对提供商的补偿成本转移至物流需求客户，此时(T－t₁)期限内客户剩余函数表示为：

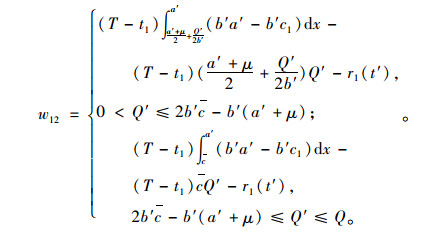
(14)

在集成商规定的价格上限内若使补偿策略对客户剩余有所提升必须实现w₁₂>w₁₁^*，但集成商补偿策略将引发上游提供商提升物流服务价格，即c₂^*>c₁^*以期实现自身收益提高。此时需求补偿策略前后利益变化有w₁₂ < w₁₁^*说明提升价格将造成客户利益损失，由此得出集成商补偿策略无法实现提供商与客户利益共同优化。

(2) 集成商价格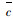再议

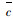
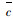
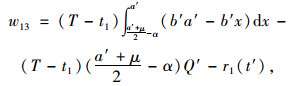
考虑集成商规定价格值时无法实现需求风险发生后提供商与顾客帕累托改进，因此需要集成商与提供商重新谈判商定价格值。分析可知，欲实现客户w₁₂>w₁₁^*，必须要求实现物流服务价格c₃ < (a′+μ)/2，为此假设谈判后物流服务价格为c₃ < (a′+μ)/2－α(0 < α < (a′+μ)/2)。计算此时需求风险发生后集成商完成补偿策略的客户剩余：

(15)

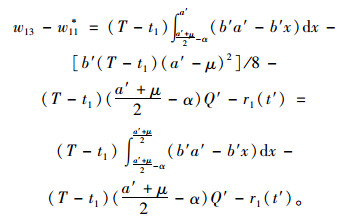
(16)

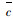
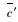
由式(16)可看出(w₁₃－w₁₁^*)对α而言为单调增函数，当α=0时有(w₁₃－w₁₁^*) < 0。而若α=(a′+μ)/2时存在(w₁₃－w₁₁^*)=[b′(T－t₁)(3a′－μ)(a′+μ)]/8－r₁(t′)，此时若要在需求风险发生后达到提升客户剩余的目的需实现(w₁₃－w₁₁^*)>0，即r₁(t′)>[b′(T－t₁)(3a′－μ)(a′+μ)]/8。在区间(0, (a′+μ)/2)内必有α′使(w₁₃－w₁₁^*)=0，且(α′, (a′+μ)/2)内(w₁₃－w₁₁^*)>0。因此当需求风险发生后，为保证客户剩余，集成商与提供商在补偿策略谈判过程中应对实施价格再议，且 < (a′+μ)/2－α′。

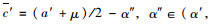
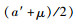
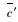
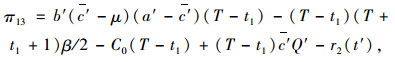
集成商与提供商完成谈判后确定提供商物流服务订购最高值为 。在交易过程中考虑提供商的利益“理性人”的性质，需求风险发生后提供商为保障自身收益最大化必会将服务价格确定为集成商所规定的最高限额。则提供商的收益函数为：

(17)

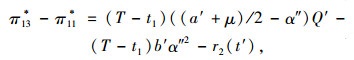
(18)

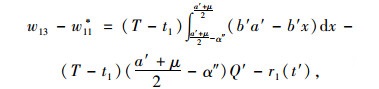
(19)

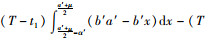
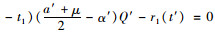
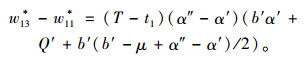
式(19)减去得：

(20)

由式(20)知在α″∈(α′, (a′+μ)/2)内收益差值(π₁₃^*－π₁₁^*)为单调减函数，将式代入提供商利益函数差可得：

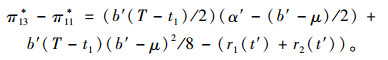
(21)

可得当α′=(b′－μ)/2时可使(π₁₃^*－π₁₁^*)取得最大值b′(T－t₁)(b′－μ)²/8－(r₁(t′)+r₂(t′))，为此若(r₁(t′)+r₂(t′))≤b′(T－t₁)(b′－μ)²/8时π₁₃^*－π₁₁^*≥0，而当α″=(a′+μ)/2时可得π₁₃^*－π₁₁^* < 0。根据单调函数性质可知必存在区间α″^*∈(α′, (b′－μ)/2)使π₁₃^*－π₁₁^*≥0，且(r₁(t′)+r₂(t′))≤b′(T－t₁)(b′－μ)²/8。集成商最终有效补偿策略为：

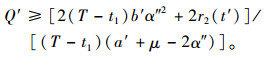
(22)

3 算例分析

考虑目前物流服务供应链现实结构，研究对象是由物流集成商主导的两层物流服务供应链，受市场供需不确定性等因素影响所引起的物流需求侧风险将导致物流服务需求发生波动，使得客户存在需求降低风险。因此，集成商须在风险阶段采用需求风险补贴机制保障物流服务供应链系统可持续运作，即当物流服务需求下降后，集成商通过提供商风险补贴实现客户剩余与提供商收益的帕累托改进。在此给出具体数值算例，用以检验所构建的补偿策略应对需求降低风险的有效性。假设物流市场需求最高价格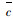 =40，其中物流服务集成商需求合约运作需求量Q=400，运作周期为一年，即T=12，物流服务需求风险发生时间节点t₁=2。考虑参数间存在的关系约束，主要参数分别设置为：a=60，a′=40，b=4，b′=4，C₀=10，β=4，μ=12，r₁(t′)=3 000，r₂(t′)=4 000。由此可知，合约初期集成商与提供商根据市场预测每时段线性需求函数D₀(c₀)=240－4c₀；需求风险发生后物流服务供应链的需求函数D₁(c₁)=160－4c₁；第t时段的提供商运作线性成本函数C_t=10+4t+12D(c)。分别研究物流集成商固定最高价格、物流集成商与提供商价格再议两种需求补贴策略模式，比较分析各补贴模式以验证集成商价格再议模式的优越性。

3.1 集成商固定最高价格模式分析

物流集成商固定最高价格情形下，将相关数值代入集成商补偿前后的利益函数值分别为π₁₁^*与π₁₂^*。其中π₁₁^*=7 440，而π₁₂^*为：

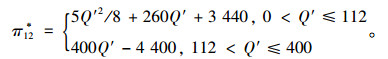
则其物流提供商的差值函数表达式为：

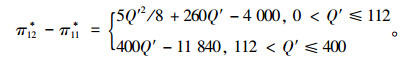
同理，数值代入后补偿前后客户剩余函数值分别为w₁₁^*与w₁₂，其中w₁₁^*=3 920，而w₁₂为：

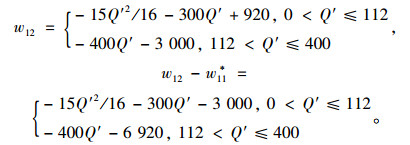
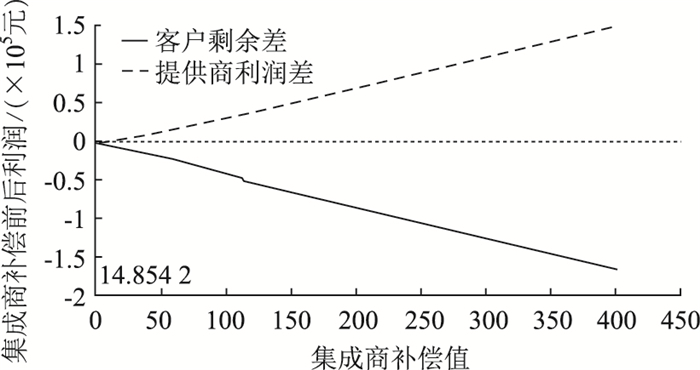
相应的w₁₂－w₁₁^*函数曲线如图 3所示，此时收到物流集成商的补偿后提供商收益差值函数在区间[0, 14.854 2]内明显提高，说明在物流服务最高固定情景中实施补偿策略可明显提升提供商收益。但在区间[0, 400]内集成商补偿策略却无法实现客户剩余的提升，因此固定最高服务价格时集成商补偿策略不能实现客户与提供商两者帕累托改进。

3.2 集成商价格再议模式分析

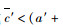
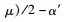
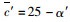
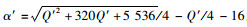
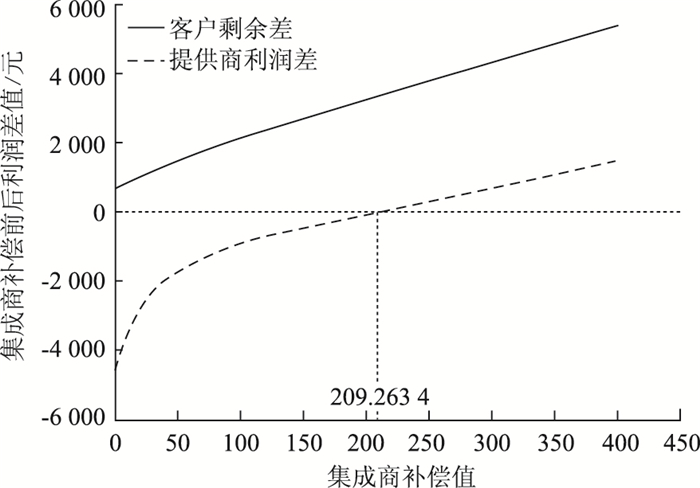
物流集成商最高价格再议情形下，按式要求假设再议后的，按其计算可得。将相关数值代入提供商利益差值函数π₁₃^*－π₁₁^*=(T－t₁)·((a′+μ)/2－α″)Q′－(T－t₁)b′α″²－r₂(t′)得：π₁₃^*－π₁₁^*=－40(α′+1)²+10Q′(25－α′)－4 000。

同理，计算w₁₃^*－w₁₁^*=(T－t₁)(α″－α′)(b′α′+Q′+b′(b′－μ+α″－α′)/2)得w₁₃^*－w₁₁^*=10×Q′²+320Q′+5 536－60，两者函数曲线如图 4所示。

可以看出，最高价格改变后收到物流集成商的补偿后客户剩余差值函数在区间[0, 400]内明显提高，说明此时集成商实施补偿策略具备有效性。关于提供商利益函数曲线，在区间[0, 209.263 4]内集成商补偿策略却无法实现提供商收益的提升，而当集成商补贴值为[209.263 4, 400]时补贴机制可实现提供商收益的增加，且在Q′=400时达到最大值。由此可知，最高价格改变时集成商的补偿策略能够实现客户与提供商的帕累托改进。

4 结论

研究以合约期内物流客户正常执行合约情况时的物流提供商收益与客户剩余模型为基准，构建出了需求降低风险期间集成商实施补偿策略下的提供商与客户剩余利润函数表达式。在集成商固定最高价格时从提供商角度出发构建集成商补偿机制，得出提供商与客户的利润差值模型，同时进一步探讨集成商改变最高价格时从客户角度出发所构建集成商补偿机制的差值函数。结果表明在物流需求风险阶段集成商改变最高价格后的补贴策略能够同时提高物流提供商与客户收益，实现双方合作利益的帕累托改进。以上研究通过价值补偿额度形成机理得出物流服务供应链运作中补贴策略机制解决方案，为物流企业健康成长提供理论指导与科学依据。