扩展功能
文章信息
- 胡郁葱, 宫曼琳, 谢昳辰, 梁燕豪
- HU Yu-cong, GONG Man-lin, XIE Yi-chen, LIANG Yan-hao
- 网络预约出租汽车营运模式的四方博弈模型
- A Four-side Game Model for Operational Mode of Online Car-hailing System
- 公路交通科技, 2020, 37(2): 130-136
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(2): 130-136
- 10.3969/j.issn.1002-0268.2020.02.017
-
文章历史
- 收稿日期: 2018-04-09
2. 现代城市交通技术江苏高校协同创新中心, 江苏 南京 210000;
3. 浙江省交通运输科学研究院, 浙江 杭州 310000;
4. 广东网上飞物流科技有限公司, 广东 广州 510032
2. Modern Urban Traffic Technology Collaborative Innovation Center of Jiangsu Universities, Nanjing Jiangsu 210000, China;
3. Zhejiang Scientific Research Institute of Transport, Hangzhou Zhejiang 310000, China;
4. Guangdong Fly-E Logistics Technology Co., Ltd., Guangzhou Guangdong 510032, China
随着互联网技术发展,以网络预约出租汽车服务(下文中简称专车)为代表的互联网出行服务正深入生活[1]。如何清晰地辨识网络预约出租汽车营运过程中涉及到的营运管理政策制定者(下文中简称管理者)、专车平台、乘客和传统出租车企业的相互关系,从社会福利最大化角度对网络预约出租汽车营运模式进行合理的规范和监管,成为促进城市交通系统协调发展必须要解决的问题。
Fisk[2]第一次提出交通领域的Stackelberg博弈模型,该模型通过管理者和出行者之间的博弈将信号控制系统最优和用户最优结合;Albert[3]构建收费道路管理者与出行者之间费用博弈的模型,为管理者制定有效的收费水平提供依据;刘立立[4]提出管理者和货运者之间的Stackelberg博弈模型,指导中小城镇的货车限行政策的制定。上述研究证明,博弈模型可以描述交通系统中多方在竞争环境下相互博弈的过程,并通过对各种博弈决策的效果进行分析,获得最佳策略。因此,可以用于涉及多方博弈的专车营运模式研究。
目前国内外对专车和传统出租车的竞争关系开展了一些研究。詹艺[5]将国内专车分别与出租车和国外约租车对比,得出发展专车服务是从出租车改革的方向。Rayle等[6]研究专车在旧金山的使用,并将其与传统出租车对比;Hall和Krueger[7]分析了以Uber为代表的专车与传统出租车对司机的吸引力;田帆等[8]基于经济学视角对专车运营模式及政策进行探究。
综上所述,由于专车对传统出租车行业带来冲击,其发展模式也一直饱受争议,这方面研究多数还处于定性阶段或基于统计数据的推断,尚不能为制定合理的专车营运模式和监管策略提供有意义的参考。本研究以广州市数据为研究背景,建立管理者、专车平台、乘客和传统出租车企业四方Stackelberg博弈模型,对几种专车营运模式进行分析,力图找到社会综合福利较好的营运模式。
1 网络预约出租汽车四方博弈模型 1.1 博弈模型概述博弈论(Game Theory)研究的是不同参与者之间利益相互制约下策略选择时的理性行为以及相应结局的一种理论。参与者(i)、策略(Si)和收益(ui(s))是描述一个博弈最基本的3个要素[9]。如果每个参与者在其他参与者的策略保持不变时,他所选择的策略使得他的收益最大,因此每个参与者都没有单独改变自己策略的激励。此时我们认为这种对局是稳定的,并将各个参与者选择的策略所组成的策略组称为一个纳什均衡[10],是求解博弈模型的一个重要手段。
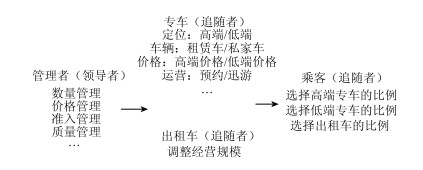
1.2 网络预约出租汽车四方博弈的基本过程本研究的博弈模型参与者包括:管理者、专车平台、乘客和传统出租车企业[11]。管理者是制定政策而使社会整体福利最大化,其他3者则是追求各自利益最大化,其博弈过程如图 1所示。
|
| 图 1 管理者、专车平台、乘客和传统出租车企业相互博弈过程 Fig. 1 Game process among administrators, online car-hailing platform, passengers and conventional taxi enterprises |
| |
设该博弈的参与主体为{a, b, c, d},a为管理者,b为专车平台,c为乘客,d为传统出租车企业。
(1) 博弈先由管理者出动,暂不考虑对专车实行数量管制、价格管制与指导,默认允许租赁车参与经营,焦点问题是“是否允许私家车参与经营”和“是否允许专车巡游”。管理者的博弈策略集Sa:
sa1为“允许私家车运营+允许专车巡游”;sa2为“允许私家车运营+只允许预约(不可巡游)”;sa3为“禁止私家车运营+允许专车巡游”;sa4为“禁止私家车运营+只允许预约(不可巡游)”。
即:Sa=(sa1, sa2, sa3, sa4)。
(2) 专车平台有两种类型车辆:假设专车经营高端专车服务时的车辆主要为租赁车,经营低端专车服务时的车辆主要为私家车。专车平台的博弈策略集Sb:
sb1为“租赁车+高端市场+高端市场价格ph”;sb2为“私家车+低端市场+低端市场价格pl”;sb3为“租赁车+私家车+高端市场+低端市场+高端市场价格ph,低端市场价格pl”。
即:Sb=(sb1, sb2, sb3)。
(3) 乘客的应对策略为选择各种出行方式的比例。设乘客选择高端专车、出租车、低端专车出行的比例为qh,qt,ql,其中qh+qt+ql=1。乘客的策略集为Sc=(qh, ql, qt)。
(4) 传统出租车企业的应对策略为当市场需求减少时,缩减其经营的规模。设政策实施后出租车经营规模与现有规模(政策实施前)的比例为φd,其中φd≤1。传统出租车企业的策略集为Sd=(φd)。
1.3 网络预约出租汽车博弈模型的建立 1.3.1 模型假设(1) 基于当前的资源和交通管理现状,专车和出租车现有的运营管理方式以及技术水平的基础。
(2) 专车博弈中仅涉及管理者、专车平台、乘客、传统出租车企业4方,其他利益相关方暂不考虑,如公共交通、私家车使用者等。
(3) 出租车现有的数量和价格管制条件不变,不考虑其他公共交通运行情况变化对专车及出租车产生的影响。
(4) 假设乘客乘坐小汽车客运服务的需求不变,不考虑和其他交通方式之间的转移。
(5) 假设在研究范围内,专车以及出租车供给的边际成本保持不变。
(6) 以天为单位,不考虑一天内不同时段之间,价格与需求的变化。
1.3.2 负外部性用ui(s)为各方收益函数;O(s)为专车平台和传统出租车企业的负外部性成本函数[12](本研究收益和成本函数取“元/km”为单位)。
计算专车平台和传统出租车企业的外部性时考虑噪音成本,环境污染成本,交通拥堵成本和交通事故成本。专车和出租车都属于小汽车,作为一个类别考虑:
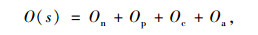
|
(1) |
式中,On为平均噪声成本;Op为空气污染成本;Oc为交通拥堵成本;Oa为交通事故成本。
(1) 噪音成本根据欧洲噪音成本[13]调整:
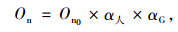
|
(2) |
式中,On0为欧洲平均噪音成本;α人为人口调整因素比值(广州与欧洲人口密度之比);αG为人均GDP调整因素比值(广州与欧洲人均GDP之比)。
(2) 环境污染成本、交通拥堵成本和交通事故成本参考国内已有研究[14]:
① 环境污染成本
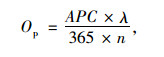
|
(3) |
式中,APC为每年因空气污染造成的经济损失;λ为小汽车造成的空气污染占总空气污染的百分比;n为小汽车平均乘坐的乘客数。
② 交通拥堵成本[15]
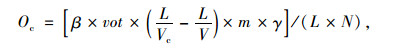
|
(4) |
式中,β为小汽车的价值系数;Vot为广州的单位时间价值;L为小汽车的日平均出行里程;Vc为小汽车出行拥挤时的速度;V为小汽车出行时的速度;m为广州的总从业人口数;γ为小汽车出行的乘车比例;N为小汽车出行的车辆总数。
③ 交通事故成本[16]
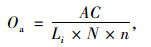
|
(5) |
式中,AC为小汽车的直接经济损失;Li为小汽车年完成的车公里数。
1.3.3 四方博弈模型本研究模型的其他函数公式和参数含义见表 1。
| 函数 | 函数意义 | 公式 | 参数含义 |
| ua(s) | 管理者收益函数 | ua(s)=[ub(s)+uc(s)+ud(s)-O(s)] | Ri(s):高端专车/低端专车/出租车收入函数(其中h代表高端专车,l代表低端专车,t代表出租车)下标a为管理者;b为专车平台;c为乘客;d为传统出租车企业。以下11个含i的参数也均按该字母含义来代表 3种出行选择,不再赘述。 pi:服务价格(元/km) qi:乘客选择高端专车/低端专车/出租车的比例(km) Ci(s):成本函数 Ci管理(s):服务管理成本(元/km) Ci运营(s):服务运营成本(元/km) Si:行驶里程(km/day) θi实载:实载率 fi油:油费(元/km) fi维修:维修费(元/month) fi车:车辆购置费(元) Ti:车辆全寿命使用时间(day) Q:乘客选择小汽车客运服务的总需求 On:平均噪声成本(元/km) Op:空气污染成本(元/km) Oc:交通拥堵成本(元/km) Oa:交通事故成本(元/km) |
| ub(s) | 专车平台收益函数 | ub(s)=[Rb(s)-Cb(s)] | |
| Rb(s) | 专车平台收入函数 | Rb(s)=Rh(s)+Rl(s)=ph×qh+pl×ql | |
| Cb(s) | 专车平台成本函数 | 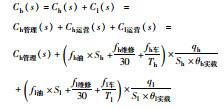
|
|
| uc(s) | 乘客收益函数 | uc(s)=[Rc(s)-Cc(s)] | |
| Rc(s) | 乘客出行效用函数 | 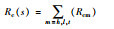
|
|
| Cc(s) | 乘客出行成本函数 | Cc(s)=(ph×qh+pt×qt+pl×ql)×Q | |
| ud(s) | 传统出租车企业收益函数 | 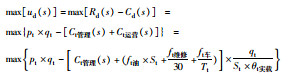
|
|
| O(s) | 专车平台和传统出租车 企业的外部性成本 |
O(s)=On+Op+Oc+Oa | |
| 注:管理成本难以调查和计算获得,由于专车公司与出租车公司的经营管理特征类似,因此参照出租车的“管理成本分摊+财务成本分摊”,作为专车的管理成本。专车公司和出租车公司的运营成本均采用小汽车运营成本的计算方法。) | |||
博弈各方目标函数:
管理者目标函数:
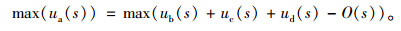
|
(6) |
专车平台目标函数:
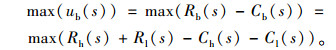
|
(7) |
乘客目标函数:
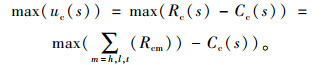
|
(8) |
传统出租车企业目标函数:
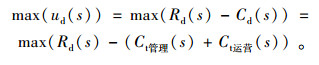
|
(9) |
本研究数据为2016年4月对广州市专车经营情况调查得到的100份数据和2015年5月14日南方都市报记者对广州市出租车行业进行问卷调查得到的数据。
2.1 博弈模型计算结果以管理策略1(sa1={允许私家车运营,允许专车巡游})为例。
假设:(1)私家车生命周期为35万km。(2)低端专车车价取9万元,高端专车车价取30万元。(3)不考虑起步价。(4)每月30天。
(1) 乘客出行效用函数
通过SPSS软件对数据建模得乘客效用函数模型为:
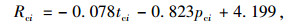
|
(10) |
式中,tci为乘客选择出行方式i时的服务时间; pci为乘客选择出行方式i的服务价格。
对模型效果检验后P < 0.001,通过显著性检验。(注:这里的P值为统计软件中输出的渐进sig值,通常用来表示检验的显著性。)
(2) 乘客出行选择logit模型
logit模型[17]的一般形式为:
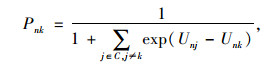
|
(11) |
式中,Pnk为个人n选择选择枝k的概率;Unj为个人n关于选择枝j的效用;Unk为个人n关于选择技术k的效用;C为所有选择枝的集合。
用SAT软件构建出行选择模型(取乘客选择出租车的效用为参照对象0,乘客选择高端专车和低端专车的效用分别为lin(h)和lin(l)):
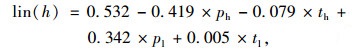
|
(11) |
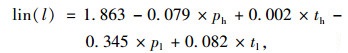
|
(12) |
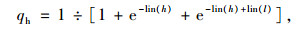
|
(13) |
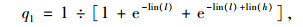
|
(14) |
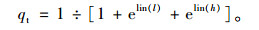
|
(15) |
对各参数进行χ2检验,结果如表 2所示:
| 参数 | 参数数目 | df | 似然比 | P值 |
| ph | 2 | 2 | 6.650 973 34 | 0.036 0* |
| th | 2 | 2 | 15.227 768 5 | 0.000 5* |
| pl | 2 | 2 | 8.801 798 81 | 0.012 3* |
| tl | 2 | 2 | 23.781 259 8 | < 0.000 1* |
模型参数检验的P值均小于0.05,满足检验标准,模型效果显著。
(3) 专车平台应对策略
将数据代入表 1中公式后得专车平台决策函数(限于篇幅不赘述计算过程):
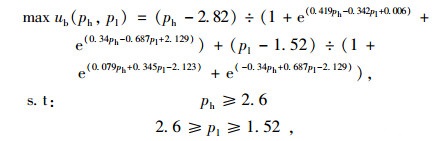
|
(16) |
解得:ph1=5.7元/km, pl1=2.6元/km,ub1max=0.880元/km。
(4) 乘客应对策略
ph1=5.7元/km,pl1=2.6元/km代入式(11)~式(15)算得:
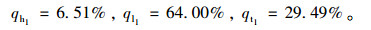
|
乘客的最优应对策略为:
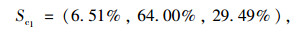
|
算得乘客最大收益:Rc1=1.707元/km, Cc1=2.802元/km, uc1max=-1.095元/km
(5) 传统出租车企业应对策略
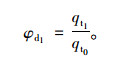
|
(17) |
已算得qt1=29.49%,出租车需求比现有需求qt0=36.2%少。得φd1=81.46%,出租车最优应对策略Sd1=(81.46%),代入数据得传统出租车企业收益:ud1max=0.220元/km。
(6) 管理者收益
先计算负外部性成本,将数据代入公式(2)算得广州市的平均噪音成本为:0.437元/km。
其他3个负外部性成本,采用陈艳玲对南京市小汽车出行成本的研究中得到的小汽车外部成本的各组成系数[8],取值为1.720,0.732,0.001元/km。
据式(14),专车平台和传统出租车企业的外部性成本:
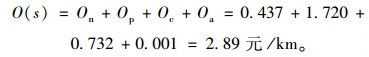
|
(18) |
管理者收益:
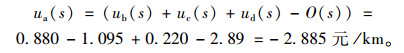
|
(19) |
(7) 福利均衡
取差异系数[18]来衡量福利均衡:
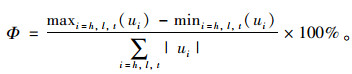
|
(20) |
管理策略1的差异系数:Φ(s1)=89.98%。
按上文方法计算其他3个管理策略和现状的相关数据,列于表 3。
| 管理策略 | 专车平台应对策略/(元·km-1) | 专车平台收益/(元·km-1) | 乘客应对策略/% | 乘客收益/(元·km-1) | 传统出租车企业应对策略/% | 传统出租车企业收益/(元·km-1) | 管理者收益/(元·km-1) | 差异系数/% |
| 现状 | 租赁车+私家车+预约 | 0.743 | qh0=14.2 ql0=49.6 qt0=36.2 |
-0.924 | 100 | 0.272 | -2.799 | 85.97 |
| 策略1 | 租赁车+私家车+巡游 ph1 =5.71 pl1=2.6 |
0.880 | qh1=6.51 ql1=64 qt1=29.49 |
-1.095 | 81.46 | 0.220 | -2.885 | 89.98 |
| 策略2 | 租赁车+私家车+预约 ph2=5.04 pl2=2.60 |
1.09 | qh2=4.46 ql2=71.42 qt2=24.12 |
-1.119 | 66.63 | 0.181 | -2.738 | 92.43 |
| 策略3 | 租赁车+巡游 ph3=5.45 |
0.120 | qh3=3.91 ql3=0 qt3=96.09 |
-0.765 | 100 | 0.749 | -2.741 | 92.66 |
| 策略4 | 租赁车+预约 ph4=5.22 |
0.079 | qh4=2.61 ql4=0 qt4=97.39 |
-0.692 | 100 | 0.730 | -2.773 | 94.74 |
| 注:这里的数值仅用于比较大小,不代表实际意义。 | ||||||||
2.2 博弈模型计算结果分析
据表 3分析:
(1) 放弃低端市场前后,在巡游和预约两种模式下专车平台收益分别从0.880元/km与1.09元/km变为0.120元/km与0.079元/km,均降低;乘客收益分别从-1.095元/km与-1.119元/km变为-0.765元/km与-0.692元/km;传统出租车企业应对策略分别从29.49%与24.12%变为96.09%与97.39%,同时传统出租车企业收益分别从0.220元/km与0.181元/km变为0.749元/km与0.730元/km,三者均提升。
专车平台放弃低端市场后,为了平衡收益,高端专车定价将提升,小部分高端专车乘客将转移到出租车,导致专车平台收益降低、乘客和传统出租车收益提升。
(2) 放弃低端市场前后,在巡游和预约两种模式下的管理者收益从-2.885元/km与-2.738元/km变为-2.741元/km与-2.773元/km,无明显变化。在模型约束的规范下,不管专车平台采取什么市场策略,整个社会福利维持着较平稳状态,其中策略2的管理者收益-2.738元/km最大。
而差异系数分别从89.98%与92.43%变成了92.66%与94.74%,提升。放弃低端市场后的专车平台提高高端专车定价,使得较大比例乘客转移到出租车,导致传统出租车企业和专车平台收益分布不公,差异系数变大。
(3) 专车平台采取低端市场和高端市场相结合的市场策略时,采取预约方式的专车平台和管理者收益分别为1.09元/km和-2.738元/km,比采取巡游方式的0.880元/km和-2.885元/km要高一些;但预约方式的乘客和传统出租车企业收益分别为-1.119元/km和0.181元/km,相比巡游方式的-1.095元/km和0.220元/km要低一些;同时预约方式的差异系数92.43%也较大于巡游方式的89.98%。
(4) 放弃低端市场时,采取预约方式拥有的乘客收益为-0.692元/km,稍高于采取巡游方式的-0.765元/km;但预约方式的专车平台、传统出租车企业和管理者收益分别为0.079,0.730,-2.773元/km,均比巡游方式的0.120,0.749元/km和-2.741元/km低;且预约方式的差异系数94.74%也大于巡游方式的92.66%。
3 结论本研究博弈模型涉及4个参与者,参与者数目多导致目标函数变多,博弈模型受制于的约束条件也相对增多,因此,本研究的模型与以往只有两三个参与者的模型相比较复杂,也更贴合实际情况。
得出结论:(1)站在管理者收益最大化和专车收益最大化角度,专车平台应选择“允许私家车运营+只允许预约(禁止巡游)”的营运模式;(2)站在乘客收益最大化和福利均衡角度,专车平台应选择“禁止私家车运营+只允许预约(禁止巡游)”的营运模式;(3)站在传统出租车企业收益最大化角度,专车平台应选择“禁止私家车运营+允许专车巡游”的营运模式。
最后综合考虑整体社会福利即管理者收益与福利均衡,建议专车选择“允许私家车运营+只允许预约(禁止巡游)”的营运模式。该模型和上述结论可为制定合理的网络预约出租汽车运营管理模式提供一定的参考。
| [1] |
刘凯, 李豫姣, 李春发, 等. 基于系统动力学的网约车准入条件政策仿真研究[J]. 公路交通科技, 2018, 35(12): 132-140. LIU Kai, LI Yu-jiao, LI Chun-fa, et al. Simulation Study on Policy of Entry Conditions of Ride-hailing Based on System Dynamics[J]. Journal of Highway and Transportation Research and Development, 2018, 35(12): 132-140. |
| [2] |
FISK C S. Game Theory and Transportation Systems Modelling[J]. Transportation Research, Part B:Methodological, 1984, 18(4/5): 301-313. |
| [3] |
ALBERT G. Analysis of the Influence of Tolls in a Congested Transport System (in Hebrew)[R]. Haifa: Teehnion-Israel Institute of Teehnology, 2001.
|
| [4] |
刘立立.基于博弈论的小城镇交通管理政策研究[D].广州: 华南理工大学, 2015. LIU Li-li. Research on Small Town Traffic Management Policy Based on Game Theory[D]. Guangzhou: South China University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10561-1015989289.htm |
| [5] |
詹艺.基于出租车管制背景下的专车市场研究[D].西安: 长安大学, 2015. ZHAN Yi. Research of Special Taxi Market Based on Taxi Regulatory Background[D]. Xi'an: Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1015802957.htm |
| [6] |
RAYLE L, DAI D. Just a Better Taxi? A Survey-based Comparison of Taxis, Transit, and Ride Sourcing Services in San Francisco[J]. Transport Policy, 2016, 45: 168-178. |
| [7] |
HALL J, KRUEGER A B. An Analysis of the Labor Market for Uber's Driver-partners in the United States[J]. Social Science Electronic Publishing, 2016, 71(3): 705-732. |
| [8] |
田帆, 常兴华. 专车运行模式及政策评价[J]. 经济与管理研究, 2016, 37(6): 98-104. TIAN Fan, CHANG Xing-hua. Operating Mode and Policies of Tailored Taxis[J]. Research on Economics and Management, 2016, 37(6): 98-104. |
| [9] |
GRUNWALD P D, DAWID A P. Game Theory, Maximum Entropy, Minimum Discrepancy and Robust Bayesian Decision Theory[J]. Annals of Statistics, 2004, 32(4): 1367-1433. |
| [10] |
JAYAWEERA S K, VAZQUEZ-VILAR G, MOSQUERA C. Dynamic Spectrum Leasing:A New Paradigm for Spectrum Sharing in Cognitive Radio Networks[J]. IEEE Transactions on Vehicular Technology, 2010, 59(5): 2328-2339. |
| [11] |
SHAHEEN S A, COHEN A P. Carsharing and Personal Vehicle Services:Worldwide Market Developments and Emerging Trends[J]. International Journal of Sustainable Transportation, 2013, 7(1): 5-34. |
| [12] |
TILLEMA T, HAMERSMA M, SUSSMAN J M, et al. Extending the Scope of Highway Planning:Accessibility, Negative Externalities and the Residential Context[J]. Transport Reviews, 2012, 32(6): 745-759. |
| [13] |
周耀东, 王嘉熙. 北京机动车环境外部成本的测算[J]. 北京理工大学学报:社会科学版, 2017, 19(6): 28-37. ZHOU Yao-dong, WANG Jia-xi. Estimate on Environment External Cost of Motor Vehicle in Beijing[J]. Journal of Beijing Institute of Technology:Social Sciences Edition, 2017, 19(6): 28-37. |
| [14] |
陈艳玲.公共交通与小汽车出行成本对比研究[D].南京: 南京林业大学, 2009. CHEN Yan-ling. A Comparative Analysis on Transport Costs between Public Transport and Cars[D]. Nanjing: Nanjing Forestry University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10298-2009201328.htm |
| [15] |
罗清玉, 隽志才, 孙宝凤, 等. 城市交通拥挤外部成本衡量方法研究[J]. 交通运输系统工程与信息, 2007, 7(5): 9-12. LUO Qing-yu, JUAN Zhi-cai, SUN Bao-feng, et al. Method Research on Measuring the External Costs of Urban Traffic Congestion[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(5): 9-12. |
| [16] |
GILES M. The Cost of Road Crashes:A Comparison of Methods and Recent Australian Estimates[J]. Journal of Transport Economics & Policy, 2003, 37(5): 95-110. |
| [17] |
HENSHER D A, GREENE W H. The Mixed Logit Model:The State of Practice[J]. Transportation, 2003, 30(2): 133-176. |
| [18] |
FABIAN E. Inversion of Z-transforms by Solving Appropriately Formulated Nonconstant Coefficient Difference Equations[J]. IEEE Transactions on Automatic Control, 2003, 28(11): 1057-1059. |
 2020, Vol. 37
2020, Vol. 37
