扩展功能
文章信息
- 蓝先林, 贾宏宇, 郑史雄, 赵金钢, 李兰平
- LAN Xian-lin, JIA Hong-yu, ZHENG Shi-xiong, ZHAO Jin-gang, LI Lan-ping
- 实际土层对高墩桥梁端碰撞的影响
- Influence of Actual Soil Layer on Pounding Beam End of High-pier Bridge
- 公路交通科技, 2020, 37(2): 82-90
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(2): 82-90
- 10.3969/j.issn.1002-0268.2020.02.011
-
文章历史
- 收稿日期: 2018-09-11
2. 贵州大学 土木工程学院, 贵州 贵阳 550025;
3. 北京工业大学 城市与工程安全减灾教育部重点实验室, 北京 100124
2. School of Civil Engineering, Guizhou University, Guiyang Guizhou 550025, China;
3. Key Laboratory of Urban Security and Disaster Engineering of MOE, Beijing University of Technology, Beijing 100124, China
地震作用下,桥梁上部结构破坏大多与桥梁碰撞有关,如San Fernando和Kobe等地震均发生过因主梁与桥台之间相对位移过大的碰撞灾害,如Hanshin桥等[1]。梁体碰撞小使得梁体局部破坏,大则发生落梁,中断交通。在Loma Prieta地震中,San Francisco-Auckland桥因支撑长度设置不足,梁体相撞导致落梁。同时,主梁与桥台之间或梁体之间碰撞会造成梁体局部破坏,而梁体下落所产生的巨大冲击力可能会造成桥墩破坏甚至全桥垮塌。碰撞导致落梁对桥梁造成极大损伤,也增加了灾后桥梁修复难度,甚至需将受损桥梁推倒重建。
国内外学者对地震作用下梁体碰撞问题进行了系列研究,Westermo[2]研究表明,强震作用下,地震动空间变化和相邻跨动力特性差异等因素均会导致梁体碰撞;Ruangrassamee等[3]研究相对位移响应谱,获得了标准相对位移反应谱,为简单桥梁结构伸缩缝宽度设置提供了参考;Bi[4-5]等基于随机振动理论,分析了场地土条件和桩土作用对碰撞间隙宽度的影响,说明桩-土相互作用对间隙宽度的影响程度;Yili Huo[6]等采用易损性分析方法研究了碰撞和斜度的相互关系对桥梁损伤概率的影响;王军文[7]等采用非线性时程方法考虑支座非线性和墩柱弹塑性对在纵向地震作用下的连续梁桥碰撞响应;李忠献[8]等基于随机振动理论和虚拟激励法,建立了桥梁临界碰撞间隙的计算方法,并研究了地震动空间效应与土-基础相互作用对隔震梁桥临界碰撞间隙的影响;贾宏宇[9]等以实际高墩铁路桥梁为研究对象,研究了不同震级和不同场地分布对桥梁碰撞间隙宽度需求的影响。基于上述研究,考虑土层对结构动力影响的较少,但是土层的作用又是抗震分析中必须考虑的因素。当地震发生时,地震波通过基岩以最快的速度从震源到桥梁所处位置,然后由基岩向上穿过土层到达结构物的基础,实际土层的分布对地震波有过滤作用,可能对基岩地震波起到放大或缩小的作用[10]。因此,土层对地震波强度的影响十分显著。刘鹏[11]、李黎[12]和刘正楠[13]等分别探究了桥梁结构在地震作用下碰撞分析的改进方法、具有隔震装置下的多跨连续梁在地震作用下的碰撞问题和高速铁路多跨连续梁的碰撞效应,但均未涉及到场地土层特性对桥梁碰撞效应的影响。研究实际场地土层分布对高墩桥梁碰撞的影响是非常必要的,而高墩桥梁伸缩缝宽度合理取值对降低桥梁碰撞概率具有重要意义。
相对于其他桥梁结构体系而言,高墩桥梁桥墩柔性较大,第一阶甚至前几阶振型为纵向振动,从而使得梁体发生纵向碰撞的概率倍增。故本研究以某高墩大跨连续刚构桥为研究对象,基于非线性抗震分析软件OPENSEES,建立伸缩缝宽度分析的全桥有限元模型,并应用DEEPSOIL软件考虑土层对地震波过滤作用,以基岩峰值加速度为强度指标,进行多点地震激励作用下的增量动力非线性分析,研究了实际场地土层分布对不同伸缩缝宽度取值下高墩连续刚构桥碰撞概率的影响。
1 有限元模型及理论介绍为了研究实际场地土层对高墩桥梁动力响应的影响,本研究选择某跨径布置为(88+168+88)m的高墩大跨预应力混凝土连续刚构桥为研究对象,该桥主梁为单箱单室的变截面形式,顶板宽12 m、底板宽8 m,梁高从跨中到墩顶按二次抛物线变化;全桥共设有2#和3#两个主墩,且均采用变截面空心矩形薄壁墩,墩高分别为75 m和103 m。全桥布置及桥位处地质情况如图 1所示。
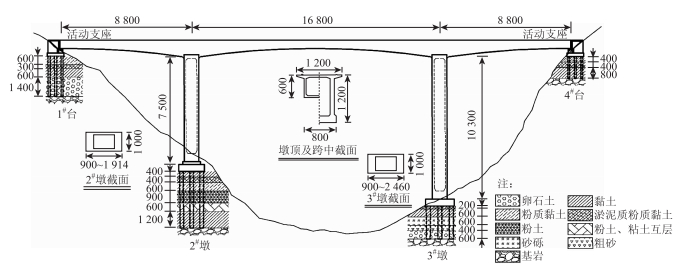
|
| 图 1 全桥布置(单位:cm) Fig. 1 Layout of bridge(unit:cm) |
| |
基于非线性有限元软件OPENSEES建立了数值有限元模型。主梁采用基于位移的梁柱单元和OPENSEES中的弹性截面联合模拟,并通过对同一单元两端节点赋予不同截面属性的方法来模拟主梁的变截面特征;地震荷载作用下,由于惯性力的梁体振动会对桥墩底部产生非常大的弯矩,使得桥墩根部进入弹塑性变形,因此,本研究基于力的梁柱单元和纤维截面来模拟桥墩的弹塑性效应,更能体现实际高墩桥梁在地震作用下的非线性行为;桥墩底部采用固结约束模拟;梁端处盆式橡胶支座采用连接单元模拟,支座滑动向的非线性行为采用双线性滞回材料模拟,并按照《公路桥梁抗震设计细则》[14]确定相关参数取值。有限元模拟中,无约束混凝土和约束混凝土的材料特性均采用Concrete02模型模拟,Concrete02模型的相关参数取值可参见文献[15];钢筋材料采用单元Steel02模拟。本研究的高墩连续刚构桥,主梁和桥墩之间采用固结,主梁和桥台均设有横向限位装置,则在有限元模型中主梁和桥墩(台)之间的横向位移均被约束,并假定碰撞是发生在桥梁纵向上。
地震作用引起的桥梁梁体之间的碰撞是一个非常复杂的动力学问题,模拟碰撞方法很多,各有优缺点。本研究采用Hertz-damp模型模拟主梁-桥台之间的碰撞。Hertz-damp模型是基于非线性弹簧和非线性黏滞阻尼器的组合来模拟碰撞,非线性弹簧和非线性黏滞阻尼器分别模拟碰撞过程中的非线性刚度和能量损失。为便于实际应用,一般将Hertz-damp模型简化为双线性刚度接触模型,碰撞力为:

|
(1) |
式中,ch为阻尼系数;kh为碰撞刚度,一般典型取值为碰撞结构物的轴向刚度(EA/L)[16-17];u1,u2为碰撞体位移;gp为相邻碰撞体之间的间距;n为Hertz系数,通常取3/2。在双折线模型中,假设Hertz-damp理论模型和简化模型的最大碰撞力Fm相等,则等效刚度keff可表示为:

|
(2) |
式中,δm为碰撞时两接触面最大入侵位移。同时,初始刚度kt1和应变强化刚度kt2表示等效刚度keff的另一种形式为:
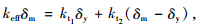
|
(3) |
式中,δy为屈服位移。碰撞力和位移所围成的区域面积可表示为:
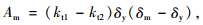
|
(4) |
碰撞过程中所耗散的能量ΔE为:

|
(5) |
式中,e为回归系数,一般取值范围为0.6~0.8。
屈服位移δy与最大侵入位移δm有如下关系:
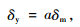
|
(6) |
式中,a为屈服系数,一般取值为0.1。
在碰撞过程中,碰撞模型耗散的能量ΔE与碰撞力-位移所围双折线区域面积Am相等,即Am=ΔE,并结合式(1)~式(6),可得:
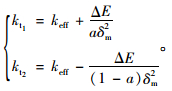
|
(7) |
由式(17)可知,只要确定碰撞刚度kh、恢复系数e,最大侵入位移δm和屈服系数a,就可以计算得出Hertz-damp模型的各参数值,本研究特征参数取值为:碰撞刚度kh=868 kN/mm3/2;Hertz系数n=3/2;恢复系数e=0.8;最大侵入位移δm=16 mm;屈服系数a=0.1;屈服位移δy=1.6 mm;等效刚度keff=3 472 kN/mm;初始刚度kt1=8 472 kN/mm;应变强化刚度kt2=2 916 kN/mm。
2 基岩地震波及土层过滤作用 2.1 基岩地震波的选取基岩地震波的选取是考虑场地土层过滤作用的分析基础,根据美国USGS规范中的相关规定,当土层地震波剪切波速Vs30>750 m/s时,为基岩地震波,基于这一标准从PEER地震波数据库(PEER ground motion database)[18]中选取了20条基岩地震波,如表 1所示。由表 1可知,基岩地震波的震级为6.20~7.62度;最大地震动加速峰值为0.862g,最小为0.018g,故所选地震波涵盖了大、中、小3级地震动。
| 序号 | 地点 | 台站 | 时间 | 场地类型 | Vs30/(m·s-1) | 震级 | 震距/km | PGA/(×g) |
| 1 | Chi-Chi | HWA003 | 1999 | A | 1 525.85 | 7.62 | 56.14 | 0.138 |
| 2 | Chi-Chi | ILA001 | 1999 | B | 909.09 | 7.62 | 103.20 | 0.025 |
| 3 | Chi-Chi | ILA063 | 1999 | B | 996.51 | 7.62 | 61.06 | 0.095 |
| 4 | Chi-Chi | TAP077 | 1999 | B | 1 022.77 | 7.62 | 119.00 | 0.034 |
| 5 | Chi-Chi | TCU085 | 1999 | B | 999.66 | 7.62 | 58.09 | 0.063 |
| 6 | Chi-Chi | CHY102 | 1999 | B | 804.36 | 6.20 | 39.30 | 0.059 |
| 7 | Chi-Chi | TAP065 | 1999 | B | 1 023.45 | 7.62 | 122.48 | 0.038 |
| 8 | Niigata | FKSH07 | 2004 | B | 828.95 | 6.63 | 52.30 | 0.143 |
| 9 | Niigata | TCGH17 | 2004 | B | 1 432.75 | 6.63 | 77.50 | 0.065 |
| 10 | Iwate | AKTH05 | 2008 | B | 829.46 | 6.90 | 39.41 | 0.085 |
| 11 | Hector Mine | LA-Griffith Park Observatory | 1999 | B | 1 015.88 | 7.13 | 185.92 | 0.018 |
| 12 | Loma Prieta | SF-Rincon Hill | 1989 | B | 873.10 | 6.93 | 74.14 | 0.093 |
| 13 | Loma Prieta | Piedmont Jr High School Grounds | 1989 | B | 895.36 | 6.93 | 73.00 | 0.084 |
| 14 | San Fernando | Pasadena-Old Seismo Lab | 1971 | B | 969.07 | 6.61 | 21.50 | 0.205 |
| 15 | Northridge-01 | Vasquez Rocks Park | 1994 | B | 996.43 | 6.69 | 23.64 | 0.151 |
| 16 | Northridge-01 | LA-Wonderland Ave | 1994 | B | 1 222.52 | 6.69 | 20.29 | 0.159 |
| 17 | Northridge-01 | Pacoima Dam (downstr) | 1994 | A | 2 016.13 | 6.69 | 7.01 | 0.434 |
| 18 | Loma Prieta | Gilroy Array #1 | 1989 | B | 1 428.14 | 6.93 | 9.64 | 0.485 |
| 19 | Loma Prieta | Los Gatos-Lexington Dam | 1989 | B | 1 070.34 | 6.93 | 5.02 | 0.443 |
| 20 | Tabas_Iran | Tabas | 1978 | B | 766.77 | 7.35 | 2.05 | 0.862 |
2.2 土层过滤效应
在地震过程中,从基岩传递到土层的剪切地震波引起土体交变应力,使土体表现出非线性特性,引起地震波的峰值加速度和频谱特性的变化。因此,考虑土层对基岩地震波的过滤作用是确定结构抗震分析地震动输入是否准确的基础。目前,频域等效线性化方法和时域直接积分的非线性方法是两种考虑土层过滤作用的常用方法。在实际工程中,地震作用下土层非线性效应明显,对基岩传播上来的地震波影响显著[19],等效线性化方法分析土层对地震波的过滤作用不够完善,因此,本研究基于DEEPSOIL软件,选用时域直接积分的非线性方法来考虑土层的非线性效应。本研究采用Matasovic等[20]提出的修正双曲线本构模型,其初始骨架曲线为:
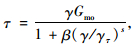
|
(8) |
式中,τ为剪应力;Gmo为初始剪切模量;γ为已知剪应变;γτ为参考剪应变;β、s为拟合参数。
参考剪应变γτ与土层特性有关,按式(9)计算:
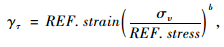
|
(9) |
式中,συ为竖向有效应力;REF.strain为参考有效应变;REF.stress为参考压应力,通常取0.18 MPa;b为拟合参数。小应变阻尼λ为:
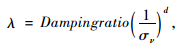
|
(10) |
式中,Dampingratio为小应变阻尼比; d为拟合参数。
本研究未考虑孔隙水压力的影响,则选用Masing法构造土层滞回曲线。并采用上述修正双曲线本构模型考虑土层深度对土层非线性参数的影响。但是进行时域非线性分析时,除土层的厚度、剪切波速、密度等参数外,还有其他参数需要确定或拟合,如表 2所示。通过对剪切模量变化曲线(G/Gmax-γ曲线)和阻尼比变化曲线(λ-γ曲线)的拟合得到拟合参数(小应变阻尼比:Dampingratio;参考压应力:REF.stress;参考有效应变:REF.strain;拟合参数:β、s、b和d)。本研究选择MRD法(Modulus reduction and damping curve fitting procedure)综合考虑了G/Gmax-γ曲线和λ-γ曲线的影响,对G/Gmax-γ曲线和λ-γ曲线都进行拟合得到计算参数。本研究依托桥梁的1#桥台、2#桥墩、3#桥墩和4#桥台处场地土层构成及各类土的土层厚度(如图 1所示),并通过钻孔资料获得土样资料(如表 2所示),G/Gmax-γ曲线和λ-γ曲线如表 3所示。
| 序号 | 土层描述 | 剪切波速/ (m·s-1) |
密度/ (kg·m-3) |
| 1 | 粉质黏土 | 150 | 1 950 |
| 2 | 淤泥质粉质黏土 | 88 | 1 850 |
| 3 | 黏土 | 190 | 1 950 |
| 4 | 粉土 | 160 | 2 010 |
| 5 | 砂砾 | 309 | 2 150 |
| 6 | 粗砂 | 256 | 2 000 |
| 7 | 卵石 | 380 | 2 050 |
| 8 | 粉土、黏土互层 | 220 | 1 950 |
| 序号 | 名称 | 参数 | 剪应变rd/(×10-4) | |||||||
| 0.05 | 0.1 | 0.5 | 1 | 5 | 10 | 50 | 100 | |||
| 1 | 粉质黏土 | G/Gmax | 0.994 | 0.988 | 0.943 | 0.892 | 0.622 | 0.452 | 0.241 | 0.136 |
| λ | 0.029 | 0.037 | 0.063 | 0.077 | 0.106 | 0.114 | 0.122 | 0.123 | ||
| 2 | 淤泥质粉质黏土 | G/Gmax | 0.860 | 0.790 | 0.600 | 0.470 | 0.165 | 0.090 | 0.015 | 0.010 |
| λ | 0.030 | 0.035 | 0.055 | 0.077 | 0.137 | 0.165 | 0.220 | 0.235 | ||
| 3 | 黏土 | G/Gmax | 0.995 | 0.990 | 0.953 | 0.910 | 0.670 | 0.504 | 0.260 | 0.139 |
| λ | 0.032 | 0.043 | 0.083 | 0.105 | 0.154 | 0.168 | 0.182 | 0.184 | ||
| 4 | 粉土 | G/Gmax | 0.994 | 0.988 | 0.943 | 0.893 | 0.625 | 0.455 | 0.246 | 0.138 |
| λ | 0.011 | 0.016 | 0.036 | 0.050 | 0.084 | 0.095 | 0.107 | 0.109 | ||
| 5 | 砂砾 | G/Gmax | 0.993 | 0.985 | 0.924 | 0.858 | 0.544 | 0.374 | 0.107 | 0.056 |
| λ | 0.004 | 0.005 | 0.021 | 0.031 | 0.074 | 0.094 | 0.124 | 0.129 | ||
| 6 | 粗砂 | G/Gmax | 0.965 | 0.935 | 0.775 | 0.660 | 0.300 | 0.250 | 0.105 | 0.090 |
| λ | 0.006 | 0.010 | 0.030 | 0.045 | 0.088 | 0.103 | 0.124 | 0.130 | ||
| 7 | 卵石 | G/Gmax | 0.990 | 0.970 | 0.900 | 0.850 | 0.700 | 0.550 | 0.320 | 0.200 |
| λ | 0.004 | 0.006 | 0.019 | 0.030 | 0.075 | 0.090 | 0.110 | 0.120 | ||
| 注:rd为土体剪应变幅值; G/Gmax为动剪切模量比; λ为阻尼比;粉土、黏土互层非线性参数与黏土相同。 | ||||||||||
为获得1#桥台、2#桥墩、3#桥墩和4#桥台处考虑土层过滤作用后的地表地震波,首先按照场地土层分布和各层土样特征值建立土层过滤效应的计算模型,非线性参数采用MRD法拟合;其次,将所选的20条基岩地震波峰值加速度均按比例调整为0.05g,0.1g,0.2g,0.3g,0.4g,0.5g,0.6g,0.7g,0.8g,0.9g和1.0g后得到220条不同峰值加速度的基岩地震波;最后,基于时域非线性方法将调整后的基岩地震波分别考虑土层对其的过滤作用。因篇幅限制,此处仅列出1#桥台、2#桥墩、3#桥墩和4#桥台处地表地震波的平均反应谱与基岩地震波平均反应谱对比图,如图 2所示。总体来看,3#桥墩处的土层对基岩地震波的平均反应谱峰值放大了1.5倍,而1#桥台、2#桥墩和4#桥台则是缩小为原来的1/4倍,因为3#墩处土层以卵石、砂砾和粗砂分布为主要成分,根据其剪切波速(表 2)可以判断该处土层较硬,其振动频率跟基岩地震波频率相近,产生共振,故对基岩地震波有放大作用。反之,1#桥台、2#桥墩和4#桥台处对基岩地震波又有缩小作用。
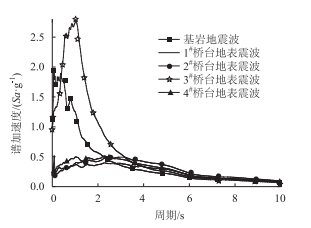
|
| 图 2 反应谱均值 Fig. 2 Average value of response spectrum |
| |
为了避免土层厚度的取值对地震波峰值加速度和反应谱值的影响,根据土层允许地震波传播的最大频率fmax确定土层厚度取值:
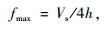
|
(11) |
式中,Vs为土层剪切波速;h为土层厚度;fmax 为土层的地震波传播最大频率,通常要求每层土的地震波最大传播频率不得小于25 Hz。
3 相对位移峰值概率地震荷载作用下,桥台与主梁端部之间的相对位移峰值随地震波的加速度峰值和频谱特性等而变化。在碰撞概率分析时,通常将相对位移峰值假定为极值分布、对数正态分布和正态分布等。为了确定相对位移峰值的概率分布形式,本研究对一致激励和多点激励下桥台-主梁相对位移响应峰值取自然对数,并进行统计分析。经分析后相对位移峰值的自然对数服从正态分布,即相对位移响应峰值服从对数正态分布。一致激励和多点激励下相对位移峰值概率分布如图 3所示。
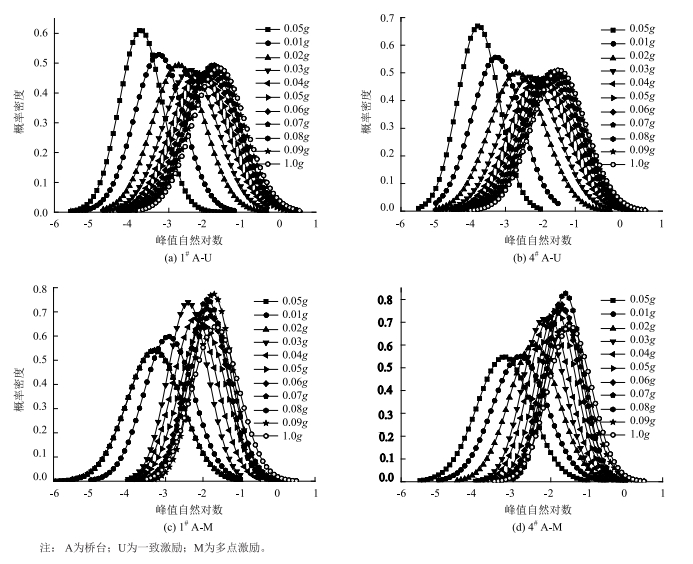
|
| 图 3 相对位移峰值概率密度 Fig. 3 Probability density of peak value of relative displacement |
| |
4 伸缩缝宽度需求值
同一峰值加速度作用下,桥台-主梁相对位移峰值xpeak 服从对数正态分布,其概率密度函数为:
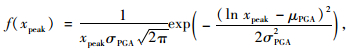
|
(12) |
式中,μPGA 、σPGA 分别为基岩地震波峰值加速度为PGA时,相对位移峰值的对数均值和对数标准差。基于对数正态分布函数的特征,可预测相对位移峰值xpeak有99.74%的概率在区间[exp(μPGA)/[exp(σPGA)]3, exp(μPGA)·[exp(σPGA)]3]内,则将该区间的上限值作为伸缩缝宽度的需求值。
本研究给出了一致激励与多点激励作用下,1#桥台和4#桥台的伸缩缝宽度需求值对比(图 4)。由图 4可见,随基岩地震波峰值加速度和伸缩缝宽度取值的同时增加,伸缩缝宽度需求值均非线性增加;一致激励作用下1#桥台和4#桥台的伸缩缝宽度需求值相差较小,而多点激励作用下1#桥台和4#桥台的伸缩缝宽度需求值相差较大,并且当基岩地震波加速度峰值为0.9g时,多点激励作用下1#桥台和4#桥台的伸缩缝宽度需求值差值最大,约差0.4 m。这是因为一致地震激励各墩底采用的都是一致的基岩地震波,使得各点激励振动一致,激起了桥梁结构反对称的变形响应。而多点激励则是考虑了土层对基岩地震波的过滤作用,各墩底土层分布不同,那么过滤后地震波频谱特性发生改变,使得各点激励不一致,这激起了结构的反对称和正对称变形。各种振动之间有相互抵消部分,使得多点激励条件下伸缩缝需求值变小;当加速度峰值达到0.2g后,一致激励作用下的伸缩缝宽度需求值,开始大于多点激励作用下的需求值,并且差值随加速度峰值的增加而增大。因此,也说明了随着地震强度的增加,一致激励会高估伸缩缝宽度需求值。
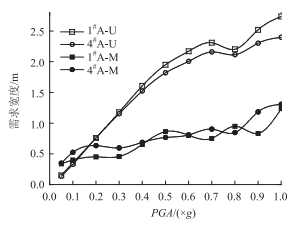
|
| 图 4 伸缩缝宽度需求值 Fig. 4 Requirement value of expansion joint width |
| |
5 碰撞概率
假设地震荷载作用下,当桥台-主梁相对位移值超过伸缩缝宽度时,桥台和主梁之间便会发生碰撞。那么,相同强度指标地震动作用下,桥台-主梁发生碰撞的概率可表示为:

|
(13) |
式中,Δi为伸缩缝宽度;Φ(·)为标准正态分布函数。
为研究伸缩缝宽度取值和场地土层过滤作用对桥台-主梁碰撞概率的影响,一致激励与多点激励作用下1#桥台和4#桥台的碰撞概率,如图 5所示。同时,按照文献[14]中对桥梁系统碰撞概率分析的方法,假设1#桥台和4#桥台的碰撞相互独立,本研究分析了文献[21]中的工况1和工况2两种情况下,桥梁系统发生碰撞概率,如图 6所示。工况1:1#和4#桥台至少有1次发生碰撞的碰撞概率;工况2:1#和4#桥台同时发生碰撞的碰撞概率。
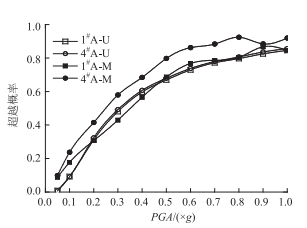
|
| 图 5 碰撞概率 Fig. 5 Pounding probability |
| |
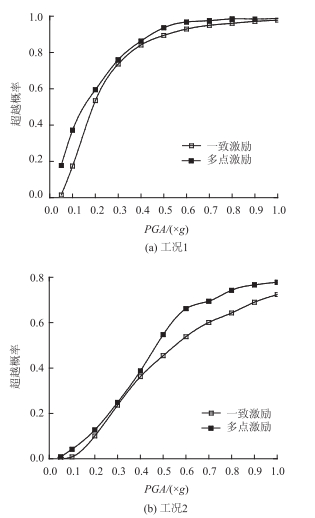
|
| 图 6 系统条件碰撞概率 Fig. 6 Conditional pounding probability of system |
| |
由图 6可见,一致激励作用下1#桥台和4#桥台的碰撞概率曲线基本重合,但是多点激励作用下1#桥台和4#桥台的碰撞概率相差较大,4#桥台比1#桥台处的碰撞概率大,因为4#桥台靠近最高墩(3#墩),高墩对桥端位移限制相对矮墩(2#墩)较弱。因土层作用而导致的多点激励对结构动力响应的影响没有统一的规律,具体桥梁需要具体分析,如随伸缩缝宽度取值的增加,1#桥台和4#桥台的碰撞概率逐渐减小;多点激励作用下4#桥台的碰撞概率在部分加速度峰值下大于一致激励作用。由图 6可见,多点激励作用下工况1和工况2的系统碰撞概率均大于一致激励作用下的系统碰撞概率;工况1时一致激励与多点激励概率基本一致,而在工况2中,多点激励比一致激励下系统碰撞概率最大相差约0.06。
6 结论以某高墩大跨连续刚构桥为研究对象,考虑实际场地土层分布对基岩地震波的过滤作用,并进行多点激励作用下的IDA非线性动力分析,结论如下:
(1) 本研究以基岩峰值加速度为强度指标的多点地震激励下梁体碰撞概率分析方法,解决了多点激励抗震分析强度指标难以确定问题。
(2) 同一地震强度指标下,桥台-主梁相对位移峰值均服从对数正态分布,随着地震强度的增加,一致激励会高估伸缩缝宽度需求值。
(3) 多点激励作用下工况1和工况2均大于一致激励作用下的系统碰撞概率;工况1时一致激励与多点激励概率基本一致,而在工况2中,多点激励比一致激励下系统碰撞概率最大相差约0.06。
| [1] |
申林.基于碰撞效应的混凝土斜拉桥地震响应特征研究[D].西安: 长安大学, 2016. SHEN Lin. Seismic Response Characteristics of Concrete Cable-stayed Bridges Considering Pounding Effects[D]. Xi'an: Chang'an University, 2016. |
| [2] |
WESTERMO B D. The Dynamic of Inter Structural Connection to Prevent Pounding[J]. Earthquake Engineering and Structural Dynamic, 1989, 18(5): 687-699. |
| [3] |
RUANGRASSAMEE A, KAWASHIMA K. Relative Displacement Response Spectra with Pounding Effect[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(10): 1511-1538. |
| [4] |
BI K, HAO H. Influence of Ground Motion Spatial Variations and Local Soil Conditions on the Seismic Responses of Buried Segmented Pipelines[J]. Structural Engineering and Mechanics, 2012, 44(5): 663-680. |
| [5] |
BI K, HAO H. Numerical Simulation of Pounding Damage to Bridge Structures under Spatially Varying Ground Motions[J]. Engineering Structures, 2013, 46: 62-76. |
| [6] |
HUO Y, ZHANG J. Effects of Pounding and Skewness on Seismic Responses of Typical Multi-span Highway Bridges Using the Fragility Function Method[J]. Journal of Bridge Engineering, 2013, 18(6): 499-515. |
| [7] |
王军文, 李建中, 范立础. 连续梁桥纵向地震碰撞反应参数研究[J]. 中国公路学报, 2005, 18(4): 42-47. WANG Jun-wen, LI Jian-zhong, FAN Li-chu. Parametric Study of Longitudinal Seismic Pounding Response for Continuous Girder Bridges[J]. China Journal of Highway and Transport, 2005, 18(4): 42-47. |
| [8] |
李忠献, 周莉, 岳福青. 地震动空间效应与土-基础相互作用效应对隔震桥梁临界碰撞间隙的影响[J]. 土木工程学报, 2010, 43(7): 85-90. LI Zhong-xian, ZHOU Li, YUE Fu-qing. Effects of Spatial Variation of Ground Motion and Soil-foundation Interaction on Critical Pounding Gap Length of Seismic Isolated Bridges[J]. China Civil Engineering Journal, 2010, 43(7): 85-90. |
| [9] |
贾宏宇, 杜修力, 李晰, 等. 地震作用下高墩铁路桥梁梁体碰撞间隙宽度需求机理分析[J]. 工程力学, 2017, 34(2): 207-215. JIA Hong-yu, DU Xiu-li, LI Xi, et al. Demand Mechanism Analysis on Pounding Separation Distance of High Pier Railway Bridges Subjected to Earthquake Excitations[J]. Engineering Mechanics, 2017, 34(2): 207-215. |
| [10] |
李兆焱, 袁晓铭. 2016年台湾高雄地震场地效应及砂土液化破坏概述[J]. 地震工程与工程振动, 2016, 36(3): 1-7. LI Zhao-yan, YUAN Xiao-ming. Seismic Damage Summarization of Site Effect and Soil Liquefaction in 2016 Kaohsiung Earthquake[J]. Earthquake Engineering and Engineering Vibration, 2016, 36(3): 1-7. |
| [11] |
刘鹏, 郑凯锋, 杨雷. 地震作用下的桥梁碰撞分析改进求解方法[J]. 公路交通科技, 2011, 28(3): 76-81. LIU Peng, ZHENG Kai-feng, YANG Lei. An Improved Algorithm for Seismic Pounding Analysis of Bridges[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3): 76-81. |
| [12] |
李黎, 叶志雄, 吴璟. 隔震连续梁桥地震作用下梁间碰撞响应的研究[J]. 公路交通科技, 2009, 26(7): 100-104. LI Li, YE Zhi-xiong, WU Jing. Analysis on Seismic Pounding Responses of Isolated Continuous Girder Bridge under Earthquake Excitation[J]. Journal of Highway and Transportation Research and Development, 2009, 26(7): 100-104. |
| [13] |
刘正楠, 陈兴冲, 张永亮, 等. 地震作用下高速铁路多联大跨连续梁桥碰撞效应研究[J]. 公路交通科技, 2018, 35(12): 63-71, 79. LIU Zheng-nan, CHEN Xing-chong, ZHANG Yong-liang, et al. Study on Pounding Effect of Multi-unit Long-span Continuous Girder Bridge in High-speed Railway under Earthquake[J]. Journal of Highway and Transportation Technology, 2018, 35(12): 63-71, 79. |
| [14] |
JTG/T B02-01—2008, 公路桥梁抗震设计细则[S]. JTG/T B02-01—2008, Guidelines for Seismic Design of Highway Bridges[S]. |
| [15] |
赵金钢, 杜斌, 占玉林, 等. OpenSEES中混凝土本构模型用于模拟结构滞回性能的对比[J]. 桂林理工大学学报, 2017, 37(1): 59-67. ZHAO Jin-gang, DU Bin, ZHAN Yu-lin, et al. Comparison of Constitutive Concrete Models in OpenSees for Hysteretic Behavior of Structures[J]. Journal of Guilin University of Technology, 2017, 37(1): 59-67. |
| [16] |
MAISON B F, KASAI K. Analysis for a Type of Structural Pounding[J]. Journal of Structural Engineering, 1990, 116(4): 957-977. |
| [17] |
MAISON B F, KASAI K. Dynamics of Pounding When Two Buildings Collide[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(9): 771-786. |
| [18] |
陆新征. 美国太平洋地震工程研究中心2018年会"计算模拟"专题大会报告简报[J]. 国际地震动态, 2018(2): 37-39. LU Xin-zheng. Brief Report on "Computational Simulation" Special Session of 2018 Conference of Pacific Earthquake Engineering Research Center[J]. Recent Developments in World Seismology, 2018(2): 37-39. |
| [19] |
李小军, 彭清. 不同类别场地地震动参数的计算分析[J]. 地震工程与工程振动, 2001, 21(1): 29-36. LI Xiao-jun, PENG Qing. Calculation and Analysis of Earthquake Ground Motion Parameters for Different Site Categories[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(1): 29-36. |
| [20] |
MATASOVIC N, VUCETIC M. Cyclic Characterization of Liquefiable Sands[J]. Journal of Geotechnical Engineering, 1993, 119(11): 1085-1821. |
| [21] |
贾宏宇, 杜修力, 李兰平, 等. 地震作用下梁体碰撞间隙宽度的概率分析方法[J]. 工程力学, 2018, 34(2): 207-215. JIA Hong-yu, DU Xiu-li, LI Lan-ping, et al. Probability Analysis of Pounding Separation Distance of Bridges Subjected to Earthquake Excitations[J]. Engineering Mechanics, 2018, 34(2): 207-215. |
 2020, Vol. 37
2020, Vol. 37

 ,
,