扩展功能
文章信息
- 秦世强, 李超, 康俊涛
- QIN Shi-qiang, LI Chao, KANG Jun-tao
- 基于规范的蝶形拱桥试验冲击系数评估
- Evaluation of Experimental Impact Coefficient of Butterfly Arch Bridge Based on Specifications
- 公路交通科技, 2020, 37(2): 55-62
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(2): 55-62
- 10.3969/j.issn.1002-0268.2020.02.008
-
文章历史
- 收稿日期: 2018-12-12
组合梁是桥梁建设中一种十分重要的桥型,钢混叠合梁组合式系杆拱桥具有承载力高、跨越能力强、结构造型优美等系列优点,在实际工程应用中得到工程师的青睐。钢混叠合梁组合式系杆拱桥因自然条件的限制,常选用的结构体系是下承式结构。这种拱桥跨度相对较大、吊杆相对较长,同等跨度桥型中其活载效应相对更加突出、动力作用十分显著。由于这种拱桥受力复杂,结构繁杂多变,研究其结构动力响应、共振分析和抗震设计等特性具有重要意义,而动力冲击系数的计算和研究是其研究内容的关键所在,对研究这种拱桥在行车过程中的动力冲击效应具有指导意义。
目前,世界各国规范对桥梁的动力冲击系数(IMpact coefficient, IM)的取值规定不尽相同,许多学者研究了车辆荷载作用下桥梁结构的动力响应,然而在该问题的一些认识上尚未达成共识[1]。Paultre[2]总结了1992年以前关于桥梁动力学和动力冲击效应评估的研究。李小珍等[3]对公路车桥耦合震动早期的试验研究和经典分析理论进行了回顾,归纳总结了公路车桥耦合振动研究中关于车桥分析模型、路面不平整度及数值计算方法等几个方面的主要成果,认为动力冲击系数与路面不平整度等有直接关系。霍学晋等[4]通过建立车桥耦合动力学模型研究了行车速度等结构设计参数对钢混叠合梁组合式系杆拱桥各构件动力冲击系数的影响,认为行车速度等结构设计参数决定结构动力冲击系数的取值。周勇军等[5]以某刚构-连续组合桥梁为依托工程,采用三轴1/2车辆模型通过正交试验表研究了影响冲击系数的显著性因素,并开展了冲击系数的敏感性因素分析。张鹤等[6]针对结构形式特殊的月牙形多拱肋钢管混凝土桁架拱桥,通过车桥耦合振动分析了影响结构冲击系数的因素,认为行车速度等设计参数决定结构动力冲击系数的取值。周勇军等[7]采用四自由度的1/2车辆模型,建立了车桥耦合振动方程,对比了传统定义法、试验测试法、现行规范法所得的冲击系数计算值并进行了修正。邓露等[8]对近20 a来国内外在公路桥梁动力冲击系数方面的研究进展进行了回顾,分别从试验研究和数值模拟两方面介绍了相关的研究进展和成果,得出了不同参数对动力冲击系数影响不同的结果。吴庆雄等[9]进行了8座钢管混凝土拱桥车振动力响应实测,对钢管混凝土拱肋和悬吊桥道系的冲击系数进行了对比分析,认为结构动力冲击系数与桥梁的跨度呈线性关系。Liu等[10]基于虚功原理,建立了车辆震动耦合模型,分析了在低速超重型车辆作用下结构的动力响应,得出结论为行车速度5 km/h的超重型车辆通过粗糙度为B级时连续梁桥的结构动力冲击系数达到最大。Wang等[11]通过桥梁荷载试验总结了动力冲击系数的取值范围,提出了一种新的验证冲击系数计算方法。Liu等[12]以大跨度铁路桥为研究对象,建立车桥系统耦合模型,计算了在不同车速下结构的冲击系数。
从上述研究可以看出,针对桥梁动力冲击系数已有较多研究成果。但目前关于桥梁冲击系数的计算方法并无统一的认识,各国公路桥梁规范对冲击系数的规定也不尽相同。对复杂桥梁而言,影响结构冲击效应的因素更多,难以用相同的计算公式去定义不同类型构件的冲击效应。因此,依托于试验来确定桥梁不同构件的冲击系数,并结合规范评估试验结果,仍是目前研究复杂桥梁冲击系数最可靠的方法。鉴于此,本研究依托一座蝶形钢管混凝土拱桥,通过动力试验确定主拱和主梁关键截面的冲击系数,在介绍试验工况、试验冲击系数计算方法的基础上,进一步利用各国规范对试验结果进行评估,同时,探讨各国规范对同类型桥梁冲击系数的适用性,试图为同类型桥梁设计过程冲击系数的计算、评估和试验方法提供参考。
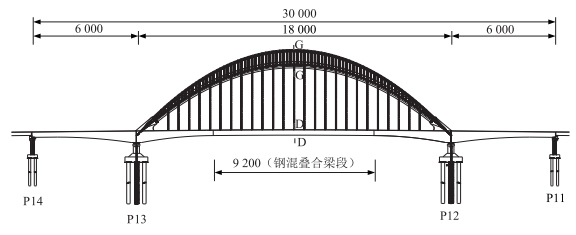
1 工程概况某蝶形拱桥主桥结构形式为钢混叠合梁组合式系杆拱,跨径组合为(60+180+60)m。主桥拱肋由主拱和副拱组成,主拱与副拱之间通过拉杆连接,拱肋外倾呈蝴蝶型,主拱外倾16°,矢跨比为1/4.326,副拱外倾26.882°,矢跨比1/3.346。主跨跨中92 m梁段采用钢混叠合梁,梁高3.0 m,主桥边跨60 m及主桥中跨44 m梁段采用变截面混凝土箱梁,支点梁高6.5 m,边跨跨中梁高3.0 m。主桥标准断面宽度为53 m,跨中宽度为71 m,按双向8车道设计,设计时速为60 km/h。图 1给出了主桥的纵向布置图。
|
| 图 1 桥梁结构纵向布置图(单位:cm) Fig. 1 Longitudinal layout of bridge structure (unit: cm) |
| |
2 桥梁动力试验工况 2.1 环境振动试验工况
环境振动试验主要测试桥跨结构在风、地脉动等微幅振动下的加速度响应,进而识别结构的模态参数。由于多数规范均根据基频来计算结构的冲击系数,因此,准确识别结构的模态参数对后续规范评估有重要的意义。在桥梁环境振动试验中,主拱共布置13个加速度测点,其中1个为参考点,其余测点通过移动传感器完成。主拱上的测点均位于吊杆与拱肋的交点附近,从拱脚附近第1根吊杆与主拱肋交点处,每隔1根吊杆布置1个加速度测点。主桥桥面共计布置21个测点,每隔15 m设置1个测点,其中1个为参考点。所有的环境振动测点处,桥梁的竖向和横向加速度响应均被记录,采样频率为80 Hz,采样时间约为5 min。试验仪器包括数据采集仪和941B型加速度传感器。
2.2 行车、跳车及制动试验工况行车试验工况主要测试主拱跨中截面(G-G)和主梁跨中截面(D-D)在测试车辆以不同车速驶过主桥时的应变时程曲线,从而根据定义计算应变冲击系数。行车试验的测试车辆与静载试验相同,采用30 t重的三轴加载车辆,轴距为(1.8+3.3) m,前轴轴重40 kN,中后轴轴重均为130 kN。行车试验中的车辆行驶速度为10,20,30,40,50 km/h。跳车试验工况中,为模拟桥梁结构的局部损伤对动力响应的影响,在车辆行驶路径上设置1个三角形障碍物,三角形底宽30 cm,高7.5 cm。跳车试验的试验车辆、测试内容与行车试验工况相同,车辆行驶速度为5,15,20,25,30 km/h。制动试验工况中,主要测试加载车辆以40 km/h速度突然制动时桥跨结构的动力响应,并以此计算制动冲击系数。试验的主要仪器设备包括动应变采集仪和应变传感器。
3 试验结果 3.1 模态参数识别模态参数识别的算法包括频域法、时域法和时频分析法,对于土木工程结构低阶模态,各种算法均能获得精确的试验模态参数。本研究选择频域峰值拾取法,利用快速傅里叶变换,将环境振动试验中获得的结构加速度响应转换至频域,并根据不同测试工况下的傅里叶谱峰值识别结构频率和振型。阻尼比采用半功率带宽法进行估算,具体估算公式为:
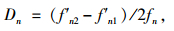
|
(1) |
式中,Dn为阻尼比;fn为第n阶频率;f′n为第n阶半功率带宽频率。由于结构阻尼机理较为复杂,各种方法识别的阻尼比均存在一定的离散性[13]。
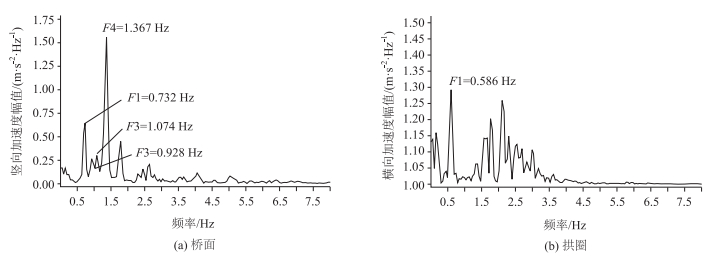
图 2给出了典型的桥面竖向频谱和拱圈横向频谱,表 1列出了试验识别出的桥梁前6阶频率和阻尼比。为评估试验模态参数的精度,基于Midas/Civil建立了主桥的有限元模型(图 3),并将计算得到的模态参数理论值列出进行对比。
|
| 图 2 实测桥梁结构振动频谱图 Fig. 2 Vibration spectra of measured bridge structure |
| |
| 序号 | 振型特征 | 自振频率/Hz | 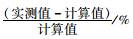
|
阻尼比 | 模态置信值 | |
| 实测值 | 计算值 | |||||
| 1 | 主梁及主拱横弯(对称) | 0.586 | 0.515 | 13.8 | 0.042 | 0.991 |
| 2 | 主拱横弯(对称) | 0.708 | 0.687 | 3.1 | 0.017 | 0.987 |
| 3 | 主拱竖弯(反对称) | 0.806 | 0.789 | 2.2 | 0.014 | 0.946 |
| 4 | 主梁横竖向(反对称) | 0.928 | 0.871 | 6.5 | 0.026 | 0.963 |
| 5 | 主梁竖弯(反对称) | 1.074 | 1.070 | 0.4 | 0.023 | 0.909 |
| 6 | 主梁竖弯(对称) | 1.367 | 1.230 | 11.1 | 0.018 | 0.961 |

|
| 图 3 主桥有限元模型 Fig. 3 FE model of main bridge |
| |
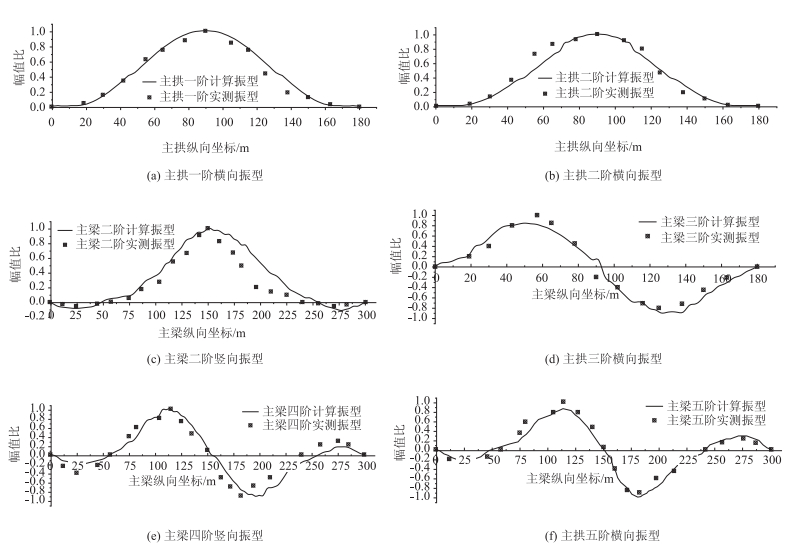
从表 1可以看出,前6阶频率试验值介于0.5~1.4 Hz之间,实测值略高于计算值。试验得到的前两阶振型特征均为主桥横向振动,表明该类型桥梁由于拱肋外倾,其横向刚度相对于竖向刚度略小。阻尼比介于0.01~0.05之间,表明主桥为低阻尼结构。图 4列出了识别的模态振型和计算值之间的对比,各阶振型的模态置信值(Modal Assurance Criterion, MAC)均高于0.9,频率相对误差控制在10%附近,表明环境振动试验得到的试验模态参数精度较高,可进一步用于后续动力冲击系数计算。
|
| 图 4 实测桥梁结构各阶振型 Fig. 4 Measured vibration modes of bridge structure |
| |
3.2 应变冲击系数
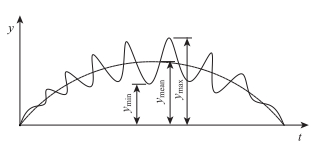
图 5为冲击系数的计算图示。
|
| 图 5 冲击系数计算 Fig. 5 Impact coefficient calculation |
| |
根据图 5,冲击系数IM的定义如下:
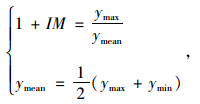
|
(2) |
式中,ymax 为动载作用下该测点最大应变值;ymean 为相应的静载作用下该测点最大应变值;ymax为相应的最大应变值;ymin 为相应的最小应变值。
根据冲击系数的定义及行车、跳车和制动工况下测试到的应变时程曲线,表 2列出了结构在各试验工程下的应变冲击系数。
| 激振 类型 |
车速/ (km·h-1) |
主梁L/2(D-D) 冲击系数 |
主拱L/2(G-G) 冲击系数 |
| 行车 | 10 | 1.05 | 1.19 |
| 20 | 1.11 | 1.12 | |
| 30 | 1.06 | 1.19 | |
| 40 | 1.06 | 1.17 | |
| 50 | 1.09 | 1.23 | |
| 跳车 | 5 | 1.66 | 1.74 |
| 10 | 1.27 | 1.60 | |
| 15 | 1.23 | 1.31 | |
| 20 | 1.48 | 1.21 | |
| 25 | 1.35 | 1.51 | |
| 30 | 1.33 | 1.48 | |
| 制动 | 40 | 1.25 | 1.39 |
根据表 2的数据可知:(1)主梁跨中截面(D-D)行车冲击系数介于1.05~1.11之间,冲击系数峰值1.11对应的车速为20 km/h;跳车冲击系数介于1.23~1.66之间,冲击系数峰值1.66对应的车速为5 km/h;40 km/h车速桥上制动时测到的主梁冲击系数为1.25。(2)主拱跨中截面(G-G)截面行车冲击系数介于1.12~1.23之间,冲击系数峰值1.23对应的车速为50 km/h;跳车冲击系数介于1.21~1.74之间,冲击系数峰值1.74对应的车速为5 km/h;制动工况下,主拱冲击系数为1.39。(3)主梁和主拱低速跳车冲击系数较大,应避免低速跳车。
4 基于规范的试验结果评估 4.1 国内外典型规范各国规范在规定公路桥梁冲击系数时,其取值规定不同。根据冲击系数的取值依据,大致可以将国内外规范分成4类:(1)将冲击系数定义成桥梁跨径的相关函数。例如我国《公路桥涵设计通用规范》(JTJ 021—89)[14]、美国LRFD Bridge Design Specifications 2017版[15]、日本Specifications for Highway Bridges(JRA1996)[16]、新西兰Bridge Manual (SP/M/022) 2013版[17];(2)将冲击系数定义成结构频率的相关函数。例如我国《公路桥涵设计通用规范》(JTG D60—2004,JTG D60—2015)[18-19]、加拿大Ontario Highway Bridge Design Code(Code OHBD 1979, Code OHBD 1983)[20-21];(3)根据桥梁的种类定义冲击系数限值。例如英国Steel, Concrete and Composite Bridges — Part 2: Specification for Loads(BS 5400-2—2006)[22];(4)根据车辆车轴数等其他方式定义桥梁冲击系数。例如加拿大Ontario Highway Bridge Design Code(Code OHBD 1991, Code OHBD 2006)[23-24]、印度Standard Specifications and Code of Practice for Road Bridges — Section II — Loads and Stresses (4th Revision) (IRC6-2000)[25]、澳大利亚Bridge Design Standard — Part 2: Design Loads (AS 5100)[26]等。不同规范按照同类指标规定冲击系数的内容基本思路一致,此处分别选择1种典型规范介绍上述4类规定方法。
4.1.1 日本规范1996版该规范将结构冲击系数定义为桥梁跨径(表 3中L为桥梁跨径)的函数,如表 3所示。表 3表明考虑卡车荷载动力效应时采用的IM对全部类型的桥梁都是一样的,而考虑车道荷载动力效应时采用的IM与桥梁类型有很大联系。
| 桥梁类型 | 加载类型 | 动力冲击系数 |
| 钢桥 | 卡车荷载和车道荷载 | 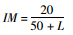
|
| 钢筋混凝土桥 | 卡车荷载 | 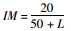
|
| 车道荷载 | 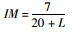
|
|
| 预应力混凝土桥 | 卡车荷载 | 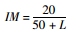
|
| 车道荷载 | 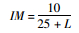
|
4.1.2 我国规范2015版
《公路桥涵设计通用规范》(JTG D60—2015)中对于混凝土桥主要构件,其冲击系数IM按照式(3)进行计算:
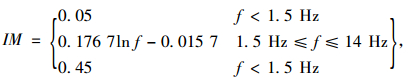
|
(3) |
式中,f为桥梁的基频。与2004版规范相比,2015版规范只是将汽车荷载的局部加载及在T梁、箱梁悬臂板上的IM由1.3修改为0.3。
4.1.3 英国规范2006版英国规范(BS 5400-2—2006)中规定了两种公路桥梁荷载,不规则交通荷载和规则交通荷载。规范在定义设计荷载时已考虑了25%的动力冲击效应,因此不再考虑冲击系数。因此,两种荷载情况下IM都采用0.25。
4.1.4 加拿大规范1979版和1983版加拿大规范Code OHBD 1979和Code OHBD 1983中的冲击系数取值与桥梁基频有关,1979版和1983版的规范根据桥梁的第1阶弯曲频率(基频)来确定IM。当第1阶弯曲频率处于2~5 Hz时,桥梁与车辆容易发生共振现象而采用了较大的IM值。然而在1991版规范中做了很大的修改。1991年版规范中规定IM的取值与车轴数相关,如表 4所示。2006年的新版规范与1991年的规范相比,唯一的区别在于桥面连接处的IM取值为0.5。其具体取值公式如下:
| 车道数 | 动力冲击系数 |
| 1 | 0.4 |
| 2 | 0.3 |
| ≥3 | 0.25 |
(1) 1979版规范中规定的IM公式(4)为:
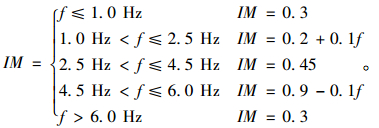
|
(4) |
(2)1983版规范中规定的IM公式(5)为:
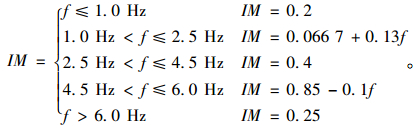
|
(5) |
(3) 1991版和2006版规范中规定的IM见表 4。
4.1.5 印度规范根据印度规范2000版,其冲击系数规定如下。
对于车队荷载:
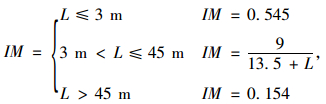
|
(6) |
式中,L为计算跨径。对于轮式车辆,IM=0.25。
4.2 规范评估结果分析从表 5可知,(1)以基频为特征值来描述结构的动力特性:以主梁冲击系数为研究对象,我国规范2004版、2015版符合情况较好,而采用加拿大规范1979版计算出的冲击系数偏高;以主拱冲击系数为研究对象,我国规范1989版符合情况较好,而采用加拿大规范1979版计算出的冲击系数偏大。(2)以跨径为特征值来描述结构的动力特性:以主梁冲击系数为研究对象,我国规范1989版等符合情况均较好;以主拱冲击系数为研究对象,印度规范符合情况较好,而相对于印度规范的其他各国规范则冲击系数偏小;(3)针对所研究的桥梁,各规范规定的冲击系数值与试验值有差异,对此类复杂桥梁的冲击系数,仍依赖于试验结果。
| 规范名称 | 冲击系数(1+IM)规范值 | 冲击系数(1+IM)实测值 | ||
| 主桥 | 主梁 | 主拱 | ||
| 我国规范 | 1989版 | 1.07 | 1.05~1.11 | 1.12~1.23 |
| 2004、2015版 | 1.05 | |||
| 美国规范 | 1989版 | 1.10 | 1.05~1.11 | 1.12~1.23 |
| 1992版 | 1.07 | |||
| 1998、2012版 | 1.15 | |||
| 日本规范 | 1996版 | 1.09 | 1.05~1.11 | 1.12~1.23 |
| 加拿大规范 | 1979版 | 1.30 | 1.05~1.11 | 1.12~1.23 |
| 1983版 | 1.20 | |||
| 2006版 | 1.25 | |||
| 英国规范 | 2006版 | 1.25 | 1.05~1.11 | 1.12~1.23 |
| 新西兰规范 | 2013版 | 1.07 | 1.05~1.11 | 1.12~1.23 |
| 澳大利亚规范 | 2004版 | 1.35 | 1.05~1.11 | 1.12~1.23 |
| 印度规范 | 2000版 | 1.25 | 1.05~1.11 | 1.12~1.23 |
5 结论
本研究介绍了某蝶形拱桥的动力试验工况,并获取了试验模态参数和应变冲击系数。结合国内外典型规范对冲击系数进行了评估,得到如下结论:
(1) 通过环境振动试验,获得了该桥的模态参数,结构基频试验值为0.586 Hz,对应的模态振型为主梁及主拱对称横向振动;通过激振试验获得了主拱和主梁跨中截面的应变冲击系数;行车工况下,主拱和主梁跨中截面应变冲击系数介于1.12~1.23之间;跳车工况下,应变冲击系数介于1.21~1.74之间;试验确定冲击系数表明,主桥结构在运营过程中应避免低速跳车荷载工况。
(2) 基于国内外典型规范评估了试验确定的冲击系数。结果表明,不同规范对桥梁冲击系数规定不同,且计算得到的冲击系数与试验值均有一定的差异;基于频率和跨径的冲击系数计算值与试验值更为接近;对复杂桥梁而言,试验仍是确定冲击系数的最可靠的方法。
| [1] |
郝向炜, 张志, 李岩, 等. 考虑桥面随机不平度的钢管混凝土拱桥冲击系数统计分析[J]. 公路交通科技, 2017, 34(3): 80-86. HAO Xiang-wei, ZHANG Zhi, LI Yan, et al. Statistical Analysis on Impact Factor of CFST Arch Bridge Considering Random Roughness of Bridge Deck[J]. Journal of Highway and Transportation Research and Development, 2017, 34(3): 80-86. |
| [2] |
PAULTRE P, CHAALLAL O, PROULX J. Bridge Dynamics and Dynamic Amplification Factors a Review of Analytical and Experimental Findings[J]. Canadian Journal of Civil Engineering, 1992, 19(2): 260-278. |
| [3] |
李小珍, 张黎明, 张洁. 公路桥梁与车辆耦合振动研究现状与发展趋势[J]. 工程力学, 2008, 25(3): 230-240. LI Xiao-zhen, ZHANG Li-ming, ZHANG Jie. State-of-the-art Review and Trend of Studies on Coupling Vibration for Vehicle and Highway Bridge System[J]. Engineering Mechanics, 2008, 25(3): 230-240. |
| [4] |
霍学晋, 蒲黔辉. 蝶形拱桥的动力冲击系数研究[J]. 振动与冲击, 2014, 33(1): 176-182, 208. HUO Xue-jin, PU Qian-hui. Impact Factors of Butterfly-shaped Arch Bridges[J]. Journal of Vibration and Shock, 2014, 33(1): 176-182, 208. |
| [5] |
周勇军, 赵煜, 史奇彬, 等. 刚构-连续组合桥梁冲击系数多因素灵敏度分析[J]. 振动与冲击, 2012, 31(3): 97-101. ZHOU Yong-jun, ZHAO Yu, SHI Qi-bin, et al. Muti-parameters Sensitivity Analysis of Impact Factors for Rigid-continuous Combined Bridge[J]. Journal of Vibration and Shock, 2012, 31(3): 97-101. |
| [6] |
张鹤, 张治成, 谢旭, 等. 月牙形多拱肋钢管混凝土桁架拱桥动力冲击系数研究[J]. 工程力学, 2008, 25(7): 118-124. ZHANG He, ZHANG Zhi-cheng, XIE Xu, et al. Theoretical Study on the Impact Factor of Crescent-shaped Multi-rib Concrete Filled Steel Tube Truss Arch Bridges[J]. Engineering Mechanics, 2008, 25(7): 118-124. |
| [7] |
周勇军, 蔡军哲, 石雄伟, 等. 基于加权法的桥梁冲击系数计算方法[J]. 交通运输工程学报, 2013, 13(4): 29-36. ZHOU Yong-jun, CAI Jun-zhe, SHI Xiong-wei, et al. Computing Method of Bridge Impact Factor Based on Weighted Method[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 29-36. |
| [8] |
邓露, 王维. 公路桥梁动力冲击系数研究进展[J]. 动力学与控制学报, 2016, 14(4): 289-300. DENG Lu, WANG Wei. Research Progress on Dynamic Impact Factors of Highway Bridges[J]. Journal of Dynamics and Control, 2016, 14(4): 289-300. |
| [9] |
吴庆雄, 黄宛昆, 陈宝春. 中、下承式钢管混凝土拱桥车振调查与动力分析[J]. 工程力学, 2013, 30(1): 147-155. WU Qing-xiong, HUANG Wan-kun, CHEN Bao-chun. Vehicle-induced Vibration Research and Dynamic Analysis for Concrete-filled Steel Tubular Arch Bridges[J]. Engineering Mechanics, 2013, 30(1): 147-155. |
| [10] |
WU Qing-xiong, HUANG Wan-kun, CHEN Bao-chun. Vehicle-induced Vibration Research and Dynamic Analysis for Concrete-filled Steel Tubular Arch Bridges[J]. Engineering Mechanics, 2013, 30(1): 147-155. |
| [11] |
王凌波, 蒋培文, 马印平. 桥梁静载试验校验系数及优化评定方法研究[J]. 公路交通科技, 2015, 32(6): 62-68. WANG Ling-bo, JIANG Pei-wen, MA Yin-ping, et al. Study on Verification Coefficient and Optimization Evaluation Method of Bridge Static Load Test[J]. Journal of Highway and Transportation Research and Development, 2015, 32(6): 62-68. |
| [12] |
LI Y L, DONG S F, BAO Y L, et al. Impact Coefficient Analysis of Long-span Railway Cable-stayed Bridge Based on Coupled Vehicle-bridge Vibration[J]. Shock and Vibration, 2015(5): 1-9. |
| [13] |
秦世强, 康俊涛, 孔凡. 桥梁工作模态分析中阻尼比识别的离散性研究[J]. 振动、测试与诊断, 2016, 36(1): 42-48, 196. QIN Shi-qiang, KANG Jun-tao, KONG Fan. Study on the Discreteness of Damping Ratio Identified from Operational Modal Analysis of Bridge Structure[J]. Journal of Vibration, Measurement and Diagnosis, 2016, 36(1): 42-48, 196. |
| [14] |
JTJ 021—89, 公路桥涵设计通用规范[S]. JTJ 021—89, General Specification for Design of Highway Bridges and Culverts[S]. |
| [15] |
AASHTO. LRFD Bridge Design Specifications[S]. Washington, D.C.: AASHTO, 2017.
|
| [16] |
JRA1996. Specifications for Highway Bridges-Part 1: Common Specifications[S].
|
| [17] |
New Zealand Transport Agency. Bridge Manual(SP/M/022)[M]. Wellington: New Zealand Transport Agency, 2013.
|
| [18] |
JTG D60—2004, 公路桥涵设计通用规范[S]. JTG D60—2004, General Specification for Design of Highway Bridges and Culverts[S]. |
| [19] |
JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General Specification for Design of Highway Bridges and Culverts[S]. |
| [20] |
Code OHBD 1979, Ontario Highway Bridge Design Code[S].
|
| [21] |
Code OHBD 1983, Ontario Highway Bridge Design Code[S].
|
| [22] |
BS 5400-2—2006, Steel, Concrete and Composite Bridges-Part 2: Specification for Loads[S].
|
| [23] |
Code OHBD 1991, Ontario Highway Bridge Design Code[S].
|
| [24] |
Code OHBD 2006, Ontario Highway Bridge Design Code[S].
|
| [25] |
IRC6-2000, Standard Specifications and Code of Practice for Road Bridges-Section Ⅱ-Loads and Stresses (4th Revision)[S].
|
| [26] |
AS 5100, Bridge Design Standard-Part 2: Design Loads[S].
|
 2020, Vol. 37
2020, Vol. 37

 ,
,