扩展功能
文章信息
- 王勇, 黄思奇, 刘永, 许茂增
- WANG Yong, HUANG Si-qi, LIU Yong, XU Mao-zeng
- 基于K-means聚类方法的物流多配送中心选址优化研究
- Study on Optimization of Logistics Multiple Distribution Center Location Based on K-means Clustering Method
- 公路交通科技, 2020, 37(1): 141-148
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 141-148
- 10.3969/j.issn.1002-0268.2020.01.017
-
文章历史
- 收稿日期: 2018-09-16
2. 电子科技大学 经济与管理学院, 四川 成都 611731
2. School of Economics and Management, University of Electronic Science and Technology of China, Chengdu Sichuan 611731, China
物流配送中心选址问题是城市物流配送网络优化的初始环节,是指在一定数目的备选址位置中选择一定数量的地址作为配送中心的规划过程。基于聚类方法的多配送中心选址问题研究,是将涉及选址多重影响因素的聚类方法与选址决策方法相结合,选择合理的配送中心数量和位置作为优化目标,进而保证物流系统规划的可持续发展。
国内外学者在配送中心选址问题研究方面已取得了较多研究成果。部分学者通过目标函数和约束条件构建定量化的数学模型进行选址问题研究,并通过启发式算法进行求解,Dan和Yu[1]提出了应用随机规划模型研究不确定需求下配送中心的选址问题。李东等[2]设计了贪婪取走的启发式方法用于研究设施失效情况下的军事物流配送中心选址问题。姜燕宁和郝书池[3]构建了以系统总成本最低为目标的库存配置与选址决策模型,研究了随机需求情形下多级配送网络的库存-选址优化问题。李明等[4]根据产销平衡的思路建立相应的数学模型研究了多物流配送中心的选址问题。Ye[5]研究了基于梯形直觉模糊信息的多准则群决策,提出了将语言属性通过模糊数转化,从而进行定量计算。而对于一些难以应用数据进行衡量的问题,定性研究体现了优越性。Awasthi等[6]提出在选址因素不确定条件下运用模糊集理论进行选址问题研究。王勇等[7]人提出先建立多配送中心评价指标体系的方法,再结合三角模糊数和语言变量值来研究多配送中心的选址问题。楼振凯和戴晓震[8]应用模糊层次分析法和改进的理想解排序法(TOPSIS)研究了模糊条件下的物流配送中心选址评价问题。贾瑞玉和宋建林[9]应用K-means方法研究了基于聚类中心优化的最佳聚类数确定方法。梁昌勇等[10]设计了基于TOPSIS方法的多属性群排序方法,并将其应用于配送中心的选址排序问题研究中。然而,考虑城市物流多配送中心选址过程的多重因素影响,并进行方法融合方面的研究设计较少。
针对城市多配送中心选址过程需要考虑较多因素且因素间具有复杂相关性的问题,首先,应用模糊理论集理论,将语言变量模糊数和梯形模糊数相结合,在建立的综合评价指标体系下对各指标权重及其各指标进行评价;其次,应用K-means聚类方法对备选配送中心进行分类;最后,应用TOPSIS方法进行各聚类中心备选址的排序计算,得出多配送中心的优化选址方案,并进行了实例验证。所提的多配送中心选址优化方法,为城市物流网络优化中的选址优化相关问题提供了新的研究思路。
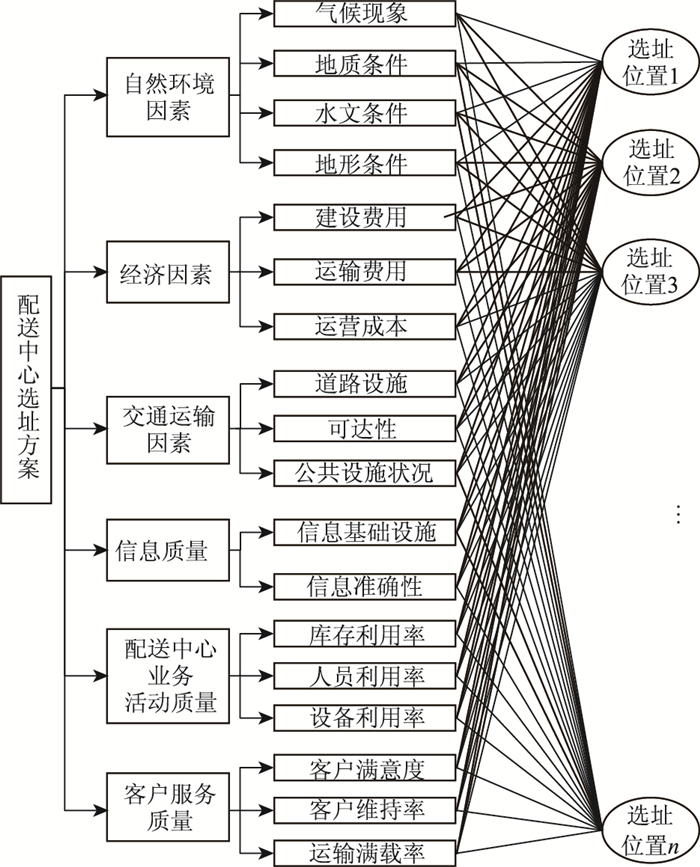
1 配送中心选址的评价指标体系和相关语言变量 1.1 配送中心选址的评价指标体系配送中心选址过程涉及到的自然环境因素(气候条件、地质条件、水文条件和地形条件)和经济因素(建设费用、运输费用和运营成本)属于确定选址的前提条件和外部因素,而选址过程涉及的交通运输因素(道路设施、可达性和公共设施状况)和信息质量(信息基础设施和信息准确性)等是确定选址的决策因素,同时配送中心业务活动质量和客户服务质量属于配送中心选址确定并建立后运营中的管理范畴,因此,将配送中心评价体系分成两级指标,并分别从自然环境因素、经济因素、交通运输因素、信息质量、配送中心业务活动质量、客户服务质量这6个方面对配送中心进行综合评价,具体如图 1所示。
|
| 图 1 多配送中心选址的评价指标体系 Fig. 1 Evaluation index system for location selection of multiple distribution center |
| |
运用梯形直觉模糊数[11-12]表示各配送中心二级准则指标下的各属性权重值和各专家对配送中心评价指标下各属性的评价值。运用模糊集成的方法,将其评价值集成到一级指标上,最终得到综合评价值。
1.2 语言变量和对应的模糊数设计根据建立的配送中心综合评价指标体系,将相关语言变量和相应的梯形模糊数,得到表 1的对应关系,运用其描述配送中心评价指标体系下各属性权重的重要度及其权重。
| 语言变量值 | 变量值缩写 | 模糊值 |
| Very poor | VP | (0.48, 0.53, 0.61, 0.63) |
| Between very poor and poor | B.VP & P | (0.56, 0.61, 0.63, 0.66) |
| Poor | P | (0.62, 0.64, 0.65, 0.72) |
| Between poor and fair | B.P & F | (0.68, 0.71, 0.73, 0.75) |
| Fair | F | (0.72, 0.74, 0.77, 0.82) |
| Between Fair and good | B.F & G | (0.77, 0.79, 0.82, 0.89) |
| Good | G | (0.82, 0.84, 0.87, 0.92) |
| Between good and very good | B.G & VG | (0.86, 0.89, 0.92, 0.94) |
| Very good | VG | (0.92, 0.94, 0.97, 0.99) |
运用上述语言变量值,结合相应的梯形直觉模糊数值,对综合评价指标体系中不同属性的重要度进行评价,从而确定属性权重。对各准则指标权重进行评价时,将语言变量值中的poor替换为low,fair替换为moderate,good替换为high,而其梯形直觉模糊数值不变,即将表 1中的语言变量值缩写转变成VL-VH。
2 基于配送中心评价指标体系的聚类研究 2.1 相关定义针对表 1中的语言变量及相应模糊数表,邀请多位专家对备选配送中心在综合评价指标体系下的二级准则指标进行评价,并对二级准则指标的自身权重进行综合评价,相关定义和符号如下:
定义1参与指标评价的专家人数为s,p表示参与评价的专家集合:p={pi|i=1, 2, …, s}。
定义2设定配送中心评价指标体系中一级指标个数为k,n1表示配送中心评价指标下一级指标的集合:n1={nt1|t=1, 2, 3,…, k}。
定义3设定评价指标体系中一级指标下的二级指标个数为m,n2表示配送中心的二级评价指标的集合:n2= {nt′2|t′=1, 2, 3, …, m}。
定义4设定备选配送中心的个数为n,D表示备选方案的集合是D={DZ|z=1, 2, …, n},通过聚类算法可将备选方案分为F类,C表示备选方案的聚类集合:C={Cg|g=1, 2, …, F}。
定义5专家i对一级指标t下第l个属性的评价值表示为:qi, tl2(i=1, 2, 3, …, s; t=1, 2, 3, …,k),也称模糊属性权重,可用梯形模糊数表示为:qi, tl2=(hi, tl2, gi, tl2, ki, tl2, fi, tl2,);专家i在二级指标t′下对选址方案z′的评价值为yi, z′, t′2(i=1, 2, …, s; z′=1, 2, …, n; t′=1, 2, …, m);专家i对方案z′在一级指标t下第l个属性上的值表示为:Yi, z′, tl2(i=1, 2, …, s; z′=1, 2, …, n′; t=1, 2, …, k),可用模糊数表示为:Yi, z′, tl2=(ai, z′, tl2, bi, z′, tl2, ci, z′, tl2, di, z′, tl2);一级准则指标t下对应备选配送中心的评价值表示为:Ut, z′1=(Tt, z′1, Qt, z′1, Ht, z′1, Et, z′1),(t=1, 2, 3, …, k; z′=1, 2, 3, …, n)。
定义6备选配送中心的聚类数据集表示为:w=(x1, x2, …, xn),其中选出的k个聚类中心表示为:(β1, β2, …, βk),每个聚类对象到聚类中心的距离使用欧式距离表示为:
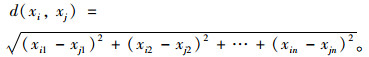
|
(1) |
定义7 Y为一个给定的数据集,假定在数据集Y中有n个聚类子集,分别表示为:y1, y2, …, yn,其中,每个聚类子集中的样本数量表示为:k1, k2, …, kn;每个聚类子集均有一个聚类中心点,其聚类中心表示为:g1, g2, …, gn。因此,设定误差平方和准则函数公式E为:

|
(2) |
备选配送中心的聚类方法包括以下两个步骤:(1)运用模糊集成方法,对备选配送中心评价指标评价体系中的二级指标进行模糊评价,再结合二级指标体系中各自的权重,将二级指标的评价值集成到一级指标上。(2)将集成到一级指标上的指标值,通过K-means算法同模糊聚类算法结合,对备选配送中心进行聚类。
2.2.1 二级准则指标下的模糊集成方法由定义5可知,Yi, z′, tl2=(ai, z′, tl2, bi, z′, tl2, ci, z′, tl2, di, z′, tl2),qi, tl2=(hi, tl2, gi, tl2, ki, tl2, fi, tl2),由多位专家对配送中心z′在一级评价指标t上的综合评价值Ut, z′1表示为:
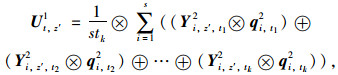
|
(3) |
式中,s为参与评价的专家人数; tk为一级指标属性t下包含的二级准则指标的个数; ⊕为矢量相加,⊗为矢量之积。
2.2.2 模糊K-means聚类方法模糊K-means聚类方法的具体实现步骤如下:
(1) 若梯形模糊数的表示形式为:w=(a, b, c, d),则可将p(w)表示为梯形模糊数的集成数值:
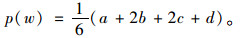
|
(4) |
由定义5可知,将集成后一级准则指标的梯形模糊数值对应的隶属度函数μt, z′1表示为:

|
(5) |
(2) 将隶属度函数μt, z′1拆分成3个属性值,分别表示为:ej, 1,ej, 2,ej, 3,并设fj(xz′)=μt, z′1,通过下式计算各子属性对应的隶属度函数值:qej, 1(xz′)=fj(xz′),qej, 2(xz′)=kj, 1-fj(xz′),qej, 3(xz′)=kj, 3-|fj(xz′)-kj, 2|,kj, 1=max{fj(x1), fj(x2), …, fj(xn)},kj, 2= 
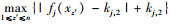
(3) 首先从备选的配送中心中选择k个对象作为初始的聚类中心,确定簇的数量为k。
(4) 将ej, 1,ej, 2,ej, 3作为聚类的输入,运用欧式距离公式计算出聚类对象到k个聚类中心的欧式距离d(xi, xj),根据欧式距离并结合各聚类中心位置划分不同的聚类单元。
(5) 在已划分好的聚类单元中,重新计算各个聚类单元的样本平均值,并将其值作为聚类单元的新中心。
(6) 重复上述步骤(4)和(5),并进行聚类结果的比较分析,进而计算公式(2)中的E值,E值越小,表示聚类结果越理想,当聚类中心不再改变或达到指定的迭代次数时,则聚类结束并得到聚类结果。
2.3 模糊聚类方法的有效性指标应用模糊K-means聚类方法[13]进行计算时,由于k值是事先拟定的,为了评判最终聚类结果的合理性,需要对聚类结果的有效性进行评价验证。聚类结果有效性[13]的评价指标可以包括两个方面,一方面是外部标准,若得出的聚类结果与参考准则保持一致,则为合理的聚类结果,否则,为不合理的聚类结果;另一方面是内部指标,即通过聚类有效性指标确定最佳的聚类数。通常应用内部指标评价聚类结果具有一定的科学性和合理性。设定DB样本的类内离散度和各聚类中心间距:
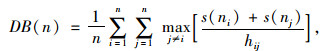
|
(6) |
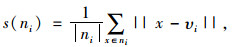
|
(7) |
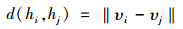
|
(8) |
式中,n为聚类数目;s(ni)和s(nj)分别为每类中的所有样本到其聚类中心的平均距离;d(hi, hj)为类与类之间的中心距离;ni为类i中的样本个数;υi,υj分别为聚类中心。由此可知,DB越小表示类与类之间的相似度越低,从而聚类结果越佳。
3 TOPSIS排序方法结合模糊聚类方法得到的聚类结果,应用TOPSIS排序方法进行聚类单元内的备选址评价排序[11]。若有h个评价对象和o个评价指标,则原始评价矩阵可表示为:

|
(9) |
对指标进行标准化和去量钢化处理,具体计算公式如下:
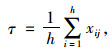
|
(10) |
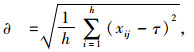
|
(11) |
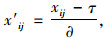
|
(12) |
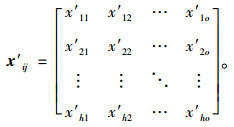
|
(13) |
TOPSIS排序方法[14]是检验各评价对象和正理想值、负理想值距离进行排序。其中,正理想值由待评价对象中每个属性值的最优值组成,而负理想值由待评价对象中每个属性值的最劣值组成,进而计算出每个方案与最优和最差值的距离。最优值和最差值分别表示为Z+和Z-,则n个评价方案的欧式距离公式如下:
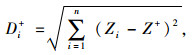
|
(14) |
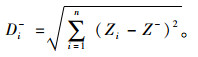
|
(15) |
而与正理想值和负理想值的相对靠近程度需通过公式
以某企业在重庆市选择配送中心为案列,经过考察后有20个备选配送中心,分别用D1,D2,…,D20来表示。同时邀请5位专家对建立的指标体系中二级准则指标下的备选配送中心的选址评价及二级准则指标权重进行评价,其中5位专家用P={P1, P2, P3, P4, P5}表示。专家运用表 1中语言变量值的模糊数,对指标评价体系下的二级准则指标的权重进行评价(如下表 2所示)。运用2.2节中提到的二级准则指标下的模糊集成方法,应用模糊集成方法将相应的二级准则指标的权重值和专家对其的评价值集成到一级指标上,然后,运用2.2.2节中提到的方法将集成到一级准则指标上的值重新拆分成3个属性值,并表示为:qej, 1, qej, 2, qej, 3。
| 二级准则指标 | 各专家对二级准则指标自身权重的评价 | ||||
| P1 | P2 | P3 | P4 | P5 | |
| t11 | B.VL & L | L | L | B.VL & L | B.VL & L |
| t12 | M | B.L & M | M | B.L & M | M |
| t13 | M | B.M & H | M | M | B.M & H |
| t14 | B.H & VH | H | VH | H | VH |
| t21 | B.H & VH | B.H & VH | H | H | B.H & VH |
| t22 | H | B.H & VH | H | B.H & VH | H |
| t23 | B.H & VH | VH | H | H | B.H & VH |
| t31 | B.L & M | M | M | M | B.L & M |
| t32 | VH | VH | B.H & VH | B.H & VH | VH |
| t33 | M | B.L & M | B.L & M | M | M |
| t41 | VH | VH | VH | VH | VH |
| t42 | B.H & VH | H | B.H & VH | H | B.H & VH |
| t51 | H | H | B.M & H | B.M & H | H |
| t52 | B.H & VH | H | B.H & VH | B.H & VH | B.H & VH |
| t53 | H | B.H & VH | H | H | B.H & VH |
| t61 | VH | B.H & VH | VH | VH | B.H & VH |
| t62 | B.H & VH | VH | VH | VH | B.H & VH |
| t63 | H | H | B.M & H | H | B.M & H |
通过表 2中二级准则指标权重的评价值和表 1中的模糊数表相结合,得到二级准则指标下的评价值,通过模糊集成方法,将二级准则指标下的评价值集成到一级准则指标上。得到各备配送中心的综合评价值,由表 3所示:
| D1 | D2 | D3 | D4 |
| (1.839, 1.951, 2.088, 2.317) | (1.834, 1.950, 2.085, 2.296) | (1.839, 1.956, 2.093, 2.304) | (1.763, 1.879, 2.010, 2.222) |
| D5 | D6 | D7 | D8 |
| (1.793, 1.907, 2.040, 2.258) | (1.936, 2.014, 2.155, 2.366) | (1.900, 2.018, 2.160, 2.359) | (1.927, 2.042, 2.187, 2.396) |
| D9 | D10 | D11 | D12 |
| (1.911, 2.022, 2.168, 2.405) | (1.914, 2.030, 2.175, 2.389) | (2.019, 2.137, 2.288, 2.491) | (1.949, 2.064, 2.211, 2.385) |
| D13 | D14 | D15 | D16 |
| (1.901, 2.012, 2.157, 2.385) | (1.919, 2.034, 2.178, 2.389) | (1.931, 2.049, 2.193, 2.396) | (1.906, 2.021, 2.162, 2.367) |
| D17 | D18 | D19 | D20 |
| (1.941, 2.062, 2.207, 2.400) | (1.923, 2.032, 2.180, 2.410) | (2.025, 2.145, 2.260, 2.496) | (1.917, 2.032, 2.177, 2.390) |
运用K-means方法对各备选配送中心进行聚类时,首先应用式(4)、(5)计算隶属度函数值,并将隶属度函数μt, z′1拆分成3个属性值[15-16],分别用qej, 1, qej, 2, qej, 3来表示,取fj(xz′)=μt, z′1,最终得到各配送中心的子属性对应的隶属度函数值,如表 4所示。
| 属性值 | 配送中心综合评价值 | |||||||||||||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | D14 | D15 | D16 | D17 | D18 | D19 | D20 | |
| qej, 1 | 2.039 | 2.033 | 2.04 | 1.961 | 1.991 | 2.107 | 2.102 | 2.13 | 2.116 | 2.119 | 2.227 | 2.153 | 2.104 | 2.122 | 2.135 | 2.106 | 2.147 | 2.126 | 2.234 | 2.121 |
| qej, 2 | 0.194 | 0.2 | 0.194 | 0.273 | 0.243 | 0.127 | 0.131 | 0.103 | 0.118 | 0.115 | 0.007 | 0.081 | 0.13 | 0.112 | 0.098 | 0.128 | 0.087 | 0.108 | 0.072 | 0.113 |
| qej, 3 | 2.185 | 2.179 | 2.186 | 2.106 | 2.136 | 2.25 | 2.248 | 2.227 | 2.241 | 2.238 | 2.13 | 2.204 | 2.25 | 2.235 | 2.222 | 2.251 | 2.21 | 2.231 | 2.123 | 2.236 |
4.2 聚类和选址方案
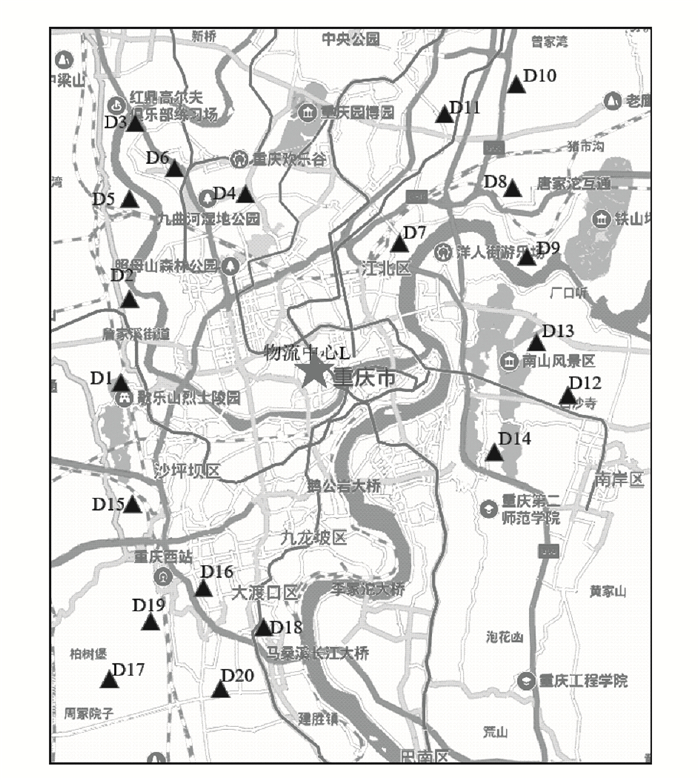
结合选址方案的时效性和合理性,本研究将聚类数目设定在3到5之间。根据上述聚类有效性指标的计算公式(6),(7),(8),具体的聚类结果和不同聚类结果的聚类有效性指标如表 5和图 2所示。
| 聚类数 | DB值 | 类别名称 | 配送中心 |
| 3类 | 1.035 | 类1 | D1 D2 D4 D7 D11 D13 D14 D15 D16 |
| 类2 | D6 D8 D12 D18 | ||
| 类3 | D3 D5 D9 D10 D17 D19 D20 | ||
| 4类 | 1.623 | 类1 | D2 D4 D7 D11 D13 D14 D16 |
| 类2 | D1 D6 D8 D15 | ||
| 类3 | D5 D12 D18 | ||
| 类4 | D3 D9 D10 D17 D19 D20 | ||
| 5类 | 1.257 | 类1 | D2 D4 D7 D14 D16 |
| 类2 | D1 D6 D8 D13 | ||
| 类3 | D11 D12 D15 D19 | ||
| 类4 | D5 D9 D18 | ||
| 类5 | D3 D10 D17 D20 |
|
| 图 2 不同聚类数目的聚类有效性指标 Fig. 2 Clustering Validity Indicators of different cluster numbers |
| |
当DB越小时,其聚类效果越好,表明聚类单元中同类别个体间的差距越小,而不同类别个体间差距越大。因此当聚类数为3时得到最佳聚类数目:{D1, D2, D4, D7, D11, D13, D14, D15, D16},{D6, D8, D12, D18},{D3, D5, D9, D10, D17, D19, D20}。为了进一步验证聚类结果的有效性,分别应用文献[17]提出的一种基于Spark框架的改进DBSCAN聚类算法和文献[18]提出的BIRCH聚类算法进行聚类比较分析,如表 6所示。
| 聚类方法 | 聚类结果 | 聚类有效性指标 |
| 模糊K-means聚类方法 | 类1 D1 D2 D4 D7 D11 D13 D14 D15 D16 类2 D6 D8 D12 D18 类3 D3 D5 D9 D10 D17 D19 D20 | 1.035 |
| 改进DBSCAN聚类算法 | 类1 D2 D4 D5 D7 类2 D1 D6 D8 D9 D11 类3 D10 D12 D15 D17 D20 类4 D13 D14 D16 D18 D19 | 1.672 |
| BIRCH聚类方法 | 类1D1 D2 D4 D11 D14 D16 类2D6 D7 D8 D12 D15 D18 D19 D13 类3D3 D5 D9 D10 D17 D20 | 1.316 |
由表 6可知,模糊K-means聚类方法计算得到的聚类有效性指标最小,聚类结果较其他两个方法更为合理。基于上述模糊K-means聚类方法的聚类结果,应用TOPSIS方法在各类中进行排序,最终选出最优配送中心位置。结合表 3中已拆分成3个属性值的结果,运用TOPSIS方法计算得到类1中Zi+=(2.227, 0.273, 2.251),Zi-=(1.961, 0.007, 2.106);类2中Zi+=(2.153, 0.127, 2.256),Zi-=(2.107, 0.081, 2.204),类3中Zi+=(2.234, 0.243, 2.241),Zi-=(1.991, 0, 2.123),运用公式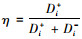
| 指标 | 类1 | ||||||||
| D1 | D2 | D4 | D7 | D11 | D13 | D14 | D15 | D16 | |
| η | 0.495 3 | 0.500 0 | 0.532 5 | 0.444 4 | 0.522 7 | 0.443 5 | 0.455 1 | 0.466 2 | 0.442 9 |
| 指标 | 类2 | ||||||||
| D6 | D8 | D12 | D18 | ||||||
| η | 0.416 8 | 0.526 3 | 0.602 3 | 0.495 1 | |||||
| 指标 | 类3 | ||||||||
| D3 | D5 | D9 | D10 | D17 | D19 | D20 | |||
| η | 0.497 7 | 0.521 1 | 0.452 3 | 0.454 5 | 0.477 3 | 0.526 6 | 0.455 9 | ||
应用模糊K-means聚类方法后,在每个聚类单元中运用TOPSIS排序方法选取一个配送中心为最终配送中心。根据上表中的计算数值,可知当η值越小,其评价结果越高。因此,选取最小的η值作为各类中的最优评价值,即选出最优配送中心为D6,D9,D16。结合图 2可知,此方法选出的配送中心位置合理。因此,基于模糊K-means聚类算法的物流多配送中心选址方法,将集成后的隶属度函数重新拆分成多个隶属度函数子属性值,能够挖掘有效的聚类属性特征和划分更合理的聚类方案,可以保证最终得到较优的配送中心选址方案。综合比较上述方法,本研究所提方法更具实践应用性。
5 结论研究了物流网络中的多配送中心选址问题,首先,对一系列备选配送中心建立了评价指标体系,通过对备选配送中心在指标体系中的二级准则指标及其权重进行综合评价,并将语言变量模糊数和梯形模糊数相结合,得到二级准则指标及其权重的评价值;其次,应用模糊集成方法将二级准则指标的评价值集成到一级准则指标上,并通过隶属度函数进行属性拆分;最后,将拆分属性值作为模糊K-means聚类方法的输入,并通过聚类有效性指标值选取合理的备选配送中心聚类方案,进而应用TOPSIS方法计算出聚类后各聚类中的排序,从而选出最优配送中心选址方案。最后,应用实例验证了所提方法的有效性,该方法也能应用到多级物流网络的配送中心选址过程中。
| [1] |
ZHUGE D, YU S, ZHEN L, et al. Multi-period Distribution Center Location and Scale Decision in Supply Chain Network[J]. Computers & Industrial Engineering, 2016, 101: 216-226. |
| [2] |
李东, 晏湘涛, 匡兴华. 考虑设施失效的军事物流配送中心选址模型[J]. 计算机工程与应用, 2010, 46(11): 3-6. LI Dong, YAN Xiang-tao, KUANG Xing-hua. Location Model for Military Logistics Distribution Centers Considering Facilities Failure[J]. Computer Engineering and Applications, 2010, 46(11): 3-6. |
| [3] |
姜燕宁, 郝书池. 基于部分跨级和集中存储模式的库存配置与选址决策模型[J]. 公路交通科技, 2016, 33(11): 152-158. JANG Yan-ning, HAO Shu-chi. Inventory Allocation and Location Decision Model Based on Partial Cross-level and Centralized Storage[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 152-158. |
| [4] |
李明, 刘航, 张晓建. 多物流配送中心的选址布局问题优化模型研究[J]. 重庆交通大学学报:自然科学版, 2017, 36(1): 97-102. LI Ming, LIU Hang, ZHANG Xiao-jian. Research on the Optimization Model of Site Selection and Layout of Logistics Distribution Center[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2017, 36(1): 97-102. |
| [5] |
YE J. Multicriteria Group Decision-making Method Using the Distances-based Similarity Measures between Intuitionistic Trapezoidal Fuzzy Numbers[J]. International Journal of General Systems, 2012, 41(7): 729-739. |
| [6] |
AWASTHI A, CHAUHAN S S, GOYAL S K. A Multi-criteria Decision-making Approach for Location Planning for urban Distribution Centers under Uncertainty[J]. Mathematical & Computer Modelling, 2011, 53(1-2): 98-109. |
| [7] |
毛海军, 王勇, 杭文, 等. 基于模糊聚类算法的多配送中心选址优化方法[J]. 东南大学学报:自然科学版, 2012, 42(5): 1006-1011. MAO Hai-jun, WANG Yong, HANG Wen, et al. Optimization Method of Multi-distribution Center Location Based on Fuzzy Clustering Algorithm[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(5): 1006-1011. |
| [8] |
楼振凯, 戴晓震. 模糊条件下配送中心选址评价方法研究[J]. 华东交通大学学报, 2017, 34(3): 81-87. LOU Zhen-kai, DAI Xiao-zhen. Study on Evaluation Methods of Distribution Center Location under Fuzzy Condition[J]. Journal of East China Jiaotong University, 2017, 34(3): 81-87. |
| [9] |
贾瑞玉, 宋建林. 基于聚类中心优化的K-means最佳聚类数确定方法[J]. 微电子学与计算机, 2016, 33(5): 62-66. JIA Rui-yu, SONG Jian-lin. K-means Optimal Clustering Number Determination Method Based on Clustering Center Optimization[J]. Microelectronics & Computer, 2016, 33(5): 62-66. |
| [10] |
梁昌勇, 戚筱雯, 丁勇, 等. 一种基于TOPSIS的混合型多属性群决策方法[J]. 中国管理科学, 2012, 20(4): 109-117. LIANG Chang-yong, QI Xiao-wen, DING Yong, et al. A Hybrid Multi-criteria Group Decision Making with TOPSIS Method[J]. Chinese Journal of Management Science, 2012, 20(4): 109-117. |
| [11] |
陈晓红, 李喜华. 基于直觉梯形模糊TOPSIS的多属性群决策方法[J]. 控制与决策, 2013, 28(9): 1377-1381. CHEN Xiao-hong, LI Xi-hua. Group Decision Making Based on Novel Trapezoidal Intuitionistic Fuzzy TOPSIS Method[J]. Control and Decision, 2013, 28(9): 1377-1381. |
| [12] |
陈良莉, 黄天民. 一种基于属性加权综合直觉梯形模糊数多属性决策方法[J]. 西南民族大学学报:自然科学版, 2017, 43(1): 76-81. CHEN Liang-li, HUANG Tian-min. Multiple Attribute Decision Method Based on Attribute Weighted Comprehensive Intuitionistic Trapezoidal Fuzzy Numbers[J]. Journal of Southwest University for Nationalities:Natural Science Edition, 2017, 43(1): 76-81. |
| [13] |
赵凤霞, 谢福鼎. 基于K-means聚类算法的复杂网络社团发现新方法[J]. 计算机应用研究, 2009, 26(6): 2041-2043. ZHAO Feng-xia, XIE Fu-ding. Detecting Community in Complex Networks Using K-means Cluster Algorithm[J]. Application Research of Computers, 2009, 26(6): 2041-2043. |
| [14] |
肖俊华, 侯云先. 综合模糊TOPSIS决策的应急物资储备库多级覆盖选址模型[J]. 工业工程, 2013, 16(1): 91-98. XIAO Jun-hua, HOU Yun-xian. An Emergency Supply Stockpile Location Model by Combining Fuzzy TOPSIS Method and Multi-level Coverage[J]. Industrial Engineering Journal, 2013, 16(1): 91-98. |
| [15] |
WANG Y, MA X L, WANG Y H, et al. Location Optimization of Multiple Distribution Centers under Fuzzy Environment[J]. Journal of Zhejiang University Science A:Applied Physics & Engineering, 2012, 13(10): 782-798. |
| [16] |
WANG Y, MA X L, LAO Y T, et al. A Fuzzy-Based Customer Clustering Approach with Hierarchical Structure for Logistics Network Optimization[J]. Expert Systems with Applications, 2014, 41(2): 521-534. |
| [17] |
宋董飞, 徐华. DBSCAN算法研究及并行化实现[J]. 计算机工程与应用, 2018, 54(24): 52-56. SONG Dong-fei, XU Hua. Research and Parallelization of DBSCAN Algorithm[J]. Computer Engineering and Applications, 2018, 54(24): 52-56. |
| [18] |
李捷承, 陶耀东, 孙咏, 等. 基于BIRCH聚类的物流配送设施选址算法[J]. 计算机系统应用, 2018, 27(9): 215-219. LI Jie-cheng, TAO Yao-dong, SUN Yong, et al. Location Algorithm of Logistics Distribution Facilities Based on BIRCH Clustering[J]. Computer Systems & Applications, 2018, 27(9): 215-219. |
 2020, Vol. 37
2020, Vol. 37
