扩展功能
文章信息
- 田秀珠, 高悦尔, 王成, 曹堉
- TIAN Xiu-zhu, GAO Yue-er, WANG Cheng, CAO Yu
- 轨道共线段公交发车班次优化
- Optimization of Bus Departure Frequency in Rail Transit Common Section
- 公路交通科技, 2020, 37(1): 115-121, 130
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 115-121, 130
- 10.3969/j.issn.1002-0268.2020.01.014
-
文章历史
- 收稿日期: 2019-03-20
2. 华侨大学, 建筑学院 福建 厦门 361021
2. School of Architecture, Huaqiao University, Xiamen Fujian 361021, China
轨道交通以其安全、节能、运量大、无污染、节约土地等优势,逐渐在我国大城市公共交通建设中占据主导地位,而且轨道交通的线路走向和常规公交的主要线路往往沿着城市客流走廊布设。轨道交通开通之前,为满足乘客出行要求,作为城市中主要公共交通工具的常规公交一般在客流需求大的路段设置密集的公交线路,导致路段交通拥堵严重,通行能力下降。轨道交通开通之后,共线段客流由常规公交转移至轨道交通,导致公交客流量和服务效果降低[1],然而密集的公交线路对道路通行能力的影响不变。为了合理利用资源,提高公共交通运营效率,缓解道路交通拥堵问题,轨道交通共线段常规公交线路调整问题亟待解决。
国外学者对轨道交通共线段常规公交线路调整的研究较少,多研究常规公交线路的服务可靠性和调度优化,并针对具体的研究方案采用相应的求解算法。Chow等[2]通过对信号配时的优化调整,提出了提高公交服务可靠性的最优控制方程和开环求解算法;Ibarra-Rojas O J等[3]将公交车的时间表和调度问题的整数线性规划模型组合成一个双目标集成模型,用∈约束方法来求解;Berrebi等[4]将公交调度问题表述为随机决策过程,用后向归纳法得到最优策略;Konstantinos等[5]根据公交运营的服务质量对公交车调度重新建模,用顺序启发式算法进行求解;Ruiz等[6]结合有关公交路线的地理数据和城市地区的经济信息,通过协调模拟和优化程序来调整公交路线。而国内学者对常规公交线路的研究主要从乘客和企业的利益角度来分析调度问题,通过构建公交发车频率的多目标模型,采用最优化搜索和遗传算法等得到最优解[7-9]。对轨道交通共线段常规公交线路调整的研究则主要集中在线网优化和线路调整两方面,线网优化主要考虑公交与轨道的协同运营、公交车辆配置,线路调整主要研究轨道交通影响下常规公交线路的取消、缩短、延伸、走向调整等。张思林[10]和陈丹等[11]分别构建了轨道交通影响范围内接运公交车的车辆配置、发车频率和常规公交线网的优化模型,并用遗传算法进行求解。其中张思林[10]量化了公交车辆运行对环境的影响,以发车间隔、满载率和车辆数限制为约束条件,以公交乘客的出行成本、公交企业的运营成本和政府的碳排成本最小为目标函数;而陈丹等[11]结合轨道交通与常规公交相互协调的特点,以公交线路长度和非直线系数为约束条件,以研究范围内乘客出行时耗最小为目标函数。李家斌[12]和房涛[13]则是对地面公交与轨道的竞争与协作进行分析,提出了地面公交线网调整目标和原则,对轨道和公交两者的网络衔接模式分类,结合线路客流特征,制订了不同的线路调整措施。李家斌等[14]还提出了轨道交通走廊上公交线路调整措施制订流程。
综上所述,国外对常规公交线路的调整多关注公交服务可靠性和公交车调度,国内对轨道交通共线段常规公交线路的调整多关注公交与轨道交通的协同运营,对公交发车班次的调整主要从乘客和企业角度出发建立优化模型并用启发式算法求解实现公交线网的调整优化,未考虑共线段常规公交线路调整之后的剩余公交线路发车班次优化问题。在公共交通优先发展政策的导向下,国内很多城市将公交专用道作为提升公交服务能力的道路空间管控措施,因此本研究将公交专用道的通行能力作为轨道交通共线段可通行常规公交车交通量的限制。根据公交车GPS数据和公交刷卡数据获取常规公交车数量和客流情况,以常规公交线路高峰小时平均满载率为目标函数,对超出公交专用道通行能力的剩余常规公交线路进行发车班次调整。
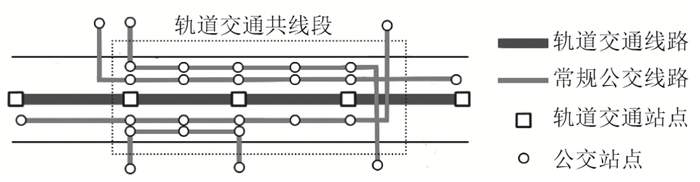
1 轨道交通共线段常规公交线路和发车班次调整数量确定 1.1 轨道交通共线段常规公交线路确定轨道交通共线段常规公交线路指:在同一客流走廊内,常规公交线路与轨道交通线路的走向全部或部分相同且都经过某一轨道站点的平行地面公交线路,如图 1所示。
|
| 图 1 轨道交通共线段常规公交线路示意图 Fig. 1 Schematic diagram of conventional bus lines in common section of rail transit |
| |
1.2 轨道交通共线段常规公交发车班次调整数量确定
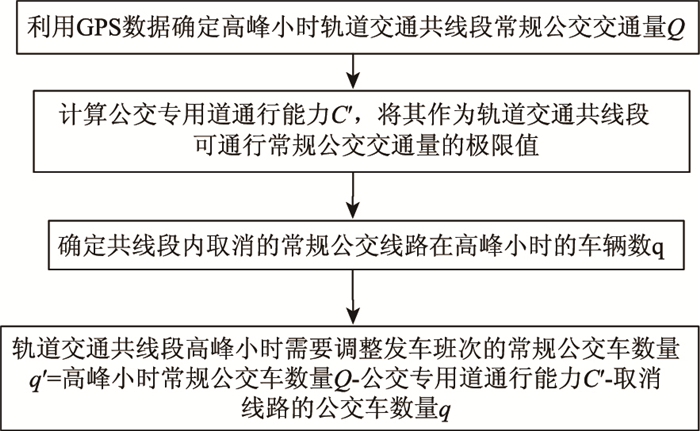
为满足高峰期间乘客对公共交通的需求,公交公司通常会在高峰期间增加常规公交的发车班次,而轨道交通开通之后,客流一般会受轨道交通的吸引而发生转移。为提高公共交通运营效率,需要对高峰期间与轨道交通共线段的常规公交线路做出调整。本研究提出以轨道交通共线段可通行常规公交的交通量极限值作为约束条件对常规公交线路进行调整,首先确定剩余常规公交线路的调整量,然后通过调整发车班次来实现对共线段常规公交车交通量的控制,即需要确定轨道交通共线段常规公交发车班次调整量,具体流程如图 2所示。
|
| 图 2 公交专用道通行能力约束下确定轨道交通共线段常规公交发车班次数量调整的流程图 Fig. 2 Flowchart of determining adjustment of frequency of conventional bus departures for rail transit common section under bus lane capacity constraints |
| |
1.2.1 公交专用道通行能力定义
公交专用道的通行能力是指在一定的运营环境和服务水平下,某个断面一段时间内单方向所能通过的承载一定乘客数量的最大公交车辆数0。根据常规公交在不同形式的公交专用道上交叉口、公交站点的车流运行状况对通行能力的折减,将公交专用道的通行能力分成3部分,分别计算公交专用道在经过交叉口、公交站点和基本路段的通行能力,取其最小值作为轨道共线段可通行常规公交交通量的标准值。
1.2.2 公交专用道通行能力模型公交专用道通行能力取经过交叉口、公交站点、基本路段通行能力的最小值(以标准公共汽车为单位),即:
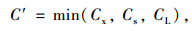
|
(1) |
式中, C′为公交专用道的通行能力;Cx,Cs,CL分别为公交专用道在信号交叉口、公交站点和基本路段的通行能力。
(1) 公交专用道在信号交叉口的通行能力
一条公交专用道在信号交叉口的设计通行能力计算公式为:
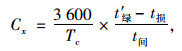
|
(2) |
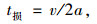
|
(3) |
式中, Cx为一条公交专用道在信号交叉口的设计通行能力;Tc为信号周期;t′绿为相位绿灯时间;t损为一个周期内的绿灯损失时间,包括启动、加速时间,一般只计加速时间损失;v为直行车辆通过交叉口的车速,一般取15 km/h;a为平均加速度,公交车取0.45 m/s2;t间为前后两车接连通过停车线的平均间隔时间,公交车平均为3.5 s。
(2) 公交站点通行能力
公交站点按照几何形状可以分为直线式和港湾式,不同形状公交站点的有效停靠效率是有差异的,通常多停靠位公交站点通行能力是单停靠位公交站点通行能力与相应几何形状公交站点的有效停靠效率的乘积[14],即:
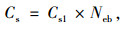
|
(4) |
其中:
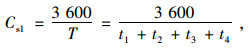
|
(5) |
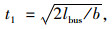
|
(6) |
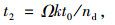
|
(7) |
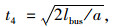
|
(8) |
式中,Cs为多停靠位公交站点通行能力;Cs1为单停靠位公交站点的通行能力;Neb为公交站点的有效停靠效率;T为1辆公交车占用公交站点的总时间;t1为车辆的进站时间,其中lbus是驶入车站时,车辆之间的最小间隔,通常取车辆长度lbus=10 m,b为进站时的制动减速度,一般取b=1.5 m/s2;t2为乘客上下车占用的时间,Ω为公共汽车的容量(人/辆),k为上下车乘客占车容量的比例,一般取k=0.3,t0为每个乘客上车或下车所用时间,平均约为2 s,nd为乘客上下车用的车门数;t3为车辆开门和关门的时间,为3.5 s;t4为车辆启动和离开车站的时间,a为车辆离开车站时的加速度,可取a=10 m/s2。
(3) 公交专用道基本路段通行能力
公交专用道基本路段的通行能力受到交叉口、公交专用道布设形式和公交站点的影响,本研究的公交专用道布设形式为路侧式+直线式公交站点。
① 交叉口影响下的公交专用道基本路段的设计通行能力
在交叉口影响下的公交专用道基本路段的设计通行能力为:
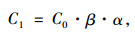
|
(9) |
其中:
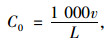
|
(10) |
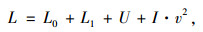
|
(11) |
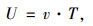
|
(12) |
式中,C1为交叉口影响下的公交专用道基本路段的设计通行能力;C0为公交专用道基本路段的可能通行能力;β为交叉口影响修正系数;α为道路分类系数;v为行驶速度;L为连续车流的车头间距;L0为停车时的车辆安全车间距,取L0=2m;L1为车辆的本身长度,取L1=10 m;v为行驶车速;I为与车重、路面阻力系数、黏着系数及坡度有关的系数,通常城市道路设计I值近似为0.054;U为司机在反应时间内车辆行驶的距离;T=1.2 s左右。根据计算结果,公交专用道基本路段的可能通行能力建议值可取1 200 pcu/h。
交叉口影响修正系数β主要取决于交叉口的控制方式及交叉口间距,其中无信号控制的交叉口,影响修正系数为1,信号控制的交叉口按照下式(13)计算得到[17]:
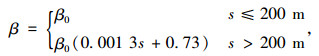
|
(13) |
式中,s为交叉口间距;β0为交叉口有效通行时间比,视路段起点交叉口控制方式而定,信号交叉口即为绿信比,如果计算的β大于1,则取β=1。
② 直线式公交站点影响下的路侧式公交专用道设计通行能力
路侧式公交专用道在只有一个直线式公交站点影响时的设计通行能力为:
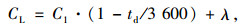
|
(14) |
式中,td为公交影响时间;λ为公交车在停靠站的到达率;其他符号含义同前。
其中公交影响时间根据公交车进出站点的过程,由公交车加减速进出站的时间、乘客上下车的时间以及公交车开关门的时间构成[18],计算公式如下:
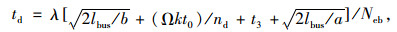
|
(15) |
式中, Neb为直线式公交站点的有效停靠效率,其他符号含义同前。
当一条公交专用道上有两个或多个公交站点时,基本路段上的设计通行能力需考虑多个站点的折减,即在前一个公交站点折减之后的通行能力基础上再做折减。
2 构建模型 2.1 问题假设(1) 以公交专用道通行能力作为轨道交通共线段可容纳常规公交车交通量的极限值;
(2) 每条常规公交线路上的客流不会流失;
(3) 常规公交车型统一,座位数和最大容量为定值。
2.2 高峰小时平均满载率高峰小时平均满载率指在高峰小时内与轨道交通共线段的常规公交在共线段内平均载客量与额定载客量之比。若轨道交通与常规公交线路共线的公交站点少于3个,公交出行的乘客一般不考虑换乘到轨道,因此将不少于3个共线公交站点的常规公交线路作为调整对象,利用高峰小时公交刷卡数据得到轨道交通共线段内每条常规公交线路的满载率。
高峰小时平均满载率用公式表达如下:
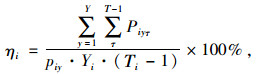
|
(16) |
式中,ηi为第i条常规公交线路在轨道共线段内高峰小时平均满载率;Piyτ为第i条常规公交线路第y辆车在轨道共线段内第τ个相邻站点间高峰小时载客量;piy为第i条常规公交线路第y辆车的额定载客量;Yi为高峰小时内第i条常规公交线路经过轨道共线段的公交车辆总数;Ti为第i条常规公交线路经过轨道共线段内的公交站点总数。
在实际生活中,部分乘客会投币上车,所以需要对由公交刷卡数据得到的满载率进行扩样,即:
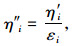
|
(17) |
式中,η″i为第i条常规公交线路扩样之后的高峰小时平均满载率;η′i为第i条常规公交线路在轨道共线段内高峰小时平均满载率;εi为第i条常规公交线路刷卡客流量与总客流量的比值。
2.3 轨道交通共线段常规公交发车班次调整模型轨道交通开通之后,部分客流转移至轨道交通,导致与轨道交通共线段的常规公交线路高峰小时平均满载率下降,为节约公共资源提出通过调整发车班次来提高高峰小时平均满载率,使与轨道交通共线段的所有常规公交线路的最小高峰小时平均满载率最大化,即:
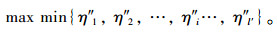
|
(18) |
从轨道交通共线段可通行常规公交的交通量、发车间隔、高峰小时平均满载率3个方面,得到如下约束条件:
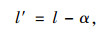
|
(19) |
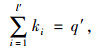
|
(20) |
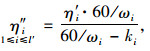
|
(21) |
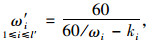
|
(22) |
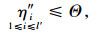
|
(23) |
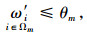
|
(24) |
式中,l为轨道交通共线段常规公交线路总数;α为轨道交通共线段被取消的常规公交线路和共线段少于3个公共站点的公交线路总和;l′表示轨道交通共线段需减少发车班次的常规公交线路总数;ki表示共线段第i条常规公交线路减少的发车班车次数;q′表示常规公交线路需减少的发车班次总量;η′i表示第i条常规公交扩样之后的高峰小时平均满载率;ωi表示第i条常规公交线路的原发车间隔;η″i表示第i条常规公交发车班次减少ki个发车班次之后的高峰小时平均满载率;ω′i表示第i条常规公交发车班次减少ki个发车班次之后的发车间隔;Θ表示常规公交车最高满载率;{Ω1,Ω2,…,Ωm,…,ΩM}表示常规公交线路根据区域划分为不同的组团;θm表示第i条常规公交线路所在第m组团的最大发车间隔。
3 模型求解 3.1 贪心算法目前国内外学者对常规公交线路的调整多从公交线网出发,以公交车流量、乘客出行成本、公交企业的运营成本、乘客等待时间等为目标函数,利用开环求解算法、∈约束方法、后向归纳法、遗传算法等进行求解。本研究对轨道交通共线段常规公交发车班次调整主要涉及高峰小时平均满载率该单变量和减班次总量、发车间隔以及满载率等多个约束条件,用单步贪心算法进行求解, 针对每条待调整公交线路进行调整,并得到每条公交线路的调整方案。贪心算法在对问题求解时,总是做出在当前看来是最好的选择;从全局来看,运用贪心策略解决的问题在运行过程中无回溯过程,具有思维复杂度低、运行效率高、空间复杂度低等优点,在满足约束条件的情况下可保证得到局部最优解。
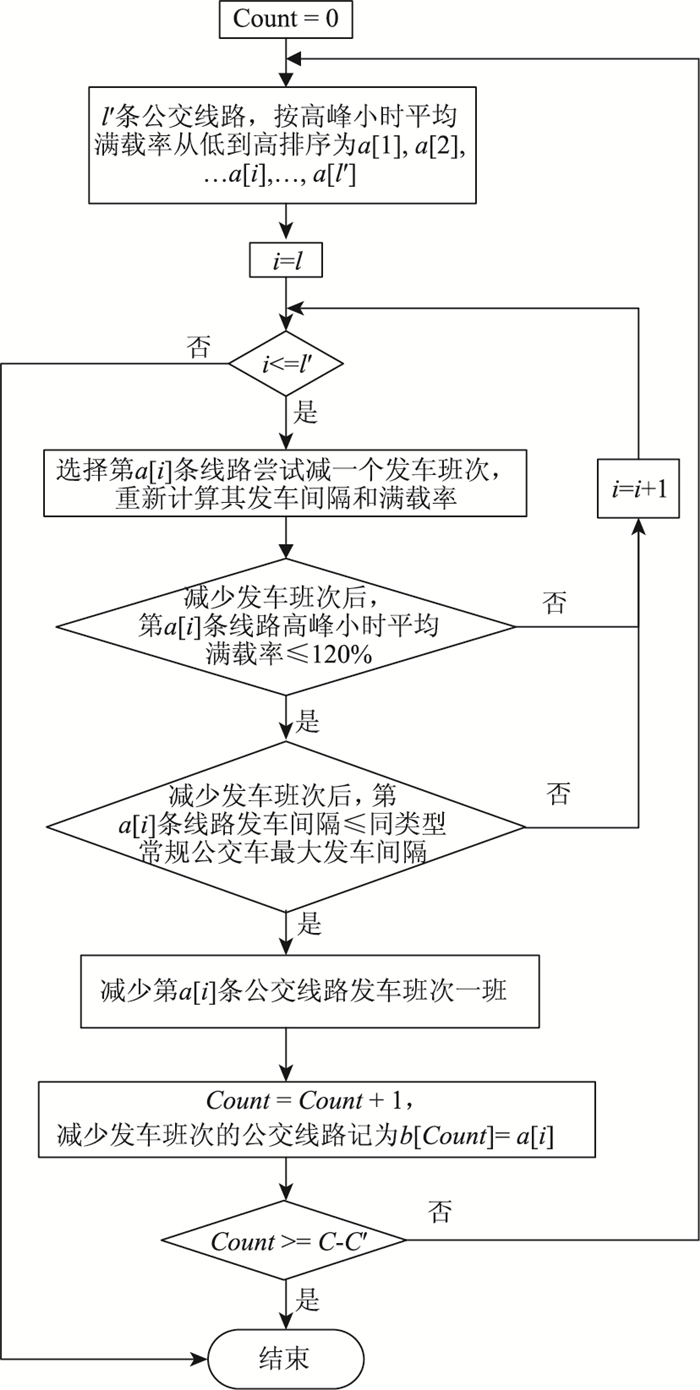
3.2 计算步骤轨道交通共线段常规公交发车班次调整流程如图 3所示。
|
| 图 3 最大等车时间和满载率约束下基于单步贪心算法的最大化最小满载率流程图 Fig. 3 Flowchart of maximizing minimum full load rate based on single-step greedy algorithm under maximum waiting time and full load rate constraints 备注:Count指减少的公交车流量;′指轨道交通共线段常规公交线路总数;高峰小时平均满载率关系为:η″a[1]≤ηa[2]≤…≤ηa[i]≤…≤ηa[l′];b[Count]记录减少发车班次的公交线路;C指轨道交通共线段常规公交现状交通量;C′指公交专用道通行能力。 |
| |
Step 1 Count表示减少的公交车数量,此时Count=0;
Step 2 计算轨道交通共线段l′条常规公交线路高峰小时扩样后的平均满载率,并按平均满载率从低到高排序:a[1], a[2], …, a[i], …, a[l′];
Step 3 选择高峰小时平均满载率低的第a[i]路公交尝试减一个发车班次,重新计算其高峰小时平均满载率和发车间隔;
Step 4 减少发车班次之后,验证第a[i]路公交高峰小时平均满载率是否小于等于120%,若满足则进行下一步,否则重新选择高峰小时平均满载率低的公交线路进行第2步;
Step 5 验证第a[i]路公交发车间隔是否小于等于所属常规公交线路类型的最大发车间隔,若满足则进行下一步,否则重新选择高峰小时平均满载率低的公交线路进行第2步;
Step 6 减少第a[i]路公交发车班次一班,此时Count=Count+1;
Step7 判断减少的公交车流量是否大于现状交通量与公交专用道通行能力之差,若大于则公交发车班次调整结束,否则按照调整之后的发车班次重新计算常规公交车高峰小时平均满载率并排序,从第2步开始,循环调整,直到满足减少的公交车流量大于轨道交通共线段常规公交减班次数量。
4 算例分析 4.1 模型参数输入将案例城市7:308:30早高峰期间由GPS数据和刷卡数据获得的轨道交通共线段常规公交的交通量和客流量作为模型的输入。根据实地调查,轨道交通开通之前高峰小时内共线段常规公交线路有27条,常规公交车有161辆。其中课题已有研究,取消4条轨道交通共线较长的公交线路,即取消28辆常规公交车。模型中涉及到的参数有:路侧式+2个直线式公交站点的公交专用道通行能力作为案例城市待研究轨道交通共线段可通行常规公交车交通量,由公式(1)到(15)得到公交专用道在信号交叉口、公交站点和基本路段的通行能力分别是,Cx=293 pcu/h,Cs=229 pcu/h,CL=356 pcu/h,所以公交专用道的通行能力C′=229 pcu/h,取公交专用道的饱和度为0.4,得到轨道交通共线段可通行常规公交车的交通量为92 pcu/h,实际通行的公交车辆数超出了共线段可通行常规公交车的交通量,常规公交车需调整的交通量为q′=41 pcu/h。所有常规公交线路的额定载客piy=70人/辆;常规公交线路刷卡客流量与总客流量的比值均为εi=66%;常规公交车最高满载率Θ=120%;常规公交线路最大发车间隔θm=20 min,由公式(16)和(17)得到待调整常规公交线路扩样之后的高峰小时平均满载率。对轨道交通共线段剩余的23条公交线路进行筛选,将经过轨道交通共线段公交站点不少于3个的常规公交线路作为调整对象,经过少于3个的常规公交线路保持发车班次不变。经过筛选,最终只对8条常规公交线路进行发车班次调整。
4.2 结果及分析按高峰小时平均满载率对8条线路进行排序,选满载率最小的进行发车班次调整,若调整之后高峰小时平均满载率和发车间隔不满足满载率和最大发车间隔的约束要求,则不调整该条线路的发车班次,若满足条件则按照图 3所示继续对常规公交线路进行调整,直到常规公交车辆数满足公交专用道通行能力的约束。
对8条常规公交线路进行发车班次调整之后,共可减少33个班次的常规公交车。调整结果如表 1所示,其中46,128,129,657路常规公交线路因达到最大发车间隔而终止调整,132,658路常规公交线路因达到最大发车间隔和最大满载率而终止调整,10,123路常规公交线路因达到最大满载率而终止调整。用单步贪心算法求解最大化最小满载率的调整发车班次数学模型最终获得常规公交调整发车班次的线路排序,以及调整前、后常规公交车满载率和发车间隔的变化。
| 公交线路 | 发车班次减少量/(pcu·h-1) | 高峰小时平均满载率/% | 发车间隔/min | ||
| 调整前 | 调整后 | 调整前 | 调整后 | ||
| 46 | 3 | 10.5 | 21.1 | 10 | 20 |
| 128 | 6 | 22.4 | 63.9 | 7 | 20 |
| 129 | 4 | 27.7 | 61.5 | 9 | 20 |
| 657 | 0 | 36.4 | 36.4 | 20 | 20 |
| 132 | 6 | 37.6 | 107.4 | 7 | 20 |
| 658 | 6 | 37.6 | 107.4 | 7 | 20 |
| 10 | 5 | 52.6 | 112.7 | 7 | 15 |
| 123 | 3 | 76.3 | 108.9 | 7 | 10 |
5 结论
本研究提出了以轨道交通共线段的常规公交线路最小高峰小时平均满载率最大化为目标函数,以轨道交通共线段可通行常规公交车交通量的极限值、最大发车间隔、最大满载率为约束条件,采用单步贪心算法对目标函数进行求解,利用公交车GPS数据和公交刷卡数据对案例城市进行算例分析,最终得到每条常规公交线路发车班次的调整方案。
本研究在一定程度上对常规公交发车班次进行了优化,但公交专用道的通行能力是基于经验公式获得,今后可通过交通仿真软件vissim对公交专用道通行能力进行验证;同时算例中由于数据的缺失,没有考虑不同线路之间刷卡率的不同和各个团组最大发车间隔的差异,且仅使用了一天的观测数据、GPS数据、公交刷卡数据,今后可补全数据做进一步完善,并根据多天运行的数据进行平均和相互验证,去除随机性;此外,共线段常规公交线路减班次调整是在客流不会流失假设条件下进行的,可根据实际情况研究调整发车班次之后客流流失模型及发车班次再调整。
| [1] |
章玉, 黄承锋, 许茂增. 中国城市公交的运营效率与服务效果研究[J]. 公路交通科技, 2017, 34(1): 154-158. ZHANG Yu, HUANG Cheng-feng, XU Mao-zeng. Operation Efficiency and Service Effectiveness of Transit in China[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 154-158. |
| [2] |
CHOW A H F, LI S, ZHONG R. Multi-objective Optimal Control Formulations for Bus Service Reliability with Traffic Signals[J]. Transportation Research Part B:Methodological, 2017, 103: 248-268. |
| [3] |
IBARRA-ROJAS O J, GIESEN R, RIOS-SOLIS Y A. An Integrated Approach for Timetabling and Vehicle Scheduling Problems to Analyze the Trade-off between Level of Service and Operating Costs of Transit Networks[J]. Transportation Research Part B:Methodological, 2014, 70(7): 35-46. |
| [4] |
BERREBI S, WATKINS K E, LAVAL J A. A Real-time Bus Dispatching Policy to Minimize Passenger Wait on a High Frequency Route[J]. Transportation Research Part B:Methodological, 2015, 81: 377-389. |
| [5] |
GKIOTSALITIS K, STATHOPOULOS A. Demand-Responsive Public Transportation Re-scheduling for Adjusting to the Joint Leisure Activity Demand[J]. International Journal of Transportation Science & Technology, 2016, 5(2): 68-82. |
| [6] |
RUIZ M, SEGUI-PONS J M, MATEU-LLADÓ J. Improving Bus Service Levels and Social Equity through Bus Frequency Modelling[J]. Journal of Transport Geography, 2017, 58: 220-233. |
| [7] |
陈茜, 牛学勤, 陈学武, 等. 公交线路发车频率优化模型[J]. 公路交通科技, 2004, 21(2): 103-108. CHEN Qian, NIU Xue-qin, CHEN Xue-wu, et al. Bus Service Frequency Optimal Model[J]. Journal of Highway and Transportation Research and Development, 2004, 21(2): 103-108. |
| [8] |
方雅君, 郑长江, 马庚华, 等. 公交发车频率优化研究[J]. 贵州大学学报:自然科学版, 2017, 34(6): 132-135. FANG Ya-jun, ZHENG Chang-jiang, MA Geng-hua, et al. Study on Bus Departure Frequency Optimization[J]. Journal of Guizhou University:Natural Science Edition, 2017, 34(6): 132-135. |
| [9] |
谷金晶, 杨艳, 张敬东. 考虑到站时间差的多层级常规公交时刻表[J]. 公路交通科技, 2016, 33(6): 128-133. GU Jin-jing, YANG yan, ZHANG Jing-dong. Timetable of Multi-level Transit Considering Arrival Time Difference[J]. Journal of Highway and Transportation Research and Development, 2016, 33(6): 128-133. |
| [10] |
张思林.城市轨道交通接运公交线网规划与运营方案优化方法研究[D].北京: 北京交通大学, 2017. ZHANG Si-lin. Approaching Feeder Bus Network Planning and Operating Scheme Linked with Urban Rail Transit[D]. Beijing: Beijing Jiaotong University, 2017. |
| [11] |
陈丹, 徐文远. 基于遗传算法的轨道交通与常规公交线路优化方案[J]. 西北大学学报:自然科学版, 2016, 46(3): 364-370. CHEN Dan, XU Wen-yuan. Optimization Scheme of Rail Transportation and Conventional Bus Lines Based on Genetic Algorithm[J]. Journal of Northwest University:Natural Science Edition, 2016, 46(3): 364-370. |
| [12] |
李家斌, 过秀成, 姜晓红, 等. 城市轨道交通运营初期地面公交线网调整策略研究[J]. 现代城市研究, 2014(10): 50-54. LI Jia-bin, GUO Xiu-cheng, JIANG Xiao-hong, et al. Research on the Adjustment Strategy of Bus Line Network in Initial Operations of Urban Mass Transit[J]. Modern Urban Research, 2014(10): 50-54. |
| [13] |
房涛, 赵贤兰, 栾长飞. 竞争性常规公交与城市轨道交通衔接调整方法研究——以青岛市地铁3号线为例[J]. 城市公共交通, 2018(8): 37-41. FANG Tao, ZHAO Xian-lan, LUAN Chang-fei. Study on the Connection Adjustment Method of Competitive Conventional Public Transport and Urban Rail Transit:Take Qingdao Metro Line 3 as an Example[J]. Urban Public Transport, 2018(8): 37-41. |
| [14] |
李家斌, 过秀成, 王峰. 城市轨道交通走廊上道路公交线路的调整措施[J]. 城市轨道交通研究, 2017, 20(10): 88-92, 133. LI Jia-bin, GUO Xiu-cheng, WANG Feng. Adjustment of Bus Lines in Urban Rail Transit Corridor[J]. Urban Mass Transit, 2017, 20(10): 88-92, 133. |
| [15] |
陈宽民, 严宝杰. 道路通行能力分析[M]. 北京: 人民交通出版社, 2003. CHEN Kuan-min, YAN Bao-jie. Highway Capacity Analysis[M]. Beijing: China Communications Press, 2003. |
| [16] |
Kittelson & Associates Inc. TCRPl00:Transit Capacity and Quality of Service Manual[M]. 2nd ed. Washington, D.C: Kittelson & Associates Inc., 2003.
|
| [17] |
任福田, 刘小明, 荣建. 交通工程学[M]. 北京: 人民交通出版社, 2003. REN Fu-tian, LIU Xiao-ming, RONG Jian. Traffic Engineering[M]. Beijing: China Communications Press, 2003. |
| [18] |
孙锋, 金茂菁, 王殿海, 等. 公交站点对路段通行能力的影响研究[J]. 北京理工大学学报, 2013, 33(12): 1284-1288. SUN Feng, JIN Mao-jing, WANG Dian-hai, et al. Study of the Effect of Bus Stop on Roadway Link Capacity[J]. Transactions of Beijing Institute of Technology, 2013, 33(12): 1284-1288. |
 2020, Vol. 37
2020, Vol. 37
