扩展功能
文章信息
- 王嘉文, 陈超, 金杨, 杨晓芳, 董洁霜
- WANG Jia-wen, CHEN Chao, JIN Yang, YANG Xiao-fang, DONG Jie-shuang
- 考虑人车交互的两相位信号控制交叉口行人专用相位设置条件
- Setting Condition of Exclusive Pedestrian Phase at Two-phase Signalized Intersections Considering Pedestrian-vehicle Interaction
- 公路交通科技, 2020, 37(1): 96-103
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 96-103
- 10.3969/j.issn.1002-0268.2020.01.012
-
文章历史
- 收稿日期: 2019-01-04
2. 上海市公安局交通警察总队, 上海 200070
2. Traffic Police Team of Shanghai Public Security Bureau, Shanghai 200070, China
常规两相位信号控制交叉口的每个相位均存在人车交互行为,如人车相互避让,减速让行等。这些交互行为导致行人与机动车通行延误增加,甚至避让失效时会进一步升级为人车交通事故,造成人身伤亡和经济损失[1]。合理设置的行人专用相位可完全消除两相位信号控制交叉口的人车交互区域,以略微提升延误为代价保证了行人过街安全[2]。在我国,自《道路交通安全法》(以下简称新交规)于2013年1月1日修订后,转弯车辆需让行交叉口正常通行行人。该法规进一步保证了信号控制交叉口的行人安全,也导致人车交互行为模式明显的改变,影响了发生人车交互时产生的延误。在部分城市,新交规发布后机动车服从率未达到100%[3-4],过街行人有概率让行机动车。即使是在同一个城市,由于交叉口设施、环境的影响等因素,人车交互行为亦存在变化[5-6]。由于人车交互时行人避让车辆或车辆避让行人时产生的交通参与者总延误估计方法不同,亟需研究不同人车交互行为下行人专用相位设置条件,通过估计并比较不同方案下交通参与者的总延误,更合理地选择交叉口信号控制模式。
行人专用相位(Exclusive Pedestrian Phase,EPP)是指信号控制交叉口所有机动车进口道均显示为红灯信号,使行人可以同时在所有方向(包括对角线)穿越交叉路口的相位[7]。针对行人专用相位的研究可以总结为优化安全性与优化通行效率两类[8]。在安全方面,许多研究认为,行人专用相位消除了机动车与行人之间的所有交互,因此有助于提高信号控制交叉口安全性能[9]。而在通行效率方面,马万经等[8]提出了一种包括交叉口行人专用相位和传统行人相位的多目标优化模型及其优化行人相位模式的求解算法。模型能够根据交叉口车辆的交通情况和行人运动确定当前最佳行人相位模式以提高交叉口运行效率。Hediyeh[10]做了更细致的研究,分析了步态参数受行人性别、年龄、群体大小、人行横道长度及行人信号指示的影响,从微观层面了解了行人的步行机制的变化和各种行人和交叉口特征的影响。韩印等[11]分析了行人流随机消散和集中消散特征的差异性,运用随机分布理论推导出右转车辆穿越行人流延误模型,得到车辆与行人交互行为时的平均延误。综合效率与安全因素,此前有诸多研究[12-13]深入分析了行人专用相位的设置条件,但大多数研究没有深入考虑人车交互行为因素。
不同人车交互行为将影响行人专用相位实施效果[12]。国内外学者研究发现交通环境因素[14-16]、行人因素[1, 10, 17]、机动车辆因素[15, 18]等均会影响信号控制交叉口人车交互行为。而人车交互行为会直接影响信号控制交叉口交通模型(包括通行能力估计模型、延误估计模型等)[17, 19],进而会改变行人专用相位的设置条件。对人车交互行为的分析方面,胡宏宇等[20]基于视频图像处理技术分析了信号交叉口人车交互行为中交互行为的辨识方法,陆斯文等[21]基于人车冲突和微观碰撞机理建立了行人过街的危险度评价指标。本研究则在上述学者研究基础上,运用交叉口视频数据分析交叉口人车交互行为,作为信号控制交叉口模型的输入条件之一。
综上,目前国内外积累了行人专用相位研究成果,提出了考虑安全性能、通行效率等方面的行人专用相位优化方法。然而,通行效率方面的研究中,大多以机动车、行人的效率指标(如延误、通行能力)或二者的组合优化为优化目标,没有充分考虑我国交通环境中以人为本的重要诉求;并且在模型中鲜有考虑我国各地人车交互行为的巨大差异,使得模型在我国不同城市的应用存在一定的误差。
本研究在以下两点内容补充了既有研究内容:(1)在行人专用相位设置条件中,创新地采用交通参与者总延误(按照每一名交通参与者计算总人×小时)作为优化目标,以体现拟设行人专用相位交叉口对交通参与者的公平性要求;(2)在交通参与者总延误估计模型中,考虑人车交互行为中行人避让机动车、机动车避让行人行为在不同城市、不同交叉口的差异性,引入了避让率因素,从而在不同人车交互行为环境下更准确地给出是否设置行人专用相位的建议值。最后,建立数值仿真模型与微观交通仿真模型,分析不同人车交互环境下设置行人专用相位条件的灵敏度及其应用效果,从而验证本研究成果的有效性以及可用性。
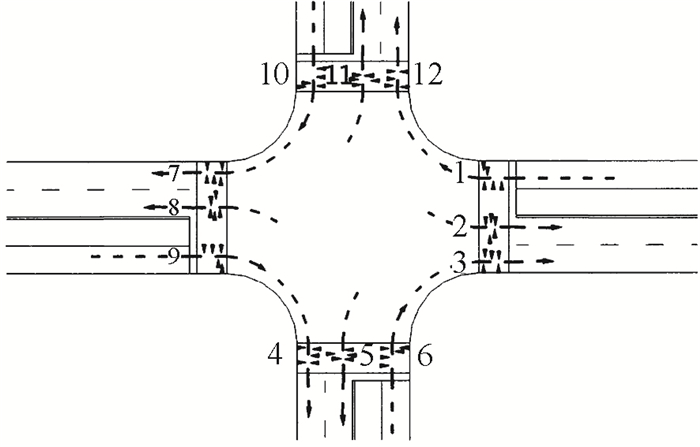
1 人车交互模型 1.1 定义两相位信号交叉口中,通常右转车辆不受信号控制。行人通行时,左转车辆将同时放行。行人在绿灯相位时间内通行过程中将与转弯车辆产生持续性人车交互,每个进口道有3个人车交互区,以四进口道交叉口为例,总计有12个人车交互区,如图 1所示。
|
| 图 1 四进口道两相位信号控制交叉口人车交互区 Fig. 1 Pedestrian-vehicle interaction region at two-phase signalized intersection with 4 entrances |
| |
在每个人车交互区会产生不同类型的人车交互行为。根据此前学者的研究[1, 22]以及本研究的信号控制交叉口建模需求,将按照以下原则分析人车交互行为:(1)因行人通行造成的机动车减速、停车、变换车道等行为记为车辆避让行人一次;(2)因机动车通行导致行人担心自身安全,因而后退或止步记为行人避让车辆一次;(3)行人绿灯信号时间内,行人因等待穿越车辆间隙,而在车道边止步记为行人避让车辆一次;(4)当一个行人在同向多条车道上分别发生多次人车交互现象时,视每次交互具体情况分别记录避让行为类型;(5)当一辆机动车与沿人行横道方向的多人在同一个人车交互区发生避让行为时,视其交互具体情况记录具体的避让行为类型。
依据上述原则,本研究引入了人车交互避让率这一变量,以支持行人专用相位设置条件中交通参与者总延误的计算。
1.2 人车交互避让率两相位信号控制交叉口中,当行人在行人信号绿灯相位过街时会与转弯机动车产生交互,必然有一方会避让另一方让对方先行,故避让行为分为车辆避让行人与行人避让车辆。定义车辆避让行人的次数与人车交互总次数的比值为车辆避让率,行人避让车辆的次数与人车交互总次数的比值为行人避让率。
车辆避让率Kc的计算公式为:
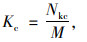
|
(1) |
式中,Nkc为车辆避让行人行为次数; M为人车交互总次数。
行人避让率Kp的计算公式为:
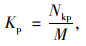
|
(2) |
式中Nkp为行人避让车辆的次数。
上述两个变量将影响行人专用相位在道路交叉口的适用性,需要在设置行人专用相位前充分调研计算。
2 交通参与者总延误估计模型本研究中,主要考虑交通参与者总延误这一指标,从通行效率角度给出行人专用相位的设置条件。因此首先需要建立两相位信号控制交叉口交通参与者总延误估计模型。
2.1 假设条件(1) 本研究中暂不考虑饱和或过饱和条件下的两相位信号控制交叉口。针对研究对象,假设车辆到达服从泊松分布。
(2) 根据本研究采集的人车交互区视频数据观测,发现行人避让机动车时机动车依旧会减速,而机动车避让行人时,鲜见行人停下来(偶尔有加速通过现象)。据此,本研究假设机动车避让行人时行人不产生延误,行人避让机动车则二者均产生延误。
(3) 由于考虑设置行人专用相位的交叉口多位于人流量较大的城市核心区或大型活动场馆等区域,往往少有的货运车辆通行,故本研究中所建模型车辆构成包含小汽车和大客车(含公交车)。
2.2 延误估计模型及行人专用相位设置条件通过交叉口的交通参与者总延误分为两部分,一部分是机动车内乘客的延误,另一部分是过街行人的延误。本研究将对设置行人专用相位前后,交通参与者总延误的变化进行建模分析。
未设置行人专用相位时,行人延误包括信号控制交叉口带来的控制延误与人车交互时产生的延误;车辆延误包括控制延误与人车交互时产生的延误。
(1) 信号控制交叉口机动车的控制延误div为:
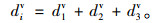
|
(3) |
本研究估计信号交叉口机动车的控制延误div时采用2010年发行的美国高速公路通行能力手册(Highway Capacity Manual,HCM)中的延误估计模型。其中,均匀延误d1v为:
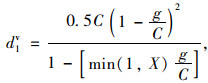
|
(4) |
式中,C为信号周期长度;g为有效绿灯时间;X为饱和度。
增量延误d2v为:
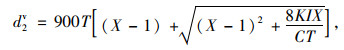
|
(5) |
式中,T为观测持续的时间;K为感应控制的增量延误修正,可查表得;I为按上游信号灯车辆换车道和调节的增量延误修正,单独交叉口取I=1;初始排队延误d3v为0。
本研究在王骏烨等[23]学者的研究基础上,推导出人车交互中机动车的延误dV的估计方法:
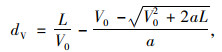
|
(6) |
式中,L为人车交互时机动车减速位置的长度;V0为发生交互时机动车的初速度;a为机动车减速时的加速度(该项取正值)。
(2) 信号控制交叉口行人控制延误d信为:

|
(7) |
式中,r为行人禁行时间,r=C-g。
人车交互时,行人延误d转i为:
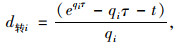
|
(8) |
式中,qi为转弯车流i的流率;τ为行人通过的最小间隔时间;t为绿灯间隔时间。
设置行人专用相位前,行人人均延误d1p为:
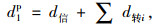
|
(9) |
得到以上数据后,可得设置行人专用相位前,通过交叉口的交通参与者总延误D1为:

|
(10) |
式中, Np为行人流量;α为行人安全系数,此系数可随行人的重要程度的提高而增大;Nc为机动车流量;M为观测时间内,设置专用相位前行人过街时人车交互数;Kc为车辆避让率;Kp为行人避让率;k为机动车平均载客数; dV1,dV2分别为车让人、人让车两种条件下,人车交互中机动车的延误。
设置行人专用相位的交叉口消除了人车交互区,行人延误包括信号控制交叉口的控制延误,车辆延误包括信号交叉口的控制延误与等待行人专用相位时间产生的延误。
设置行人专用相位,行人延误d2p为:
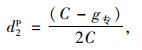
|
(11) |
式中g专为行人专用相位时间。
设置行人专用相位后,并规定行人必须在行人专用相位内通行,所有通过交叉口的交通参与者总延误D2为:
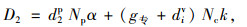
|
(12) |
从通过交叉口所有通行者的总延误角度分析,设置行人专用相位的条件为:
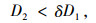
|
(13) |
式中,D1为设置行人专用相位前交通参与者总延误;D2为设置行人专用相位后交通参与者总延误;δ为调整系数,δ≥1,考虑到设置行人专用相位带来的安全性能的提升,应允许延误的小幅提升。其中,δ的取值因结合工程实践与模型灵敏度分析结果给出。本研究将在灵敏度分析部分讨论δ的取值方法。
综上所述,当D2≤δD1时,交叉口可以设置行人专用相位,当D2>δD1时,不推荐设置行人专用相位。
3 数值分析 3.1 人车交互行为回归分析因不同交叉口人车交互行为特征存在差异,本研究将基于人车交互区视频数据,采用回归分析方法对不同交叉口的人车交互次数、行人流量、机动车流量间的关系展开研究。
回归模型表达式为:

|
(14) |
式中,M为人车交互次数; Np为行人流量; Nc为机动车流量; A, B, C为回归模型的各项参数。
本研究以上海市北京路-常德路交叉口人车交互视频为例,以车流量、人流量为变量指标,建立行人车辆交互次数回归预测模型。该交叉口为两相位信号控制交叉口,本研究以常德路南、北进口为研究对象,基于在平峰期随机抽样的4 h人车交互区视频数据,记录了每次人车交互行为发生时的5 min内行人与机动车流量。在随机抽样数据中,人流量以5 min计分布于34~63人区间内(均值为52人);车流量以5 min计分布于42~67辆区间内(均值为51辆),二者均近似泊松分布;期间共观测到了183次人车交互。在上述案例条件下,应用回归分析建立交互次数与车辆及行人通过量的线性模型,回归分析得出表达式:
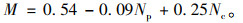
|
(15) |
经检验,模型的拟合优度R2值为0.976,表明考虑了人车数量的交互次数模型预测结果拟合较理想。对模型的总体性进行F检验(见表 1),F值为743.3,显著程度参数sig为0,表明行人车辆交互行为与人流车流量的关系可以近似为线性关系。对各项参数进行T检验(见表 2),机动车流量的显著程度为0,行人流量的显著程度为0.03,常数项的显著程度为0.52,表明机动车流量、行人流量及常数项可以在该案例条件下估计北京路-常德路交叉口的人车交互次数,验证了本方法在小型两相位信号控制交叉口平峰期低流量条件下的适用性。
| 回归平方和 | 残差平方和 | 自由度 | 期望平方 | F | sig |
| 5 200.6 | 129.4 | 39 | 2 600.3 | 743.3 | 0 |
| 非标准化系数 | T | Sig | 95%置信区间 | |||
| 回归系数 | 标准误差 | 下限 | 上限 | |||
| 常数项 | 0.53 | 0.83 | 0.64 | 0.52 | -1.14 | 2.22 |
| 人流量 | -0.09 | 0.04 | -2.23 | 0.03 | -0.18 | 0 |
| 车流量 | 0.25 | 0.04 | 5.69 | 0 | 0.16 | 0.34 |
在183次人车交互中,有27次行人避让机动车,156次机动车避让行人。根据式(1)和式(2)可以得出北京路-常德路交叉口行人的避让率为15%,车辆的避让率为85%。
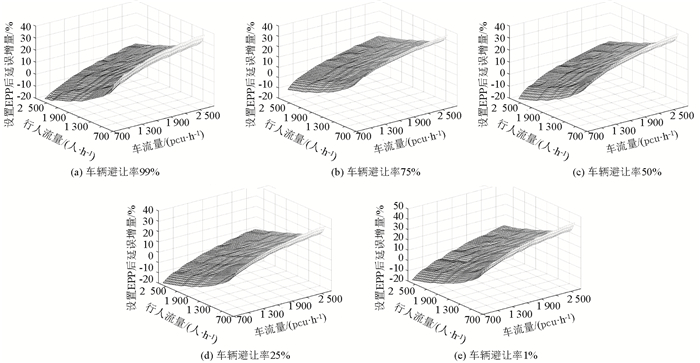
3.2 灵敏度分析为了分析本研究提出模型中各参数的灵敏度,按照应用要求分别设置模型中各项参数。在本次灵敏度分析中,讨论不同行人机动车流量下,设置行人专用相位后交通参与者总延误变化。本研究分析了车辆完全避让行人(车辆避让率99%)、大多数车辆避让行人(车辆避让率75%)、人车避让率相当(车辆避让率50%)、大多数行人避让车辆(车辆避让率25%)、车辆完全不避让行人(车辆避让率1%)5种情况,如图 2所示。
|
| 图 2 不同避让率条件下模型灵敏度分析 Fig. 2 Model sensitivity analysis at different avoidance rates |
| |
从上述分析中本研究得出以下结论:
(1) 在机动车流量相同时,行人流量越多,设置行人专用相位后延误增量越小,更具备设置条件。
(2) 车辆避让率越高,设置行人专用相位后延误增量越小。说明避让率对交叉口交通参与者总延误具有较大影响,本研究将避让率作为模型变量是重要的。
为了确定式(13)中调整系数δ在不同工况下的取值,本研究分析了调整系数δ取值对行人专用相位设置条件的影响。
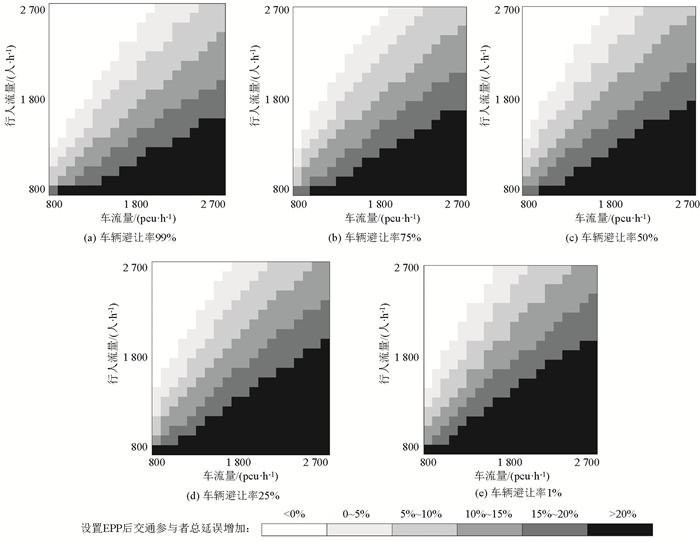
图 3展示了调整系数δ取1~1.2的情况,可以看出在各类避让率条件下,δ取值越大均使得推荐设置行人专用相位的流量范围有所扩展。基于本研究分析结果,在实际工程应用中,建议在商业区等人流密集交叉口取值1.15~1.2偏重人流安全;在住宅区、休憩场所附近的交叉口取值1.05~1.15兼顾效率与安全;在工业区、郊区的交叉口取值1~1.05偏重效率。
|
| 图 3 调整系数取值分析 Fig. 3 Analysis of adjustment factor value |
| |
4 仿真验证
使用车辆完全避让行人,避让比例99%的情况进行VISSIM仿真检验。仿真场景以上文所示的典型两相位信号双向四车道交叉口为例,在两个场景中分别进行仿真。由于设置行人专用相位后,行人可进行对角线过街,故输入行人流量与不设置行人专用相位时不同。各方向流量输入如表 3所示。
| 项目名称 | 场景1 | 场景2 |
| 左转车流量/(pcu·h-1) | 200 | 100 |
| 直行车流量/(pcu·h-1) | 150 | 75 |
| 右转车流量/(pcu·h-1) | 150 | 75 |
| 设置EPP时行人流量/(人·h-1) | 83 | 166 |
| 不设置EPP时行人流量/(人·h-1) | 125 | 250 |
在VISSIM中建立路网,东西向次路为南北向主路让行,车辆为行人让行。对于每一个仿真场景,分别选取5种不同的随机数种子进行5次仿真试验,以降低结果的随机影响。在以上两个场景中分别进行仿真检验,仿真结果如表 4所示。
| 评价指标 | 场景1 | 场景2 | |||
| 未设置EPP | 设置EPP | 未设置EPP | 设置EPP | ||
| 机动车内乘客延误/h | 111.3 | 132.1 | 41.3 | 49.4 | |
| 平均排队长度/m | 34.4 | 21.7 | 4.35 | 7.16 | |
| 机动车通过量/pcu | 1 890 | 1 954 | 1 017 | 1 021 | |
| 行人延误/h | 19.5 | 11.6 | 25.9 | 15.4 | |
| 行人通过量/人 | 1 306 | 1 272 | 2 604 | 2 607 | |
| 总延误/h | 125.8 | 143.7 | 67.2 | 64.8 | |
场景1交叉口在设置行人专用相位后,机动车内乘客延误增加,机动车排队长度增加,行人延误降低,交叉口交通参与者的总延误增加,可见在场景1交叉口设置行人专用相位是不合理的。
场景2交叉口在设置行人专用相位后,机动车内乘客的延误增加,机动车的通过量增加,行人延误降低,行人的通过量增加,交叉口交通参与者的总延误降低。在本例中,总延误降低了4%左右,此结果与灵敏度分析中结果相符,表明在场景2设置行人专用相位是合理的,证明了本研究提出的行人专用相位设置条件的模型有效性。
5 结论文章研究了两相位信号控制交叉口人车交互时的避让行为,提出了避让率概念;建立了考虑避让率的交通参与者总延误估计模型,以设置行人专用相位前后的交通参与者总延误变化作为指标,并给出设置条件;进而基于人车交互区视频数据回归分析了人车交互次数与机动车、行人流量的关系,估计避让率;并对不同避让率下的行人专用相位设置效果进行灵敏度分析,针对不同城市区域分别给出设置条件。本研究分析结果表明当机动车流量不变时,行人流量越高设置行人专用相位效果越好,且避让率会影响设置行人专用相位效果,将避让率纳入行人专用相位设置的输入条件十分重要。最后,建立了微观交通仿真模型,验证了本研究提出的行人专用相位设置条件的有效性。在本研究考虑的交通参与者总延误之外,交叉口通行能力及安全性能亦是行人专用相位设置条件的重要影响因素,未来将基于行人专用相位交叉口视频数据,进一步研究调整系数的确定方法,给出同时考虑安全、效率的行人专用相位设置条件。
| [1] |
XIN X Y, JIA N, MA S F, et al. Empirical and Simulation Study of Traffic Delay at Un-signalized Crosswalks due to Conflicts between Pedestrians and Vehicles[J]. Transportmetrica B:Transport Dynamics, 2018, 7(1): 637-656. |
| [2] |
MA W J, LIAO D B, LIU Y, et al. Optimization of Pedestrian Phase Patterns and Signal Timings for Isolated Intersection[J]. Transportation Research Part C:Emerging Technologies, 2015, 58: 502-514. |
| [3] |
艾冠韬, 邓院昌, 舒凡. 广州市机动车人行横道让行行为及影响因素分析[J]. 中国安全生产科学技术, 2016, 12(12): 133-137. AI Guan-tao, DENG Yuan-chang, SHU Fan. Analysis on Yielding Behavior and Its Influencing Factors of Motor Vehicle at Pedestrian Crosswalk in Guangzhou[J]. Journal of Safety Science and Technology, 2016, 12(12): 133-137. |
| [4] |
周竹萍, 王炜, 任刚, 等. 信号交叉口行人交通冲突特性及影响因素分析[J]. 东南大学学报:自然科学版, 2014, 44(6): 1294-1298. ZHOU Zhu-ping, WANG Wei, REN Gang, et al. Analysis on Characteristics and Influential Factors of Pedestrian Conflicts with Vehicles at Signalized Intersections[J]. Journal of Southeast University:Natural Science Edition, 2014, 44(6): 1294-1298. |
| [5] |
周竹萍, 王炜, 任刚, 等. 信号控制交叉口行人个体过街行为选择模型[J]. 东南大学学报:自然科学版, 2013, 43(3): 664-668. ZHOU Zhu-ping, WANG Wei, REN Gang, et al. Choice Model of Pedestrian Crossing Behavior at Signalized Intersections[J]. Journal of Southeast University:Natural Science Edition, 2013, 43(3): 664-668. |
| [6] |
FU T, MIRANDA-MORENO L, SAUNIER N. A Novel Framework to Evaluate Pedestrian Safety at Non-signalized Locations[J]. Accident Analysis & Prevention, 2018, 111: 23-33. |
| [7] |
KATTAN L, ACHARJEE S, TAY R. Pedestrian Scramble Operations:Pilot Study in Calgary, Alberta, Canada[J]. Transportation Research Record:Journal of the Transportation Research Board, 2009, 2140: 79-84. |
| [8] |
MA W J, LIU Y, HEAD K L. Optimization of Pedestrian Phase Patterns at Signalized Intersections:A Multi-objective Approach[J]. Journal of Advanced Transportation, 2014, 48(8): 1138-1152. |
| [9] |
IVAN J N, MCKERNAN K, ZHANG Y H, et al. A Study of Pedestrian Compliance with Traffic Signals for Exclusive and Concurrent Phasing[J]. Accident Analysis & Prevention, 2017, 98: 157-166. |
| [10] |
HEDIYEH H, SAYED T, ZAKI M H. The Use of Gait Parameters to Evaluate Pedestrian Behavior at Scramble Phase Signalized Intersections[J]. Journal of Advanced Transportation, 2015, 49(4): 523-534. |
| [11] |
韩印, 张楠, 马万达, 等. 右转车辆穿越行人流的延误模型[J]. 交通运输工程学报, 2010, 10(6): 121-126. HAN Yin, ZHANG Nan, MA Wan-da, et al. Delay Models of Right-turning Vehicle Crossing through Pedestrian Flow[J]. Journal of Traffic and Transportation Engineering, 2010, 10(6): 121-126. |
| [12] |
ZHANG Y H, MAMUN S A, IVAN J N, et al. Safety Effects of Exclusive and Concurrent Signal Phasing for Pedestrian Crossing[J]. Accident Analysis & Prevention, 2015, 83: 26-36. |
| [13] |
杨晓光, 马万经, 林瑜. 两相位信号控制交叉口行人专用相位设置条件研究[J]. 公路交通科技, 2005, 22(1): 127-131. YANG Xiao-guang, MA Wan-jing, LIN Yu. Criterion of Setting Exclusive Pedestrian Phases at Two-phase Signalized Intersections[J]. Journal of Highway and Transportation Research and Development, 2005, 22(1): 127-131. |
| [14] |
VAN HOUTEN R, MALENFANT J E L, BLOMBERG R, et al. High-visibility Enforcement on Driver Compliance with Pedestrian Right-of-way Laws:4-year Follow-up[J]. Transportation Research Record, 2018, 2660(1): 58-65. |
| [15] |
STAPLETON S, KIRSCH T, GATES T J, et al. Factors Affecting Driver Yielding Compliance at Uncontrolled Midblock Crosswalks on Low-speed Roadways[J]. Transportation Research Record, 2017, 2661: 95-102. |
| [16] |
孟虎, 陈艳艳, 刘花. 信号交叉口行人过街遵章率预测模型[J]. 公路交通科技, 2012, 29(12): 114-118, 132. MENG Hu, CHEN Yan-yan, LIU Hua. Prediction Model for Pedestrian Obeying Traffic Rule at Signalized Intersections[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 114-118, 132. |
| [17] |
慈玉生, 郑淑妮, 赵韩涛. 基于过街人数分布的路段机动车延误经验模型[J]. 重庆交通大学学报:自然科学版, 2018, 37(6): 76-80. CI Yu-sheng, ZHENG Shu-ni, ZHAO Han-tao. Empirical Model of Road Segment Vehicle Delay Based on Numerical Distribution of Pedestrians' Crossing[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2018, 37(6): 76-80. |
| [18] |
赵靖, 杨晓光. 行人-自行车对两种交叉口设计模式通行能力的影响[J]. 公路交通科技, 2016, 33(8): 114-119, 126. ZHAO Jing, YANG Xiao-guang. Impact of Pedestrian and Bicycle on Capacity of Two Design Types of Intersection[J]. Journal of Highway and Transportation Research and Development, 2016, 33(8): 114-119, 126. |
| [19] |
WEI D L, XU H, KUMFER W, et al. Vehicular Traffic Capacity at Unsignalized Crosswalks with Probabilistic Yielding Behavior[J]. Transportation Research Record, 2015, 2483: 80-90. |
| [20] |
胡宏宇, 李志慧, 魏巍, 等. 基于模糊逻辑的信号交叉口人车冲突判别方法[J]. 吉林大学学报:工学版, 2014, 44(3): 637-641. HU Hong-yu, LI Zhi-hui, WEI Wei, et al. Fuzzy Logic Based Pedestrian-vehicle Conflict Discrimination at Signalized Intersection[J]. Journal of Jilin University:Engineering and Technology Edition, 2014, 44(3): 637-641. |
| [21] |
陆斯文, 方守恩, 李刚. 城市道路人车冲突和碰撞概率微观模型研究[J]. 同济大学学报:自然科学版, 2009, 37(12): 1627-1632. LU Si-wen, FANG Shou-en, LI Gang. Study on Probabilistic Microscopic Models for Pedestrian-vehicle Traffic Conflict and Collision on Urban Road[J]. Journal of Tongji University:Natural Science Edition, 2009, 37(12): 1627-1632. |
| [22] |
VAN HAPEREN W, DANIELS S, DE CEUNYNCK T, et al. Yielding Behavior and Traffic Conflicts at Cyclist Crossing Facilities on Channelized Right-turn Lanes[J]. Transportation Research Part F:Traffic Psychology and Behaviour, 2018, 55: 272-281. |
| [23] |
王俊骅, 方守恩. 行人机动车冲突模型及其行人过街风险控制应用[J]. 同济大学学报:自然科学版, 2009, 37(9): 1191-1195. WANG Jun-hua, FANG Shou-en. Pedestrian-Vehicle Conflict Model and Its Application to Pedestrian Crossing Street Risk Control[J]. Journal of Tongji University:Natural Science Edition, 2009, 37(9): 1191-1195. |
 2020, Vol. 37
2020, Vol. 37
