扩展功能
文章信息
- 董洁霜, 卞春, 王嘉文, 林诗悦, 刘魏巍
- DONG Jie-shuang, BIAN Chun, WANG Jia-wen, LIN Shi-yue, LIU Wei-wei
- 数据驱动的两相位信号控制交叉口行人专用相位动态设置方法
- A Method for Dynamic Setting Exclusive Pedestrian Phase of Data-driven Two-phase Signal Control Intersection
- 公路交通科技, 2020, 37(1): 85-95
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 85-95
- 10.3969/j.issn.1002-0268.2020.01.011
-
文章历史
- 收稿日期: 2018-08-13
2. 上海市公安局交通警察总队, 上海 200070
2. Traffic Police Team of Shanghai Public Security Bureau, Shanghai 200070, China
中国现行的交叉口交通控制信号大多针对机动车交通流设置[1],对交叉口行人通行效率及公平性的优化较少。而在城区商业区(核心区)交叉口环境下,行人流量大并且往往行人交通是其主要服务对象之一。在该环境下需要保证行人的通行安全、通行效率及通行公平性,从而提升交叉口服务水平。行人专用相位(Exclusive Pedestrian Phases,EPP)可减少人车冲突,为行人提供安全便利的步行环境,该方法是提高城市行人通行效率的有效手段[1-2]。国内外学者对行人专用相位进行了一系列的相关研究。早在20世纪50年代国外学者展开了对行人专用相位的研究,一方面是基于安全的研究,另一方面是基于效率的研究[1]。行人专用相位是为了给信号交叉口即将到来的车辆显示红色信号, 以便行人可以同时在交叉口对角线及侧向通过交叉口[3], 消除了车辆和行人之间的冲突以提高安全性,减少了行人在交叉口过街的距离,提高了便利性。Ivan等[4]比较了行人信号控制的两种类型,一种是常规信号相位,另一种是行人专用相位。Zhang等[5]提出了这两种相位模式下的行人冲突数与车辆相互作用严重性预测模型,并得出建议仅在行人服从率高的地区设置行人专用相位。Alhajyasen[6]提出了一种考虑人车交通冲突概率和预期冲突严重程度的安全措施, 引入PET(post-encroach ment time)、TTC(time to collision)和速度等影响因素,建立了交叉口安全评价指标体系CI(Conflict index),并通过对实际交叉口的数据分析,验证了评价指标的有效性。Ma等[7-8]提出了一个模拟行人专用相位的适应性分析方法,并与常规信号相位进行对比;并在考虑了过街行人需求且降低车辆延误的基础上开发了行人专用相位驱动与常规并行相位驱动控制的信号控制逻辑;研究发现车辆需求、行人需求、车辆转弯率和行人交叉口的通过率等因素共同决定了行人专用相位的性能和使用范围;同年也提出了一种针对这两种相位模式的多目标优化模型及其优化行人相位模型的求解算法,模型将根据交叉口车辆的行驶情况和行人移动确定当前最佳行人相位模式。Medina等[9]研究行人的个体和群体的行为特征,如自由流穿越人行横道的速度,为交叉口信号配时提供了重要依据,以减少因设置行人专用相位导致的车辆延误。Hediyeh等[10]针对行人专用相位做了更深入的研究,分析了步态参数(步长和步频)受行人性别、年龄、群体大小、人行横道长度及行人信号指示的影响,从微观层面了解了行人步行机制的变化和各类行人与交叉口特征的影响。国内亦有诸多学者对该问题展开研究,杨晓光等[11]运用穿越理论推导出行人在交叉口通行时穿越行人的转弯车辆通行能力模型和行人延误模型,论证了交叉口行人专用相位的设置条件。袁黎等[12]探讨路口实施行人专用信号的可行性,兼顾路口交通安全与效益指标,建立安全效益评价方法,得出结论应在行人流量较高或车流右转比较大的路口实施行人专用相位。钱大琳等[13]针对道路等级相差较大的两相位信号控制交叉口,提出了一种针对行人专用相位修改的交叉口信号控制方案。赵靖等[14]提出了一种利用下游交叉口红灯信号时间来为路段行人提供专用过街信号相位的行人过街横道信号控制方法。
综上,考虑行人流量和车辆流量的动态行人专用相位优化方法是最前沿的研究领域,此前的研究中较少考虑到人车公平性的优化问题。因此本研究在前人的研究基础上,分析了交叉口行人与机动车发生冲突时的相互影响,以城区商业区(核心区)交叉口作为研究对象,并基于视频检测数据得出的行人与机动车流量,实时估计设置行人专用相位前后行人与机动车的吞吐量(throughput),提出数据驱动的两相位交叉口动态设置行人专用相位模型,通过比较设置行人专用相位前后交叉口的行人、机动车的流量比(按通行人数计)差值,在下个周期选用使得交叉口二者饱和度之差最小的相位方案,在保证通行效率的同时,使得人与机动车能在人均占有道路时空资源较公平的条件下通过交叉口,以保证人与车通过交叉口的效率与公平性。
本研究的主要贡献包括:(1)将过街行人和机动车中的人流量作为变量,并加入行人重要程度指标,以考虑过街行人与机动车中的人流量大小关系,针对人流密集且需要保证行人过街效率的交叉口,提出了将过街行人和机动车均换算成“标准人”的吞吐量的估计与评级方法,为动态设置行人专用相位的判别提供理论支撑;(2)考虑了新信息环境下,可通过动态采集行人和机动车实时流量的技术来实现交叉口每周期的流量数据更新,并将每周期采集的交叉口人车流量的实时数据作为数据驱动的行人专用相位的设置公平性模型的输入变量,指导了在城区商业区(核心区)交叉口动态设置行人专用相位的自适应判别;(3)在动态模型的方案选择上,以行人与机动车(按行人计)的饱和度之差最小为优化目标,考虑了交叉口通过的行人数量与机动车中的行人数量的公平性,保证过街行人与机动车中的人能更公平地通过交叉口。
1 交叉口机动车与行人冲突特性分析本研究是基于数据驱动以研究相位设置方法,是以每个信号周期中的行人和机动车作为研究目标,实则是将交叉口每小时的通行能力细分成每个周期的吞吐量。因此本研究将基于前人对交叉口行人和机动车通行能力的研究,分析影响交叉口行人和机动车的冲突特性,得出行人和机动车每周期吞吐量的计算公式。本研究重点研究城区商业区(核心区)交叉口,在这类交叉口中,交通参与者主要以过街行人、小汽车、公交车为主,因此研究对象仅考虑这3类交通参与者。
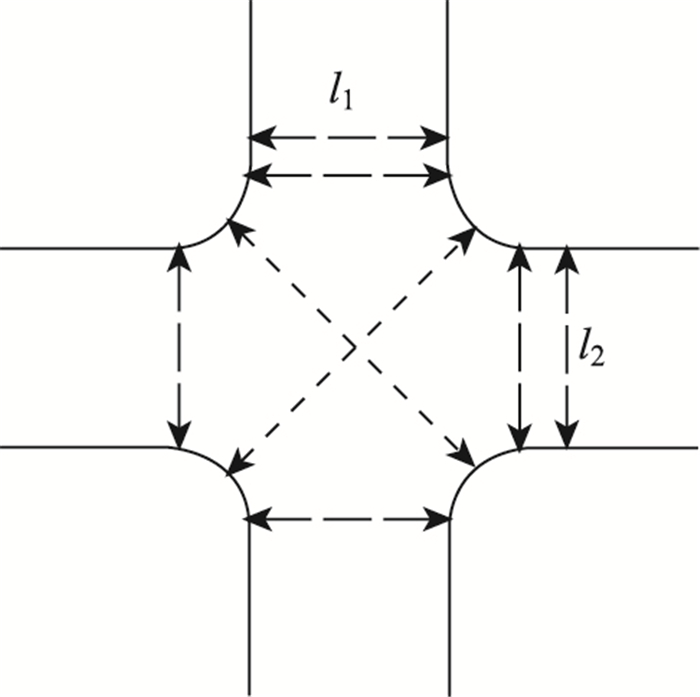
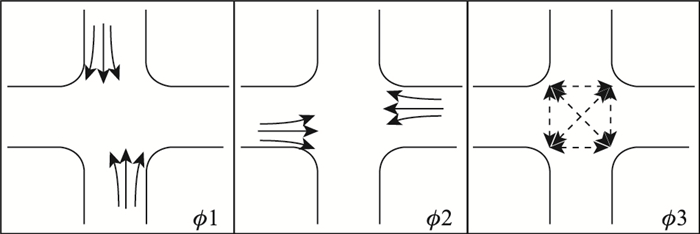
路口行人专用相位是从时间上将行人与机动车流分离,顾名思义,行人过街时有一个专门的相位通过,此时所有方向的机动车均禁止通过交叉口;反之,无论哪个方向的机动车通行时,所有方向的行人均不能通过交叉口。在该种类型的相位情况下,行人过街多采用斜穿方式设置人行横道,如图 1所示。设置行人专用相位后,较未设置行人专用相位之前,多出一个相位(ϕ3),以供行人通行,两相位行人专用相位信号设置图见图 2。
|
| 图 1 行人专用相位时段行人过街示意图 Fig. 1 Schematic diagram of pedestrian crossing in EPP |
| |
|
| 图 2 两相位行人专用相位信号设置 Fig. 2 Setting two-phase pedestrian dedicated phase signal |
| |
1.1 行人对机动车吞吐量的影响分析
(1) 设置行人专用相位前后机动车的吞吐量
本研究在停止线法计算车辆通行能力的基础上,分别讨论设置行人专用相位前后公交车、小汽车每个周期吞吐量的变化情况。信号控制交叉口通行能力的计算方法主要有以下4种:饱和流率法、停止线法、停车线法、冲突点法。其中停车线法是中国计算信号控制交叉口通行能力的常用方法之一,该方法以前后两车接连通过停车线的平均间隔时间为基础,分别就左转、直行和右转车道通行能力给出计算模型[15],如式(1)~(3)所示。
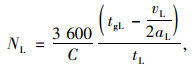
|
(1) |
式中,tL为左转车辆通过停车线的车头时距;vL为左转车辆的通过速度;aL为左转车辆的加速度;vT为直行车辆的通过速度;aT为直行车辆的加速度;tT为直行车辆通过停车线的车头时距;tR为右转车辆通过停车线的车头时距;NL,NT,NR分别表示左转、直行和右转车道的通行能力。
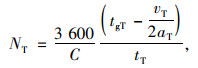
|
(2) |
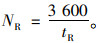
|
(3) |
对于各进口道,在每个周期内,有效绿灯时间除了加速损失时间,还应包括相位切换初期时行人集中过街,导致车辆不能通过交叉口产生的损失时间tl。假设每个周期内,行人过街流量为Qp,其中在相位切换初期时行人集中过街的数量所占比例为θ1,人行横道宽为d,过街行人与转弯车辆的安全距离为s,行人平均占地面积为A(通过查阅HCM的A为0.75×0.75m2的矩形)。
(1) 相位切换初期时行人集中过街时,行人占满一排时,一排所站的人数n。
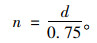
|
(4) |
(2) 相位切换初期时行人集中过街,一排行人占人行道长度L。
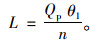
|
(5) |
(3) 因行人集中过街导致车辆损失的行驶时间tl。
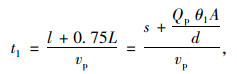
|
(6) |
式中, vp为行人步行平均速度1. 2~1. 5 m/s,取1.2 m/s; l为行为过街长度,即人行横道长度, 这种情况可以通过设置行人信号灯进行迟起早断控制解决[1]。如果交叉口采取这种信号控制方法,视作车辆通过交叉口时不受到相位切换的影响,不发生时间损失,即tl=0。
只有相应左转和右转车辆会在相位切换初期受到行人集中过街的影响,直行车辆不受影响,每个周期每个进口道小汽车和公交车的吞吐量如式(7)~(12)所示:
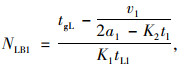
|
(7) |
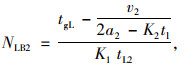
|
(8) |
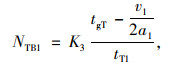
|
(9) |
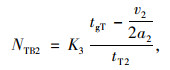
|
(10) |
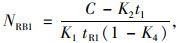
|
(11) |
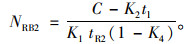
|
(12) |
切换至行人专用相位之后,在一个信号周期内,行人专用相位时段内车辆不能通行。该周期内其余时段的车辆吞吐量如式(13)~(18)所示:
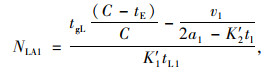
|
(13) |
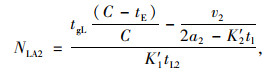
|
(14) |
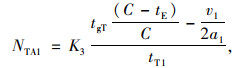
|
(15) |
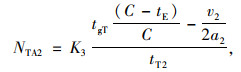
|
(16) |

|
(17) |
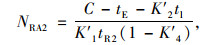
|
(18) |
式中, NLB1,NTB1,NRB1与NLA1,NTA1,NRA1分别为设置行人专用相位前后每条左转车道、直行车道和右转车道每个周期内公交车的吞吐量;NLB2,NTB2,NRB2与NLA2,NTA2,NRA2分别为设置行人专用相位前后每条左转车道、直行车道和右转车道每个周期内小汽车的吞吐量; tgL,tgT分别为一个周期内左转和直行信号时长;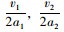
本研究是在李文勇对于平面人行横道通行能力研究的基础上[17-18],考虑右转车辆对行人过街的影响,在不设置行人专用相位的情况下建立行人吞吐量, 如式(19)所示:
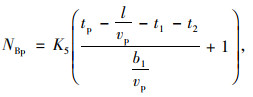
|
(19) |
式中, NBp为没有插入行人专用相位时交叉口过街行人的吞吐量; tp为行人过街绿灯时间长度; l为行人过街长度; b1为前后行人间距,取0.75 m;t1为等待过街的行人对灯色变换的反应时间,造成的损失很短,可忽略不记;t2为红灯末行人因安全感降低使流量未达饱和所造成的损失,经实测为2 s;K5为右转专用车道对行人通行的影响的折减系数。
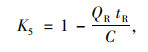
|
(20) |
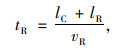
|
(21) |
式中, QR为当前周期内右转车辆的的实时流量; tR为右转车辆用人行道的时间; C为周期时长; lC为换算车辆长度,取6 m; lR为行人与右转车辆的最小安全距离; vR为右转车速,经实测在2.22~4.17 m/s之间,取2.78 m/s。
切换至行人专用相位之后,行人每周期的吞吐量分成两部分计算,一部分是行人专用相位时段,另一部分是除了行人专用相位以外的时段。
第1部分,在行人专用相位的时段内,行人的吞吐量NAp1。行人过街示意图如图 1所示,公式推导过程如下所示:
分别求通过四边和斜对角线人行横道的行人吞吐量。以长为l1的人行横道为例。
(1) 行人过街的最短时间ts
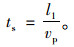
|
(22) |
(2) tE时段内一条长l1为人行横道能通过的人数M1。
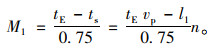
|
(23) |
(3) 2条长为人行横道能通过的人数Ml1
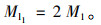
|
(24) |
(4) 同理可得,6条人行横道每个周期总共能通过的人数NAp1。
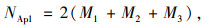
|
(25) |
式中, NAp1为设置行人专用相位后,行人专用相位时段的过街行人的吞吐量;M1为(每周期内)长度为l1的人行横道可通过的行人数;M2为(每周期内)长度为l2的人行横道可通过的行人数;M3为(每周期内)斜对角线的人行横道可通过的行人数。
第2部分,在C-t专的时间段内,即在行人专用相位周期的非行人专用相位时段内,行人依旧可以如正常相位时过街,相当于计算行人在正常两相位周期为C-tE的交叉口的吞吐量。
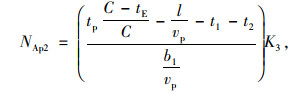
|
(26) |
式中, NAp2为设置行人专用相位后,每个周期非行人专用相位时段的过街行人的吞吐量。
设置行人专用相位后,行人吞吐量公式表示如式(27)所示。
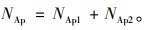
|
(27) |
本研究考虑到在人流密集区域,转弯车辆与行人之间会产生更大的相互影响,也会导致更多的人车冲突,会使得机动车排队的情况发生,也可能会导致行人因避让车辆而不能一次过街,会影响行人的通行效率和体验。因此需要加强对交叉口的行人、非机动车和机动车的管理和控制,以此来提高交叉口的安全性,同时减少人车冲突,从而减少对行人、非机动车和机动车的通行能力的影响。本研究从信号控制的角度,对交叉口的机动车和行人在时间上和空间上进行分离,以减少交通冲突的影响,提高交叉口的通行效率和安全性。
2.1 基本假设本研究中做以下假设:
(1) 每周期各交叉口进口道车流量不超过其吞吐量,即此处讨论车流量不饱和的情况。
(2) 因主要研究城区商业区(核心区)的交叉口,车辆主要以小型客车(私家车)及公交车为主,所以在本研究中车辆不考虑货车、自行车、电动车等,只包括小型客车(私家车)及公交车。
(3) 行人通过人行横道的速度保持不变,且没有加速过程,可看作瞬间提速。行人的步行速度较机动车而言较低,机动车有加减速损失时间,而行人的加减速时间可忽略不计,故可看作瞬间减速。
(4) 插入行人专用相位后,信号周期时长保持不变,只在原周期时长的基础上减去行人专用相位时长,即设置前后相位绿信比保持不变,行人专用相位时长在本研究中取行人过街最短绿灯时间[9]。目的是保证在动态设置行人专用相位时有较高的技术可行性。
(5) 行人过街时不考虑对向人流的干扰,也不考虑同向行人的横向干扰。因为行人过街时会受到对向行人在同一步行带上相遇而降低速度,假设行人过街都靠右行走,不存在两个方向相遇而导致速度降低。同时同方向也会因为行人行走速度不同导致超越前人的情况,也会导致行走速度变化,本研究假设行人速度一致,不存在超越行为的情况发生。
(6) 公交车和小汽车起步加速阶段的速度和加速度与其行驶方向无关。
(7) 交叉口各进口道公交车占总流量的比例相同。
2.2 目标函数及约束条件设置行人专用相位前后交叉口每个周期人的总流量比之差的绝对值Φ1,Φ2分别如式(28)~(29)所示:
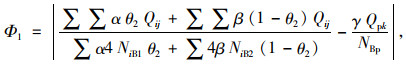
|
(28) |
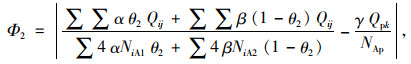
|
(29) |
式中,Φ1,Φ2分别为设置行人专用相位前、后交叉口当前周期车的人均流量比与行人流量比之差的绝对值;Qij为当前周期第j个方向进口道第i个行车方向(左转、直行、右转)车道的实时车流量(i=1, 2, 3,j=1, 2, 3, 4);Qpk为第k条人行横道上当前周期的实时人流量(k=1, 2, 3, 4);NiB1,NiA1分别为设置行人专用相位前、后各行车方向(左转、直行、右转)车道的当前周期公交车的吞吐量;NiB2,NiA2分别为设置行人专用相位前、后各行车方向(左转、直行、右转)车道的当前周期小汽车的吞吐量;NBp,NAp分别为设置行人专用相位前、后过街行人的吞吐量;α为公交车平均载客率;β为小汽车平均载客率;γ为行人的重要程度调整系数;θ2为公交车占当前周期实时车流量的比例。
运用0-1规划构建目标函数如式(30)所示:
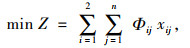
|
(30) |
s.t. xij=0或1,(i=1, 2,j=1, 2,…,n),
Φ1j=Φ1,x1j=0,当Φ1<Φ2,
Φ2j=Φ2,x2j=1,当Φ1≥Φ2,
式中, Φij为第j个周期内使用第i个相位方案时车的人均流量比与行人流量比之差的绝对值; xij为决策变量,x1j=0时为第j个周期不插入行人专用相位的正常信号方案; x2j=1时为第j个周期插入行人专用相位之后的信号方案;n为n个信号周期。
2.3 模型数值分析及灵敏度分析为验证模型的理论分析结果,对式(30)进行数值分析。以仿真两相位信号交叉口为例,进口道为直左车道和右转车道两车道,具体参数设置详见表 1。
| 参数名称 | 不插入行人专用相位 | 插入行人专用相位 | |
| 信号周期时长C/s | 90,无全红时间 | ||
| 南北相位有效绿灯时间/s | 42 | 35 | |
| 东西相位有效绿灯时间/s | 42 | 35 | |
| 黄灯时长/s | 3 | ||
| 行人专用相位时长/s | — | 14 | |
| 交叉口人行横道宽度/m | 4 | ||
| 车道宽度/m | 3.5 | ||
| 公交车平均载客率/(人·辆-1) | 30 | ||
| 小汽车平均载客率/(人·辆-1) | 1.5 | ||
| 左转车流量占直左车道流量比例 | 0.3 | ||
| 行人重要程度调整系数 | 1 | ||
| 每周期内行人集中过街占总人数的比例 | 0.4 | ||
| 公交车占当前周期实时车流量的比例 | 作为灵敏度分析参数,取值在0~0.4之间 | ||
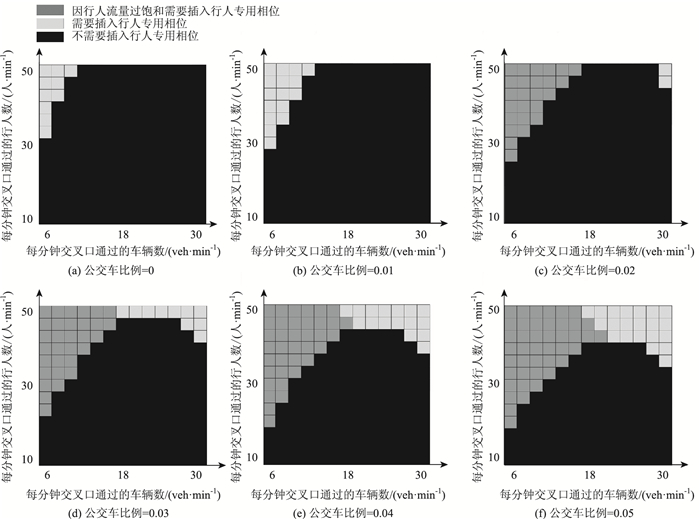
分析结果如图 3所示,在曲线上方的部分,表示在相应的行人流量和公交车流量的情况下需要插入行人专用相位;反之,在曲线下方的部分则表示不需要插入。
|
| 图 3 不同公交车比例下(0~0.05)的行人专用相位插入临界曲线 Fig. 3 EPP inserting critical curves in different bus ratios (0~0.05) |
| |
通过图 3可以看出,在没有公交车行驶的交叉口,不需要通过设置行人专用相位调节行人与机动车通过交叉口的流量,即可使行人与机动车较为公平地通过交叉口。随着公交车比例的上升,设置行人专用相位的效果越明显,因为公交车的平均载客率高,在不设置行人专用相位的情况下,过街行人会影响车辆的正常行驶,使得通过交叉口的机动车数量下降,过街行人越多,对其影响越大,所以在高人流量的情况下考虑设置行人专用相位减少行人对车辆行驶的干扰,使得行人与机动车尽可能公平地通过交叉口。
不设置行人专用相位时,行人过街时会与左转和右转两股车流产生冲突,使车辆每周期的吞吐量降低,与此同时,行人也会受到转弯车流的影响,导致其每周期吞吐量降低。而设置行人专用相位之后,会导致车辆的有效绿灯时间降低,也会影响每周期车辆的吞吐量。因此需要在特定的时段设置行人专用相位减少机动车对过街行人的影响,从而提高行人每周期的吞吐量。
具体来说,当行人流量较低时,行人虽然会在其过街期间与左转和右转两股车流产生冲突,影响机动车每周期的吞吐量,但因为行人总体流量较少,对车辆的干扰较少;插入行人专用相位反而会减少车辆的有效绿灯时间使得机动车吞吐量减少更多,因此在人流量较低时,无论车流量多与少,不插入行人专用相位是更好的选择。
随着人流量的增加,过街行人与转弯车辆的冲突也随之增加,在车流量较少的情况下,可通过插入行人专用相位减少行人对转弯车辆的影响,可达到二者流量比差值最小的目标;随着车流量的增加,插入行人专用相位以减少人对车辆行驶影响的效果与不设置时行人专用相位时行人对转弯车辆的影响相同,即出现图中水平线的情况;随着机动车流量的继续增加,插入行人专用相位以减少行人对车辆行驶的影响的效果已经超过了不设置时行人专用相位时行人对转弯车辆的影响,因此在人流量较高且车流量较高的信号周期内,选择不插入行人专用相位以使得二者流量比差值最小。
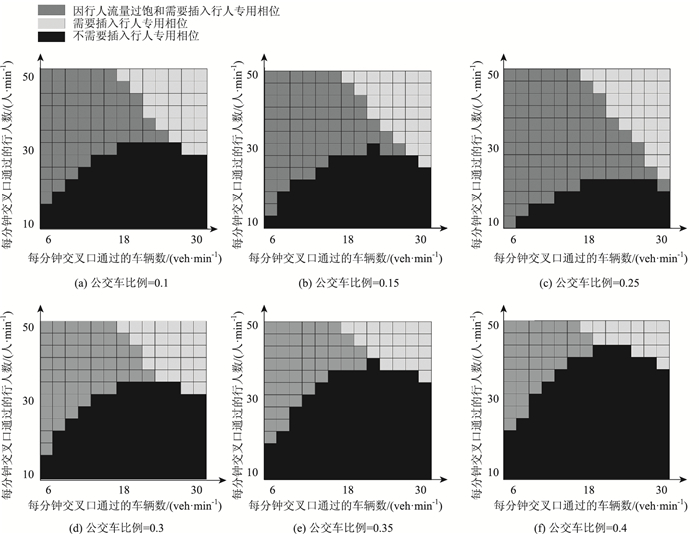
因为公交车的平均载客率较高,因此公交车数量较少(公交车比例在0~0.05范围内)时,机动车中的交通参与者与过街行人数量的差别不大,不需要设置行人专用相位来保证二者的通行公平性;而随着公交车比例的上升,机动车内交通参与者的数量明显上升,需要考虑机动车与过街行人流量直接的相互关系,在公交车比例为0.1~0.3的范围内(如图 4所示),临界曲线上下分布情况较为平均,说明在公交车比例为0.1~0.3的交叉口,采用动态设置行人专用相位的信号控制方法时对公平性的控制效果最佳,换言之这种情况下交叉口的过街行人与机动车中的交通参与者能更为公平地通过交叉口,以体现以人为本的思想。
|
| 图 4 不同公交车比例下(0.1~0.4)的行人专用相位插入临界曲线 Fig. 4 EPP inserting critical curves in different bus ratios (0.1~0.4) |
| |
另一方面,从图 3和图 4的灰色区域中可以看出,是由于在不设置行人专用相位的情况下行人流量过饱和, 所以需要设置行人专用相位,说明了在行人流量较大机动车流量较少的情况下设置行人专用相位后增加了行人通过交叉口的吞吐量。
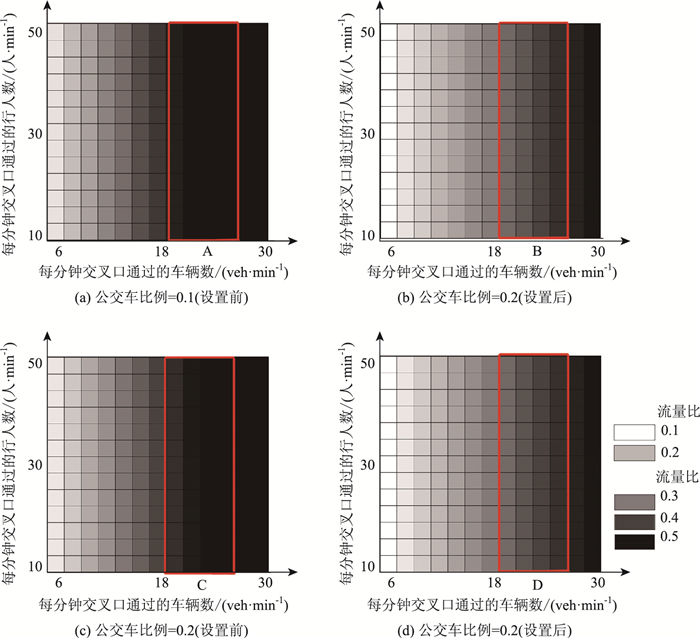
与此同时,本研究是在考虑了设置行人专用相位前后,对机动车和行人的通行效率影响不大的情况下,才考虑人车通行均衡的问题。从图 5中可以看出,在不同的公交车比例下(分别为0.1和0.2),设置行人专用相位前后,只在图中A,B,C,D 4个区域机动车流量比有明显差异,但对比设置前后流量比均不超过0.2,在可接受范围内,说明设置行人专相位后,对机动车的通行效率影响不大,同时大幅提高了行人交叉口的吞吐量。
|
| 图 5 不同公交车比例下设置行人专用相位前后机动车流量比对比图 Fig. 5 Comparison of traffic volumes before and after setting EPP in different bus ratios |
| |
3 行人专用相位动态设置判定流程及相位切换方法 3.1 行人专用相位动态设置判定流程
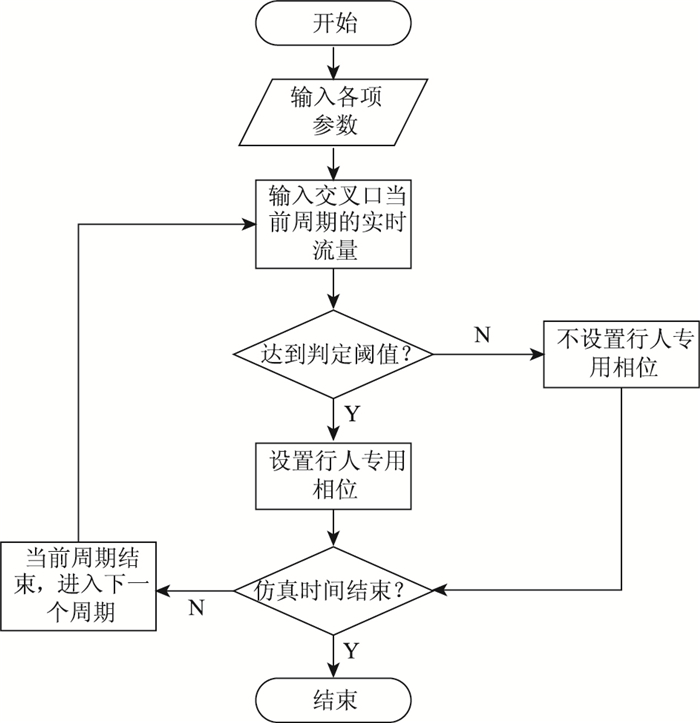
本模型的行人专用相位动态设置判定流程图如图 6所示。
|
| 图 6 行人专用相位动态设置判定流程图 Fig. 6 Flowchart of EPP dynamic setting decision |
| |
3.2 相位切换方法
对于实施本研究动态设置行人专用相位的交叉口,通过算法结合实时流量计算得出达到判定阈值的条件时,为确保交叉口车辆驾驶员充分接收信息,应事先在交叉口各信号灯上方或地面显眼处设置LED显示屏,以提示驾驶员在本周期结束下个周期起步阶段依旧停止不能通行,等待行人专用相位时段结束方可通行。尤其要注意各进口道右转车辆的信息提示,因为在未使用该方法的正常交叉口右转车辆不受信号灯控制。同时在人行道行人等待过街处也应设置LED显示屏,以提示行人下个周期是行人专用相位,注意信号灯指示准备过街。还可以在交叉口设置初期,配合交警指挥,以提高驾驶员和行人对动态设置行人专用相位信号配时方案的熟悉程度。
4 仿真试验 4.1 试验设计以仿真交叉口为例进行分析,交叉口处于人流较密集的地区,各个入口的直行、左转、右转机动车道宽度均为3.5 m,人行横道宽4 m;每个进口道均为两车道,一条是右转车道,另一条是直左车道,因本研究仿真交叉口较小,故不设置安全岛。交叉口对机动车采取两相位信号控制。具体交叉口参数与上节数值分析时的参数设定保持一致(如表 1所示)。
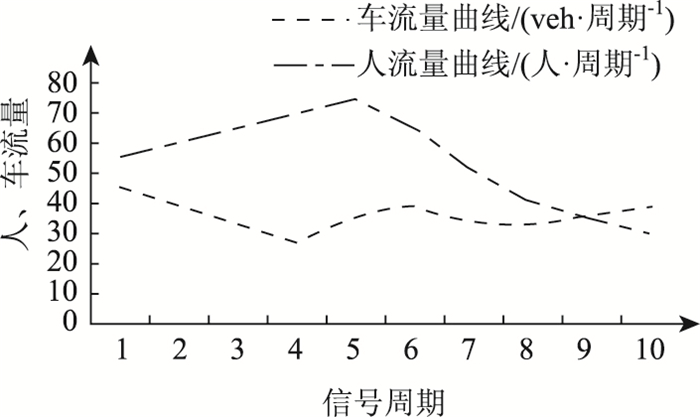
仿真试验针对上述交叉口,选取不设置行人专用相位(条件1)、设置行人专用相位(条件2)和通过各周期实时流量动态判定插入行人专用相位与否(条件3)3种仿真条件,考虑到行人流量与机动车流量有波动变化,所以设置10个周期内该交叉口的每个进口道的车流量和交叉口总人流量的实时数据流量如图 7所示。
|
| 图 7 各周期内人、车流量变化曲线 Fig. 7 Curves of pedestrian-vehicle volumes in each cycle |
| |
4.2 参数标定
笔者通过对上海市北京路常德路等交叉口进行视频监测(对视频的观测时长为15 min),得到了仿真需要的参数输入值。需要标定的参数有车头时距调整系数、设置行人专用相位前后行人波动系数。行人专用相位动态设置仿真试验需要标定的参数如表 2所示。
| 参数指标 | 描述及标定取值 |
| K1 | 结合上海市静安区北京西路与常德路交叉口视频数据,回归分析得车头时距的调整系数,取0.6 |
| K′1 | |
| K2 | 设置行人专用相位之前行人的波动系数,取2 |
| K′2 | 设置行人专用相位之后行人的波动系数,取0.8 |
| K3 | 结合上海市静安区北京西路与常德路交叉口视频数据,回归分析得直行机动车受到左转机动车影响的折减系数,取0.6 |
| K4 | 结合上海市静安区北京西路与常德路交叉口视频数据,回归分析得设置行人专用相位之前行人与右转机动车产生冲突的折减系数K4=1-0.03×(2-1.78+0.14×Q人) |
| K′4 | 结合上海市静安区北京西路与常德路交叉口视频数据,回归分析得设置行人专用相位之后行人与右转车辆产生冲突的折减系数K′4=1-0.01×(2-1.78+0.14×Q人) |
4.3 仿真结果分析
对于每一种仿真条件,分别选取5种不同的随机数种子进行5次仿真试验,以降低结果的随机影响。仿真时段长为15 min。具体结果及各项指标对比详见表 3。
| 仿真条件 | 不设置行人专用相位 | 设置行人专用相位 | 动态设置行人专用相位 |
| 交叉口小汽车通过量/veh | 302 | 305 | 310 |
| 交叉口公交车通过量/veh | 28 | 29 | 29 |
| 交叉口行人通过量/veh | 507 | 612 | 619 |
| 人均通过量差值/人 | 786 | 739 | 716 |
| 平均速度/(km·h-1) | 15.953 | 9.783 4 | 12.296 6 |
| 机动车总延误时间/h | 3.464 4 | 10.282 2 | 6.532 4 |
| 行人总延误时间/h | 2.256 8 | 6.521 2 | 4.265 94 |
| 机动车总行程时间/h | 12.215 | 20.896 4 | 13.656 96 |
| 行人行程时间/h | 7.481 6 | 13.570 4 | 9.044 3 |
由表 3可以看出,在不设置行人专用相位(条件1)的情况下,路网的平均速度最高、机动车和行人总延误时间最少、总行程时间最短,但交叉口的人车通过总量最少,且公平程度(人均通过量差值)相较其他两种仿真条件而言,最不公平(差值最大);在设置行人专用相位(条件2)的情况下,路网的平均速度最低、机动车和行人总延误时间最长、总行程时间最长,而交叉口机动车的人车通过总量有明显增加;在动态设置行人专用相位(条件3)的情况下,平均速度较仿真条件2稍有下降,机动车和行人总延误和总行程时间介于条件1和条件2之间,且交叉口能通过的交通量最大,交叉口通过的行人与机动车的公平程度最高。其他指标效果也类似,具体详见附录。综上所述,在实际仿真的情况下,动态设置行人专用相位总体说来有较好的应用前景,可以保证行人与机动车更为公平地通过交叉口,同时提高交叉口可通过的交通量并对交叉口的通行效率的影响不大。
5 结论本研究利用交叉口人车冲突特性的思想,考虑两相位信号控制交叉口行人与机动车的相互影响,提出了以行人与机动车(按行人计)的饱和度之差最小为优化目标的数据驱动的两相位交叉口行人专用相位动态设置模型。把行人专用相位设置与否作为决策变量,以行人和机动车(按通行人数计)通过交叉口的流量差值最小为目标函数。通过VISSIM仿真,结果表明该模型可行有效,通过根据交叉口实时人车流量数据,实时判定动态设置行人专用相位与否,达到了在保证行人安全过街的同时,也保证了进口道机动车的通行效率,从整体上保证了行人与机动车的通行公平性。
后续研究可考虑对行人专用相位时长进行优化,考虑交叉口信号控制绿信比的自适应优化,通过每周期实时人流量和车流量,确定下个周期是否应插入的行人专用相位并确定行人专用相位时长。因本文中只考虑了车流不过饱和的情况,故后续研究还可对车流量过饱和的情况进行讨论。后续研究还可以讨论其他情况的交叉口,如生活性交叉口、主城区车流人流量密集交叉口等情况。
| [1] |
杨晓光, 陈白磊, 彭国雄. 行人交通控制信号设置方法研究[J]. 中国公路学报, 2001, 14(1): 73-76, 80. YANG Xiao-guang, CHEN Bai-lei, PENG Guo-xiong. Study of the Way of Setting Pedestrian's Traffic Control Signal[J]. China Journal of Highway and Transport, 2001, 14(1): 73-76, 80. |
| [2] |
KNEIDL A, HARTMANN D, BORRMANN A. A Hybrid Multi-scale Approach for Simulation of Pedestrian Dynamics[J]. Transportation Research Part C:Emerging Technologies, 2013, 37(3): 223-237. |
| [3] |
KASEMSUPPAKORN P, KARIMI H A. A Pedestrian Network Construction Algorithm Based on Multiple GPS Traces[J]. Transportation Research Part C:Emerging Technologies, 2013, 26(1): 285-300. |
| [4] |
IVAN J N, MCKERNAN K, ZHANG Y, et al. A Study of Pedestrian Compliance with Traffic Signals for Exclusive and Concurrent Phasing[J]. Accident Analysis & Prevention, 2017, 98: 157-166. |
| [5] |
ZHANG Y, MAMUN S A, IVAN J N, et al. Safety Effects of Exclusive and Concurrent Signal Phasing for Pedestrian Crossing[J]. Accident Analysis & Prevention, 2015, 83: 26-36. |
| [6] |
ALHAJYASEEN W K M. The Development of Conflict Index for the Safety Assessment of Intersections Considering Crash Probability and Severity[J]. Procedia Computer Science, 2014, 32: 364-371. |
| [7] |
MA W, HAN B, AN K, et al. Investigating the Applicability of Exclusive Pedestrian Phase at Two-phase Actuated Controlled Intersections[J]. Journal of Advanced Transportation, 2015, 49(6): 752-767. |
| [8] |
MA W, LIU Y, HEAD K L. Optimization of Pedestrian Phase Patterns at Signalized Intersections:A Multi-Objective Approach[J]. Journal of Advanced Transportation, 2015, 48(8): 1138-1152. |
| [9] |
MEDINA J C, LO E G, BENEKOHAL R F. Analyzing Pedestrian Behavior during Exclusive Pedestrian Phases for Improved Intersection Signal Timing[C]//2014 Second Transportation & Development Congress, Orlando: American Society of Civil Engineers, 2014: 410-419.
|
| [10] |
HEDIYEH H, SAYED T, ZAKI M H. The Use of Gait Parameters to Evaluate Pedestrian Behavior at Scramble Phase Signalized Intersections[J]. Journal of Advanced Transportation, 2015, 49(4): 523-534. |
| [11] |
杨晓光, 马万经, 林瑜. 两相位信号控制交叉口行人专用相位设置条件研究[J]. 公路交通科技, 2005, 22(1): 127-131. YANG Xiao-guang, MA Wan-jing, LIN Yu. Criterion of Setting Exclusive Pedestrian Phases at Two-phase Signalized Intersections[J]. Journal of Highway and Transportation Research and Development, 2005, 22(1): 127-131. |
| [12] |
袁黎, 葛兴, 雷智鹢. 信号交叉口行人专用相位安全效益评价方法研究[J]. 中国安全科学学报, 2014, 24(3): 85-90. YUAN Li, GE Xing, LEI Zhi-yi. Research on Method for Evaluating Safety and Efficiency of Exclusive Pedestrian Phase[J]. China Safety Science Journal, 2014, 24(3): 85-90. |
| [13] |
钱大琳, 陈小红. 基于行人专用相位的交叉口信号控制优化模型[J]. 中国公路学报, 2013, 26(5): 140-147. QIAN Da-lin, CHEN Xiao-hong. Signal Control Optimization Model at Intersection by Modifying Pedestrian Phase[J]. China Journal of Highway and Transport, 2013, 26(5): 140-147. |
| [14] |
赵靖, 马万经, 杨晓光. 考虑下游交叉口的路段行人过街优化控制模型[J]. 同济大学学报:自然科学版, 2014, 42(10): 1536-1542. ZHAO Jing, MA Wan-jing, YANG Xiao-guang. Signal Control Model for Mid-block Pedestrian Crossing with Consideration of Downstream Intersection[J]. Journal of Tongji University:Natural Science Edition, 2014, 42(10): 1536-1542. |
| [15] |
杨晓光, 赵靖, 马万经, 等. 信号控制交叉口通行能力计算方法研究综述[J]. 中国公路学报, 2014, 27(5): 148-157. YANG Xiao-guang, ZHAO Jing, MA Wan-jing, et al. Review on Calculation Method for Signalized Intersection Capacity[J]. China Journal of Highway and Transport, 2014, 27(5): 148-157. |
| [16] |
赵星, 任刚. 信号交叉口车头时距特性分析[J]. 交通运输工程与信息学报, 2010, 8(1): 103-108. ZHAO Xing, REN Gang. Analysis of Vehicle Headway Characters at a Signalized Intersection[J]. Journal of Transportation Engineering and Information, 2010, 8(1): 103-108. |
| [17] |
李文勇, 陈学武, 王庆, 等. 路段人行横道通行能力及过街绿灯时间计算[J]. 武汉理工大学学报:交通科学与工程版, 2006, 30(5): 751-754. LI Wen-yong, CHEN Xue-wu, WANG Qing, et al. Algorithm of Mid-block Street Crossing Capacity and Cross-street Green Time[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2006, 30(5): 751-754. |
| [18] |
郑祖武, 李康, 徐吉谦, 等. 现代城市交通[M]. 北京: 人民交通出版社, 1998. ZHENG Zu-wu, LI Kang, XU Ji-qian, et al. Modern Urban Traffic[M]. Beijing: China Communications Press, 1998. |
 2020, Vol. 37
2020, Vol. 37
