扩展功能
文章信息
- 刘晨凯, 郑万山
- LIU Chen-kai, ZHENG Wan-shan
- 基于模态识别的短索索力识别方法
- An Estimation Method of Short Cable Force Based on Modal Identification
- 公路交通科技, 2020, 37(1): 74-84
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 74-84
- 10.3969/j.issn.1002-0268.2020.01.010
-
文章历史
- 收稿日期: 2019-03-20
2. 桥梁工程结构动力学国家重点实验室, 重庆 400067
2. State Key Laboratory of Bridge Engineering Structural Dynamics, Chongqing 400067, China
拉索索力的变化通常是结构退化的关键指标,同时也影响结构的内力分布[1],准确快速地评估索力是非常重要的。频率法由于其方便的激励方式和可靠的测量精度,成为最广泛应用的技术。对于长索,频率法测试精度满足工程应用。但是对于短索,经典索力计算公式是在理想的两端铰接条件下得到的, 对于一般边界条件将面临计算长度选取的难题[2];同时,拉索抗弯刚度的选取对索力测试精度的影响同样不容忽视。
针对一般边界条件下的短索索力识别,前人进行了大量的研究。2007年Nerio Tullini等人在已知拉索抗弯刚度前提下,除拉索两端振幅为零的边界条件外,引入3个已知测点的振幅,建立方程组,求解得到拉索索力及两端的转角刚度[3]。2011年Suzhen Li等人在已知拉索抗弯刚度前提下,选取至少5个测点的振动数据,利用挠度函数和应变函数之间的关系式得到方程组,最终求得索力与两端的支撑刚度和转角刚度[1]。2015年李柯君等人在已知拉索抗弯刚度前提下,利用拉索的某个自振频率和相应振型的几个振动分量,在未知边界条件的情况下识别索力,最终确定拉索的边界等效弹簧的刚度值[4]。2015年晏班夫等人提出的方法将零幅度点间的距离作拉索计算长度代入到索力计算式中,从而求得索力[5]。
除了各阶模态频率及质量参数外,现有测试理论仍需要在获取拉索截面抗弯刚度信息的基础上才能实现索力识别[1-6]。实际拉索通常是由钢绞线或者平行钢丝构成的,其内部钢丝间的黏结力大小存在离散性,因此即使是同一型号的拉索,不同拉索的截面抗弯刚度也具有离散性的特征。在已知拉索型号的前提下,拉索的实际抗弯刚度仍难以确定。因此有必要开展在未知抗弯刚度的前提下,一般边界条件的短索索力识别研究。
1 理论公式推导 1.1 理论公式推导受恒定拉力欧拉伯努利梁振动方程的通解表达式[7]为:
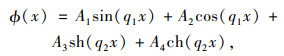
|
(1) |
式中,A1,A2,A3,A4为常数;q1= 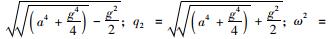
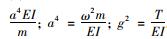
又知:
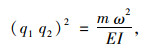
|
(2) |
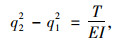
|
(3) |
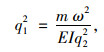
|
(4) |
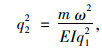
|
(5) |
式中, EI为索的抗弯刚度; m为线质量; T为索的拉力; ω为拉索自振圆频率。
下面对索力计算公式进行整理,以得到一个适用于一般边界条件的索力计算公式。
将式(5)代入式(3)中得:

|
(6) |
化简得:

|
(7) |
又因

|
(8) |
可得:
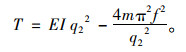
|
(9) |
同理将式(4)代入式(2)中得:

|
(10) |
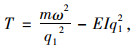
|
(11) |

|
(12) |
当边界条件为两端铰接时,索力计算公式[7]为:
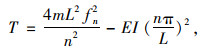
|
(13) |
式中,L为拉索总长,其振型函数为ϕ(x)=A1sin(q1x),半波长为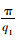
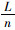

对适用于梁模型而边界条件复杂的短索,可以使用式(12)计算索力。计算索力所需获取的参数有拉索每延米质量参数m、自振频率f、参数q1及抗弯刚度EI,质量参数m及各阶自振频率均易获得,则索力识别的关键转变为参数q1及抗弯刚度EI的识别问题。
在具体参数识别时,振型函数中非线性项括号内有两个未知数,假设仍然能够通过建立方程组求解。通过某阶模态下5个已知点的振型可以建立方程组:
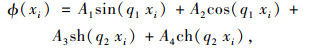
|
(14) |
式中i=1, 2, 3, 4, 5。
令
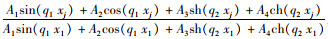
可得:
A1sin(q1xj)+A2cos(q1xj)+A3sh(q2xj)+A4ch(q2xj)= λj1[A1sin(q1x1)+A2cos(q1x1)+A3sh(q2x1)+A4ch(q2x1)],即A1[sin(q1xj)-λj1sin(q1x1)]+A2[cos(q1xj)-λj1cos(q1x1)]+A3[sh(q2xj)-λj1sh(q2x1)]+A4[ch(q2xj)-λj1ch(q2x1)]=0,式中j=2, 3, 4, 5。
由以上方程组可知,即使增加方程的数量,对括号内的未知数求解并没有帮助。括号内的未知参数q1, q2通常的求解方法是,将方程组转化成矩阵形式,然后利用系数行列式等于0来求解。q1,q2满足式(2)、式(3),加上行列式等于0,已知方程数量为3个,未知参数为q1,q2,T,EI 4个,有无穷解。
因此在未知拉索抗弯刚度EI的情况下,只能采用曲线拟合的方法通过多个点的振型数据来拟合振型函数通解,得到参数值q1,q2,从而求得索力值及拉索抗弯刚度。
2 短索索力测试方法研究根据前文的分析可知,在未知拉索抗弯刚度的情况下,只能通过曲线拟合来获取未知参数q1,q2的值。拟合得到参数q1,q2的值后,有两种方式来求得索力值及抗弯刚度:
(1) 同时识别参数q1,q2,然后通过二者的关系式求得拉索索力及抗弯刚度EI;
(2) 识别参数q1,q2其中的一项,选用索力计算公式(7)或者(12)计算索力值,抗弯刚度由不同阶模态建立的形如式(7)或式(12)的方程组联立求解得到。
2.1 短索模态振型特征本研究通过分析各类边界条件下梁模型的各阶模态振型特征,得到如下结论:
进行索力识别时,应以三角函数项的识别为主,即以参数q1的识别为主。因此,本研究采用的索力计算公式是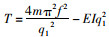
根据前文分析结果可推出一个基于识别参数q1的短吊杆索力识别的方法。具体测试步骤如下:
(1) 测量无支撑段拉索长度,计算传感器布点位置并布设传感器。
理论上在拉索的全长段均可以布设传感器,但是由于边界条件附近振动较弱,信噪比较差,不建议在边界附近取点。结合拉索的振型特征提出两种推荐布点方案,具体最优布点位置及数量方案仍需进一步做研究。同时需要指出的是,各传感器所测量的振动方向应一致,若振动测量方向为竖直向上则各传感器均布置为竖直方向。
6测点方案:取6个点布设传感器,假设无支撑段的拉索长度为1,则各点的相对布设位置如图 1所示。

|
| 图 1 6传感器布置方案 Fig. 1 Arrangement of 6 sensors |
| |
8测点方案:取8个点布设传感器,假设无支撑段的拉索长度为1,则各点的相对布设位置如图 2所示。

|
| 图 2 8传感器布设位置 Fig. 2 Arrangement of 8 sensors |
| |
这种不等间距的传感器布设方法既能适用于低阶模态的振型函数拟合,同时也能满足高阶模态振型函数拟合的需要。显然测点数量更多时,得到的振型数据更加丰富,由此拟合得到的振型函数也更加接近真实振型函数。
(2) 对拉索进行激励,采集各传感器同步时程信息。
(3) 对时程数据进行傅里叶变换查看频率。通过所得频谱图判断各阶频率是否等间距,若为等间距则使用弦模型方法计算,若不等间距则采用梁模型方法计算。
(4) 应用随机子空间法获得各点振型数据。
随机子空间法(Stochastic Subspace Identification-SSI)[8-10]是基于环境振动模态参数识别的时域方法,不需要人工激励,能准确识别系统的频率,能很好的识别系统的模态振型和阻尼,确定系统的阶次是该方法的关键。稳定图法是一种比较新颖的确定系统阶次的方法,但该方法容易识别出虚假模态。常军等人[11]对稳定图法进行了改进,用模态置信因子来消除虚假模态,将阻尼比的标准放松至40%,提高了随机子空间方法的识别精度。
本研究应用的即是随机子空间结合稳定图的方法来识别各阶模态振型,稳定图示例如图 3所示。

|
| 图 3 稳定图示例 Fig. 3 Example of a stabilization diagram |
| |
(5) 预估各阶振型半波长范围并拟合拉索梁模型振型函数。
选用MATLAB中的lsqcurvefit函数[12]对得到的振型数据进行拟合[13],可得到整个振型函数的表达式,各参数的初始值在预估范围内程序随机选择,最后通过一些评价标准来检验拟合的准确度并选出最优拟合。拟合结果评价标准有[14]:残差平方和(Sum of Squares for Error)、均方根(Root Mean Square)、相关系数(Coefficient Of Correlation)、决定系数(Coefficient Of Determination)、卡方系数(Chi-Square)。
(6) 代入公式计算拉索索力及EI。索力使用一阶模态频率进行计算,即: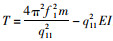
抗弯刚度EI通过第1和n两阶模态联立方程组求解得来,两阶模态的索力计算公式分别为:
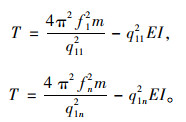
|
(15) |
由以上两式可得EI表达式为:
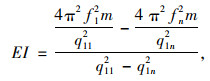
|
(16) |
式中,f1,fn分别表示第一阶频率和第n阶频率;q11,qn1分别表示第1阶模态的参数q1和第n阶模态的参数q1。当计算得到的某个索力值偏离其他大多数索力值较大时,将该索力计算结果去掉,再求剩余索力的平均值。
2.3 测试方法流程图本研究测试方法流程图如图 4所示。

|
| 图 4 测试方法流程图 Fig. 4 Flowchart of test method |
| |
2.4 误差来源及适用范围分析 2.4.1 误差来源分析
短索索力识别方法的误差主要来源于以下几个方面:
(1) 欧拉伯努利梁模型带来的误差;
(2) 各传感器的振动测量方向不一致导致所得振型与实际振型存在偏差;
(3) 噪声的影响;
(4) 测点的布置位置及数量。
2.4.2 适用范围本方法是基于欧拉伯努利梁理论得到的,运用本方法进行索力估算时必须满足以下条件[15]:
(1) 不考虑索剪切变形的影响;
(2) 索在横向作微振动, 沿轴线方向位移忽略不计;
(3) 索自由振动, 不受横向力作用;
(4) 不考虑索的阻尼的影响;
(5) 不考虑索的自重影响。
3 数值模拟索力识别研究为了验证提出的索力测试方法的实用性,进行有限元模拟短索索力测试[16]。
采用6弹簧边界条件下beam3梁单元来模拟拉索,如图 5所示,模型两端点约束轴向位移,用combin14单元模拟弹簧,通过整体降温来模拟拉索张拉,打开PSTRES。通过改变各弹簧的刚度来模拟边界条件的改变。假设拉索阻尼为瑞利阻尼[17],阻尼比取5e-3,α=6.3e-3,β=3.2e-6。

|
| 图 5 短索模型示意图 Fig. 5 Schematic diagram of short cable model |
| |
拉索各项参数为:直径D=0.15 m,全长L=5 m,L1=0.5 m,L2=0.6 m,索力T=10 000 kN,无量纲参数7.18,每延米质量m=139.96 kg/m。各弹簧刚度参数值见表 1。
| 弹簧刚度编号 | k1 | k2 | k3 | k4 | k5 | k6 |
| 参数值/(N·m-1) | 1e+11 | 1e+12 | 1e+7 | 1e+8 | 1e+6 | 1e+10 |
根据推荐布点方法选取图 6中位置点的响应数据做索力识别计算。
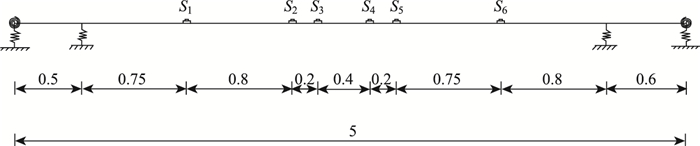
|
| 图 6 测点布置(单位:m) Fig. 6 Arrangement of measuring points (unit:m) |
| |
对各点的时域振动数据进行傅里叶变换[18]后可得各阶模态频率如表 2所示。
| 模态阶数 | 识别频率/Hz | 实际频率/Hz |
| 1阶 | 42.25 | 42.249 |
| 2阶 | 101.02 | 101.06 |
| 3阶 | 183.88 | 184.09 |
| 4阶 | 292.76 | 293.59 |
| 5阶 | 427.47 | 430.06 |
| 注:此处的1,2,3阶编号为各阶频率按从小到大排列所得,但本例为数值模拟,各阶频率均有对应的理论频率值,所以能够确定各阶模态具体的阶数,实际识别时要确定具体的模态阶数仍需振型数据来辅助确认。 | ||
应用随机子空间法处理数据后得到的稳定图如图 7所示,选取小于500 Hz的5阶模态,并导出各阶模态相应的振型见表 3。将各阶模态振型数据代入到曲线拟合程序中,拟合结果及评价指标分别如表 4、表 5所示。

|
| 图 7 稳定图 Fig. 7 Stabilization diagram |
| |
| 模态阶数 | 频率/Hz | S1 | S2 | S3 | S4 | S5 | S6 |
| 1阶 | 42.25 | 0.750 8 | 1 | 0.998 4 | 0.915 9 | 0.838 2 | 0.404 4 |
| 2阶 | 101.02 | 1 | 0.157 0 | -0.160 0 | -0.718 2 | -0.905 0 | -0.809 2 |
| 3阶 | 183.88 | 0.493 1 | -0.931 4 | -0.942 9 | -0.413 1 | 0.019 2 | 1 |
| 4阶 | 292.76 | -0.369 7 | -0.362 1 | 0.236 1 | 1 | 0.901 2 | -0.949 0 |
| 5阶 | 427.47 | -0.987 0 | 0.919 5 | 1 | -0.172 8 | -0.813 5 | 0.544 6 |
| 模态阶数 | 拟合所得q1 | 实际q1 | q1识别误差/% | 拟合所得q2 | 实际q2 | q2识别误差/% |
| 1阶 | 0.854 1 | 0.853 7 | 0.04 | 1.670 2 | 1.671 1 | -0.05 |
| 2阶 | 1.565 9 | 1.591 6 | -1.61 | 6.548 0 | 2.144 0 | 205.40 |
| 3阶 | 2.298 4 | 2.295 5 | 0.12 | 2.405 3 | 2.708 0 | -11.18 |
| 4阶 | 2.998 5 | 2.989 2 | 0.31 | 1.963 4 | 3.316 5 | -40.80 |
| 5阶 | 3.695 5 | 3.677 9 | 0.48 | 2.643 1 | 3.948 5 | -33.06 |
| 模态阶数 | 均方根 | 残差平方和 | 相关系数 | 决定系数 | 卡方系数 |
| 1阶 | 2.01e-08 | 2.42e-15 | 1 | 1 | 1.29e-15 |
| 2阶 | 6.49e-06 | 2.53e-10 | 1 | 1 | -2.94e-10 |
| 3阶 | 4.09e-10 | 1.01e-18 | 1 | 1 | 9.37e-18 |
| 4阶 | 5.16e-04 | 1.60e-06 | 1 | 1 | 1.32e-06 |
| 5阶 | 3.65e-09 | 7.98e-17 | 1 | 1 | -5.94e-17 |
由表 5中各评价指标可知,本次拟合结果比较准确。由表 4可知,q1的识别精度较高;随着模态阶数的提升,q2的识别误差增大,甚至程序拟合所得结果不能满足q1 < q2。将各阶模态振型图与对应的拟合所得曲线放图 8中进行对比。
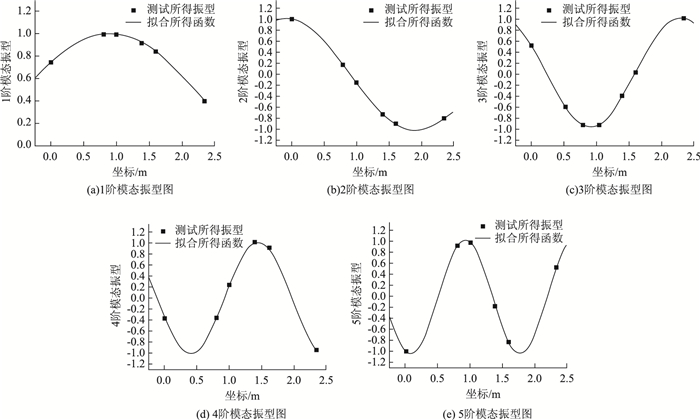
|
| 图 8 各阶模态振型图 Fig. 8 Curves of each order modal vibration shape 注:图中横坐标轴以最左端1号传感器测点为坐标原点,向右为正方向,单位为m。 |
| |
根据已知的质量参数,各阶模态的频率与q1参数值,采用1阶频率进行索力计算,抗弯刚度EI由1阶与其他阶模态联立方程组求解得到,并代入梁模型索力计算式(12)中计算索力值,结果如表 6所示。
| EI来源 | EI/(×103kN·m2) | 索力/(×103kN) | 误差/% |
| 1, 2阶联立 | 5.50 | 9.51 | 4.94 |
| 1, 3阶联立 | 4.80 | 10.02 | -0.19 |
| 1, 4阶联立 | 4.74 | 10.06 | -0.62 |
| 1, 5阶联立 | 4.67 | 10.11 | -1.10 |
其中:实际拉索索力为10 000 kN,抗弯刚度为4 845.85 kN·m2。
4 试验索力识别研究 4.1 试验简介为进一步验证短索索力测试方法的有效性,进行了实验室索力测试试验。
试验采用人工敲击拉索,不采集输入信号,通过输出信号来识别拉索索力,采样频率均为1 000 Hz。试验系统流程图如图 9所示,系统由试验装置、振动测量部分以及数据处理部分组成。

|
| 图 9 试验系统流程图 Fig. 9 Flowchart of test system |
| |
本试验共使用8个型号为8310A10的加速度计,其量程为±10g,灵敏度为0.02 mV/g,频响范围为0~1 000 Hz。数据采集仪为德维创生产的DEWE2-A4,现场照片如图 10所示。

|
| 图 10 数据采集仪DEWE2-A4照片 Fig. 10 Photo of data acquisition instrument DEWE2-A4 |
| |
试验借助于招商局重庆交科院的拉索疲劳试验设备,在拉索处于静止状态时,应用本方法对拉索索力进行测试。试验装置示意图及现场照片分别如图 11、图 12所示。

|
| 图 11 试验装置示意图 Fig. 11 Schematic diagram of test device |
| |

|
| 图 12 试验装置及拉索现场照片 Fig. 12 Photo of test device and cable |
| |
所用拉索符合规范《斜拉桥热挤聚乙烯高强钢丝拉索技术条件》(GB/T 18365—2001)规定,型号为PES(C)7-421,弹性模量为195 GPa,单根钢丝直径为7 mm,钢丝数量为421,钢丝束公称截面积为162.02 cm2,拉索总的钢丝束拉索外径为181 mm,质量参数m=134.9 kg/m,拉索张拉端安装有锚索计,在本次试验时,锚索计显示索力T=9 848 kN。受现场条件所限,拉索有部分长度范围内无法布设加速度传感器,在原有推荐的8测点方案的基础上调整了传感器的布设位置,拉索及传感器位置示意图及现场照片分别如图 12、图 13所示。

|
| 图 13 拉索及传感器位置示意图(单位:m) Fig. 13 Schematic diagram of cable and sensor positions(unit:m) |
| |
试验步骤:
(1) 测量可布设传感器段拉索长度,计算传感器布点位置并布设传感器。
(2) 对拉索进行激励,采集各传感器时程信息。
(3) 对时程数据进行傅里叶变换查看频率。通过所得频谱图判断各阶频率是否等间距,若为等间距则使用弦模型方法计算,若不等间距则采用梁模型方法计算。
(4) 应用随机子空间法获得各点振型数据。
(5) 预估各阶振型半波长范围并拟合拉索梁模型振型函数。
(6) 代入公式计算拉索索力及EI。
4.2 试验结果与索力识别试验所得各点时程数据如图 14所示。
|
| 图 14 各传感器加速度响应图 Fig. 14 Acceleration response of each sensor |
| |
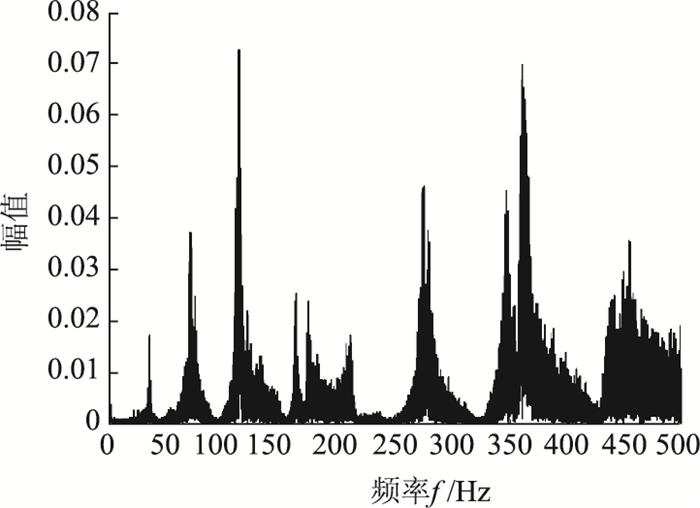
对各测点加速度时程数据进行傅里叶变换后可得各点频域加速度响应图,其特征如图 15所示。
|
| 图 15 S1频域加速度响应 Fig. 15 Frequency domain acceleration response of S1 |
| |
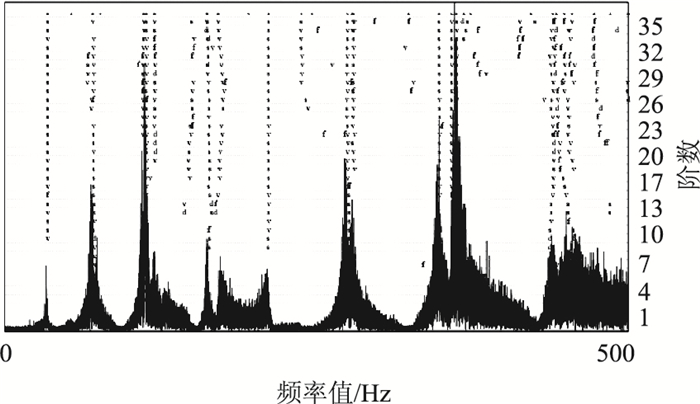
使用随机子空间法处理后可得稳定图如图 16所示,选取几阶相对稳定的模态提取相应的振型,其结果如表 7所示。

|
| 图 16 稳定图 Fig. 16 Stabilization diagram |
| |
| 频率/Hz | 频率差/Hz | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
| 33.3 | — | 0.39 | 0.51 | 0.68 | 0.80 | 0.96 | 0.99 | 1.00 | 0.97 |
| 70.3 | 37.0 | 0.83 | 0.95 | 1.00 | 0.94 | 0.41 | 0.07 | -0.22 | -0.56 |
| 112.2 | 41.9 | 1.00 | 0.91 | 0.46 | 0.08 | -0.84 | -0.96 | -0.89 | -0.62 |
| 210.4 | 98.2 | 0.02 | 0.53 | 1.00 | 0.83 | -0.55 | -0.90 | -0.83 | -0.34 |
| 274.4 | 64.0 | 0.67 | 1.00 | 0.59 | -0.12 | -0.76 | -0.19 | 0.41 | 0.84 |
将各阶模态振型数据代入到曲线拟合程序中,拟合结果及评价指标分别如表 8、表 9所示。
| 模态阶数 | 拟合所得q1/m-1 | (π/q1)/m |
| 1阶 | 0.707 1 | 4.44 |
| 2阶 | 1.203 1 | 2.61 |
| 3阶 | 1.767 8 | 1.78 |
| 4阶 | 2.579 9 | 1.22 |
| 5阶 | 3.035 9 | 1.03 |
| 模态阶数 | 均方根 | 残差平方和 | 相关系数 | 决定系数 | 卡方系数 |
| 1阶 | 5.14e-03 | 2.11e-04 | 0.999 734 | 0.999 469 | 1.40e-04 |
| 2阶 | 4.36e-03 | 1.52e-04 | 0.999 974 | 0.999 94 | 5.66e-05 |
| 3阶 | 2.37e-02 | 4.51e-03 | 0.999 653 | 0.999 051 | -2.81e-03 |
| 4阶 | 1.08e-02 | 9.29e-04 | 0.999 88 | 0.999 761 | 2.69e-04 |
| 5阶 | 2.24e-02 | 4.01e-03 | 0.999 214 | 0.998 429 | -3.18e-03 |
由表 9中各评价指标可知,本次拟合结果比较准确。现将各阶模态振型图与对应的拟合所得曲线放入图中进行对比,如图 17所示。
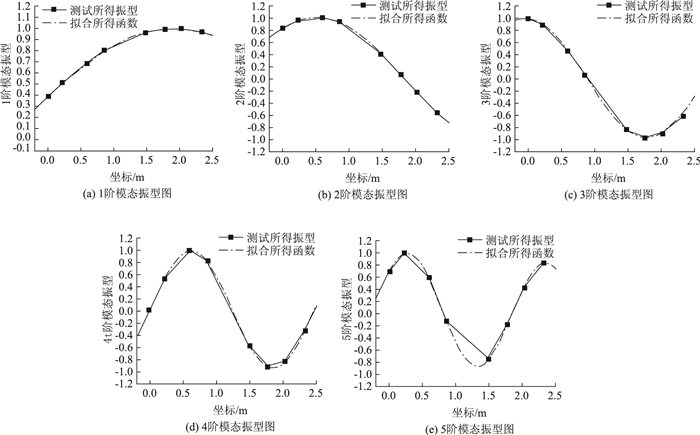
|
| 图 17 各阶模态振型 Fig. 17 Curves of each order modal vibration shape 注:图中横坐标轴以最左端1号传感器测点为坐标原点,向右为正方向,单位为m。 |
| |
实际测试的过程中存在某阶模态未能识别得到,结合各点的频域响应图及振型图可知3阶与4阶之间的模态未能识别,但是从表 7的频率差可以看出相邻两阶模态间的频率差在逐渐增大,即弦模型在此已经不再适用,应该选用梁模型来计算索力。
此时已知条件有:质量参数m,各阶模态的频率与q1参数值,采用1阶频率进行索力计算,抗弯刚度EI由1阶与其他阶模态联立方程组求解得到,并代入梁模型索力计算式(12)中计算索力值,其结果见表 10。
| EI来源 | EI/(×103 kN·m2) | 索力/(×103 kN) | 误差/% |
| 1, 2阶联立 | 6.67 | 8.47 | 14.01 |
| 1, 3阶联立 | 3.67 | 9.97 | -1.23 |
| 1, 4阶联立 | 3.84 | 9.89 | -0.40 |
| 1, 5阶联立 | 3.64 | 9.99 | -1.42 |
其中:锚索计测得索力为9 848 kN。
由表 10可知,抗弯刚度由1阶与3,4,5阶模态联立方程组求解得到时,误差较小;当抗弯刚度由1阶与2阶模态联立方程组求解得到时,识别误差较大。可能的原因有两个:(1)2阶模态的振型识别有较大误差;(2)拟合参数q1过程中产生的误差较大。
从以上结果可知,本方法在进行一次试验的情况下可得到多个索力值,在确定所测拉索索力值时,可将偏离其他大多数索力值的结果去掉,再求索力平均值,本试验所得平均值如表 11所示。
| EI/(×103kN·m2) | 索力/(×103 kN) | 索力误差/% | |
| 修正平均值 | 3.72 | 9.95 | -1.02 |
由表 11可知,本次试验所得索力值精度能够满足工程实际需要。
最后将本研究提出的测试方法与经典测试方法进行对比。由于经典测试方法涉及到拉索的计算长度及抗弯刚度的选取,因此计算长度分别取拉索全长、拉索无套筒段长度、1阶模态的π/q1,抗弯刚度分别取每根钢丝抗弯刚度的代数和、将钢束视为实体进行计算所得EI。
采用1阶频率作基频代入经典理论公式进行索力计算,两类经典索力测试方法计算结果见表 12。
| 理论模型 | 计算长度/m | EI/(kN·m2) | 索力/(×103kN) | 误差/% |
| 弦模型 | 6.43 | — | 24.73 | -151.11 |
| 4.5 | — | 12.11 | -22.99 | |
| 4.44 | — | 11.81 | -19.88 | |
| 梁模型 | 6.43 | 9.68 | 24.73 | -151.08 |
| 4 073.45 | 23.76 | -141.23 | ||
| 4.5 | 9.68 | 12.11 | -22.96 | |
| 4 073.45 | 11.14 | -13.11 | ||
| 4.44 | 9.68 | 11.80 | -19.86 | |
| 4 073.45 | 10.83 | -10.01 |
由表 11及表 12可知,计算长度的选取不慎引起的索力测试误差巨大;对于梁模型,实际抗弯刚度的取值范围巨大,EI的选取引起的索力测试误差不容忽视。本研究方法测得的抗弯刚度为3 715.48 kN·m2,介于钢丝实体与独立体代数和之间,相对来说更接近于视拉索为实体的计算所得。
本研究的测试方法能够同时避免计算长度与抗弯刚度的选取问题,提高了索力测试的精度。
5 结论本研究通过推导整理梁单元索力计算公式,采用有限元模拟短索,研究了短索索力测试方法,并进行了索力测试数值模拟与实验室拉索索力测试,得到了如下结论:
(1) 在梁模型理论的基础上整理得到一个适用于一般边界条件的索力计算公式,并指出两端铰接边界条件下的索力计算公式为梁模型新公式的一种特殊形式。
(2) 结合随机子空间法及曲线拟合技术推出了一种基于模态分析且未知拉索抗弯刚度的前提下,能够适用于一般边界条件的短索索力识别方法,并分析了其适用范围及测试误差可能的来源。
(3) 通过索力测试数值模拟与实验室拉索索力测试试验,验证了短索索力测试方法的可行性与适用性,索力识别精度能够满足工程需要。
| [1] |
LI SU-ZHEN, REYNDERS EDWIN, MAES KRISTOF, et al. Vibration-based Estimation of Axial Force for a Beam Member with Uncertain Boundary Conditions[J]. Journal of Sound and Vibration, 2013, 332(4): 795-806. |
| [2] |
周正茂. 振型节点法估算短索索力的数值分析[J]. 公路交通科技, 2013, 30(12): 107-113, 131. ZHOU Zheng-mao. Numerical Analysis on Mode Node Method for Estimation of Tension in Short Cable[J]. Journal of Highway and Transportation Research and Development, 2013, 30(12): 107-113, 131. |
| [3] |
REBECCHI G, TULLINI N, LAUDIERO F. Estimate of the Axial Force in Slender Beams with Unknown Boundary Conditions Using One Flexural Mode Shape[J]. Journal of Sound and Vibration, 2013, 332(18): 4122-4135. |
| [4] |
李柯君.基于模态特性的未知边界条件下索力识别[D].合肥: 合肥工业大学, 2015. LI Ke-jun. Modal Characteristics-based Identification of Cable Tension with Unknown Boundary Condition[D]. Hefei: Hefei University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10359-1015650053.htm |
| [5] |
YAN B F, YU J Y, SOLIMAN M, et al. Estimation of Cable Tension Force Independent of Complex Boundary Conditions[J]. Journal of Engineering Mechanics, 2015, 141(1): 06014015. |
| [6] |
郑罡, 王鹏, 唐光武. 桥梁索结构[M]. 北京: 人民交通出版社, 2015. ZHENG Gang, WANG Peng, TANG Guang-wu. Bridge Cable Structures[M]. Beijing: China Communications Press, 2015. |
| [7] |
吴文清, 王成树, 刘国昌, 等. 大跨度系杆拱桥柔性吊杆张力监测和参数识别研究[J]. 公路交通科技, 2007, 24(1): 69-73. WU Wen-qing, WANG Cheng-shu, LIU Guo-chang, et al. Flexible Hanger Rods Tension Measurement and Parameter Identification in Large-span Tied Arch Bridge[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 69-73. |
| [8] |
OVERSCHEE PETER VAN, MOOR BART DE. Subspace Identification for Linear Systems[M]. Boston: Kluwer Academic Publisher, 1996.
|
| [9] |
NANDAGOPALAN S. Engineering Applications of Correlation and Spectral Analysis[J]. Technometrics, 1994, 36(2): 220-221. |
| [10] |
张笑华, 任伟新, 禹丹江. 结构模态参数识别的随机子空间法[J]. 福州大学学报:自然科学版, 2005, 33. ZHANG Xiao-hua, REN Wei-xin, YU Dan-jiang. Structural Modal Parameter Identification Applying Stochastic Subspace Identification[J]. Journal of Fuzhou University:Natural Sciences Edition, 2005, 33(S1): 46-49. |
| [11] |
常军, 张启伟, 孙利民. 稳定图方法在随机子空间识别模态参数中的应用[J]. 工程力学, 2007, 24(2): 39-44. CHANG Jun, ZHANG Qi-wei, SUN Li-min. Application of Stabilization Diagram for Modal Parameter Identification Using Stochastic Subspace Method[J]. Engineering Mechanics, 2007, 24(2): 39-44. |
| [12] |
COLEMAN T F, LI Y. On the Convergence of Reflective Newton Methods for Large-scale Nonlinear Minimization Subject to Bounds[J]. Mathematical Programming, 1994, 67(1/2/3): 189-224. |
| [13] |
罗成汉, 刘小山. 曲线拟合法的Matlab实现[J]. 现代电子技术, 2003, 26(20): 16-17, 20. LUO Cheng-han, LIU Xiao-shan. Realization Method to Curve Fitting Based on Matlab[J]. Modern Electronic Technique, 2003, 26(20): 16-17, 20. |
| [14] |
《数学辞海》编辑委员会. 数学辞海:第4卷[M]. 北京: 中国科学技术出版社, 2002. Editorial Board of Mathematics Dictionary. Mathematics Dictionary:Volume 4[M]. Beijing: Science and Technology of China Press, 2002. |
| [15] |
徐霞飞.考虑边界条件影响的吊索索力估算与试验[D].长沙: 中南大学, 2008. XU Xia-fei. Estimation and Test of Tie-bars Force Considering Boundary Conditions[D]. Changsha: Central South University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10533-2009237851.htm |
| [16] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. WANG Xin-min. Numerical Analysis of Engineering Structure Using ANSYS Software[M]. Beijing: China Communications Press, 2007. |
| [17] |
克拉夫R, 彭津J.结构动力学[M].王光远, 译.北京: 科学出版社, 1981. CLOUGH R, PENZIEN J. Structural Dynamics[M]. WANG Guang-yuan, translated. Beijing: Science Press, 1981. |
| [18] |
王普明, 郭建英. 信号处理技术[M]. 郑州: 黄河水利出版社, 2011. WANG Pu-ming, GUO Jian-ying. Signal Processing Technology[M]. Zhengzhou: The Yellow River Water Conservancy Press, 2011. |
 2020, Vol. 37
2020, Vol. 37
