扩展功能
文章信息
- 肖泽荣
- XIAO Ze-rong
- 有初应力的钢管混凝土桁式拱结构平面内受力性能试验研究
- Experimental Study on In-plane Stress Performance of CFST Truss Arch Structure with Initial Stress
- 公路交通科技, 2020, 37(1): 66-73
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 66-73
- 10.3969/j.issn.1002-0268.2020.01.009
-
文章历史
- 收稿日期: 2018-04-20
目前,钢管混凝土拱桥在我国的数量增长较快,成为了一种较重要的桥型[1]。在跨度较大的钢管混凝土拱桥大多采用格构式截面。钢管混凝土拱桥通常采用极限状态法进行验算,即应用等效梁柱法把钢管混凝土拱结构等效成钢管混凝土柱,通过极限状态法进行极限承载力的验算。对钢管混凝土桁式拱的极限承载能力研究表明,钢管混凝土桁式拱结构的受力特性受到矢跨比以及荷载形式的影响。文献[2]制作了钢管混凝土桁式拱模型进行了试验,研究表明:钢管混凝土桁式拱节间腹杆受到较大的力;在达到极限荷载前没有节点破坏,有很好的整体性;达到极限荷载后,直腹杆屈曲,斜腹杆剪切破坏,然后主弦管失稳。
由钢管自身和灌注的混凝土产生的重力,都会使钢管拱肋在形成组合结构之前产生初应力。初应力对钢管混凝土拱的极限承载能力的影响,有学者对此问题展开了研究,研究大部分集中在有限元分析方面。研究表明[3-11]:初应力对钢管混凝土拱结构极限承载力的影响不可忽略,其极限承载能力最大可下降10%;不同拱肋形式受初应力影响的程度不同,极限承载能力最大可下降超过30%;初应力的存在会降低拱肋面外极限承载能力;不同的加载方式会导致初应力对钢管混凝土的承载能力影响不同; 初应力使拱的塑性变形特征更明显,对其变形影响较大;对失稳形式没有影响。文献[12] 4根钢管混凝土单圆管拱初应力试验表明:随着初应力增加,钢管混凝土构件的极限承载力非线性下降,且最大下降幅度超过了10%;文献[13-18]研究表明, 初应力对于钢管混凝土构件的极限承载力影响的大小与长细比、偏心率有关,而拱结构还与矢跨比有关。
考虑初应力的钢管混凝土桁式拱试验开展较少。而目前,已建和在建的钢管混凝土桁式拱桥的数量不断增加,跨径也不断增大[1]。跨径越大,初应力也越大,影响也越显著,因此,需开展该方面的研究。为此,在文献[2]的基础上,对有初应力的钢管混凝土桁式拱结构模型进行试验研究, 研究有初应力对钢管混凝土桁拱平面内受力性能的影响,为有初应力的钢管混凝土桁拱承载能力计算提供参考。
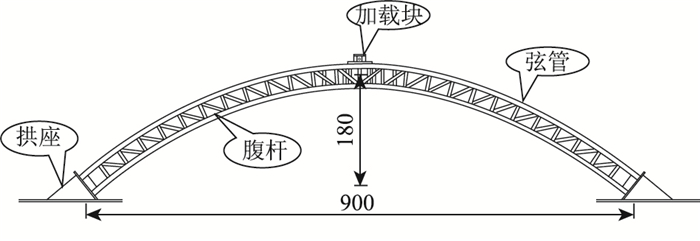
1 试验概况 1.1 试件设计试验设计制作了1根钢管混凝土桁式拱结构,初应力度为0.1。模型计算跨径为9 m,矢跨比为1/5,矢高为1.8 m,拱轴线为二次抛物线。拱结构模型如图 1所示。
|
| 图 1 试验拱模型全构造(单位:cm) Fig. 1 Structure of test arch model (unit: cm) |
| |
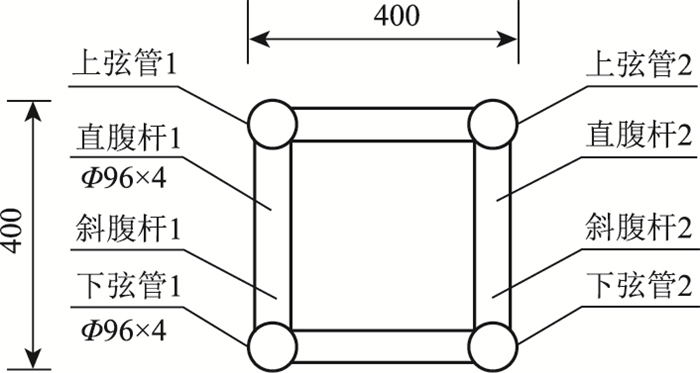
桁拱截面的长与宽均为400 mm,上下弦管的尺寸为Φ89 mm×4 mm,直腹杆、斜腹杆与平腹杆尺寸都为Φ48 mm×2 mm。桁拱截面如图 2所示。为了便于描述和分析,同一节间的桁拱截面,其左侧的杆件记为按其部位记为上弦管1、下弦管1、直腹杆1和斜腹杆1;同样,右侧杆件记为上弦管2、下弦管2、直腹杆2和斜腹杆2。
|
| 图 2 桁拱截面尺寸(单位:mm) Fig. 2 Sectional dimensions of truss arch (unit: mm) |
| |
拱脚下有三角形的底座,拱脚和底座垂直。在底座钢板处设置地锚,用于防止拱座滑动。
设计制作了加载块用于桁拱跨中的集中力加载。为使加载点的钢管受力均匀,在拱顶加载点范围内的钢管外面多焊接1层10 mm厚的钢板。为了防止局部破坏,在跨中的拱肋两侧各多焊接了4根钢管,同时在相邻的节间也多焊接了1根钢管。在跨中加载点下相邻两个节间外测的两根加强钢管处,横向焊接两根相互交叉的钢管和2根横缀管。所有焊接的钢管的尺寸也为Φ48 mm×2 mm。
钢管为Q235钢,测量的钢材的平均弹性模量为2.1×105 MPa,泊松比为0.283。屈服强度为260 MPa,极限抗拉强度为350 MPa,屈服应力对应的应变为1 018 με。灌注的混凝土等级为C30,实测28天混凝土立方体抗拉强度平均值为25.6 MPa, 弹性模量为3.0 MPa。
1.2 试验加载荷载加载分为两个阶段,第1个阶段为施加初应力阶段,此时的拱肋为空钢管;第2阶段为管内灌注混凝土并养护完成后,混凝土与钢管共同承担荷载。
第1阶段:进行初应力的施加和采集。第1阶段的荷载加载完毕后,试件静置3到5天直至其趋于稳定。这期间通过再次测量和分析应变数据来判断试件是否稳定。施加初应力时,每级增加1 kN,每级荷载保持3~5 min,然后进行读数与采集。
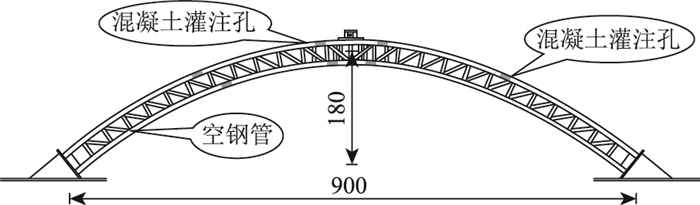
第2阶段:第1阶段结束后,在试件管内灌注混凝土,浇注时采用上、下弦管错孔灌,分别在桁拱上弦管第7,12,15,20节间和下弦管第8,13,14,19节间上方开孔灌注混凝土,并监测桁拱的应变和挠度, 如图 3所示。混凝土灌注孔为矩形,尺寸为8 m×4 cm。混凝土养护28 d后,钢管与混凝土形成整体,再对桁拱继续加载,直至破坏。随着试验的进行,每级荷载增加的幅度也随之改变,试验初期每级增加5 kN;当桁拱达到弹塑性阶段后,每级增加3 kN;当所加荷载达到极限荷载值的75%,每级增加2 kN,直至极限荷载;当荷载超过极限荷载,采用不停机加载至桁拱破坏。
|
| 图 3 混凝土灌注孔示意(单位:cm) Fig. 3 Schematic diagram of concrete pouring holes(unit:cm) |
| |
1.3 测点布置
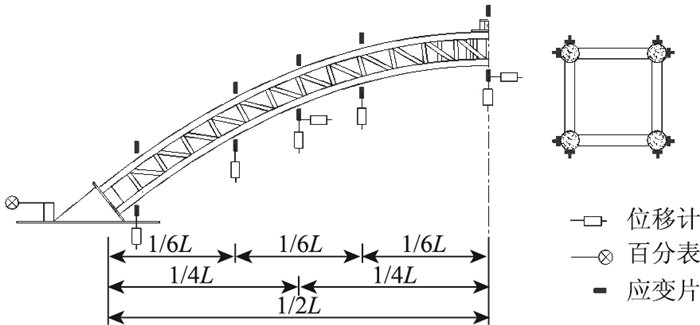
在桁拱上选取9个截面做为控制截面,分别为桁拱的左右拱脚截面以及拱肋的6等分截面和4等分截面, 在控制截面上设置测点。控制截面处,在弦管外侧贴横向和纵向应变片,腹杆和横缀管也设置应变片。控制截面的下弦管下方设置位移计,测量桁拱的竖向位移。在桁拱的4等分截面处设置横向位移计。在拱脚两端设置百分表用以测定拱座的位移。测点布置如图 4所示。
|
| 图 4 桁式拱应变片、位移计与百分表布置 Fig. 4 Layout of strain gauges, displacement meters and dial indicator on truss arch |
| |
2 试验现象与破坏模式 2.1 试验现象描述
先对桁拱进行初应力的加载,由布置在拱脚截面沿弦管方向的应变片可知,当跨中单点加载至5 t(由于弦管上有开孔,不能准确计算空钢管桁拱的承载力,荷载加到5 t(约49 kN))时就停止施加压力,初应力度达到0.1,用两台螺旋式手动千斤顶代替油压千斤顶,此时应变基本不变。比较各截面,拱顶受到加载点集中力的影响较大,拱顶的压应变最大;L/4截面处的应变较小,有压应变也有拉应变;拱脚应变居于两者之间,且上、下弦管的应变相近,拱脚的弯矩较小。
桁拱内浇注混凝土28 d后,进行第2阶段的试验加载。加载初期,桁拱变形较小,拱座百分表指针无转动,拱座无位移。拱顶三分段的拱肋向下变形;靠近拱脚的三分段向上变形,但是变形幅度较小。L/3和2L/3是变形状态发生改变的位置。
荷载小于200 kN时,结构处于弹性状态。之后荷载增加,结构进入弹塑性状态而无初应力拱在荷载达到250 kN进入弹塑性状态。这是因为初应力的存在,增大了钢管的应力,从而使其提早进入弹塑性状态。荷载达到370 kN时,桁拱跨中部分向下变形逐渐增大。此时上下弦管变形一致,说明桁拱整体性良好。荷载达到400 kN时,靠近拱脚的三分段向上变形明显。此时第9个节点和第15个节点处(接近三分点位置)的直腹杆下端部的钢管鼓起。当荷载达到430 kN时,跨中向下变形加大,且变形形式变为向下微凸的弧线,跨中直接承受拱顶的集中荷载,受影响最大。此时,位于跨中的两个相邻节间的直腹杆下部钢管出现了隆起。荷载达到450 kN时,在加载点相邻节间的直腹杆下部都出现了钢管隆起的现象。这说明此时桁拱顶部塑性区域向左右两侧发展,且桁拱没有出现节点破坏,表现出良好的整体性。
当荷载达到473 kN时,结构变形明显加快,结构无法持续承受该荷载,荷载值开始减小,说明该荷载值为其极限承载能力值,其值与无初应力拱极限承载能力值510 kN相比,减小7.3%。之后不停机继续加载直至结构破坏。荷载下降至466 kN时在加载点相邻4个节间处与接近三分点节间处的直腹杆下端部鼓起范围更大;跨中的斜腹杆沿腹杆四周在邻近接头部位拉裂,在邻近三分点处截面的斜腹杆,在靠近节点位置完全拉断。同时,2L/3截面附近的上弦管拼接焊缝拉裂,结构破坏严重。与文献[2]拱结构相比说明,初应力的存在不会改变桁拱的破坏模式,但是会使其破坏现象更明显。在整个试验过程中,拱座的位移很小,拱脚处没有变形,认为拱结构处于固接状态。拱肋平面外位移很小,将本次试验当作平面内受力。试验过程中出现焊缝部分破坏的现象,说明初应力的存在会增大上弦管的拉应力。钢管混凝土拱桥拱肋的拼装基本是逐段拼焊形成拱结构,实际工程中要确保焊缝质量。

|
| 图 5 拱达到极限荷载力后腹杆破坏情况 Fig. 5 Failure mode of webs when arch at ultimate loading |
| |
2.2 有初应力桁拱与无初应力桁拱破坏模式比较
在达到极限承载能力之前,有初应力的钢管混凝土桁拱表现出较好的整体性,没有发生局部的破坏。这表明有初应力的钢管混凝土桁拱与无初应力的钢管混凝土桁拱有相同的受力特性,腹杆屈曲,并先于弦管破坏。
初应力的存在占据了钢管的部分承载力,使得有初应力钢管混凝土拱和无初应力钢管混凝土相比,进入弹塑性的状态提前,对应荷载值减小20%;有、无初应力的钢管混凝土桁拱在最大承载力时的变形相差较大,荷载值减小7.3%,最大竖向位移减小12.1%,即有初应力的桁拱变形能力下降显著。破坏现象也更加显著,继续加载后主弦管焊缝处拉裂,三分点处斜腹杆全部拉裂。
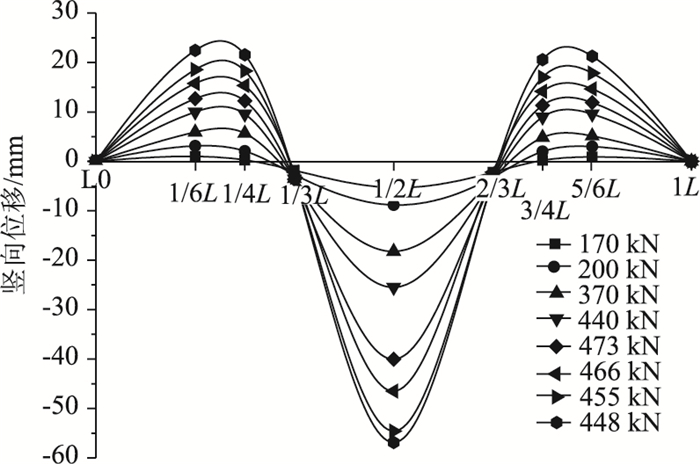
3 有初应力桁拱弦管荷载-竖向位移曲线由图 6可知,与文献[2]桁拱相比,本桁拱在荷载作用下变形较大。当荷载小于200 kN时,桁拱变形较小,处于弹性状态,在六等分截面和四等分截面处基本没有竖向位移,拱脚处也没有位移。当荷载达到370 kN时,桁拱跨中加载点向下位移达到了18.2 mm,变形明显。荷载达到473 kN时,跨中截面向下位移迅速增加,达到40 mm,桁拱的左、右三分段变形也变得明显,最大位移超过了10.0 mm。此时荷载达到最大,继续不停机加载,变形继续增加,荷载减小。当荷载达到466 kN时,跨中加载点位移变得更大,达到46.5 mm。当荷载为448 kN时,加载点截面向下位移为56.9 mm。
|
| 图 6 桁拱竖向位移过程曲线 Fig. 6 Vertical displacement curves of truss arch |
| |
在单点集中力加载的工况下,桁拱的变形形态表现出对称性,变形形态为“M”形。破坏形态如图 7所示。

|
| 图 7 桁拱变形破坏情况 Fig. 7 Deformation of truss arch |
| |
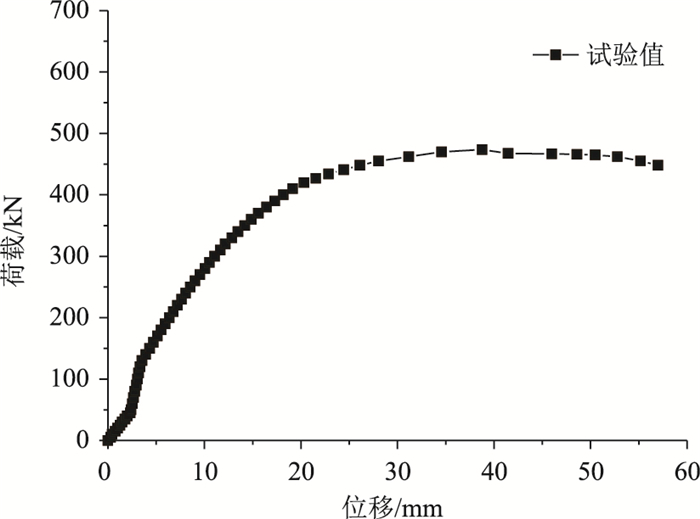
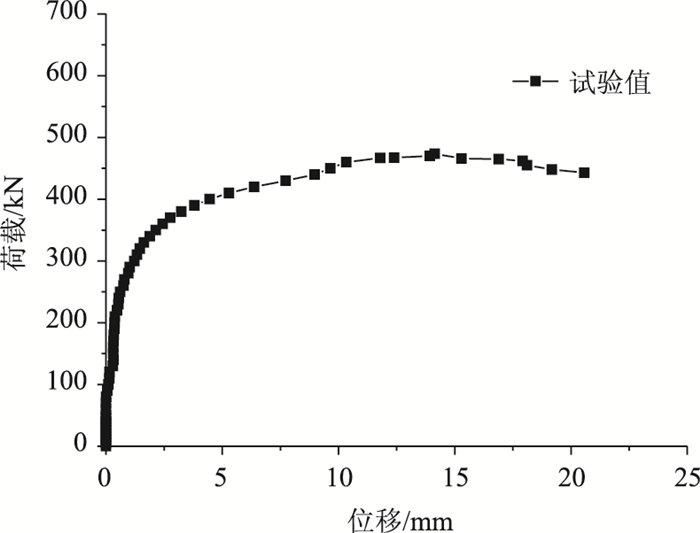
图 8为跨中截面的荷载-平均竖向位移曲线。图 9为1/4截面处的荷载-平均竖向位移曲线。从图 8与图 9可以看出,除了初应力加载阶段,当荷载低于200 kN时,荷载与位移基本上呈线性变化。之后随着荷载不断增加,曲线斜率不断变小,荷载与位移变为非线性关系,说明桁拱结构进入了弹塑性状态。桁拱顶部上弦管最大平均竖向位移为57.3 mm;桁拱1/4截面上弦管最大平均竖向位移为20.6 mm。当达到极限荷载473 kN后,继续加载,位移继续增大,荷载减小。相比之下无初应力拱的拱顶最大竖向位移为45.5 mm,极限荷载为510 kN,有初应力桁拱极限承载能力降低了7.3%最大竖向位移下降12.1%。
|
| 图 8 桁拱跨中上弦管荷载-平均竖向位移曲线 Fig. 8 Load-average vertical displacement curves of upper chord tube at mid-span of truss arch |
| |
|
| 图 9 1/4截面上弦管荷载-平均竖向位移曲线 Fig. 9 Load-average vertical displacement curves of upper chord tube at 1/4 section |
| |
4 有初应力桁拱的荷载-应变曲线 4.1 主弦管荷载-应变曲线
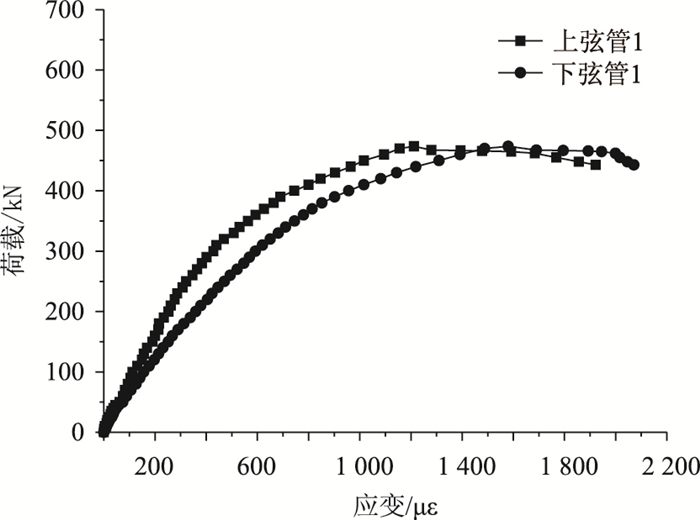
从图 10中可知,相同荷载时,拱脚的下弦管的应变比上弦管稍大,但相对来说拱脚截面的偏心距不大。当荷载达到473 kN时,荷载值达到最大,上弦管和下弦管的应变分别达到1 252με和1 580με,此后无法持续承载,荷载开始下降。
|
| 图 10 有初应力桁拱拱脚弦管荷载应变-曲线 Fig. 10 Load-strain curves of arch foot chord tube of truss arch with initial stress |
| |
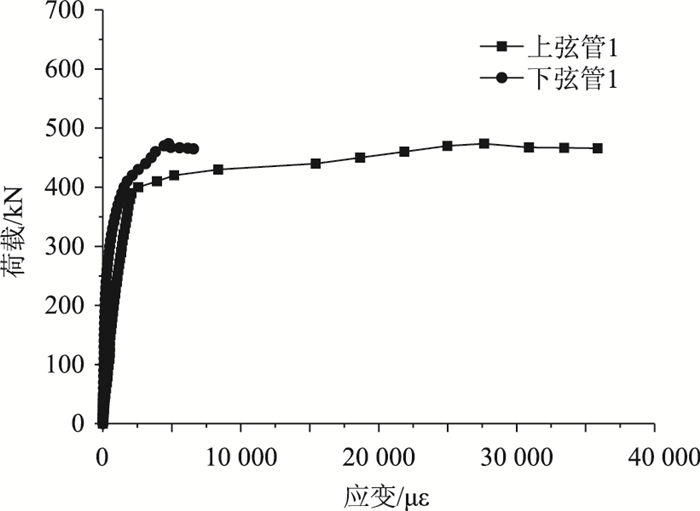
从图 11可知,随着荷载的增加,应变增加较快,且上弦管应变更大,这表明跨中截面的偏心距较大。与文献[2]无初应力桁拱相比,有初应力桁拱在荷载较小时就进入了弹塑性阶段。有初应力桁拱荷载达到370 kN时进入弹塑性阶段,荷载达到473 kN时达到极限荷载。上弦管出现明显的转折,变形快速增加,但整个结构能够继续提升承载能力,说明桁拱有很好的延性,在其失效前有明显的预兆。
|
| 图 11 有初应力桁拱拱顶弦管荷载-应变曲线 Fig. 11 Load-strain curves of arch crown chord tube of truss arch with initial stress apex of arch chord |
| |
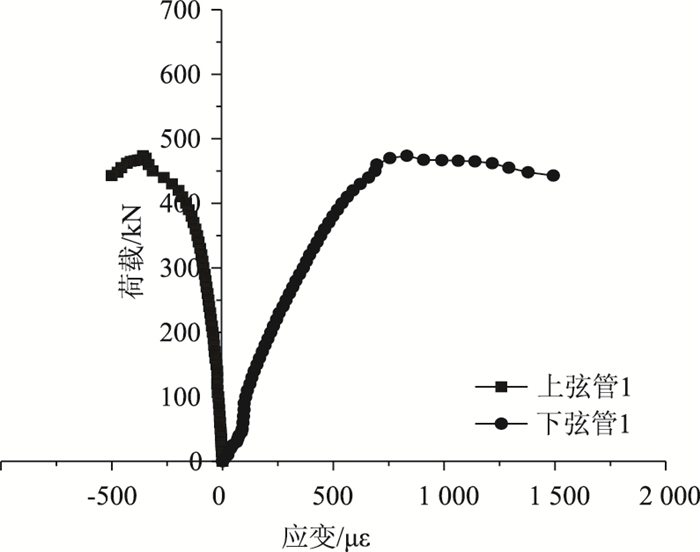
由图 12可知,1/4截面上弦管受拉,下弦管受压。在整个试验过程中,上弦管未达到屈服,处于弹性状态;而下弦管最终屈服,处于弹塑性状态。
|
| 图 12 有初应力桁拱1/4截面弦管荷载-应变曲线 Fig. 12 Load-strain curves of chord tube at 1/4 section of truss arch with initial stress |
| |
4.2 腹杆荷载-应变曲线
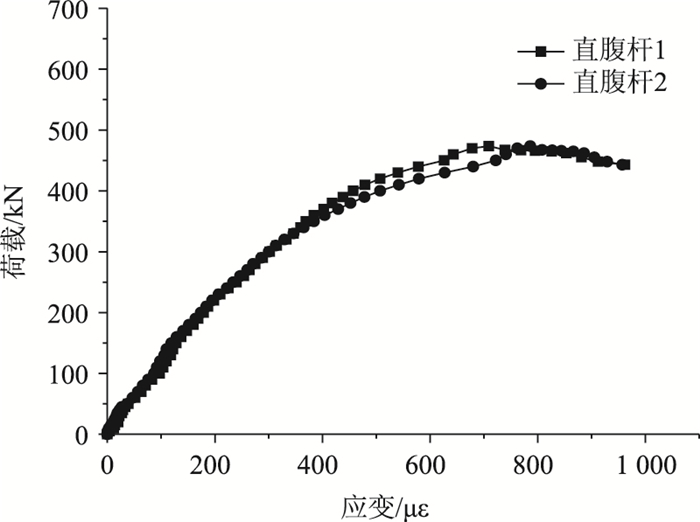
图 13为第1节间的两根直腹杆的荷载-应变曲线。由图 13可见,有初应力桁拱拱脚截面的直腹杆承受径向剪力较小,应变不大,最大应变达到962 με,未达到屈服应变。
|
| 图 13 拱脚直腹杆的荷载-应变曲线 Fig. 13 Load-strain curves of arch foot straight web members |
| |
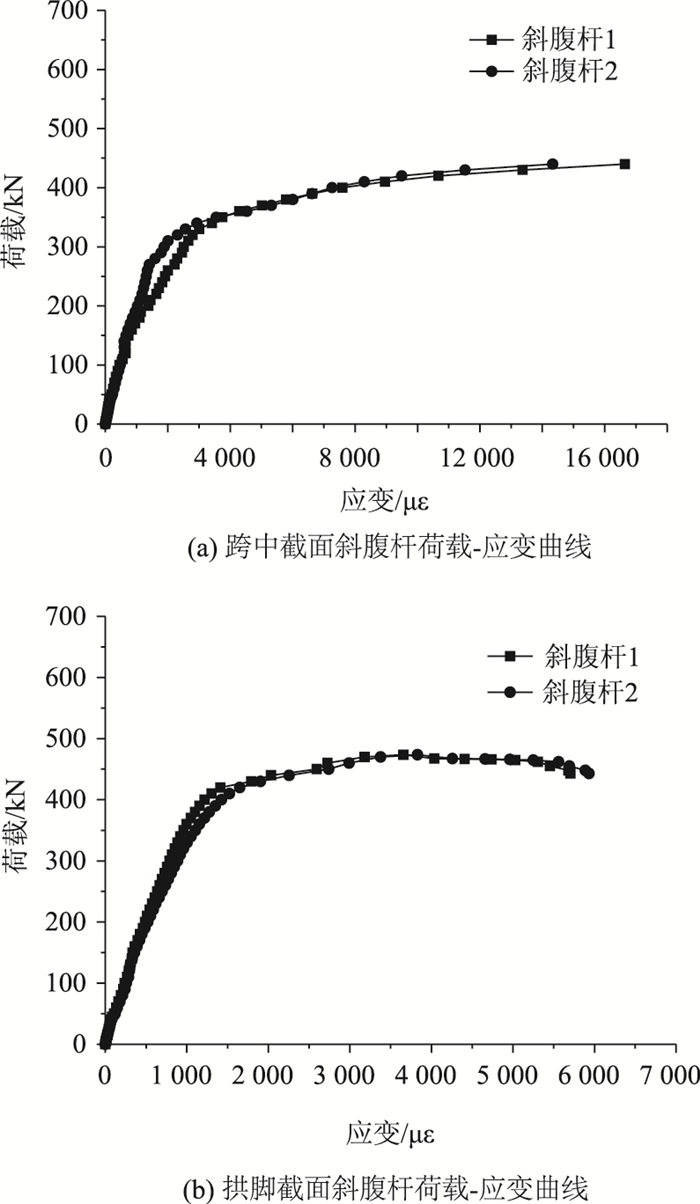
图 13(a)为第12个节间的两根斜腹杆的荷载-应变曲线,图 14(b)为第1节间的两根斜腹杆。由图 14(a)和14(b)可知,当荷载达到370 kN时,跨中截面与拱脚截面斜腹杆已经进入弹塑性状态,应变加快。当荷载超过拱的极限荷载之后,拱结构失去承载能力,荷载值不断下降。当荷载下降至466 kN时,跨中截面斜腹杆最大拉应变为1 664 με,拱脚截面斜腹杆最大压应变为5 692 με。
|
| 图 14 斜腹杆的荷载-应变曲线 Fig. 14 Load-strain curves of diagonal web members |
| |
5 结论
(1) 试验结果表明,在跨中单点集中力加载的工况下,有初应力钢管混凝土桁拱变形呈现出对称形态,变形大致成“M”形。其中,L/3至2L/3段部分向下变形较显著,跨中向下最大位移达到;左拱脚至1L/3段部分和2L/3至右拱脚段部分发生向上变形。
(2) 有初应力钢管混凝土桁拱在达到极限承载力前,有较好的整体性,没有出现节点破坏;当达到极限荷载时,直腹杆屈曲,继续加载后斜腹杆在节点处拉裂。结构的腹杆先于弦管破坏,直腹杆发生屈曲先于斜腹杆出现拉裂。
(3) 初应力的存在,占据了钢管部分承载力,使其提前进入弹塑性状态(弹性极限状态对应荷载值减小20%);达到极限荷载时,极限承载能力降低7.3%,降低变形能力,竖向位移减小12.1%。初应力的存在不改变破坏模式,但是加剧了破坏现象,破坏后继续加载,位于三分点附近的两个相邻节间其斜腹杆全部拉裂,主弦管拼接焊缝拉裂。
| [1] |
陈宝春, 韦建刚, 周俊, 等. 我国钢管混凝土拱桥应用现状与展望[J]. 土木工程学报, 2017, 50(6): 50-61. CHEN Bao-chun, WEI Jian-gang, ZHOU Jun, et al. Application of Concrete-filled Steel Tube Arch Bridges in China:Current Status and Prospects[J]. China Civil Engineering Journal, 2017, 50(6): 50-61. |
| [2] |
黄福云, 钱海敏, 陈宝春, 等. 钢管混凝土桁式拱结构平面内受力性能试验研究[J]. 建筑结构学报, 2015, 36(12): 116-124. HUANG Fu-yun, QIAN Hai-min, CHEN Bao-chun, et al. Experimental Study on In-plane Mechanical Behavior of Concrete-filled Steel Tubular Truss Arch[J]. Journal of Building Structures, 2015, 36(12): 116-124. |
| [3] |
周水兴, 刘琪, 陈湛荣. 钢管初应力对哑铃型钢管砼拱桥极限承载力影响分析[J]. 工程力学学报, 2008, 25(7): 159-178. ZHOU Shui-xing, LIU Qi, CHEN Zhan-rong. Effect of Initial Stress on Bearing Capacity of Dumbbell Concrete-filled Steel Tube Arch Bridge[J]. Engineering Mechanics, 2008, 25(7): 159-178. |
| [4] |
周水兴, 张敏, 王小松. 钢管初应力对钢管砼拱桥承载力影响非线性分析[J]. 计算力学学报, 2010, 27(4): 677-681. ZHOU Shui-xing, ZHANG Min, WANG Xiao-song. Nonlinear Analysis of Steel Tube Initial Stress Effect in Steel Tube on Bearing Capacity for CFST Arch Bridges[J]. Chinese Journal of Computational Mechanics, 2010, 27(4): 677-681. |
| [5] |
杨孟刚, 曹志光. 初应力对大跨度钢管混凝土拱桥极限承载力的影响[J]. 铁道科学与工程学报, 2010, 7(4): 7-10. YANG Meng-gang, CAO Zhi-guang. Influence of Initial Stress on the Ultimate Bearing Capacity of Long-span CFST Arch Bridges[J]. Journal of Railway Science and Engineering, 2010, 7(4): 7-10. |
| [6] |
赵跃宇, 易壮鹏, 王连华. 初始应力对钢管混凝土拱桥面内极限承载能力的影响[J]. 湖南大学, 2007, 34(3): 1-5. ZHAO Yue-yu, YI Zhuang-peng, WANG Lian-hua. Effects of Initial Stress on the In-plane Ultimate Bearing Capacity of CFST Arch Bridges[J]. Journal of Hunan University:Natural Science Edition, 2007, 34(3): 1-5. |
| [7] |
邓继华, 邵旭东. 初应力对钢管混凝土拱肋节段极限承载力影响的有限元分析[J]. 中外公路, 2007, 27(3): 104-109. DENG Ji-hua, SHAO Xu-dong. Finite Element Analysis of Influence of Initial Stress on Ultimate Bearing Capacity of Concrete-filled Steel Tubular Arch Ribs[J]. Journal of China & Foreign Highway, 2007, 27(3): 104-109. |
| [8] |
邓继华, 邵旭东. 钢管混凝土拱极限承载力计算及相关参数分析[J]. 长沙理工大学学报, 2004, 1(3/4): 24-30. DENG Ji-hua, SHAO Xu-dong. Computation of Ultimate Bearing Capacity Load for Concrete Filled Steel Tube (CFST) Arch Bridge and Analysis of the Relevant Factor[J]. Journal of Changsha University of Science & Technology:Natural Science Edition, 2004, 1(3/4): 24-30. |
| [9] |
邓继华, 邵旭东. 钢管混凝土拱空间极限承载力高精度分析[J]. 中南公路工程, 2005, 30(2): 59-62. DENG Ji-hua, SHAO Xu-dong. Precision Analysis on Spatial Limit Bearing Capacity of Concrete-filled Steel Tubular Arch[J]. Journal of Central South Highway Engineering, 2005, 30(2): 59-62. |
| [10] |
于洪刚, 周水兴, 陈强, 等. 中山大桥钢管初始应力稳定计算分析[J]. 重庆交通学院学报, 2006, 25(1): 5-7. YU Hong-gang, ZHOU Shui-xing, CHEN Qiang, et al. The Analysis of Initial Stress about Stability and Bearing Capacity of Zhongshan Bridge[J]. Journal of Chongqing Jiaotong University, 2006, 25(1): 5-7. |
| [11] |
黄福云.有初应力的钢管混凝土实肋拱的极限承载力研究[D].福建: 福州大学, 2008. HUANG Fu-yun. Study on Ultimate Bearing Capacity of Concrete Filled Steel Tubular Arch with Initial Stress[D]. Fuzhou: Fuzhou University, 2008. |
| [12] |
韦建刚, 黄福云, 陈宝春. 初应力对钢管混凝土单圆管拱极限承载力影响的研究[J]. 工程力学, 2010, 27(7): 103-112. WEI Jian-gang, HUANG Fu-yun, CHEN Bao-chun. Research on the Influence of Initial Stress to Ultimate Load Carrying Capacity of Concrete Filled Steel Tubular (Single Tube) Arches[J]. Engineering Mechanics, 2010, 27(7): 103-112. |
| [13] |
张晓庆, 钟善桐, 闫善章, 等. 初应力对钢管混凝土偏压构件承载力影响的试验研究[J]. 哈尔滨建筑大学学报, 1997, 30(1): 50-56. ZHANG Xiao-qing, ZHONG Shan-tong, YAN Shan-zhang, et al. Experimental Study about the Effect of Initial Stress on Bearing Capacity of Concrete Filled Steel Tubular Members under Eccentric Compression[J]. Journal of Harbin University of Civil Engineering and Architecture, 1997, 30(1): 50-56. |
| [14] |
黄福云, 陈宝春, 李建中, 等. 有初应力的钢管混凝土格构柱试验研究[J]. 建筑结构学报, 2013, 34(6): 29-36. HUANG Fu-yun, CHEN Bao-chun, LI Jian-zhong, et al. Study on Mechanical Performance of CFST Laced Columns Considering Initial Stress by Finite Element Method[J]. Journal of Building Structures, 2013, 34(6): 29-36. |
| [15] |
周海龙, 周水兴. 钢管初应力对钢管混凝土单圆管拱极限承载力影响的研究[J]. 公路工程, 2013, 38(5): 72-74. ZHOU Hai-long, ZHOU Shui-xing. Research on the Influence of Tubular Initial Stress to Ultimate Bearing Capacity of Concrete-filled Steel Tube (Single Tube) Arch Rib[J]. Highway Engineering, 2013, 38(5): 72-74. |
| [16] |
宋福春.钢管混凝土桁肋拱桥面外稳定性研究[D].福州: 福州大学, 2009. SONG Fu-chun. Study on Out-of-plane Stability of Concrete Filled Steel Tubular Rib Arch Bridge[D]. Fuzhou: Fuzhou University, 2009. |
| [17] |
陈宝春, 肖泽荣, 韦建刚. 钢管混凝土哑铃型拱肋灌注混凝土时的截面应力分析[J]. 中国公路学报, 2005, 18(1): 73-76. CHEN Bao-chun, XIAO Ze-rong, WEI Jian-gang. Analysis on Stresses of Dumbbell-shaped Cross-section of CFST Arch Rib during Concrete Pouring Construction[J]. China Journal of Highway and Transport, 2005, 18(1): 73-76. |
| [18] |
肖泽荣. 福州市金鸡山飞虹桥概念设计和结构分析[J]. 福建建筑, 2017(6): 107-109. XIAO Ze-rong. The Conceptual Design and Structural Analyses of Feihong Bridge at the Jinjishan Park in Fuzhou[J]. Fujian Architecture & Construction, 2017(6): 107-109. |
 2020, Vol. 37
2020, Vol. 37
