扩展功能
文章信息
- 唐茂林, 王鹏, 李翠娟
- TANG Mao-lin, WANG Peng, LI Cui-juan
- 考虑行人舒适度的空间缆索悬索桥车致振动控制
- Control of Vehicle-induced Vibration of Suspension Bridge with Spatial Cable Considering Pedestrian Comfort
- 公路交通科技, 2020, 37(1): 58-65
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 58-65
- 10.3969/j.issn.1002-0268.2020.01.008
-
文章历史
- 收稿日期: 2018-07-30
2. 长江勘测规划设计研究有限责任公司, 湖北 武汉 430010
2. Changjiang Institute of Survey, Planning, Design and Research, Wuhan Hubei 430010, China
高速地铁通过桥梁时,对结构的作用是随时间变化的周期性荷载,在某特定轨道不平顺谱影响下,可能使荷载激励频率与结构自振频率一致,引起结构共振。共振导致结构产生较大的动力响应,影响桥上行人舒适度,此时有必要对结构进行振动控制。许海亮[1]研究了路面不平整度激励下车路耦合振动,得出路面不平整度越差路面产生的振动位移也越大;Den Hartog[2]首次提出了STMD系统在结构受到简谐力作用下的最优参数求解方法;Han[3]等利用阻尼比相同、调谐频率等间隔分布的MTMD系统有效控制了结构振动;李春祥[4-5]对MTMD进行了大量动力分析,得出MTMD系统具有更好的有效性和鲁棒性;樊健生[6]研究发现人-桥共振时采用MTMD将比单个TMD具有更高的减振效率;王文熙[7]研究了TMD系统在自身参数偏离下的减振有效性和可靠性问题, 并给出增强TMD系统有效性和可靠性的一些建议。张铎等[8]基于移动简谐荷载列模型,研究了地铁过桥时,谐振频率、荷载列移速等对共振效应的影响;肖新标等[9]研究了TMD对不同速度简谐荷载激励下桥梁动力响应的控制效果;郭文华[10]等提出TMD可有效抑制高速铁路简支箱梁的共振效应;王浩等[11]研究了TMD对南京长江大桥车致振动竖向加速度的控制效果;靖仕元[12]对长沙磁浮工程道岔梁,采用多重调谐质量调谐阻尼器(TMD)的方式控制一定激振频率带的振动,达到控制频率能全覆盖;徐家云[13]研究得出TMD能够较好地减小重载铁路桥梁的振动响应。已有车致振动控制方面的研究大都是基于铁路简支梁或者连续梁桥,对带有人行道的大跨度空间缆索悬索桥车致振动方面的研究较少。
目前一些城市市政桥梁不仅承受地铁轨道交通,还布置有人行道,对于这类桥梁,地铁过桥时振动问题突出,有必要对其行人走行舒适度进行研究。本研究以某座跨度为(45+330+60) m的市政轨道交通悬索桥为背景,依据表 1中德国EN03[14]规范规定的采用峰值加速度作为评价准则,研究地铁荷载作用下桥上行人的走行舒适度。该桥边跨为平行缆,主跨为外张式空间缆,吊索间距为7.5 m,主梁采用桁架与箱梁的组合梁,在桥塔处连续通过,上层桥面承受双向地铁荷载,下层桥面布置有6 m宽的人行道。该桥实际设计中,两岸桥塔塔顶横向间距并不相同,矮塔侧塔顶I.P点横向间距为43 m,高塔侧塔顶I.P点横向间距为47.4 m,吊索下吊点横向间距34.4 m。
| 等级 | 名称 | 竖向 |
| 1 | 很舒适 | < 0.5 |
| 2 | 中度舒适 | 0.50~1.00 |
| 3 | 不舒适 | 1.00~2.50 |
| 4 | 不可忍受 | >2.50 |
1 桥梁结构振动分析
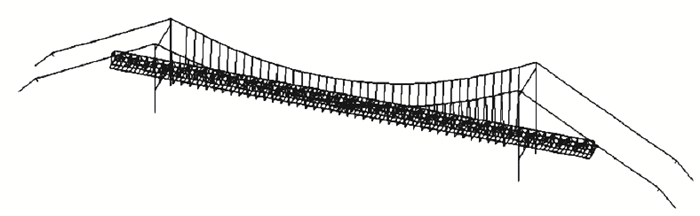
悬索桥具有强烈的非线性[15],导致结构的响应与外载荷激励的变化不成比例。悬索桥的车桥振动分析为瞬态非线性分析,因此在ANSYS中建立结构三维有限元模型如图 1所示。其中采用link10单元模拟吊杆和主缆,采用beam4单元模拟主塔和主梁,考虑车辆激励在ANSYS进行瞬态非线性时程分析。
|
| 图 1 有限元模型 Fig. 1 Finite element model |
| |
1.1 动力特性分析
动力特性是桥梁全局动态刚度指标的重要体现,是桥梁动力分析的基础。桥梁结构的动力特性主要包括结构的振型、自振频率、模态质量等,本研究主要研究在地铁激励下该桥的竖向振动,表 2展示了该桥前三阶竖弯振型的关键参数。
| 阶数 | 频率/(rad·s-1) | 模态质量/kg | 振型 |
| 2 | 2.07 | 1.41E+07 | 一阶竖弯 |
| 5 | 2.95 | 2.47E+03 | 二阶竖弯 |
| 13 | 5.29 | 2.38E+06 | 三阶竖弯 |
1.2 考虑轨道不平顺的车致振动分析
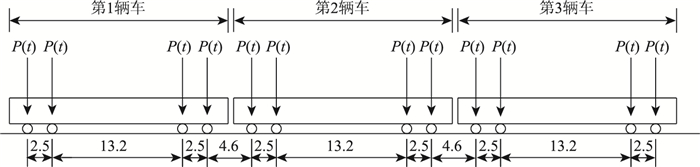
地铁车辆作用主要由轨道不平顺引起的简谐荷载和常量的轴重荷载叠加而成。地铁激励的简谐荷载幅值近似取为[8]P=0.2·Po=32 kN,地铁主轴重Po=160 kN,则实际车辆荷载即可等效为图 2中按特定间距排列的简谐荷载。该桥设计地铁为由6辆车编组的A型地铁,图中只示意了3辆,地铁激励大小为:
|
| 图 2 地铁简谐荷载(单位:kN) Fig. 2 Simple harmonic load of subway(unit:kN) |
| |
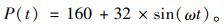
|
(1) |
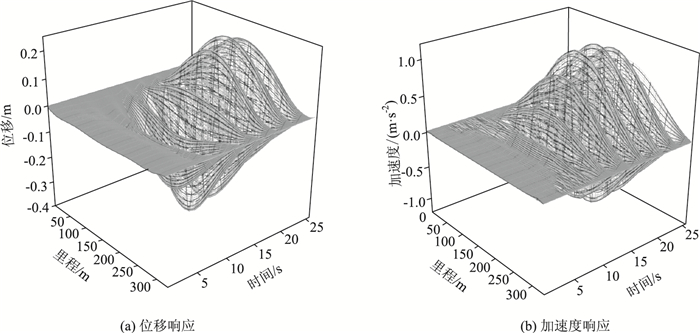
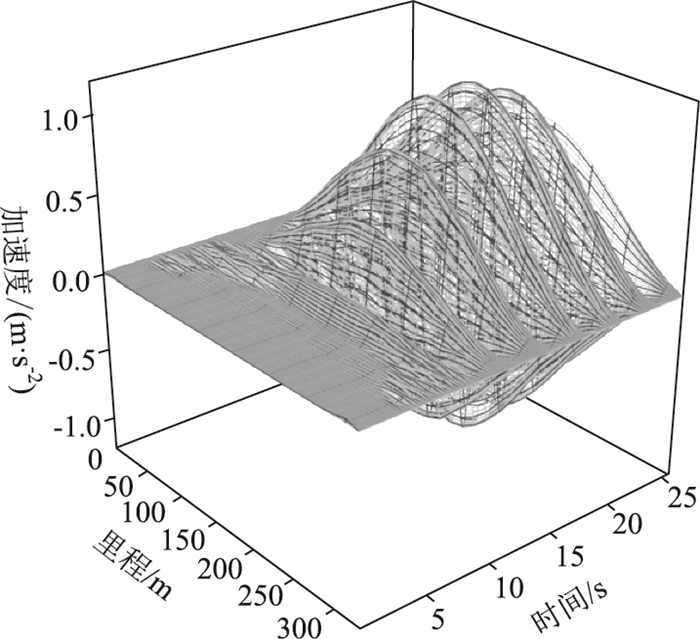
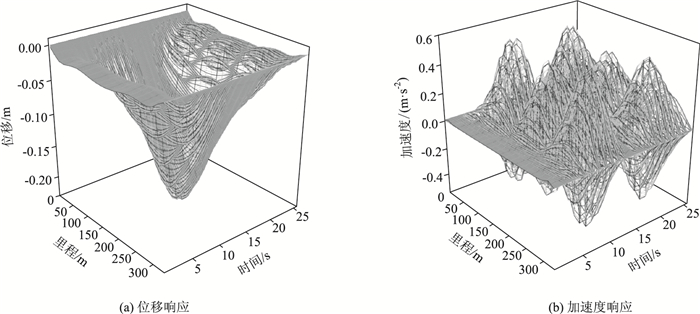
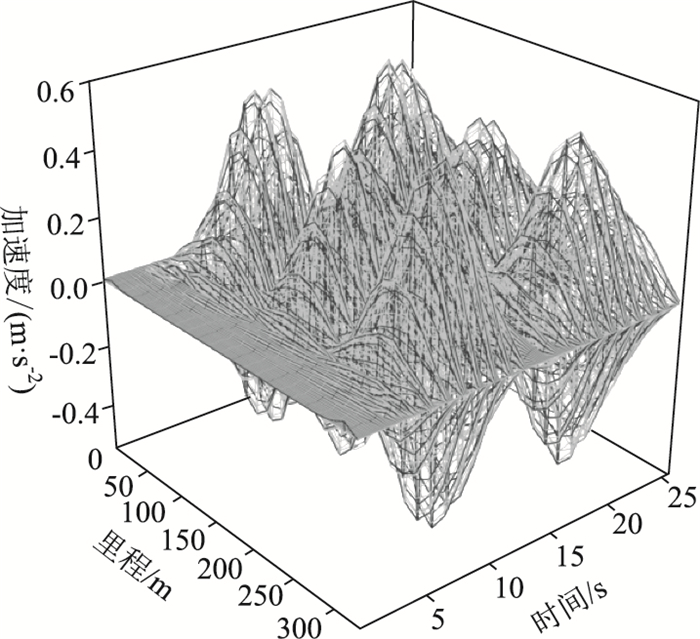
确定荷载模式以后,在该桥上下游加载相向而行的两列简谐地铁荷载列,模拟地铁在桥上会车,谐振频率分别与该桥的一阶和三阶竖弯模态频率相同,由于二阶竖弯模态质量不大,并不能激发结构共振,此处不做研究。图 3~图 4为移动简谐荷载列作用下,主跨330 m范围内主梁位移和加速度时程变化图,从图中数据可以看出,在列车荷载激励下,结构分别被激发了一阶和三阶竖弯共振,且一阶竖弯模态频率简谐荷载列激励下,结构的位移和加速度响应都要比三阶频率简谐荷载作用下的响应大。结构被激发一阶竖弯共振时,主梁最大位移值为-0.393 m,最大加速度值为1.122 m/s2,行人走行舒适度等级为“不舒适”;激发三阶竖弯共振时,主梁最大位移响应为-0.224 m,最大加速度响应为0.492 m/s2,行人走行舒适度处于“很舒适”等级。
|
| 图 3 一阶竖弯频率简谐荷载下结构响应 Fig. 3 Structural responses under first-order vertical bending frequency harmonic loading |
| |
|
| 图 4 三阶竖弯频率简谐荷载下结构响应 Fig. 4 Structural responses under third-order vertical bending frequency harmonic loading |
| |
2 基于TMD的结构振动控制
上一节研究发现,当轨道不平顺的谐振频率与一阶竖弯模态频率相同时,行人走行舒适度处于“不舒适”等级,采用TMD对主梁振动进行控制是有必要的。
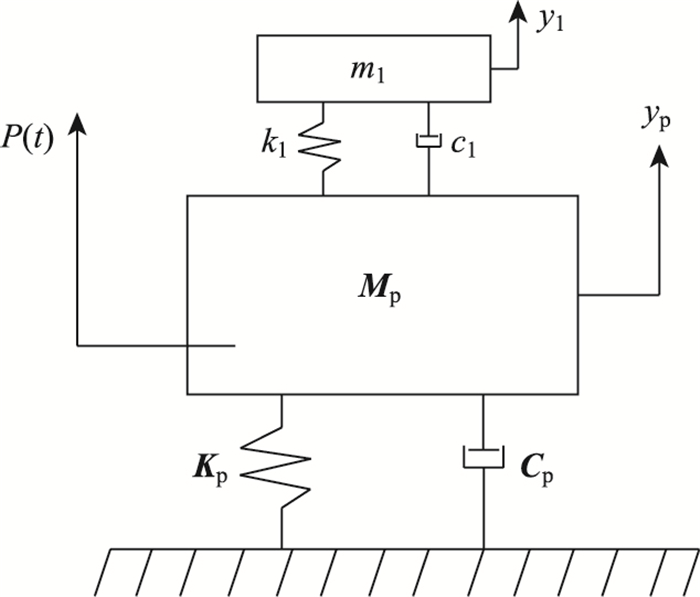
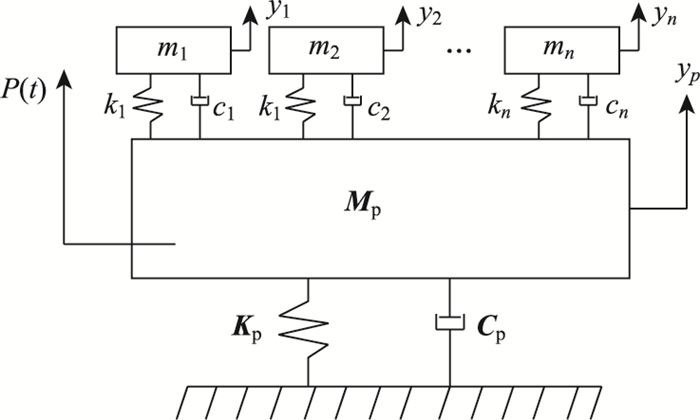
2.1 抑振原理待控结构简化为质量矩阵只有一个自由度的质量块Mp; 结构阻尼系数为Cp; 刚度系数为Kp; 在待控结构上装置TMD系统进行振动控制。单调谐频率质量阻尼器(STMD)系统只有单个子TMD;多调谐频率质量阻尼器(MTMD)系统具有多个子TMD,子TMD的自振频率以结构被控模态频率为中心,按一定的间隔对称分布。每一个子TMD都由一个质量为mi的质量块、一个刚度系数为ki的弹簧以及一个阻尼系数为ci的线弹性阻尼器组成。根据子TMD频率特点可以发现,STMD系统只能对一个频率点进行控制,而MTMD系统则能对一个小的频率段进行控制。该桥利用STMD与MTMD系统进行振动控制的力学模型如图 5、图 6所示。在主梁振幅响应最大区域安装N个子TMD,每个子TMD质量、刚度和阻尼矩阵分别为mi,ki,ci。可以把主梁运动微分方程写成如下非矩阵形式:
|
| 图 5 STMD力学模型 Fig. 5 Mechanical model of STMD |
| |
|
| 图 6 MTMD力学模型 Fig. 6 Mechanical model of MTMD |
| |
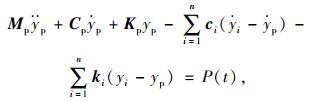
|
(2) |
式中,yp(x, t)为主梁在车辆激励下各点的位移; P(t)为所计入轨道不平顺影响后的地铁激励。假设第i个子TMD的位移响应为yi(x, t),可以得出如下第i个TMD的受力平衡方程式:
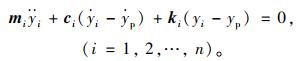
|
(3) |
采用Den Hartog最佳参数确定方法[2]确定TMD最优参数,其中最优频率比:
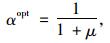
|
(4) |
最优阻尼比:
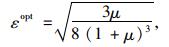
|
(5) |
TMD主要物理参数:
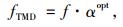
|
(6) |
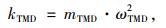
|
(7) |
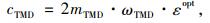
|
(8) |
式中, f为主结构待控振型自振频率;μ为阻尼器质量与结构模态质量之比; ω为角频率。
此处考虑到恒载挠度,STMD系统质量比μ取0.02。依据以上方法,得出针对该桥一阶竖弯模态振动控制的STMD系统主要参数如表 3所示。
| 待控振型 | TMD个数 | mTMD/kg | αopt | εopt | kTMD/(kN·m-1) | cTMD/ (kN·s·m-1) |
| 一阶竖弯 | 1 | 2.82E+05 | 0.980 | 0.084 | 1.16E+06 | 9.63E+04 |
文献[4-5]介绍了MTMD主要参数的计算方法,其中平均频率为:
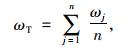
|
(9) |
第j个子TMD的频率为:
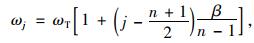
|
(10) |
频率间隔为:
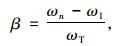
|
(11) |
调谐频率系数:

|
(12) |
则每个子TMD的调频系数:

|
(13) |
总质量比:

|
(14) |
平均阻尼比系数:
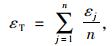
|
(15) |
式中, ωs为桥梁结构的自振频率; ms为对应模态下的模态质量,调谐频率系数与平均阻尼比可由公式(4)~(5)计算得到。一个TMD系统有n个子TMD,ωj为第j个子TMD的角频率;ω1为第1个TMD的角频率;mj为第j个子TMD的质量; εj为第j个子TMD的阻尼比。
由等量分析原则,此处MTMD系统总质量比也取0.02、最优频率间隔取0.16,采用5个质量与阻尼比相同,阻尼系数与刚度系数不同的子TMD对结构进行振动控制。依据上述方法,计算针对该桥一阶竖弯振动控制的MTMD系统参数如表 4所示。
| TMD编号 | mj/kN | rj | ωj/ (rad·s-1) | kj/ (kN·m-1) | cj/ (kN·s·m-1) |
| 1 | 5.64E+04 | 0.929 | 1.924 | 2.09E+05 | 8.36E+03 |
| 2 | 5.64E+04 | 0.955 | 1.978 | 2.21E+05 | 8.59E+03 |
| 3 | 5.64E+04 | 0.981 | 2.032 | 2.33E+05 | 8.83E+03 |
| 4 | 5.64E+04 | 1.007 | 2.086 | 2.46E+05 | 9.06E+03 |
| 5 | 5.64E+04 | 1.033 | 2.140 | 2.59E+05 | 9.30E+03 |
2.3 振动控制分析
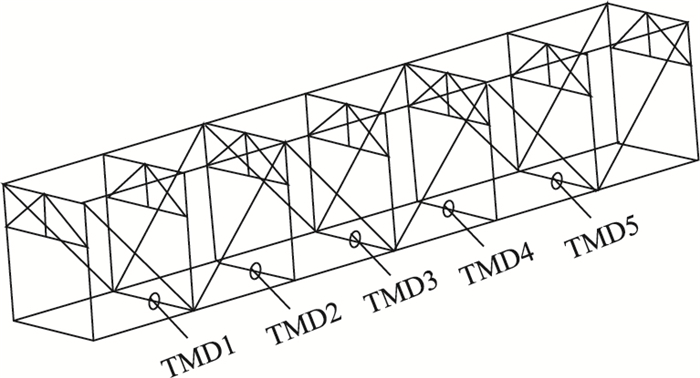
在有限元模型中采用mass21单元模拟阻尼器的质量,采用combin14单元模拟阻尼器的弹簧刚度和阻尼刚度,并将mass21单元与结构联系在一起。已有研究表明,在满足空间要求的情况下,尽可能的把TMD布置在主梁动力响应最大的位置,其抑振效果最好[16]。如图 7所示,可以在桁架下层桥面跨中5片下横梁中间预设节点板,将整个TMD系统装配在图中位置,最大限度减小结构振动。
|
| 图 7 TMD系统在主梁上的布置图 Fig. 7 Layout of TMD system on main girder |
| |
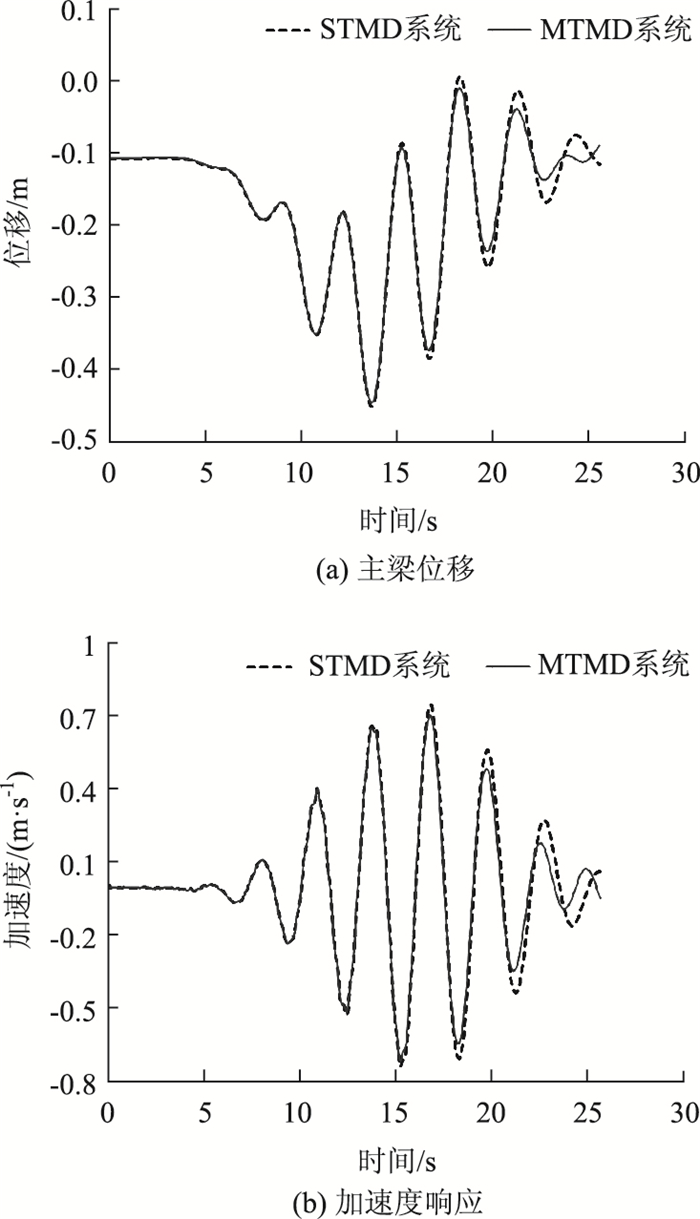
本研究主要针对一阶振动进行控制,将表 3、表 4设计的STMD与MTMD系统布置在上述主梁跨中位置。图 8为双向地铁过桥时,两类系统控制下跨中主梁位移、加速度时程曲线。从中可以看出STMD系统控制下结构最大加速度为0.751 m/s2,有效降低了33.2%;MTMD系统控制下结构最大加速度为0.712 m/s2,有效降低了36.6%。两类系统都实行人舒适度进入“中度舒适”等级,对比分析结果可以发现,MTMD系统具有更好的抑振效果。
|
| 图 8 跨中主梁位移、加速度响应时程曲线 Fig. 8 Time-history curves of displacement and acceleration response of main girder at midspan |
| |
2.4 参数敏感性分析
TMD在加工制造时存在加工误差,可能引起自身参数与设计值不相符,影响抑振效果[17]。此处对STMD、MTMD系统的子TMD主要参数存在误差时的抑振能力进行研究,结果可作为TMD参数优化设计的依据,也可对分析TMD制造误差影响抑振效果提供参考。在表 3、表 4设计参数的基础上,分别让质量、刚度、阻尼参数按下述3种状态发生偏移。
状态1:在刚度和阻尼保持不变的情况下,各子TMD质量按其设计参数的0.7,0.85,1.15,1.3倍发生改变;
状态2:在质量和阻尼保持不变的情况下,各子TMD刚度按其设计参数的0.7,0.85,1.15,1.3倍发生改变;
状态3:在质量和刚度保持不变的情况下,各子TMD阻尼按其设计参数的0.7,0.85,1.15,1.3倍发生偏改变。
图 9绘出了跨中加速度响应极值随着子TMD质量、刚度、阻尼发生偏移时的变化情况。从中可以看出:子TMD质量发生偏移时,系统的抑振效果会下降;刚度增加15%获得更好的抑振效果,此时STMD与MTMD系统控制下结构最大加速度为0.731,0.681 m/s2,分别降低了34.8%,39.3%;随着子TMD阻尼的增加,系统的减振效率呈单调下降趋势,但影响不明显。
|
| 图 9 加速度峰值随TMD偏移变化曲线 Fig. 9 Curves of acceleration maximum value vs. deviation of TMD |
| |
3 鲁棒性分析 3.1 结构自身频率变化的鲁棒性分析
桥梁在运营期间,结构可能产生收缩徐变[18],建筑材料也可能存在老化现象,导致结构实际自振频率与TMD设计时所采用的并不一致,进一步对STMD与MTMD系统的抑振效果带来影响。为实现结构自振频率改变,本研究将该桥跨矢比由8.5修改为9.5,结构一阶竖弯模态频率降到1.95 rad/s,进而研究抑振系统在结构自身频率改变后的鲁棒性能。表 5列出了频率变化后,双向地铁激励下两类系统的抑振效果,从中可以发现,MTMD系统依旧具有较高的有效率,跨中加速度减小了32.4%,STMD系统减小了29.7%。由此可见,MTMD抑振系统具有更好的鲁棒性,能更长久保障桥上行人舒适度。
| 关键位置 | 无控制 | STMD系统 | MTMD系统 | ||||
| 加速度 | 加速度 | 降幅/% | 加速度 | 降幅/% | |||
| 1/4跨 | 0.606 | 0.442 | 27.1 | 0.429 | 29.3 | ||
| 1/2跨 | 1.041 | 0.731 | 29.7 | 0.704 | 32.4 | ||
| 3/4跨 | 0.628 | 0.432 | 31.2 | 0.420 | 33.1 | ||
3.2 TMD个数对抑振系统鲁棒性的影响
保证质量比为2%不变的前提下,分别将13个,9个,5个,1个子TMD装置原桥主梁跨中,研究MTMD系统鲁棒性随子TMD个数的变化情况。随着子TMD个数的减少,单个子TMD的质量与体积也将增加。采用9个子TMD时,可以考虑将子TMD布置在下横梁与下弦杆交点处的节点板,同一个下横梁与两片桁架的节点处就可以布置两个子TMD;采用13个子TMD时,可以同时将子TMD布置在下横梁与两片桁架的节点以及下横梁中间的节点,同一个下横梁上就可以布置3个子TMD。这样尽可能的将TMD布置在桥梁跨中附近,可使TMD系统发挥更好的抑振效果。
分析过程中,激励荷载选用前文介绍的地铁模型,模拟双向地铁在桥上会车,地铁谐振频率为1.87 rad/s。作用地铁激励频率与该桥一阶竖弯模态频率2.07 rad/s偏移时,各类MTMD系统的加速度响应如图 10所示,从中可以发现,主梁的加速度响应极值随着TMD个数的增加有所下降,但幅度逐渐减弱,趋于平缓。因此,适当的增加TMD个数,可以有效解决激励荷载频率改变对桥上行人舒适度带来的影响。
|
| 图 10 加速度峰值随TMD个数变化曲线 Fig. 10 Curves of acceleration maximum value vs. number of TMD |
| |
4 结论
本研究依托某市政轨道交通空间缆索体系悬索桥,以桥上行人走行舒适度为出发点,对该结构在考虑轨道不平顺影响的简谐地铁荷载激励下的动力响应进行分析,并分别研究了调谐质量阻尼器STMD以及MTMD系统对结构的抑振效果。本研究主要结论如下:
(1) 该桥一阶竖弯振型模态质量较大,当轨道不平顺的谐振频率接近该模态频率时,容易激发结构共振,引起桥上行人走行不适。
(2) 无阻尼器时,跨中加速度响应极值为1.122 m/s2;STMD系统控制下结构最大加速度为0.731 m/s2,有效降低了34.8%;MTMD系统控制下结构最大加速度为0.681 m/s2,有效降低了39.3%。添加阻尼器使桥上行人舒适度从“不舒适”进入“中度舒适”。
(3) 结构自身频率发生改变时,MTMD系统也能较好地控制结构振动,鲁棒性良好;另外,随着TMD个数的增加,MTMD系统的鲁棒性进一步提高。
| [1] |
许海亮, 何炼, 何兆才. 考虑路面不平整度因素的车路耦合系统非线性数值模型[J]. 公路交通科技, 2017, 34(8): 23-28. XU Hai-liang, HE Lian, HE Zhao-cai. A Nonlinear Numerical Model of Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 23-28. |
| [2] |
HARTOG H D J P. Mechanical Vibrations[M]. New York: Dover Publications, 1947: 126-131.
|
| [3] |
HAN B, LI C. Characteristics of Linearly Distributed Parameter-based Multiple-tuned Mass Dampers[J]. Structural Control & Health Monitoring, 2008, 15(6): 839-856. |
| [4] |
李春祥, 周岱. 基于位移响应控制时不同激励下MTMD性能的比较研究[J]. 振动与冲击, 2004, 23(2): 52-54. LI Chun-xiang, ZHOU Dai. Comparative study on Performance of Displacement Response Control Based MTMD for STructures under Various Excitations[J]. Journal of Vibration and Shock, 2004, 23(2): 52-54. |
| [5] |
LI C X. Performance of Multiple Tuned Mass Dampers for Attenuating Undesirable Oscillations of Structures under the Ground Acceleration[J]. Earthquake Engineering & Structural Dynamics, 2015, 29(9): 1405-1421. |
| [6] |
樊健生, 李泉, 聂建国. 人群激励下梁式人行桥振动控制和MTMD优化设计[J]. 土木工程学报, 2010, 43(8): 73-80. FAN Jian-sheng, LI Quan, NIE Jian-guo. Crowds-induced Vibration Control of Beam Footbridge Equipped with Multiple Tuned Mass Dampers[J]. China Civil Engineering Journal, 2010, 43(8): 73-80. |
| [7] |
王文熙, 华旭刚, 王修勇, 等. TMD系统在自身参数随机偏离下的减振有效性和可靠性分析[J]. 振动与冲击, 2016, 35(1): 228-234. WANG Wen-xi, HUA Xu-gang, WANG Xiu-yong, et al. Vibration Reduction Validity and Reliability of a TMD System Under Random Deviation of its Own Parameters[J]. Journal of Vibration and Shock, 2016, 35(1): 228-234. |
| [8] |
张铎, 李小珍. 移动简谐荷载列作用下简支梁竖向动力响应的解析解及其应用研究[J]. 应用力学学报, 2014, 31(1): 144-149. ZHANG Duo, LI Xiao-zhen. Analysis and Application of Vertical Dynamic Response of Simply Supported Beam Bridge under Moving Harmonic Load Series[J]. Chinese Journal of Applied Mechanics, 2014, 31(1): 144-149. |
| [9] |
肖新标, 沈火明. 移动荷载作用下的桥梁振动及其TMD控制[J]. 振动与冲击, 2005, 24(2): 58-61, 149. XIAO Xin-biao, SHEN Huo-ming. Vibration and the TMD Control of Bridges under Moving Loads[J]. Journal of Vibration and Shock, 2005, 24(2): 58-61, 149. |
| [10] |
郭文华, 路萍. TMD对高速列车通过简支箱梁桥时的振动控制研究[J]. 振动与冲击, 2008, 27(11): 42-45, 196-197. GUO Wen-hua, LU Ping. Vibration Suppression for Simply Supported Bridges Passed by High-speed Trains Using Tuned Mass Dampers (TMD)[J]. Journal of Vibration and Shock, 2008, 27(11). |
| [11] |
王浩, 刘海红, 陶天友, 等. TMD对列车作用下大跨钢桁架桥的振动控制研究[J]. 振动工程学报, 2014, 27(3): 385-391. WANG Hao, LIU Hai-hong, TAO Tian-you, et al. Vibration Control of Long-span Steel Truss Bridge Subjected to Train Loadings Using TMD[J]. Journal of Vibration Engineering, 2014, 27(3): 385-391. |
| [12] |
靖仕元. 多重调谐质量调谐阻尼器的磁浮道岔减振方案[J]. 铁道工程学报, 2019, 36(4): 80-83, 89. JING Shi-yuan. Damping Method for Maglev Transit Switches Based on Multiple Tuned Mass Damper[J]. Journal of Railway Engineering Society, 2019, 36(4): 80-83, 89. |
| [13] |
徐家云, 胡晶晶, 张璨. 重载列车作用下桥梁振动荷载识别及减振控制[J]. 华中科技大学学报:自然科学版, 2018, 46(2): 46-50. XU Jia-yun, HU Jin-jin, ZHANG Can. Vibration Load Identification and Vibration Control of Bridge under Heavy-haul Train[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2018, 46(2): 46-50. |
| [14] |
EN03.2008, Human Induced Vibrations of Steel Structures[S].
|
| [15] |
唐茂林, 强士中, 沈锐利. 悬索桥成桥主缆线形计算的分段悬链线法[J]. 铁道学报, 2003, 25(1): 87-91. TANG Mao-lin, QIANG Shi-zhong, SHEN Rui-li. Segmental Catenary Method of Calculating the Cable Curve of Suspension Bridge[J]. Journal of the China Railway Society, 2003, 25(1): 87-91. |
| [16] |
王鹏.公轨人三线合一空间缆索悬索桥动力响应与行人走行舒适度研究[D].成都: 西南交通大学, 2018. WANG Peng. Study on Dynamic Response and Pedestrian Comfort Relying on Rail-cum-road-cum-sidewalk Suspension Bridge with Spatial Cables[D]. Chengdu: Southwest Jiaotong University, 2018. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=1018825384.nh |
| [17] |
郑宇欣.基于TMD的大跨度悬索桥时域抖振控制研究[D].成都: 西南交通大学, 2017. ZHENG Yu-xin. Study on Buffeting Control of Long-span Suspension Bridge in Time-domain Based on Tuned Mass Dampers[D]. Chengdu: Southwest Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017138074.htm |
| [18] |
陈旭, 莫南明, 邱志刚, 等. 混凝土松弛系数的实用计算[J]. 公路交通科技, 2018, 35(3): 36-45. CHEN Xu, MO Nan-ming, QIU Zhi-gang, et al. Practical Calculation of Concrete Relaxation Coefficient[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 36-45. |
 2020, Vol. 37
2020, Vol. 37
