扩展功能
文章信息
- 万亮, 杨和平, 倪啸, 肖杰
- WAN Liang, YANG He-ping, NI Xiao, XIAO Jie
- 单向土工格栅加筋膨胀土的拉拔力计算公式研究
- Study on Calculation Formula of Pullout Force of Expansive Soil Reinforced by Uniaxial Geogrid
- 公路交通科技, 2020, 37(1): 32-41
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 32-41
- 10.3969/j.issn.1002-0268.2020.01.005
-
文章历史
- 收稿日期: 2019-10-12
2. 安徽省农垦集团有限公司, 安徽 合肥 230000
2. Anhui Agricultural Reclamation Group Co., Ltd., Hefei Anhui 230000, China
众所周知,土的抗拉强度极低,抗剪强度也很弱,通过土中加筋构成的筋土复合体,当外力作用时,筋土间的相互作用能限制土体侧向位移,等效于给其施加一侧压力增量,从而提高了土的整体性。土工格栅作为一种新型加筋材料,特别是单向土工格栅,由高分子聚合物(PP-聚丙烯或HDPE-高密度聚乙烯)通过挤压2薄板再冲成规则孔网,后经纵向拉伸而成型,其工艺过程使高分子成定向排列并形成分布均匀、节点强度高的长椭圆形网状整体结构,因而其韧性好、强度高、耐腐蚀,加之生产过程相对简单且经济,已迅速成为当前土中加筋的主打材料。
美国学者MeGown[1]认为,对加筋土结构而言,起加固作用的都是筋材的抗拔阻力,主张用拉拔试验测定其界面强度,同时以获取土中加筋材料的应力-应变关系。法国的Schlosser[2]指出拉拔试验的优点在于能反应土体压密和剪胀效应,并可较好模拟加筋材料在土内的工作条件。《土工合成材料测试规程》(SL 235—2012)[3]明确提出直剪摩擦试验不适合土工格栅等材料,拉拔摩擦试验才适用确定各种性质和状态的土与各类土工格栅的相互作用。现场实测结果也表明,拉拔试验能较好模拟加筋土中筋材的加筋行为,是现行加筋结构物设计中获得合适界面参数的最好方法。Moraci、王家全、张正、郑俊杰、徐超等[4-8]的拉拔试验研究主要针对双向和三向土工格栅,单向格栅因横肋间距宽,做拉拔试验要求仪器的尺寸足够大,一般实验室无法进行,故目前开展单向土工格栅拉拔特性试验研究的甚少。
采用单向土工格栅加筋膨胀土边坡的柔性支护新技术, 在膨胀土地区公路修筑成套技术研究项目主要依托工程——广西宁明膨胀土路段的成功创立,以及随后在百隆、南宁外环、北京西六环高速及云桂高铁等膨胀(岩)土路段的推广应用,迫切需有膨胀土中单向格栅加筋的拉拔作用力分析计算方法。目前,研究土中加筋的理论虽较多,如界面摩擦作用、约束增强作用、张力膜、加筋垫层的应力扩散作用、加筋导致土地应力状态和位移场改变的作用理论以及剪切带理论等[9],但实际工程更关心或看重的是加筋体破坏前筋土间作用的最大拉拔力,只有把握了它才能在工程设计中合理确定筋材铺设的层间距及埋入长度,而格栅生产商则可根据它对筋材的孔隙率、横肋厚度及间距等产品参数做出相应改进。
Moraci[4]、Wilson-Fahmy、Koerner、Jewell、杨广庆、蔡春、王家全等[10-15]都研究过不同加筋土中拉拔力计算公式,均认为该力主要由表面摩擦力与横肋侧面阻力两者构成,但已有计算公式的设计参数较多,尤其确定筋土界面摩擦角时,不易快速、准确获取,妨碍了其在实际工程的应用,更不用说帮助筋材厂家改进产品。目前,不同工况下膨胀土中单向格栅加筋能提供多大拉拔力,且如何方便确定还无合适方法。
为此,本研究基于自主研制的大型数控拉拔试验系统所开展大量试验的测试结果,重新分析膨胀土中加筋单向格栅的纵、横肋分别对拉拔力所做贡献,借鉴已有研究提出的各拉拔力计算方法,针对单向格栅及膨胀土的特点,先设计完成不同边界、材料条件下百色膨胀土中加筋拉拔试验,研究提出单向格栅加筋膨胀土的拉拔力计算公式,后开展宁明、百色两种膨胀土的相应拉拔试验,通过比对测试结果来验证所建计算公式的合理可行性,以期为膨胀土路基处治工程设计及土工格栅产品改型提供便利。
1 初步研究提出的最大拉拔力计算式Wilson-Fahmy[10]、Koerner[11]、Jewell[12]等进行加筋土大型拉拔试验,分析得出土中加筋的拉拔阻力由3部分组成,并提出极限抗拔阻力F计算公式:

|
(1) |
式中,F1,F2,F3分别为纵、横肋提供的极限摩擦阻力和横肋的端承侧面阻力;Al为纵肋表面积;At为横肋表面积;δ为土与格栅界面的摩擦角;Ab,σ′n,Nq分别为横肋的端承面积、格栅表面的有效正应力及承载能力因子。
Moraci[4]等通过开展双向土工格栅与粗粒土的拉拔试验,分析提出另一种简单确定拉拔阻力PR的计算公式:
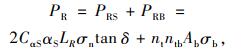
|
(2) |
式中,PRS为拉拔力中的摩擦部分;PRB为拉拔力中的剪切部分;CαS为格栅表面摩擦折减系数;LR为格栅长度;n为横肋根数;ntb为单根横肋节点数;σn为测试时的法向应力;σb为作用于横肋单元上的承载应力。
杨广庆[13]等进行单向土工格栅加筋粗粒土拉拔试验,研究提出一新的单宽拉拔阻力pt的计算公式:

|
(3) |
式中,B为土工格栅拉筋宽度;L为计算的拉筋长度;φp为筋/土界面的摩擦角;B0为土体膨胀对格栅产生附加应力的宽度。
蔡春[14]等对带加强肋单向土工格栅加筋砂土实施了拉拔试验,经分析提出如下拉拔阻力T计算公式:
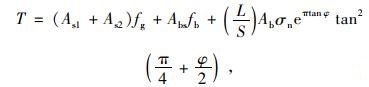
|
(4) |
式中,As1、As2分别为土工格栅的上、下表面(已扣除加强肋面积)承受法向应力的面积;Abs为加强肋上端面的面积;fg为土与格栅表面间的摩擦系数;fb为加强肋的端面与填料间摩擦系数;L为筋材长度;S为横肋间距;Ab为加强肋侧面承受阻力的面积。
王家全[15]等完成双向土工格栅加筋砂土的拉拔试验后,分析提出筋土界面的极限拉拔阻力Pr为:
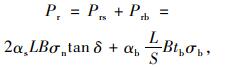
|
(5) |
式中,Prs为格栅表面与砂土滑动产生的界面摩擦力分量;Prb为格栅拉拔时横肋与砂土挤压咬合产生的承载力分量;αs为格栅实体表面积与其嵌固面积之比值;αb为计算格栅横肋承载力分量时可用前端面积的分数;L/S为嵌固段中横肋的条数;tb为横肋的厚度;σb为作用在横肋单元上的法向压力。
研究上述拉拔力计算式的形式和特点,不难看出它们大多是建立在先确定好筋、土界面间摩擦角及加筋格栅的纵、横肋面积基础之上。其中的界面摩擦角,则需经完成不同法向压力下格栅与土的直剪或拉拔试验后分析推算而定,因采用全尺寸格栅断面试验所得的最大拉拔力中包含有横肋阻力,而实际测得的却是筋土界面的换算内摩擦角,不能真实反映筋材表面与土间摩擦力。就分析格栅的纵、横肋面积而言,单向土工格栅的生产工艺是由挤压、冲取规则孔网,后经纵向拉伸而成型,故它纵、横肋之间的界限通常较难划清,而纵、横肋各自的面积也就更不易精确确定。
分析单向土工格栅生产的工艺特点,格栅拉伸成形后单位宽度的两根横肋间的孔隙面积为一定值,这样采取去除参与剪切部分单向土工格栅的横肋后,再埋入膨胀土中实施拉拔,格栅发生整体滑动时所产生的最大拉拔力,即是其上、下表面所受到的摩擦力,由此便可推算出格栅与填土间摩擦系数。此外,学者们对筋土间的拉拔阻力各用不同符号表示,为方便建立公式,本研究基于已有学者研究成果并考虑文献[3]中使用的拉拔力符号,初步提出如下形式单向土工格栅加筋膨胀土最大拉拔力F的计算公式:

|
(6) |
式中,μ为格栅表面与填料间摩擦系数;A为格栅面积(长×宽);e为格栅孔隙率(单位宽度两横肋间孔隙面积除以其间距);P为格栅表面作用的法向压力;n为横肋的根数;Fb为格栅单根横肋提供的端承侧面阻力。
显然,公式(6)简洁明了,仅μ和Fb为待定参数。
2 确定公式参数的试验及其方案设计 2.1 拉拔试验设备采用自主研发的大型数控拉拔试验系统(CS-LB01)[16]。设备的主要优点:(1)尺寸大:1.2 m(长)× 0.5 m(宽)×0.5 m(高);(2)拉拔试验过程可采取恒速或恒力控制;(3)适用于各类土;(4)上下双面气囊并配置稳压伺服系统使加载方式更合理;(5)侧壁摩擦对试验的影响得以消除;其数据采集系统可精确获取土中加筋的位移与拉力间关系。CS-LB01的主体部分见图 1,表 1给出其主要性能指标,可见试验接触面尺寸大且可施加较大荷载并产生大的相对位移。整个系统由拉拔测试主机、压力伺服控制、数据采集系统及压实与起吊辅助设备4部分组成(见图 2)。

|
| 图 1 CS-LB01设备 Fig. 1 Photograph of CS-LB01 equipment |
| |
| 箱体尺寸/cm | 荷载 | 最大位移/mm | 位移表精度 | 拉拔速度/(mm·min-1) | 数据采集间隔/s | ||||
| 长 | 宽 | 高 | 垂直力/MPa | 水平力/kN | |||||
| 120 | 50 | 50 | 0~1 | 30 | 80 | 0.1% | 0~3 | 1~30 | |

|
| 图 2 CS-LB01结构组成示意图(单位:mm) Fig. 2 Schematic diagram of CS-LB01 structure (unit:mm) |
| |
2.2 试验所用材料
填料为两种典型的广西膨胀土——百色棕黄色残积土(百色土)和宁明灰黑页岩风化土(宁明土),考虑土的微观指标测试难而复杂,土性试验均委托中科院地质与地球物理研究所完成,主要测试结果见表 2。单向土工格栅是产于湖北某公司的RS35PP、RS50PP和浙江绍兴某塑料有限公司的TGDG35,其物理特性指标见表 3,网格的结构见图 3,其中的标注MD表示纵向,TD表示横向。鉴于目前各厂家的单向土工格栅产品横肋均只一种形式和规格,为方便测试研究,笔者分批次剪去参与试验格栅的横肋,使其成为不同横肋数格栅用于拉拔试验(见图 4)。
| 膨胀土名 | 天然含水率/% | 液限/% | 塑限/% | 最佳含水率/% | 最大干密度/ (g·cm-3) | 填土压实度/% | 比表面积/ (m2·g-1) | (< 0.074 mm)细粒含量/% | 自由膨胀率/% |
| 百色土 | 30.1 | 60.6 | 21.9 | 15.5 | 1.86 | 90 | 264 | 98.6 | 115 |
| 宁明土 | 25.0 | 57.3 | 31.0 | 14.5 | 1.82 | 90 | 226 | 93.7 | 42 |
| 格栅型号 | 尺寸/cm | 孔隙面积/ cm2 | 厚度/cm | 孔隙率/% | 拉伸屈服强度/ (kN·m-1) | 屈服伸长率/% | 5%伸长率拉伸强度/(kN·m-1) | ||
| MD | TD | 肋 | 节点 | ||||||
| RS35PP | 22.21 | 1.78 | 31.01 | 0.05 | 0.17 | 78.54 | >35 | <10 | >20 |
| RS50PP | 27.14 | 1.88 | 40.17 | 0.08 | 0.22 | 78.56 | >50 | <10 | >30 |
| TGDG35 | 15.22 | 1.10 | 13.17 | 0.06 | 0.14 | 78.53 | >35 | <10 | >20 |

|
| 图 3 单向土工格栅的网格结构 Fig. 3 Grid structure of uniaxial geogrid |
| |

|
| 图 4 单向土工格栅剪去横肋示意图 Fig. 4 Schematic diagram of cut transverse ribs from uniaxial geogrid |
| |
2.3 试验方案设计 2.3.1 直剪试验
建立拉拔力计算式需得到试验土样抗剪强度相关指标,本研究按土工试验规程,对百色膨胀土在25%含水率及重型击实90%压实度条件下制备土样,分别于50,100,150和200 kPa的法向压力下完成直接剪切试验。
2.3.2 拉拔试验(1) 为获得式(6)中摩擦系数μ与端承侧面阻力Fb两个重要参数,设计了两组恒速拉拔(1 mm/min)试验,拟完成25%含水率、90%压实度、法向压力50 kPa下百色土的拉拔测试,具体方案见表 4。
| 试验方案 | 试验土样 | 格栅型号 | 格栅尺寸(长×宽)/cm×cm | 横肋数量/根 | 法向压力/kPa |
| 1 | 百 色 土 |
RS50PP | 60×42 | 0 | 50 |
| 80×42 | |||||
| 100×42 | |||||
| 120×42 | |||||
| 2 | 百 色 土 |
RS50PP | 60×42 | 0 | 50 |
| 1 | |||||
| 2 | |||||
| 3 |
(2) 为检验不同格栅横肋的端承侧面阻力测试值与理论分析计算值之间的符合程度,并验证本研究公式(6)的合理性,同样按1 mm/min拉拔速度,开展两种膨胀土(填土含水率25%、压实度90%)与不同型号及横肋数格栅、设定的4组不同法向压力下拉拔试验,详细设计方案见表 5。
| 试验方案 | 试验土样 | 格栅型号 | 格栅尺寸(长×宽)/cm×cm | 横肋数量/根 | 法向压力/kPa |
| 3 | 百 色 土 |
TGDG35 | 60×42 | 2 | 50 |
| 3 | |||||
| RS35PP | 2 | ||||
| 3 | |||||
| RS50PP | 2 | ||||
| 3 | |||||
| 4 | 百 色 土 |
RS50PP | 60×42 | 3 | 50 |
| 80×42 | 4 | ||||
| 100×42 | 5 | ||||
| 5 | 宁 明 土 |
TGDG35 | 60×42 | 2 | 50 |
| 60×42 | 3 | ||||
| 120×42 | 5 | ||||
| 6 | 百 色 土 |
RS50PP | 60×42 | 3 | 50 |
| 100 | |||||
| 150 |
3 试验测试的结果 3.1 直剪试验
按《公路土工试验规程》(JTGE40—2007)[17]中土样制备程序配制了25%含水率的百色土土样,分别完成法向压力为50,100,150,200 kPa的直剪试验,测得图 5所示各剪应力与剪切位移关系曲线,分析整理测试成果得抗剪强度与法向压力之间关系(见图 6),由此求得土的黏聚力C为68.9 kPa,内摩擦角φ为17.09°。

|
| 图 5 剪应力与剪切位移关系曲线 Fig. 5 Curves of shear stress vs. shear displacement |
| |

|
| 图 6 剪应力与法向压力关系 Fig. 6 Relation between shear stress and normal pressure |
| |
3.2 拉拔试验
对改变格栅横肋数量、尺寸、型号的不同加筋膨胀土,分别实施恒速拉拔(1 mm/min),共完成6组设定拉拔试验,通过宽度换算,分别得到如下各组单宽拉拔力与拉拔时间的关系曲线。
3.2.1 试验方案1测试结果采用RS50PP型格栅,按试验设计(见表 4)剪去不参与剪切部分的横肋后,加筋于百色土中,埋入格栅的尺寸(cm×cm)分别为60×42,80×42,100×42,120×42,施加50 kPa法向压力后完成拉拔试验,测试结果见图 7和表 6。

|
| 图 7 不同长度RS50PP格栅的拉拔曲线 Fig. 7 Pullout curves of RS50PP geogrid with different lengths |
| |
| 填料 | 格栅型号 | 法向压力/kPa | 格栅尺寸(长×宽)/cm×cm | 横肋数/根 | 最大单宽拉拔力/kN |
| 百色土 | RS50PP | 50 | 60×42 | 0 | 5.83 |
| 80×42 | 0 | 7.87 | |||
| 100×42 | 0 | 9.24 | |||
| 120×42 | 0 | 11.49 |
3.2.2 试验方案2测试结果
将埋入尺寸60×42,横肋数为0,1,2,3根的RS50PP型格栅,分别铺设在百色土中并施加50 kPa法向压力,共完成4次拉拔试验。测试曲线及分析结果分别见图 8和表 7。

|
| 图 8 不同横肋根数RS50PP格栅的拉拔曲线 Fig. 8 Pullout curves of RS50PP geogrid with different transverse ribs |
| |
| 填料 | 格栅型号 | 法向压力/kPa | 格栅尺寸(长×宽)/cm×cm | 横肋数/根 | 最大单宽拉拔力/kN |
| 百色土 | RS50PP | 50 | 60×42 | 0 | 5.59 |
| 1 | 7.21 | ||||
| 2 | 9.00 | ||||
| 3 | 10.60 |
3.2.3 试验方案3测试结果
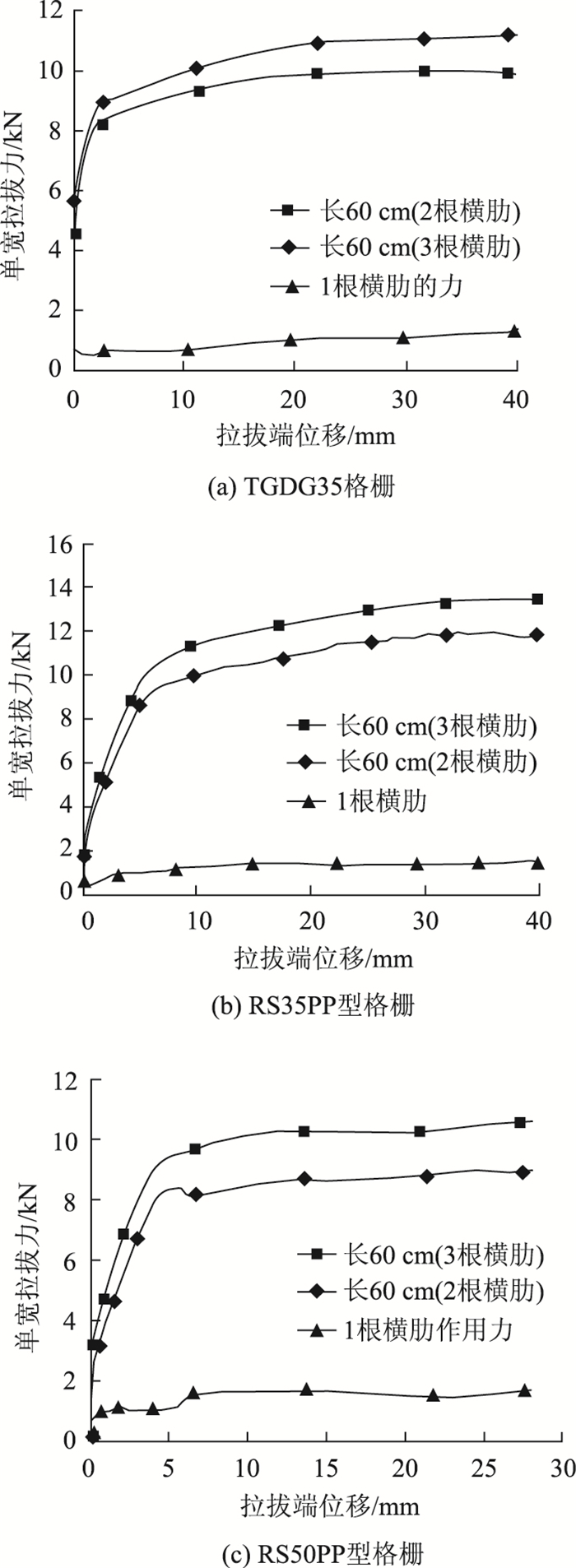
TGDG35,RS35PP,RS50PP型3种格栅,其横肋数分别为3根和2根,埋入百色土的尺寸均为60×42(cm×cm),在50 kPa法向压力下完成3组拉拔试验,获得各自的测试曲线。将3根肋的拉拔力测值减2根肋的对应值,即求得1根横肋的拉拔力分析值,各组的测试、分析结果分别见图 9和表 8。
|
| 图 9 不同横肋数RS50PP格栅拉拔曲线 Fig. 9 Pullout curves of RS50PP geogrid with different transverse ribs |
| |
| 填料 | 格栅型号 | 3根横肋最大单宽拉拔力/kN | 2根横肋最大单宽拉拔力/kN | 最大单宽1根横肋阻力/kN | 横肋占总拉拔力的百分比/% |
| 百色土 | TGDG35 | 11.09 | 9.94 | 1.15 | 31.1 |
| RS35PP | 13.14 | 11.66 | 1.48 | 33.8 | |
| RS50PP | 10.60 | 9.00 | 1.60 | 45.3 |
3.2.4 方案4拉拔测试结果
分别将埋入尺寸为60×42(3根横肋),80×42(4根横肋),100×42(5根横肋)的RS50PP型格栅加筋百色土,在法向压力50 kPa下完成3次拉拔试验,测试和分析结果见图 10、表 9。

|
| 图 10 不同尺寸RS50PP格栅拉拔曲线 Fig. 10 Pullout curves of RS50PP geogrid with different sizes |
| |
| 填料 | 格栅型号 | 法向压力/kPa | 格栅尺寸(长×宽)/cm×cm | 横肋数/根 | 最大单宽拉拔力/kN |
| 百色土 | RS50PP | 50 | 60×42 | 3 | 10.60 |
| 80×42 | 4 | 14.13 | |||
| 100×42 | 5 | 17.04 |
3.2.5 方案5拉拔测试结果
分别将埋入尺寸(cm×cm)60×42(2根横肋)、60×42(3根横肋),120×42(5根横肋)的TGDG35型格栅加筋宁明土,在50 kPa法向压力下完成3次拉拔试验,测试和分析结果见图 11、表 10。

|
| 图 11 不同横肋数和长度TGDG35格栅拉拔曲线 Fig. 11 Pullout curves of TGDG35 geogrid with different sizes and lengths |
| |
| 填料 | 格栅型号 | 法向压力/kPa | 格栅尺寸(长×宽)/cm×cm | 横肋数/根 | 最大单宽拉拔力/kN |
| 宁明土 | TGDG35 | 50 | 60×42 | 2 | 9.98 |
| 60×42 | 3 | 11.82 | |||
| 120×42 | 5 | 21.59 |
3.2.6 方案6拉拔测试结果
埋入尺寸(cm×cm)为60×42的RS50PP型格栅加筋百色土,在50,100,150 kPa法向压力下完成拉拔试验,所得测试和分析的结果分别见图 12和表 11。

|
| 图 12 不同法向压力下RS50PP格栅拉拔曲线 Fig. 12 Pullout curves of RS50PP geogrid under different normal pressures |
| |
| 填料 | 格栅型号 | 法向压力/kPa | 格栅尺寸(长×宽)/cm×cm | 横肋数/根 | 最大单宽拉拔力/kN |
| 百色土 | RS50PP | 50 | 60×42 | 3 | 10.60 |
| 100 | 60×42 | 3 | 12.93 | ||
| 150 | 60×42 | 3 | 18.33 |
4 公式参数的分析确定及合理性验证 4.1 分析确定公式参数 4.1.1 表面摩擦系数
分析方案1试验结果,由于是已去除横肋的格栅被整体匀速从土中拔出,可认为该最大拉拔力就是格栅表面与土的滑动摩擦力,用它除以格栅宽度B,换算成最大单宽拉拔力,即得到单宽摩擦力f摩。将格栅孔隙率e代入2L(1-e)中得到该单宽摩擦力所对应的有效摩擦面积,再由μ=f摩/2L(1-e)P即求得该型号格栅与填土间摩擦系数。表 12给出不同长度格栅的μ,分析表中各μ值可知它较为稳定,极差为平均值的6.2%,故可取其平均值0.447 4作摩擦系数。
| 格栅型号 | 格栅长度L/cm | 单宽摩擦力f摩/kN | 法向压力P/kPa | 格栅孔隙率e | 摩擦系数μ |
| RS50PP | 60 | 5.83 | 50 | 0.785 6 | 0.453 2 |
| 80 | 7.87 | 50 | 0.785 6 | 0.458 8 | |
| 100 | 9.24 | 50 | 0.785 6 | 0.431 0 | |
| 120 | 11.49 | 50 | 0.785 6 | 0.446 6 |
4.1.2 单根横肋端承侧面阻力
基于表 7测试结果,将横肋数1,2,3根的测试最大拉拔力值分别减去0根横肋的对应值,经宽度换算后得1,2,3根单宽横肋对土的端承侧面阻力值,代入均值μ(0.447 4),即可算出其对应的摩擦力,将测得的最大单宽拉拔力减去该摩擦力,得单宽横肋端承侧面阻力计算值(见表 13),表中的实测值与计算值较为接近。将表中测试值除以对应横肋数,得单根单宽横肋的端承侧面阻力Fb,分别为1.62,1.52,1.67 kN,3值平均为1.60 kN,其极差为均值的9.4%。
| 格栅型号 | 格栅长度L/cm | 横肋数n/根 | 最大单宽拉拔力/kN | 横肋端承侧面阻力/kN | |
| 测试值 | 计算值 | ||||
| RS50PP | 60 | 0 | 5.59 | — | — |
| 60 | 1 | 7.21 | 1.62 | 1.45 | |
| 60 | 2 | 8.63 | 3.04 | 2.87 | |
| 60 | 3 | 10.60 | 5.01 | 4.84 | |
4.2 最大拉拔力计算公式的合理性验证 4.2.1 验证不同格栅横肋端承侧面阻力测试值
学者们普遍认同的格栅横肋端承侧面阻力Fb计算公式为[18]:

|
(7) |
式中,Ab为横肋的端承面积;c为土的黏聚力;σn为格栅表面的法向压力;Nc、Nq为端承侧面阻力影响因子,其中,Nc=cot φ(Nq-1),Nq则根据分析横肋破坏的3种机理[19-20]表达式分别加以确定:
剪切破坏机理:

|
(8) |
冲切破坏机理:

|
(9) |

|
(10) |
将式(8)~(10)分别代入式(7),可算得TGDG35,RS35PP,RS50PP型格栅加筋百色土的单根单宽端承侧面阻力(见表 14)。表 14中分列了各计算值与测试值,可见,式(10)计算值与测试值最接近;式(8)次之;式(9)计算值最小,偏安全。
| 格栅型号 | 公式(8)/kN | 公式(9)/kN | 公式(10)/kN | 试验测试值/kN |
| TGDG35 | 1.38 | 0.55 | 1.22 | 1.15 |
| RS35PP | 1.73 | 0.69 | 1.53 | 1.48 |
| RS50PP | 2.24 | 0.89 | 1.98 | 1.60 |
4.2.2 本研究公式用于不同尺寸格栅的合理性验证
将前分析所得RS50PP型格栅加筋百色土的μ=0.447 4及Fb=1.60 kN代入式(6),求出法向压力50 kPa,100×42(5根横肋)、80×42(4根横肋)、60×42(3根横肋)条件下各自最大单宽拉拔力(见表 15),对比分析表中计算值与测试值(见表 9)可知,公式计算值与测试结果相差无几。
| 格栅型号 | 格栅长度L/cm | 横肋数/根 | 法向压力P/kPa | 计算值/kN | 测试值/kN |
| RS50PP | 60 | 3 | 50 | 10.56 | 10.60 |
| RS50PP | 80 | 4 | 50 | 14.07 | 14.13 |
| RS50PP | 100 | 5 | 50 | 17.59 | 17.04 |
4.2.3 本研究公式用于不同类型膨胀土的合理性检验
分析表 10测试结果,将求得的Fb=1.84 kN、μ=0.489 1代入式(6),得埋长120 cm格栅的最大拉拔力F=21.78 kN,与测试值21.59 kN非常接近。
5.2.4 本研究公式分析拉拔摩擦系数的合理性验证文献[3]提供的拉拔摩擦系数确定方法是先求界面拉拔摩擦强度τp,后将其除以施测法向压力P,即求得拉拔摩擦系数f,具体计算公式如下:

|
(11) |

|
(12) |
式中,F为最大拉拔力;L、B为埋入土中格栅的长与宽。
由表 11,按(11)(12)式分析,得τp及f与P关系(见图 13、14),可知:τp随P增大线性增大;f随P增大呈幂函数曲线关系减小,P较小时f减幅较大;P>100 kPa后,减幅变小;当P>150 kPa后,减幅逐渐消失。

|
| 图 13 拉拔摩擦强度与法向压力关系 Fig. 13 Relation between pullout friction strength and normal pressure |
| |

|
| 图 14 拉拔摩擦系数与法向压力曲线 Fig. 14 Curves of pullout friction coefficient vs. normal pressure |
| |
将式(6)代入式(11)和(12),得新的f计算式:

|
(13) |
将前分析所得RS50PP型格栅加筋百色土的μ=0.447 4代入式(13),可求得0根横肋时的f=μ(1-e)= 0.096,与按文献[3]法确定0根横肋150 kPa法向压力下的f值(0.101 8)基本一致(见图 14)。可见P越大,f值越接近μ(1-e)之值。
5 结论(1) 抓住影响加筋土中格栅与填料相互作用的关键设计两组试验,先做去除横肋格栅拉拔试验求得筋土间摩擦系数,后测试确定单根格栅横肋的端承侧面阻力,顺利突破了本研究的技术瓶颈,从而建立简洁明了的单向土工格栅加筋膨胀土拉拔力计算公式。
(2) 比较目前普遍认同确定格栅横肋端承侧面阻力的3种理论,本单向土工格栅加筋膨胀土系统拉拔试验的结果表明,普朗特理论做分析较为合适,剪切破坏机理的计算值偏大,冲切破坏机理计算值偏小。
(3) 用不同尺寸、型号单向土工格栅加筋两种膨胀土的系统拉拔试验测试成果,对比按本研究公式计算所得各边界条件下的最大拉拔力值,验证了本研究的合理正确性。
(4)《土工合成材料测试规程》提出的筋土界面拉拔摩擦强度τp、拉拔摩擦系数f与法向压力P间的关系合理,本研究由拉拔力计算公式重新导出的f计算式(13)更直观,参数也更明确且易获取,其计算值随P值增大将无限接近μ(1-e)。
(5) 目前厂家生产单向格栅的产品参数尚无统一标准,所提供的横肋阻力与表面摩擦力比例不尽合理,有了本研究公式,只需完成简单拉拔试验并提供材料相应参数即可准确预测拉拔力,既方便加筋膨胀土的工程设计,还能不增用料而优化参数后生产较大拉拔力的单向土工格栅产品。
| [1] |
MEGOWN A, ANDRAWES K Z, KABIR M H. Load Extension Testing of Geotextiles Confined in Soil[C]//Proceedings of the 2nd International Conference on Geotextiles. Las Vegas: Industrial Fabrics Association International, 1982: 793-798.
|
| [2] |
SCHLOSSER F, LONG N T. Recent Results in French Research on Reinforced Earth[J]. Journal of the Construction Division, 1974, 100(CO3): 223-237. |
| [3] |
SL 235-2012, 土工合成材料测试规程[S]. SL 235-2012, Specification for Test and Measurement of Geosynthetics[S]. |
| [4] |
MORACI N, GIOFFRE D. A Simple Method to Evaluate the Pullout Resistance of Extruded Geogrids Embedded in a Compacted Granular Soil[J]. Geotextiles and Geomembranes, 2006, 24(2): 116-128. |
| [5] |
王家全, 周岳富, 夏雨, 等. 新型可视土工拉拔试验仪的研发与应用[J]. 岩土工程学报, 2016, 48(4): 718-725. WANG Jia-quan, ZHOU Yue-fu, XIA Yu, et al. Development and Application of New Visual Pullout Test Apparatus for Geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 2016, 48(4): 718-725. |
| [6] |
张正, 刘振华. 土工格栅与黄土相互作用机制的拉拔试验研究[J]. 兰州工业学院学报, 2018, 25(1): 1-6. ZHANG Zheng, LIU Zhen-hua. Study on the Interaction Mechanism between the Geogrid and Loess[J]. Journal of Lanzhou Institute of Technology, 2018, 25(1): 1-6. |
| [7] |
郑俊杰, 周燕君, 赖汉江, 等. 格栅加筋砂土拉拔试验界面特性的离散元模拟[J]. 华中科技大学学报:自然科学版, 2014, 42(8): 104-108. ZHENG Jun-jie, ZHOU Yan-jun, LAI Han-jiang, et al. DEM Analysis of Characteristic of Interface between Geogrid and Sand in Pull-out Test[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014, 42(8): 104-108. |
| [8] |
徐超, 廖星樾. 土工格栅与砂土相互作用机制的拉拔试验研究[J]. 岩土力学, 2011, 32(2): 423-428. XU Chao, LIAO Xing-yue. Researches on Interaction Mechanism between Geogrid and Sand by Pull-out Tests[J]. Rock and Soil Mechanics, 2011, 32(2): 423-428. |
| [9] |
包承纲. 土工合成材料界面特性的研究和试验验证[J]. 岩土工程学报, 2006, 25(9): 1735-1744. BAO Cheng-gang. Study on Interface Behavior of Geosynthetics and Soil[J]. Chinese Journal of Geotechnical Engineering, 2006, 25(9): 1735-1744. |
| [10] |
WILSON-FAHMY R F, KOERNER R M, SANSONE L J. Experimental Behavior of Polymeric Geogrids in Pullout[J]. Journal of Geotechnical Engineering, 1994, 120(4): 661-667. |
| [11] |
KOERNER R M, WAYNE M H, CARROLL R G. Analytic Behavior of Geogrid Anchorage[C]//Proceedings of Geosynthetics'89 Conference. San Diego: [s. n.], 1989: 525-536.
|
| [12] |
JEWELL R A, MILLIGAN G W E, SARSBY R W, et al. Interaction between Soil and Geogrids[C]//Proceedings of a Conference on Polymer Grid Reinforcement. London: Thomas Telford, 1984: 18-30.
|
| [13] |
杨广庆, 李广信, 张保俭. 土工格栅界面摩擦特性试验研究[J]. 岩土工程学报, 2006, 28(8): 948-952. YANG Guang-qing, LI Guang-xin, ZHANG Bao-jian. Experimental Studies on Interface Friction Characteristics of Geogrids[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 948-952. |
| [14] |
蔡春, 张孟喜, 赵岗飞, 等. 带加强肋单向土工格栅的拉拔试验[J]. 岩土力学, 2012, 33(1): 53-64. CAI Chun, ZHANG Meng-xi, ZHAO Gang-fei, et al. Pull-out Test of Uniaxial Geogrid with Strengthening Ribs[J]. Rock and Soil Mechanics, 2012, 33(1): 53-64. |
| [15] |
王家全, 陆梦梁, 周岳富, 等. 土工格栅纵横肋的筋土承载特性分析[J]. 岩土工程学报, 2018, 40(1): 186-193. WANG Jia-quan, LU Meng-liang, ZHOU Yue-fu, et al. Bearing Characteristics of Reinforced Soil with Longitudinal and Transverse Ribs of Geogrids[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 186-193. |
| [16] |
杨和平, 万亮, 郑健龙. 大型数控拉拔试验系统的研制及应用[J]. 岩土工程学报, 2007, 29(7): 1080-1084. YANG He-ping, WAN Liang, ZHENG Jian-long. Development and Application of Large Scale Numerical Control Pullout Test System[J]. Chinese Journal ofGeotechnical Engineering, 2007, 29(7): 1080-1084. |
| [17] |
JTGE40-2007, 公路土工试验规程[S]. JTGE40-2007, Test Methods of Soils for Highway Engineering[S]. |
| [18] |
PETERSON L M, ANDERSON L R. Pullout Resistance of Welded Wire Mesh Embeded in Soil[R]. Logan: Civil and Environmental Engineering Department, Utah State University, 1980.
|
| [19] |
陈榕, 郝冬雪, 栾茂田, 等. 土工格栅横肋与纵肋加筋机理研究[J]. 建筑材料学报, 2013, 16(3): 544-548. CHEN Rong, HAO Dong-xue, LUAN Mao-tian, et al. Reinforcement Mechanism of Transverse and Longitudinal Geogrid Ribs[J]. Journal of Building Materials, 2013, 16(3): 544-548. |
| [20] |
CARDILE G, GIOFFRE D, MORACI N, et al. Modelling Interference Between the Geogrid Bearing Members Under Pullout Loading Conditions[J]. Geotextiles and Geomembranes, 2017, 45: 169-177. |
 2020, Vol. 37
2020, Vol. 37
