扩展功能
文章信息
- 王文真, 申爱琴, 郭寅川, 张东, 李得胜
- WANG Wen-zhen, SHEN Ai-qin, GUO Yin-chuan, ZHANG Dong, LI De-sheng
- 基于图像分析的粗集料形状特征参数及分布规律
- Shape Feature Parameters and Distribution Rule of Coarse Aggregate Based on Image Analysis
- 公路交通科技, 2020, 37(1): 25-31
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 25-31
- 10.3969/j.issn.1002-0268.2020.01.004
-
文章历史
- 收稿日期: 2018-07-12
2. 南京工业大学 道路工程研究所, 江苏 南京 210009
2. Institute of Road Engineering, Nanjing Tech University, Nanjing Jiangsu 210009, China
我国沥青路面的早期破坏现象严重,许多新建高等级公路沥青路面的设计寿命为20 a,但实际上使用3~5 a后均出现不同程度上的破坏[1],集料的级配组成不合理是导致沥青路面寿命大大缩减的一个重要因素。研究表明沥青混凝土材料是由多种材料组成的,具有复杂结构的非均值、多相多层次的复合体系[2],且沥青混合料的级配组成特性受集料的形状特征影响显著,进而影响到沥青混合料的力学强度和路用性能[3]。因此,应当深入研究和分析集料的形状特征。
Tutumluer等[4]使用一种用于分析粗集料几何特征的装置,基于具有不同几何特征的集料进行了离散元模拟,该方法对于高效收集粗集料的几何特征很有效,可以完成各种参数的同时采集。Wang等[5]用傅立叶级数分析了沥青混合料的图像特征,以评估它们的尺寸、形状、棱角性和纹理。Wang等[6]使用X射线断层扫描和激光扫描获得三维表面数据后比较得出,两种扫描重建均可有效地评估粗细集料的尺寸、表面积和体积。张肖宁等[7]结合工业CT扫描技术与图像处理法,并引入模式识别领域的算法分析了沥青混合料中集料的形状和材质。王端宜等[8]通过MATLAB程序处理CT图像,完成三维模型重建,获得了三维几何信息。汪海年等[9-10]设计了多角度光照入射的方法,克服了在拍摄过程中可能出现的图像阴影对形状特征的影响。涂新斌等[11]用图像分析方法研究了不同岩石颗粒的形态特征,并提出了一系列二维形状参数。李嘉[12]设计了一套图像采集装置,并采用自主研发的Image-proplus图像分析软件来识别粗集料图像,对粗集料的棱角性进行定量研究。熊琴[13-14]在图像处理的基础上通过长短轴、矩形度、形状指数和棱角性等指标,较好地评价了集料颗粒的形状特征。
目前传统测试方法对于粗集料的几何形状特征如长细比、扁平度等,往往只能采用一些定性的描述进行分类,缺乏定量分析的手段[15],而且受试验仪器的限制,集料的形状特征不易获得。为定量表征集料的形状特征,并通过合理的形状特征为集料的级配设计提供理论依据,本研究提出一种集料二维形状特征的简易测试系统,结合数字图像处理技术,对各形状特征进行测试和对比分析,得到矩形度、形状指数和棱角性等形状特征指标。对各参数的统计分布规律进行研究,并分析形状特征参数与级配的相关性,为判断混合料加工合格性、确定混合料级配范围提供依据。
1 试验原材料及试验方案 1.1 试验原材料本研究对不同粒径的粗集料进行图像分析,粗集料采用玄武岩集料,其特性参数见表 1。
| 岩性 | 表观相对密度 | 毛体积相对密度 | 压碎值/% | 磨光值 | 粒径范围/mm |
| 玄武岩 | 2.866 | 2.823 | 16.5 | 62 | 4.75~19 |
1.2 试验方案
本研究对象为不同粒径集料颗粒的整体形状特征,集料最终投影面的形状受具体摆放位置的影响。集料二维形状只是某个投影面的形状,可能无法代表整个集料的特性,因而更无法由此来判断不同粒径的情况[13],所以考虑选择大样本。根据统计学规律,粒径小的颗粒其形状差异更大,故粒径越小样本数越大。本研究选取的样本数量见表 2。
| 粒径大小/mm | 19 | 16 | 13.2 | 9.5 | 4.75 |
| 数量/个 | 200 | 200 | 200 | 300 | 500 |
主要试验方案如下:
首先,将试验原材料进行筛分,得到不同粒径大小的集料;其次将集料清洗干净,利用烘箱烘干,使用墨汁对集料进行均匀染色;最后,再次烘干后均匀平铺在空白A3纸上,采集粗集料图像。
集料二维形状特征参数的简易测试系统包括:测试平台、单反相机(尼康D7000,像素4 928×3 264)、三脚架(TRIOPO)。将A3白纸放置在平台正中位置,人工将集料样品规则地排布在白纸上。固定三脚架高度为50 cm,使相机保持水平,使用单反相机从上方摄取集料样品的图像。把1元硬币放在集料中,保证照片上能清楚读出硬币条纹,并且集料不能有阴影出现,避免影响读数的准确。
此外,为使集料颜色和背景颜色差异明显,染色后烘干时间不宜过长,烘干至无明显墨迹即可,并立即进行图像采集。为防止产生重影,每张A3纸上的集料数量不超过20个。为避免室内外光线强弱差异太大而产生的图像阴影等影响,拍摄时间宜选择在清晨或傍晚时分,外界光线与室内光线差异不明显时进行拍摄,在需要时打开测试平台底部的LED灯进行辅助照明。
1.3 图像处理在获取试验集料图像后,需要得到每个集料颗粒的轮廓形状,同时,若将集料一颗颗进行单独拍摄,工作量大,所以采用MATLAB软件进行编程,对集料图像进行增强和分割处理。
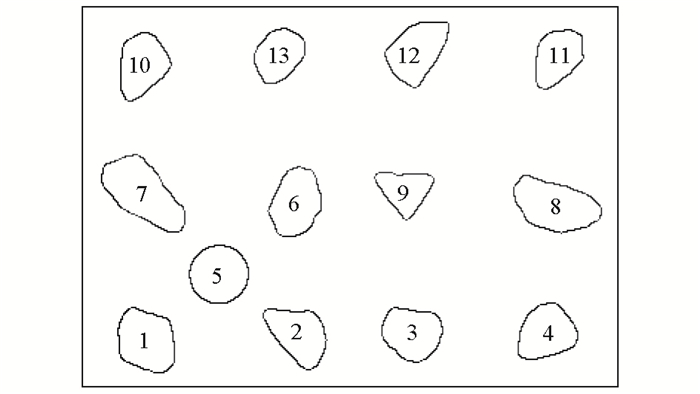
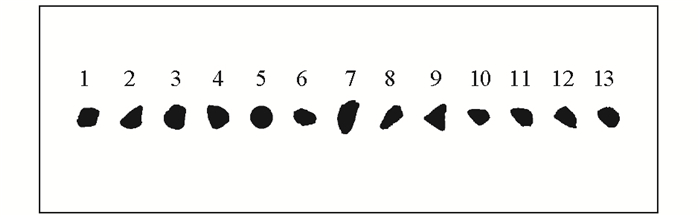
将Sobel梯度算子[16](图 1)直接作为边缘检测的模板,实现图像的边缘检测,边缘检测结果见图 2。为获取每颗集料颗粒的形状特征参数,通过设置灰度阈值来确定待分割物体的边界。二值化后的阈值分割处理结果如图 3所示。

|
| 图 1 Sobel算子模板 Fig. 1 Sobel operator template |
| |
|
| 图 2 边缘检测结果 Fig. 2 Edge detection result |
| |
|
| 图 3 图像分割结果 Fig. 3 Image segmentation result |
| |
进一步通过MATLAB软件编程计算集料图像的大小指标:长轴、短轴、周长和面积,利用大小指标换算得到粗集料的形状特征参数。
2 试验结果及分析 2.1 粗集料形状特征参数(1) 矩形度
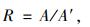
|
(1) |
式中,R为矩形度;A为颗粒图像的面积;A′为颗粒最小外接矩形。矩形度的大小反映集料对其最小外接矩形的充满程度。
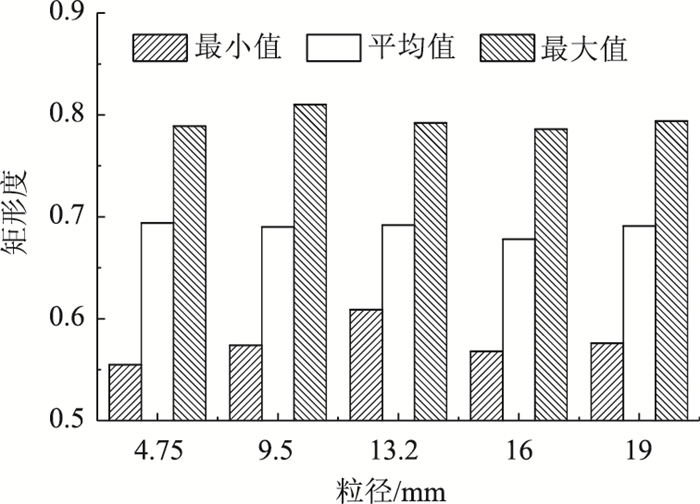
根据数理统计原理进行统计分析[17-19],对不同粒径的玄武岩集料的总体特征进行计算。集料矩形度的分布结果见图 4,其概率密度累积分布见图 5。
|
| 图 4 不同粒径集料颗粒的矩形度 Fig. 4 Rectangularity of aggregate particles with different particle sizes |
| |
|
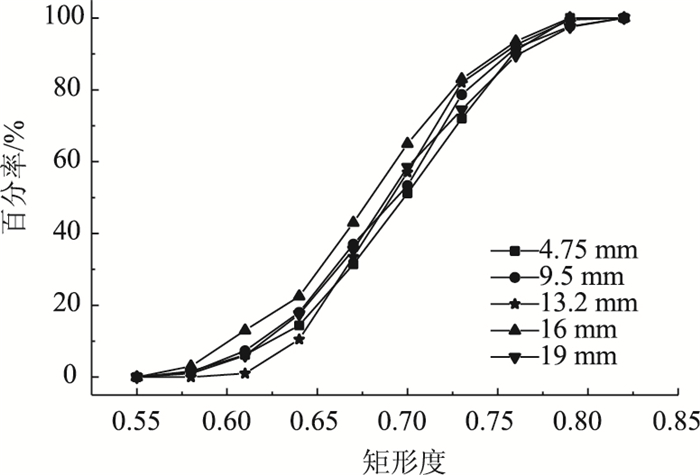
| 图 5 矩形度的概率密度累积分布 Fig. 5 Probability density cumulative distribution of rectangularity |
| |
由图 4可知,不同粒径集料颗粒的矩形度代表值(平均值)与矩形度最大值变化呈现出一致性,且矩形度平均值与最大值的变化幅度均很小,变化幅度小于3.05%。矩形度最小值随着粒径的增大先增加后减小,粒径为13.2 mm的集料颗粒的矩形度最小值比粒径为4.75 mm的高出9.73%。不同粒径矩形度的代表值近似处于最大值和最小值之间,说明矩形度值的差异性较小。
由图 5可以看出,13.2 mm和19 mm粒径的集料颗粒概率密度累积分布曲线最平滑,9.5 mm粒径的次之,4.75 mm和16 mm粒径的集料颗粒概率密度累积分布曲线较曲折,其中13.2 mm粒径集料的矩形度分布较集中,主要集中在0.61~0.79之间。粒径为9.5 mm的集料颗粒矩形度的概率密度累积分布曲线更接近“S”型曲线中线,结合图 4,其矩形度的代表值近似处于最大值和最小值之间,说明9.5 mm粒径的集料矩形度分布更为均匀。
(2) 形状指数
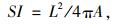
|
(2) |
式中,SI为形状指数;L为颗粒边界的周长;A为颗粒图像的面积。
形状指数是反映颗粒形状特征比较重要的一个指标,该指标表征集料接近圆形的程度。圆形是沥青混凝土骨架结构中最忌讳的一种形状,形状指数越大对应集料的性能越好。
不同粒径集料颗粒的形状指数对比分析见图 6,其概率密度累积分布见图 7。
|
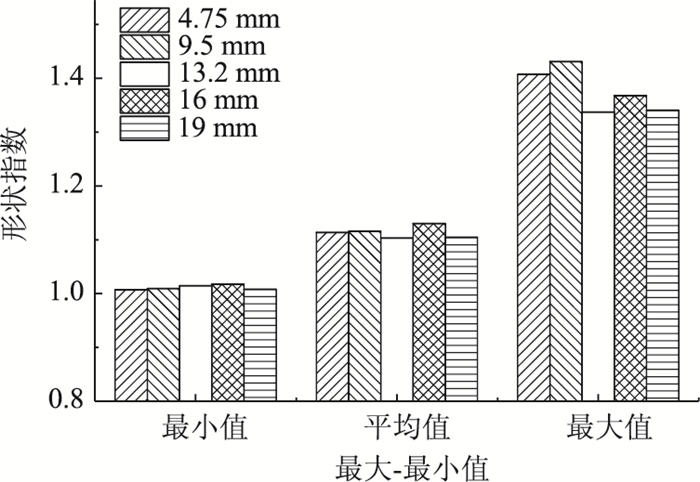
| 图 6 不同粒径集料颗粒的形状指数对比 Fig. 6 Comparison of shape indicators of aggregate particles with different particle sizes |
| |
|
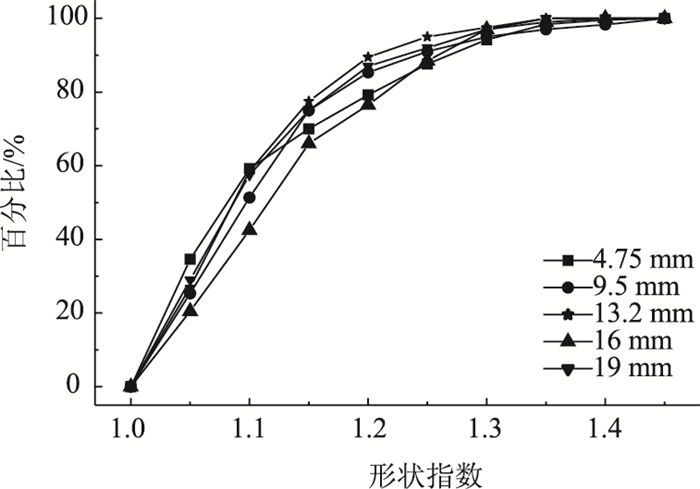
| 图 7 形状指数的概率密度累积分布 Fig. 7 Cumulative distribution of probability density of shape indicator |
| |
由图 6可以看出,不同粒径集料颗粒的形状指数代表值与形状指数的最小值变化均不明显,形状指数最小值的变化幅度不大于1.04%,代表值的变化幅度不大于2.46%。形状指数的代表值数值上更接近其最小值,与最大值相差较大,说明形状指数的差异性较大,且形状指数大的颗粒较少。形状指数的最大值随着粒径的增大而变化,没有明显的变化规律,但表现出与代表值同步变化。
由图 7可知,13.2 mm和19 mm粒径集料的形状指数位于5种粒径形状指数的上界,分布较集中,其概率密度累积分布曲线也比较平滑。4.75 mm和16 mm粒径的集料颗粒概率密度累积分布曲线较曲折。不同粒径形状指数的取值都处在5种粒径形状指数的包络线图中,因此,可以通过计算形状指数来评价粗集料加工是否符合规格,要求加工后粗集料的形状指数应不小于目标包络线的下限值。同时可以量化混合料级配范围的大小,从而为今后确定混合料的合理级配提供参考依据。
(3) 棱角性
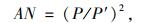
|
(3) |
式中,AN为棱角性;P为颗粒轮廓周长;P′为等效椭圆周长。
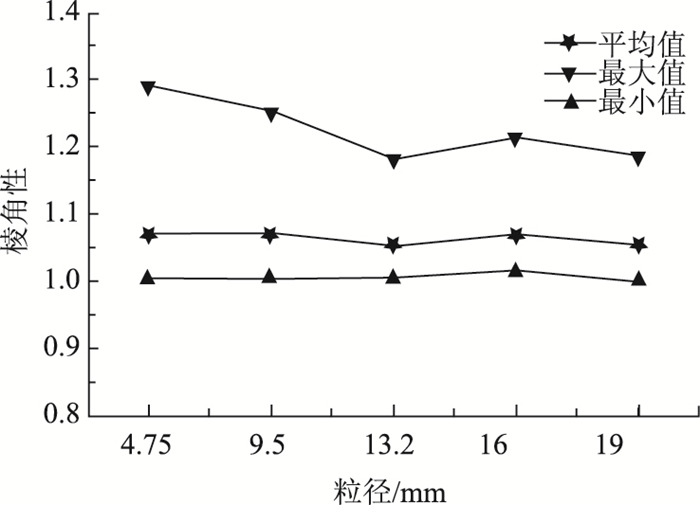
基于等效椭圆的棱角性指数是反映集料轮廓的另一个重要指标,表征的是轮廓的复杂程度,反映了集料颗粒轮廓上角度的变化。不同粒径集料颗粒的棱角性对比分析见图 8,其概率密度累积分布见图 9。
|
| 图 8 不同粒径集料颗粒的棱角性对比 Fig. 8 Comparison of angularity of aggregate particles with different particle sizes |
| |
|
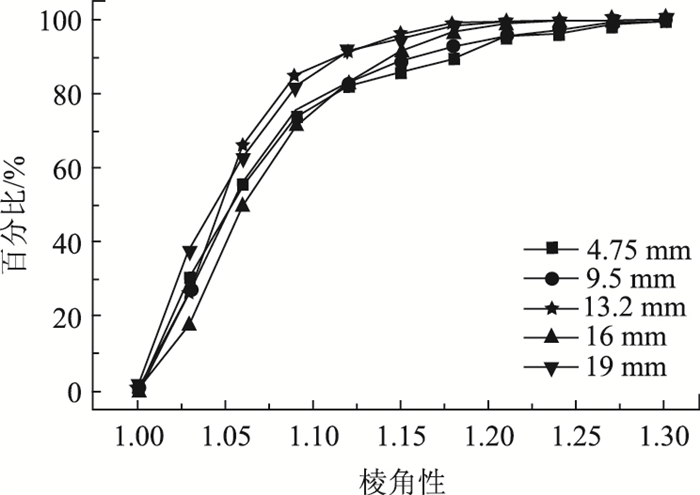
| 图 9 棱角性的概率密度累积分布 Fig. 9 Cumulative distribution of probability density of angularity |
| |
由图 8可以看出,集料颗粒棱角性代表值的走势与其最小值趋于一致,且其值更接近其最小值,说明棱角性的差异性较大,同时棱角性数值大的颗粒较少,棱角性大于平均值的颗粒约占总颗粒的26.4%。棱角性的最大值随着粒径的增大而变化,没有明显的变化规律。
由图 9可知,13.2 mm和19 mm粒径集料的棱角性位于5种粒径棱角性的上界,分布范围小,分布集中,主要集中在1.03~1.18之间。16 mm粒径的集料棱角性分布集中性次之,4.75 mm粒径的集料颗粒棱角性分布范围最广。所有粒径集料的棱角性主要分布在其最小值-平均值部分,当棱角性大于平均值,特别是大于1.20后,其概率密度累积分布呈现水平状,说明棱角性在其值达到1.20后分布较为稀疏,即棱角性大于1.20的集料颗粒较少。
2.2 形状特征参数与级配的相关性为确定集料的形状特征参数对混合料级配的影响,采用人工干扰的方式,配置15组具有不同粒径颗粒含量的粗集料,放大粗集料间形状特征的差异性,为相关性分析提供更有利的数据支撑。具体操作如下。
挑选5种不同的粗集料,按不同比例进行合理组合,得到15组不同级配的粗集料,如表 3所示。
| 编号 | 粒径/mm | |||||
| 4.75 | 9.5 | 13.2 | 16 | 19 | 平均 | |
| JZ1 | 1 | 0 | 0 | 0 | 0 | 4.750 |
| JZ2 | 1 | 1 | 0 | 0 | 0 | 7.125 |
| JZ3 | 1 | 1 | 1 | 0 | 0 | 9.150 |
| JZ4 | 0 | 1 | 0 | 0 | 0 | 9.500 |
| JZ5 | 1 | 1 | 1 | 1 | 0 | 10.863 |
| JZ6 | 0 | 1 | 1 | 0 | 0 | 11.350 |
| JZ7 | 1 | 1 | 1 | 1 | 1 | 12.490 |
| JZ8 | 0 | 1 | 1 | 1 | 0 | 12.900 |
| JZ9 | 0 | 0 | 1 | 0 | 0 | 13.200 |
| JZ10 | 0 | 1 | 1 | 1 | 1 | 14.425 |
| JZ11 | 0 | 0 | 1 | 1 | 0 | 14.600 |
| JZ12 | 0 | 0 | 0 | 1 | 0 | 16.000 |
| JZ13 | 0 | 0 | 1 | 1 | 1 | 16.067 |
| JZ14 | 0 | 0 | 0 | 1 | 1 | 17.500 |
| JZ15 | 0 | 0 | 0 | 0 | 1 | 19.000 |
| 注:表中JZ1表示该组集料粒径全部为4.75 mm;JZ2表示该组集料为粒径4.75 mm和9.5 mm各一半,以此类推。 | ||||||
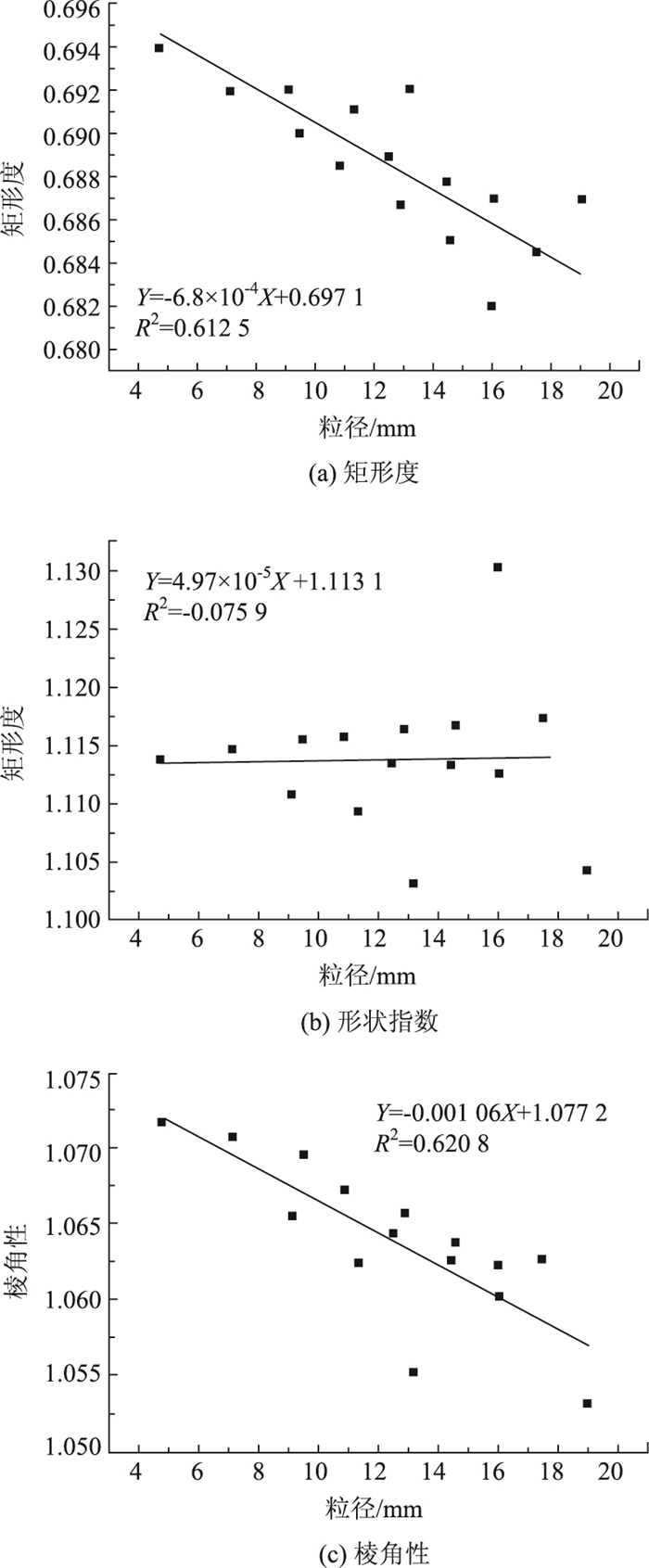
利用粗集料二维形状特征参数的简易测试系统对上述粗集料组合进行测试,利用MATLAB进行处理计算,分别得到不同粒径组合的粗集料的矩形度、形状指数和棱角性。基于最小二乘法的线性回归模型,分析形状特征参数与集料级配之间的关系,相关性分析结果如图 10所示。
|
| 图 10 形状特征参数与级配相关性 Fig. 10 Correlations between shape parameters and gradation |
| |
由图 10可以看出,矩形度和棱角性与级配表现出良好的相关性,其相关性指数R2分别为0.612 5和0.620 8;而形状指数的分布分散无规律,其值与级配不相关。矩形度与级配的关系式为:Rectangularity=-6.8×10-4 (Particle Size)+0.697 1;棱角性与级配的关系式为:Angularity=-0.001 06 (Particle Size) + 1.077 2。
随着集料粒径的增大,即混合料级配逐渐变粗时,矩形度值逐渐减小;反之,说明矩形度越大级配越细。同理,随着集料粒径的增大,即混合料级配逐渐变粗时,棱角性逐渐减小,则说明棱角性越小则级配越粗。因此,可以用矩形度和棱角性指标来表征级配的粗细程度,并为混合料级配设计的提供理论依据。
3 结论(1) 本研究选用玄武岩粗集料,对不同粒径的二维指标的矩形度、形状指数和棱角性利用图像处理和数理统计方法进行了大量的试验分析。结果表明,不同粒径的玄武岩颗粒形状特征参数具有一定的统计规律。
(2) 矩形度是所有形状特征参数中差异性最小的,可以认为是3个指标中相对最可靠的指标。矩形度和形状指数指标的代表值随粒径走向趋势与其指标值最大值趋于一致,而棱角性指标代表值的走向趋势与其指标值最小值趋于一致,且其值更接近于最小值,指标值大于平均指标的颗粒数量约占颗粒总量的26.4%。
(3) 粒径为9.5 mm的集料颗粒矩形度的概率密度累积分布曲线更接近“S”型曲线中线,分布较均匀,而13.2 mm和19 mm粒径集料的形状指数和棱角性分布集中,其概率密度累积分布曲线较平滑。形状指数和棱角性指标的差异性较大,其分布表现为指标值小的颗粒多,指标值大的颗粒分布稀疏。
(4) 矩形度和棱角性指标与集料粒径表现出良好的相关性,可以利用矩形度和棱角性指标来表征混合料级配的粗细,并为混合料级配设计提供理论依据。而形状指数可以评价集料加工是否符合规格,要求加工时集料的形状指数值应不小于目标包络线的下限值,进一步确定混合料的级配范围。
| [1] |
黎逢亮.基于图像处理的路用碎石形态评价指标的研究[D].长沙: 长沙理工大学, 2013. LI Feng-liang. Study on Evaluation Indicator of Road Gravel Morphology Based on Image Processing[D].Changsha: Changsha University of Science & Technology, 2013. http://d.wanfangdata.com.cn/Thesis/Y2306357 |
| [2] |
杨群, 郭忠印, 陈立平, 等. 级配碎石分形特征分析及其在路面工程中的应用[J]. 建筑材料学报, 2006, 9(4): 418-422. YANG Qun, GUO Zhong-yin, CHEN Li-ping, et al. Fractal Analysis of Gradation Aggregate and Its Applications in Pavement Engineering[J]. Journal of Building Materials, 2006, 9(4): 418-422. |
| [3] |
杜小婷, 汪海年. 基于图像分析的粗集料三维形态指标研究[J]. 公路, 2013(8): 250-254. DU Xiao-ting, WANG Hai-nian. A Study on Three-Dimensional Shape Indicatores of Coarse Aggregates Based on Image Analysis[J]. Highway, 2013(8): 250-254. |
| [4] |
TUTUMLUER E, HUANG H, BIAN X C. Geogrid-aggregate Interlock Mechanism Investigated through Aggregate Imaging-based Discrete Element Modeling Approach[J]. International Journal of Geomechanics, 2012, 12(4): 391-398. |
| [5] |
WANG L B, PARK J Y, MOHAMMAD L N. Quantification of Morphology Characteristics of Aggregate From Profile Images[C]//Transportation Research Board 82nd Annual Meeting. Washington, D.C.: Transportation Research Board, 2003.
|
| [6] |
WANG L, DRUTA C, ZHOU Y, et al. Three-dimensional Aggregate Evaluation Using Laser and X-ray Scanning[C]//Transportation Research Board 87th Annual Meeting. Washington, D.C.: Transportation Research Board, 2008.
|
| [7] |
张肖宁, 段跃华, 李智, 等. 基于X-ray CT的沥青混合料材质分类方法[J]. 华南理工大学学报:自然科学版, 2011, 39(3): 120-124. ZHANG Xiao-ning, DUAN Yue-hua, LI Zhi, et al. Classification of Asphalt Mixture Materials Based on X-ray Computed Tomography[J]. Journal of South China Cniversity of Technology:Nature Science Edition, 2011, 39(3): 120-124. |
| [8] |
王端宜, 胡迟春, KUTAYE. 沥青混合料集料微观结构的三维重构与计算[J]. 建筑材料学报, 2011, 14(1): 41-46. WANG Duan-yi, HU Chi-chun, KUTAY E. Three Dimensional Reconstruction and Calculation of Aggregate Structure in Asphalt Mixture[J]. Journal of Building Materials, 2011, 14(1): 41-46. |
| [9] |
汪海年, 郝培文. 粗集料二维形状特征的图像描述[J]. 建筑材料学报, 2009, 12(6): 747-751. WANG Hai-nian, HAO Pei-wen. Digital Description of Two-dimensional Shape Characteristics of Coarse Aggregate[J]. Journal of Building Materials, 2009, 12(6): 747-751. |
| [10] |
汪海年, 郝培文, 胡世通. 粗集料形态特征研究与应用[J]. 公路, 2008(10): 180-184. WANG Hai-nian, HAO Pei-wen, HU Shi-tong. Research and Application of Coarse Aggregate Morphology Characteristics[J]. Highway, 2008(10): 180-184. |
| [11] |
涂新斌, 王思敬. 图像分析的颗粒形状参数描述[J]. 岩土工程学报, 2004, 26(5): 659-662. TU Xin-bin, WANG Si-jing. Description of Particle Shape Parameters in Image Analysis[J]. Journal of Geotechnical Engineering, 2004, 26(5): 659-662. |
| [12] |
李嘉, 林辉. 基于数字图像处理的粗集料棱角性量化研究[J]. 公路交通科技, 2008, 25(7): 27-31. LI Jia, LIN Hui. Quantification Research of Coarse Aggregate Angularity Based on Digital Image Processing[J]. Journal of Highway and Transportion Research and Development, 2008, 25(7): 27-31. |
| [13] |
熊琴.粗集料形状特征的数字图像分析[D].重庆: 重庆交通大学, 2011. XIONG Qin. Digital Image Analysis of Shape Features of Coarse Aggregate[D]. Chongqing: Chongqing Jiaotong University, 2011. |
| [14] |
熊琴, 王旭东, 张蕾. 数字图像处理技术在粗集料形状方面的研究综述[J]. 路基工程, 2012(1): 7-10. XIONG Qin, WANG Xu-dong, ZHANG Lei. Research Summary of Digital Image Processing Technology on Coarse Aggregate Morphology Characteristics[J]. Subgrade Engineering, 2012(1): 7-10. |
| [15] |
边学成, 李公羽, 李伟, 等. 基于双平面镜三维成像的粗粒料形状特征分析[J]. 土木工程学报, 2014, 47(9): 135-144. BIAN Xue-cheng, LI Gong-yu, LI Wei, et al. Morphology Analysis of Coarse Aggregate Based on 3D Imaging Method by Using Two Planar Mirrors[J]. China Civil Engineering Journal, 2014, 47(9): 135-144. |
| [16] |
杨德平, 孙显录, 管殿柱. MATLAB 8.5基础教程[M]. 北京: 机械工业出版社, 2016. YANG De-ping, SUN Xian-lu, GUAN Dian-zhu. MATLAB 8.5 Basic Course[M]. Beijing: China Machine Press, 2016. |
| [17] |
GB4882-85, 数据的统计处理和解释正态性检验[S]. GB4882-85, Statistical Interpretation of Data-Normality Test[S]. |
| [18] |
茆诗松, 周纪芗. 概率论与数理统计[M]. 北京: 中国统计出版社, 2007. MAO Shi-song, ZHOU Ji-xiang. Probability Theory and Mathematical Statistics[M]. Beijing: China Statistics Press, 2007. |
| [19] |
周品, 赵新芬. MATLAB数理统计分析[M]. 北京: 国防工业出版社, 2009. ZHOU Pin, ZHAO Xin-fen. Mathematical MATLAB Mathematical Statistical Analysis[M]. Beijing: National Defense Industry Press, 2009. |
 2020, Vol. 37
2020, Vol. 37
