扩展功能
文章信息
- 周丹, 马泽欣, 刘黎萍, 孙立军
- ZHOU Dan, MA Ze-xin, LIU Li-ping, SUN Li-jun
- 基于足尺加速加载试验的现役沥青路面疲劳特性研究
- Study on Fatigue Performance of In-service Asphalt Pavement Based on Full-scale Accelerated Loading Test
- 公路交通科技, 2020, 37(1): 17-24
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(1): 17-24
- 10.3969/j.issn.1002-0268.2020.01.003
-
文章历史
- 收稿日期: 2018-04-09
2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804;
3. 江西省交通设计研究院有限责任公司, 江西 南昌 330022
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China;
3. Jiangxi Provincial Communications Design & Research Institute Co., Ltd., Nanchang Jiangxi 330022, China
路面结构承载能力可描述为路面结构在达到预定损坏状况之前,还能承受多少次行车荷载作用或者还能服务多少年,它反映了路面结构抵抗荷载和环境的能力[1]。沥青路面的结构承载能力评价可以选取变形和模量为主要指标,依托现场路面检测或是足尺加速加载(APT)试验以及室内试验对沥青面层的高温变形和疲劳损伤特性进行研究[2-6]。
APT试验是目前道路工程所有研究中最能接近实际行车荷载状况的模拟方法,近年来常被用于研究沥青路面的车辙抗力[7]、传统疲劳开裂[8-9]以及新型Top-down开裂[10],为指导路面结构与材料设计提供了许多有益的结论。
对于沥青混合料室内疲劳性能评价,目前常用的方法有:四点小梁弯曲疲劳试验、两点梯形梁疲劳试验、直接拉伸疲劳试验和劈裂疲劳试验[11-12]。劈裂疲劳试验的优点是试件容易制备,既适用于室内成型混合料试件,又适用于现场取芯试件,且试验结果离散性较小,是一种常用的室内疲劳试验方法[13]。鉴于本研究主要是评价现场取芯试件的疲劳性能,所以主要采用劈裂疲劳试验方法。
为了研究高速公路现役沥青路面的疲劳特性,本研究在上海现役高速公路上选取了3个不同沥青层厚度的路段进行了APT试验,研究了沥青面层的模量随加速加载作用次数的变化规律。并于APT试验结束后,在各加载区的轮迹带和非加载区进行了取芯,通过室内试验对经受不同加速加载次数作用的现役沥青混合料的疲劳特性进行了研究。
1 试验方法简介 1.1 足尺加速加载试验南非研制的MLS66属于最新型的加速加载试验设备,可以模拟真实轮载作用到实际路面上,有效试验长度6.6 m,6组加载轮在一个近似椭圆的轨道上循环运行,最高加载速度达6 000次/h,试验轮可选单轮或双轮,一般的双轮荷载为75 kN,轮架的最高速度可达6 m/s,22 km/h。本次加速加载试验采用的加载速度为MLS66最大加载速度(6 000次/h),采用75 kN的双轮进行加载。
本次加速加载测试区的沥青层结构与足尺加速加载试验状况见表 1。在1号和2号加载区,分别连续进行了63.4和55万次加载,平均每日加载7万次。在3号加载区,当前25万次加载完成后,加载车向前移动半个车身长度并进行了15万次加载。因此,3号加载区可以分为3个加载段,这3个加载段分别经历了25万次、40万次和15万次加速加载作用。
| 加载区 | 沥青层总厚度/cm | 上面层厚度/cm | 中面层厚度/cm | 下面层厚度/cm | 总加载次数/万次 |
| 1号加载区 | 10 | 4 | 5 | — | 63.4 |
| 2号加载区 | 18 | 4 | 5 | 9 | 55 |
| 3号加载区 | 15 | 4 | 5 | 6 | 40 |
1.2 沥青层地震波模量检测
加速加载试验过程中,地震波地质分析仪PSPA(Portable seismic pavement analyzer)被用于测定路面沥青层的地震波模量。地震波路面分析技术是美国德克萨斯州大学开发的无损路面检测技术,可在不破坏路面的前提下获得路面结构的地震波模量,为路面力学计算及施工验收提供重要依据。它的原理是通过测量一个地震波发生器和两个接收器之间传播的瑞利波波速,利用路面材料的泊松比,计算接收器下方路面表层的平均地震波模量。
为了准确评价加速加载作用对轮迹带下地震波模量的影响,各加速加载试验区分别设置了20个地震波模量检测点,其具体设置情况是在两条轮迹的中心和外边缘分别沿着加载方向均匀设置5个检测点。地震波模量检测在每天加载开始前进行,每次检测分别在每个测点分别沿垂直加载方向和平行加载方向各读取10个数据。每次检测共有400个地震波模量检测结果。
1.3 劈裂试验本研究采用的劈裂试验包括劈裂强度试验和劈裂疲劳试验,采用仪器为MTS材料试验仪。劈裂试验试件选用分层切割的10 cm直径芯样。根据我国试验规程[14],劈裂强度试验温度采用15 ℃,加载速率采用50 mm/min,每种工况的沥青混合料分别进行3次平行试验。劈裂疲劳试验温度采用15 ℃,控制模式为应力控制,波形为10 Hz半正弦波,不插入间歇时间,以试件完全断裂为破坏标准,每种工况的沥青混合料根据其劈裂强度选取3个应力水平各进行3次平行试验。
2 现场检测结果与分析 2.1 开裂现象观测结果与分析对于1号加载区,至37.5万次加载,在轮隙中心处可以观测到多段宽度约为1~4 mm的裂缝。至63万次加载,裂缝宽度明显增长,最宽位置的开裂宽度约有15 mm。
对于2号加载区,在经过23.7万次加速加载作用后,轮隙中心处观测到宽度约为1 mm的多段微裂缝,之后裂缝的宽度和长度不断发展,在经过45.8万次加速加载作用后部分裂缝的宽度增大为3~4 mm,在经过55万次加速加载作用后,轮迹带外边缘出现了宽度约1 mm的多段纵向裂缝。
对于3号加载区,在经过13.2万次加速加载作用后,在轮隙位置处开始观测到多段微裂纹,在经过19.4万次加速加载作用后,这些微裂纹的宽度发展至1 mm。在经过35.9万次加速加载作用后,轮隙中心位置处的多段裂缝发展相连,部分裂缝的宽度发展达到2 mm。
加载结束后,在这些裂缝处进行了取芯,发现轮隙间裂缝和轮迹带外边缘裂缝都为自上而下发展的裂缝,且裂缝的发展深度较浅,仅出现在上面层内。
根据3个加速加载试验段的路面开裂状况可以看出,多段纵向微裂缝首先产生在两条轮迹带之间的轮隙中心处,随着加速加载作用次数的增加,多段微裂缝的宽度和长度不断增大并最终互相连通,当达到一定加速加载作用次数后,轮迹带外边缘处开始出现纵向裂缝。同时可以看出,路面厚度越薄的结构越容易出现开裂且裂缝宽度发展越快。

|
| 图 1 路面开裂现象 Fig. 1 Pavement crack phenomenon |
| |
2.2 沥青层地震波模量检测结果与分析
在开始加速加载试验前,于加载段轮迹带上、加载设备内轮迹带外和加载设备外分别取芯埋设了温度传感器。温度传感器埋置方法为在每个试验位置在轮迹下和轮迹外各取一个芯样,然后在各沥青层中间(以2号加载区为例,深度为2,7,14 cm)打孔埋入温度传感器,放回原位,用沥青封好空隙,如图 2所示。温度数据的记录使用无纸温度记录仪24 h记录。

|
| 图 2 温度传感器埋设 Fig. 2 Embedding temperature sensor |
| |
根据APT试验过程中的路面温度检测结果发现,在APT试验的开始阶段,路面温度不断上升,经历了前10万次加载后,路面温度基本保持稳定。由于在各加载区进行地震波模量检测时的路面的温度不同,因此需要对各个加载区的地震波模量检测结果进行温度修正。根据各加载区的地震波模量检测结果,可以由已有研究[15]得到的沥青路面地震波模量随温度变化的规律进行温度修正,见式(1)。
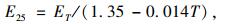
|
(1) |
式中,E25和ET分别为25 ℃和检测温度T下的地震波模量。
各加载区的两条轮迹带分别在轮迹带中心和轮迹带边缘位置处沿加载方向均匀布置有5个地震波模量检测点。对于各加载区的地震波模量检测结果的平均值,根据每次检测时沥青层的平均温度,采用式1对地震波模量进行修正,修正后的地震波模量计算结果见表 2~表 4。
| 累积加载作用次数/万次 | 地震波模量检测结果/GPa | 沥青层平均温度/℃ | 修正后地震波模量/GPa |
| 12.5 | 1.558 | 31.45 | 1.712 |
| 17.5 | 1.408 | 34.35 | 1.620 |
| 20.5 | 1.369 | 34.9 | 1.589 |
| 26.5 | 1.308 | 37.15 | 1.576 |
| 32.5 | 1.364 | 33.7 | 1.553 |
| 37.5 | 1.243 | 40.1 | 1.577 |
| 42 | 1.472 | 29.55 | 1.572 |
| 57 | 1.329 | 33.75 | 1.514 |
| 累积加载作用次数/万次 | 地震波模量检测结果/GPa | 沥青层平均温度/℃ | 修正后地震波模量/GPa |
| 7.2 | 2.732 | 34.9 | 3.173 |
| 11 | 2.416 | 36.7 | 2.887 |
| 17.4 | 2.467 | 37.1 | 2.970 |
| 23.7 | 2.257 | 37.3 | 2.727 |
| 29.9 | 2.095 | 40.7 | 2.684 |
| 36.2 | 1.951 | 42.2 | 2.572 |
| 42.6 | 1.824 | 44.7 | 2.518 |
| 45.8 | 1.859 | 45.3 | 2.596 |
| 52.5 | 1.808 | 45.8 | 2.551 |
| 55 | 1.834 | 43.4 | 2.472 |
| 累积加载作用次数/万次 | 地震波模量检测结果/GPa | 沥青层平均温度/℃ | 修正后地震波模量/GPa |
| 7.2 | 2.309 | 37.5 | 2.798 |
| 13.2 | 2.092 | 38.3 | 2.572 |
| 19.4 | 1.919 | 40.8 | 2.465 |
| 25.3 | 1.884 | 40.4 | 2.404 |
| 30.1 | 1.847 | 40.6 | 2.363 |
根据温度修正后的地震波模量可以建立其随加速加载作用次数的变化规律,如图 3所示。根据图 3可以看出,随着加速加载作用次数的增加,路面沥青层的地震波模量不断降低。沥青层的地震波模量与加速加载作用次数具有较好的指数函数关系。

|
| 图 3 地震波模量随加速加载作用次数的变化 Fig. 3 Seismic wave modulus varying with accelerated loading times |
| |
将APT试验开始前的地震波模量检测结果看作APT试验中路面沥青层的初始地震波模量。由图 3可以看出,1号和2号加载区分别具有最小和最大的初始地震波模量,表明沥青层越厚的路面具有越大的地震波模量,且随加速加载作用次数降低的速率也越快。由于沥青混合料的疲劳损伤可以由其模量随加载作用的衰变规律进行表征,路面沥青层的地震波模量与加速加载作用次数之间较好的相关关系可以作为现役沥青路面疲劳损伤特性的描述。
3 室内试验结果与分析APT试验结束后,在各加载区轮迹带上进行了取芯,通过劈裂试验评价了加速加载作用对现场沥青混合料疲劳抗力的影响。此外,在2号加载区外的未加载位置也进行了取芯,作为用于对照的非加载区混合料。
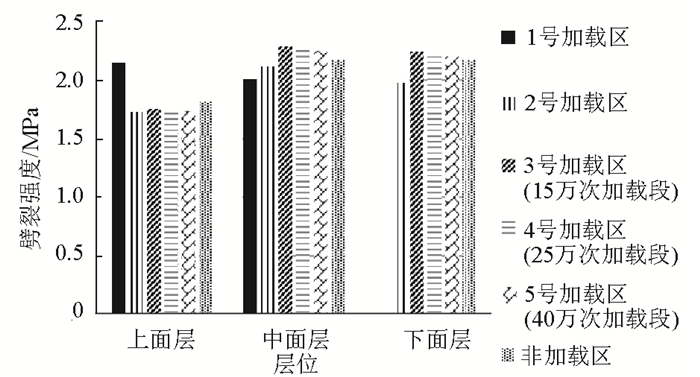
3.1 劈裂强度试验结果与分析根据劈裂强度试验结果可以计算得到各加载区沥青混合料的劈裂强度,见图 4。由图 4可以看出,1号加载区上面层混合料的劈裂强度最高,而其他加载区上面层混合料的劈裂强度总体上随加载次数增加而降低。非加载区各层位混合料的劈裂强度均比2号加载区混合料略高。随着加载次数的增加,3号加载区各层位混合料的劈裂强度略有降低。综上可见,不同加载区的现役沥青混合料的劈裂强度总体上比较接近,并随着加速加载作用次数的增加略有降低。
|
| 图 4 各加载区沥青混合料劈裂强度试验结果 Fig. 4 Result of splitting test on asphalt mixture of each loading section |
| |
3.2 劈裂疲劳试验结果与分析
基于现役沥青混合料的劈裂强度,选取了不同应力比,进行了劈裂疲劳试验。为了保证疲劳寿命介于合理的区间,体现出疲劳破坏的特性,根据文献[13]所推荐的沥青混合料劈裂疲劳试验应力比,本研究对于上面层混合料选取的应力比为0.3, 0.4, 0.5,对于中、下面层混合料选取的应力比为0.25, 0.3, 0.4。
劲度模量是反映沥青混合料在特定温度和加载条件下的应力应变关系的参数。研究沥青混合料劲度模量的变化规律对认识其疲劳性能具有重要作用。根据规范[14],劲度模量计算采用下式:
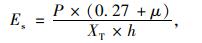
|
(2) |
式中,Es为劲度模量;P为竖向荷载峰值;μ为泊松比;XT为水平径向变形幅值;h为试件高度。
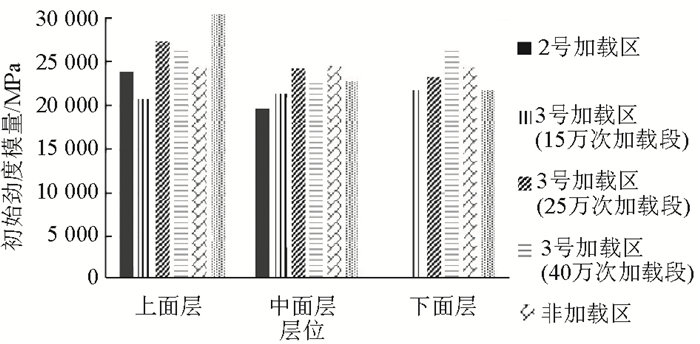
对于沥青混合料的疲劳试验,通常可以将第50周期的劲度模量作为其初始劲度模量。图 5给出了在应力比为0.3时,各加载区各层位沥青混合料的初始劲度模量。
|
| 图 5 各加载区沥青混合料劈裂疲劳试验初始劲度模量 Fig. 5 Initial stiffness modulus of asphalt mixture in each loading section obtained by splitting fatigue test |
| |
由图 5可以看出,随着加速加载作用次数的增加,上面层沥青混合料的初始劲度模量总体上不断降低。而各加载区中、下面层沥青混合料的初始劲度模量总体上比较接近。对比各沥青层混合料的初始劲度模量变化规律可以看出,加速加载作用对上面层混合料疲劳抗力的影响比中、下面层沥青混合料更加显著。
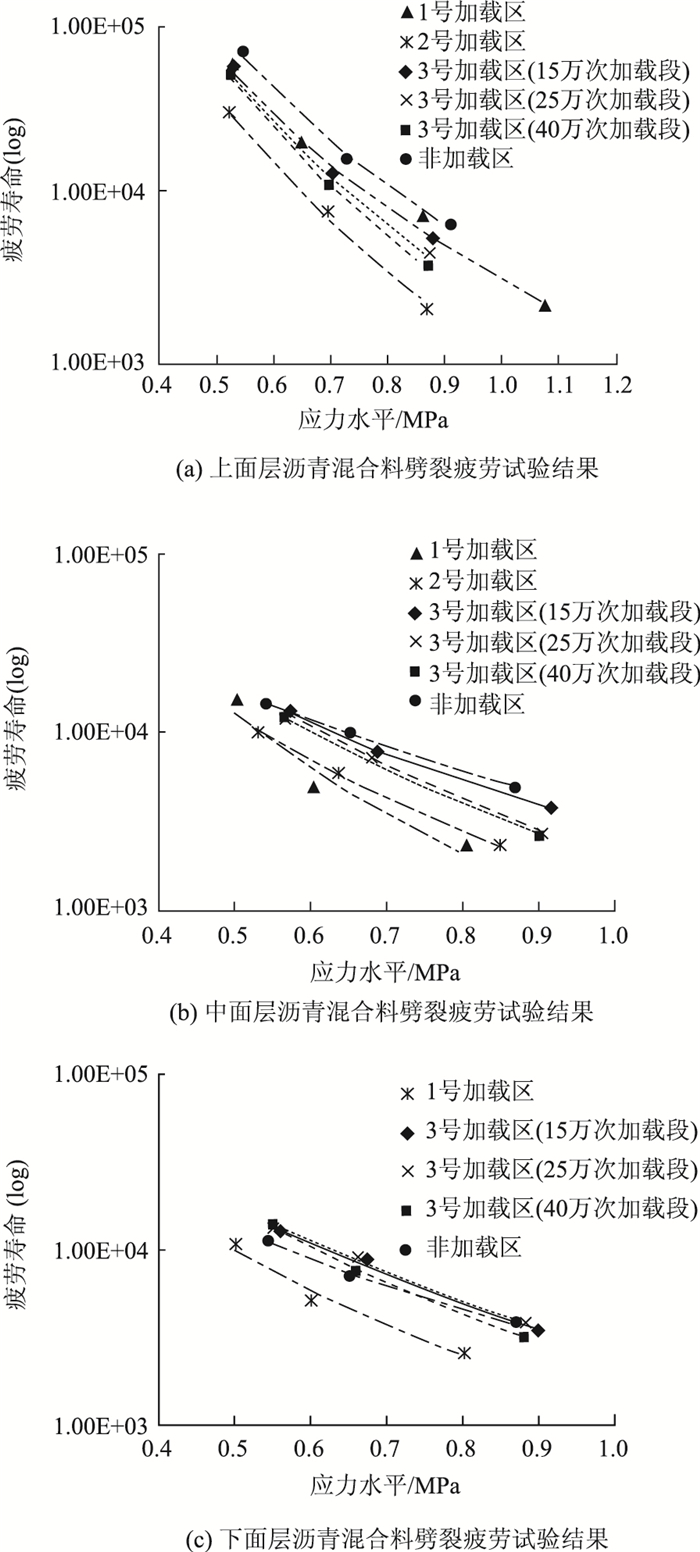
劈裂疲劳试验过程中,试件完全破坏时所对应的加载循环次数可以作为其疲劳寿命。根据不同应力水平下劈裂疲劳试验的结果,可以得到各加载区沥青混合料的劈裂寿命与试件中心拉应力的关系,见图 6。
|
| 图 6 各加载区沥青混合料劈裂疲劳试验结果 Fig. 6 Result of splitting fatigue test on asphalt mixture in each loading section |
| |
由图 6(a)可以看出,在相同的应力水平下,随着加速加载作用次数的增加,现役沥青混合料的疲劳抗力逐渐降低。其中,2号加载试验段上面层沥青混合料具有最低的劈裂强度和初始劲度模量,且该加载区在APT试验过程中的平均路面温度最高,因此其疲劳寿命最低。
由图 6(b)可以看出,在相同的应力水平下,非加载区和3号加载区中面层混合料的疲劳寿命最长。1号加载区中面层混合料的劈裂强度和初始劲度模量最低导致其疲劳寿命最短。
由图 6(c)可以看出,在相同的应力水平下,3号加载区下面层混合料的疲劳寿命最长。而2号加载区下面层混合料的劈裂强度最低导致其疲劳寿命最短。
综上可以看出,尽管各个加载区具有不同的沥青层厚度和加载工况,相同层位沥青混合料的疲劳寿命总体上随着加速加载作用次数的增加而降低,且劈裂强度和初始劲度模量较低的在役沥青混合料具有相对较低的疲劳寿命。
采用现象学疲劳模型回归现役混合料疲劳寿命与应力水平的关系,见式(3)。
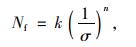
|
(3) |
式中, Nf为疲劳寿命;σ为应力;k和n为模型参数。
根据式(3)可以拟合得到各加载区各层位沥青混合料的疲劳模型参数,见表 5。由表 5可以看出,随着加速加载作用次数的增加,各加载区沥青混合料的疲劳模型参数“k”总体上不断变小,导致疲劳寿命不断降低。相比于中面层和下面层混合料,上面层混合料的疲劳模型参数“k”随加速加载作用次数的变化更加明显,表明加速加载作用对上面层混合料的疲劳性能的影响更为显著。
| 层位 | 非加载区 | 3号加载区(15万次加载段) | 3号加载区(25万次加载段) | 3号加载区(40万次加载段) | 2号加载区 | 1号加载区 | |||||||||||
| k | n | k | n | k | n | k | n | k | n | k | n | ||||||
| 上面层 | 4 246.0 | 4.721 | 4 052.7 | 4.197 | 3 708.4 | 4.157 | 2 467.5 | 4.687 | 856.7 | 5.389 | 3 074.7 | 4.408 | |||||
| 中面层 | 3 050.5 | 2.684 | 2 065.0 | 3.723 | 2 403.2 | 3.129 | 2 149.0 | 3.368 | 2 008.0 | 2.641 | 961.6 | 3.840 | |||||
| 下面层 | 1 904.6 | 2.609 | 2 770.8 | 2.990 | 2 770.3 | 2.750 | 2 744.4 | 2.702 | 1 379.6 | 2.459 | — | — | |||||
根据劈裂疲劳试验的初始劲度模量和疲劳寿命变化规律可以看出,随着加速加载作用次数的增加,沥青层的疲劳抗力总体上不断下降,这与现场路面沥青层地震波模量的变化规律是一致的。劈裂疲劳试验能够更好地描述加速加载作用对不同层位混合料疲劳特性的影响。上面层混合料的疲劳抗力随加载作用次数增加而衰减的程度相比中、下面层混合料更显著。
3.3 现役沥青混合料剩余疲劳寿命预估根据国内外对于现场沥青混合料疲劳寿命预估方法的研究[16-17],通常的做法是基于转换因子建立起沥青混合料室内疲劳试验结果与现场疲劳性能之间的联系。
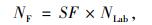
|
(4) |
式中,NF为现场疲劳寿命; NLab为室内疲劳寿命; SF为转换因子。
在实际路面结构中,沥青混合料在轮载与温度的共同作用下会出现一系列的应变响应,因此需要根据一定累计损伤假设对这些不同状况下的响应进行考虑。一种常用的方法是采用荷载循环比的线性累加,即Miner法则[18]来进行累计损伤的计算。Miner法则的基本原理如式(5)所示。

|
(5) |
式中,ni为在应力水平i下交通荷载实际作用次数,Ni为在应力水平i下容许的荷载作用次数。
对于本研究中经历了不同加速加载作用次数的沥青混合料,基于转换因子将室内疲劳寿命转换为现场剩余疲劳寿命,根据Miner法则可以建立如下关系:

|
(6) |
式中,NLab1为经历了N1次加速加载作用的现役沥青混合料的室内疲劳寿命; NLab2为经历了N2次加速加载作用的现役沥青混合料的室内疲劳寿命。
对式(6)进行整理,得到现场与室内疲劳寿命的转换因子的计算式。

|
(7) |
基于2号加载区及在其附近非加载区所取的现役沥青混合料的劈裂疲劳试验结果,可以对不同结构层位的沥青混合料的转换因子进行计算,并在此基础上对现役沥青混合料的剩余疲劳寿命进行预估。本研究中,以0.4应力比下的劈裂疲劳试验结果进行计算分析, 分别计算上面层、中面层和下面层沥青混合料的转换因子并根据式(4)对现役沥青混合料的剩余疲劳寿命进行预估,结果见表 6。
| 结构层位 | 非加载区劈裂疲劳寿命 | 55万次加载区劈裂疲劳寿命 | 转换因子 | 剩余疲劳寿命预估结果/次 |
| 上面层 | 16 484 | 7 154 | 58.95 | 421 725 |
| 中面层 | 4 614 | 2 995 | 339.71 | 1 017 450 |
| 下面层 | 2 900 | 2 370 | 1 037.74 | 2 458 396 |
根据表 6可以看出,对于上面层沥青混合料,在0.4应力比下的一次劈裂疲劳试验加载等效于58.95次加速加载作用,对于已经历55万次加速加载作用的2号加载区轮迹带下沥青混合料,其剩余疲劳寿命约为42万次加速加载作用。而对于中面层和下面层沥青混合料,其转换因子更大,预估得到的剩余疲劳寿命,即现役沥青混合料疲劳失效时所需的额外加速加载作用次数也更多。
4 结论(1) 在加速加载试验的初期阶段,双轮的轮隙间首先出现了多段微裂缝,随着加载次数的增加,轮隙间微裂缝逐渐发展贯通,而在一定加速加载作用次数之后,轮迹带外边缘处开始出现多段平行于轮迹带的裂缝。
(2) 随着加速加载作用次数的增加,路面沥青层的地震波模量不断降低。沥青层的地震波模量与加速加载作用次数具有较好的指数函数关系,可以作为现役沥青路面疲劳损伤特性的描述。
(3) 不同加载区的现役沥青混合料的劈裂强度总体上比较接近,随着加速加载作用次数的增加,现役沥青混合料的劈裂强度总体上具有降低的趋势,但变化程度不大。
(4) 现役沥青混合料的劈裂疲劳试验结果表明,随着加速加载作用次数的增加,沥青混合料的初始劲度模量和劈裂疲劳寿命总体上不断下降,且加速加载作用对上面层混合料疲劳抗力的影响相比中、下面层混合料更为显著。
(5) 基于Miner法则可以建立现役沥青混合料的劈裂疲劳试验结果与实际加载作用次数间的关系,并对现役沥青混合料的剩余疲劳寿命进行了预估。
| [1] |
郝大力.路面性能的评价与分析研究[D].西安: 长安大学, 2000. HAO Da-li. Study on Pavement Performance Evaluation and Analysis[D]. Xi'an: Chang'an University, 2000. http://d.wanfangdata.com.cn/Thesis_Y410487.aspx |
| [2] |
孟书涛. 半刚性基层沥青路面性能的加速加载试验研究[J]. 公路交通科技, 1997, 14(1): 59-64. MENG Shu-tao. Research on the Bituminous Pavement Performance of Semi Rigid Base under the Accelerated Loading Facility (ALF)[J]. Journal of Highway and Transportation Research and Development, 1997, 14(1): 59-64. |
| [3] |
YEO I, SUH Y, MUN S, et al. Development of a Remaining Fatigue Life Model for Asphalt Black Base Through Accelerated Pavement Testing[J]. Construction & Building Materials, 2008, 22(8): 1881-1886. |
| [4] |
MATEOS A, AYUSO P, JAUREGUI C. Shift Factors for Asphalt Fatigue from Full-scale Testing[J]. Transportation Research Record, 2011, 2225: 128-136. |
| [5] |
WU J T, YE F, WU Y T. Analysis on Three-direction Strain of Asphalt Pavement Structure Based on Accelerated Pavement Testing[J]. Advanced Materials Research, 2011, 255: 3426-3431. |
| [6] |
陈少幸, 张肖宁, 孟书涛, 等. 基于ALF加速加载试验的沥青层疲劳损伤[J]. 公路交通科技, 2012, 29(1): 18-22. CHEN Shao-xing, ZHANG Xiao-ning, MENG Shu-tao, et al. Fatigue Damage in Asphalt Layer Based on ALF Accelerated Loading Test[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 18-22. |
| [7] |
JI X P, ZHENG N X, HOU Y Q, et al. Application of Asphalt Mixture Shear Strength to Evaluate Pavement Rutting with Accelerated Loading Facility (ALF)[J]. Construction and Building Materials, 2013, 41: 1-8. |
| [8] |
JURADO M, GIBSON N, CELAYA M, et al. Evaluation of Asphalt Damage and Cracking Development with Seismic Pavement Analyzer[J]. Transportation Research Record, 2012, 2304: 47-54. |
| [9] |
陈少幸.沥青路面疲劳性能加速加载试验研究[D].广州: 华南理工大学, 2007. CHEN Shao-xing. Study of Fatigue Performance of Asphalt Pavement by Accelerated Loading Test[D]. Guangzhou: South China University of Technology, 2007. http://d.wanfangdata.com.cn/Thesis/Y1184147 |
| [10] |
ZOU J, ROQUE R, BYRON T. Effect of HMA Ageing and Potential Healing on Top-down Cracking Using HVS[J]. Road Materials and Pavement Design, 2012, 13(3): 518-533. |
| [11] |
SHU X, HUANG B, VUKOSAVLJEVIC D. Laboratory Evaluation of Fatigue Characteristics of Recycled Asphalt Mixture[J]. Construction and Building Materials, 2008, 22(7): 1323-1330. |
| [12] |
HUANG B, SHU X, VUKOSAVLJEVIC D. Laboratory Investigation of Cracking Resistance of Hot-mix Asphalt Field Mixtures Containing Screened Reclaimed Asphalt Pavement[J]. Journal of Materials in Civil Engineering, 2011, 23(11): 1535-1543. |
| [13] |
许志鸿, 李淑明, 高英, 等. 沥青混合料疲劳性能研究[J]. 交通运输工程学报, 2001, 1(1): 20-24. XU Zhi-hong, LI Shu-ming, GAO Ying, et al. Research on Fatigue Characteristic of Asphalt Mixture[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 20-24. |
| [14] |
JTG E20-2011, 公路工程沥青及沥青混合料试验规程[S]. JTG E20-2011, Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering[S]. |
| [15] |
NAZARIAN S, ALVARADO G. Impact of Temperature Gradient on Modulus of Asphaltic Concrete Layers[J]. Journal of Materials in Civil Engineering, 2007, 18(4): 492-499. |
| [16] |
AL-QADI I L, NASSAR W N. Fatigue Shift Factors to Predict HMA Performance[J]. International Journal of Pavement Engineering, 2003, 4(2): 69-76. |
| [17] |
YU J, TSAI B W, ZHANG X, et al. Development of Asphalt Pavement Fatigue Cracking Prediction Model Based on Loading Mode Transfer Function[J]. Road Materials & Pavement Design, 2012, 13(3): 501-517. |
| [18] |
RAJBONGSHI P, DAS A. A Systematic Approach of Field Calibration of Fatigue Equation for Asphalt Pavements[J]. Road Materials and Pavement Design, 2009, 10(1): 109-124. |
 2020, Vol. 37
2020, Vol. 37
