扩展功能
文章信息
- 高大威, 郑腾飞, 李向阳
- GAO Da-wei, ZHENG Teng-fei, LI Xiang-yang
- 基于有限元法的螺纹参数化建模与有效性分析
- Analysis on Parametric Modeling of Bolt Based on FEM and Efficiency
- 公路交通科技, 2019, 36(12): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 152-158
- 10.3969/j.issn.1002-0268.2019.12.019
-
文章历史
- 收稿日期: 2018-03-09
螺纹联接是机械零部件组合中常见的一种联接方式, 它有着装配拆卸方便、经济性好等优点。对于汽车行业, 随着技术的飞速发展, 在综合实力愈发接近下, 振动噪声舒适性逐渐成为吸引消费者的重要因素。而螺纹联接作为汽车零部件联接的4种(螺纹联接、焊接、铆接、粘胶联接)常用方式之一, 是汽车上应用最为广泛的一种紧固形式, 直接影响着车身和底盘系统的连接刚度, 对整车性能起到至关重要的作用。尤其在汽车底盘上的螺纹联接, 由于车身地板钣金冲压成型工艺制造精度以及成型面的复杂性等问题, 造成在螺栓预紧过程中被夹持的钣金之间产生反向变形力, 导致螺栓预紧力下降, 进而紧固力矩不足, 使得在底盘与车身联接处产生窜动异响甚至导致安全事故发生。长期以来由于螺纹联接结构的重要性和复杂性, 国内外相关学者对螺纹连接可靠性, 紧固理论等一直进行着研究和讨论, 但在螺纹联接预紧力衰退机理上一直缺少统一认识。
有限元分析法是对于结构力学分析迅速发展起来的一种现代计算方法。几十年来, 有限元法理论及其算法趋于成熟, 在求解复杂工程问题方面应用非常广泛, 为螺纹联接力学行为分析提供了一种有效途径。而有限元基本思想是把连续的几何结构离散成有限个单元, 并在每一个单元中设定有限个节点, 从而将连续体看作仅在节点处相连接的一组单元的集合体, 因此进行有限元仿真分析的前提是建立尽可能精确又便于计算实现的单元模型[1]。建立的有限元模型通常有轴对称模型[2]、四面体网格自由划分模型[3]、六面体网格模型[4-8]。由于轴对称模型是对螺纹联接简化的一种模型, 忽略了螺纹升角, 不能很好地反映螺纹松动过程; 而四面体网格模型计算精度较差, 不适合对螺纹啮合表面进行应力应变分析。在螺纹有限元模型有效性验证上, 广泛以日本学者YAMATOTO提出的螺纹负载理论计算方法为参考, 其中陈海平等[2]在螺纹副承载分布规律研究、以及何竞飞等[5]提出的螺栓联接精确建模方法中均采用了YAMATOTO理论法进行有限元模型的有效性验证, 并都做了光弹试验, 结果一致表明以YAMATOTO理论法进行螺纹联接有限元模型有效性验证具有可靠性。
本研究利用螺纹轮廓数学公式, 获取螺纹轮廓截面, 通过划分初始层横截面上的壳单元和结合螺纹基本牙型参数, 实现无螺纹三维实体模型的六面体网格参数化建模。为验证模型的有效性, 以一定预紧力作用下通过YAMATOTO理论法计算的各扣螺纹负载结果为参考, 在满足设定参数相同条件下进行有限元法仿真计算, 两种方法的计算结果相吻合, 验证了模型的有效性。为螺纹联接承载分布规律、预紧力松退机理及螺纹副设计等研究提供了一种易于实现的螺纹有限元参数化建模方法。
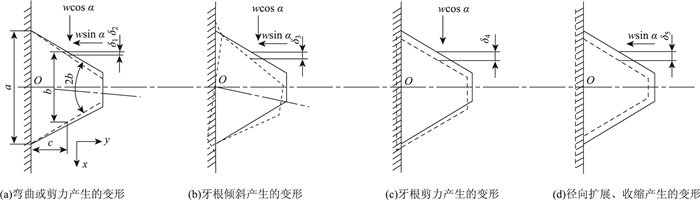
1 螺纹联接力学行为传统理论研究螺纹联接结构应该具有足够的夹紧力防止被夹持件分开或出现泄露, 如果还承受剪切载荷, 也需要防止被夹持件之间出现相互滑移[9-17], 影响比较深远的是日本YAMATOTO提出的一系列理论[18]。但是YAMATOTO理论建立的前提假设是:在对螺纹牙的弹性变形和螺纹牙轴向力分布的分析时, 忽略考虑螺纹面和支撑面上摩擦力的影响, 且不考虑材料的塑形变形。在此假设条件下, 将螺纹牙截面看作平面横梁, 然后将引起螺纹牙弹性变形的因素分为弯曲产生的变形、剪切力产生的变形、牙根倾斜产生的变形、牙根剪切变形产生的变形和径向扩展、收缩产生的变形5个部分, 如图 1(a)所示, 在梯形截面横梁y=c处位置上每单位宽度受一为w(x方向分力为wcos α, y方向分力为wsin α)的斜面垂直力, 求出各变形因素在横梁y=c处产生的x方向上的变形, 根据各部分变形叠加推出螺纹牙的变形。
|
| 图 1 各种原因造成的螺纹牙变形示意图 Fig. 1 Schematic diagram of deformations of thread caused by various causes |
| |
(1) 弯曲产生的变形δ1、剪切产生的变形δ2:如图 1(a)中虚线变形所示, 计算由弯曲力矩产生的挠度δ1时, 假设梯形截面横梁变形为平面变形; 计算由剪切力产生的挠度δ2时, 假设梯形任意截面上的剪切应力按抛物线分布。则
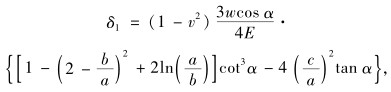
|
(1) |
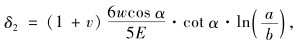
|
(2) |
式中, E为材料的纵向弹性模量; v为材料的泊松比。
(2) 牙根倾斜产生的变形δ3:由螺纹牙受弯曲力矩T=cwcos α-(b/2)wsin α, 使螺纹牙根底面发生倾斜, 如图 1(b)中虚线所示。力作用点处的倾斜变形为:
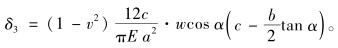
|
(3) |
(3) 牙根剪切变形产生的变形δ4:如图 1(c)中虚线所示, 假设牙根截面上剪切应力wcos α/a均匀分布, 则由剪切变形引起的O点沿x方向的位移与力作用点处位移一致, 所以
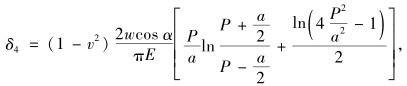
|
(4) |
式中P为螺纹的螺距。
(4) 径向扩展、收缩产生的变形δ5:螺纹牙作用力w的径向分力为wsin α, 螺栓沿径向收缩, 螺母向外扩展, 所以对于外螺纹和内螺纹轴向变形分别为
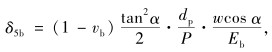
|
(5) |
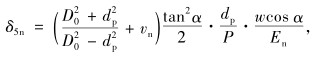
|
(6) |
式中, 外螺纹和内螺纹材料的纵向弹性模量、泊松比分别为Eb, vb和En, vn; dp为螺纹直径; D为螺母。
根据以上各变形分量叠加可得外螺纹与内螺纹的变形分别为:
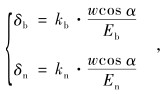
|
(7) |
式中, kb为外螺纹弹性变形综合系数; kn为内螺纹弹性变形综合系数。
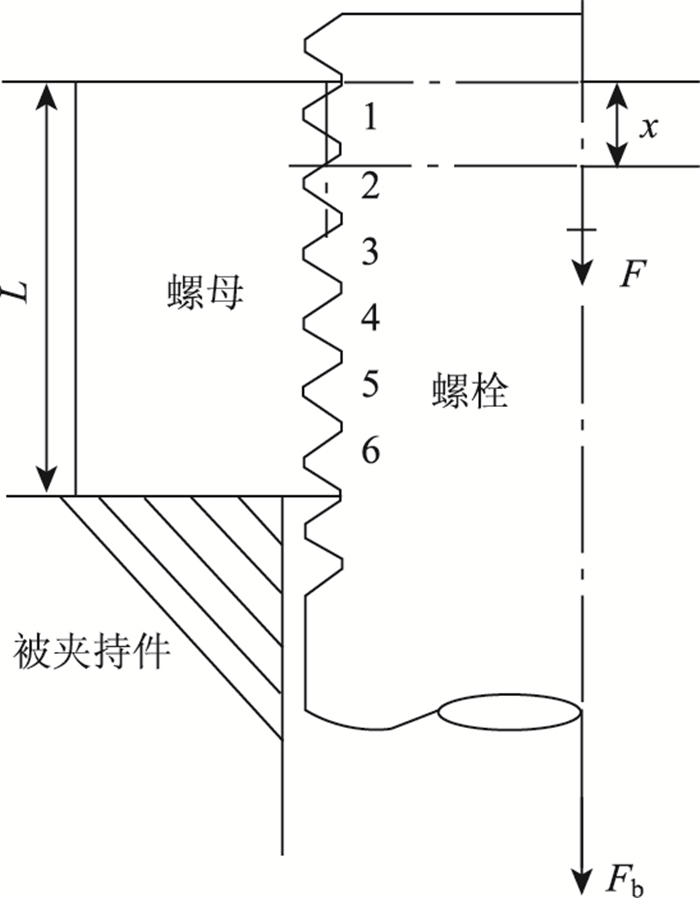
上述理论推导由于忽略了材料的塑形变形及界面之间的摩擦力, 使得计算结果与实际工况下螺纹负载分布具有一定误差, 但在对螺纹负载分布规律研究和对螺纹有限元模型有效性验证上仍然具有重要的参考意义。如图 2所示螺纹联接, Fb为螺栓杆所受轴向载荷, 设以螺母自由面为起点, 距离自由面距离为x的螺纹截面轴向负载为F。
|
| 图 2 啮合螺纹部分轴向力示意图 Fig. 2 Schematic diagram of axial force of meshing thread part |
| |
根据YAMATOTO螺纹牙轴向力分布理论, 得到F和Fb关系公式如下:
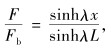
|
(8) |
式中, 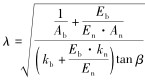
式中, L为螺母高度; Ab为螺栓截面积; An为螺母截面积; Eb为外螺纹材料纵向弹性模量; En为内螺纹材料纵向弹性模量; β为螺纹升角。
2 螺纹联接有限元参数化建模在螺纹联接的有限元分析研究中, 由于螺纹六面体网格划分较为复杂, 大部分采用梁单元模型、实体螺杆模型、轴对称模型和四面体单元模型等, 这些模型存在着过简、计算精度差、未考虑螺纹及螺纹升角等问题, 因此本研究对螺纹六面体网格参数化建模方法进行研究。前人在螺纹联接上实现螺纹参数化精确建模主要有两种方式:一种是利用螺纹轮廓数学模型, 获取几何参数, 建立可实现理想六面体网格划分的有限元模型, 此方式网格划分质量依赖于实体模型精度和对实体的精细分割, 另外在对实体进行扫掠生成网格时的质量控制过程较为繁琐[5]。另一种是利用螺纹轮廓数学模型, 运用MTALAB软件计算出螺纹区域上所有节点坐标和节点编号, 导入有限元软件ABAQUS后对不同区域模型进行布尔运算并压缩重合节点, 此方式前提需要精确的各单元节点编号和坐标公式推导, 并需要预先判断网格大小和分布, 此外需要具有一定的编程能力[6], 整体网格质量仍然依赖于初始层螺纹横截面壳单元的布局。对于一般螺纹紧固件, 本研究利用螺纹轮廓数学模型, 获取螺纹轮廓截面并合理布局截面上周向网格分布; 结合螺纹牙型几何参数, 在保留牙型最小特征尺寸的基础上合理判断轴向网格分布, 实现无螺纹三维实体模型的六面体网格参数化建模。本研究提出的螺纹六面体网格参数化建模方法同样是在利用螺纹轮廓数学模型的基础上, 直接以最关键的螺纹横截面壳单元划分为关注对象, 省去了螺纹实体建模, 也无需进行单元和节点编号及坐标计算, 降低了螺纹六面体网格参数化建模的复杂度。
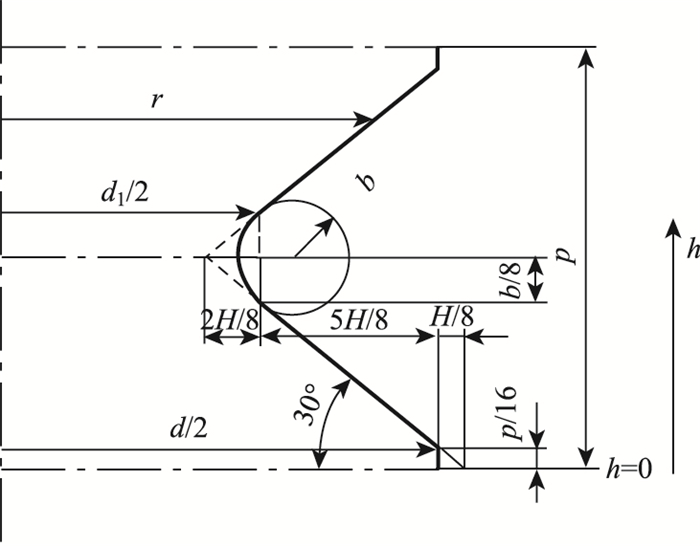
如图 3螺纹基本牙型示意图所示, 根据牙型线到螺纹轴线的距离r具有的一定规律性和周期性, 在半各螺距P/2内, 可将螺纹牙型线分为3个部分:牙顶、牙侧、牙底。
|
| 图 3 螺纹基本牙型示意图 Fig. 3 Schematic diagram of basic thread profile |
| |
则外螺纹牙型线到螺纹轴线距离r的表达式为:
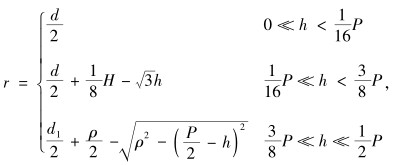
|
(9) |
式中, 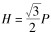
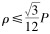
同理, 忽略内螺纹牙底弧线, 则内螺纹牙型线到螺纹轴线距离R的表达式为:
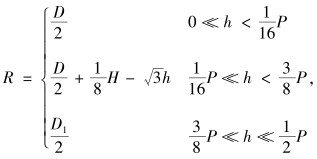
|
(10) |
式中, D为内螺纹外径; D1为内螺纹内径。
由图 3螺纹基本牙型还可得知在1个螺距内外螺纹牙顶为最小特征, 因此在对螺纹轴向分布网格时应保留牙顶特征。设在轴向尺寸为1/8P的牙顶上划分n层网格, 则1个螺距内轴向网格分布为8n层, 相邻层间夹角为360/8n度, 为保证相邻层之间能通过旋转360/8n度后单元节点达到完全重合, 周向螺纹轮廓线上网格分布数量应为8nk个, 这也就使得后一层单元网格能完全由前一层得到, 以此确保螺纹的螺旋特性。其中, n和k均为正整数。
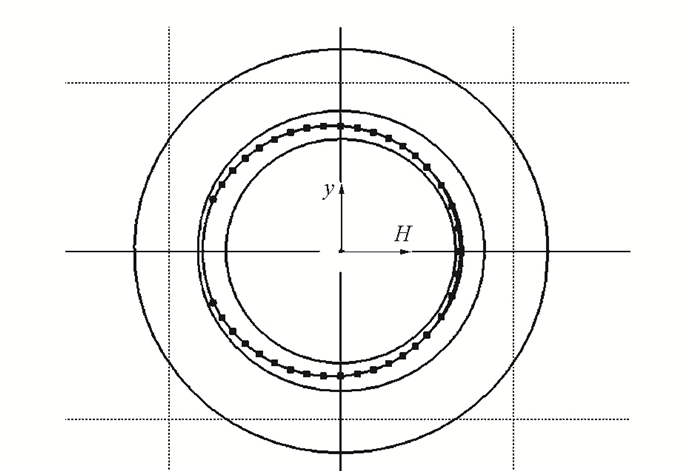
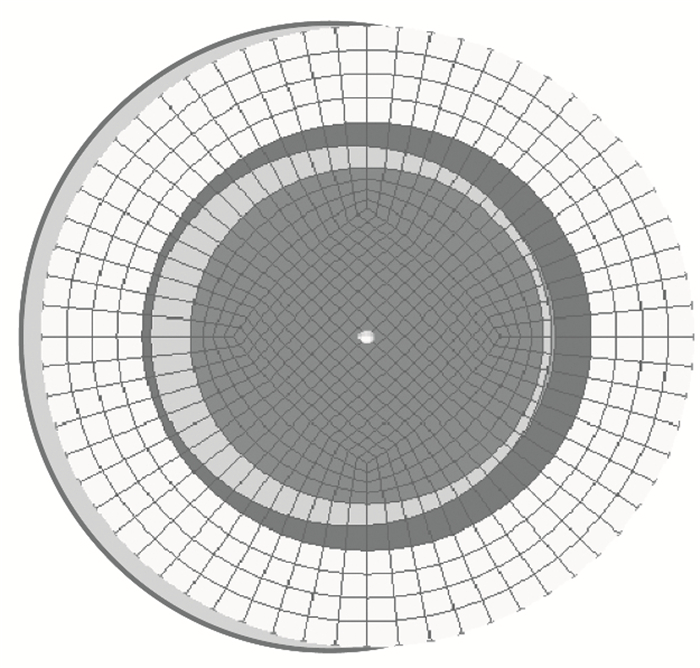
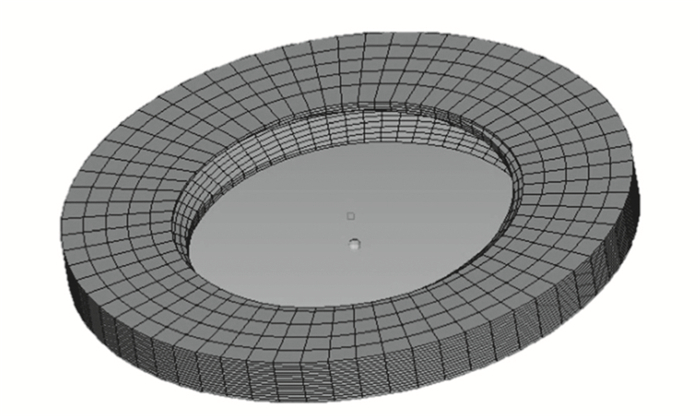
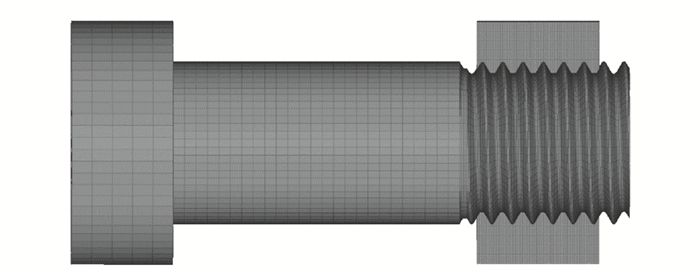
采用上述方法对螺距为2 mm的M16标准螺栓螺母进行有限元建模, 根据螺纹线距离表达式合理均匀取点, 再以样条线连接作出螺纹轮廓线。为了保证所建螺纹网格周向单元均匀分布、质量更优且减少后续操作步骤, 分别在轮廓线内、外侧内建立两条圆线且使其与轮廓线的最小距离相同, 如图 4所示。在HyperMesh中将两条新建圆线的周向上分别均匀排布64个节点, 即对应将螺纹轮廓线在周向上均分成了64份, 划分出壳单元网格, 如图 5所示。轴向上在表征螺纹最小特征尺寸的牙顶上划分2层网格, 则一个螺距内轴向网格分布为16层, 相邻层间夹角为22.5°。对已生成的初始层壳单元网格进行拉伸、复制、平移、旋转操作, 并对属于螺纹牙侧部分上的最外层网格节点做位置恢复, 最终得到一个螺距的完整内、外螺纹六面体精细网格, 如图 6、图 7所示。由螺纹牙型的周期性对一个牙型网格进行相应复制、平移操作即可获得完整内、外螺纹六面体网格。对于螺杆和螺纹连接部分, 采用6层分布逐级消除图 5所示螺纹周向上的小单元, 合理完成过渡, 最终获得含有6圈啮合螺纹的有限元模型, 如图 8所示。
|
| 图 4 螺纹轮廓线 Fig. 4 Thread profile |
| |
|
| 图 5 螺纹横截面壳单元划分 Fig. 5 Shell element division of thread cross-section |
| |

|
| 图 6 一个螺距外螺纹六面体网格划分 Fig. 6 Hexahedral meshing of single pitch external thread |
| |
|
| 图 7 一个螺距内螺纹六面体网格划分 Fig. 7 Hexahedral meshing of single pitch internal thread |
| |
|
| 图 8 含6圈啮合螺纹的有限元模型 Fig. 8 FE model with 6-ring meshing thread |
| |
利用上述建模方法与其他建模方法对GB/T5782—2000M16x95螺栓建模对比如表 1所示。
| 建模方法 | 单元类型 | 网格划分方法 | 单元总数/个 | 节点总数/个 |
| 传统建模方法 | 四面体 | 根据实体自由划分free | 865 539 | 230 080 |
| 专利CN102332047A方法 | 六面体 | 根据实体模型扫描(Mapped) | 217 881 | 250 040 |
| 本研究建模方法 | 六面体 | 无实体模型, 壳单元拉伸、复制、旋转 | 131 072 | 144 141 |
3 螺纹有限元模型的有效性验证
在有限元仿真分析软件ABAQUS中[12], 为与YAMATOTO理论法计算结果作对比分析, 需要满足预紧力大小等参数相同, 且考虑当接触摩擦系数为零时因滑移量过大导致仿真计算难以收敛的问题, 这里定义接触摩擦系数均为0.05, 螺纹横截面积Ab取以有效直径dp=d2为直径的圆柱横截面积, 弹性模量E=210 GPa, 忽略材料的塑性变形, 设定螺栓预紧轴力Fb=10 kN, 啮合螺纹扣数N=6, 即螺纹轴向力Fb将分布在6扣螺纹上。通过有限元仿真得到的螺栓、螺母应力云图如图 9、图 10所示, 可以看出螺纹牙底为应力集中区域, 且越靠近被夹持件越明显, 说明螺纹负载并不是均匀分布, 靠近被夹持件的螺纹负载有增大趋势; 在后处理VIEW CUT模块中提取内螺纹轴向负载, 外螺纹负载以相同方法提取, 得到的各扣螺纹轴向力F结果如表 2所示; 同时根据YAMATOTO理论公式(8)计算出各螺纹负载。

|
| 图 9 外螺纹应力分布云图(单位:MPa) Fig. 9 Nephogram of stress distribution of external thread(unit:MPa) |
| |

|
| 图 10 内螺纹应力分布云图(单位:MPa) Fig. 10 Nephogram of stress distribution of internal thread(unit:MPa) |
| |
| 螺距序号 | x/mm | 外螺纹各扣螺纹负载/kN | 内螺纹截面轴向力/kN | 外螺纹截面轴力与螺杆拉伸力比 |
| 1 | 2 | 0.838 | 0.885 | 0.050 8 |
| 2 | 4 | 1.052 | 1.912 | 0.156 4 |
| 3 | 6 | 1.352 | 3.243 | 0.280 9 |
| 4 | 8 | 1.768 | 4.982 | 0.427 2 |
| 5 | 10 | 2.278 | 7.213 | 0.612 2 |
| 6 | 12 | 2.712 | 10 | 0.852 7 |
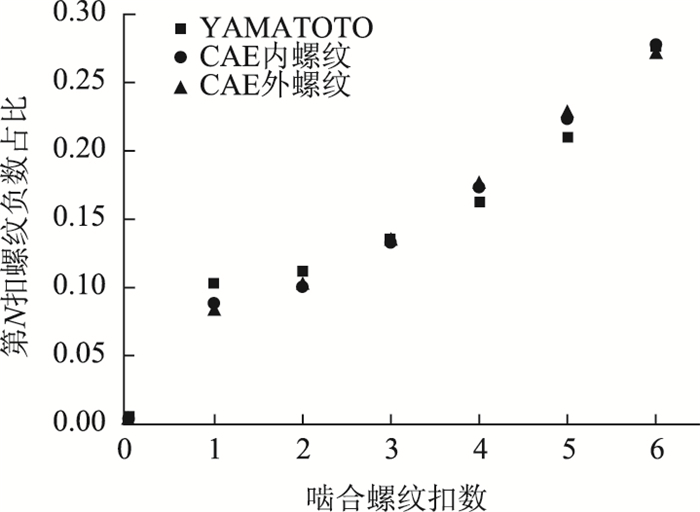
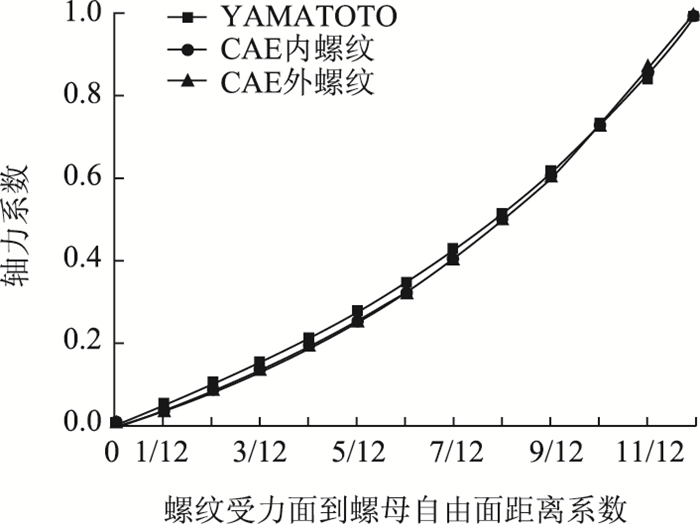
对有限元法与YAMATOTO理论法计算得到的各扣螺纹轴向负载结果进行对比验证, 各扣螺纹负载与轴向预紧力占比分布如图 11所示、螺纹区域内不同螺纹截面的轴力系数分布如图 12所示, 可以看出两种方法在各扣螺纹负载情况以及不同螺纹截面轴力系数分布上均具有吻合性, 且内、外螺纹负载几乎完全重合符合实际情况, 表明本研究所提出的螺纹六面体网格参数化建模方法具有有效性。
|
| 图 11 各扣螺纹负载占比分布验证 Fig. 11 Verification of distribution of thread load proportions |
| |
|
| 图 12 不同螺纹截面负载系数分布验证 Fig. 12 Verification of distribution of load coefficients of different thread sections |
| |
4 结论
本研究提出了一种易于实现的螺纹六面体网格参数化建模方法。在一定预紧力作用下, 通过进行YAMATOTO理论法计算和有限元法仿真计算, 并将结果作对比验证得出以下结论:
(1) 通过计算分析得出螺纹各扣负载情况具有不均匀性, 且越靠近被夹件的螺纹负载占比越高。当螺纹摩擦系数取0.05时, 得到第3扣螺纹的轴力系数在0.3~0.4之间, 即靠近被夹件的第4~6扣螺纹轴向负载占总负载的60%~70%, 其中第6扣螺纹的负载约占总负载的30%。
(2) 通过有限元仿真计算与YAMATOTO法理论计算, 在各扣螺纹负载情况与不同螺纹截面轴力系数分布规律上, 两种方法的计算结果相吻合, 表明根据本研究提出的螺纹六面体网格参数化建模方法具有有效性。
| [1] |
张建伟. 有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2014. ZHANG Jian-wei. Finite Element Analysis: From Entry to Mastery[M]. Beijing: China Machine Press, 2014. |
| [2] |
陈海平, 曾攀, 方刚, 等. 螺纹副承载的分布规律[J]. 机械工程学报, 2010, 46(9): 171-178. CHEN Hai-ping, ZENG Pan, FANG Gang, et al. Load Distribution of Bolted Joint[J]. Journal of Mechanical Engineering, 2010, 46(9): 171-178. |
| [3] |
IZUMI S, YOKOYAMA T, IWASAKI A, et al. Three-dimensional Finite Element Analysis of Tightening and Loosening Mechanism of Threaded Fastener[J]. Engineering Failure Analysis, 2005, 12(4): 604-615. |
| [4] |
杨广雪, 谢基龙, 谢云叶. 基于有限元的一种新型螺母的防松机理研究[J]. 工程力学, 2010, 27(12): 224-228, 243. YANG Guang-xue, XIE Ji-long, XIE Yun-ye. Study on Mechanism of Anti-loosening of a New Type of Nut Based on FEM[J]. Engineering Mechanics, 2010, 27(12): 224-228, 243. |
| [5] |
何竞飞, 杨鸣, 万闯建. 螺栓联接的精确建模与有限元分析[J]. 机械设计与研究, 2014, 30(4): 62-65. HE Jing-fei, YANG Ming, WAN Chuang-jian. Bolt Joint Modeling with Accurate Geometry and Finite Element Analysis Based on ANSYS[J]. Machine Design and Research, 2014, 30(4): 62-65. |
| [6] |
刘建华.轴向激励下螺栓连接结构的松动机理研究[D].成都: 西南交通大学, 2016. LIU Jian-hua. Research on Loosening Mechanism of Bolted Joints under Axial Excitation[D]. Chengdu: Southwest Jiaotong University, 2016. |
| [7] |
侯世远.螺纹联接松动机理研究[D].北京: 北京理工大学, 2015. HOU Shi-yuan. Study on Loosening Mechanism of Threaded Connection[D].Beijing: Beijing Institute of Technology, 2015. |
| [8] |
北京强度环境研究所.一种MJ螺栓及螺母有限元网格建模方法: 中国, CN106202639A[P]. 2016-12-07. Beijing Institute of Strength and Environment. A Finite Element Modeling Method for MJ Bolt Joint: China, CN106202639A[P]. 2016-12-07. |
| [9] |
BICKFORD J H. Introduction to the Design and Behavior of Bolted Joints: Non-gasketed Joints[M]. Beijing: China Architecture & Building Press, 2016.
|
| [10] |
万闯建.组合转子拉杆螺纹副滑移机理研究[D].长沙: 中南大学, 2014. WAN Chuang-jian. Study on Slip Mechanism of Combined Rotor Rod Thread[D]. Changsha: Central South University, 2014. |
| [11] |
MURPHY J, BLANCHET T A. Load Redistribution on Lead Screw Threads Wearing under Varying Operating Conditions[J]. Journal of Tribology, 2008, 130: 1-13. |
| [12] |
MONTGOMERY J. Boundary Condition Influences on Shank Stress in 3D Solid Bolt Simulation[C]//2008 Abaqus Users' Conference. Providence: Ds Simulia, 2008.
|
| [13] |
YOKOYAMA T, OLSSON M, IZUMI S, et al. Investigation Into the Self-loosening Behavior of Bolted Joint Subjected to Rotation Loading[J]. Engineering Failure Analysis, 2012, 23: 35-43. |
| [14] |
ZHANG M, JIANG Y, LEE C H. Finite Element Modeling of Self-loosening of Bolted Joint[J]. Journal of Mechanical Design, 2007, 129(2): 218-226. |
| [15] |
赵登峰, 曾国英. 振动环境中螺纹联结松动过程的研究[J]. 振动与冲击, 2010, 9(10): 175-178. ZHAO Deng-feng, ZENG Guo-ying. Unintentional Unscrewing of Screw Joints under Vibration Condition[J]. Journal of Vibration and Shock, 2010, 9(10): 175-178. |
| [16] |
缪宏, 左敦稳, 汪洪峰. 冲击载荷对飞机起落架螺纹连接的影响[J]. 振动与冲击, 2010, 29(2): 208-211. MIAO Hong, ZUO Dun-wen, WANG Hong-feng. Effect of Impact Load on Threaded Connection of an Aircraft Landing Gear[J]. Journal of Vibration and Shock, 2010, 29(2): 208-211. |
| [17] |
酒井智次.螺纹紧固件连接工程[M].柴之龙, 译.北京: 机械工业出版社, 2016. SAKAI J. Thread Fasteners Connection Engineering[M]. CHAI Zhi-long, translated. Beijing: China Machine Press, 2016. |
| [18] |
YAMATOTO A. The Theory and Computation of Threads Connection[M]. Tokyo: Yokendo, 1980.
|
 2019, Vol. 36
2019, Vol. 36
