扩展功能
文章信息
- 龚雨兵, 张立杰, 张德峰
- GONG Yu-bing, ZHANG Li-Jie, ZHANG De-feng
- 摩擦片表面凸起对汽车干式离合器滑摩噪声的影响
- Influence of Surface Bump in Friction Plate on Automotive Dry Clutch Slide Noise
- 公路交通科技, 2019, 36(12): 145-151
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 145-151
- 10.3969/j.issn.1002-0268.2019.12.018
-
文章历史
- 收稿日期: 2018-04-08
干式离合器具有传递效率高、压盘压紧力稳定、操纵力小等优点, 在汽车上得到广泛应用[1]。某些离合器在接合滑摩过程中会产生低频滑摩噪声, 严重影响乘车舒适性, 增加维修成本, 浪费大量资源。离合器滑摩噪声属于摩擦引起的振动和噪声。对于此类型振动噪声, 国内外学者利用解析法、数值分析法以及试验法等研究方法进行了大量研究[2-15]。特别是以制动尖叫噪声(brake squeal)为研究对象, 发现摩擦面形貌[2-3]、摩擦面实际接触倾角[4-6]或凸起[7]以及接触压力[8]等对制动尖叫噪声的产生有重要影响。但是现有研究中关于离合器滑摩噪声(clutch slide noise)的研究则很少。本研究采用复特征值分析方法, 以是否发生滑摩噪声为指标, 以理想离合器(从动盘摩擦片不存在凸起)为对比, 研究了从动盘摩擦片表面正弦凸起对离合器滑摩噪声产生的影响。
1 有限元建模 1.1 复特征值理论近年来, 基于复模态理论的复特征值分析方法已经成为摩擦噪声的主流分析方法[9, 14]。在工业应用中, 复特征值分析方法成为唯一的可用方法[15]。汽车干式摩擦离合器其动力学方程可以用以下二阶非齐次微分方程描述[11]:
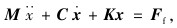
|
(1) |
式中, M为质量矩阵; C为阻尼矩阵(包含摩擦阻尼); K为刚度矩阵; ẍ为加速度向量; ẋ为速度向量; x为位移向量; Ff为摩擦力向量。把式(1)改为如式(2)所示。

|
(2) |
式中Kf为包含摩擦力的非对称刚度矩阵。其特征值方程为:

|
(3) |
式中, λ为特征值, φ为对应的特征向量。
由于压盘和飞轮分别与从动盘摩擦片之间存在摩擦力, 阻尼矩阵C和刚度矩阵Kf为非对称矩阵。方程(3)在实空间里无法解耦, 必须采用复模态分析的方法。复模态分析方法有两种途径, 分别是状态空间法和拉氏变换法。拉氏变换法将求解问题转换到复域(或S域)中进行求解。在复域中, 式(3)特征值可表示为:

|
(4) |
式中, σ为特征值实部; ω为特征值虚部。
如果复模态的特征值具有非正实部, 则该阶模态是稳定的。反之, 如果复模态的特征值具有正实部, 则该阶模态是不稳定的[9-13], 从而可能激发噪声, 相应的虚部即为发生振动噪声的频率。因此, 复特征值方法可以判断噪声发生趋势以及特有噪声频率。
针对离合器总成, 基于ANSYS软件的复特征值分析方法为:首先, 对离合器模型进行非线性静力学分析, 仿真离合器工作时的真实接触状态, 软件忽略阻尼矩阵C并将压盘与摩擦片之间的摩擦力作为外力引入到振动微分方程, 使原本对称的刚度矩阵变成非对称矩阵。其次, 利用线性摄动法, 对引入摩擦后的非对称刚度矩阵进行复模态分析。根据得到的复特征值实部的正负来判断系统是否稳定。由于在分析中忽略了材料阻尼的影响, 分析结果存在过预测。有研究认为阻尼比ζ≤-0.01的不稳定模态才能发出滑摩噪声[10]。由于各阶不稳定模态的阻尼比ζ符号总是与实部符号相反, 在实部绝对值远小于虚部绝对值时, 阻尼比数值大小近似等于实部与虚部的比值, 为便于观察, 把ζ≤-0.01的不稳定模态转换成∣ζ∣≥0.01进行表示。
1.2 离合器摩擦片表面局部接触 1.2.1 现象在某汽车维修服务站对一些出现离合器滑摩噪声的故障车辆进行拆机检查, 发现故障车离合器从动盘摩擦片表面上, 在其铆钉附近位置, 具有较明显的局部接触特征。而正常车辆离合器摩擦片, 其表面接触较均匀, 未出现明显局部接触现象。正常车辆摩擦片表面与故障离合器摩擦片表面分别如图 1(a)和(b)所示。因此推测离合器摩擦片局部接触特征有可能是产生离合器滑摩噪声的重要影响因素。

|
| 图 1 离合器从动盘 Fig. 1 Driven disk of clutch |
| |
1.2.2 局部接触原因
在该离合器制造工艺中, 摩擦片铆钉铆接采用铆压工艺。由于工艺中铆接压力一致性难以控制, 因此铆接时部分铆钉变形过大或过小, 使得铆钉处摩擦片发生凸起变形。在实际生产工艺检测中, 一般通过端面跳动检查来检测摩擦片的表面凸起是否在工艺要求范围内, 并对不合格件通过专用工具进行二次校正。但校正件容易在使用中产生二次端面跳动超差[16]。因此, 摩擦片铆钉孔附近的表面凸起造成了摩擦片在与压盘滑动接触过程中出现局部接触与磨损。
1.2.3 摩擦片局部接触仿真模型根据实际故障件离合器从动盘摩擦片的局部接触特征, 不失一般性, 假定在摩擦片两组铆钉孔之间, 摩擦片厚度存在符合正弦分布的凸起, 如图 2所示。

|
| 图 2 摩擦片正弦分布凸起 Fig. 2 Sine type distributed bumps on friction disc surface |
| |
摩擦片厚度分布如式(5)所示:

|
(5) |
式中, h为摩擦片实际厚度; h0为摩擦片名义厚度; Am为最大凸起高度; λ为波长(值为πri/3, ri为摩擦片内半径); θ为角弧度。
1.3 有限元模型以ϕ260离合器为原型建立有限元模型, 为便于计算, 对从动盘内花键部分进行简化, 忽略内花键的齿槽部分。有限元模型如图 3所示。

|
| 图 3 有限元模型 Fig. 3 Finite element models |
| |
单元总数为270 568个, 节点总数为850 144个。在压盘与摩擦片之间建立相对滑动摩擦接触(采用Augmented Lagrange算法), 其他零件之间建立绑定/bonding接触(采用MPC算法)。压盘、摩擦片等关键零部件的材料参数如表 1所示。
| 部件名称 | 密度/(kg·m-3) | 弹性模量/Pa | 泊松比 |
| 压盘 | 7 200 | 1.1E+11 | 0.26 |
| 摩擦片 | 2 595 | 1.5E+09 | 0.25 |
| 减震弹簧 | 7 850 | 2E+11 | 0.3 |
| 减振器盖 | 7 800 | 2.07E+11 | 0.3 |
在典型滑摩工况下, ϕ260膜片弹簧工作点压紧力为5 000 N, 从动盘摩擦片与压盘之间摩擦系数为0.4, 摩擦片材料为雷贝斯托某型号材料, 摩擦片内直径为160 mm、外直径为260 mm。
根据离合器实际工作时的受力及约束情况, 在压盘齿顶处施加力载荷; 在压盘孔位置施加限制径向位移的位移约束; 在从动盘内花键处施加限制径向位移和切向转动的位移约束; 在从动盘摩擦片与飞轮接触的外表面施加零位移约束(模拟飞轮的刚性作用); 在压盘与摩擦片之间建立摩擦接触对, 并生成内部滑移运动, 指定摩擦系数与转速。
2 结果与分析 2.1 摩擦片凸起高度对滑摩噪声的影响压盘工作压紧力为5 000 N、摩擦系数为0.4时, 名义传递转矩为420 N·m; 转速为650 r/min。不同凸起高度对应的离合器总成不稳定模态的实部(不稳定系数)和虚部(频率)如表 2所示。
| 凸起高度/mm | 不稳定模态1 | 不稳定模态2 | 不稳定模态3 | 不稳定模态4 | |||||||
| 虚部 | 实部 | 虚部 | 实部 | 虚部 | 实部 | 虚部 | 实部 | ||||
| 0 | 2 122.9 | 2.277 4 | |||||||||
| 0.1 | 1 805.5 | 12.581 | 2 024.7 | 36.247 | 2 129.6 | 1.948 | |||||
| 0.2 | 1 599.2 | 12.825 | 1 840.7 | 33.881 | |||||||
| 0.3 | 1 492.1 | 12.105 | 1 748.8 | 31.096 | 2 126.5 | 0.251 41 | |||||
| 0.4 | 1 420.9 | 11.322 | 1 685.7 | 29.766 | 2 126.5 | 0.332 03 | |||||
| 0.5 | 1 392.4 | 12.152 | 1 668.8 | 28.759 | |||||||
| 0.6 | 1 316.2 | 0.278 27 | 1 320.8 | 12.705 | 1 602.6 | 27.373 | 2 126.1 | 0.471 03 | |||
| 0.7 | 1 283.9 | 9.503 4 | 1 563.9 | 26.364 | 2 126.3 | 0.129 52 | |||||
从表 2可以看出, 与理想状态(凸起高度0 mm)对比, 摩擦片存在凸起时, 不稳定模态个数增加以及不稳定系数增加, 表明离合器滑摩噪声的发生趋势增大。
不同凸起高度对应的离合器总成不稳定模态的实部(不稳定系数)和虚部(频率)如图 4所示。在图 4中若仅考虑阻尼比∣ζ∣≥0.01的不稳定状态, 则可以看出, 随着凸起高度的增加, 不稳定模态的虚部逐渐降低, 意味着凸起高度的增加会导致滑摩噪声更趋于低频; 此外, 凸起高度增加时不稳定模态的实部相对减小, 意味着噪声发生强度略有降低。

|
| 图 4 离合器总成不稳定模态的实部和虚部 Fig. 4 Real part and imagine part of instability mode of clutch assembly |
| |
摩擦片凸起高度为0.3 mm时, 噪声强度较大的2阶不稳定模态振型分别如图 5所示。其中图 5(a)为1 492.1 Hz的不稳定振型, 表现为摩擦片切向摆动模态与压盘圆周摆动模态发生耦合, 图 5(b)为1 748.8 Hz时的不稳定振型, 表现为摩擦片弯曲模态与压盘弯曲模态发生耦合。

|
| 图 5 不稳定振型 Fig. 5 Instability modes |
| |
2.2 接触分析
接触压力分布状况是影响模态耦合的重要因素之一, 接触压力分布的差别是导致不稳定模态计算结果差别的原因[17-18]。对离合器摩擦片不同凸起高度下的接触压力进行分析比较, 为研究摩擦片凸起高度对滑磨噪声的影响机制提供基础。
2.2.1 接触状态理想模型与凸起模型(凸起高度0.3 mm)从动盘摩擦片接触状态分别如图 6所示, 其中不同颜色分别表示远离接触、接近接触、接触滑移和粘连等不同接触状态。由图 6(a)可知, 不存在凸起时, 摩擦片整个表面都为接触状态。由图 6(b)可知, 存在凸起时, 仅摩擦片凸起区域与压盘进行接触, 其他区域表现为未接触。

|
| 图 6 接触状态 Fig. 6 Contact statuses |
| |
2.2.2 滑动距离
理想模型与凸起模型(凸起高度0.3 mm)从动盘摩擦片与压盘间的滑动距离分别如图 7所示。

|
| 图 7 滑动距离 Fig. 7 Sliding distances |
| |
由图 7(a)可知, 理想摩擦片在接触区域的滑动距离随着摩擦片半径的增大而线性增大。由图 7(b)可知, 对于存在凸起的摩擦片, 凸起区域的滑动距离随着摩擦片半径的增大而增大, 非凸起区域与压盘不存在实际接触, 没有相对滑动(滑动距离为0 mm)。
2.2.3 接触压力理想模型与0.1 mm凸起高度下从动盘摩擦片接触压力分别如图 8所示。0.2~0.7 mm凸起高度下的摩擦片接触压力分布规律与0.1 mm凸起高度下基本类似, 只是数值变化。不同凸起高度下的最大接触压力值如表 3所示。

|
| 图 8 凸起接触压力 Fig. 8 Contact pressures of bump |
| |
| 凸起高度/mm | 摩擦面最大接触压力/MPa |
| 0 | 0.529 33 |
| 0.1 | 2.656 6 |
| 0.2 | 3.153 2 |
| 0.3 | 3.587 3 |
| 0.4 | 3.717 2 |
| 0.5 | 4.136 5 |
| 0.6 | 4.179 1 |
| 0.7 | 4.225 2 |
结合图 8和表 3可以看出, 理想摩擦片其接触压力分布相对均匀, 凸起情形下接触压力则仅存在于凸起接触区域上。这也使得凸起区域接触压力明显大于理想摩擦片接触压力。随着凸起高度由0.1 mm增加到0.7 mm, 最大接触压力数值相应由2.65 MPa增加到4.22 MPa, 说明随着凸起增加, 最大接触压力随之增大。此外, 由图 8可以看出, 对于理想模型和凸起模型, 接触压力都是外缘压力大, 内缘压力小。这是由于压紧力载荷施加在压盘齿顶上, 而压盘齿顶靠近外缘所致(可参见图 3(a))。外缘区域接触压力较大, 预示该处磨损也会较大, 这一仿真结论与图 1(b)中摩擦片局部接触区外缘磨损较大的实际磨损状态相符, 说明了接触压力分析模型的有效性。不同凸起高度下接触压力存在差异, 可能进而产生不同的模态耦合特性及滑磨噪声频率。
3 实车试验 3.1 试验测试在某市汽车维修服务站对存在滑摩噪声的车辆进行实车噪声数据采集。该车辆为皮卡型汽车, 采用ϕ260离合器。试车方法如下:在泥泞的上坡路试车:挂1档起步加速, 在行驶过程中切换到高档位并继续加速。采用北京东方振动和噪声研究所INV3018A型智能信号采集处理分析仪, INV9212型声强传感器测试探头放置于驾驶室内记录噪声信号。测试结果发现, 故障车辆在半离合加速时出现滑摩噪声, 噪声具有明显间歇性, 与摩擦噪声发生特性相符[14]。对噪声进行频率采样, 得到3个主要的噪声频率分别为494, 634, 1 378 Hz(噪声强度≥100 dB), 如图 9所示。

|
| 图 9 滑摩噪声频谱图 Fig. 9 Vehicle for slide noise spectrogram |
| |
并且1 378 Hz区域附近的噪声发生强度最大。对故障车离合器进行返厂测试, 各项性能参数如膜片弹簧压紧力、摩擦片摩擦系数均符合技术要求, 从动盘摩擦片的端面全跳动在0.6 mm左右。
3.2 对比分析典型滑摩工况下, 即膜片弹簧压紧力为5 000 N, 从动盘摩擦片摩擦系数为0.4, 摩擦片表面存在凸起0.3 mm(实测中全跳动0.6 mm)的情况下, 复特征值分析法预测有3阶不稳定频率, 分别为1 492, 1 748 Hz和2 126 Hz。对比试验结果, 复特征值分析法结果接近噪声发生强度最大的1 378 Hz(预测频率为1 492 Hz), 两者相差8.2%;另外, 复特征值方法没有预测出强度较低的实测低频噪声频率494, 634 Hz, 出现了所谓的漏阶现象。这可能主要是由于忽略了材料阻尼以及仿真模型中对摩擦片凸起的正弦简化导致。
4 结论针对离合器滑摩噪声, 采用复特征值分析方法分析了摩擦片表面凸起对滑摩噪声的影响并与试验数据进行对比。可总结如下:
(1) 摩擦片表面凸起会明显增大滑摩噪声的发生趋势。
(2) 摩擦片表面凸起高度增加, 离合器滑摩噪声趋于低频。
(3) 复特征值方法基本预测出实测最大强度的噪声频率, 同时出现了漏阶现象。
(4) 摩擦片表面凸起值增加, 最大接触压力值增大。
| [1] |
林世裕, 范海荣, 刘学章, 等. 膜片弹簧与碟形弹簧离合器的设计与制造[M]. 南京: 东南大学出版社, 1995: 18-20. LIN Shi-yu, FAN Hai-rong, LIU Xue-zhang, et al. Design and Manufacutring of Diaghgram Spring Cltuch and Belleville Springs Cltuch[M]. Nanjing: Southeast University Press, 1995: 18-20. |
| [2] |
王东伟, 莫继良, 王正国, 等. 沟槽织构化表面影响摩擦振动噪声机理[J]. 机械工程学报, 2013, 49(23): 112-116. WANG Dong-wei, MO Ji-liang, WANG Zheng-guo, et al. Mechanism of the Effect of Groove-textured Surface on the Friction Vibration and Noise[J]. Journal of Mechanical Engineering, 2013, 49(23): 112-116. |
| [3] |
WANG X C, MO J L, OUYANG H, et al. Squeal Noise of Friction Material with Groove-textured Surface: An Experimental and Numerical Analysis[J]. Journal of Tribology, 2016, 138(2): 21401. |
| [4] |
VAYSSIERE C, BAILLET L, LINCK V, et al. Influence of Contact Geometry and Third Body on Squeal Initiation: Experimental and Numerical Studies[C]// Proceedings of WTC 2005 World Tribology Congress Ⅲ. Washington, D.C.: ASME, 2005.
|
| [5] |
ZHANG L, YU Z, LÜ H. Influence of Surface Run-out on Disc Brake Squeal[J]. Journal of Vibroengineering, 2013, 15(2): 520-531. |
| [6] |
吕红明, 张立军, 余卓平. 接触表面不平度对摩擦尖叫噪声的影响[J]. 摩擦学学报, 2011, 31(5): 473-479. LÜ Hong-ming, ZHANG Li-jun, YU Zhuo-ping. Effects of Surface Roughness on the Friction-induced Squeal Noise[J]. Tribology, 2011, 31(5): 473-479. |
| [7] |
BONNAY K, MAGNIER V, BRUNEL J F, et al. Influence of Geometry Imperfections on Squeal Noise Linked to Mode Lock-in[J]. International Journal of Solids and Structures, 2015, 75-76: 99-108. |
| [8] |
HETZLER H, WILLNER K. On the Influence of Contact Tribology on Brake Squeal[J]. Tribology International, 2012, 46(1): 237-246. |
| [9] |
陈光雄, 戴焕云, 曾京, 等. 踏面制动尖叫噪声的有限元分析[J]. 机械工程学报, 2009, 45(3): 203-207. CHENG Guang-xiong, DAI Huan-yun, ZENG Jing, et al. Finite Element Analysis of the Squeal Propensity for a Pad-wheel Tread Brake System[J]. Journal of Mechanical Engineering, 2009, 45(3): 203-207. |
| [10] |
侯俊, 过学迅. 基于有限元方法的盘式制动器制动噪声研究[J]. 机械设计, 2008, 25(8): 50-52. HOU Jun, GUO Xue-xun. Braking Noise Study on Disc Typed Brake Based on Finite Element Method[J]. Journal of Machine Design, 2008, 25(8): 50-52. |
| [11] |
张光荣, 谢敏松, 黎军, 等. 摩擦片偏磨引起的汽车制动低鸣噪声[J]. 机械工程学报, 2013, 49(9): 81-86. ZHANG Guang-rong, XIE Ming-song, LI Jun, et al. Vehicle Brake Moan Noise Induced by Brake Pad Taper Wear[J]. Journal of Mechanical Engineering, 2013, 49(9): 81-86. |
| [12] |
陈康.盘式制动啸叫的实验研究与仿真分析[D].哈尔滨: 哈尔滨工业大学, 2014. CHEN Kang. Experimental Research and Simulation on Disc Brake Squeal[D]. Harbin: Harbin Institute of Technology, 2014. |
| [13] |
韦健, 孙跃东, 王书文, 等. 基于ABAQUS的盘式制动尖叫分析[J]. 机械设计与制造, 2016(6): 151-154. WEI Jian, SUN Yue-dong, WANG Shu-wen, et al. Research on Brake Squeal Based on ABAQUS[J]. Machinery Design & Manufacture, 2016(6): 151-154. |
| [14] |
张立军, 刁坤, 孟德建, 等. 摩擦引起的振动和噪声的研究现状与展望[J]. 同济大学学报:自然科学版, 2013, 41(5): 765-772. ZHANG Li-jun, DIAO Kun, MENG De-jian, et al. Friction-induced Vibration and Noise Research: the Status Quo and Its Prospect[J]. Journal Tongji University: Natural Science Edition, 2013, 41(5): 765-772. |
| [15] |
CANTONI C, CESARINI R, MASTINU G, et al. Brake Comfort: A Review[J]. Vehicle System Dynamics, 2009, 47(8): 901-947. |
| [16] |
方向东. 离合器从动盘总成端面跳动校正工艺的研究[J]. 湖北农机化, 2015(6): 60-61. FANG Xiang-dong. Study on Correction Process of Surface Run-out of Clutch Driven Plate[J]. Hubei Agricultural Mechanization, 2015(6): 60-61. |
| [17] |
OUYANG H, BAKAR A R A, LI L. A combined Analysis of Heat Conduction, Contact Pressure and Transient Vibration of a Disk Brake[J]. International Journal of Vehicle Design, 2013, 51(1/2): 190-206. |
| [18] |
张立军, 孟德建, 孙俊刚. 通风盘制动器盘-块接触位置变化对尖叫复模态分析的影响[J]. 汽车工程, 2016, 38(2): 242-247. ZHANG Li-jun, MENG De-jian, SUN Jun-gang. The Impact of Disc-pad Contact Position Variation on the Complex Modal Analysis of Ventilated Disc Brake Squeal[J]. Automotive Engineering, 2016, 38(2): 242-247. |
 2019, Vol. 36
2019, Vol. 36
