扩展功能
文章信息
- 崔洪军, 李雨生, 朱敏清, 李霞, 宋长柏
- CUI Hong-jun, LI Yu-sheng, ZHU Min-qing, LI Xia, SONG Chang-bai
- 无人驾驶汽车共享调度方法研究
- Study on Scheduling Method of Shared Driverless Vehicles
- 公路交通科技, 2019, 36(12): 110-116
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 110-116
- 10.3969/j.issn.1002-0268.2019.12.014
-
文章历史
- 收稿日期: 2018-09-25
2. 河北工业大学 建筑与艺术学院, 天津 300401
2. School of Architecture and Art, Hebei University of Technology, Tianjin 300401, China
使用共享无人驾驶车辆(Shared autonomous vehicles, SAV), 顾客可以通过电话、网络等通讯工具定制出行服务(出发地、目的地、允许合乘人数、最大等待时间、目的地到达时间等), SAV将自动完成接送顾客(含沿途顾客), 完成服务后车辆自动驶回停车场或接送新顾客。SAV相对于常规公交具有服务个性化、准时、舒适、灵活(门到门)的显著优势, 相对于网约车(滴滴、UBER), SAVs运营成本更低, 而且可以实现车辆完全可控(用户匹配、路径选择等), 在环境污染、交通安全、交通拥堵等方面SAV同样有着积极的作用。
调度问题(VRP)产生于公路交通运输规划, 并很快成为运筹学与组合优化领域的前沿和研究热点。目前无人驾驶技术的发展如火如荼, 对于无人驾驶车辆的共享调度问题, 引起了国内外学者的高度重视。A.Karbassi等[1]开发出一种启发式算法来解决无人驾驶汽车共享系统中车辆行驶路线和到达时间问题。N.Masoud[2]提出了一种乘坐匹配算法, 通过考虑乘坐用户的偏好, 最大限度地减少系统中服务的乘客转移数量和自动驾驶汽车的等待时间。J.P. Hanna[3]提出了一种可以降低系统的空闲行程的车辆匹配聚类算法。W.Herbawi[4]等利用多目标蚁群优化算法来解决共享车辆中的多目标路径规划问题。J.Alonso-Mora[5]等研究了一种用于无人驾驶汽车乘坐共享的算法, 该算法可以根据在线需求和车辆位置生成最佳路线。A.Y. S. Lam[6]等对遗传算法进行改进, 来解决共享无人驾驶调度问题。N.A等[7]等开发了减少整个共享无人驾驶系统用户车辆里程的优化算法。国内对共享无人驾驶系统研究较少, 力帆、百度、盼达[8]将在无人驾驶领域展开战略合作, 推动无人驾驶在共享汽车商业化场景的实际应用。李雪[9]等提出了基于近似动态规划的动态车辆调度算法。唐静媛[10]运用图论和Dijkstra算法从网络拓扑图中找到最短路径, 以动态路径规划, 计算权值, 得出无人共享车最优路径。J.Yuan等[11]提出了一种分布式的调度方法, 详细分析了调度的时间约束。J.Alonso-Mora等[12]分析得出使用共享无人驾驶汽车可以减少城市道路上75%的汽车数量。
以上研究虽然建立了调度模型, 但是对共享无人驾驶汽车的供需停放问题缺乏深入研究, 并且缺乏对算法是否最优性的检验, 基于此本研究从共享无人驾驶汽车的供需停放问题入手, 建立了共享无人驾驶汽车供需停放多约束条件的调度模型并设计了一种调度优化分配算法来满足用户需求并实现系统效益最优化。
1 问题表述共享自动驾驶汽车与各种车载通信技术联系在一起, 具有高度的自行控制能力, 可以高效率和灵活性协作地响应瞬时情况, 准确高效地提供点对点服务及动态的共享乘坐服务。文献[13-18]中详细介绍了SAV的调度问题, 以及如何预测行驶路线和计算服务完成时间以实现系统性能的最优化。在SAV调度问题中, 系统需要在动态的环境下实现乘客与SAV的合理匹配, 具体来说, 就是在一定范围的区域内, 有多辆SAV在行驶, 同时有多名乘客有不同的搭乘需求, 而且乘客的出发点和目的地己经确定, 并且在上、下车的位置有一定的服务时间限制, 乘客必须在规定的服务时间范围内搭乘或离开。但是现有的研究对未行驶的SAV如何调度缺少相关研究且调度算法缺少优化验证, 本研究主要对不同的SAV和多个用户进行合理匹配及合理安排限制时间进行深入研究, 逐步计算一组给定容量SAV与对应请求之间的最优分配。
2 模型建立 2.1 符号定义(1) 网络结构:使用G(V, ε)表示有向图, 其中V为区域中需要服务的位置; ε为连接这些位置的路段, 以便可以用G完全描述SAV的路线。对于i, j∈V, 每个边(i, j)∈ε与单个成本费用cij和行程时间tij相关联, tij为SAV从i到j的时间。cij通常代表路段(i, j)的距离。
(2) 请求:乘客的服务请求由R表示。每个r∈R由5个因素(sr, dr, Tr, [er, lr], qr)构成。sr和dr分别为乘客的出发地和目的地; Tr为最大乘坐时间, 超过这个时间会导致顾客不满。[er, lr]为服务开始时间的取值范围。qr为请求r中所需的空余座位。
(3) 车辆:用K为系统中所有可以调度的SAV。每个k∈K由5个指标(ak, tk0, 
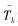


本节将对SAV车辆调度问题进行约束限制, 建立SAV车辆调度问题模型, 以获取最小成本为目标对行程时间tij、乘客请求集R等以上给定的参数进行限制约束。首先给出决策变量:

|

|

|
以SAV系统总运营成本函数最小化为目标, 构建数学模型可表示为:

|
(1) |

|
(2) |

|
(3) |

|
(4) |

|
(5) |

|
(6) |

|
(7) |

|
(8) |

|
(9) |

|
(10) |

|
(11) |

|
(12) |

|
(13) |

|
(14) |

|
(15) |
此外有:

|

|
tki为k到达出发点i需要的时间; fik为离开i之前车辆k的乘客数量。式(1)定义了目标函数总成本最小。式(2)表示对每个服务需求自动驾驶车辆只能提供一次服务。式(3)表示每辆SAV不进行服务时将回到停车站点。式(4)定义了k的起始点有一个净流出车辆, xakik为起点ak到目的地i的行程, 其中N+(ak)和N-(ak)分别表示出发点ak的驶入和驶出车辆的集合。
本研究拟解决的问题是在一定范围的区域内, 对于给定的一组请求R={r1, …, rn}和SAV车辆K={k1, …, km}及包括乘客在内的实时动态环境下, 如何将SAV更加合理地分配给需要服务的用户并实现用户的合乘, 达到系统效益最优。其他外在条件设置为理想状态, 所以暂不考虑道路拥挤对行驶时间带来的影响, 当调度中心收到乘客请求后通过调度算法, 将合适的SAV指派给乘客, 最后通过算法计算系统选取SAV的最优路径为乘客服务。具体步骤如下:
(1) 第1步利用乘客发出的请求, 系统获取乘客的起点和目的地, 分析区域内部哪些请求可以成对组合, 以及哪些车辆可以服务这些乘客的请求。
(2) 第2步系统对乘客请求以及所需行程进行分析, 以找到能够满足乘客需求和行程路线的车辆, 同时需要满足所有的约束条件。此时, 一个请求可能包含多种途径, 一次行程可能会有多个候选车辆执行。
(3) 最后一步根据第2步确定的多组请求-路线-车辆分配图, 确定每辆车与乘客行程整个系统的最佳分配, 此时可以转换成一个整数线性规划问题, 如图 1所示。

|
| 图 1 无人驾驶车辆分配步骤 Fig. 1 Allocation steps of driverless vehicle |
| |
图 1(a)中有4个请求和两辆车(黑色三角形表示乘客目的地)的街道网络示例, 且车辆1中包含1名乘客(所以车辆1开始已有固定的目的地), 车辆2无乘客。图 1(b)是无人驾驶车辆和请求的匹配图, 这张图表示所有请求和车辆匹配的可能性。图 1(c)确定无人驾驶车辆对所有乘客的服务顺序组合。图 1(d)由算法确定解决方案实现最佳分配, 其中车辆1为请求2和3提供服务, 车辆2为请求1和4提供服务, 并确定两辆车对分配请求的最佳路线。
对于车辆-请求匹配图:
对该方法的第一步是计算图 1(a)哪些请求可以成对组合, 以及图 1(b)哪些车辆可以针对当前乘客个别地提供哪些请求。如果请求可以满足模型约束, 则无人驾驶车辆将为其提供服务, 则请求r和车辆k被连接。这就是说, 如果行程travel(k, r)返回有效的旅行, 现有的无人驾驶车辆将在系统要求的最长等待时间和延迟时间限制下接受请求r, 并由边e(r, v)表示二者已匹配成功。
对于请求-路线-车辆分配图, 此图是在车辆-请求匹配图的基础上进一步研究所有可行的行程T={T1, …Tn}。如果区域内自动驾驶车辆可以与乘客的请求组合, 同时满足模型约束, 则行程是可行的。每个请求可能会产生多个可行的行程, 每个行程可能会由不同的车辆来服务。e(r, T)表示请求r和行程T之间相匹配构成的边, e(T, k)表示行程T和车辆k之间相匹配构成的边。
整个算法由以下3部分构成, 伪代码如下所示。
(1) 分析请求-路线-车辆
如表 1所示, 计算可行的请求-路线-车辆分配算法按行程需求增加的顺序进行迭代, 其中τ为所有的可行行程。对于每条边e(T, k), 都会有一定的最大成本进行限制。对于每辆无人车, 都可以设置一个最大等待时间, 超过这个时间将不再服务。这样可以优化解决方案, 提高计算效率, 减少不必要的行程。
1:τ≠ |
| 2:对于每个无人车k∈K继续 |
3:τi≠ ∀i∈{1, …, k} ∀i∈{1, …, k} |
| 4:[对于1个需求的行程] |
| 5:对于车辆-请求匹配图的边e(r, k)继续 |
| 6:τ1←T={r}; 添加e(r, T)和e(T, k) |
| 7:[对于2个需求的行程] |
| 8:对所有{r1}, {r2}∈τ1和e(r1, r2)∈车辆请求匹配图继续 |
| 9:若travel(k, {r1, r2})是有效的, 则 |
| 10:τ2←T={r1, r2}; 添加e(rn, T)和e(T, k) |
| 11:[对于m个需求的行程] |
| 12:对于m∈{3, …, k}继续 |
| 13:对于所有T1, T2∈τm-1及|T1∪T2|=m继续 |
| 14:Denote T1∪T2={r1, …rm} |
| 15:若∀n∈{1, …m}, {r1, …rm}\rn∈τm-1, 则 |
| 16:若travel(k, T1∪T2)是有效的, 则 |
| 17:τm←T=T1∪T2 |
| 18:添加e(rn, T), ∀rn∈T, 和e(T, v) |
| 19:τ←∪n∈{1, …, k}τn |
根据可能行程和系统的请求-路线-车辆分配图, 计算出行车辆的最佳分配。这可以转化为一个整数线性规划问题(ILP)。首先, 通过贪婪分配方法, 计算出ILP优化的初始值。
(2) 贪婪分配
贪婪分配以减小行程数量和增加成本的方式进行迭代, 将行程分配给车辆。该方法在最大限度减少成本的同时最大限度地提高请求的数量。表 2描述了贪婪分配使成本目标函数最小化。其中

1:  |
| 2:对于m=k; m>0;m继续 |
| 3:Sm=sort e(T, k)在成本增加上, ∀T∈τk, k∈K |
4:当Sm≠  继续 继续 |
| 5:pop e(T, k)←Sm |
| 6:若∀r∈T, r∉Ro和k∉Ko, 则 |
| 7:Ro←{∀r∈T}; Ko←k |
| 8:∑ greedy←e(T, k) |
(3) 最优分配
以贪婪分配为基础, 进行最优分配。对于请求-路线-车辆分配图中的行程Ti∈τ和车辆kj∈K之间的每个边e(Ti, kj)引入二元变量εi, j∈{0, 1}。如果εi, j=1, 则车辆kj被分配到行程Ti。由εTK为在请求-路线-车辆分配图中边e(Ti, kj)的{i, j}集合。为每个请求rk∈R引入另一变量χk∈{0, 1}, 如果相关请求rk不能由任何车辆提供并且被忽略, 则χk=1。定义变量χ={εij, χk; ∀e(Ti, kj); ∀rk∈R},

|

|
TkR为在请求-路线-车辆分配图中的边e(rk, Ti); TiT为在请求-路线-车辆分配图中的边; e(Ti, kj)分别为与请求相关的行程和可以为每次行程提供服务的车辆。ck为还未服务的请求所需的成本。如表 3所示, 通过求解由上述变量, 成本和约束条件定义的ILP优化来找到最优分配。SAV的整个调度匹配过程如图 2所示。

|
| 图 2 SAV调度匹配算法流程 Fig. 2 Flowchart of SAV scheduling matching algorithm |
| |
4 算例分析
为验证算法的有效性及性能, 以某地区OD调查的真实数据作为基础, 将本研究提出的算法与基于聚类的拼车算法[3]应用MATLAB进行仿真模拟对比分析(基于聚类的拼车算法复杂度较低, 且匹配成功率较高)。取设置固定车辆数M=1 200, 每辆车的最大容量为3, 设置最长等待时间5 min, 试验中地图为10×10的网格每个网格的平均距离为1 km。
试验环境:在Intel Core i7-7500 CPU和2.5 GHz, 16 GB RAM的计算机上执行模拟。对算法运行时间、匹配成功率、乘客平均等待时间进行对比分析, 结果如图 3~图 5所示。

|
| 图 3 算法运行时间对比图 Fig. 3 Comparisons of operation time of algorithms |
| |

|
| 图 4 匹配成功率对比 Fig. 4 Comparison of matching success rates |
| |

|
| 图 5 平均等待时间对比 Fig. 5 Comparison of average waiting time |
| |
由图 3可知, 两种算法的平均运行时间随着乘客请求数量的增加而增大, 在请求数为2 000, 2 400, 2 800, 3 200, 3 600时, 本研究算法的平均运行时间比聚类算法分别降低3, 8, 14, 18, 20 ms, 本研究算法运行时间在整体上比聚类算法降低12.6 ms。
由图 4可知, 由于系统中SAV总数为定值, 随着乘客数量的增加, 两种算法的匹配成功率下降。在人车需求比为1, 1.5, 2, 2.5, 3时, 本研究算法的匹配成功率比聚类算法分别提高1.1%, 2.3%, 4.1%, 6.2%, 7.4%。总体上本研究算法的匹配成功率比聚类算法提高4.2%。
由图 5可知, 随着乘客请求的数量增加, 乘客的平均等待时间也随之增大。当乘客请求数量为2 000, 2 400, 2 800, 3 200, 3 600时, 本研究算法等待时间比聚类算法分别低2.1%, 3.4%, 4.5%, 6.0%, 7.7%, 整体降低约4.9%。使用本研究算法整体上降低了乘客等待时间, 使顾客得到更高效的服务。
5 结论通过本研究得出的成果如下:
(1) 基于乘客对无人驾驶汽车实时动态的需求, 建立了共享无人驾驶汽车调度约束限制模型, 并对供需停放问题进行深入研究。
(2) 设计了适用于一定范围区域内动态的共享无人驾驶汽车-乘客-行程路线匹配算法, 并详细的介绍了车辆-路线-乘客请求的分配过程, 以贪婪分配为基础进行改进, 经过迭代, 求得最优解。
(3) 与已有的聚类算法从算法运行时间、匹配成功率、乘客平均等待时间3个角度进行对比分析, 结果证明本研究算法的更为高效。
(4) 本研究对于道路拥挤对行驶时间的影响缺乏深入分析, 后续研究可以将研究问题深化, 探讨复杂外界环境下SAV如何调度。
| [1] |
KARBASSI A, BARTH M. Vehicle Route Prediction and Time of Arrival Estimation Techniques for Improved Transportation System Management[C]// Proceedings of IEEE 2003 Intelligent Vehicles Symposium. Columbus, USA: IEEE 2013.
|
| [2] |
MASOUD N, JAYAKRISHNAN R. A Real-time Algorithm to Solve the Peer-to-peer Ride-matching Problem in a Flexible Ridesharing System[J]. Transportation Research Part B: Methodological, 2017, 106: 218-236. |
| [3] |
HANNA J P, ALBERT M, CHEN D, et al. Minimum Cost Matching for Autonomous Carsharing[J]. IFAC Papers On Line, 2016, 49(15): 254-259. |
| [4] |
HERBAWI W, WEBER M. Ant Colony VS. Genetic Multiobjective Route Planning in Dynamic Multi-hop Ridesharing[C]// 2011 IEEE 23rd International Conference on Tools with Artificial Intelligence. Boca Raton: IEEE, 2011.
|
| [5] |
ALONSO-MORA J, SAMARANAYAKE S, WALLAR A, et al. On-demand High-capacity Ride-sharing via Dynamic Trip-vehicle Assignment[J]. Proceedings of the National Academy of Sciences, 2017, 37(1): 462-467. |
| [6] |
LAM A Y S, LEUNG Y W, CHU X. Autonomous-vehicle Public Transportation System:Scheduling and Admission Control[J]. IEEE Transaction on Intelligent Transportation Systems, 2016, 2(5): 1210-1226. |
| [7] |
NIELS A, AGATZ H, Alan L E, et al. Dynamic Ride-sharing: A Simulation Study in Metro Atlanta[J]. Transportation Research Part B: Methodological, 2011, 45(9): 1450-1464. |
| [8] |
佚名. 力帆与百度合作2018年测试无人驾驶共享车[J]. 汽车与配件, 2017(33): 20. Anon. Lifan Cooperated with Baidu to Test Driverless Shared Cars in 2018[J]. Automobile & Parts, 2017(33): 20. |
| [9] |
李雪, 聂兰顺, 齐文艳, 等. 基于近似动态规划的动态车辆调度算法[J]. 中国机械工程, 2015, 26(5): 682-688, 693. LI Xue, NIE Lan-shun, QI Wen-yan, et al. An Algorithm of Dynamic Vehicle Scheduling Problem Based on Approximate Dynamic Programming[J]. China Mechanical Engineering, 2015, 26(5): 682-688, 693. |
| [10] |
唐静媛, 陈宇晴. 基于无人驾驶共享车路径优化的讨论[J]. 消费导刊, 2017, 13(1): 51. TANG Jing-yuan, CHEN Yu-qing. Discussion on Route Optimization for Driverless Shared Vehicles[J]. Consumption Guide, 2017, 13(1): 51. |
| [11] |
YUAN J, ZHENG Y, ZHANG L, et al. Where to Find my Next Passenger[C]// The 6th International Conference on Ambient Systems. Beijing: [s.n.], 2011.
|
| [12] |
ALONSO-MORA J, SAMARANAYAKE S, WALLAR A, et al. On-demand High-capacity Ride-sharing via Dynamic Trip-vehicle Assignment[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(3): 462-467. |
| [13] |
LAM A Y S, LEUNG Y W, CHU X. Autonomous Vehicle Public Transportation System[C]// 2014 International Conference on Connected Vehicles and Expo (ICCVE). Vienna: IEEE, 2014.
|
| [14] |
WANG H, LI Z, ZHU X, et al. A Full Service Model for Vehicle Scheduling in One-way Electric Vehicle Car-sharing Systems[C]// IOV 2015 Proceedings of the Second International Conference on Internet of Vehicles-Safe and Intelligent Mobility. Berlin: Springer-Verlag, 2015: 25-36.
|
| [15] |
OSTERMANN J, KOETTER F. Energy-management-as-a-service: Mobility Aware Energy Management for a Shared Electric Vehicle Fleet[C] // 2016 5th International Conference on Smart Cities and Green ICT Systems. Rome: IEEE, 2016: 1-11.
|
| [16] |
KARBASSI A, BARTH M. Vehicle Route Prediction and Time of Arrival Estimation Techniques for Improved Transportation System Management[C]// IEEE 2003 Intelligent Vehicles Symposium: IEEE, 2003: 511-516.
|
| [17] |
AGATZ N A, ERERA A L, SAVELSBERGH M W P, et al. Dynamic Ride-sharing: A Simulation Study in Metro Atlanta[J]. Transportation Research Part B: Methodological, 2011, 45(9): 1450-1464. |
| [18] |
WANG H, LI Z, ZHU X, et al. A Full Service Model for Vehicle Scheduling in One-way Electric Vehicle Car-sharing Systems[C] // International Conference on Internet of Vehicles: Safe and Intelligent Mobility. Switzerland: Springer, 2015: 25-36.
|
 2019, Vol. 36
2019, Vol. 36

 , ∀rk∈R
, ∀rk∈R