扩展功能
文章信息
- 陶兴旺, 孙宗光, 陈一飞
- TAO Xing-wang, SUN Zong-guang, CHEN Yi-fei
- 基于监测响应的斜拉桥车重车速识别
- Identification of Vehicle Load and Speed on Cable-stayed Bridge Based on Monitoring Response
- 公路交通科技, 2019, 36(12): 87-93
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 87-93
- 10.3969/j.issn.1002-0268.2019.12.011
-
文章历史
- 收稿日期: 2019-05-31
车辆荷载识别可作为桥梁损伤机理研究的基础,同时为交通规划提供可靠的车载信息。建立准确的用于疲劳分析的车辆荷载模型也是进行桥梁疲劳可靠性评估的重要基础。近年来车辆动态称重系统WIM在一些公路和桥梁上被越来越多地采用。WIM可以在不中断交通的情况下获得计算车速、车重、轴重等数据,对于公路和桥梁的设计分析与运营管理将发挥着重要作用。但WIM系统成本较高,安装复杂,需在路面开挖布置混凝土基坑或凹槽,且精度受路面刚度与不平整度的影响较大[1]。20世纪80年代前后,学者们提出了桥梁动态称重系统BWIM[2]。BWIM是通过测量桥梁在车辆载荷作用下的结构响应,运用反问题求解方法获得车辆轴重等信息的测量技术[3-4]。与传统的WIM相比,B-WIM的优点有:(1)桥梁长度比WIM的秤台长得多,车辆称重时间长,因此称重精度受车辆动态载荷的影响小;(2)车辆通行速度快,缓解了称重精度与车辆通行速度之间的矛盾;(3)不与车轮直接接触,安装和维修不干扰交通且对路面无损害,耐久性得到保障;(4)可结合桥梁健康监测设计,亦可重复利用,费用较低。一般认为BWIM主要适合于结构简单的小型桥梁[5-6]。
近年来,逐渐开展了较大桥梁的BWIM可行性研究。陈惟珍等[7]根据刚桁架桥上的实测应变采用BWIM方法进行车辆荷载识别。张福俭[8]提出了一种基于斜拉索振动监测的斜拉桥上车辆荷载及其参数识别方法。以南京长江三桥为背景,通过数值仿真验证了所提出方法在一定噪声水平下的有效性。王蕾等[9]将移动荷载的识别转化为荷载形函数拟合系数的识别,并以某大跨刚构-连续预应力混凝土桥梁为背景,进行移动荷载识别的数值仿真研究,证明该方法在5%以下的噪声时能快速并准确识别移动荷载。谭金华等[10]基于桥梁运营状态监测的应变, 建立了识别过桥车辆荷载的一种BWIM方法。结合某大桥实例分析表明该方法能够较精确识别稀疏交通状态下车辆数量、大小、作用位置。还有研究将神经网络方法应用于简支梁桥的车辆荷载识别[11-12]。
这些研究对BWIM在一般桥梁结构上的应用做了积极地探索,同时也看到受到结构形式简单、小跨径桥梁或数值仿真的局限。目前,大多数健康监测系统都安装于大跨度桥梁,尤其是斜拉桥和悬索桥。健康监测系统能够提供更丰富的响应类型和数据量,将桥梁动态称重技术与健康监测相结合,既有利于提高大型桥梁的车辆荷载识别精度,同时也能提高监测数据的利用率,因此,是一个值得进一步深入研究的课题。本研究基于运营状态的监测响应,应用神经网络方法对通过斜拉桥的重车荷载识别进行了初步探讨。基于相似公路上实测车流统计模型拟定车流荷载,通过车桥耦合响应分析建立网络的训练和精度检验样本。然后,采用斜拉桥实际运营状态下的监测响应(索力和应变)提取特征参数并组成网络输入向量来识别车重和车速。
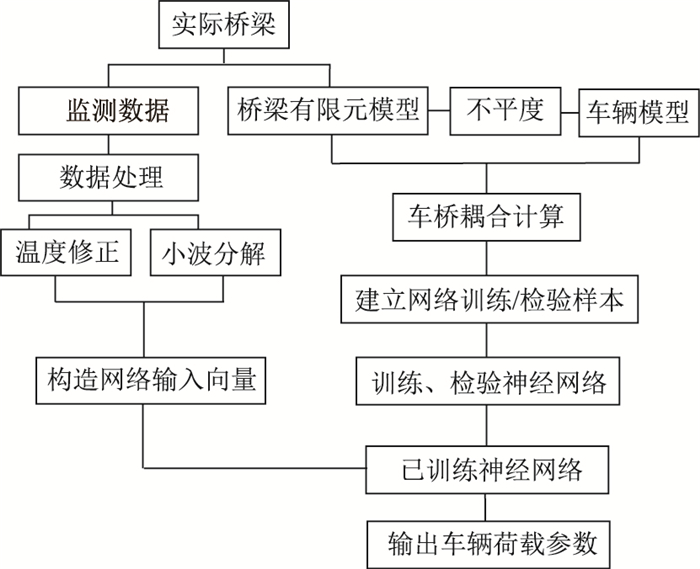
1 基于神经网络的识别方法神经网络车辆荷载识别的基本思路是,基于高精度模型进行车桥耦合响应模拟,由各个工况的结构响应特征参数和对应的车辆荷载参数构造网络的训练对(输入向量和目标向量),对网络进行训练和训练精度检验。然后基于实际桥梁的监测系统,对运营响应进行数据处理并提取特征参数,组成用于车辆荷载识别的网络输入向量,经上述训练好的网络完成实际车辆荷载的识别。上述流程如图 1所示。
|
| 图 1 网络识别流程图 Fig. 1 Flowchart of network identification |
| |
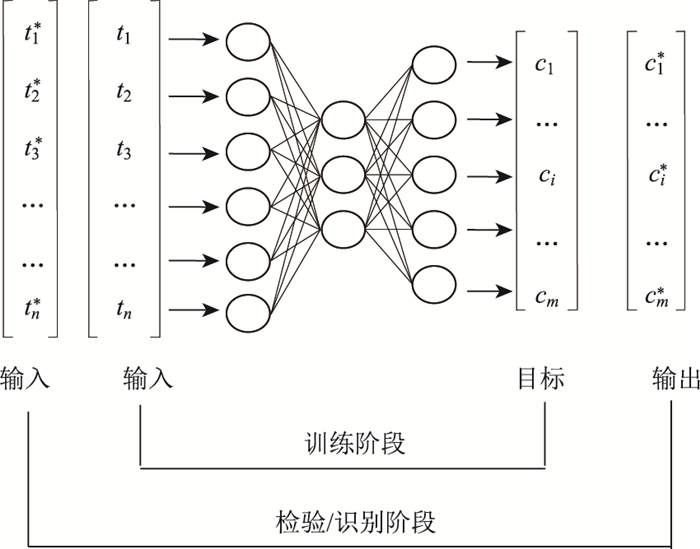
实践表明,BP网络的非线性映射能力使之具有较好系统识别性能,图 2为其训练与检验/识别过程的示意图[13]。向量t和c分别为训练阶段的网络输入样本(模拟的结构响应特征参数)和规定的目标输出(已知的车辆荷载参数)。向量t*和c*分别为检验/识别阶段网络的输入样本(实测响应特征参数)和输出结果(车辆识别结果)。通常网络训练完成后可先用已知车辆情况下的数据进行训练精度检验,满足要求后,再应用于实际车辆的识别。网络检验的过程和识别过程是相似的。一般对不同类型的原始数据参数可按各自的最大值进行归一化处理。
|
| 图 2 BP神经网络训练与检验/识别示意图 Fig. 2 Schematic diagram of BP Network training and inspection/ identification |
| |
2 斜拉桥车辆荷载识别 2.1 训练样本的建立 2.1.1 车桥模型
(1) 桥梁模型
本研究以某大桥航道桥及其健康监测系统为背景,该桥为一座分离双箱梁双塔双索面斜拉桥,主跨为260 m,采用五跨连续半漂浮结构体系,斜拉索采用平行索布置。
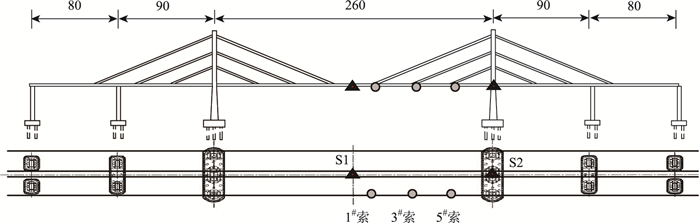
如图 3所示为本研究拟选用的索力与应变监测点布置图,其中S1测点为主梁跨中截面顶板应变计,S2测点为主塔处主梁底板应变计;1#索、3#索、5#索采用光纤栅式压力传感器测量索力。
|
| 图 3 斜拉桥索力与应变计布置(单位:m) Fig. 3 Arrangement of cable tensions and strain gauges on cable-stayed bridge(unit:m) |
| |
此传感器是通过外界物理参量对光纤布拉格波长的调制来获取传感信息,是一种波长调制型光纤传感器,具有高精度、抗干扰能力强、测量范围广等优点。能够准确采集斜拉桥索力信号。建立三维有限元模型,通过荷载试验和监测结果,运用迭代优化设计及响应面法对桥梁结构的振型频率与索力进行修正,从而保证了结构模型的精度[14]。
(2) 车辆模型
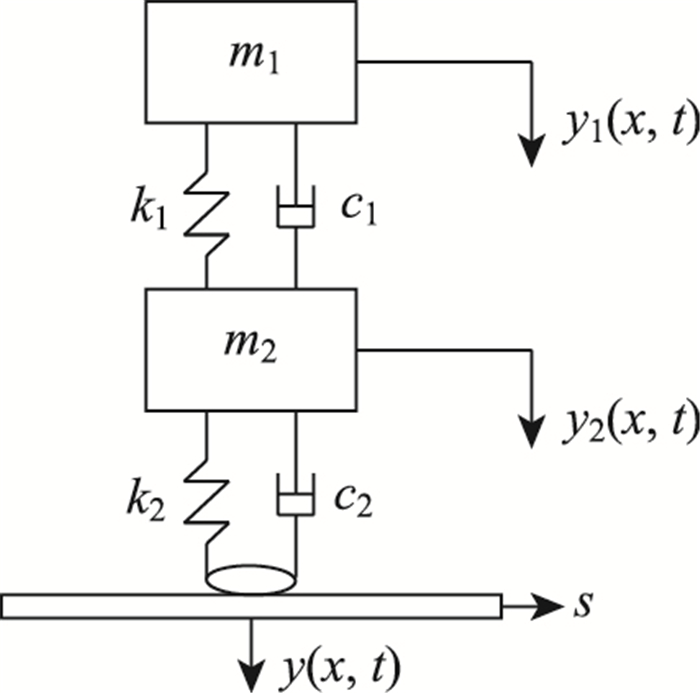
常用的单车模型有三维模型和二维1/2、1/4等简化模型。当车辆模型达到一定精度后对于较大型桥梁的耦合响应,上述不同简化模型的差异较小[15]。本研究主要目标是基于实测响应识别车速车重,因此单车选用相对简单适用的1/4车辆模型(如图 4所示),相关参数选用见参考文献[16-17]。
|
| 图 4 1/4车辆模型 Fig. 4 Quarter vehicle model |
| |
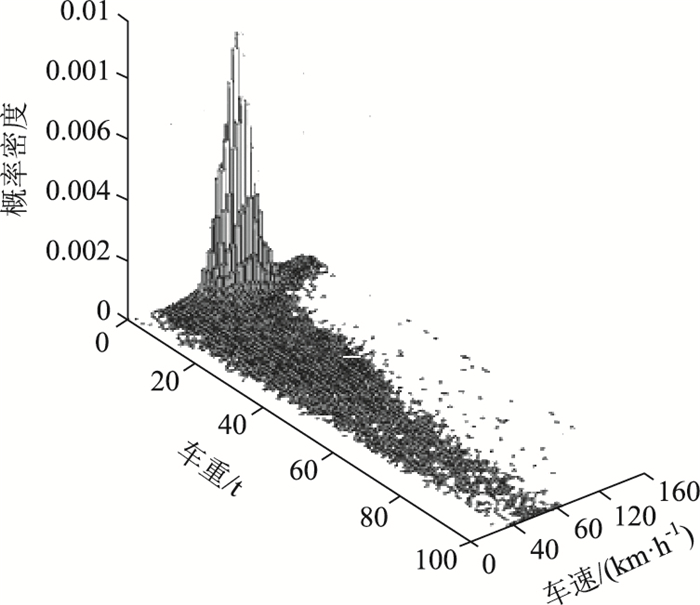
车队模型是基于相似公路上车辆监测结果建立的。相似公路实测车流样本车速车重联合分布模型如图 5所示。基于上述实测车流联合概率分布模型,对下列车速和车重进行了车流组合,用于车桥耦合模拟分析,车速:20,60,90,120,150 km/h;车重:5,10,30,60,90,120,150,180 t。在此基础上对模拟结果进行线性差值,扩大样本数量。
|
| 图 5 实测车流样本车速车重联合分布概率密度 Fig. 5 Joint distribution probability density of vehicle speeds and weights of measured vehicle flow samples |
| |
(3) 桥面不平度
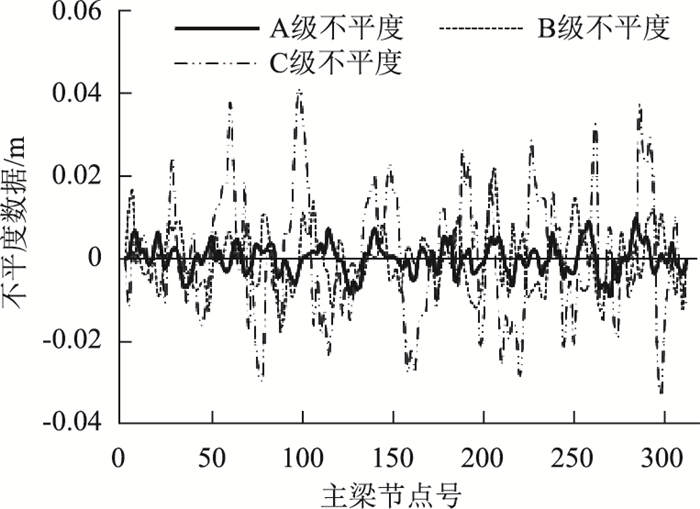
根据我国《车辆振动输入路面不平度表示方法》(GB7031—86)[18]给定的位移功率密度谱函数,即式(1),并结合实际斜拉桥模型生成不同等级的桥面不平度数据,本研究选用的为A级不平度,如图 6所示。
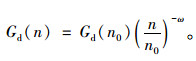
|
(1) |
|
| 图 6 路面不平度 Fig. 6 Road surface roughness |
| |
2.1.2 车桥耦合响应与数据处理
(1) 车桥耦合响应
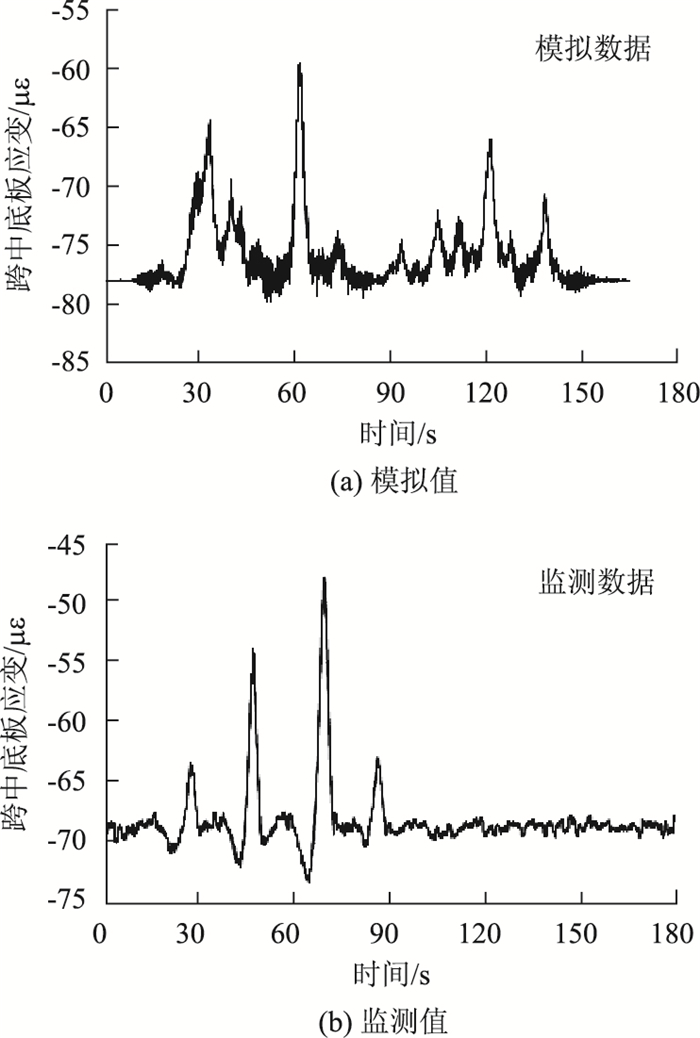
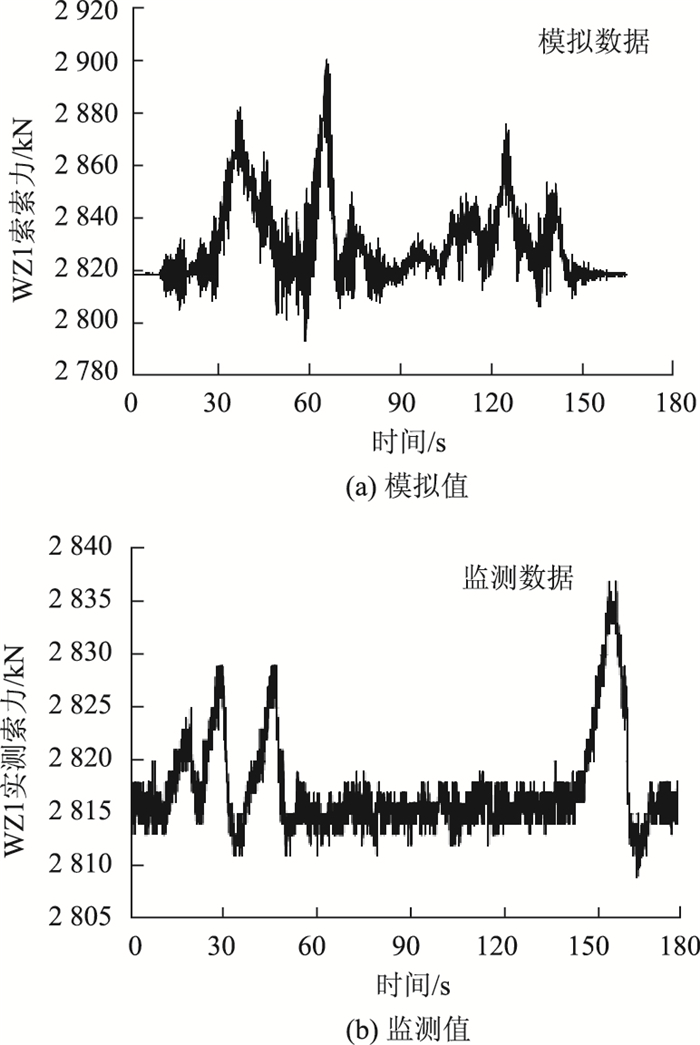
首先,车队加载进行车桥耦合分析[14],并通过相似条件下实测响应对模型进行校正。由于车流是根据实际统计模型生成,模拟结果与实测结果只能在统计意义上具备可比性。因此,图 7和图 8给出的是部分计算响应与相似条件下的实际监测响应在形态上的对比情况。然后,对上节拟定的车辆荷载工况分别进行车桥耦合分析,从而获得各工况下结构的模拟响应。
|
| 图 7 主梁跨中截面纵向应变模拟数据与监测数据对比 Fig. 7 Comparison of simulation data and monitoring data of longitudinal strain of girder mid-span section |
| |
|
| 图 8 WZ1索力模拟数据与监测数据对比 Fig. 8 Comparison of simulation data and monitoring data of WZ1 cable force |
| |
(2) 数据的处理
对于车辆荷载引起的桥梁索力(应变)变化通常以时间为周期,所含信息中高频信号所占比重较大,此种信号正好可以通过这种具有带通滤波功能的小波分析法进行分解与重构,将车辆激励响应、随机干扰部分进行有效分离。
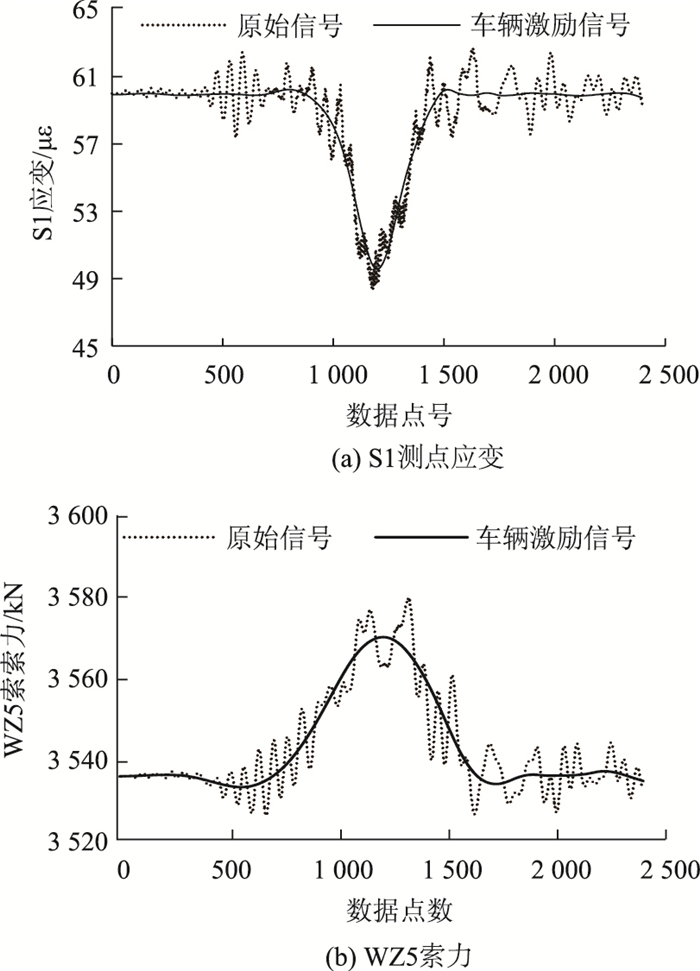
图 9所示为利用MATLAB小波工具箱的Daubechies小波对S1应变和WZ5索力原始数据进行处理的情况。其他测点索力与应变数据处理方式相同,不再赘述。经过小波数据处理,使结果更接近过桥车辆的静态响应,从而提高了响应特征参数提取的准确性。
|
| 图 9 索力与应变原始信号与车辆激励信号对比 Fig. 9 Comparison of original signals and vehicle excitation signals of cable force and strain |
| |
2.2 网络构造与训练/检验 2.2.1 网络构造
网络输入输出节点数,取决于网络的输入输出参数个数。对于车辆荷载识别,输入参数宜选用对车辆荷载作用更为敏感的测点响应进行构造。通过分析,并结合具体斜拉桥监测系统测点布置,选用参数和组成网络输入向量为:
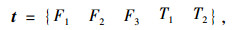
|
(2) |
式中F1,F2,F3分别为WZ5,WZ3,WZ1斜拉索索力;T1为WZ5与WZ3索力峰值点时间差;T2为S1与S2测点应变峰值点时间差。对车辆荷载识别车速V和车重W,输出向量为:
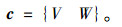
|
(3) |
运用MATLAB神经网络工具箱,经过大量试验最终确定两个隐含层神经元个数分别为25和2,即确定的BP网络结构为5-25-2-2。隐含层传递函数选用tansig,输出层传递函数选用pourlin。
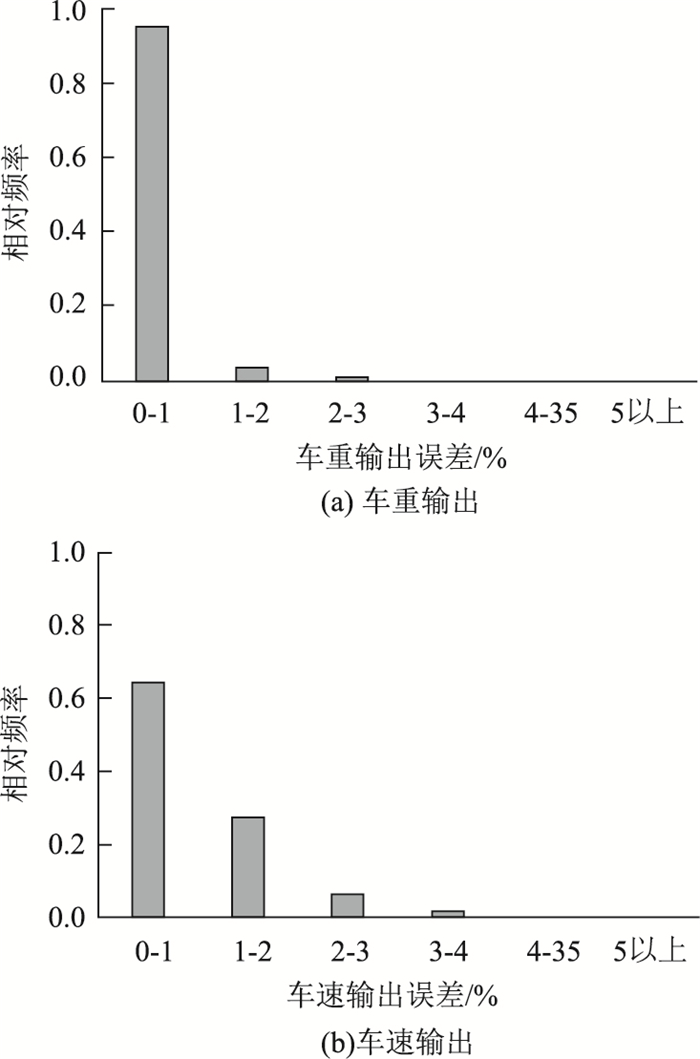
2.2.2 网络训练及检验在模拟各工况车桥耦合响应的基础上,利用线性插值法共得到数据样本2 916组,其中2 616组数据用于训练,300组数据用于训练精度检验。在模拟计算中加入5%随机噪声,网络经过837次迭代后收敛。由300组检验结果的误差分布来评价网络训练精度,结果如图 10所示。可见,车重输出误差都在3%以内,其中90%以上在1%之内。车速输出误差在1%之内的占60%以上,绝大多数车速误差都在3%以内。表明网络训练的精度较高,达到预期效果。
|
| 图 10 网络训练精度检验 Fig. 10 Network training accuracy test |
| |
2.3 基于监测响应的车辆识别
基于某桥实际监测系统,选取2012年6月10日下午4:00—4:16时段的WZ5,WZ3,WZ1索力与S1和S2测点应变监测数据,采用上述数据处理方法进行原始监测数据的处理,然后提取斜拉桥索力的车辆响应特征值F1,F2,F3和两测点索力、应变车辆响应的时间差T1,T2,按照式(2)和式(3)的结构形式构造识别阶段网络输入向量t*。运用上述训练并经过精度检验的网络。
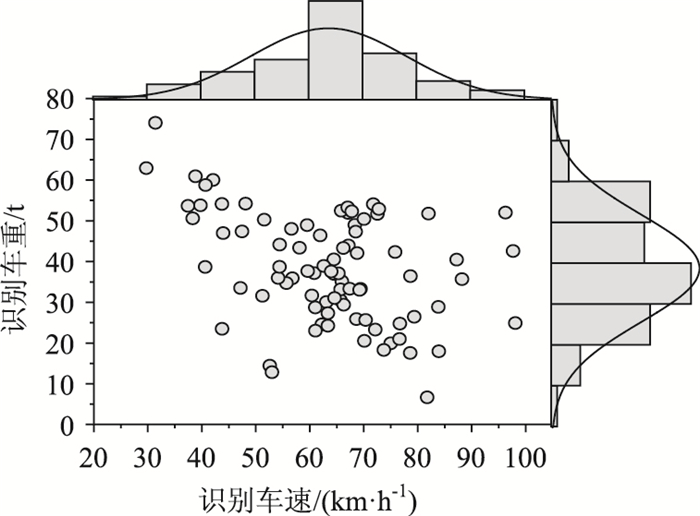
进行实际车辆荷载识别。在实际监测过程中,由于无法获取过桥车辆的车重车速,依据监测系统监测的索力与应变信号作为网络输入,运用神经网络识别出的车速车重只能进行“识别预测”,统计其车速车重的分布规律并与相似公路实测车流车速车重联合分布相比较证明符合一定的规律性。识别结果由图 11可见,车速分布近似于正态分布,均值约在65 km/h。车重分布的范围相对较宽,10 t以下的小型车辆较难识别。车速车重总体上呈现负相关特性,并具一定离散性。
|
| 图 11 车重、车速识别统计结果 Fig. 11 Statistical result of vehicle weight and speed identification |
| |
3 结论
将BP神经网络与斜拉桥监测系统相结合的方式进行车速车重识别是可行的。根据系统监测的索力与应变数据在一定程度上能够识别出车速与车重。当网络的样本足够,网络结构选择恰当时,可获得较好的精度。
从识别结果来看,车速分布近似于正态分布,车重分布范围相对较宽,但10 t以下的小型车辆较难识别。车速车重总体上呈现负相关特性,并具一定离散性。这些特征与图 5相似公路实测车流样本车速车重联合分布实际情况基本吻合。本研究基于桥梁现有监测系统进行斜拉桥过桥车辆荷载识别研究分析,能够实时了解车辆在斜拉桥上运营状态,同时为交通规划提供可靠的车载信息,对超载超速车辆进行监测与控制,在斜拉桥的设计、运营、维护以及安全评估方面具有非常重要的意义。
| [1] |
JACOB B, DE LA BEAUMELLE V F. Improving Truck Safety Potential of Weigh-in-motion Technology[J]. IATSS Search, 2010, 34(1): 9-15. |
| [2] |
李小年, 陈艾荣, 马如进. 桥梁动态称重研究综述[J]. 土木工程学报, 2013, 46(3): 79-85. LI Xiao-nian, CHEN Ai-rong, MA Ru-jin. Review of Bridge Weigh-in-motion[J]. China Civil Engineering Journal, 2013, 46(3): 79-85. |
| [3] |
SNYDER R, MOSES F, KRISS M. Bridge Weigh-in-motion System: USA, 5111897[P]. 1972-05-12.
|
| [4] |
MOSES F. Weigh-in-motion System Using Instrumented Bridges[J]. Transportation Engineering Journal, 1979, 105(3): 233-249. |
| [5] |
张征文, 杨飞, 赵建峰, 等. 基于WIM数据的简支梁桥车辆荷载效应分析[J]. 公路交通科技, 2014, 31(5): 86-92. ZHANG Zheng-wen, YANG Fei, ZHAO Jian-feng, et al. Analysis on Traffic Load Effect of Simply Supported Beam Bridge Based on WIM Data[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 86-92. |
| [6] |
COST 323, European Specification on Weigh-in-motion of Road Vehicles[S].
|
| [7] |
陈惟珍, 王志平, 徐俊. 一种用于钢桁架桥的BWIM方法[J]. 桥梁建设, 2009, 22(4): 72-75. CHEN Wei-zhen, WANG Zhi-ping, XU Jun. A BWIM Method Used for Steel Truss Bridges[J]. Bridge Construction, 2009, 22(4): 72-75. |
| [8] |
张福俭, 李惠. 基于拉索振动监测的车辆荷载识别研究[J]. 土木工程与管理学报, 2013, 30(1): 1-5. ZHANG Fu-jian, LI Hui. Vehicle Loads Identification Through Vibration Monitor of Stay Cables[J]. Journal of Civil Engineering and Management, 2013, 30(1): 1-5. |
| [9] |
王蕾, 侯吉林, 欧进萍. 基于荷载形函数的大跨桥梁结构移动荷载识别[J]. 计算力学学报, 2012, 29(2): 153-158, 177. WANG Lei, HOU Ji-lin, OU Jin-ping. Moving Force Identification Based on Load Shape Function for a Long-span Bridge Structure[J]. Chinese Journal of Computational Mechanics, 2012, 29(2): 153-158, 177. |
| [10] |
谭金华, 陈惟珍, 程飞. 基于运营状态监测数据识别过桥车辆荷载[J]. 桥梁建设, 2006, 22(1): 22-24. TAN Jin-hua, CHEN Wei-zhen, CHENG Fei. Identifying of Passing Vehicle Load Based on Information Obtained from Monitoring of Bridge Operation State[J]. Bridge Construction, 2006, 22(1): 22-24. |
| [11] |
李忠献, 陈锋, 王波. 基于BP神经网络的桥上移动荷载分阶段识别方法[J]. 工程力学, 2008, 25(9): 85-92. LI Zhong-xian, CHEN Feng, WANG Bo. A BP Neural Network-based Stage Identification Method for Moving Loads on Bridges[J]. Engineering Mechanics, 2008, 25(9): 85-92. |
| [12] |
杨慧.基于动态响应的简支梁桥移动荷载识别研究[D].包头: 内蒙古科技大学, 2014. YANG Hui. Moving Load Identification of Simply Supported Girder Bridge Based on Dynamic Response[D]. Baotou: Inner Mongolia University of Science and Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-11973-1014080306.htm |
| [13] |
孙宗光, 陈一飞, 邵元, 等. 基于模型试验的悬索桥结构损伤识别研究[J]. 工程力学, 2014, 31(6): 132-137. SUN Zong-guang, CHEN Yi-fei, SHAO Yuan, et al. Model Test Study on Damage Identification for Suspension Bridges[J]. Engineering Mechanics, 2014, 31(6): 132-137. |
| [14] |
陈一飞.基于长期监测的索桥结构分析评价与识别[D].大连: 大连海事大学, 2018. CHEN Yi-fei. Analytic Evaluation and Identification of Cable Bridge Structure Based on Long-term Monitoring[D]. Dalian: Dalian Maritime University, 2018. |
| [15] |
孙宗光, 陈一飞. 桥梁结构健康监测分析与评价[M]. 北京: 中国建筑工业出版社, 2017: 203-210. SUN Zong-guang, CHEN Yi-fei. Health Monitoring Analysis and Evaluation for Bridge Structures[M]. Beijing: China Architecture & Building Press, 2017: 203-210. |
| [16] |
周玉民, 谈至明, 刘伯莹. 1/4车-路耦合动力学模型研究[J]. 同济大学学报:自然科学版, 2012, 40(3): 408-413. ZHOU Yu-min, TAN Zhi-ming, LIU Bo-ying. Quarter Vehicle-road Coupling Dynamics Models[J]. Journal of Tongji University:Natural Science Edition, 2012, 40(3): 408-413. |
| [17] |
戴君. 基于四分之一车辆模型的具有随机结构参数车辆的随机动力分析[J]. 振动与冲击, 2010, 29(6): 211-215, 246. DAI Jun. Stochastic Dynamic Analysis of Vehicles with Random Parameters Based on a Quarter-car Model[J]. Journal of Vibration and Shock, 2010, 29(6): 211-215, 246. |
| [18] |
GB7031—86, 车辆振动输入-路面平度表示方法[S]. GB7031—86, Vehicle Vibration-Describing Method for Road Surface Irregularity[S]. |
 2019, Vol. 36
2019, Vol. 36
