扩展功能
文章信息
- 顾斌, 高望, 谢甫哲, 雷丽恒
- GU Bin, GAO Wang, XIE Fu-zhe, LEI Li-heng
- 基于历史气象参数的桥梁结构日照温度作用代表值研究
- Study on Representative Values of Solar Temperature Action on Bridge Structure Based on Historical Meteorological Parameters
- 公路交通科技, 2019, 36(12): 79-86, 93
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 79-86, 93
- 10.3969/j.issn.1002-0268.2019.12.010
-
文章历史
- 收稿日期: 2018-10-25
置于自然环境中的混凝土结构桥梁,长期遭受太阳辐射、大气温度变化等环境因素的影响,在这些环境因素影响作用下,结构内部将产生非线性温度分布,从而产生明显的温度效应[1]。为确保桥梁结构物的安全使用,许多国家的桥梁规范对桥梁结构的日照温度梯度分布模型和温度作用代表值进行了规定,但由于地域气候环境的差异,时有文献[2-5]研究表明,规范对桥梁结构温度作用代表值的规定是偏不安全的。
迄今为止,国内外许多学者对桥梁结构日照温度作用代表值进行了研究。如Maes[6]、Li[5]和Lucas[7]分别使用工程实测数据,对桥梁的日照温度作用代表值进行了概率统计分析,其中Maes[6]和Li[5]等的分析结果超出了他们本国规范的规定值;我国的雷笑[4]、丁幼亮[8]、陶翀[2]和刘扬[9]等,也均基于长期工程实测数据对桥梁结构的温度作用代表值进行了计算分析,其中雷笑[4]和陶翀[2]等均根据分析结果指出,现行公路桥规对混凝土箱梁日照温度作用代表值的规定是偏不安全的。使用长期工程实测数据,对桥梁结构日照温度作用的代表值进行研究是最直接有效的方法,其结果也最可靠,但获取数据的成本较高、周期较长,而且由于地域环境因素和桥梁结构的差异,该方法得到的结果对不同地区或不同结构形式桥梁的参考意义有限。故部分学者又转而使用历史气象数据对桥梁结构的日照温度作用代表值进行研究。如彭友松[10]和Lee[3]等从历史气象数据中选择了一些日太阳辐射总强度高、大气日最高温度高、大气日温差大以及风速小的气象数据,对混凝土箱梁的竖向日照温差代表值进行了计算分析;Soukhov[11]、肖建庄[12]和顾斌[13]等分别将日太阳辐射总量、日最高(低)温度和日平均风速进行了概率统计分析,并用这些气象参数的代表值对桥梁结构温度作用的代表值进行了计算分析;使用部分不利工况的气象数据或气象参数的代表值,对桥梁结构日照温度作用代表值进行研究的方法简单方便,但不能反应真实情况,误差可能较大,因此,Larsson[14]和Caner[15]等又提出了使用逐时气象数据对桥梁结构温度作用代表值进行研究的方法,并验证了其准确性。但该方法需要有长期的太阳辐射、大气温度和风速等逐时气象数据,而我国大多数城市由于气象台站观测条件的限制,只有日照时数、日最高与最低温度和日平均风速等日值气象数据。
鉴于此,本研究将基于气象学和桥梁工程学现有的研究成果,提出使用日照时数、日最高与最低温度和日平均风速,计算桥梁结构温度作用代表值的方法,并使用某混凝土箱梁桥工程实例对其可行性进行验证,最后又基于计算分析数据,提出预测混凝土箱梁竖向日照温差的方法。该研究成果将为桥梁工程以及其他土木工程结构日照温度效应的研究提供参考和借鉴。
1 温度作用时程分析的基本原理日照辐射条件下,桥梁表面与周围环境每时每刻都进行着辐射换热和对流换热。在传热学基本原理的基础上,采用有限单元法,可以建立桥梁结构温度场的时程分析方法,从而得到温度场随时间的变化规律。
桥梁结构受日照温度作用产生的温度场实质上是一个三维非稳态温度场问题。为简化计算工作,一般可忽略构件纵向的温度梯度,按平面问题计算温度场[1],用二维热传导方程表示,再加上适当的边界条件和初始条件,就可以运用数值方法进行求解。
二维平面导热微分方程为:

|
(1) |
式中,T为混凝土瞬时温度;t为时间;ρ为密度;c为比热容;λ为导热系数。
在日照辐射作用下,桥梁表面与外界的热交换边界条件可以表示为:

|
(2) |
式中,Γ为箱梁的边界;n为边界的法线方向;hc为对流热交换系数;Ta(t)为外界大气温度;q(t)为已知边界上的热流密度。
2 气象参数的时程模型在应用气象学研究领域,太阳辐射、大气温度和风速等气象参数的研究已经基本成熟。本节将给出由日照时数、日最高温度、日最低温度和日平均风速的日值气象数据计算逐时太阳辐射强度、逐时大气温度和逐时平均风速的方法。
2.1 逐时太阳辐射量目前国内外关于日太阳辐射总量计算、逐时太阳辐射量计算以及直接辐射和散射辐射的分离计算已有较多的研究成果。由日照时数向逐时太阳辐射量的转换主要分为3步:第1步由日照时数求日太阳辐射总量;第2步由日太阳辐射总量求逐时太阳辐射量;第3步对逐时太阳辐射量进行直散分离,求得逐时太阳直射和散射辐射量。具体过程如下。
(1) 日太阳辐射总量计算
目前国内外关于日太阳总辐射量的计算方法有很多,其中由Perman提出的关于日照百分率线性计算模型应用最为广泛,计算公式如下[16]:

|
(3) |

|
(4) |

|
(5) |

|
(6) |

|
(7) |
式中,IGc为地表水平面日太阳辐射总量;IHc为大气层上界水平面日太阳辐射总量;a,b为经验系数;s为日照百分率;Hr为日照时数;H0为可日照时数,即从日出到日落这段时间;ws为日出时的太阳时角,正午时刻太阳时角为0,其他时刻太阳时角为距离正午的时间乘以15;φ为纬度;δ为赤纬角;n为天数,自1月1日开始计算。
(2) 逐时太阳辐射量计算
目前C-P & R模型已经相对比较成熟,使用率和准确性都很高,本研究采用C-P & R模型计算逐时太阳总辐射数据,计算公式如下[17]:
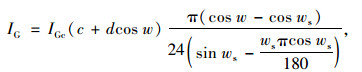
|
(8) |
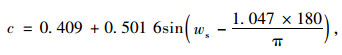
|
(9) |

|
(10) |
式中, IG为地表水平面逐时太阳辐射量;w为太阳时角。
(3) 逐时太阳直射和散射辐射强度计算
在桥梁结构日照温度场的计算中,需要知道倾斜面的太阳辐射量,而倾斜面的辐射量是由水平面的直射和散射间接求出的,所以需要将总辐射分离成直射和散射。在直散分离的研究中,大部分采用晴天指数(即水平面总辐射强度与水平面天文辐射强度之比)的分离模型。计算公式如下[18]:

|
(11) |

|
(12) |
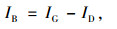
|
(13) |
式中,ID为逐时太阳散射辐射总量;kt为晴空指数,即地表水平面逐时太阳辐射量与大气层上界水平面逐时太阳辐射量的比值;IH为大气层上界水平面逐时太阳辐射量;IB为地表水平面逐时太阳直接辐射总量。
2.2 逐时大气温度在一年中,每一天的气温变化规律, 除了某些日子会发生突变以外,一般都较为一致,即1天之中最低温度发生在日出时左右,最高温度发生在下午两点左右。对逐时气温的计算,计算公式如下[19]:

|
(14) |
式中,Ta(t)为一天中t时刻的大气温度;Tmax-1和Tmin+1分别为前一天大气日最高温度和后一天大气日最低温度;Tmax、Tmin分别为当天大气日最高温度和日最低温度;ts为日出时间,即为-ws/15。
2.3 逐时风速与太阳辐射和大气温度不同,日风速值分布的离散性交大,无明显规律[12]。鉴于风速的变化规律较差,且最不利日照温度作用基本发生在晴天且风速较小的时候,因此,参照文献[12]取逐时风速均等于日平均风速。
3 桥梁结构日照温度作用代表值计算本研究桥梁结构日照温度作用代表值计算方法的流程如图 1所示,整个流程主要分为3步:

|
| 图 1 桥梁结构日照温度作用代表值的计算流程 Fig. 1 Calculation process of representative values of solar temperature action on bridge structure |
| |
(1) 历史气象数据处理
根据第2节处理方法,编写程序将历史气象数据(日照时数、日最高温度、日最低温度、日平均风速)转换成桥梁结构日照温度场分析所需要的逐时气象数据。
(2) 桥梁结构逐时日照温度场的计算分析
根据目标桥梁,建立桥梁主要构件的二维日照温度场有限元模型,使用该模型对桥梁结构的逐时日照温度场进行计算(具体建模方法和温度场边界条件的处理参见文献[20])。
为节省模型的计算时间,应事先对目标桥梁结构日照温度场的分布特点进行分析。对温度变化剧烈的地方尽量多划分单元,温度变化缓慢的地方尽量少划分单元,总之,在保证计算精度的前提下,尽量减少模型的单元数量。
(3) 极值统计分析
通过最不利年(日)日照温度荷载的极值统计分析,可得具有一定重现期的日照温度作用代表值。极值统计分析是研究随机变量小概率事件的统计分析方法,这种方法在水文、气象、地震与工程等许多领域得到广泛应用。极值理论中,极值分布的模型一共3种,即Gumbel、Frechet和Weibull极值分布,为了判断哪一种极值分布模型能较好地适用于样本数据,一种最直接简单的方法就是使用概率纸[21]。概率纸是按某种分布函数设计的一种特殊的坐标纸,其横轴与观测变量有关,纵轴与累积概率有关,这样对于每个连续的分布函数,都可以设计出一种坐标纸,使该分布函数在坐标纸上的图形呈一条直线。
4 工程实例验证本研究以文献[2]中的杭州市某大桥为例,对其日照温度作用的代表值进行计算分析。
4.1 工程概况某大桥位于杭州市周边地区,该桥为双薄壁墩连续刚构桥,跨径布置为(58+3×108+58)m,铺装层厚度为10 cm。呈西北-东南走向,中心线与正北方向夹角55°。主梁采用预应力混凝土变高度箱梁,跨中梁高2.5 m,中支点处梁高5.5 m,箱梁底板按照二次抛物线接顺,其中跨中箱梁截面如图 2所示。

|
| 图 2 跨中箱梁截面(单位:cm) Fig. 2 Cross-section of box girder at mid-span(unit:cm) |
| |
4.2 模型验证
本研究使用文献[2]中所给材料热参数,对该箱梁的温度场进行了计算,图 3为测点2-2和2-3的实测温度和模拟温度的对比图(测点位置见文献[2]),从图中可以看出,计算温度与实测温度吻合均良好,两者不仅在规律上相似,且误差也均在1.5 ℃之内,因此,可以说明本研究建立的有限元模型可以准确地模拟箱梁的实际温度场。

|
| 图 3 模拟温度和实测温度对比图 Fig. 3 Comparison betiveen simulated temperature and measured temperature |
| |
4.3 历史气象数据
本研究使用某桥所在地杭州市1962—2001年这40年的历史气象数据对其日照温度作用代表值进行计算分析。
图 4和图 5分别为杭州市1962—2001年这40年期间日照时数和经式(3)~式(7)转换后日太阳辐射总量的变化情况(a、b参数的取值见文献[16])。从图中可以看出,日照时数和日太阳辐射总量具有明显的年变化规律,在这40年中,每年的最大日照时数在12.1~13.5 h之间波动,最大日太阳辐射总量在27.3~30.2 MJ/m2之间波动。

|
| 图 4 杭州市1962—2001年日照时数的变化情况 Fig. 4 Sunshine hours of Hangzhou City from 1962 to 2001 |
| |

|
| 图 5 杭州市1962—2001年日太阳辐射总量的变化情况 Fig. 5 Daily total solar radiations of Hangzhou City from 1962 to 2001 |
| |
图 6为杭州市1962—2001年这40年期间日最高温度和日最低温度的变化情况。从图中可以看出,日最高温度和日最低温度也具有明显的年变化规律,每年最大和最小日最高温度分别在35.7~39.9 ℃和-3.7~3.6 ℃之间波动,最大和最小日最低温度分别在26.4~29.2 ℃和-9.6~-2.2 ℃之间波动。

|
| 图 6 杭州市1962—2001年日最高、低温度的变化情况 Fig. 6 Daily maximum and minimum air temperatures of Hangzhou City from 1962 to 2001 |
| |
图 7为杭州市1962—2001年这40年期间日平均风速变化情况,从图中可以看出,日平均风速没有明显的变化规律,随机性较大,但多集中在6 m/s之内。

|
| 图 7 杭州市1962—2001年日平均风速的变化情况 Fig. 7 Daily average wind speeds of Hangzhou City from 1962 to 2001 |
| |
4.4 温度作用代表值的计算分析
使用ANSYS有限元软件,建立某大桥跨中箱梁截面的二维日照温度场有限元模型,模型中材料参数的取值与原文献相同。
使用逐时气象数据和建立的日照温度场有限元模型,对目标桥梁的逐时日照温度场进行仿真模拟。通过对仿真结果的提取和处理,得到每年最不利竖向日照温差如图 8所示。从图中可以看出,每年最不利竖向日照温差在14.3~18.4 ℃之间波动,不同年之间最不利竖向日照温差的差距可达4.1 ℃。

|
| 图 8 年最不利竖向日照温差变化情况 Fig. 8 Annual most unfavorable solar vertical temperature differences |
| |
经极值统计分析,年最不利竖向日照温差的累积概率服从Gumbel(15.445,0.819)分布,根据极值分布函数,可得重现期为50年的代表值为18.65 ℃,比原文的研究结果高1.47 ℃,比规范的规定值高4.65 ℃。分析原因为:原文实测值的时间跨度较短,其分布情况不能代表 50年跨度时间内竖向日照温差的分布情况;图 5~图 7中也可以看出,每一年的日照时数、日太阳辐射总量、日最高和最低温度等参数都是变化的,从图 9也可以看出,不同年的最不利日照竖向温差可能相差较大,故短时间实测数据的计算结果可能有一定误差;我国《公路桥涵设计通用规范》对温度日照温度梯度的规定是在参考美国AASHTO规范的基础上修改确定的,对于铺装层厚度为10 cm沥青混凝土箱梁的日照温差,全国统一规定为14 ℃,因此,不能考虑到具体地区的差异。

|
| 图 9 本研究预测结果与其他研究预测结果的对比情况 Fig. 9 Comparison of predicted results between our study and other studies |
| |
5 竖向日照温差的预测研究
为了方便桥梁日照温度作用的设计计算,近些年国内外一些学者基于有限元参数分析或实测数据分析,提出了一系列混凝土箱梁竖向日照温差的预测公式。比如Lee[22]和Abid[23]等提出了使用逐时太阳辐射量、大气温度和风速预测桥梁竖向日照温差的公式,分别如式(18)~式(20)所示;雷笑[24]和陶翀[2]等提出了使用大气温度预测桥梁竖向日照温差的公式,分别如式(18)~式(21)所示。
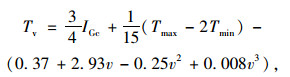
|
(18) |
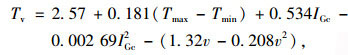
|
(19) |
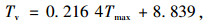
|
(20) |
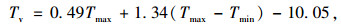
|
(21) |
式中,Tv为竖向日照温差;v为风速。
本研究通过对气象参数和竖向日照温差数据的分析研究,得出以下规律:(1)日太阳辐射总量对竖向日照温差的影响最大,二者之间有着很强的线性相关关系,其相关性系数约为0.969。(2)当天的日最高温度对竖向日照温差有一定影响,二者也有一定的相关性,其相关系数约为0.664。(3)前两天大气温度对竖向日照温差有一定影响,即前两天气温越低,越容易出现较大的竖向日照温差,也即处于升温过程中的天气,较容易出现较大的竖向温差。(4)风速对竖向温差的影响与日太阳辐射总量有关,日太阳辐射总量越大时,风速对竖向日照温差的影响越大,影响规律也越明显,当日太阳辐射总量较小的时候,风速对竖向日照温差的影响较小,同时也无明显关系。
根据以上规律,本研究提出的混凝土竖向日照温差的预测公式如式(22)所示:

|
(22) |
式中,n1,n2,n3,n4,n5,n6为待拟合系数;Tmin-1和Tmin-2分别为前一天和前两天的日最低温度;α为桥面铺装层材料的短波吸收系数。
使用模拟数据对式(22)进行了拟合,拟合后的预测公式如式(23)所示。

|
(23) |
图 9为本研究公式和Lee、Abid、雷笑和陶翀公式预测结果的对比情况,从图中可以看出:本研究公式预测值与模拟值的相关系数(R)最高,约为0.96,且预测平均绝对误差(AEE)也最小,约为0.47 ℃;Lee和Abid公式预测值与本研究模拟值的相关性虽然也较高,分别约为0.91和0.92,但预测值的平均绝对误差偏高,原因可能与地域气候环境因素的差异和他们预测的对象没有铺装层有关,因此,热边界条件的不一样,导致了预测结果的偏差;雷笑和陶翀公式预测值与本研究模拟值的相关性明显低于Lee、Abid和本研究的预测公式,而且预测值的平均绝对误差也较大,原因是他们考虑的因素较少,所以预测值的离散性较大。因此,相对来说本研究公式的预测效果较好。
为验证本研究预测公式的适用性,本研究又使用其他文献的实测结果对式(23)进行了验证(见表 1,表中日照辐射和大气温度由桥址所在城市或附近城市的历史气象数据经统计分析得到,风速统一取0.5 m/s),从表中可以看出,本研究公式的预测结果与其他文献的研究结果吻合程度较好。
6 结论
(1) 在现有气象学研究成果的基础上,使用日照时数、大气日最高温度、大气日最低温度和日平均风速建立了桥梁结构日照温度场时程分析所用的气象参数时程模型。
(2) 提出了使用日照时数、日最高温度、日最低温度和日平均风速计算桥梁结构温度作用代表值的方法,并通过工程实例对其可行性进行了验证。
(3) 杭州市某地区铺装层厚度为10 cm沥青混凝土的混凝土箱梁桥50年一遇竖向日照温差代表值为18.65 ℃,高出了规范的规定值。
(4) 根据分析数据,总结了气象参数对混凝土箱梁竖向日照温差的影响规律,并根据影响规律提出了铺装层厚度为10 cm沥青混凝土的混凝土箱梁竖向日照温差预测公式,该公式可为类似结构桥梁以及和杭州市类似气候地区桥梁结构温度效应的研究提供参考和借鉴。
| [1] |
刘兴法. 混凝土结构的温度应力分析[M]. 北京: 人民交通出版社, 1991. LIU Xing-fa. Analysis on Thermal Stress of Concrete Structures[M]. Beijing: China Communications Press, 1991. |
| [2] |
陶翀, 谢旭, 申永刚, 等. 基于概率分析的混凝土箱梁温度梯度模式[J]. 浙江大学学报:工学版, 2014, 48(8): 1353-1361. TAO Chong, XIE Xu, SHEN Yong-gang, et al. Study on Temperature Gradient of Concrete Box Girder Based on Probability Analysis[J]. Journal of Zhejiang University:Engineering Science Edition, 2014, 48(8): 1353-1361. |
| [3] |
LEE J H. Investigation of Extreme Environmental Conditions and Design Thermal Gradients during Construction for Prestressed Concrete Bridge Girders[J]. Journal of Bridge Engineering, 2012, 17(3): 547-556. |
| [4] |
雷笑, 叶见曙, 王毅. 日照作用下混凝土箱梁的温差代表值[J]. 东南大学学报:自然科学版, 2008, 38(6): 1105-1109. LEI Xiao, YE Jian-shu, WANG Yi. Representative Value of Solar Thermal Difference Effect on PC Box-girder[J]. Journal of Southeast University:Natural Science Edition, 2008, 38(6): 1105-1109. |
| [5] |
LI D N, MAES M A, DILGER W H. Thermal Design Criteria for Deep Prestressed Concrete Girders Based on Data from Confederation Bridge[J]. Canadian Journal of Civil Engineering, 2004, 31(5): 813-825. |
| [6] |
MAES M A, DILGER W H, BALLYK P D. Extreme Values of Thermal Loading Parameters in Concrete Bridges[J]. Canadian Journal of Civil Engineering, 1992, 19(6): 935-946. |
| [7] |
LUCAS J, VIRLOGEUX M, LOUIS C. Temperature in the Box Girder of the Normandy Bridge[J]. Structural Engineering International, 2005, 15(3): 156-165. |
| [8] |
DING Y L, WANG G X. Estimating Extreme Temperature Differences in Steel Box Girder Using Long-term Measurement Data[J]. Journal of Central South University, 2013, 20(9): 2537-2545. |
| [9] |
刘扬, 张海萍, 邓扬, 等. 基于实测数据的悬索桥钢箱梁温度场特性研究[J]. 中国公路学报, 2017, 30(3): 56-64. LIU Yang, ZHANG Hai-ping, DENG Yang, et al. Temperature Field Characteristic Research of Steel Box Girder for Suspension Bridge Based on Measured Data[J]. China Journal of Highway and Transport, 2017, 30(3): 56-64. |
| [10] |
彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都: 西南交通大学, 2007. PENG You-song. Studies on Theory of Solar Radiation Thermal Effects on Concrete Bridges with Application[D]. Chengdu: Southwest Jiaotong University, 2007. |
| [11] |
SOUKHOV D. Representative Values of Thermal Actions for Concrete Bridges[J]. Progress in Structural Engineering and Materials, 2000, 2(4): 495-501. |
| [12] |
肖建庄, 宋志文, 赵勇, 等. 基于气象参数的混凝土结构日照温度作用分析[J]. 土木工程学报, 2010, 43(4): 30-36. XIAO Jian-zhuang, SONG Zhi-wen, ZHAO Yong, et al. Analysis of Solar Temperature Action for Concrete Structure Based on Meteorological Parameters[J]. China Civil Engineering Journal, 2010, 43(4): 30-36. |
| [13] |
顾斌, 陈志坚, 陈欣迪. 基于气象参数的混凝土箱梁日照温度场仿真分析[J]. 东南大学学报:自然科学版, 2012, 42(5): 950-955. GU Bin, CHEN Zhi-jian, CHEN Xin-di. Simulation Analysis for Solar Temperature Field of Concrete Box Girder Based on Meteorological Parameters[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(5): 950-955. |
| [14] |
LARSSON O, THELANDERSSON S. Estimating Extreme Values of Thermal Gradients in Concrete Structures[J]. Materials and Structures, 2011, 44(8): 1491-1500. |
| [15] |
CANER A, GULKAN P, MAHMOUD K, et al. Turkish Solar Radiation Zones for Segmental Box Girder Bridge Design under Temperature Gradient Loading[M]. Berlin: Springer International Publishing, 2016: 77-89.
|
| [16] |
赵伟, 顾骏强, 杨军, 等. 杭州太阳日总辐射变化特征分析[J]. 资源科学, 2009, 31(9): 1587-1591. ZHAO Wei, GU Jun-qiang, YANG Jun, et al. The Calculation Method and Characteristics of Daily Global Solar Radiation in Hangzhou City[J]. Resources Science, 2009, 31(9): 1587-1591. |
| [17] |
LIU B Y H, JORDAN R C. The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation[J]. Solar Energy, 1960, 4(3): 1-19. |
| [18] |
CHOI S, CHA S W, OH B H, et al. Thermo-hygro-mechanical Behavior of Early-age Concrete Deck in Composite Bridge under Environmental Loadings. Part 1:Temperature and Relative Humidity[J]. Materials and Structures, 2011, 4(7): 1325-1346. |
| [19] |
LORENZO E. Energy Collected and Delivered by PV Modules[M]. Hoboken: Handbook of Photovoltaic Science and Engineering, 2011.
|
| [20] |
顾斌, 陈志坚, 陈欣迪. 大尺寸混凝土箱梁日照温度场的实测与仿真分析[J]. 中南大学学报:自然科学版, 2013, 44(3): 1252-1261. GU Bin, CHEN Zhi-jian, CHEN Xin-di. Measurement and Simulation on Solar Temperature Field of Large Size Concrete Box Girder[J]. Journal of Central South University:Science and Technology Edition, 2013, 44(3): 1252-1261. |
| [21] |
史道济. 实用极值统计方法[M]. 天津: 天津科学技术出版社, 2006. SHI Dao-ji. Practical Methods of Extreme Value Statistics[M]. Tianjin: Tianjin Science and Technology Press, 2006. |
| [22] |
LEE J H, KALKAN I. Analysis of Thermal Environmental Effects on Precast, Prestressed Concrete Bridge Girders:Temperature Differentials and Thermal Deformations[J]. Advances in Structural Engineering, 2012, 15(3): 447-459. |
| [23] |
ABID S R, TAYŞI N, ÖZAKÇA M. Experimental Analysis of Temperature Gradients in Concrete Box-girders[J]. Construction and Building Materials, 2016, 106(C): 523-532. |
| [24] |
雷笑, 叶见曙, 王毅, 等. 基于长期观测的混凝土箱梁温度与应变分析[J]. 江苏大学学报:自然科学版, 2010, 31(2): 230-234, 239. LEI Xiao, YE Jian-shu, WANG Yi, et al. Analysis of Concrete Box-girder Temperature and Strain Based on Long Term Observation[J]. Journal of Jiangsu University:Natural Science Edition, 2010, 31(2): 230-234, 239. |
| [25] |
李英华.基于长期健康监测的连续刚构梁桥的性能分析与演化规律研究[D].广州: 华南理工大学, 2012. LI Ying-hua. Performance Analysis and Evolution of Continuous Rigid Frame Bridge Based on Long-term Health Monitoring[D]. Guangzhou: South China University of Technology, 2012. |
 2019, Vol. 36
2019, Vol. 36

