扩展功能
文章信息
- 冯忠居, 李少杰, 董芸秀, 郝宇萌, 胡海波
- FENG Zhong-ju, LI Shao-jie, DONG Yun-xiu, HAO Yu-meng, HU Hai-bo
- 高填方盖板涵垂直土压力分布特性及计算理论
- Vertical Earth Pressure Distribution Characteristics and Calculation Theory of High Fill Culvert
- 公路交通科技, 2019, 36(12): 69-78
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 69-78
- 10.3969/j.issn.1002-0268.2019.12.009
-
文章历史
- 收稿日期: 2018-08-27
2. 中铁建设集团有限公司, 北京 100040;
3. 中交第二公路勘察设计研究院有限公司, 湖北 武汉 710065
2. China Railway Construction Group Co., Ltd., Beijing 100040, China;
3. CCCC Second Highway Consultants Co., Ltd., Wuhan Hubei 710065, China
随着我国高等级公路在山岭区的建设发展,以盖板涵为常用型式的涵洞结构物越来越多。然而由于高等级公路线形标准的要求和地形条件限制,使得山区高等级公路的高填方路基及相应的高填方盖板涵较多。高填方作用下涵顶会发生不同程度的应力集中现象[1-9],一方面,涵顶垂直土压力设计取值偏小时,荷载长期作用下将引起涵洞纵向开裂;另一方面,土压力取值偏大会造成涵洞材料浪费。因而,涵顶垂直土压力作为盖板涵结构设计计算中的主要荷载之一,其取值影响着盖板涵结构设计安全可靠与经济合理性。
国内外计算涵洞土压力的理论研究较多,1913年,马斯顿学者等人[10]基于散体材料极限平衡条件推导出涵洞土压力公式,该公式较早考虑了涵顶垂直土压力集中现象。随后,曾国熙教授[11]在上述马斯顿散体极限平衡理论的基础上加以修正,考虑了土体黏聚力的作用提出了修正公式。1981年,顾安全教授[1]从变形条件出发,以弹性理论为基础提出了上埋式管道土压力的计算公式。之后,很多学者大都在马斯顿理论与顾安全理论的基础上对涵洞土压力公式进行修正。文献[12]基于模型试验结果和修正的马斯顿理论提出了管涵土压力计算模型和计算公式。文献[13]采用理论分析和数值模拟的方法研究了高填方涵洞垂直土压力分布特征和变化规律,并对顾安全土压力理论计算公式进行了修正。文献[14-16]根据高填方涵洞的土压力变化规律及拱效应特点,提出了高填方涵洞的非线性土压力计算理论和方法。文献[17-18]通过现场试验研究了盖板涵台背及涵顶垂直土压力的分布规律和土压力随填土荷载的增长规律。上述研究成果在涵洞土压力方面取得了较大进展,但各种理论公式没有考虑涵顶垂直土压力分布特性,只是把涵顶垂直土压力简化为均布荷载,其计算结果与实际情况不可避免的存在较大差异;上述研究成果未探明填土性质对涵顶垂直土压力分布特性的影响,更没有将其运用于土压力公式计算,不能准确地将涵顶垂直土压力量化。因此,有必要对高填方盖板涵垂直土压力计算理论展开研究。
通过离心模型试验与有限元软件研究高填方盖板涵涵顶垂直土压力分布特性与填土变形规律,利用正交试验分析涵顶土压力不均匀系数与填土性质的关系,得到涵顶土压力不均匀系数回归公式,建立考虑涵顶土压力分布特性的高填方盖板涵土压力分析模型,推导涵顶垂直土压力计算公式,以期完善高填方涵洞土压力理论。
1 离心模型试验与数值模拟方法 1.1 模型设计 1.1.1 离心模型试验相似率高填方盖板涵的离心试验相似关系主要取决于:(1)涵洞的结构尺寸及埋置深度等几何因素;(2)涵周土特性;(3)涵洞结构材料特性;(4)土体的初始应力状态。本次试验根据相似理论和量纲分析理论对试验模型的各物理量进行确定[17, 19-20],将与原型的应力、应变和位移有关的物理量表示为:
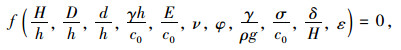
|
(1) |
式中, H为涵顶填土高度;h为涵洞的突出高度;D为涵洞的计算跨径;ρ为土的密度;g为重力加速度;d为涵洞盖板的厚度;γ为填土材料重度;c0,φ为内摩擦角;E,v为泊松比;σ, ε, δ分别为涵洞和土体应力、应变、位移。
高填方盖板涵离心试验相似律见表 1。
| 参数 | 几何 | 填土材料 | 初始应力 | 涵洞结构反应 | |||||||||||||
| 原型 | H/h | D/h | d/h | φ | γh/c0 | E/c0 | v | γ/ρg | d′/h | σ0/ c0 | σ/c0 | ε | δ/H | ||||
| 模型 | H/h | D/h | d/h | φ | γh/c0 | E/c0 | v | γ/ρg | d′/h | σ0/c0 | σ/c0 | ε | δ/H | ||||
| 是否相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | 相似 | ||||
表 1中,d′为土粒直径。从表中可看出,模型与盖板涵实际原型各物理量指标均相似,故采用离心模型试验模拟高填方涵洞问题在理论上是可行的。
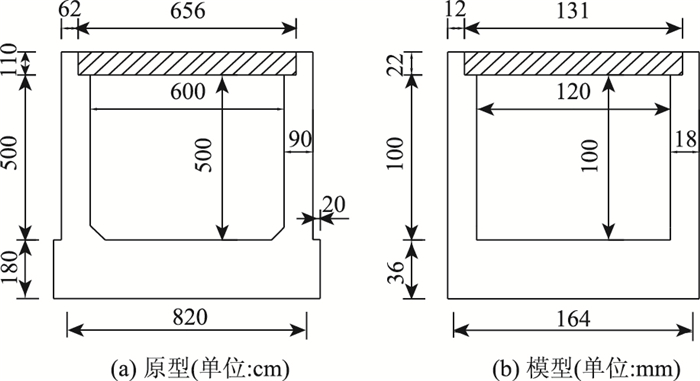
1.1.2 涵洞模型设计涵洞材料采用有机玻璃,其弹性模量E与混凝土材料接近,有机玻璃和混凝土在弹性阶段内应力、应变关系特性相似。模型箱尺寸为700 mm(长)×360 mm(宽)×680 mm(高),试验模型根据原型按1:50比例缩尺制作,为了方便模型放入模型箱,模型长度设计为300 mm,涵洞原型与模型的参数详见图 1。在试验前,先在模型箱内侧涂上液体硅油,以尽量减小地基土和填土与箱壁间的摩擦作用产生的试验误差。试验中填土采用砂质粉土,最优含水量为19.0%,最大干密度为2.0 g/cm3,三轴试验测得的黏聚力为8 kPa,内摩擦角为28°。地基土的最优含水量为15%,最大干密度为2.2 g/cm3,黏聚力与内摩擦角分别为15 kPa,20°。地基土层厚度为100 mm,在盖板涵基础下铺设40 mm厚的砂垫层。首先,按照要求填筑涵洞地基,加速度设置与施加时间分别为50g,3.5 h(实际相当于1 a),保证土体充分固结,之后让模型静止一段时间使之恢复。然后相继在地基上放置涵洞、分层填土,每层填高20 mm(实际填高1 m),涵顶最大填高为400 mm(实际填高20 m)。填筑土体的过程中进行夯实,在每层土压密后进行下一层土的填筑。上述步骤完成后再设置加速度为50g,施加时间为1 h(实际当于104 d)。
|
| 图 1 盖板涵原型-模型尺寸示意图 Fig. 1 Schematic diagram of dimensions of prototype and model of cover culvert |
| |
1.1.3 测试元件的布设
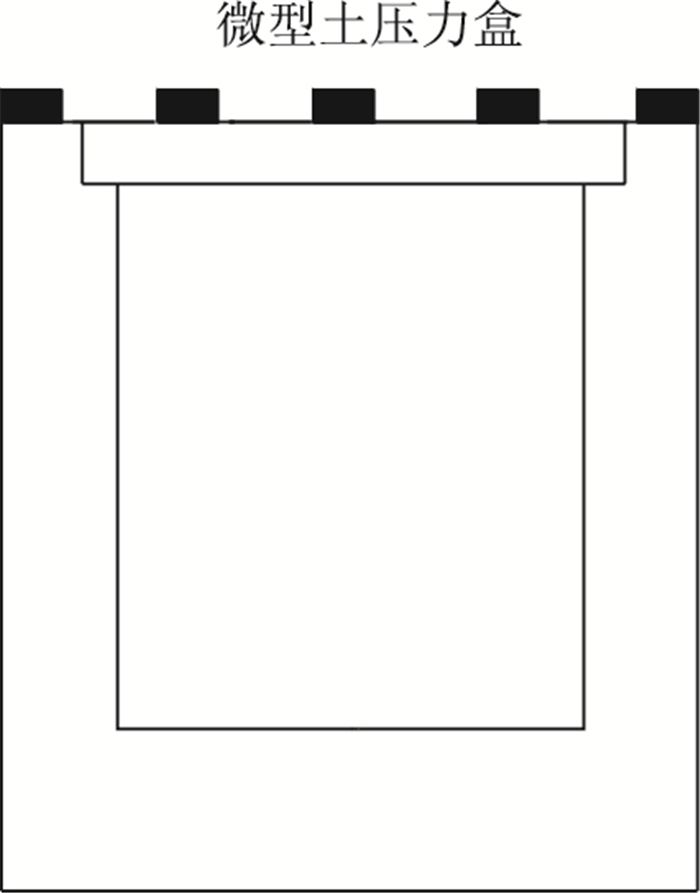
本试验主要揭示不同填高下的盖板涵涵顶土压力及沉降分布规律,测试元件包括土压力盒及沉降标,涵顶布设5个土压力盒。其中为了减小试验仪器的尺寸效应产生的试验误差,试验过程中土压力盒采用微型土压力盒,埋设时紧贴涵身-填土界面,盖板涵模型具体测试元件布设及微型土压力盒如图 2、图 3所示。为了准确观测涵顶填土沉降,通过在模型箱外侧绘制格栅,布设测试标,用数码相机定点拍摄运动模型箱内模型变化,利用计算机对数字图像进行处理,经测量软件处理后得到涵顶土体位移。
|
| 图 2 土压力盒布设图 Fig. 2 Layout of soil pressure boxes |
| |

|
| 图 3 微型土压力盒 Fig. 3 Micro earth pressure box |
| |
1.2 数值模拟方法
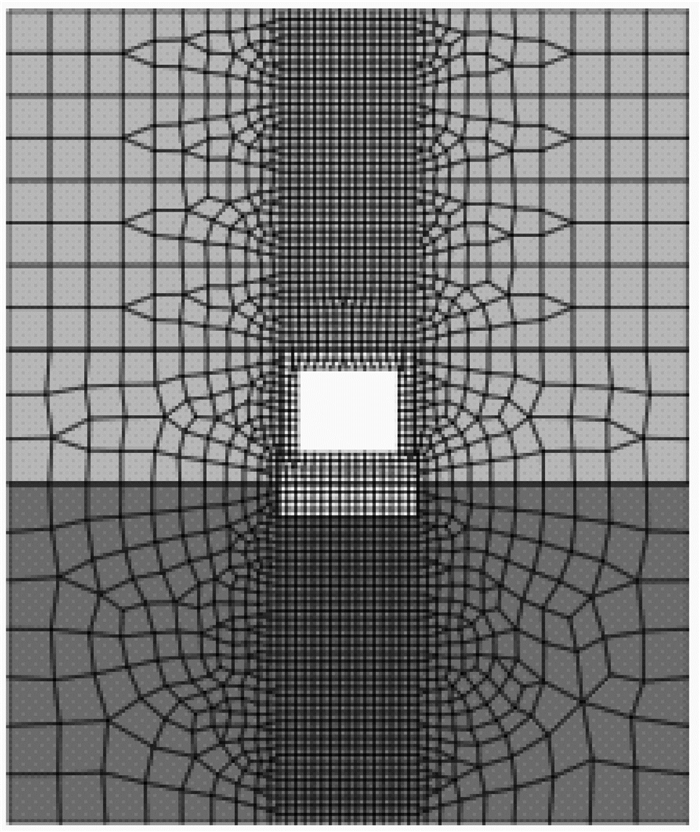
采用有限元软件进行模拟分析,结合盖板涵所处边界、受力特性等情况,视为平面应变问题。采用逐渐增加计算域内网格的数量来模拟分层填土过程,不考虑填土固结等因素的影响。填土与地基土选择理想弹塑性M-C模型模拟,盖板涵采用弹性模型模拟。盖板涵与土体之间的非线性接触采用Coulomb定律描述[7],界面中的属性助手可通过盖板涵与土体的参数自动计算接触参数。计算模型两侧仅约束水平位移,模型底部同时约束水平和竖向位移。如图 4所示,模型水平方向宽度为40 m,地基土厚度为20 m。其中涵洞类型为盖板涵,涵洞净高度为5 m,净宽度为6 m,顶板和侧墙厚度分别为1.1, 0.9 m;基础尺寸为8.2 m2×1.8 m2,在基础下面铺设2.0 m厚的砂垫层。土体及混凝土参数与离心模型试验取值相同,具体参数如表 2、表 3所示。
|
| 图 4 模型网格划分 Fig. 4 Model gridding |
| |
| 材料名称 | 弹性模量E0/MPa | 泊松比v | 容重γ/(kN·m-3) | 黏聚力/ c/kPa | 内摩擦角φ/(°) |
| 填土 | 15 | 0.35 | 20 | 10 | 25 |
| 地基土 | 40 | 0.2 | 19 | 15 | 20 |
| 混凝土 | 3×104 | 0.2 | 25 | — | — |
| 名称 | 法向刚度模量Kn/(kN·m-3) | 切向刚度模量Kt/(kN·m-3) | 虚拟厚度系数tv | 强度折减系数R |
| 接触 | 8.15×105 | 7.41×104 | 0.1 | 0.9 |
2 试验及数值模拟成果分析
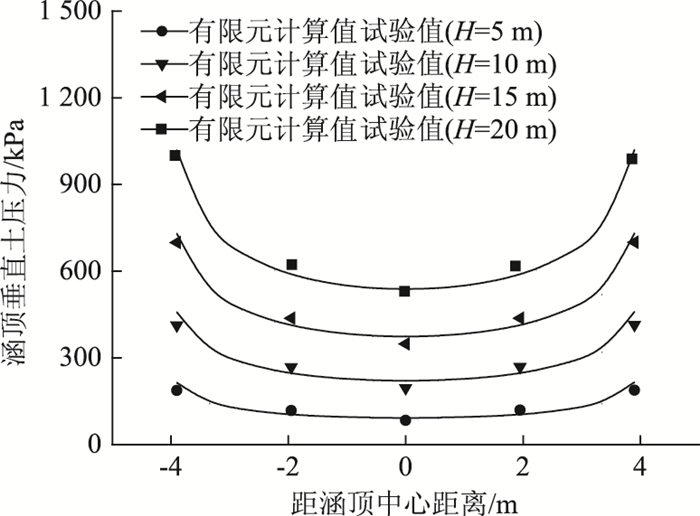
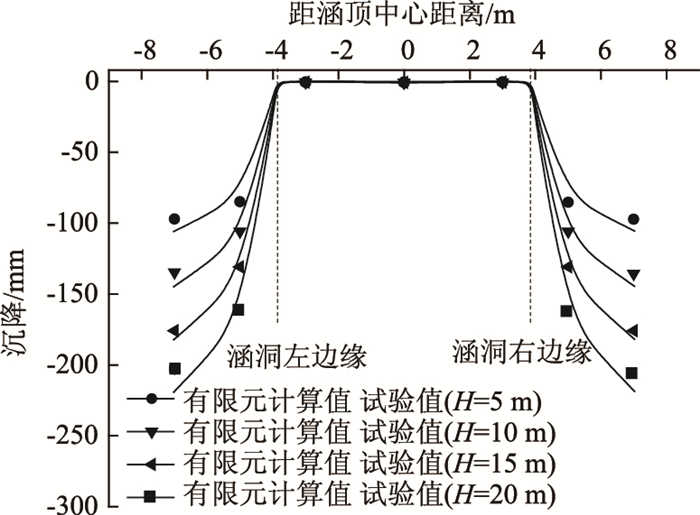
图 5~图 6给出了盖板涵涵顶垂直土压力及填土沉降随填土高度增加的变化规律。可以看出,不同填土高度下涵顶垂直土压力与填土沉降的试验值与有限元计算值较为吻合,验证了有限元计算的准确性。分析得出:涵顶垂直土压力沿跨径呈“马鞍形”对称分布,即“中间小两端大”,且随着涵顶填土高度的增加,“马鞍形”分布特性越显著,涵顶两端垂直土压力总体可达涵顶中心垂直土压力的2倍左右。涵顶垂直土压力大于上覆土重,涵顶产生应力集中现象。这种现象产生的原因在于涵顶平面填土沉降的分布规律,从图 6可以看出,涵顶左右边缘内的填土沉降很小,涵顶左右边缘外填土发生较大沉降,这就使得涵顶外填土对涵顶内填土产生附加土压力,导致涵顶垂直土压力普遍大于上覆土自重。另一方面,涵顶内填土沉降“小且均匀”的分布特点足以说明涵顶中心并不是由于挠曲而产生卸荷,主要是因为涵顶左右边缘受附加土压力的影响较大,使得涵顶两侧的土压力明显大于中心土压力,涵顶垂直土压力为不均匀分布。
|
| 图 5 不同填高涵顶垂直土压力沿跨径变化曲线 Fig. 5 Curves of vertical earth pressure on top culvert at different fill heights along span |
| |
|
| 图 6 不同填高涵顶填土沉降变化曲线 Fig. 6 Curves of settlement of fill on culvert top at different fill heights |
| |
3 正交试验设计与分析 3.1 正交试验设计
顾安全教授曾将涵洞简化为倒置的基础,以弹性理论研究涵顶土压力,并得到一定程度的认可[1]。《土质学与土力学》中提到地基土在弹性变形范围内,基底压力呈“马鞍形”分布[21],这种分布特性与地基土性质密切相关,综上说明涵顶土压力与基底压力的分布特性相同,下面通过正交试验研究不同填土体参数对涵顶土压力不均匀系数If(涵顶中心土压力与涵顶两端土压力的比值)的影响。选取与填土性质相关的5个指标的变化区间,按照4水平确定步长,各因素在不同水平的取值如表 4所示。
| 影响因素 | 变化区间 | 步长 | 水平取值 | |||
| 1 | 2 | 3 | 4 | |||
| 填土高度/m | 5~20 | 5 | 5 | 10 | 15 | 20 |
| 弹性模量/MPa | 15~30 | 5 | 15 | 20 | 25 | 30 |
| 泊松比 | 0.25~0.40 | 0.05 | 0.25 | 0.30 | 0.35 | 0.40 |
| 容重/(kg·m-3) | 16~22 | 2 | 16 | 18 | 20 | 22 |
| 内摩擦角/(°) | 15~45 | 10 | 15 | 25 | 35 | 45 |
3.2 正交试验成果分析
根据表 4中各因素在不同水平的取值,进行5因素4水平正交试验,其中因素A~E分别表示填土的高度、弹性模量、泊松比、容重以及内摩擦角。各因素在表 4中选取对应水平的取值,对表 5中16种组合情况分别建立有限元模型计算涵顶土压力不均匀系数If,计算结果见表 5。
| 试验号 | 列号 | If | 涵顶中心垂直土压力/kPa | 涵顶两端垂直土压力/kPa | ||||
| A | B | C | D | E | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0.472 | 76.61 | 162.12 |
| 2 | 1 | 2 | 2 | 2 | 2 | 0.487 | 85.90 | 176.22 |
| 3 | 1 | 3 | 3 | 3 | 3 | 0.420 | 91.51 | 217.88 |
| 4 | 1 | 4 | 4 | 4 | 4 | 0.340 | 95.24 | 280.12 |
| 5 | 2 | 1 | 2 | 3 | 4 | 0.411 | 208.11 | 506.35 |
| 6 | 2 | 2 | 1 | 4 | 3 | 0.495 | 244.34 | 493.62 |
| 7 | 2 | 3 | 4 | 1 | 2 | 0.494 | 172.23 | 348.64 |
| 8 | 2 | 4 | 3 | 2 | 1 | 0.548 | 200.45 | 365.78 |
| 9 | 3 | 1 | 3 | 4 | 2 | 0.544 | 398.67 | 732.85 |
| 10 | 3 | 2 | 4 | 3 | 1 | 0.583 | 360.76 | 618.80 |
| 11 | 3 | 3 | 1 | 2 | 4 | 0.455 | 331.33 | 728.19 |
| 12 | 3 | 4 | 2 | 1 | 3 | 0.498 | 301.25 | 604.91 |
| 13 | 4 | 1 | 4 | 2 | 3 | 0.445 | 445.37 | 1 000.83 |
| 14 | 4 | 2 | 3 | 1 | 4 | 0.422 | 407.88 | 966.54 |
| 15 | 4 | 3 | 2 | 4 | 1 | 0.518 | 565.23 | 1 091.18 |
| 16 | 4 | 4 | 1 | 3 | 2 | 0.557 | 554.44 | 995.40 |
根据表 5中的涵顶土压力不均匀系数的计算值分别计算因素δ在每一种水平上的试验值的平均数,计算公式如下所示,其中Kiδ表示因素δ在每种水平上的试验值的总和,kiδ表示因素δ在每一种水平上的验值的平均数,Yp, Yq, …, Ys分别为每种水平上的试验值,n为每种水平上试验值的数量。
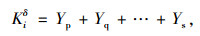
|
(2) |
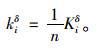
|
(3) |
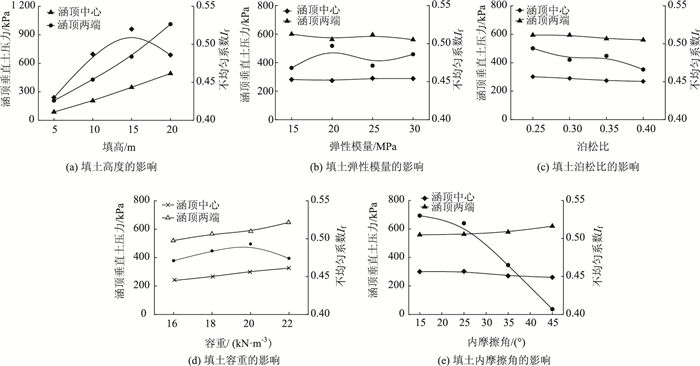
按照上述公式计算影响因素填土的高度、弹性模量、泊松比、容重以及内摩擦角分别在4水平上的试验值的平均数,以实际水平为横坐标,影响因素的试验平均值为纵坐标建立影响因素对涵顶土压力不均匀系数的影响曲线如图 7所示。
|
| 图 7 不同填土参数对涵顶土压力不均匀系数影响曲线 Fig. 7 Curves of influence of different fill parameters on non-uniformity coefficient of soil pressure on culvert top |
| |
从图 7可以看出,随着填土高度以及容重的增加,涵顶土压力的均匀性先提高后减小;涵顶土压力的均匀性与填土的内摩擦角、泊松比呈负相关,涵顶土压力的均匀性与填土的弹性模量总体呈正相关。涵顶土压力不均匀系数与涵顶两端及中心土压力的变化幅度密切相关。根据极差分析原理,试验值的极差越大,影响因素对涵顶土压力不均匀系数的影响程度越大。填土的高度、弹性模量、泊松比、容重以及内摩擦角对应的试验值的极差分别为0.09,0.029,0.028,0.022,0.123,不同因素对涵顶土压力不均匀系数If敏感程度的大小顺序为:内摩擦角>填土的高度>弹性模量>泊松比>容重,因此在计算If时应重视内摩擦角与填土高度的的影响。
3.3 涵顶土压力不均匀系数If的确定采用经验公式法对涵顶土压力不均匀系数If进行回归,得到不均匀系数的公式为:
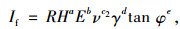
|
(4) |
式中,H为涵顶填土高度;E为填土的弹性模量;ν为填土的泊松比;γ为填土的容重;φ为填土的内摩擦角;R为综合影响因子;a,b,c2,d,e为各因素的影响系数。
对式(4)两边同时取对数,可得:
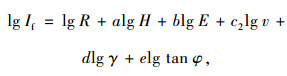
|
(5) |
令Y=lg If,C1=lg R,X1=lg H,X2=lg E,X3=lg v,X4=lg γ,X5=lg tan φ,则:
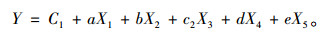
|
(6) |
式(6)经运算后得线性回归公式,根据正交试验表 5中的数据,利用SPSS数据分析软件进行回归分析求解线性回归方程系数,如表 6所示。
| 影响系数 | R | a | b | c2 | d | e |
| 填土 | 0.265 5 | 0.112 | 0.017 | -0.14 | -0.005 | -0.201 |
将影响系数代入式(4),可得涵顶土压力不均匀系数If公式:
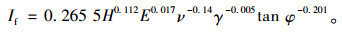
|
(7) |
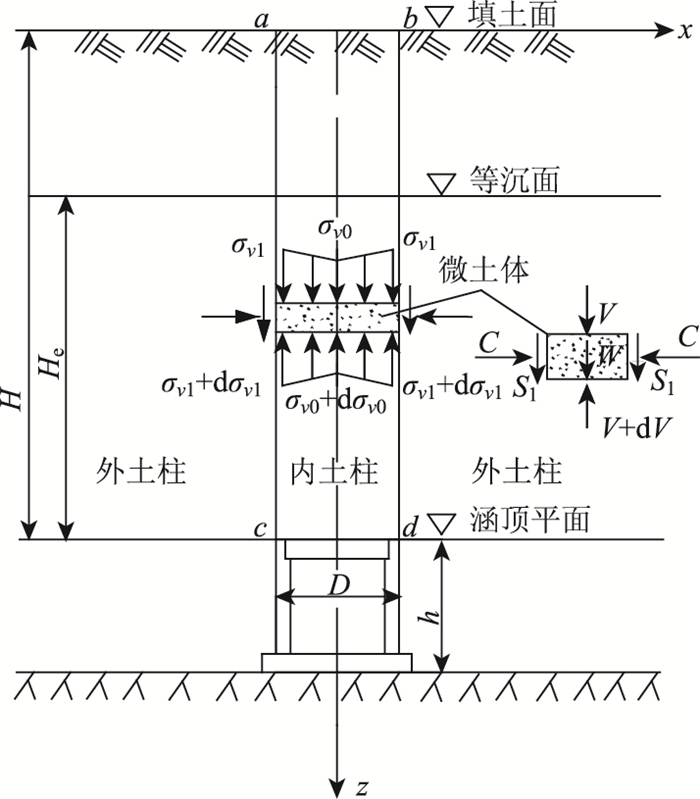
针对涵顶垂直土压力的不均匀分布特性,建立高填方盖板涵土压力分析模型。如图 8所示,盖板涵的宽度为D,高度h。由涵顶开始的填土高度为H,涵顶填土等沉面高度He[13]。图中同时给出了涵顶上部内土柱的土压力分布形式(中间小两边大)。内土柱土层自重W,竖向应力V和V+dV,其不仅受到外土柱对内土柱的侧压力C,同时承担外土柱传递过来的剪切力S1。
|
| 图 8 高填方盖板涵垂直土压力分析模型 Fig. 8 Vertical earth pressure analysis model of cover culvert with high fill |
| |
4.1 计算假定
分析模型建立以下假设:(1)内外土柱的分界为垂直平面,在土体沉陷变形过程中,内外土柱通过其分界面作相对运动,并产生剪切力S1,忽略填土黏聚力的影响;(2)极限平衡状态假定:滑动面间的相对运动,用极限状态表示;(3)内土柱的垂直土压力σv沿盖板涵宽度范围内水平方向为“V形”对称分布,由涵顶两端向中心线性递减,而不是均匀分布,这是区别于马斯顿理论的地方。
4.2 公式推导如图 7所示,假设土的容重为γ,涵顶以上的内土柱abcd高度的dz微土体作为隔离体,其平衡方程可表示为:
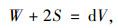
|
(8) |
式中,W为微土体的重量:
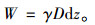
|
(9) |
S为内外土柱间滑动界面的摩擦力,根据假定(2)有:
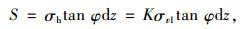
|
(10) |
式中,σh为内外土桩间滑动界面的法向应力;K为土体侧压力系数;经文献[13]验证K取主动土压力系数较为准确:
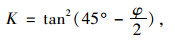
|
(11) |
式中, φ为土体内摩擦角;σv1为内外土柱分界面处竖向应力。
根据假定(3),通过积分可表示微土体竖向应力矢量的合力:
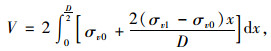
|
(12) |
进一步求解可得:
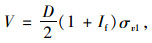
|
(13) |
式中,If为涵顶垂直土压力不均匀系数,用式(9)计算;Wf为涵顶垂直土压力分布系数,定义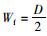
将式(9)~式(13)代入式(8),可得:
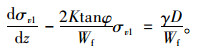
|
(14) |
当H≤He时,由边界条件:z=0,σv1=0对微分方程(12)积分得:
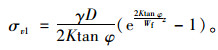
|
(15) |
当H≥He时,由边界条件:z=H-He,σv1=γ·(H-He)对微分方程(12)积分得:
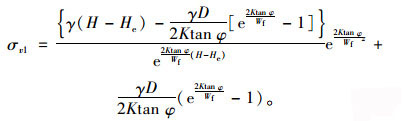
|
(16) |
当z=H时,式(15)、式(16)即为盖板涵涵顶两端垂直土压力公式。
综上所述,当时,盖板涵涵顶中心及两端垂直土压力分别为:
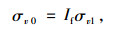
|
(17) |
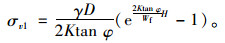
|
(18) |
距涵顶中心距离为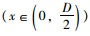
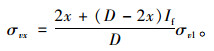
|
(19) |
当H≥He时,盖板涵涵顶中心及两端垂直土压力分别为:
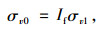
|
(20) |
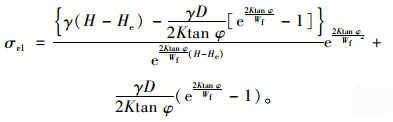
|
(21) |
距涵顶中心距离为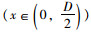
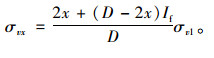
|
(22) |
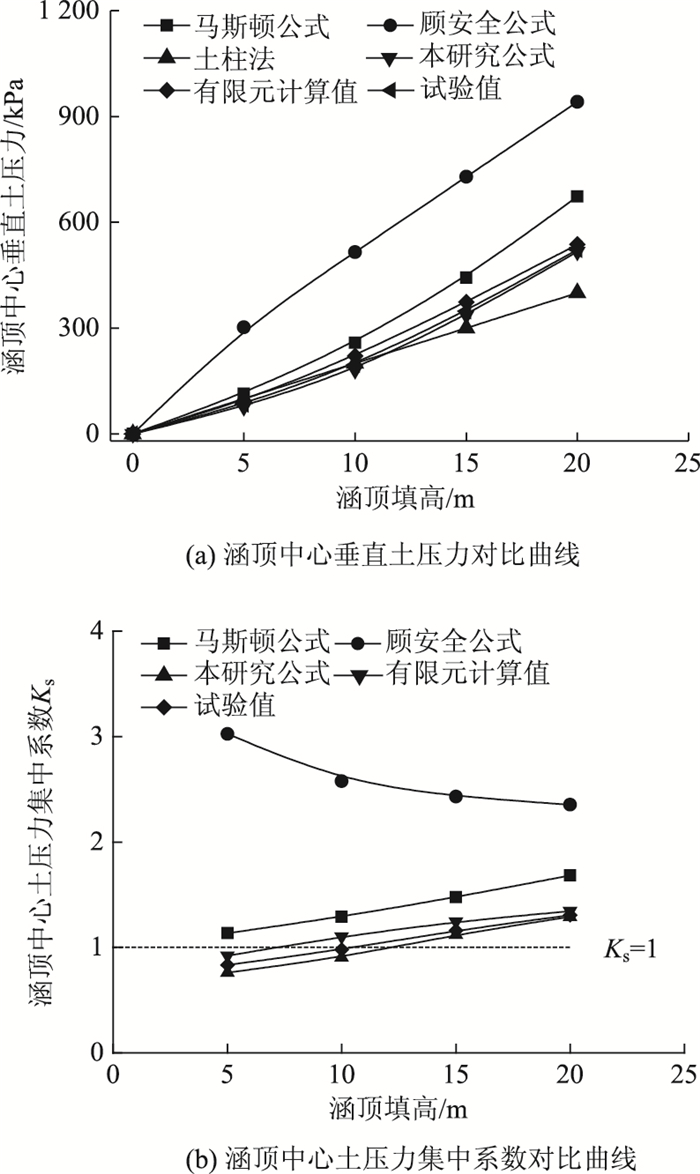
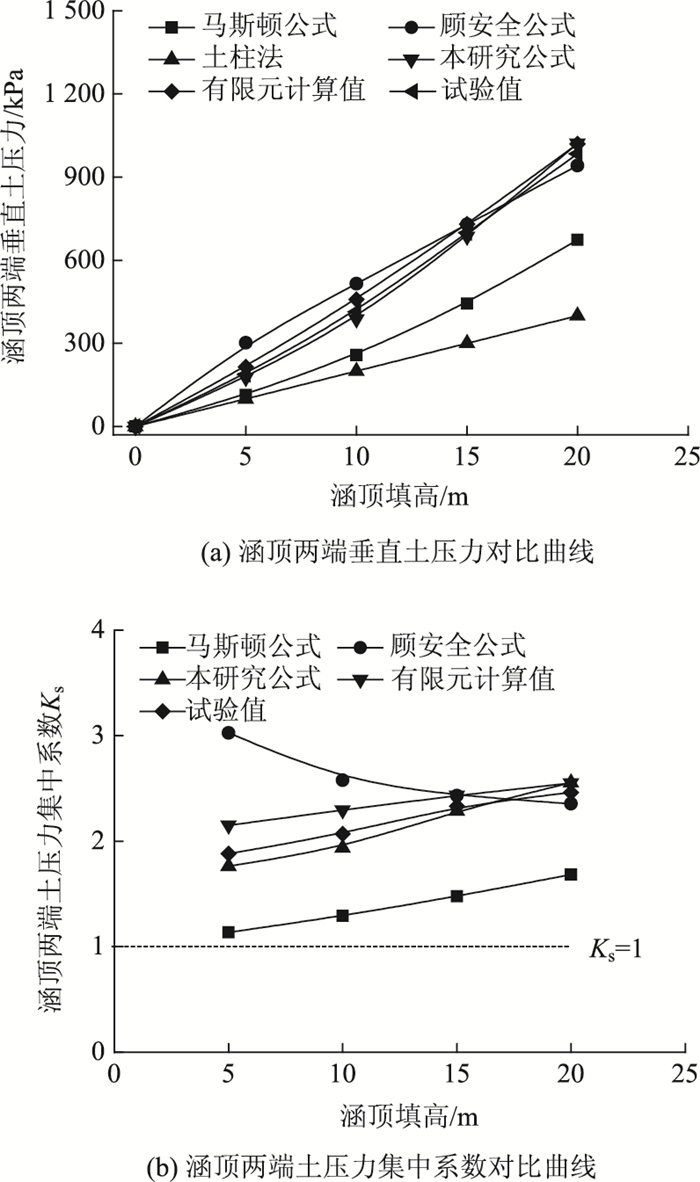
不同涵顶填高作用下,各土压力理论计算公式与数值模拟及模型试验得出的涵顶垂直土压力及集中系数对比曲线如图 9、图 10所示。从图 9、图 10(a)中可以看出,随着涵顶填高的增加,土柱法计算得出的涵顶垂直土压力呈线性增长,其他计算方法得出的涵顶垂直土压力呈非线性增长。通过数值模拟及模型试验成果可知涵顶产生应力集中现象,因此土柱法计算结果不能真实反映涵洞的受力情况。此外,盖板涵涵顶垂直土压力呈“马鞍形”分布,Marston公式与顾安全公式没有考虑涵顶垂直土压力的分布形式,只是简单地把涵顶垂直土压力当做均布荷载,这两种方法计算结果与数值模拟存在较大差异。文中公式通过引入涵顶垂直土压力不均匀系数反映涵顶垂直土压力沿跨径“中间小两边大”的分布规律,将涵顶垂直土压力分布形式简化为“V形”,使其计算得出的涵顶垂直土压力变化规律与数值模拟及模型试验成果最为吻合。从图 9、图 10(b)中可以看出,顾安全公式计算得出的涵顶土压力集中系数随填高逐渐减小,其他方法得出的涵顶土压力集中系数随填高逐渐增大,说明涵顶应力集中现象逐步加剧,其中涵顶两侧的应力集中程度明显大于涵顶中心附近。通过上述分析可以说明文中提出的计算模型较好反映了涵洞的受力状态。
|
| 图 9 涵顶中心土压力及集中系数对比曲线 Fig. 9 Comparison curves of earth pressure on center of culvert top and concentration coefficient |
| |
|
| 图 10 涵顶两端土压力及集中系数对比曲线 Fig. 10 Comparison curves of soil pressure on both ends of culvert top and concentration coefficient |
| |
6 结论
本研究采用离心模型试验与数值模拟结合的方法,研究了高填方盖板涵涵顶土压力及填土沉降变化规律,推导了考虑涵顶土压力分布形式的计算公式,得到以下主要结论:
(1) 盖板涵涵顶垂直土压力沿跨径呈“马鞍形”分布,涵顶两端垂直土压力总体可达涵顶中心垂直土压力的2倍左右,涵顶填土差异沉降是揭示涵顶土压力集中现象与分布特性的内在因素。
(2) 随着填土高度以及容重的增加,涵顶土压力不均匀系数先增加后减小,涵顶土压力不均匀系数与填土的内摩擦角、泊松比呈负相关,与填土的弹性模量总体呈正相关,不同填土参数对涵顶土压力不均匀系数敏感程度的大小顺序为:内摩擦角>填土的高度>弹性模量>泊松比>容重。
(3) 文中提出的盖板涵土压力分析模型较好反映了涵顶垂直土压力“中间小两边大”的分布特性,与其他计算理论的结果相比,计算值能较好反映涵洞实际受力情况。
(4) 涵顶两侧应力集中程度明显大于涵顶中心附近,顶板中心处的压力并非超出上覆填土自重很多,在工程设计中应重视盖板涵涵顶土压力分布特性。
| [1] |
顾安全. 上埋式管道及洞室垂直土压力的研究[J]. 岩土工程学报, 1981, 3(1): 3-15. GU An-quan. Investigation of the Vertical Earth Pressure on Projecting Conduit and Underground Chamber under a High Embankment[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(1): 3-15. |
| [2] |
冯忠居. 大型沟埋式蛋型管道土压力的非线性有限元分析[J]. 西安公路交通大学学报, 1996, 16(4): 23-27. FENG Zhong-ju. The Analysis of the Soil Pressure of Large Egg-shapped Ditch Conduit by Finite Element[J]. Journal of Xi'an Highway University, 1996, 16(4): 23-27. |
| [3] |
冯忠居, 乌延玲, 贾彦武, 等. 钢波纹管涵洞受力与变形特性模拟试验研究[J]. 岩土工程学报, 2013, 35(1): 187-192. FENG Zhong-ju, WU Yan-ling, JIA Yan-wu, et al. Model Tests on Force and Deformation Characteristics of Corrugated Steel Pipe Culvert[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 187-192. |
| [4] |
冯忠居, 李少杰, 郝宇萌, 等. 基于填土-涵洞-地基共同作用机制的涵洞减载数值模拟研究[J]. 公路, 2018, 63(6): 50-57. FENG Zhong-ju, LI Shao-jie, HAO Yu-meng, et al. Research on Numerical Simulation of Culvert Load Reduction Based on Interaction Mechanism of Filled Soil-culvert-base[J]. Highway, 2018, 63(6): 50-57. |
| [5] |
郭婷婷, 顾安全. 减荷措施下涵洞土压力与填土变形数值计算[J]. 交通运输工程学报, 2010, 10(5): 12-16, 29. GUO Ting-ting, GU An-quan. Numerical Simulation of Soil Pressure and Deformation for Culvert with Load-reducing Measures[J]. Journal of Traffic and Transportation Engineering, 2010, 10(5): 12-16, 29. |
| [6] |
马强, 郑俊杰, 张军, 等. 高填方涵洞减载机制与数值分析[J]. 岩土力学, 2010, 31(增1): 424-429. MA Qiang, ZHENG Jun-jie, ZHANG Jun, et al. Mechanism Analysis and Numerical Simulation on Load Reduction for Culvert Beneath High Filling[J]. Rock and Soil Mechanics, 2010, 31(S1): 424-429. |
| [7] |
邓国华, 邵生俊. 填埋式涵洞上覆土压力的有限元分析[J]. 岩石力学与工程学报, 2004, 23(增1): 4356-4360. DENG Guo-hua, SHAO Sheng-jun. FEM Analysis on Earth Pressure of Embedded Culvert in Subgrade or Dike[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S1): 4356-4360. |
| [8] |
KANG J, PARKER F, YOO C H. Soil-structure Interaction and Imperfect Trench Installations for Deeply Buried Concrete Pipes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(3): 277-285. |
| [9] |
KIM K, YOO C H. Design Loading on Deeply Buried Box Culverts[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(1): 20-27. |
| [10] |
MARSTON A, ANDERSON A O.The Theory of Loads on Pipes in Ditches and Tests of Cement and Clay Drain Tile and Sewer Pipe[R].City of Ames: Iowa Engineering Experiment Station, 1913.
|
| [11] |
曾国熙. 土坝下涵管竖向土压力的计算[J]. 浙江大学学报, 1960, 33(6): 79-97. ZENG Guo-xi. Calculation of Vertical Earth Pressure on Culvert under Dam[J]. Journal of Zhejiang University, 1960, 33(6): 79-97. |
| [12] |
郑俊杰, 赵建斌, 陈保国. 高路堤下涵洞垂直土压力研究[J]. 岩土工程学报, 2009, 31(7): 1009-1013. ZHENG Jun-jie, ZHAO Jian-bin, CHEN Bao-guo. Vertical Earth Pressure on Culverts under High Embankments[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1009-1013. |
| [13] |
申文明, 边学成, 唐晓武, 等. 低填方上埋式管涵土压力的模型试验和理论研究[J]. 岩土工程学报, 2010, 32(7): 1017-1022. SHEN Wen-ming, BIAN Xue-cheng, TANG Xiao-wu, et al. Model Tests and Theoretical Studies on Earth Pressure on Shallow Positive Buried Culverts[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 1017-1022. |
| [14] |
杨锡武, 张永兴. 山区公路高填方涵洞的成拱效应及土压力计算理论研究[J]. 岩石力学与工程学报, 2005, 24(21): 89-95. YANG Xi-wu, ZHANG Yong-xing. Study on Arch Action and Earth Pressure Theory for Culverts under High Embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 89-95. |
| [15] |
杨锡武, 张永兴. 公路高填方涵洞土压力变化规律及计算方法研究[J]. 土木工程学报, 2005, 38(9): 119-124. YANG Xi-wu, ZHANG Yong-xing. A Study on the Earth Pressure Theory for High Fill Culverts[J]. China Civil Engineering Journal, 2005, 38(9): 119-124. |
| [16] |
周兴涛, 陈保国, 简文星, 等. 沟埋涵洞土拱效应及涵顶垂直土压力研究[J]. 地下空间与工程学报, 2015, 11(4): 957-964. ZHOU Xing-tao, CHEN Bao-guo, JIAN Wen-xing, et al. Soil Arching Effect and Vertical Earth Pressure on Trench Installation Culverts[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(4): 957-964. |
| [17] |
马强, 郑俊杰, 李丽华, 等. 装配式盖板涵土压力和变形的现场试验研究[J]. 应用基础与工程科学学报, 2014, 22(2): 364-374. MA Qiang, ZHENG Jun-jie, LI Li-hua, et al. Field Test on the Earth Pressure and Deformation of An Assembled Slab Culvert[J]. Journal of Basic Science and Engineering, 2014, 22(2): 364-374. |
| [18] |
陈保国, 骆瑞萍, 孙金山. 上埋式盖板涵受力特性及影响因素研究[J]. 岩土力学, 2011, 32(1): 199-206. CHEN Bao-guo, LUO Rui-ping, SUN Jin-shan. Study of Stress Characteristics and Its Influencing Factors of Embankment Installation Slab-culverts[J]. Rock and Soil Mechanics, 2011, 32(1): 199-206. |
| [19] |
康佐, 杨晓华, 谢永利, 等. 高填路堤下涵洞病害机理[J]. 长安大学学报:自然科学版, 2006, 26(2): 22-26, 30. KANG Zuo, YANG Xiao-hua, XIE Yong-li, et al. Disease Mechanism of Culvert under Embankment of Special High-stacked Soil[J]. Journal of Chang'an University:Natural Science Edition, 2006, 26(2): 22-26, 30. |
| [20] |
边学成, 申文明, 马祖桥, 等. 不同填土管涵土压力模型试验和数值模拟研究[J]. 土木工程学报, 2012, 45(1): 127-133. BIAN Xue-cheng, SHEN Wen-ming, MA Zu-qiao, et al. Model Test and Numerical Simulation of Earth Pressure on Culvert under Different Earth Backfill Conditions[J]. Journal of Civil Engineering, 2012, 45(1): 127-133. |
| [21] |
钱建固. 土质学与土力学[M]. 北京: 人民交通出版社, 2015. QIAN Jian-gu. Soil Properties and Soil Mechanics[M]. Beijing: China Communications Press, 2015. |
 2019, Vol. 36
2019, Vol. 36
