扩展功能
文章信息
- 赵秋, 陈孔生, 陈平, 赵云鹏
- ZHAO Qiu, CHEN Kong-sheng, CHEN Ping, ZHAO Yun-peng
- 钢桥面板U肋对接焊缝疲劳细节有限元分析方法
- A FEM for Analysing Fatigue Details of U-rib Butt Welds of Steel Bridge Deck
- 公路交通科技, 2019, 36(12): 53-61
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 53-61
- 10.3969/j.issn.1002-0268.2019.12.007
-
文章历史
- 收稿日期: 2017-08-15
2. 辽宁省交通规划设计院有限责任公司, 辽宁 沈阳 110166
2. Liaoning Provincial Transport Planning and Design Institute, Shenyang Liaoning 110166, China
自第1座正交异性钢桥面板建造完成以来,正交异性钢桥面板由于其承载能力大、自重轻等优势,在世界范围内得到了大量的应用。但是,由于正交异性钢桥面板使用年限的增加,各种疲劳问题也随之出现,甚至造成多起事故,给社会带来了巨大的损失[1]。经过国内外大量的实践和研究,总结出4个在钢桥面板中最容易出现疲劳裂纹的焊接部位[2-3]。U肋对接焊缝细节就是4个部位之一,而纵肋在桥面体系中作为主梁发挥作用,保证它的正常受力尤为重要。
2003年,在日本Kinuura桥的U肋纵向对接焊缝处发现了大量疲劳裂纹,Kentaro Yamada[4]等人对该细节展开研究。通过过去在常幅应力下的实测结果和通过线弹性损伤理论的预测结果比较表明:大多数的疲劳裂缝是在2~3 mm的不完全焊透下产生的。唐亮、黄李骥[5]等人开展正交异性钢桥面板足尺模型疲劳试验研究,研究表明,U肋对接焊缝细节的疲劳强度等级相当于欧洲规范Eurocode中的71类细节。吉伯海等人[6-7]以江阴大桥为例,采用数值模拟的方法,研究了车轮行驶位置对钢桥面板U肋对接焊缝疲劳性能的影响,并进一步在江阴大桥各车道U肋对接焊缝处布设测点,测得该桥一天的应变历程曲线,对其疲劳寿命进行评估,结果表明:当轮载距离焊缝大于600 mm时,轮载对焊缝的疲劳性能影响可忽略不计;U肋下缘弧形段疲劳损伤严重,容易产生疲劳裂纹;慢车道U肋对接焊缝的疲劳寿命远远不能满足设计要求,因此需要对慢车道U肋对接焊缝寿命给予特别关注。
但是上述研究成果对于正交异性钢桥面板的设计来说,没有直接的参考性。疲劳细节在车辆荷载作用下产生的应力是影响其疲劳性能的关键参数,而荷载加载方法和有限元分析模型的网格划分对分析结果又有重大影响。因此有必要开展U肋对接焊缝疲劳细节的疲劳分析方法研究。
1 疲劳分析模型 1.1 纵肋相关疲劳细节对于纵肋的相关细节,AASHTO[8],EUROCODE[9]和我国的《公路钢结构桥梁设计规范》(JTG D64—2015)[10]都给进行了疲劳细节分类。图 1显示了带垫板的全熔透对接焊缝、不带垫板的双面全熔透对接焊缝和纵肋下方横梁挖孔的纵肋处共3个疲劳细节,未包括纵肋下方横梁不挖孔结构,规范中各疲劳细节的疲劳应力为弯曲正应力幅。AASHTO,EUROCODE及我国钢桥规范的常幅疲劳极限对比如表 1所示。
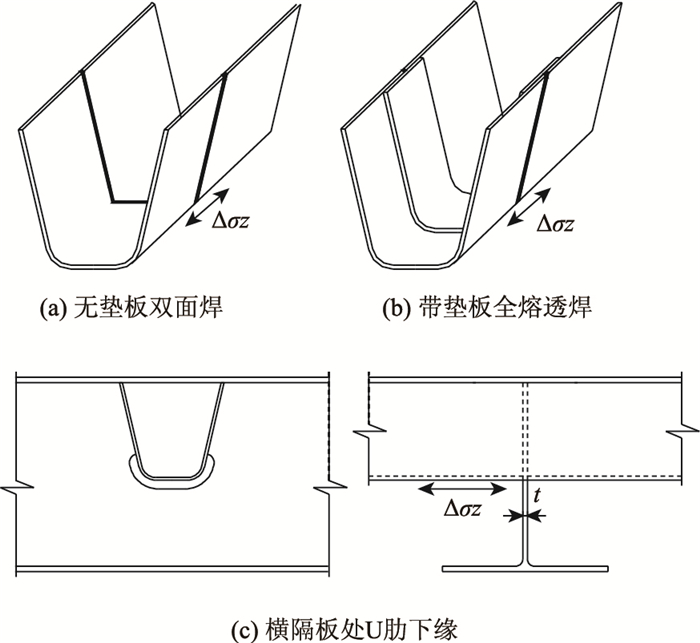
|
| 图 1 纵肋相关疲劳细节 Fig. 1 Fatigue details of longitudinal rib |
| |
| 疲劳细节 | 常幅疲劳极限[σ0] /MPa | |||
| AASHTO | EUROCODE | JTG D64—2015 | ||
| (a) | 31 | 71 | 70 | |
| (b) | 69 | 焊缝沿箭头方向磨平 | 112 | 110 |
| 焊缝余高不大于焊缝宽度10%,且光滑过度到表面 | 90 | 90 | ||
| 焊缝余高不大于焊缝宽度的20% | 80 | 80 | ||
| (c) | 48.3 | U肋腹板厚度t < 12 | 80 | 80 |
| U肋腹板厚度t>12 | 71 | 70 | ||
从表 1可以看出,我国的《公路钢结构桥梁设计规范》基本是参考欧洲规范EUROCODE编制的,分类比较详细。而美国AASHTO手册对于疲劳细节(b)的分类略为粗糙,所以取得常幅疲劳极限也偏于保守。
美国《正交异性钢桥梁的设计、建造和维修手册》指出应该考虑纵肋与横隔板连接区域纵肋上的垂直局部应力Δσy。但是对该细节的研究还不很成熟,所以未对该细节进行分类。其细节具体位置和应力方向如图 2所示。
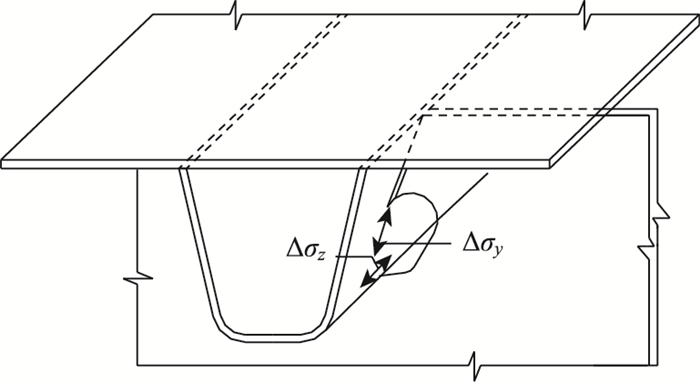
|
| 图 2 纵肋疲劳细节与疲劳应力方向 Fig. 2 Fatigue details and stress direction of longitudinal rib |
| |
1.2 有限元计算模型
在疲劳荷载作用下,正交异性钢桥面板的荷载效应是局部的,因此可采用局部钢箱梁节段模型进行有限元分析[11-14],以保证在降低模型复杂性的情况下,还能得到与实际受力情况基本一致的结果。以某钢箱梁桥为例,其主要尺寸参数如下:梁宽为33.10 m,梁高为4.50 m,横隔板间距2.50 m,横隔板厚22 mm,桥面板的顶板厚度为14 mm,U肋板厚为8 mm,U肋间距为600 mm。取出其中5道横隔板的节段长度,利用Abaqus软件进行有限元分析,建模方式与文献[15]一致。

|
| 图 3 钢箱梁节段模型 Fig. 3 Segment model of steel box girder |
| |
2 网格划分大小分析
美国AASHTO规范[8]对横梁与纵肋连接处附近的网格划分进行了规定,但并没有对桥面板其他疲劳细节的网格划分给出详细的推荐。因此,有必要研究U肋网格大小变化对U肋各疲劳细节应力变化的影响,以便进行桥面板疲劳分析时正确选取网格大小。
2.1 横隔板处为了使得计算结果偏于保守,与U肋连接处的横隔板附近的网格大小取为U肋腹板厚度t。横隔板与U肋连接处附近的U肋腹板网格大小分别划分为0.5t,t,2t,4t和8t,对计算结果进行比较,横隔板与U肋相关处细部网格划分见图 4(以1t, 4t网格大小为例)。当U肋网格与横梁腹板网格不同时,两个面相交区域的网格就会产生不协调,所以需要在与U肋相连接的横隔板区域设置网格过渡区域,U肋网格大小不同时如图 4所示。
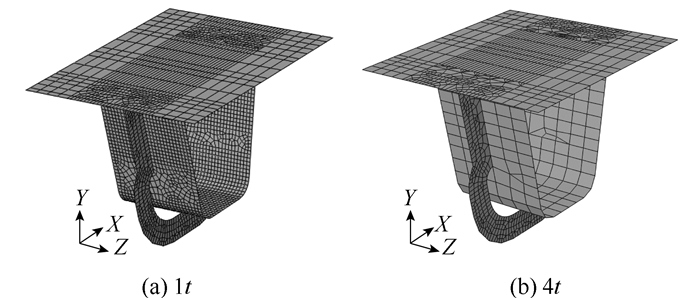
|
| 图 4 U肋与横隔板连接区域网格划分 Fig. 4 Mesh partition of U-rib and diaphragm connection area |
| |
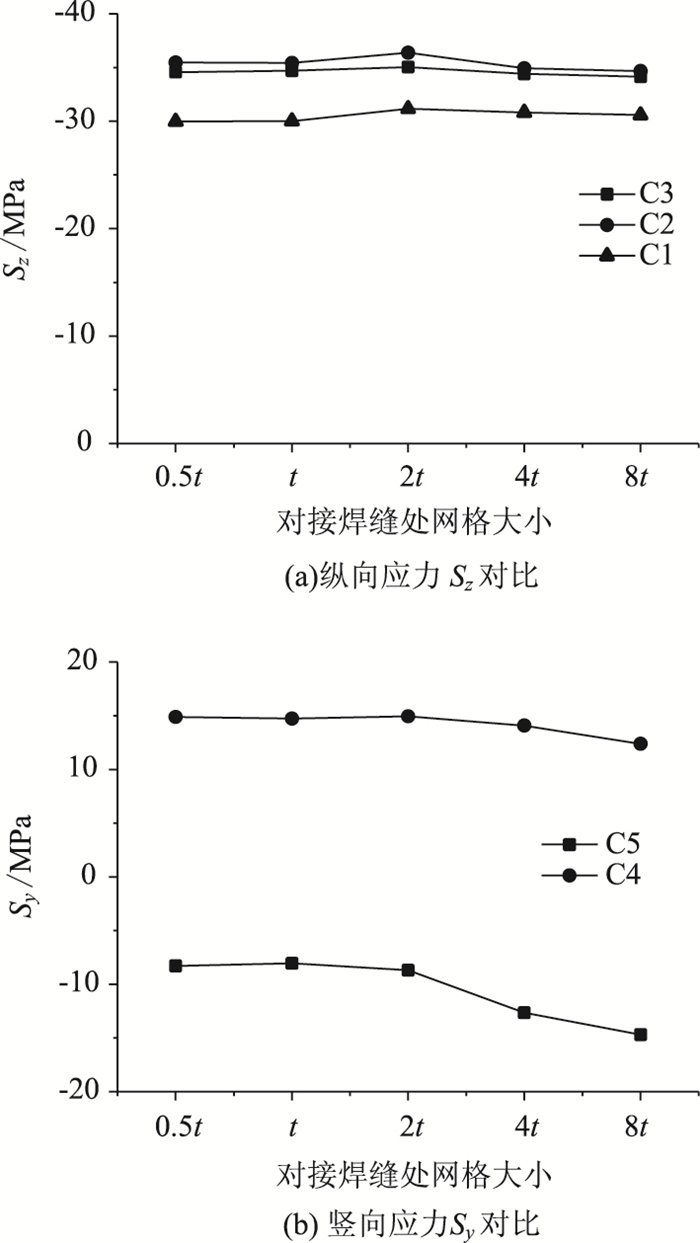
在U肋与横隔板相交处正上方布置一个车轮荷载,分析在相同荷载作用下U肋下缘对接焊缝处C1,C2,C3位置的纵向应力Sz和C4,C5处的竖向应力Sy并进行比较。其位置和计算结果如图 5和图 6所示。
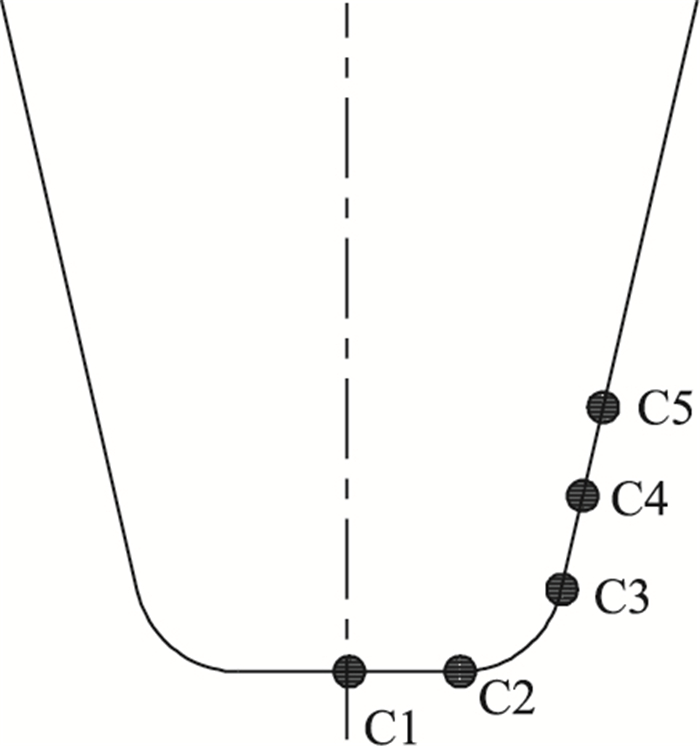
|
| 图 5 应力提取点示意图 Fig. 5 Schematic diagram of stress extraction point |
| |
|
| 图 6 不同网格大小下提取的应力对比 Fig. 6 Comparison of stresses in different mesh sizes |
| |
在建有限元模型时,为了使计算结果足够精确,网格必须划分得足够小,所以以0.5t为标准进行分析。由图 6(a)可知,网格划分大小由0.5t变化为8t,其应力大小相对于0.5t时变化的百分比分别为0.4%, 3.9%, 2.7%, 2.0%,网格大小对应力结果影响较小。由图 6(b)可知,网格大小从0.5t变化为8t,其应力大小相对于0.5t时变化的百分比分别为3.0%, 4.7%, 52.5%, 77.1%,网格大小为2t时,计算偏差较小,当达到4t时对应力影响特别大。由此可知,横隔板与U肋连接处附近的U肋腹板网格大小最大取为2t时较为合适。
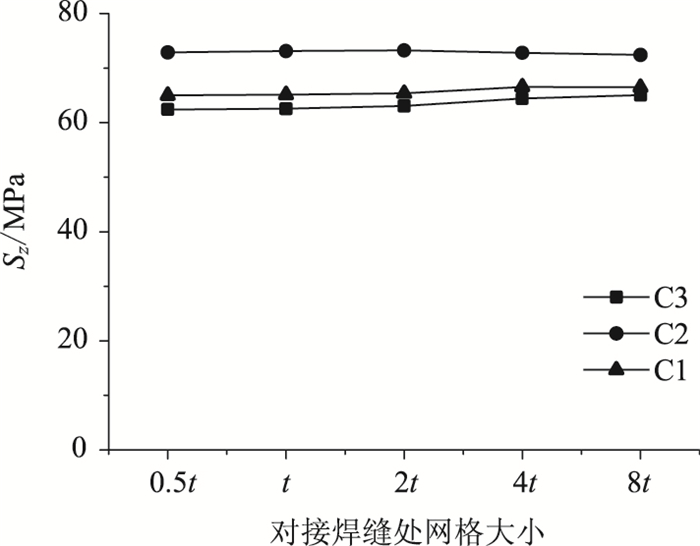
2.2 非横隔板处为了进一步分析横隔板间U肋对接疲劳细节网格划分大小对所提取应力大小的影响,取U肋跨中局部进行网格分析,其加载方式和横隔板处网格分析时一致。在横隔板附近的U肋网格划分大小取为t,横隔板间U肋跨中局部区域网格大小分别取0.5t, t, 2t, 4t, 8t进行应力分析,测点依然为图 6中的C1,C2,C3点。只是在U肋跨中位置即无横隔板位置不考虑U肋对接疲劳细节的竖向应力,只考虑纵向应力。应力对比结果如图 7所示。
|
| 图 7 网格大小变化时的应力对比 Fig. 7 Comparison of stresses in different mesh sizes |
| |
从图 7可知,当网格大小在2t以及2t以内的时候应力值较为稳定,当网格大小大于2t的时候开始出现波动状态。网格大小由0.5t变化为8t,其应力大小相对于0.5t时的变化值最大百分比分别为0.3%, 0.58%, 3.2%, 4.3%,因此跨中处U肋腹板网格大小取到8t较为合适。
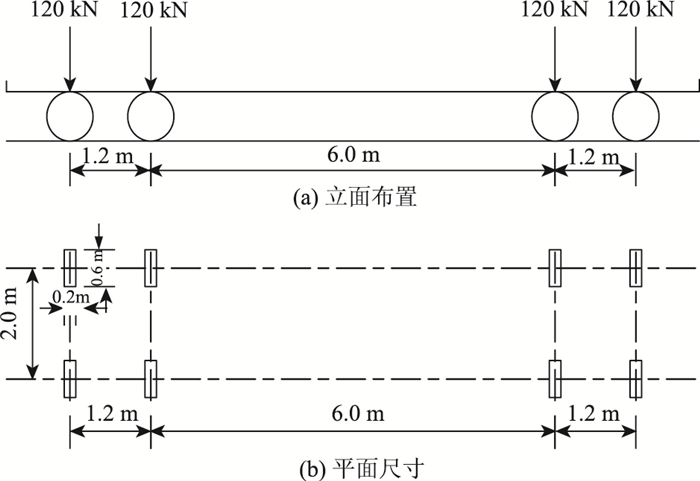
3 疲劳荷载 3.1 荷载模型
|
| 图 8 疲劳荷载模型 Fig. 8 Fatigue load model |
| |
对有限元模型进行加载时,只需要取后轴车轮组或前轴车轮组进行加载即可[15]。在相同车辆荷载作用下,细节在不同的横向位置表现出不同的荷载效应。因此,需要对同一细节在不同横向位置时进行分析,以得到最不利细节位置。
3.2 疲劳荷载加载方式简述由于采用影响面分析获得疲劳细节的最不利加载方式比较费时,因此在进行疲劳分析时,往往会在保证计算结果精确度的情况下,对加载方式进行简化。相关规范并没有对疲劳荷载的简化加载方式进行说明,国内外文献在这方面给出了不同的加载方式。下文将对这些文献中的加载方式进行总结分类。
美国AASHTO手册[8]通过车轮纵向移动得到细节的最大应力后,为减少车轮的横向位置布置数量,在该纵向位置将轮载分别置于U肋正上方、U肋间和U肋腹板上方,进行最不利细节横向位置分析,最后在最不利横向位置处将荷载纵向移动以获得应力历程。湖南大学邵旭东[16]在此基础上采取了6个加载方式来确定每一个细节的横向最不利位置,加载方式如图 9、图 10所示,分别为3个横向位置和2个纵向位置组合,从而省略了最初的确定最不利横断面时荷载的纵向移动分析。
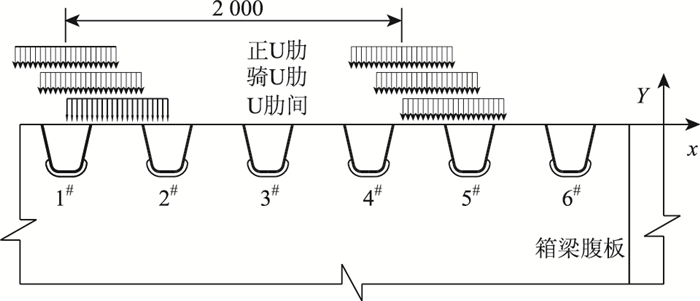
|
| 图 9 车轮横向加载(单位:mm) Fig. 9 Lateral loading of wheel (unit: mm) |
| |
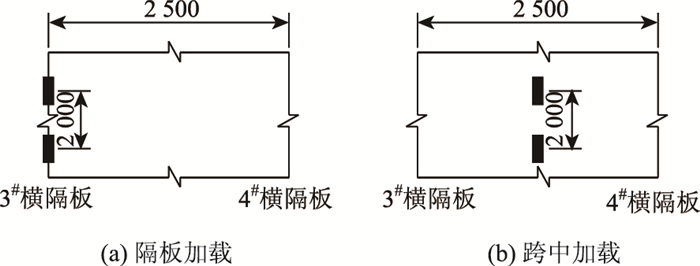
|
| 图 10 车轮纵向加载(单位:mm) Fig. 10 Longitudinal loading of wheel(unit: mm) |
| |
西南交通大学高科[17]、吴月峰[18]以疲劳车辆荷载在车道中心线向箱梁中心线方向偏移0.25 m处为起点,逐步向悬挑端移动,并以车道中心线向悬挑端方向偏移0.25 m处为终点,以获得横向的最不利位置。最后在这个位置将荷载纵向移动以获得应力历程。该种横向加载方式的加载范围有限,有可能找不到横向最不利的加载位置。因此引入一种更为合理的加载方式:从车道的最左侧以一定的荷载步长(如50 mm)横向移动到车道最右侧,最终获得横向最不利位置,具体加载过程如图 11所示。
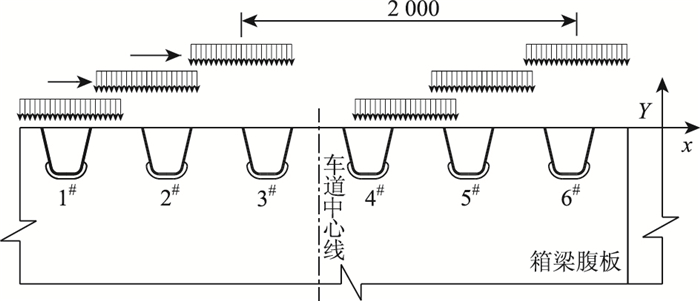
|
| 图 11 车轮横向加载(单位:mm) Fig. 11 Lateral loading of wheel (unit: mm) |
| |
上述3种不同的疲劳荷载加载方法主要是横向加载方式不同。方式1:将车轮荷载分别置于各U肋正上方、U肋间和U肋腹板正上方(图 9);方式2:将疲劳车辆荷载置于车道中心线左右各0.25 m范围内进行横向移动加载;方式3:将疲劳荷载置于车道宽度范围内从左到右进行横向移动加载(图 11)。
为了验证U肋对接疲劳细节的纵向应力历程是否合理,对各细节进行影响面分析,然后将影响面分析结果与其他方式分析结果进行对比,将此定义为加载方式4,其分析方法及对比方式同文献[15]。
3.3 加载位置与加载方式分析疲劳细节分析的主要参数是其在移动荷载作用下的应力幅,而应力幅需要通过疲劳细节在最不利移动荷载作用下的最大应力和最小应力来求得,因此疲劳分析的关键步骤在于获取疲劳细节在最不利荷载作用下最大应力和最小应力。
文献[16]将荷载放置在横隔板间跨中和横隔板上近似为获得细节最大应力和最小应力的荷载位置。下面以U肋对接疲劳细节为例,分析此方法的有效性,对比方法同文献[15]。将U肋对接疲劳细节从1#到11#进行编号,荷载纵向移动时在横向的位置和该车道处各细节编号如图 12所示。以图 12中靠近车轮荷载处的2#,3#,4#和5#U肋对接疲劳细节的应力提取点为例。假设U肋对接疲劳细节在两横隔板间跨中断面和1/5断面,在单轴疲劳荷载纵向移动作用下,U肋对接细节应力变化如图 13(a)所示,图中拉应力为正,压应力为负。
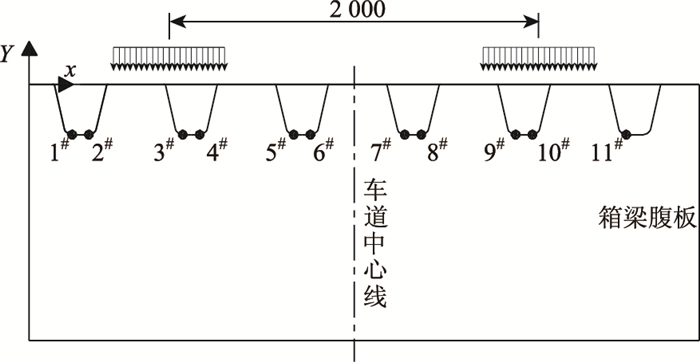
|
| 图 12 荷载横向位置及细节编号图(单位:mm) Fig. 12 Lateral position of load and detail numbers (unit: mm) |
| |
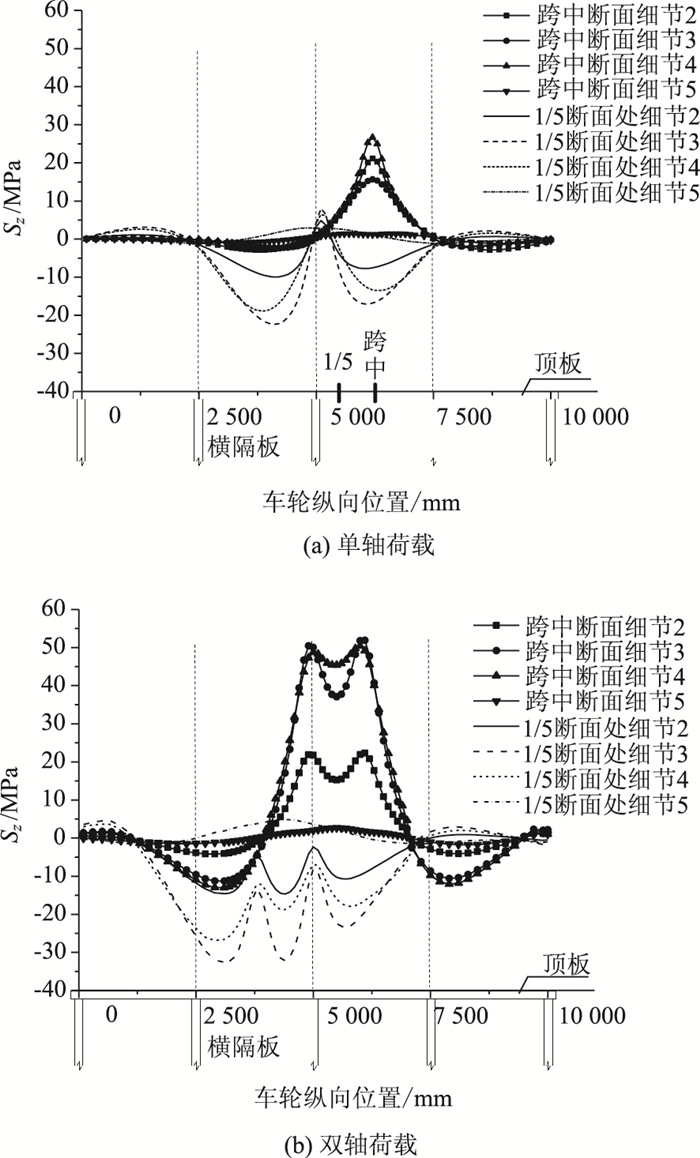
|
| 图 13 细节随荷载纵向移动应力变化历程 Fig. 13 Detail varying with longitudinal moving load |
| |
由图 13(a)可知,在单轴纵向移动荷载作用下,跨中断面处2#,3#,4#U肋对接疲劳细节主要处于受拉状态,应力历程曲线仅有一个拉应力峰值点,对应的轮载恰好位于跨中断面。1/5断面处2#,3#,4#U肋对接疲劳细节的应力历程曲线出现两个压应力峰值点,仅第2个峰值点对应的轮载位置则恰好位于跨中断面。两个断面中,5#U肋对接疲劳细节距离荷载位置较远,因此得到的应力大小几乎为0。从以上结果可以判断将荷载放置在横隔板间跨中和横隔板上获取细节最大应力和最小应力的简化加载方式并不准确。
U肋对接疲劳细节的影响面面积相对于其他细节大,这将会导致疲劳车轮的双轴轮组的前后轴均对其产生有影响。因此,在分析时,应进行双轴加载。在车辆中心线与车道中心线重合位置进行纵向移动加载,结果如图 13(b)所示。荷载纵向位置由车辆荷载后轴组中心线确定。
由图 13(b)可得,跨中处2#,3#,4#U肋对接疲劳细节的应力历程曲线经历了两个拉应力峰值点,所对应的荷载位置分别为横隔板处和横隔板间2/5L附近处,且均有一个轮载位于横隔板正上方。在双轴纵向移动荷载作用下,1/5L断面处2#,3#,4#U肋对接疲劳细节主要处于受压状态,应力历程曲线经历了3个压应力峰值点,与跨中处细节相似,各个峰值点对应轮载位置之间的纵向距离均为1 200 mm, 相当于前后轴之间的距离。应力峰值点所对应的荷载位置分别为横隔板间1/5L处和4/5L处,既不在跨中断面,也不在隔板处,进一步说明简化加载方式的不准确性。
对比图 14(a)和图 14(b)可知,汽车轴数越多,在其作用下,疲劳细节应力历程曲线峰值点越多且越大;单轴情况下,当轴载位于横隔板上时,对U肋对接疲劳细节的应力响应几乎为0。而双轴情况下,当车辆荷载后轴组位于横隔板上时,另一个位于横隔板间的轮组使得U肋对接疲劳细节产生压应力;跨中断面U肋对接疲劳细节的应力幅远大于1/5断面U肋对接疲劳细节的应力幅。因此,下文将以两横隔板跨中断面U肋对接疲劳细节为例子进行分析。
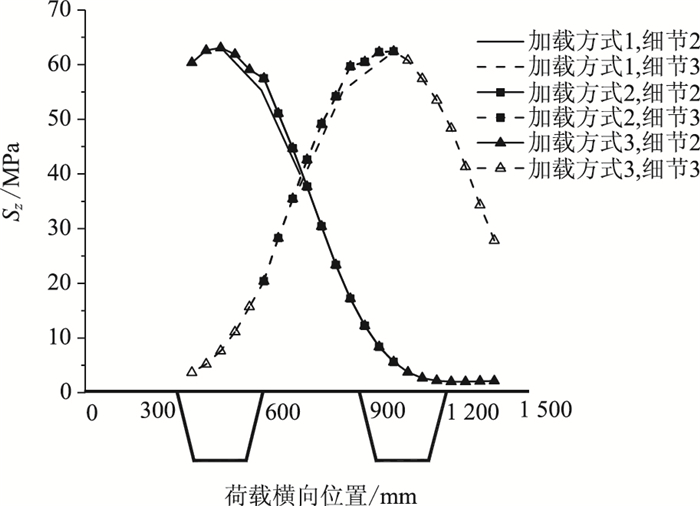
|
| 图 14 不同加载方式下应力最高点断面细节的应力变化 Fig. 14 Stress variations of the highest section details under different loading modes |
| |
以车轮主轮迹线下U肋对接疲劳细节2#、3#点为例,在应力最高点断面用3种加载方式进行横向加载分析。细节在不同加载方式下的应力变化如图 14所示。
从图 14可以看出,在加载方式1和加载方式3下,2#U肋和3#U肋对接疲劳细节应力曲线达到了最大值。加载方式2由于加载范围有限,导致不能准确获取细节的最不利荷载横向位置。因此综合比较可知,加载方式1以最简化的加载方式得到了细节的最不利横向位置,该方式较为合理。
3.4 最不利细节的应力历程分析根据上节分析结果,本节分别采取加载方式1和加载方式4进行最不利细节2#的应力历程分析比较,其影响面应力图如图 15所示。
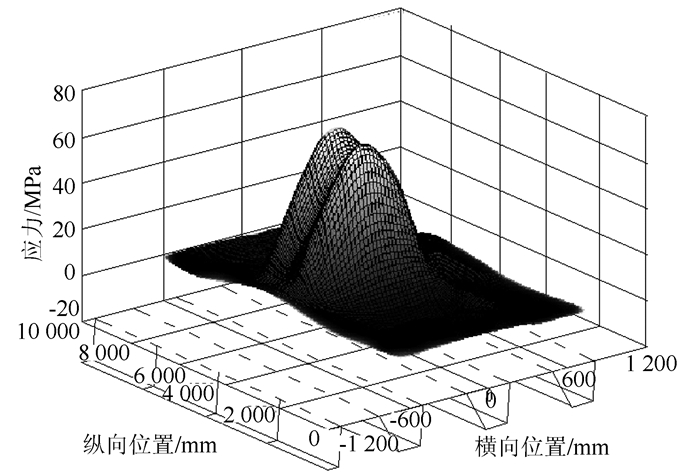
|
| 图 15 应力影响面图 Fig. 15 Curved surface of stress influence |
| |
从图 15中的影响面可知,U肋对接焊缝的影响面横桥向范围为700 mm,顺桥向范围为1 900 mm。超出这个范围的车辆荷载对U肋对接焊缝的影响可忽略不计。两种加载方式得到的细节应力历程如图 16所示。
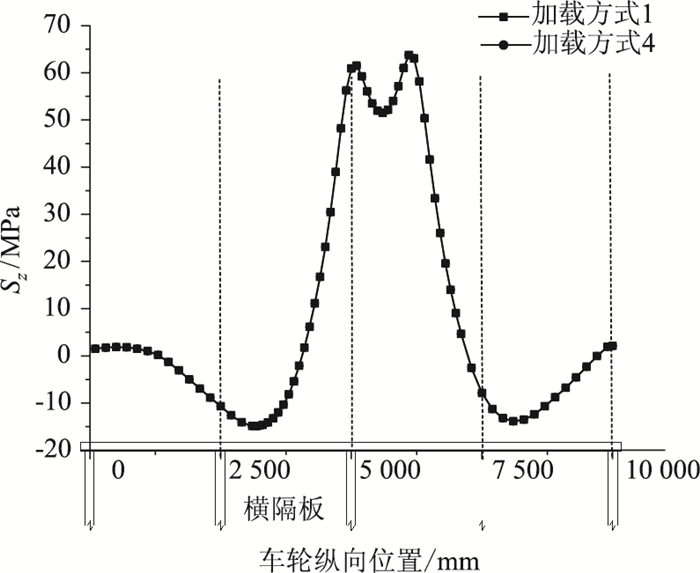
|
| 图 16 纵向应力历程 Fig. 16 Longitudinal stress history |
| |
由图 16可看出,两种加载方式得到U肋对接疲劳细节2#的最不利横向加载位置为同一位置,因此最终得到该细节的纵向应力历程曲线完全重合。由此可以判断:加载方式1可以准确确定U肋对接疲劳细节的最不利位置。
3.5 加载区域网格大小与加载步长影响(1) 加载区域网格大小影响
以跨中处U肋对接焊缝细节为例,将轮载置于U肋正上方,进行纵向加载,分析加载区域内顶板网格大小对U肋对接焊缝处疲劳细节应力结果的影响。网格大小分别取为12.5,25,50 mm和100 mm时,U肋对接焊缝细节应力历程图如图 17所示。
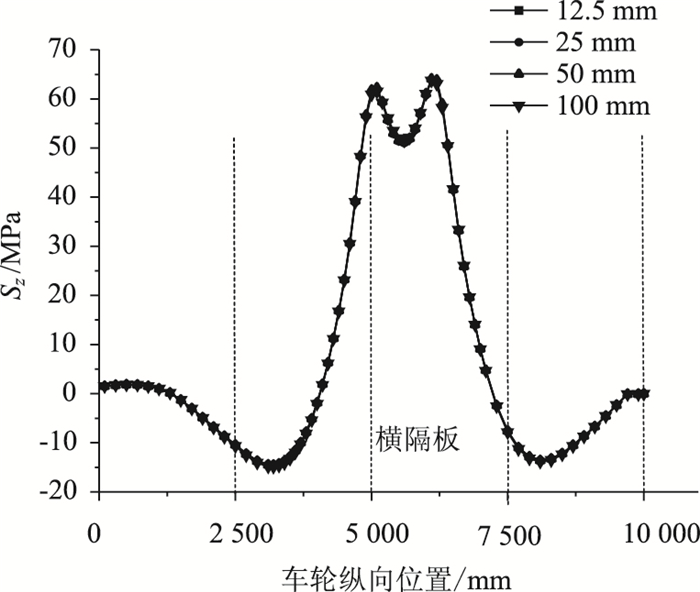
|
| 图 17 不同顶板网格大小时的应力历程 Fig. 17 Stress history in different deck mesh sizes |
| |
从图 17可得,顶板网格大小从12.5 mm增大为100 mm,细节的应力历程曲线几乎完全重合。可以确定顶板网格大小取到100 mm也可得到满意的结果。
(2) 加载步长影响
取顶板网格大小为50 mm,随加载步长改变而变化的应力历程曲线如图 18所示。
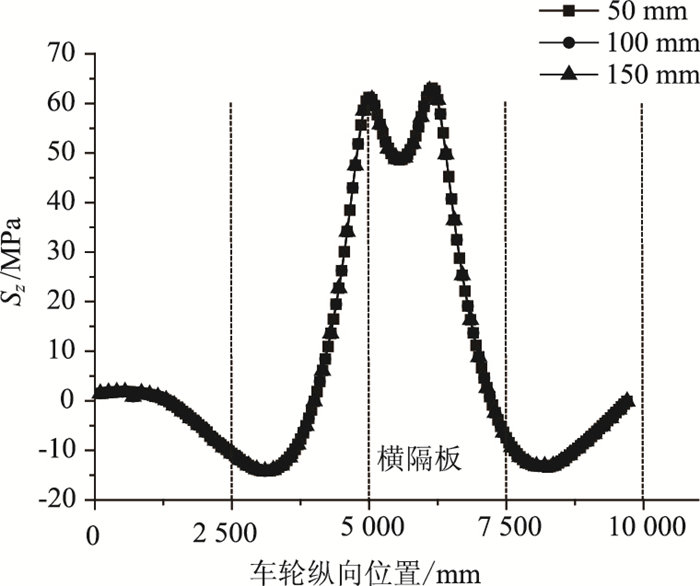
|
| 图 18 不同加载步长时U肋对接疲劳细节应力历程 Fig. 18 Stress history of fatigue details of U-rib butt weld in different loading steps |
| |
从图 18可知,加载步长的变化影响着提取得到的应力点的个数。加载步长越小,得到的应力点个数越多,得到的结果也更靠近实际的应力峰值点。
(3) 加载区域网格大小、加载步长同时变化的影响
网格大小和加载步长以相同的值同时变化时,U肋对接焊缝细节应力历程图如图 19所示。
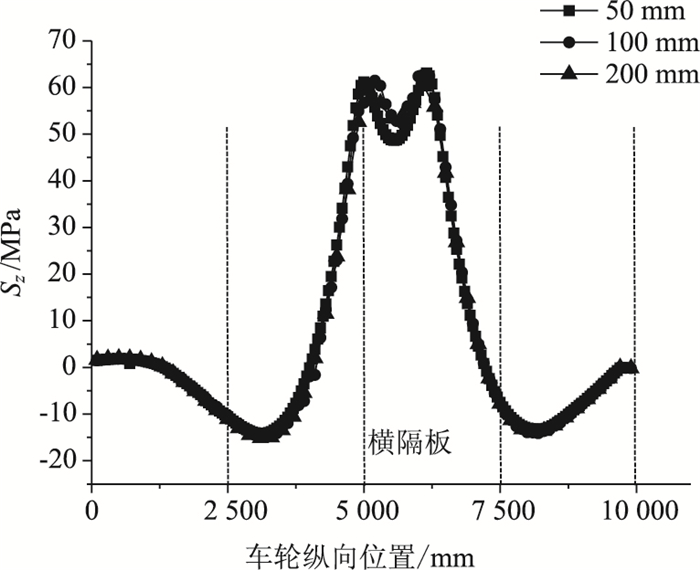
|
| 图 19 U肋对接疲劳细节应力历程 Fig. 19 Stress history of fatigue details of U-rib butt weld |
| |
由图 19可知,不同网格大小与加载步长下,应力峰值相对于50 mm时变化分别为0.48%和4.4%。可以确定在对U肋对接焊缝细节进行有限元分析时,网格大小与加载步长同时取到100 mm,也可得到满意的结果。
4 结论(1) 由U肋网格划分大小分析可知,U肋与横隔板连接处附近U肋网格大小最大取为2t时,也可保证计算精度≥95%。横隔板间U肋对接焊缝处的U肋网格大小最大可取到8t。
(2) 车轮位置与U肋对接焊缝横桥向距离大于700 mm,或纵桥向距离大于1 900 mm时,对U肋对接焊缝的影响可忽略。
(3) 由于U肋对接疲劳细节的影响面面积相对比较大,单轴加载不合理,需要考虑双轴组的叠加效应;另外,U肋对接细节的最值应力需要将轮载进行纵向移动来获取,而不是近似地将其位置布置于横隔板间和横隔板上。
(4) 将荷载分别布置于U肋正上方、U肋间和U肋腹板上方来确定U肋对接焊缝细节最不利横向位置,既简化了加载步骤,又能得到较为精确的结果。
(5) 当顶板网格大小不大于100 mm时,对U肋对接疲劳细节应力大小的结果影响非常小,可忽略不计;而加载步长的大小决定了所提取的应力点的个数,步长越小,所取得的结果越靠近实际的应力峰值点,对于U肋对接疲劳细节,加载步长取到100 mm所提取的应力已足够接近实际值。
(6) 通过分析认为对于U肋对接疲劳细节,正确的应力幅分析过程为:首先将疲劳车辆的双轴组纵向中心线与车道中心线相对应进行纵向加载,获得U肋对接细节取得应力最大值时对应的轮载纵向位置,然后在该纵向位置进行横向移动加载,确定U肋对接细节最不利的横向位置,最后在该最不利横向位置进行纵向加载获取纵向应力历程曲线,再通过应力历程曲线计算该细节的应力幅。
| [1] |
艾丽.疲劳荷载作用下钢桥疲劳寿命与延寿方法研究[D].武汉: 武汉科技大学, 2015. AI Li. Research on Fatigue Life and Prolong Life Method of Steel Bridge under Fatigue Loads[D].Wuhan: Wuhan University of Science and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10488-1015582438.htm |
| [2] |
曾志斌. 正交异性钢桥面板典型疲劳裂纹分类及其原因分析[J]. 钢结构, 2011, 26(2): 9-15. ZENG Zhi-bin. Classification and Reasons of Typical Fatigue Cracks in Orthotropic Steel Deck[J]. Steel Construction, 2011, 26(2): 9-15. |
| [3] |
张允士, 李法雄, 熊锋, 等. 正交异性钢桥面板疲劳裂纹成因分析及控制[J]. 公路交通科技, 2013, 30(8): 75-80. ZHANG Yun-shi, LI Fa-xiong, XIONG Feng, et al. Cause Analysis and Control Measures of Fatigue Cracks in Orthotropic Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2013, 30(8): 75-80. |
| [4] |
XIAO Z G, YAMADA K, INOUE J, et al. Fatigue Cracks in Longitudinal Ribs of Steel Orthotropic Deck[J]. International Journal of Fatigue, 2006, 28(4): 409-416. |
| [5] |
唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112-122. TANG Liang, HUANG Li-ji, LIU Gao, et al. Fatigue Experimental Study of a Full-scale Steel Orthotropic Deck Model[J]. China Civil Engineering Journal, 2014, 47(3): 112-12. |
| [6] |
朱伟, 吉伯海, 傅中秋. 轮迹位置对钢桥面板U肋对接焊缝疲劳性能的影响[J]. 广西大学学报:自然科学版, 2014, 40(4): 998-1005. ZHU Wei, JI Bo-hai, FU Zhong-qiu. Fatigue Influence for Wheels Position of the Orthotropic Steel Bridge Deck of U-rib Butt Weld[J]. Journal of Guangxi University: Natural Science Edition, 2014, 40(4): 998-1005. |
| [7] |
王益逊, 吉伯海, 姚悦, 等. 正交异性钢桥面板U肋对接焊缝疲劳损伤度分析[J]. 工业建筑, 2016, 46(6): 161-165. WANG Yi-xun, JI Bo-hai, YAO Yue, et al. Study of the Fatigue Damage Behavior of U-rib Butt Welds of Orthotropic Steel Bridge Deck[J]. Industrial Construction, 2016, 46(6): 161-165. |
| [8] |
AASHTO. AASHTO LRFD Bridge Design Specifications [S]. Washington, D.C.: American Association of State Highway and Transportation Officials, 2012.
|
| [9] |
ENV 1993-2: Eurocode 3, Design of Steel Structures, Part 2-Steel Bridges[S].
|
| [10] |
JTG D64—2015, 公路钢结构桥梁设计规范[S]. JTG D64—2015, Specifications for Design of Highway Steel Bridge[S]. |
| [11] |
孟凡超, 苏权科, 卜一之, 等. 正交异性钢桥面板的抗疲劳优化设计研究[J]. 公路, 2014(10): 1-5. MENG Fan-chao, SU Quan-ke, BU Yi-zhi, et al. Optimized Design of Anti-fatigue for Orthotropic Steel Bridge Deck[J]. Highway, 2014(10): 1-5. |
| [12] |
卜一之, 王一莹, 崔闯. 新型正交异性钢桥面板关键部位疲劳性能研究[J]. 世界桥梁, 2015, 43(5): 20-24. BU Yi-zhi, WANG Yi-ying, CUI Chuang. Study of Fatigue Performance of Key Parts of New-Type Orthotropic Steel Deck[J]. World Bridges, 2015, 43(5): 20-24. |
| [13] |
李丽娟, 崔闯, 卜一之, 等. 铺装层对正交异性钢桥面板疲劳性能影响效应研究[J]. 世界桥梁, 2016, 44(5): 48-52. LI Li-juan, CUI Chuang, BU Yi-zhi, et al. Study of Influential Effects of Pavement on Fatigue Performance of Orthotropic Steel Deck Plate[J]. World Bridges, 2016, 44(5): 48-52. |
| [14] |
崔闯, 卜一之, 张清华, 等. 基于热点应力法的正交异性钢桥面板疲劳寿命评估[J]. 桥梁建设, 2014, 44(4): 62-67. CUI Chuang, BU Yi-zhi, ZHANG Qing-hua, et al. Fatigue Life Assessment of Orthotropic Steel Deck Plate Based on Hot Spot Stress Method[J]. Bridge Construction, 2014, 44(4): 62-67. |
| [15] |
赵秋, 陈孔生. 钢桥面板U肋-顶板连接焊缝疲劳细节分析方法[J]. 沈阳建筑大学学报:自然科学版, 2018, 34(1): 53-65. ZHAO Qiu, CHEN Kong-sheng. Analysis Method for Fatigue Details of U Rib to Deck Welded Joint in Steel Bridge Deck[J]. Journal of Shenyang Jianzhu University: Natural Science Edition, 2018, 34(1): 53-65. |
| [16] |
丁楠, 邵旭东. 轻型组合桥面板的疲劳性能研究[J]. 土木工程学报, 2015, 48(1): 74-81. DING Nan, SHAO Xu-dong. Study on Fatigue Performance of Light-weighted Composite Bridge Deck[J]. China Civil Engineering Journal, 2015, 48(1): 74-81. |
| [17] |
高科.基于断裂力学的正交异性钢桥面板疲劳性能研究[D].成都: 西南交通大学, 2012. GAO Ke. Study on Fatigue Performance of Orthotropic Steel Deck Based on Fracture Mechanics[D]. Chengdu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1015338462.htm |
| [18] |
吴月峰.正交异性钢桥面板热点应力的疲劳寿命评估[D].成都: 西南交通大学, 2012. WU Yue-feng. Fatigue Life Evaluation Based on Hot Spot Stress Method of Orthotropic Steel Deck[D]. Chengdu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1015340553.htm |
 2019, Vol. 36
2019, Vol. 36
