扩展功能
文章信息
- 唐仁华, 历永杰
- TANG Ren-hua, LI Yong-jie
- 基于全概率法的锚杆挡墙中锚杆设计
- Design of Anchor in Anchored Retaining Wall Based on Full Probability Method
- 公路交通科技, 2019, 36(12): 47-52
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 47-52
- 10.3969/j.issn.1002-0268.2019.12.006
-
文章历史
- 收稿日期: 2017-10-16
2. 华杰工程咨询有限公司, 北京 100029
2. Chelbi Engineering Consultants, Inc., Beijing 100029, China
安全度控制的设计方法分为定值法和概率法。定值法包括单一安全系数法、容许应力法和多系数法。概率法包括近似概率设计法(分项系数法)和全概率法。岩土工程的传统设计方法是建立在经验基础上的定值法,随着设计理论和设计方法的进步,有逐步转向以概率为基础的极限状态法的趋势。目前对于边坡锚杆方面的可靠性分析已有较多研究成果。朱川曲等[1-3]对巷道锚杆支护结构可靠性进行了深入研究。邓志平等[4]通过蒙特卡洛法模拟进行边坡可靠度分析,取得了较好效果,但未深入探讨锚杆作用效果。唐仁华等[5-8]对边坡上的多排锚杆系统进行了体系可靠度分析。王辉等[9]对加锚复合土钉支护体系的可靠度进行了分析与论证。董建华等[10]运用可靠度理论分析了地震加速度分布特征对锚固边坡稳定性的影响。以上研究虽然均属于可靠性分析,但对其逆过程可靠度设计亦有一定的参考意义。相对而言,涉及锚杆可靠度设计的研究成果较少。刘昌清等[11]提出了基于极限状态的锚杆挡墙的设计步骤与方法,该法实际上还是属于近似概率设计法。王玉杰等[12]探讨了在锚杆杆体抗拉强度、注浆体与锚杆黏结强度、注浆体与周围岩土层黏结强度这3种核算模式下锚杆抗拔安全系数和可靠指标之间的关系,该研究已经触及到了全概率设计,只是其中相关变量特别是锚杆设计抗拔强度的变异系数取值来源依据不强。本研究将在深入分析重要相关参数变异系数取值的基础上,提出边坡锚杆全概率设计流程,并编制程序对算例进行详细具体的分析计算。
1 锚杆参数全概率设计流程根据结构极限状态方程进行的可靠指标计算,通常是在各种参数已知的前提下完成的,采用的计算方法或程序只能用于可靠度校核,并不能直接用于可靠度设计。然而,在实际工程应用中,通常需要在一个预期目标可靠度指标的条件下,对结构的尺寸进行规划设计,即可靠度设计。为此,必须建立一种可靠度设计的计算流程。
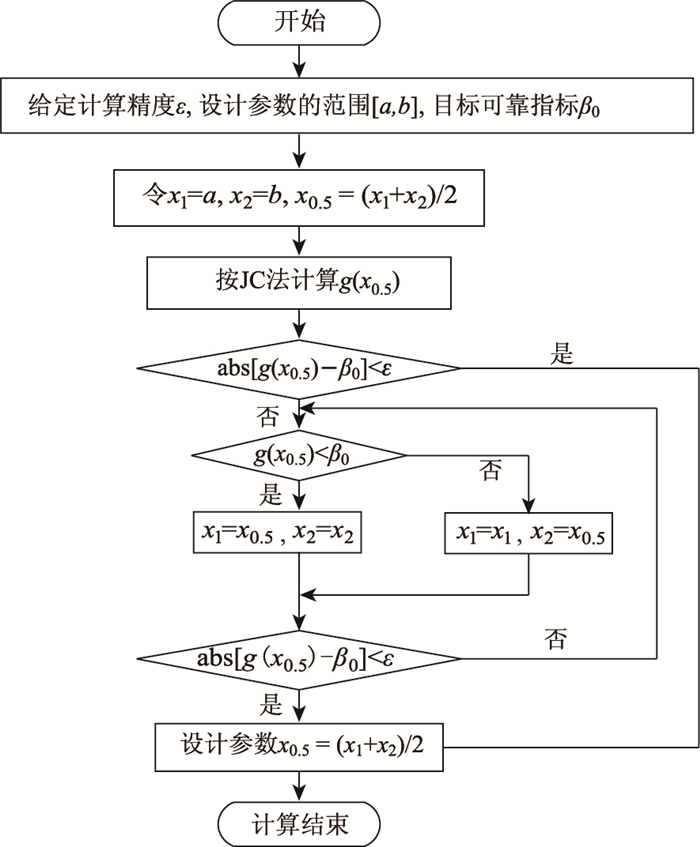
设极限状态下的结构功能函数为z=f(x1, x2, …, xn),式中变量的均值和变异系数已知,则可采用精度相对较高的验算点法编制程序求得其可靠指标[13]。即可靠度指标可以写成这些变量的函数β=g(x1, x2, …, xn),若要对第i个变量xi的均值进行设计,在其他参数不变的条件下,则可靠度指标即为这一变量的单调函数β=g(xi)。可靠度设计是在目标可靠指标β0值及其他各参数均值和变异系数已知的条件下求某个设计参数的均值(此设计参数的变异系数也已给出),一般不能轻易通过求函数β=g(xi)的反函数来求得。因为在可靠指标的常用计算方法中,中心点法虽然计算简单,无需迭代,但是计算结果误差较大。验算点法基本可以满足精度要求,但是其方法需要迭代计算,故其反函数较难直接获得。而优化方法是由特定的几何意义引申得到的,其逆过程则不适用。二分法最初用于解方程,通过每次把函数的零点所在区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值。后来很多学者把它用到强度折减法求边坡的安全系数上来,本研究将它用于结构的全概率设计,计算流程如图 1所示。
|
| 图 1 基于二分法锚杆全概率设计流程 Fig. 1 Full probability design process of anchor based on dichotomy |
| |
其中参数初值的选择并不一定要取变量范围的两个端点值,只需满足g(x1) < β0 < g(x2)即可。
由此可见,此设计方法的前提是目标可靠指标已知且所有参数的变异系数已知。因此需对每个参数的变异系数进行重点分析,使其取值有据可寻,才能保证设计结果的合理与可靠。
2 锚杆极限状态功能函数及其设计参数变异性与目标可靠度分析根据《建筑边坡工程技术规范》(GB50330—2013)[14],锚杆的轴向拉力标准值计算式为:
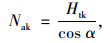
|
(1) |
式中,Nak为锚杆轴向拉力标准值;Htk为锚杆所受水平拉力标准值,即主动土压力标准值的水平分量eahk与锚杆水平间距和排距的乘积;α为锚杆倾角。
2.1 锚杆钢筋截面面积设计钢筋抗拉极限状态下的功能函数为:
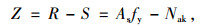
|
(2) |
式中,Z为结构功能函数;R为结构抗力;S为结构作用效应;As为锚杆钢筋截面面积;fy为钢筋屈服强度。
2.2 锚杆锚固长度设计土质边坡中,锚固体与周围土体的黏结强度远小于水泥砂浆与钢筋的黏结强度,锚固通常破坏模式为锚固体与周围土体黏结破坏。锚杆抗拔极限状态功能函数为:
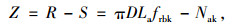
|
(3) |
式中,D为锚固体直径;La为锚固体长度;frbk为土体与锚固体黏结强度的标准值。
2.3 锚杆参数均值及其变异性分析由锚杆的功能函数可知,涉及的随机变量主要为钢筋屈服强度fy、土体与锚固体的黏结强度frbk、主动土压力标准值的水平分量eahk。
对于岩土类材料,由于其强度参数空间差别性较大,不便于统计,材料强度标准值即为其名义值(非统计方法确定的值),在可靠度计算时可不需变换而直接视为均值。对于钢筋这种已有大量统计结果的材料,材料的均值还需根据标准值进行换算。
根据《混凝土结构设计规范》(GB50010—2010)[15]附录及其条文说明,钢筋强度均值计算式为:
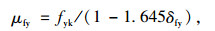
|
(4) |
式中,μfy为钢筋屈服强度平均值;fyk为钢筋屈服强度标准值;δfy为钢筋屈服强度变异系数,根据2008—2010年对全国的统计结果,HRB335钢筋的变异系数为0.074 3。
对岩土变量而言,eahk与土压力系数相关,其均值可直间根据土层的黏聚力和内摩擦角的名义值计算得到,变异系数与主动土压力系数一致。彭大鹏[16]通过严密的数学推导,给出了主动土压力系数的变异系数的近似计算式:
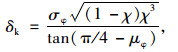
|
(5) |
式中,δk为主动土压力系数的变异系数;μφ和σφ分别为内摩擦角的均值和标准差;χ为中间变量,计算式为:
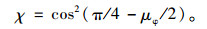
|
(6) |
可见,eahk的变异系数δk可根据该土层内摩擦角的相关参数计算得到。Lee等[17]通过调查指出,砂土的内摩擦角变异系数δφ的范围为0.05~0.15,黏土黏聚力变异系数的范围为0.2~0.5,内摩擦角变异系数δφ的范围为0.12~0.56。
对于frbk而言,均值即为其标准值,实际设计工程的勘察报告会给出。若无试验数据,可参照规范[14]给定的范围取值。由于目前针对frbk没有大量的统计数据,其变异系数可参照黏聚力变异系数取值。
2.4 可靠指标与安全系数关系分析早期结构设计的中心安全系数实际上为抗力均值与荷载效应均值之比,即:
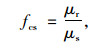
|
(7) |
式中,fcs为中心安全系数;μr为定值法设计时结构抗力的均值;μs为定值法设计时荷载效应的均值。
考虑抗力和荷载为随机变量,设结构功能函数为Z=R-S,则当R和S为正态分布时,
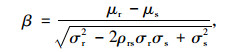
|
(8) |
式中,β为可靠指标;σr为结构抗力标准差;σs为荷载标准差;ρrs为抗力与荷载的相关系数。
联合式(7)和(8),并将标准差用变异系数替代,则有:
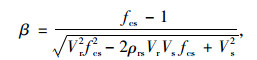
|
(9) |
式中Vr和Vs分别为抗力与荷载的变异系数。
同理,当R和S均为对数正态分布时,
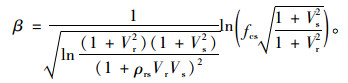
|
(10) |
可见,可靠指标与安全系数有对应关系,且对于固定的某个可靠指标,变异系数不同,则安全系数会不同。
3 算例分析某土质边坡,安全等级为二级,采用锚杆挡墙支护,其中锚杆倾角为15°,锚固体直径为130 mm,筋体采用HRB335钢筋,屈服强度标准值为335 MPa,土体与锚固体极限黏结强度标准值为50 kPa,锚杆水平间距为2 m,排距为2.2 m,其主动土压力标准值的水平分量eahk为18 kPa,土体内摩擦角为20°。
3.1 随机变量参数变异性分析将钢筋屈服强度、土体与锚固体黏结强度、土压力水平分量均视为按正态分布的随机变量,其他参数均视为常量。
由上文所述,土体与锚固体黏结强度的均值μfrb=50 kPa,变异系数参考范围为0.2~0.5,取中间值δfrb=0.35;据式(4),δfy=0.074 3,μfy=381.646 1 MPa;内摩擦角度均值μφ=20°,由于其变异系数范围为0.12~0.56,取中间值δφ=0.34,代入式(5)与(6),计算得主动土压力水平分量的变异系数δk=0.252 6,对应δk的变化范围则为0.089 2~0.416 0,而均值即为μea=18 kPa。
3.2 目标可靠指标选取及设计计算根据文献[10],对于二级永久性边坡,岩土锚杆锚固体抗拔安全系数定为2.4,锚杆杆体抗拉安全系数定为2.0。
联合式(9)和式(2),并将fcs=2.0,δfy= 0.074 3,δk=0.252 6及δk∈[0.089 2,0.416 0]代入,得β=3.412 2及β∈[2.263 8,5.769 8]。
联合式(9)和式(3),并将fcs=2.4,δfrb=0.35及δfrb∈[0.2,0.5],δk=0.252 6及δk∈[0.089 2,0.416 0]代入,得β=1.596 1及β∈[1.102 3,2.867 6]。
可见,锚固体抗拔的可靠指标明显低于锚杆杆体抗拉的可靠指标,主要是由于黏结强度的变异系数远大于钢筋屈服强度的变异系数。
接下来按图 1流程进行参数设计。由于基本变量均为正态分布,可采用设计验算点法替代JC法计算功能函数的可靠指标。
先对钢筋截面积As进行设计。首先按定值法计算:
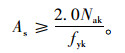
|
(11) |
将Nak=2×2.2×18/cos15°=82.0 kN,fyk=335×103 kPa代入式(11)得:
As≥489.6 mm2,选择钢筋直径为25 mm,符合要求。
按全概率设计,功能函数为:
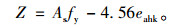
|
(12) |
暂定目标可靠指标为3.0,按图 1流程编程计算,结果为As=400.9 mm2。
| 迭代次数 | 可靠指标 | 验算点坐标 | 截面面积范围/mm2 |
| 1 | 4.926 9 | (297.66, 35.90) | [100, 1 000] |
| 2 | 1.849 1 | (360.35, 25.68) | [100, 550] |
| 3 | 3.513 4 | (330.49, 31.71) | [325, 550] |
| 4 | 2.712 4 | (346.09, 28.94) | [325, 437.5] |
| 5 | 3.120 8 | (338.41, 30.38) | [381.2, 437.5] |
| 6 | 2.918 6 | (342.29, 29.67) | [381.2, 409.4] |
| 7 | 3.020 2 | (340.36, 30.03) | [395.3, 409.4] |
| 8 | 2.969 5 | (341.32, 29.85) | [395.3, 402.3] |
| 9 | 2.994 9 | (340.84, 29.94) | [398.8, 402.3] |
| 10 | 3.007 5 | (340.60, 29.99) | [400.6, 402.3] |
| 11 | 3.001 2 | (340.72, 29.96) | [400.6, 401.5] |
| 12 | 2.998 0 | (346.78, 29.95) | [400.6, 401.0] |
| 13 | 2.999 6 | (340.75, 29.96) | [400.8, 401.0] |
| 14 | 3.000 4 | (340.74, 29.96) | [400.9, 401.0] |
| 15 | 3.000 0 | (340.74, 29.96) | [400.9, 400.9] |
然后,变化不同的目标可靠指标,则设计结果如表 2所示。
| 目标可靠指标 | 锚杆截面设计面积/mm2 |
| 2 | 334.6 |
| 2.2 | 347.4 |
| 2.4 | 360.4 |
| 2.6 | 373.7 |
| 2.8 | 387.2 |
| 3 | 400.9 |
| 3.2 | 415 |
| 3.4 | 429.3 |
| 3.6 | 443.9 |
| 3.8 | 458.8 |
| 4 | 474 |
| 4.2 | 489.7 |
| 4.4 | 505.7 |
| 4.6 | 522.1 |
| 4.8 | 539 |
| 5 | 556.4 |
从表 2中可见,当目标可靠指标为4.2时,锚杆横截面积设计结构与按《建筑边坡工程技术规范》设计结果一致。
接下来对锚固段长度进行设计。同样先按定值法设计。
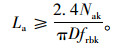
|
(13) |
将Nak=82.0 kN,frbk=50 kPa,D=0.13 m代入上式,得La≥9.64 m。
按全概率设计,功能函数为:
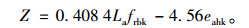
|
(14) |
暂定目标可靠指标为1.6,按图 1流程编程计算结果为La=9.68 m。
| 迭代次数 | 可靠指标 | 验算点坐标 | 锚固体长度范围/m |
| 1 | 1.504 9 | (24.93, 20.10) | [3.0, 15.0] |
| 2 | 1.846 9 | (18.58, 19.97) | [9.0, 15.0] |
| 3 | 1.699 7 | (21.33, 20.06) | [9.0, 12.0] |
| 4 | 1.609 5 | (23.00, 20.09) | [9.0, 10.5] |
| 5 | 1.559 2 | (23.93, 20.10) | [9.0, 9.75] |
| 6 | 1.584 8 | (23.46, 20.09) | [9.375, 9.75] |
| 7 | 1.579 3 | (23.23, 20.09) | [9.562 5, 9.75] |
| 8 | 1.603 4 | (23.12, 20.09) | [9.656 3, 9.75] |
| 9 | 1.600 4 | (23.17, 20.09) | [9.656 3, 9.703 1] |
| 10 | 1.598 8 | (23.20, 20.09) | [9.656 3, 9.679 7] |
| 11 | 1.599 6 | (23.19, 20.09) | [9.668 0, 9.679 7] |
| 12 | 1.600 0 | (23.18, 20.09) | [9.673 8, 9.679 7] |
然后,变化不同的目标可靠指标,则设计结果如表 4所示。
| 目标可靠指标 | 锚固段长度/m |
| 1.1 | 6.90 |
| 1.2 | 7.33 |
| 1.3 | 7.81 |
| 1.4 | 8.35 |
| 1.5 | 8.97 |
| 1.6 | 9.68 |
| 1.7 | 10.50 |
| 1.8 | 11.48 |
| 1.9 | 12.65 |
| 2.0 | 14.09 |
从表 4中可见,当目标可靠指标为1.6时,锚固长度与按《建筑边坡工程技术规范》设计结果一致。
综上可知,将《建筑边坡工程技术规范》设计结果对照换算成全概率设计结果后发现,锚杆截面面积的目标可靠指标(4.2)远高于锚固段长度的目标可靠指标(1.6)。实际工程中亦是如此,钢筋很少被拉断,土质边坡中锚杆的失效模式多见于锚固体与周围岩土体黏结破坏的情况。
4 结论(1) 提出了基于二分法的锚杆全概率设计流程并编制了计算程序,该程序一般经十几次迭代即可算出任意目标可靠指标下的锚杆直径或锚固段长度。
(2) 该方法可在其他结构功能函数只包含1个设计变量的全概率设计中推广,对应功能函数中包含2个甚至多个设计变量的情况则需在此基础上进一步研究。
(3) 通过算例计算并与《建筑边坡工程技术规范》设计结果进行对比分析,结合工程实际情况,建议对锚杆截面面积进行全概率设计时将目标可靠指标取为4.0,对锚固段长度进行全概率设计时将目标可靠指标取为2.0。
值得指出的是,本研究中锚杆所受荷载采用了土压力荷载,在陡坡中的锚杆挡土墙中可以适用[18],但若在未设挡墙的锚固边坡中使用则并不合适,此时应采用潜在滑动面的下滑荷载来计算锚杆荷载,而搜索最优滑动面将会导致锚杆的功能函数变得极为复杂,可作为后续重点研究方向。
| [1] |
朱川曲, 张道兵, 朱海燕. 基于蒙特-卡罗法的煤巷锚杆支护结构可靠性分析[J]. 中国安全科学学报, 2008, 18(4): 146-150. ZHU Chuan-qu, ZHANG Dao-bing, ZHU Hai-yan. Reliability Analysis on Bolt Support Structure of Coal Roadway Based on Monte-Carlo[J]. China Safety Science Journal, 2008, 18(4): 146-150. |
| [2] |
王卫军, 侯朝炯. 回采巷道煤帮锚杆支护可靠性分析[J]. 岩石力学与工程学报, 2001, 20(6): 813-816. WANG Wei-jun, HOU Chao-jiong. Reliability Analysis on Coal Wall Bolting of Extraction Gallery[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 813-816. |
| [3] |
何满潮, 苏永华, 孙晓明, 等. 锚杆支护煤巷稳定性可靠度分析[J]. 岩石力学与工程学报, 2002, 21(12): 1810-1814. HE Man-chao, SU Yong-hua, SUN Xiao-ming, et al. Reliability Analysis of Stability of Coal Roadway Supported by Rock-bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(12): 1810-1814. |
| [4] |
邓志平, 李典庆, 曹子君, 等. 考虑地层变异性和土体参数变异性的边坡可靠度分析[J]. 岩土工程学报, 2017, 39(6): 986-995. DENG Zhi-ping, LI Dian-qing, CAO Zi-jun, et al. Slope Reliability Analysis Considering Geological Uncertainty and Spatial Variability of Soil Parameters[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 986-995. |
| [5] |
唐仁华, 陈昌富. 系统可靠性理论在肋柱锚杆体系中的应用[J]. 公路交通科技, 2011, 28(1): 37-41. TANG Ren-hua, CHEN Chang-fu. System Reliability Theory Applied to Ribbed Anchor System[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 37-41. |
| [6] |
唐仁华, 陈昌富. 锚杆挡土墙可靠度分析与计算方法[J]. 岩土力学, 2012, 33(5): 1389-1394. TANG Ren-hua, CHEN Chang-fu. Analysis and Calculation Method of Reliability of Anchored Retaining Wall[J]. Rock and Soil Mechanics, 2012, 33(5): 1389-1394. |
| [7] |
唐仁华, 陈昌富, 梁冠亭. 框架预应力锚杆挡墙的系统可靠性分析[J]. 岩石力学与工程学报, 2013, 32(12): 2520-2526. TANG Ren-hua, CHEN Chang-fu, LIANG Guan-ting. System Reliability Analysis of Frame Prestressed Anchor Bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2520-2526. |
| [8] |
唐仁华, 陈昌富, 梁冠亭. 框架式预应力锚固系统分阶段可靠性分析[J]. 岩土力学, 2014, 35(1): 217-225. TANG Ren-hua, CHEN Chang-fu, LIANG Guan-ting. Reliability Analysis in Stages for Frame-type Prestressed Anchor System[J]. Rock and Soil Mechanics, 2014, 35(1): 217-225. |
| [9] |
王辉, 杨向前, 郜新军. 加锚复合土钉支护体系可靠度分析与实证[J]. 广西大学学报:自然科学版, 2016, 41(1): 212-218. WANG Hui, YANG Xiang-qian, GAO Xin-jun. Reliability Analysis and Demonstration of Composite Soil Nailing Retaining System Enhanced with Prestressed Anchor[J]. Journal of Guangxi University: Natural Science Edition, 2016, 41(1): 212-218. |
| [10] |
董建华, 董旭光, 朱彦鹏. 随机地震作用下框架锚杆锚固边坡稳定性可靠度分析[J]. 中国公路学报, 2017, 30(2): 41-47. DONG Jian-hua, DONG Xu-guang, ZHU Yan-peng. Reliability Analysis on Stability of Slope Reinforced by Frame with Pre-stress Anchors Under Random Earthquake Action[J]. China Journal of Highway and Transport, 2017, 30(2): 41-47. |
| [11] |
刘昌清, 罗一农, 魏永幸. 基于极限状态法的锚杆挡土墙设计研究[J]. 铁道工程学报, 2014, 31(11): 15-19. LIU Chang-qing, LUO Yi-nong, WEI Yong-xing. Design Research of Anchor Rod Retaining Wall Structure Based on Limit State Design Method[J]. Journal of Railway Engineering Society, 2014, 31(11): 15-19. |
| [12] |
王玉杰, 徐佳成, 汪小刚, 等. 基于可靠度分析的锚杆抗拔安全系数取值标准研究[J]. 岩土工程学报, 2012, 34(2): 303-308. WANG Yu-jie, XU Jia-cheng, WANG Xiao-gang, et al. Criteria for Determining Factor of Safety of Anchor against Pull-out by Using Reliability Analysis[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 303-308. |
| [13] |
张明, 金峰. 结构可靠度计算[M]. 北京: 科学出版社, 2015. ZHANG Ming, JIN Feng. Structural Reliability Calculation[M]. Beijing: Science Press, 2015. |
| [14] |
GB50330—2013, 建筑边坡工程技术规范[S]. GB50330—2013, Technical Code for Building Slope Engineering [S]. |
| [15] |
GB50010—2010, 混凝土结构设计规范[S]. GB50010—2010, Code for Design of Concrete Structures[S]. |
| [16] |
彭大鹏. 土压力系数的概率分析[J]. 岩土工程学报, 1994, 16(6): 117-122. PENG Da-peng. Probability Analysis of Soil Pressure Coefficient[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(6): 117-122. |
| [17] |
LEE I K, WHITE W, INGLES O G. Geotechnical Engineering[M]. Marshfield: Pitman Publishing Inc., 1983.
|
| [18] |
朱彦鹏, 王秀丽, 周勇. 支挡结构设计计算手册[M]. 北京: 中国建筑工业出版社, 2008. ZHU Yan-peng, WANG Xiu-li, ZHOU Yong. Handbook for Structural Design and Calculation of Supporting Structure[M]. Beijing: China Architecture and Building Press, 2008. |
 2019, Vol. 36
2019, Vol. 36
