扩展功能
文章信息
- 李海莲, 林梦凯, 王起才
- LI Hai-lian, LIN Meng-kai, WANG Qi-cai
- 基于IFA-SVM的高速公路沥青路面使用性能预测
- Prediction of Performance of Expressway Asphalt Pavement Based on IFA-SVM
- 公路交通科技, 2019, 36(12): 8-14, 78
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(12): 8-14, 78
- 10.3969/j.issn.1002-0268.2019.12.002
-
文章历史
- 收稿日期: 2019-04-18
高速公路随着路龄的变化和交通流量的急速增长,使沥青路面的损坏及病害越来越严重,导致路面养护工作量越来越大。如何开展科学养护决策,关键环节是要对养护沥青路面的使用性能进行预测分析。国内外许多学者根据高速公路沥青路面的结构性能、功能性能、车辙性能、安全性能的路面损坏情况、平整度、车辙、抗滑性能等评价指标基础测试数据,采用确定方法及不确定性数学理论,提出了不同的高速公路沥青路面性能预测模型及方法,对高速公路沥青路面使用性能进行了比较有效的预测分析[1-4]。然而伴随着信息技术的不断发展,我国高速公路基础数据库得以进一步完善,利用大数据理论及智能信息处理方法对这些数据进行科学分析和研究,结合路面使用性能综合评价结果,研究建立更加有效的路面使用性能预测模型,进一步提高预测方法的通用性和预测结果精度,为高速公路养护管理方案制定及科学决策等提供理论支撑显得更加迫切。
本研究根据支持向量机(Support Vector Machine,SVM)在非线性预测中学习泛化能力强的特点,结合改进的萤火虫算法(Improved Firefly Algorithm,IFA)对SVM模型性能参数进行寻优选择,构建了基于IFA-SVM的高速公路沥青路面使用性能预测模型,选择相关性能指标实现对高速公路沥青路面使用性能的回归预测和综合分析。
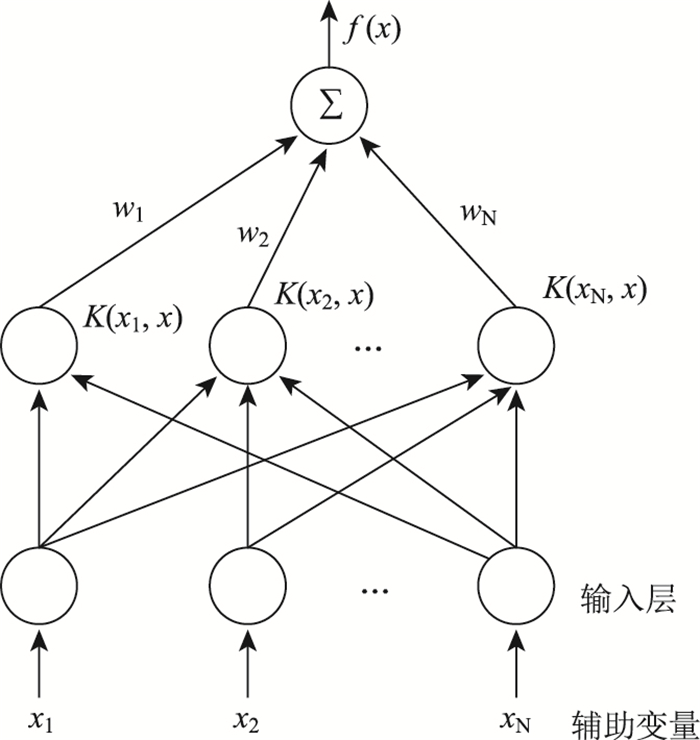
1 SVM的基础理论假设SVM算法的训练数集D={(xi, yi)|i=1, 2, …, n},其中输入量为xi,输出量是yi,建立x的映射函数Φ(x),然后利用函数f(x)=w×Φ(x)+b在高维数特征空间H中对数据集进行拟合,并引入核函数来求得非线性回归的结果[5],其结构示意图如图 1所示。
|
| 图 1 支持向量机结构 Fig. 1 SVM structure |
| |
SVM算法的具体回归过程如下:
(1) 利用函数f(x)=w×Φ(x)+b对数据集进行拟合,并根据最优目标函数,求解非线性支持向量。约束条件如下:
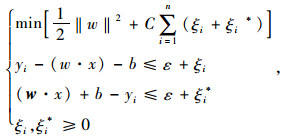
|
(1) |
式中,引入惩罚系数C>0用来控制对错分样本数据的惩罚度; ε是拟合精度且大于0;ξi, ξi*是松驰因子; w是权向量; b为偏置。
(2) 利用Lagrange函数对上述非线性问题进行优化[6-7]。
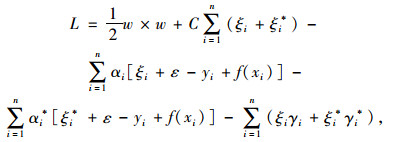
|
(2) |
式中, αi,αi*,γi,γi*是Lagrange因子,且都大于等于0,满足以下约束条件:
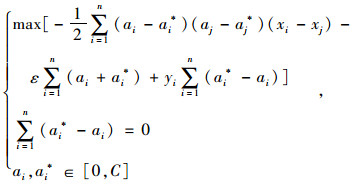
|
(3) |
(3) 引入高斯核函数K(xi, xj)=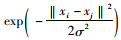
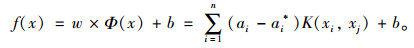
|
(4) |
FA算法的基本思想是利用在一定范围内发光低的萤火虫向发光高的萤火虫移动,从而有效实现寻找最优解。通常在最优化问题求解过程中,假设所有的萤火虫都是同性的且都会被其他萤火虫吸引,彼此间的吸引力与萤火虫的亮度成正比,同时目标函数影响其亮度[8-9]。为了克服FA算法寻优过程中萤火虫随着迭代次数的增加而发生随机移动,进一步提高全局的寻优搜索能力,加快算法的收敛速度,本研究对传统FA算法进行改进。具体步骤如下:
(1) 计算萤火虫的亮度和吸引度。设I和β分别表示萤火虫的亮度和吸引度。分别定义如下:
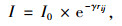
|
(5) |
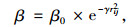
|
(6) |
式中,rij为萤火虫i、j间的距离;I0为在r=0处的初始亮度;γ为亮度吸收系数;β0为在r=0处的原始吸引度。
(2) 萤火虫叠加寻优。设在寻优过程中,萤火虫i被萤火虫j吸引移动的叠加位置为:
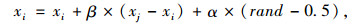
|
(7) |
式中α为移动步长因子,且α∈[0, 1],rand为[0, 1]上随机因子数。
(3) 萤火虫领域寻优。为了克服寻优过程中萤火虫随着迭代次数的增加而发生随机移动,分别在xi±2阶半径内随机选取xi1和xi2两个萤火虫,在整个种群中随机选取xi3和xi4两个萤火虫,增加萤火虫i被萤火虫j吸引移动的两个领域候选解x′i和x″i,从而在xi、x′i和x″i中选取亮度最亮的更替xi,加快算法的精确收敛[10]。x′i和x″i计算公式如下:
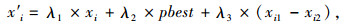
|
(8) |
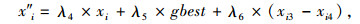
|
(9) |
式中,λi(i=1, 2, …, 6)是[0, 1]区间的调节系数,且λ1+λ2+λ3=1,λ4+λ5+λ6=1;pbest是经过第t次迭代后得到的最大目标函数值,gbest是当前全局最大目标函数值。
(4) 动态调整搜索步长。为了提高全局的寻优搜索能力,在后续寻优过程中采用动态调整算法搜索步长α来平衡全局搜索能力。
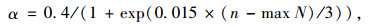
|
(10) |
式中, n是迭代次数; max N是最大迭代次数。
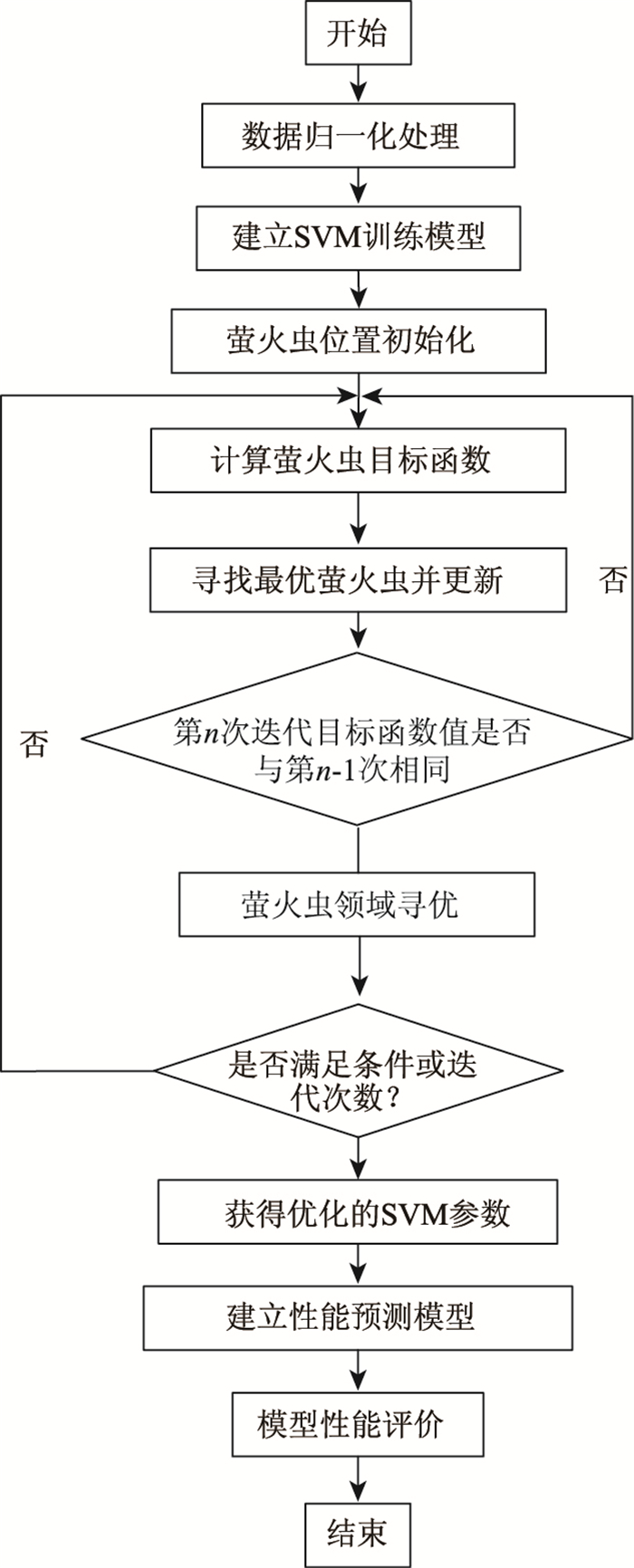
3 基于IFA-SVM沥青路面使用性能预测模型根据高速公路沥青路面使用性能基本评价指标,结合SVM和改进的FA领域寻优算法,建立基于IFA-SVM沥青路面使用性能预测模型,具体流程如图 2所示。
|
| 图 2 基于IFA-SVM的沥青路面使用性能预测流程 Fig. 2 Flowchart of predicting asphalt pavement performance based on IFA-SVM |
| |
具体预测步骤如下:
(1) 基础数据归一化处理。确定高速公路沥青路面使用性能预测模型对应的训练数据集及测试数据集,并对评价指标基础数据进行归一化。
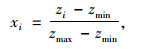
|
(11) |
式中zi为评价指标基础序列数据。
(2) 迭代寻优IFA-SVM模型参数。
① 初始化SVM算法各个基本参数,将所有SVM可选参数模拟为相应的萤火虫并且随机分布,将参数优化过程看作对最优萤火虫的寻找过程[11-14]。
② 以沥青路面使用性能训练集的预测性能作为SVM的目标函数值,计算萤火虫的目标函数值。
③ 根据萤火虫的目标函数值确定其亮度,并对其进行逆序排序,找到当前最优目标函数值对应的萤火虫,并按照公式(7)对萤火虫进行更新。
④ 当第n次迭代目标函数值与前一次迭代目标函数值相同时,执行改进寻优策略。分别增加萤火虫i被萤火虫j吸引移动的两个领域候选解x′i和x″i,选取最亮的萤火虫再次迭代。
⑤ 若迭代次数等于maxN或满足停止迭代的条件,则转至步骤⑥,否则转至步骤②继续迭代寻优。
⑥ 输出最大目标函数值及其对应的萤火虫,即得到SVM算法的相关最优参数。
(3) 使用最优参数对沥青路面使用性能测试集进行预测,经过反归一化处理后,得到实际沥青路面使用性能预测值。
(4) 结果分析。利用相对误差系数和均方根误差系数对预测结果进行比较分析。其中均方根误差计算公式如下:
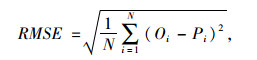
|
(12) |
式中, Oi为实际值; Pi为预测值。
4 实例预测及分析根据西部高寒地区地形特征及气候条件,选取G6京藏高速公路白银段段沥青路面进行模型预测。K1423-K1557.4路段为沥青路面,里程全长134.4 km,双向4车道。近7年路面使用性能指标检测值如表 1所示。
| 检测年份 | 路面分项指标(上行) | 路面分项指标(下行) | |||||||
| PCI | RCI | RDCI | SRI | PCI | RCI | RDCI | SRI | ||
| 2012 | 92.5 | 93.5 | 86.6 | 96.2 | 99.3 | 92.8 | 87.1 | 86.7 | |
| 2013 | 92.3 | 93.2 | 86.2 | 95.7 | 99.1 | 92.6 | 86.2 | 85.9 | |
| 2014 | 91.8 | 92.9 | 85.6 | 95.2 | 98.8 | 92.4 | 85.3 | 85.6 | |
| 2015 | 91.6 | 92.7 | 84.1 | 73.0 | 98.7 | 92.1 | 82.9 | 72.8 | |
| 2016 | 91.1 | 92.5 | 80.4 | 95.1 | 89.5 | 91.8 | 81.6 | 93.7 | |
| 2017 | 85.1 | 92.2 | 87.7 | 94.9 | 76.7 | 91.7 | 87.9 | 93.2 | |
| 2018 | 85.3 | 92.1 | 87.4 | 94.5 | 82.3 | 90.5 | 86.5 | 92.8 | |
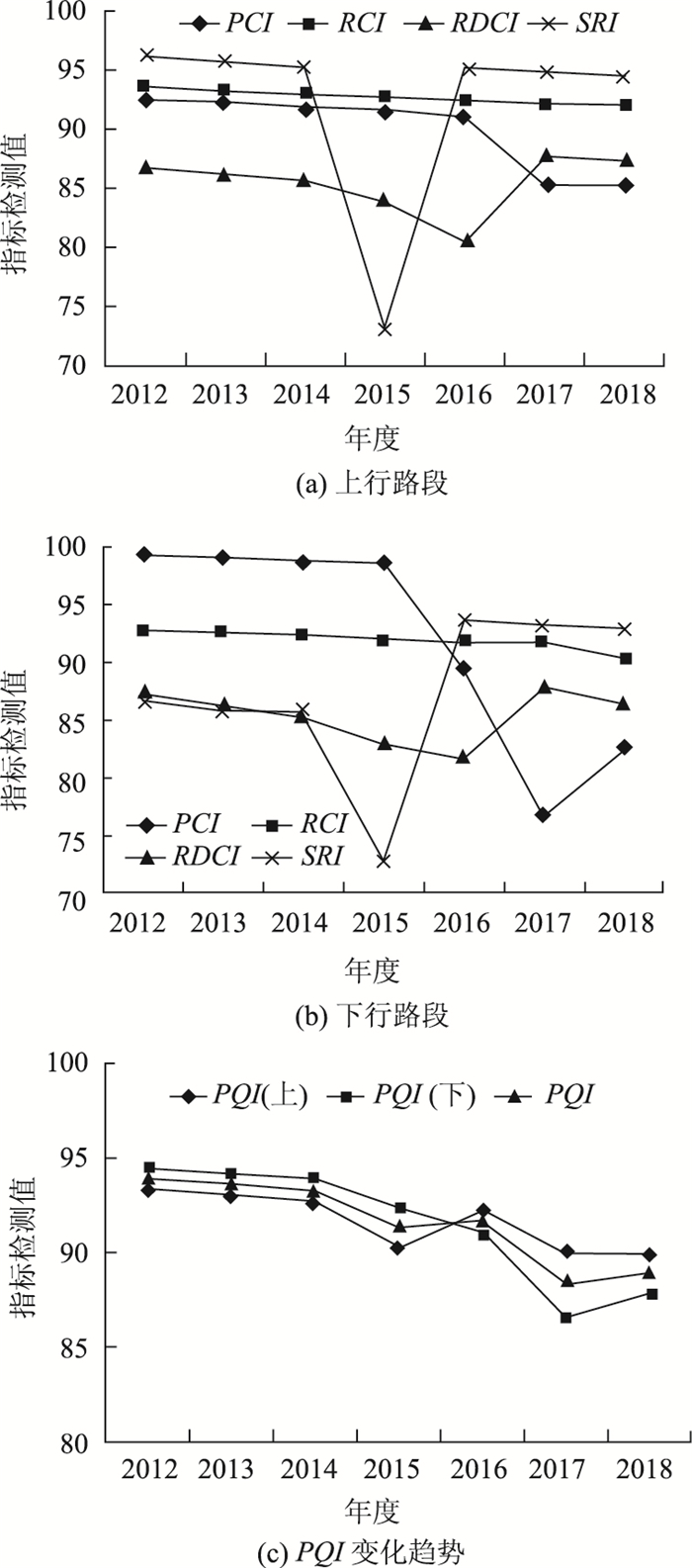
本路段上、下行行车道沥青路面各项评价指标变化趋势如图 3所示。
|
| 图 3 G6(白银段)高速公路各年路面使用性能变化趋势 Fig. 3 Change trend of annual pavement performance of G6 (Baiyin section) expressway |
| |
由图 3可知,G6京藏高速公路白银段随着通车时间的不断增加,沥青路面使用性能整体呈明显的衰减趋势,其中SRI在2015年衰减最大,PCI和RDCI衰减程度远大于RCI。
4.1 数据预处理(1) 数据准备。以G6京藏高速公路白银段(K1423-K1557.4)2012年至2017年上下行路面使用性能检测数据作为训练集,以2018年上下行路面使用性能检测数据作为测试集,构造基础数据表如表 2所示。
| 编号 | 检测年份 | 路面分项指标 | 备注 | |||
| PCI | RCI | RDCI | SRI | |||
| 1 | 2012 | 92.5 | 93.5 | 86.6 | 96.2 | 上行 |
| 2 | 2012 | 99.3 | 92.8 | 87.1 | 86.7 | 下行 |
| 3 | 2013 | 92.3 | 93.2 | 86.2 | 95.7 | 上行 |
| 4 | 2013 | 99.1 | 92.6 | 86.2 | 85.9 | 下行 |
| 5 | 2014 | 91.8 | 92.9 | 85.6 | 95.2 | 上行 |
| 6 | 2014 | 98.8 | 92.4 | 85.3 | 85.6 | 下行 |
| 7 | 2015 | 91.6 | 92.7 | 84.1 | 73.0 | 上行 |
| 8 | 2015 | 98.7 | 92.1 | 82.9 | 72.8 | 下行 |
| 9 | 2016 | 91.1 | 92.5 | 80.4 | 95.1 | 上行 |
| 10 | 2016 | 89.5 | 91.8 | 81.6 | 93.7 | 下行 |
| 11 | 2017 | 85.1 | 92.2 | 87.7 | 94.9 | 上行 |
| 12 | 2017 | 76.7 | 91.7 | 87.9 | 93.2 | 下行 |
| 13 | 2018 | 85.3 | 92.1 | 87.4 | 94.5 | 上行 |
| 14 | 2018 | 82.3 | 90.5 | 86.5 | 92.8 | 下行 |
(2) 归一化处理。对G6京藏高速公路白银段沥青路面使用性能评价指标基础数据进行归一化处理,结果如表 3所示。
| 编号 | 检测年份 | PCI | RCI | RDCI | SRI |
| 1 | 2012 | 0.699 1 | 1.000 0 | 0.826 7 | 1.000 0 |
| 2 | 2012 | 1.000 0 | 0.766 7 | 0.893 3 | 0.594 0 |
| 3 | 2013 | 0.690 3 | 0.900 0 | 0.773 3 | 0.978 6 |
| 4 | 2013 | 0.991 2 | 0.700 0 | 0.773 3 | 0.559 8 |
| 5 | 2014 | 0.668 1 | 0.800 0 | 0.693 3 | 0.957 3 |
| 6 | 2014 | 0.977 9 | 0.633 3 | 0.653 3 | 0.547 0 |
| 7 | 2015 | 0.659 3 | 0.733 3 | 0.493 3 | 0.008 5 |
| 8 | 2015 | 0.973 5 | 0.533 3 | 0.333 3 | 0.000 0 |
| 9 | 2016 | 0.637 2 | 0.666 7 | 0.000 0 | 0.953 0 |
| 10 | 2016 | 0.566 4 | 0.433 3 | 0.160 0 | 0.893 2 |
| 11 | 2017 | 0.371 7 | 0.566 7 | 0.973 3 | 0.944 4 |
| 12 | 2017 | 0.000 0 | 0.400 0 | 1.000 0 | 0.871 8 |
| 13 | 2018 | 0.380 5 | 0.533 3 | 0.933 3 | 0.927 4 |
| 14 | 2018 | 0.247 8 | 0.000 0 | 0.813 3 | 0.854 7 |
4.2 沥青路面使用性能预测
选择2012—2017年的G6京藏高速公路白银段沥青路面表面损坏状况指数(PCI)数据为例,对其进行预测。在时间序列重构时,选择嵌入维数为4,输出维数为1,即训练模型有4个输入1个输出,也就是说用过去2年的路面表面损坏状况指标来预测第3年的路面表面损坏状况。
(1) 建立SVM训练模型。以2012—2017年的沥青路面表面损坏状况指数(PCI)归一化值构成训练数据集,2018年的数据作为测试数据集,具体模型输入数据如表 4所示。
| 编号 | x′(i) | x′(i+1) | x′(i+2) | x′(i+3) | y′(i) |
| 1 | 0.699 1 | 1.000 0 | 0.690 3 | 0.991 2 | 0.668 1 |
| 2 | 1.000 0 | 0.690 3 | 0.991 2 | 0.668 1 | 0.977 9 |
| 3 | 0.690 3 | 0.991 2 | 0.668 1 | 0.977 9 | 0.659 3 |
| 4 | 0.991 2 | 0.668 1 | 0.977 9 | 0.659 3 | 0.973 5 |
| 5 | 0.668 1 | 0.977 9 | 0.659 3 | 0.973 5 | 0.637 2 |
| 6 | 0.977 9 | 0.659 3 | 0.973 5 | 0.637 2 | 0.566 4 |
| 7 | 0.659 3 | 0.973 5 | 0.637 2 | 0.566 4 | 0.371 7 |
| 8 | 0.973 5 | 0.637 2 | 0.566 4 | 0.371 7 | 0.000 0 |
| 9 | 0.637 | 0.566 4 | 0.371 7 | 0.000 0 | 0.380 5 |
| 10 | 0.566 4 | 0.371 7 | 0.000 0 | 0.380 5 | 0.247 8 |
(2) 参数选择与优化。核函数的选择和参数优化可以大大提高SVM的泛化能力。由于RBF核函数在非线性逼近方面有着良好的性能,本研究在IFA-SVM中选择了RBF核函数。同时根据迭代寻优IFA-SVM模型参数方法,设置种群数量N=50,maxN=200,γ=0.01,初始步长α=0.2,并选取Ackley函数和Sphere函数分别进行仿真测试,使每一个函数单独运行50次,根据函数收敛速度及仿真结果[15-18],比较分析确定IFA-SVM模型的参数分别为:C=2.15,ε=0.54,γ=0.75。
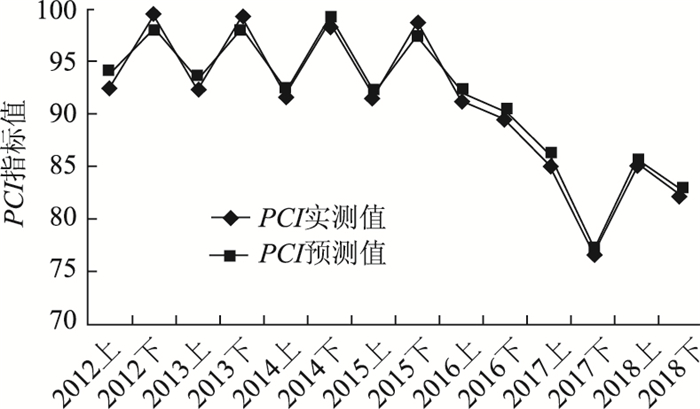
(3) 根据IFA-SVM模型以上参数,对G6京藏高速公路白银段上、下行沥青路面的表面损坏状况指数(PCI)进行预测,并通过反归一化求得对应的PCI值。其中对2018年的沥青路面表面损坏状况指数(PCI)预测值分别是0.402 7和0.261 1,反归一化求得对应的PCI值分别是85.8和82.6。具体预测结果对比如图 4所示。
|
| 图 4 G6(白银段)高速公路各年路面PCI性能预测结果对比 Fig. 4 Comparison of annual PCI performance prediction results of G6 (Baiyin section) expressway |
| |
由图 4可以看出,对G6京藏高速公路白银段上、下行沥青路面表面损坏状况指数(PCI)的预测值与实测值特别接近,两条曲线的拟合度很高。这表明利用IFA-SVM模型预测高速公路沥青路面使用性能是可行和有效的。
4.3 沥青路面使用性能预测结果与分析按照以上方法,同理对G6京藏高速公路白银段(K1423-K1557.4)沥青路面使用性能的RCI,RDCI和SRI进行预测。并同标准FA-SVM预测方法的结果进行对比分析,预测结果的精度分别如表 5和图 5所示。
| 指标 | 实测值 | 预测值 | 相对误差% | RMSE | |||||
| FA-SVM | IFA-SVM | FA-SVM | IFA-SVM | FA-SVM | IFA-SVM | ||||
| PCI上行 | 85.3 | 84.6 | 85.8 | 0.820 6 | 0.586 2 | 0.982 3 | 0.412 3 | ||
| PCI下行 | 82.3 | 83.5 | 82.6 | 1.458 1 | 0.364 5 | ||||
| RCI上行 | 92.1 | 93.5 | 93.1 | 1.520 1 | 1.085 8 | 1.216 6 | 0.824 6 | ||
| RCI下行 | 90.5 | 89.5 | 91.1 | 1.105 0 | 0.663 0 | ||||
| RDCI上行 | 87.4 | 88.6 | 88.3 | 1.373 0 | 1.029 7 | 1.772 0 | 0.696 4 | ||
| RDCI下行 | 86.5 | 88.7 | 86.9 | 2.543 4 | 0.462 4 | ||||
| SRI上行 | 94.5 | 95.3 | 94.9 | 0.846 6 | 0.423 3 | 1.140 2 | 0.570 2 | ||
| SRI下行 | 92.8 | 94.2 | 93.5 | 1.508 6 | 0.754 3 | ||||
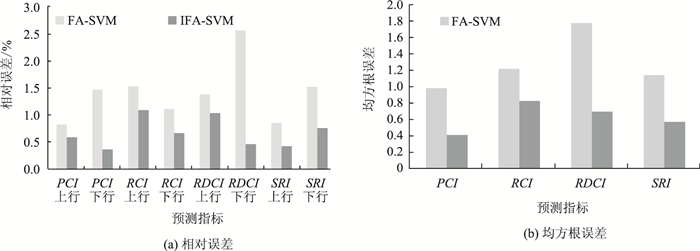
|
| 图 5 IFA-SVM与FA-SVM预测结果精度比较 Fig. 5 Comparison of accuracy of IFA-SVM and FA-SVM prediction results |
| |
由表 5和图 5结果可知,采用标准FA-SVM对G6京藏高速公路白银段(K1423-K1557.4)路面使用性能各个指标进行预测,其相对误差最大达2.543 5%,最小为0.820 6%,而利用IFA-SVM模型预测结果的相对误差最值分别为1.085 8%和0.365 4%,且其均方根误差(RMSE)均小于标准FA-SVM方法。结果表明,IFA-SVM模型在高速公路沥青路面使用性能预测时,收敛速度更快,精度高于标准的FA-SVM,预测值更加接近实测值。
5 结论随着我国高速公路的快速发展,用传统定性法预测高速公路沥青路面使用性能已经不能满足养护决策的实际需要,本研究通过对沥青路面使用性能预测影响因素及传统预测方法的系统总结和分析的基础上,结合支持向量机理论和改进萤火虫算法,建立了基于IFA-SVM的预测模型。
(1) 在基于IFA-SVM的高速公路沥青路面使用性能预测模型中引入领域搜索及可变步长策略,克服了寻优过程中萤火虫随着迭代次数的增加而发生随机移动问题,加速了SVM模型性能参数寻优选择。并通过非线性映射构建高维空间最优超平面,选择对应性能指标对高速公路沥青路面使用性能进行有效预测,为沥青路面使用性能预测提高了一种新思路。
(2) 通过与标准FA-SVM预测的实例结果比较分析,IFA-SVM模型在高速公路沥青路面使用性能预测时收敛速度更快、精度更高,预测值更加接近实测值。
| [1] |
敬超, 张金喜. 沥青路面性能预测研究综述[J]. 中外公路, 2017, 37(5): 31-35. JING Chao, ZHANG Jin-xi. Review of Prediction of Asphalt Pavement Performance[J]. Journal of China & Foreign Highway, 2017, 37(5): 31-35. |
| [2] |
孔祥杰, 张金喜, 袁晓斌, 等. 沥青路面抗车辙性能影响因素研究[J]. 中外公路, 2016, 36(3): 43-48. KONG Xiang-jie, ZHANG Jin-xi, YUAN Xiao-bin, et al. Research on Factors Affecting Rutting Resistance of Asphalt Pavement[J]. Journal of China & Foreign Highway, 2016, 36(3): 43-48. |
| [3] |
于琳. 高速公路沥青路面在役期衰变特性研究[J]. 交通世界, 2016(25): 16-19. YU Lin. Study on Decay Characteristics of Asphalt Pavement in Service[J]. Transpoworld, 2016(25): 16-19. |
| [4] |
孙立军, 刘喜平. 路面使用性能的标准衰变方程[J]. 同济大学学报:自然科学版, 1995(5): 512-518. SUN li-jun, LIU Xi-ping. General Deterioration Equation for Pavement Performance[J]. Journal of Tongji University:Natural Science Edition, 1995(5): 512-518. |
| [5] |
金年生, 陈飞, 苗超杰. 基于灰色-马尔科夫理论的沥青路面性能预测研究[J]. 公路交通技术, 2018, 34(5): 17-20, 26. JIN Nian-sheng, CHEN Fei, MIAO Chao-jie. Study on the Prediction of Asphalt Pavement Performance Based on Grey-Markov Theory[J]. Technology of Highway and Transport, 2018, 34(5): 17-20, 26. |
| [6] |
杨国峰, 王浩仰, 潘玉利. 基于混合效应模型的沥青路面使用性能预测[J]. 公路交通科技, 2018, 35(8): 19-27. YANG Guo-feng, WANG Hao-yang, PAN Yu-li. Prediction of Asphalt Pavement Performance Based on Mixed Effect Model[J]. Journal of Highway and Transportation Research and Development, 2018, 35(8): 19-27. |
| [7] |
刘黔会, 张挣鑫, 黄方林, 等. 基于支持向量机的沥青路面使用性能预测探究[J]. 公路工程, 2018, 43(2): 201-205. LIU Qian-hui, ZHANG Zheng-xin, HUANG Fang-lin, et al. Studied on Performance Prediction of Asphalt Pavement Based on Support Vector Machine[J]. Highway Engineering, 2018, 43(2): 201-205. |
| [8] |
FISTER I, FISTER I Jr, YANG X S, et al. A Comprehensive Review of Firefly Algorithms[J]. Swarm and Evolutionary Computation, 2013, 13: 34-46. |
| [9] |
ZHANG C H, TIAN Y J, DENG N Y. The New Interpretation of Support Vector Machines on Statistical Learning Theory[J]. Science in China Series A: Mathematics, 2010, 53(1): 151-164. |
| [10] |
范文婷, 王晓. 基于改进萤火虫寻优支持向量机的PM2.5预测[J]. 计算机系统应用, 2019, 28(1): 134-139. FAN Wen-ting, WANG Xiao. PM2.5 Forecasting Based on Improved Firefly Optimization SVM[J]. Computer Systems & Applications, 2019, 28(1): 134-139. |
| [11] |
王晓静, 彭虎, 邓长寿, 等. 基于均匀局部搜索和可变步长的萤火虫算法[J]. 计算机应用, 2018, 38(3): 715-721. WANG Xiao-jing, PENG Hu, DENG Chang-shou, et al. Firefly Algorithm Based on Uniform Local Search and Variable Step Size[J]. Journal of Computer Applications, 2018, 38(3): 715-721. |
| [12] |
陈仕周, 李山, 熊峰, 等. 基于GA-灰色神经网络的沥青路面使用性能预测[J]. 重庆交通大学学报:自然科学版, 2019, 38(2): 44-50. CHEN Shi-zhou, LI Shan, XIONG Feng, et al. Forecasting of Asphalt Pavement Performance Based on GA-gray Neural Network[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2019, 38(2): 44-50. |
| [13] |
张金喜, 孔祥杰, 韩丁丁, 等. 不同养护模式下的高速公路沥青路面状况指数预测模型[J]. 北京工业大学学报, 2016, 42(1): 74-80. ZHANG Jin-xi, KONG Xiang-jie, HAN Ding-ding, et al. Prediction Model of Asphalt Pavement PCI of Expressway under Different Maintenance Conditions[J]. Journal of Beijing University of Technology, 2016, 42(1): 74-80. |
| [14] |
白琦峰, 钱振东, 吴春颖. 基于实测验证的沥青路面力学模型研究[J]. 公路交通科技, 2011, 28(5): 39-43. BAI Qi-feng, QIAN Zhen-dong, WU Chun-ying. Study on Asphalt Pavement Mechanical Model Based on Calibration of Measurement[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 39-43. |
| [15] |
杜二鹏, 马松林, 景海民. 基于灰色系统理论的沥青路面使用性能预测[J]. 同济大学学报:自然科学版, 2010, 38(8): 1161-1164. DU Er-peng, MA Song-lin, JING Hai-min. Asphalt Pavement Performance Prediction Model Based on Gray System Theory[J]. Journal of Tongji University:Natural Science Edition, 2010, 38(8): 1161-1164. |
| [16] |
李涛, 王辉明, 胡宗琪. 基于熵权-正态云模型的沥青路面使用性能评价[J]. 土木工程与管理学报, 2019, 36(4): 190-196. LI Tao, WANG Hui-ming, HU Zong-qi. Application of Asphalt Pavement Performance Evaluation Based on Entropy Weight-normal Cloud Model[J]. Journal of Civil Engineering and Management, 2019, 36(4): 190-196. |
| [17] |
巩建, 常成利, 程珊珊, 等. 基于弯沉的沥青路面使用性能评价模型[J]. 公路交通科技, 2016, 33(7): 40-46. GONG Jian, CHANG Cheng-li, CHENG Shan-shan, et al. An Asphalt Pavement Performance Evaluation Model Based on Deflection[J]. Journal of Highway and Transportation Research and Development, 2016, 33(7): 40-46. |
| [18] |
王昌衡, 柏理想, 邓珊. 基于熵权组合预测与粗糙模糊集的沥青路面使用性能分析[J]. 公路交通科技, 2016, 33(4): 12-19. WANG Chang-heng, BAI Li-xiang, DENG Shan. Analysis of Asphalt Pavement Performance Based on Entropy Weight Combination Forecast and Rough Fuzzy Set[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 12-19. |
 2019, Vol. 36
2019, Vol. 36
