扩展功能
文章信息
- 王勇, 黄秋彬, 刘永, 许茂增
- WANG Yong, HUANG Qiu-bin, LIU Yong, XU Mao-zeng
- 基于客户重要度的混合时间窗车辆路径问题研究
- Study on Vehicle Routing Problem with Mixed Time Windows Based on Importance of Customers
- 公路交通科技, 2019, 36(11): 151-158
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 151-158
- 10.3969/j.issn.1002-0268.2019.11.020
-
文章历史
- 收稿日期: 2018-07-30
2. 电子科技大学 经济与管理学院,四川 成都 611731
2. School of Economics and Management,University of Electronic Science and Technology of China,Chengdu Sichuan 611731,China
车辆路径问题是物流配送的核心问题之一[1],而考虑客户点时间窗限制的问题是传统车辆路径问题的拓展。传统的VRPTW是在满足客户需求量和时间窗限制的前提下,研究配送成本和惩罚成本总和最小的车辆路径问题,但较少涉及客户重要度对物流配送企业的意义研究。国内外学者在基于客户重要度的车辆路径优化问题的研究主要集中在基于客户属性的聚类问题和基于客户优先级的车辆路径问题研究两个方面,并已取得了许多研究成果。在基于客户属性的聚类研究中,Li[2]等运用层次聚类法对客户进行了聚类,并提出了改进策略。Chicco[3]在研究了企业的客户属性的基础上使用不同的聚类方法进行聚类,并进行了比较与总结。Kuo[4]等提出了一种基于人工免疫算法的聚类方法并证明了其优越性。Chen[5]等针对电子商务客户的特殊性进行了相关的聚类研究。在基于客户优先级的车辆路径问题研究上,罗孝羚[6]等应用K-means方法研究了城郊公交网络的优化设计问题。Vidal[7]等提出一种混合遗传算法用于解决VRPTW问题。李明燏[8]等提出了一种改进的禁忌搜索算法研究了带时间窗和异构车队的车辆路径问题。潘立军[9]等人基于时差的插入法设计了带时间窗送取货的遗传算法,并在实例计算中验证了该算法的优越性。符卓[10]等针对软时间窗的需求依订单拆分车辆路径问题设计了一种禁忌搜索算法求解。王勇[11]等基于客户多重特性,运用TOPSIS和动态规划相结合的方法对客户进行优先级排序。然而,从实际案例出发研究基于客户重要度的车辆路径优化问题,并考虑不同客户的软硬时间窗异质性,进而探讨基于客户重要度的混合时间窗的车辆路径优化问题方面的研究涉及较少。
传统VRPTW研究中通常采用硬时间窗管理和软时间窗管理两种方式[12-13],在竞争愈加激烈的物流行业,提高顾客满意度尤其是重要客户的满意度是物流企业一个重要战略目标,对重要客户进行硬时间窗管理是保障重要客户满意度的有效措施。因此,本研究在基于客户重要度的VRPTW问题研究中,采取对客户进行混合时间窗的差异管理策略。
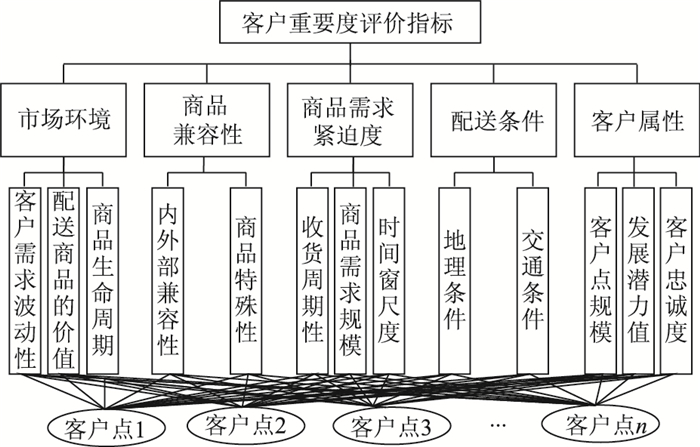
1 客户重要度的指标体系和相关变量 1.1 客户重要度的评价指标体系物流配送网络中的客户点存在多重属性特征,结合国内外相关文献[14-15]和物流配送需求客户点的走访调研结果,构建客户重要度的评价指标体系,将客户重要度评价指标体系分为两层,从市场环境、商品兼容性、商品需求紧迫度、配送条件、客户属性等5个方面对客户重要度进行综合评价,具体如图 1所示。
|
| 图 1 客户重要度评价指标体系 Fig. 1 Evaluation indicator system for importance of customers |
| |
1.2 语言变量设计及对应的三角模糊数
基于客户重要度的评价指标体系,设计语言变量值及对应的三角模糊数(见表 1),对不同属性下客户的重要度和不同属性自身权重进行评价。
| 语言变量值 | 变量缩写 | 模糊数 |
| Exceedingly low | EL | (0.52 0.58 0.61) |
| Between exceedingly low and low | B.EL & L | (0.58 0.61 0.64) |
| Low | L | (0.61 0.64 0.69) |
| Between low and moderate | B.L & M | (0.68 0.71 0.74) |
| Moderate | M | (0.71 0.74 0.79) |
| Between moderate and high | B.M & H | (0.76 0.79 0.86) |
| High | H | (0.81 0.84 0.89) |
| Between high and exceedingly high | B.H & EH | (0.86 0.89 0.92) |
| Exceedingly high | EH | (0.91 0.94 0.96) |
针对不同指标属性下的客户重要度进行综合评价时,从EL~EH中选取;而评价准则指标时,用Poor替换Low,Fair替换Moderate,Good替换High,表 1中相应的语言变量值缩写转变成EP~EG,但与其对应的模糊数值保持不变。
2 基于客户重要度的聚类研究 2.1 相关定义基于客户重要度的聚类研究相关变量定义如表 2所示。
| 变量 | 定义 |
| r | 决策者数 |
| n | 客户点数量 |
| m | 一级指标数 |
| m2 | 二级指标数 |
| B | 决策者集合,B={Bu|u=1,2,3,…,r} |
| U1 | 一级准则指标集合,U1={μt1|t=1,2,…,m} |
| U2 | 二级准则指标集合,U2={Ut2′|t′=1,2,…,m2} |
| X | 客户点集合,X={xi|i=1,2,3,…,n} |
| Hu,tl2 | 专家u对一级准则指标t下第l个属性的评价值Hu,tl2=(hu,tl2,gu,tl2,ku,tl2),其中u=1,2,…,r; t=1,2,…,m |
| Xu,i,tl2 | 专家u对客户i在一级准则指标t下第l个属性的评价值,Xu,i,tl2=(au,i,tl2,bu,i,tl2,cu,i,tl2),其中u=1,2,…,r; i=1,2,…,n; t=1,2,…,m |
| Wt,i1 | 客户i在一级准则指标t上相应的综合客户重要度评价值,Wt,i1=(Tt,i1,Qt,i1,Lt,i1),其中t=1,2,3,…m; i=1,2,3,…,n |
| ts | 一级准则指标属性t下二级准则指标的数量为s |
| vi | 客户i的重要度综合评价值,i=1,2,3,…,n |
| ft(xi) | 用于拆分的一级准则集成属性值 |
| ii,jj | 两个n′维属性下的数据对象,ii=(xi1,xi2,…,xin′),jj=(ji1,ji2,…,jin′) |
| d(xii,xjj) | 两个样本之间的距离,d(xii,xjj)=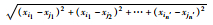
|
| Meandist(s) | 样本平均距离,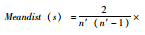 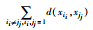
|
| cw | 第w个簇的中心 |
| W | 簇的数量 |
| Meandist(xi,cw) | 第w个簇中每个聚类单元到其聚类中心的平均距离 |
| Ia | 聚类有效性指标值 |
| E | 样本中的所有对象与其所属聚类中心之间的欧式距离的平方和,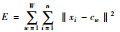
|
2.2 客户重要度的聚类优化算法
通过模糊聚类算法与k-means算法相结合对客户重要度进行聚类,进而对客户点进行差异管理提供决策依据。
2.2.1 二级准则指标的集成方法客户i在一级准则指标属性t上客户重要度的综合评价值为[8]:
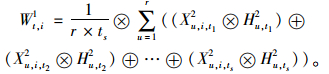
|
(1) |
假定三角模糊数为Y=(a,b,c),其中,a,b,c为相应模糊数,则三角模糊数可以集成为[8]:
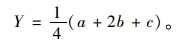
|
(2) |
Wt,i1可用三角模糊数表示为Wt,i1=(Tt,i1,Qt,i1,Lt,i1),其中,T′t,i,Q′t,i,L′t,i为相应模糊数,将二级准则指标集成到一级准则指标的隶属度函数值ut,i1表示为:
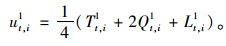
|
(3) |
步骤1:将集成得到的一级准则指标属性值进行拆分,得到rt,1,rt,2,rt,3共3个分属性值[8],同时令ft(xi)=ut,i1,然后通过式(4)来计算出各子属性对应的隶属度函数值:
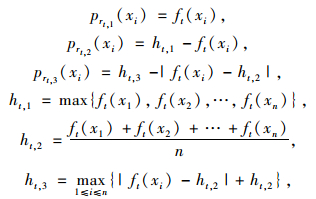
|
(4) |
式中,t=1,2,…,m;n为被评价客户的总数。
计算出各子属性对应的隶属度函数值prt,1(xi),prt,2(xi),prt,3(xi),则客户重要度综合评价值vi可表示为:
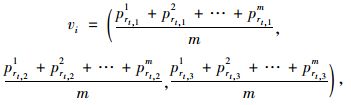
|
(5) |
式中,i=1,2,3,…,n;n为被评价的客户点数量;m为一级准则指标的个数。
步骤2:确定簇的数量w,从n个客户中随机选取w个对象作为初始聚类中心点。
步骤3:将vi作为聚类输入,计算出数据集中每个点到w个聚类中心的距离d(xii,xjj),并将每个数据对象划分到离它最近的聚类中心所属的类中。
步骤4:运用式(3)重新计算出每个簇的新中心,重复步骤3,每次聚类结束都需与上次聚类结果进行对比并判断聚类结果是否发生变化。
步骤5:计算E值,若E值收敛,则聚类结束,并输出聚类结果。反之,则返回步骤3,继续迭代,直至E值收敛或者聚类划分结果不再出现变化为止。
2.3 聚类有效性指标针对不同簇数下的聚类结果,为选取最佳聚类方案,设计聚类有效性指标如下:
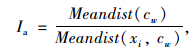
|
(6) |
式中,Meandist(cw)为w个簇中心之间的平均距离;Meandist(xi,cw)为w个簇中每个聚类单元到其聚类中心的平均距离,因此,当Ia最大时聚类结果最优。
3 差异管理策略下的路径优化研究 3.1 混合时间窗车辆路径优化研究基于聚类结果,计算每类中客户重要度评价值的平均值average(vir′),其中r′=1,2,…,w,设定重要客户判定指标如下:
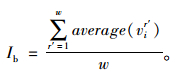
|
(7) |
建立混合时间窗的车辆路径优化模型,可以设定假设条件如下:
(1) 配送车辆由配送中心出发,且完成配送任务后必须返回配送中心;
(2) 客户点总数为n,且客户点的位置取客户点的实际经纬度坐标参与计算;
(3) 在进行客户差异管理过程中,根据客户重要程度而采用对应的时间窗服务管理。
考虑混合时间窗的车辆路径优化研究中,相关变量定义如表 3所示。
| 变量 | 定义 |
| NN | 所需配送的客户点集合 |
| i,j | 编号,其中客户编号为1,2,…,n,配送中心编号为0 |
| k | 车辆编号,k=(1,…,K) |
| ci,j | 客户i到客户j的运输距离,其中i≠j |
| α | 车辆行驶的单位成本 |
| β | 单位车辆的固定维护成本 |
| Q | 车辆的最大荷载量 |
| di | 客户i的需求量,且maxdi≤Q,d0=0 |
| ei | 客户i允许的最早接受服务时间 |
| li | 客户i允许的最晚接受服务时间 |
| si | 车辆k到达客户点i进行服务的时间,其中s0=0 |
| x0jk | 车辆k从配送中心行驶到客户点j,此时x0jk=1,否则x0jk=0, |
| xijk | 车辆k从客户点i行驶到客户点j,此时xijk=1,否则xijk=0, |
| Mi | 违反时间窗时对应的惩罚值 |
| snr | 任意车辆配送客户点的子集合,|snr|表示子集合中客户点的数量,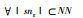
|
以配送总成本最小和车辆使用数最小为目标函数,建立带混合时间窗的车辆路径优化数学模型如下:
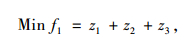
|
(8) |
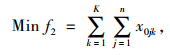
|
(9) |
其中:
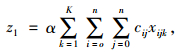
|
(10) |
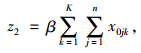
|
(11) |
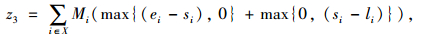
|
(12) |
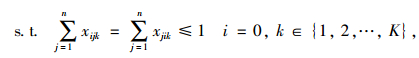
|
(13) |
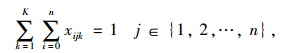
|
(14) |
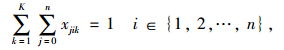
|
(15) |
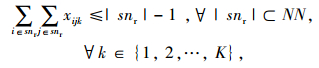
|
(16) |
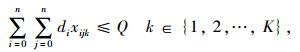
|
(17) |
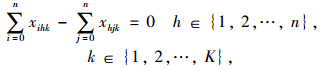
|
(18) |
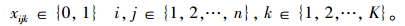
|
(19) |
式(8)表示配送总成本最小化;式(9)表示车辆使用数最小化;式(10)表示车辆的行驶成本;式(11)表示车辆的维护成本;式(12)表示违反时间窗的惩罚成本;式(13)表示配送车辆均从配送中心出发并最终返回配送中心;式(14)、(15)表示每个客户点均被一辆车服务一次;式(16)表示消除子回路;式(17)表示每辆车的总配送量不超过车辆的荷量;式(18)表示流量守恒,即车辆到达客户点后必须离开;式(19)表示变量取值范围。
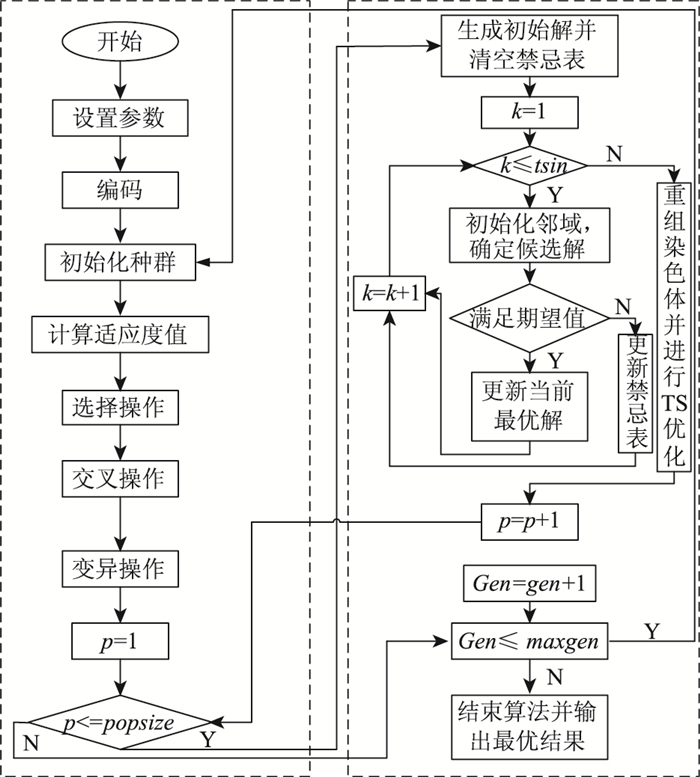
3.2 GA-TS混合算法研究智能算法中的遗传算法和禁忌搜索算法常应用于VRPTW的优化研究中[16-17],其中,遗传算法的全局搜索能力较强,但局部搜索能力较弱,而禁忌搜索算法拥有自适应存储记忆功能,局部搜索能力较强,但全局优化能力较差。本文设计了遗传-禁忌混合算法(GA-TS)用于求解混合时间窗的车辆路径优化模型,算法流程如图 2所示:其中p为遗传操作中当前种群个数;popsize为种群规模;Gen为当前迭代次数; maxgen为最大迭代次数;k为禁忌搜索当前迭代次数;tsin为禁忌搜索最大迭代次数。
|
| 图 2 GA-TS混合算法流程图 Fig. 2 Flowchart of GA-TS hybrid algorithm |
| |
4 算例分析 4.1 实例相关数据
本研究以重庆某企业的城市配送网络为案例,选取具有代表性的50个客户点,其中D为配送中心,C1~C50为客户点,专家对二级准则指标自身权重评价如表 4所示,客户信息如表 5所示。在路径优化研究中,设定车辆的荷载量为20,车速为1,车辆单位行驶成本为10元,车辆维护成本为100元。算法中参数设定为:最大迭代次数为500,交叉概率为0.8,变异概率为0.1,初始种群个数为50,禁忌搜索长度为20。
| 二级准则指标 | 各专家对二级准则指标自身权重的评价 | ||
| B1 | B2 | B3 | |
| U11 | B.P & F | F | F |
| U12 | G | G | G |
| U13 | F | EG | G |
| U21 | G | B.G & EG | G |
| U22 | B.F & G | F | B.F & G |
| U31 | G | B.G & EG | G |
| U32 | G | B.F & G | B.F & G |
| U33 | B.F & G | EG | G |
| U41 | B.G & EG | G | EG |
| U43 | F | F | B.F & G |
| U51 | EG | F | F |
| U52 | B.F & G | G | F |
| U53 | EG | B.F & G | B.G & EG |
| 客户点 | di | ei | li |
| C1 | 1.5 | 5 | 12 |
| C2 | 5 | 6 | 8 |
| C3 | 3 | 2.5 | 6.5 |
| C4 | 2.5 | 3 | 15 |
| C5 | 3 | 4 | 18 |
| C6 | 2.6 | 3.5 | 8 |
| C7 | 2.7 | 16 | 20 |
| C8 | 3 | 5 | 9 |
| C9 | 2.8 | 4 | 8 |
| C10 | 3 | 7 | 10.5 |
| C11 | 2.1 | 20 | 23 |
| C12 | 1.8 | 21 | 24 |
| C13 | 3.2 | 20.5 | 24 |
| C14 | 2.4 | 1 | 8 |
| C15 | 3.8 | 2.5 | 5.5 |
| C16 | 1.3 | 4.5 | 8 |
| C17 | 1.8 | 5.5 | 12 |
| C18 | 2.1 | 10 | 14 |
| C19 | 2 | 11.5 | 16 |
| C20 | 3 | 14 | 17.5 |
| C21 | 3.2 | 15 | 20 |
| C22 | 2.6 | 12.5 | 17 |
| C23 | 2.9 | 13 | 18 |
| C24 | 5 | 16 | 19.5 |
| C25 | 3.2 | 17 | 21 |
| C26 | 2.4 | 5 | 20 |
| C27 | 5 | 8 | 12 |
| C28 | 2.6 | 5 | 16 |
| C29 | 4.1 | 16 | 19 |
| C30 | 3.8 | 2 | 5 |
| C31 | 1.5 | 3.5 | 10.5 |
| C32 | 2.4 | 5 | 15 |
| C33 | 2.8 | 6 | 10 |
| C34 | 1.9 | 8 | 14 |
| C35 | 1.8 | 8.5 | 16.5 |
| C36 | 3.4 | 7 | 13.5 |
| C37 | 2.7 | 5 | 15.5 |
| C38 | 4 | 3 | 17 |
| C39 | 3.3 | 2 | 15 |
| C40 | 3.1 | 12 | 24 |
| C41 | 2.6 | 4 | 15 |
| C42 | 2.3 | 2 | 16 |
| C43 | 2.9 | 7 | 12 |
| C44 | 1.5 | 5 | 8 |
| C45 | 4.6 | 6 | 9 |
| C46 | 3 | 13 | 24 |
| C47 | 2 | 10 | 20 |
| C48 | 2.8 | 11.5 | 18 |
| C49 | 3.3 | 3.5 | 20 |
| C50 | 1.5 | 7 | 24 |
4.2 聚类结果分析
基于混合时间窗的特性,将聚类数设定在2~4之间,具体聚类结果和不同聚类结果下聚类有效性指标如表 6~表 8所示。
| 类别 | 客户点 | |
| 2类 | A | C2 C6 C8 C15 C23 C27 C30 C35 C38 C43 C45 C1 C3 C4 C5 C7 C9 C10 C11C12 C13 C14 C16 C17 C18 |
| B | C19 C20 C21 C22 C24 C25 C26 C28 C29 C31 C32 C33 C34 C36 C37 C39 |
|
| 类别 | 客户点 | |
| 3类 | A | C2 C6 C15 C23 C27 C30 C35 C38 C43 C45 |
| B | C1 C3 C4 C5 C8 C10 C11 C12 C29 C33 C41 C49 C7 C9 C13 C14 C16 C17 C18 C19 C20 C21 C22 C24 C25 C26 |
|
| C | C28 C31 C32 C34 C36 C37 C39 C40 C42 C44 C46 C47 C48 C50 |
|
| 类别 | 客户点 | |
| 4类 | A | C6 C8 |
| B | C2 C15 C23 C27 C30 C35 C38 C43 C45 | |
| C | C1 C3 C4 C5 C10 C11 C12 C29 C33 C41 C44 C49 | |
| D | C7 C9 C13 C14 C16 C17 C18 C19 C20 C21 C22 C24 C25 C26 C28 C31 C32 C34 C36 C37 C39 C40 C42 C46 C47 C48 C50 |
|
当Ia=11.21时,聚类结果分为2类,具体聚类结果如表 6所示。
当Ia=10.53,聚类结果分为3类,具体聚类结果如表 7所示。
当Ia=9.64,聚类结果分为4类,具体聚类结果如表 8所示。
由上述聚类结果可知,当聚类数为2时,Ia=11.21最大,此时聚类结果最符合“类间分明、类内紧凑”,因此聚类数为2时的聚类结果最佳。当聚类数超过2时,可采用重要客户判定指标Ib进行判定。如聚类数为3时,此时Ib=0.47,A,B,C类中客户重要度平均值分别为0.52,0.46,0.43,故将A类客户定义为重要客户,B和C类客户则定义为非重要客户,而对于非重要客户可以根据实际情况进行再次分类计算。
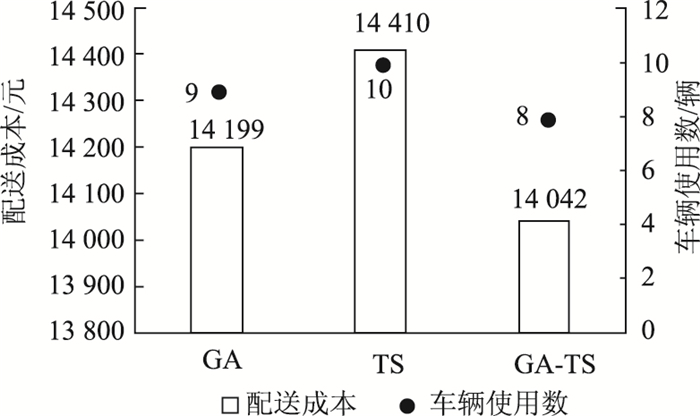
4.3 算法比较基于上述聚类结果,为验证GA-TS算法的优越性,运用GA-TS算法进行最佳聚类结果下的车辆路径优化,并与GA[18]及TS[8]算法优化结果进行比较,如图 3和表 9所示。
|
| 图 3 不同算法的最优计算结果比较 Fig. 3 Comparison of optimal calculation results of different algorithms |
| |
| 算法 | 运行次数 | 优化解 | 优化解出现次数 | 平均计算时间/s |
| GA | 20 | 14 199 | 12 | 159 |
| TS | 20 | 14 410 | 10 | 198 |
| GA-TS | 20 | 14 042 | 15 | 146 |
由图 3和表 9所示,在基于聚类结果的路径优化过程中,分别应用3种算法进行20次路径优化计算,相比GA,TS算法,GA-TS算法在总配送成本和车辆使用数上均取得了较优结果。在20次的优化计算过程中,GA-TS算法优化解的出现了15次,GA算法和TS算法的优化解分别出现了12次和10次。此外,GA-TS算法的平均计算时间为146 s,而GA和TS算法的平均计算时间分别为159 s和198 s。
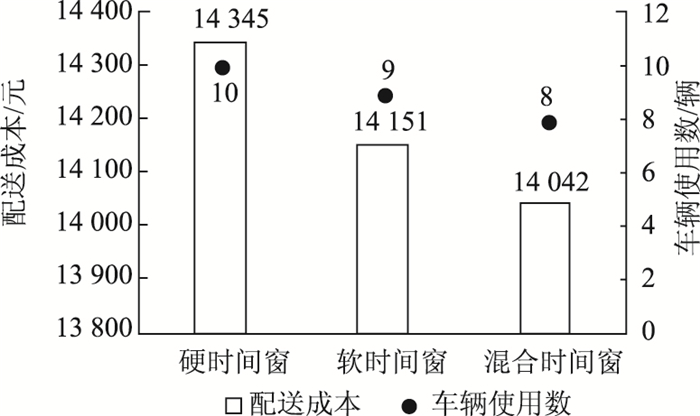
4.4 路径优化结果及分析为证明本研究所提方法的有效性,分别采用硬、软时间窗管理方法对算例进行计算比较,具体比较结果如表 10及图 4所示。
| 管理策略 | 车辆使用数/辆 | 配送总成本/元 |
| 硬时间窗管理 | 10 | 14 345 |
| 软时间窗管理 | 9 | 14 151 |
| 混合时间窗管理 | 8 | 14 042 |
|
| 图 4 不同时间窗类型下配送成本和车辆数的比较 Fig. 4 Comparison of delivery costs and vehicle numbers under different time windows types |
| |
通过不同管理策略下的结果对比分析可知,在基于客户重要度的路径优化研究中,对物流企业客户进行混合时间窗差异化管理,能够保证重要客户的满意度,还能有效降低车辆使用数和配送成本。该对比结果说明客户进行差异管理策略对考虑客户优先级的路径优化研究具有较高参考价值。
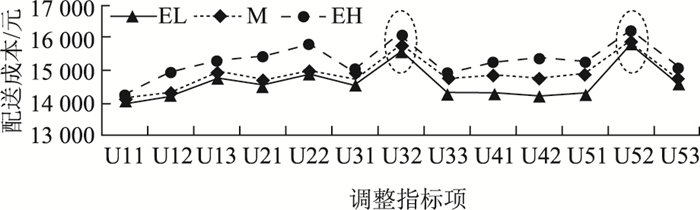
4.5 敏感性分析为了进一步研究不同指标权重对路径优化的影响,调整指标权重设定,将表 4中的U11,U12,U13,U21,U22,U31,U32,U33,U41,U42,U51,U52,U53依次全部更改为EL,M,EH,EL & M,EL & M & EH和EH & M,其中EL & M & EH表示13个指标中前4个调整为EL,中间5个调整为M,最后4个调整为EH,同时其他指标权重保持不变。在每次调整后计算出优化路径的配送成本,具体结果如图 5和图 6所示。
|
| 图 5 U11-U53指标依次全部调整为EL,M,EH的配送成本比较 Fig. 5 Comparison of dispatch costs when adjusting U11-U53 indicators to EL,M and EH |
| |
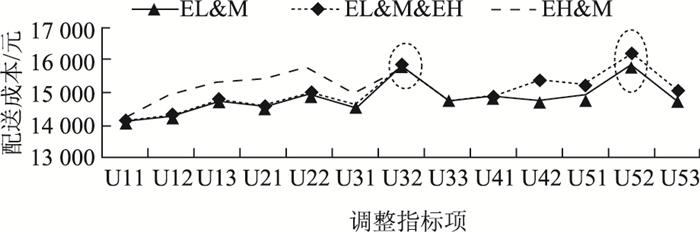
|
| 图 6 U11-U53指标依次调整为EL & M,EL & M & EH,EH & M的配送成本比较 Fig. 6 Comparison of dispatch costs when adjusting U11-U53 indicators to EL & M,EL & M & EH and EH & M |
| |
通过敏感度分析,可以发现将U11~U53的13个指标项依次调整为EL,M,EH,EL & M,EL & M & EH和EH & M时,优化成本仍稳定在一定区间内,证明所提评价体系的合理性。同时通过图 5和图 6可以看出随着指标权重的增加,相应的配送成本也随之增加,原因在于指标提高后导致聚类后的重要客户数也随之增加,进而导致配送成本增加。此外,通过图 5和图 6可以看出在对U32和U52进行指标调整时,成本波动程度相比其他指标更为激烈,说明本研究所提的评价指标体系中商品需求规模和发展潜力值两个指标的敏感性较高,因此,企业在客户重要度评估过程中需要对商品需求规模和发展潜力值两个指标进行详细分析和评价,这样可以保证重要客户满意度的前提下有效降低物流的配送成本,为物流企业长远发展战略实现夯实基础。
5 结论本研究针对传统车辆路径优化片面追求成本最小化而忽视客户重要度的问题进行研究,提出先进行基于客户重要度的聚类分析,然后进行客户差异管理策略的路径优化,并结合实例进行了方法验证和敏感性分析研究。试验计算结果分析表明,文中所提的研究方法适用于定制需求服务的城市物流配送过程,并能更好地应用到基于客户重要度的混合时间窗车辆路径问题优化研究中,进而为后续研究提供相应方法借鉴。
| [1] |
SOLOMON M M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints[J]. Operations Research, 1987, 35(2): 254-265. |
| [2] |
LI J, WANG K, XU L. Chameleon Based on Clustering Feature Tree and Its Application in Customer Segmentation[J]. Annals of Operations Research, 2008, 168(1): 225-245. |
| [3] |
CHICCO G. Overview and Performance Assessment of the Clustering Methods for Electrical Load Pattern Grouping[J]. Energy, 2012, 42(1): 68-80. |
| [4] |
KUO R J, CHIANG N J, CHEN Z Y. Integration of Artificial Immune System and K-means Algorithm for Customer Clustering[J]. Applied Artificial Intelligence, 2014, 28(6): 577-596. |
| [5] |
CHEN X J, PENG S, HUANG J Z. Local PurTree Spectral Clustering for Massive Customer Transaction Data[J]. IEEE Intelligent Systems, 2017, 32(2): 37-44. |
| [6] |
罗孝羚, 蒋阳升. 基于K-means聚类的城郊公交网络设计[J]. 公路交通科技, 2018, 35(5): 115-120,134. LUO Xiao-ling, JIANG Yang-sheng. Design of Transit Network between Urban Area and Suburb Based on K-means Clustering[J]. Journal of Highway and Transportation Research and Development, 2018, 35(5): 115-120,134. |
| [7] |
VIDAL T, CRAINIC T G, GENDREAU M. A Hybrid Genetic Algorithm for Multidepot and Periodic Vehicle Routing Problems[J]. Operations Research, 2012, 60(3): 611-624. |
| [8] |
李明燏, 梁丽萍, 鲁燕霞. 基于改进禁忌搜索算法的车辆路径问题模型[J]. 公路交通科技, 2017, 34(10): 108-114. LI Ming-yu, LIANG Li-ping, LU Yan-xia. A Model of Vehicle Routing Problem Based on Improved Tabu Search Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 34(10): 108-114. |
| [9] |
潘立军, 符卓. 求解带时间窗取送货问题的遗传算法[J]. 系统工程理论与实践, 2012, 32(1): 120-126. PAN Li-jun, FU Zhuo. Genetic Algorithm for the Pickup and Delivery Problem with Time Windows[J]. Systems Engineering-Theory & Practice, 2012, 32(1): 120-126. |
| [10] |
符卓, 刘文, 邱萌. 带软时间窗的需求依订单拆分车辆路径问题及其禁忌搜索算法[J]. 中国管理科学, 2017, 25(5): 78-86. FU Zhuo, LIU Wen, QIU Meng. A Tabu Search Algorithm for the Vehicle Routing Problem with Soft Time Windows and Split Deliveries by Order[J]. Chinese Journal of Management Science, 2017, 25(5): 78-86. |
| [11] |
王勇, 毛海军, 刘永, 等. 基于客户点多重特性的车辆路线优化[J]. 华南理工大学学报:自然科学版, 2014, 42(2): 116-124. WANG Yong, MAO Hai-jun, LIU Yong, et al. Optimization of Vehicle Routing Problem Based on Multiple Customer Characteristics[J]. Journal of South China University of Technology, 2014, 42(2): 116-124. |
| [12] |
SUN P, VEELENTURF L P, HEWITT M, et al. The Time-dependent Pickup and Delivery Problem with Time Windows[J]. Transportation Research Part B:Methodological, 2018, 116: 1-24. |
| [13] |
SCHNEIDER M. The Vehicle-routing Problem with Time Windows and Driver-specific Times[J]. European Journal of Operational Research, 2016, 250(1): 101-119. |
| [14] |
WANG Y, MA X L, XU M Z, et al. Vehicle Routing Problem Based on a Fuzzy Customer Clustering Approach for Logistics Network Optimization[J]. Journal of Intelligent & Fuzzy Systems, 2015, 29(4): 1427-1442. |
| [15] |
WANG Y, MA X, LAO Y, et al. A Fuzzy-based Customer Clustering Approach with Hierarchical Structure for Logistics Network Optimization[J]. Expert Systems with Applications, 2014, 41(2): 521-534. |
| [16] |
QI M Y, LIN W H, LI N, et al. A Spatiotemporal Partitioning Approach for Large-scale Vehicle Routing Problems with Time Windows[J]. Transportation Research Part E:Logistics and Transportation Review, 2012, 48(1): 248-257. |
| [17] |
TAŞ D, DELLAERT N, VAN WOENSEL T, et al. The Time-dependent Vehicle Routing Problem with Soft Time Windows and Stochastic Travel Times[J]. Transportation Research Part C:Emerging Technologies, 2014, 48: 66-83. |
| [18] |
张华庆, 张喜. 改进遗传算法在车辆路径问题中的应用[J]. 交通信息与安全, 2012, 30(5): 81-86. ZHANG Hua-qing, ZHANG Xi. Application of Improved Genetic Algorithm in Vehicle Routing Problem[J]. Journal of Transport Information and Safety, 2012, 30(5): 81-86. |
 2019, Vol. 36
2019, Vol. 36
