扩展功能
文章信息
- 胡正云
- HU Zheng-yun
- 乘用车城市行驶工况构建方法研究
- Study on Construction Method of Urban Driving Cycle of Passenger Vehicles
- 公路交通科技, 2019, 36(11): 142-150
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 142-150
- 10.3969/j.issn.1002-0268.2019.11.019
-
文章历史
- 收稿日期: 2019-06-06
车辆尾气排放已经成为了环境污染的重要因素。目前,我国已经意识到了控制汽车尾气排放的重要性。同时对汽车尾气执行更加严格的排放标准。汽车尾气以及其他性能的排放测定是试验室中在试验台上完成,以此来模拟出车辆的实际行驶情况,因此研究人员开发出了多种车辆和不同行驶状况的模型,这就是车辆行驶工况。它代表着在测试地区该类型车辆的行驶速度变化规律。另外,行驶工况对于了解该地区的交通状况也有着十分重要的参考价值。
不同城市或地区,其驾驶模式是在不断变化。所以在一个具体城市或地区建立的可用工况往往不适用于其他城市或地区,因此,研发和制定符合具体城市或地区实际交通状况的车辆行驶工况,是目前主要的研究方向。[1-2]
姜平等人利用马尔科夫方法[3],保留了车辆实际行驶过程中速度及加速度变换的随机性,但其利用极大似然估计法分类时考虑因素为速度与加速度,不能全面反映行驶信息;且其在片段连接阶段的规则设置简单,对其合成精度也有很大的影响。
石琴等人在短行程法的基础上,考虑到在传统聚类分析中,会对聚类结果产生较大影响的因素之一是初始聚类中心的选择,为了避免此问题,其对初始聚类中心的选择进行了优化[4]。在传统聚类的基础上,加入了SOFM神经网络理论,提高了聚类分析的可靠性,进而增强合成工况的可靠性。但其并没有摆脱短行程法的桎梏,仍存在较大误差。
行驶工况的构建方法一般由以下几个方面组成:车辆行驶数据采集和存储、数据处理、合成工况和工况合理性验证。而合成工况是构建车辆行驶工况的最为关键的一步,采用不同的合成方法决定了该工况能够是否反映了车辆实际的行驶特征。国内外的很多研究人员和从业者开发出了很多合成方法。本研究针对传统马尔科夫方法构建工况其分类条件单一及小概率事件丢失的问题,提出一种利用蒙特卡洛模拟进行优化的方法,完成西安市乘用车行驶工况的构建。与其它方法构建的工况相比,使用本研究方法建立的工况精度较高;与各类标准工况相比,使用本文方法建立的工况更符合西安市的实际情况。
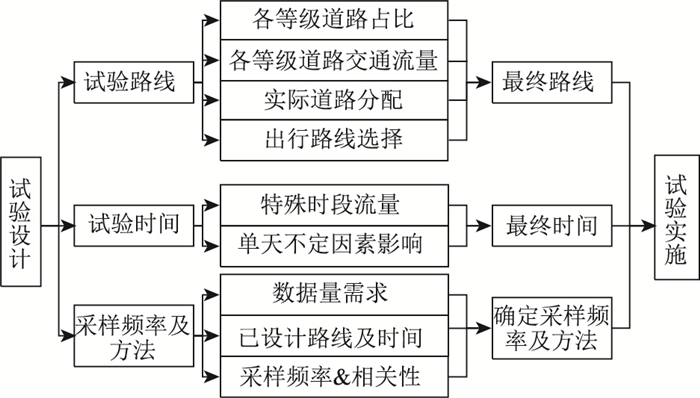
1 试验方案设计行驶工况的试验设计对最终工况是否符合地区实际具有极大的影响。而行驶工况的试验设计主要包含试验路线设计、试验时间设计及采样频率及采样方法设计[7-16]。本研究的行驶工况试验方案具体流程如图 1。
|
| 图 1 试验总体设计方案 Fig. 1 Overall design scheme of test |
| |
1.1 循环工况试验路线设计
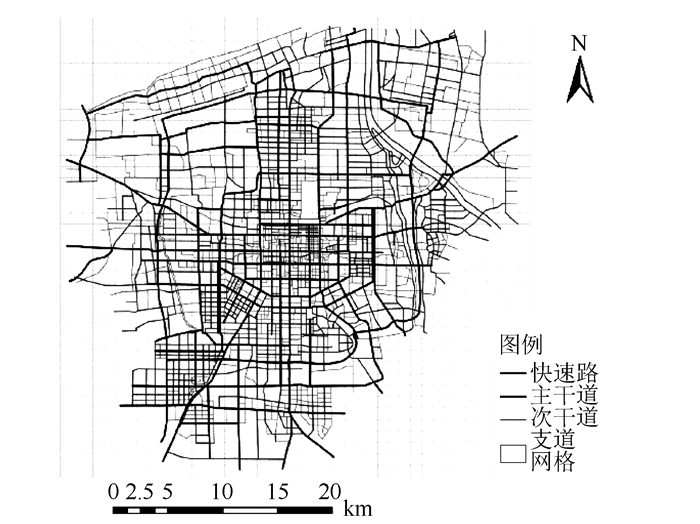
为了得到最终试验路线中各等级道路所占的比例,需要结合西安市实际各等级道路分布情况以及各等级道路上的车流量等信息综合考虑,各等级道路分布如图 2所示。故本研究对西安市实际道路分布及车流量情况进行了调查[17]。
|
| 图 2 西安市不同等级道路分布图 Fig. 2 Distribution of different grades of roads in Xi'an City |
| |
通过道路分布图的参考进行计算得到西安市不同等级道路长度特征参数如表 1所示[17]。
| 道路等级 | 快速路 | 主干道 | 次干道 | 支路 |
| 道路长度/km | 141 | 597 | 1 001 | 823 |
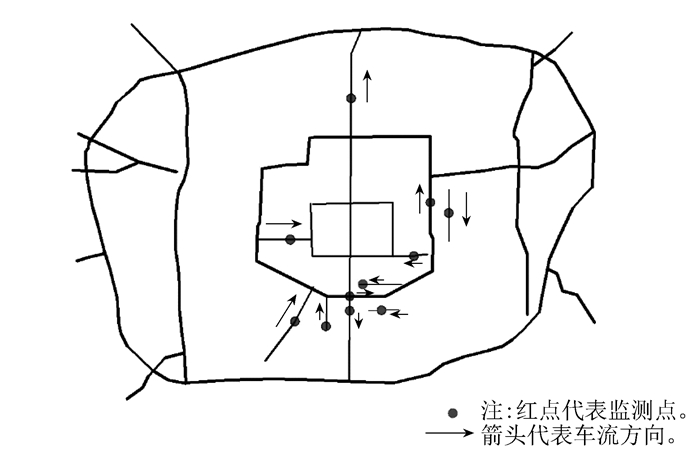
为得到西安市各等级道路的交通流量情况,本研究对西安市各等级道路进行了交通流量检测,根据西安市整体道路特征和道路分布,为了得到快速路、主干道、次干道以及支路的交通流量,本研究选取了四种不同等级道路上的具有代表性的观察点,进行了11 d的交通流量监测。各观察点的位置以及车辆行驶方向如图 3所示。
|
| 图 3 交通流量观察点分布图 Fig. 3 Distribution of traffic volume observation points |
| |
根据得到的11个观察点共11 d的监控数据,对数据进行分析处理,获得一周内各种等级道路交通总流量平均值如表 2所示。
| 道路等级 | 快速路 | 主干道 | 次干道 | 支路 |
| 交通总量平均值 | 47 065 | 24 414 | 14 928 | 5 588 |
得到交通流量数据后,为得到西安市构建循环工况需要的试验样本数据量,本研究采用参数估计的方法来确定随机抽样中的必要样本容量[8]。通过计算,在方差未知的条件下,西安市道路必要样本容量为38.46 km。
得到必要样本容量后,依据层次分析法(AHP)进行实际试验道路长度的计算。
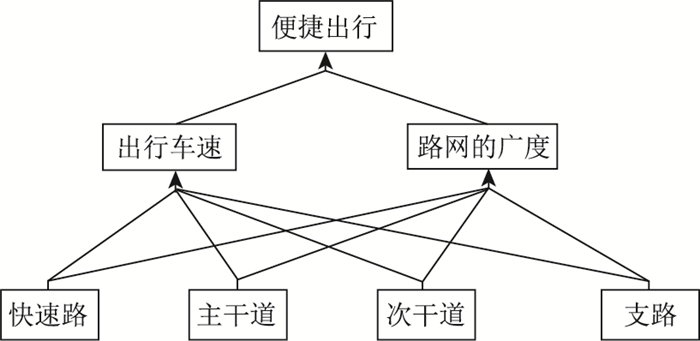
根据之前的分析结果得到了此次构建工况所需要的样本容量,再结合西安市不同等级道路总长度以及所占路网总长度的比例和相对应道路上的交通流量,利用YAAHP软件,建立层次分析决策模型,如图 4所示。计算出的试验样本中各等级道路所占比例及对应的长度如表 3所示。
|
| 图 4 驾驶人最佳出行方式模型 Fig. 4 Driver's optimum travel mode model |
| |
| 道路等级 | 快速路 | 主干道 | 次干道 | 支路 |
| 比例 | 0.299 6 | 0.248 0 | 0.268 5 | 0.183 9 |
| 长度/km | 11.52 | 9.54 | 10.33 | 7.07 |
根据得到的试验道路信息,结合西安市实际道路分布以及所需样本容量和各等级道路比例及长度,设计了包含商业区、工业区、文化区以及生活区等不同城市区域的试验路线图如图 5所示路线。

|
| 图 5 试验路线示意图 Fig. 5 Schematic diagram of test route |
| |
1.2 循环工况试验时间设计
试验时间部分,为采集到各种交通状况下的车辆运行数据,采样时间的规划应覆盖每天早高峰、晚高峰、低谷期等有特殊交通流量的时段,且为避免单天试验因天气、交通事故等不定因素对试验结果造成的影响,应连续多天进行采集。故试验采样时间设计为连续一周之内每天早7:30出发、中午12:30出发、晚5:30出发按设计路线进行整圈的测试,其中早、晚阶段均为高峰期阶段,中午阶段为低谷期阶段,保证各种交通状况都能被全面适量的采集。其具体情况如表 4所示。
| 采样时间 | 早上 | 中午 | 下午 |
| 周一至周天 | 7:30~10:00 | 12:30~15:00 | 17:30~20:00 |
1.3 循环工况试验数据采集设计
在数据采集过程中,为了构建出具有代表性的西安市城市工况,应该选取城市中保有量较大的车型,综合考虑,本次试验采用的车辆为比亚迪E6纯电动乘用车。采集参数如表 5所示。
| 参数 | 符号 |
| 运行时间 | T |
| 行车速度 | v |
| 行驶里程 | s |
| 位置经度 | ° |
| 位置纬度 | ° |
2 数据处理
在传统马尔科夫方法构建行驶工况的过程中,认定车辆下一个时刻的状态仅与当前时刻车辆的运行状态有关,其通过对数据的分类,得到车辆在不同状态之间的转换关系,进而进行频数统计,从而得到车辆状态的马尔科夫状态转移概率矩阵。这种方法将车辆的行驶过程分为加速、减速、匀速、怠速等类型的片段,其分类方法主要是依靠最大似然估计法。利用车辆的速度加速度状态进行划分,将平均速度与平均加速度相似的片段归为一类,其分类依据单一,因此可能导致分类结果中零碎片段极多,且在全面代表车辆行驶状态上也略显不足,为解决此问题,本研究引入了主成分分析及聚类分析法进行数据的划分,设置多种特征参数,从而全面反映车辆状态,使得分类结果更为精确。而且传统马尔科夫方法在得到转移矩阵后进行各片段选取时,主要依照转移概率矩阵中概率的大小情况进行选取,即在已知状态i时,在其下一时刻可能发生的状态j中选取转移概率最大的作为下一状态。该方法虽然选择了最大概率发生事件作为连接依据,但其却规避了小概率事件发生的可能性,在一定程度上损失了车辆运行的信息,故而合成工况在一定程度上降低了准确性。为解决这一问题,本研究引入了蒙特卡洛模拟法进行状态转移的确定。本研究中试验数据处理的具体流程如图 6。

|
| 图 6 数据处理流程图 Fig. 6 Flowchart of data processing |
| |
2.1 数据去噪与平滑
经过分析发现,由于各种原因,采集到的数据中存在异常值,为了剔除异常值,需要对数据进行去噪和平滑[13]。故利用限幅滤波法及递推平均滤波算法去除数据的脉冲噪声与高频噪声。其如式(1),式(2),处理前后对比如图 7所示。
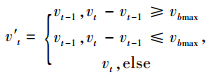
|
(1) |
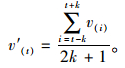
|
(2) |

|
| 图 7 处理前后对比图 Fig. 7 Comparison of data before and after processing |
| |
2.2 数据划分
将数据划分为加速、减速、匀速、怠速的片段,参照相关论文[13],分段时的加速度阈值一般选取为0.15m/s2,依照式(3)规则对数据进行划分:

|
(3) |
经此方法处理,共得到15 682个行驶片段,用以进行后续处理。
2.3 主成分分析数据划分后,为将片段分为不同的类型,需对片段设置片段特征参数,利用主成分分析进行降维处理,并最终通过聚类分析进行片段类型的划分。
在主成分分析阶段,首先设置片段特征参数,本研究设置有10个片段特征参数,分别为:最高车速Vmax、最低车速Vmin、平均车速Vmean、车速标准差Sv、最大加速度Amax、最小加速度Amin、平均加速度Amean、加速度标准差SA、始末速度差Vsd、片段时间长度T。
主成分分析中,因为每个特征参数的量纲不同,数值相差较大,需要对数据进行标准化处理,处理过程如式(4),经过处理之后,每一列数据的均值为0,方差为1。设yij为未经标准化处理的第i个样本的第j个变量,xij为标准化后第i个样本的第j个变量。由此得到标准化处理后的数据矩阵Xn×m,如式(5)所示。

|
(4) |

|
(5) |
得到Xn×m后利用公式(6)求解变量之间的相关系数,式中rij为变量xi与xj之间的相关系数,从而得到相关系数矩阵R。
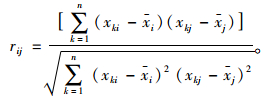
|
(6) |
利用相关系数矩阵求解其特征根与相应的特征向量,即解方程|λ-R|=0,计算出其m个特征根,并令λ1≥λ2≥…λm≥0。并对每个λk利用Rb=λkb便可以得到每个特征跟对应的特征向量bk,使用公式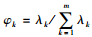
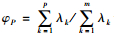
经主成分分析后,得到各主成分及其累积贡献率,如表 6。
| 主成分 | 方差总计 | 贡献率 | 累积贡献率 |
| 1 | 3.697 | 36.972 | 36.972 |
| 2 | 2.192 | 21.917 | 58.889 |
| 3 | 1.843 | 18.434 | 77.323 |
| 4 | 1.163 | 11.630 | 88.953 |
| 5 | 0.895 | 8.951 | 97.905 |
| 6 | 0.134 | 1.344 | 99.249 |
| 7 | 0.053 | 0.530 | 99.779 |
| 8 | 0.015 | 0.150 | 99.929 |
| 9 | 0.007 | 0.071 | 100.000 |
| 10 | 4.140E-15 | 4.140E-14 | 100.000 |
主成分及累积贡献率结果如表 8,得到的图样如图 8,前4个主成分方差均大于1且累积贡献率为88.953%,超过85%[15],分析之后,本研究选择前四个主成分,用以进行后续数据的处理。
| 类型 | 平均速度/(km·h-1) | 平均加速度/(m·s-2) |
| 1 | 36.018 3 | -0.013 |
| 2 | 7.478 7 | 0.017 4 |
| 3 | 45.908 6 | -0.184 |
| 4 | 25.139 6 | -0.591 9 |
| 5 | 26.866 8 | 0.573 9 |
| 6 | 10.891 1 | 0.250 6 |
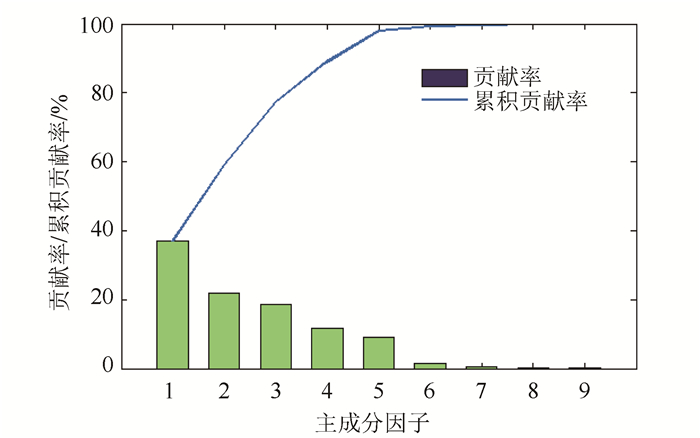
|
| 图 8 主成分贡献率及累积贡献率 Fig. 8 Principal component contribution rate and cumulative contribution rate |
| |
2.4 聚类分析
在本研究聚类分析阶段,利用主成分分析得到的4个主成分作为聚类分析的数据来源,进行数据的聚类分析。根据车辆一般行驶的规律,预先设计分类数目为6类,从而进行聚类分析。
本研究利用SPSS软件进行了聚类分析,分析结束后,15 682个片段归为6类,其分类结果如表 7。
根据分类结果,统计6类中各类的速度及加速度特征,结果如表 8。
本研究利用分类情况进行了其分布图的统计如图 9,X轴为片段运行平均速度,Y轴为片段运行平均加速度,Z轴为该片段距离类中心的距离。

|
| 图 9 聚类分析结果 Fig. 9 Cluster analysis result |
| |
由分类特征结果,可知第一类为高速匀速行驶,特征为平均速度较高、平均加速度较低;第二类为低速匀速行驶,特征为平均速度和平均加速度都较低;第三类为弱减速行驶,特征为平均速度较高、平均加速度中等;第四类为强减速行驶,特征为平均速度中等、平均加速度极低;第五类为强加速行驶,特征为平均速度中等,平均加速度极高、第六类为弱加速行驶,特征为平均速度较低、平均加速度较高。
3 工况合成本研究中工况合成采用马尔科夫理论,马尔科夫由两个关键的部分组成,一是状态空间,二是转移概率矩阵。定义一个事件为:当前时刻的状态为状态i,下一时刻的状态为状态j,则这个事件发生的概率称之为从状态i转移到状态j的概率。在马尔科夫理论中,下一时刻所处的状态只与当前时刻所处状态相关,具有无后效性。如果状态空间中存在K个状态,就会有K×K个转移概率,形成一个转移概率矩阵,矩阵中每一个元素的行坐标代表着当前时刻的状态,列坐标代表了下一时刻的状态,故而可以通过转移概率矩阵了解下一时刻各状态发生的概率,选取下一时刻采样点的状态。
蒙特卡洛模拟法是一种通过设定随机过程生成时间序列,将复杂的变化简化为简单的随机性事件的方法。蒙特卡洛模拟法特别适用于利用马尔科夫合成工况时,下一个片段的选取问题。在本方法的应用中,聚类分析得到的6种状态类型,即高速匀速行驶、低速匀速行驶、弱减速行驶、强减速行驶、强加速行驶、弱加速行驶等六类,作为马尔科夫过程的状态空间,依照数据间的关系可以计算出6种状态类型之间的转移概率,得到转移概率矩阵。在此基础上不利用转移概率最大者作为下一状态的选取依据,而采用蒙特卡洛模拟法,由于当前时刻转移到下一时刻的所有状态的转移概率之和为1,且每个状态的转移概率均在0~1之间,因此可以将其概率分布在长度为1的直线上,故而可以利用程序产生一个随机数,使之服从[0, 1]之间的均匀分布,根据随机数的取值,观测其落在哪一区间内,从而选择下一片段所处的状态。此方法可以完美规避传统马尔科夫方法造成小概率事件丢失的问题,从而提高合成工况的精确性。
3.1 马尔科夫状态转移概率矩阵获取聚类完成后,可进行工况的合成工作。根据聚类结果,将所分的六类作为状态空间,统计每一片段归属于哪一类,从而得到六类之间的状态转移频数矩阵,进而通过式(7)得到六类之间的状态转移概率矩阵[15]。式中Nij代表当前状态为i,下一状态为j的频数,pij代表当前状态为i,下一状态为j的概率。
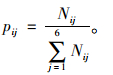
|
(7) |
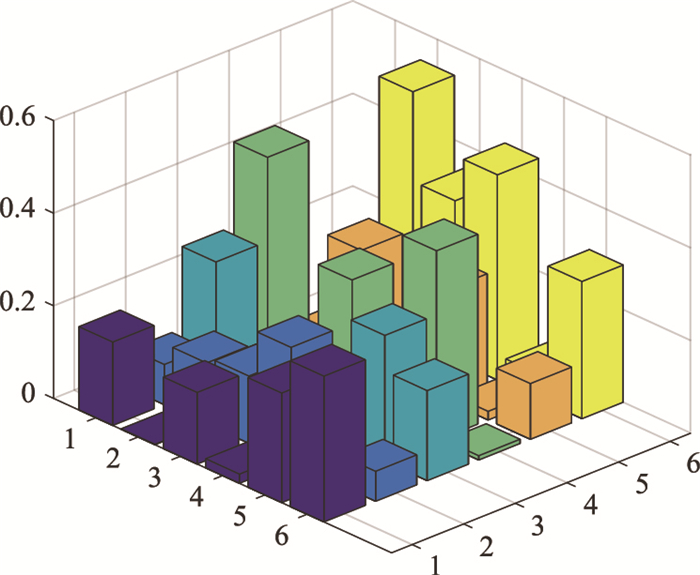
通过统计各类之间的转移频数关系,并利用公式(1)处理后,得其状态转移概率矩阵如下:
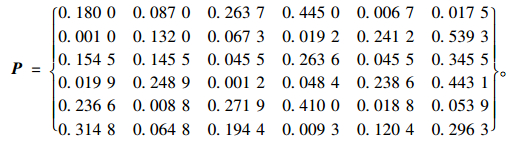
|
|
| 图 10 概率转移矩阵图 Fig. 10 Probabilistic transfer matrix graph |
| |
3.2 蒙特卡洛模拟法合成工况
在工况最终合成方面,根据马尔科夫状态转移矩阵,采用静态蒙特卡洛模拟法[16]进行工况合成。首先,设置了总体特征参数,用以进行备选工况与总体原始数据之间的对比。其中设置的总体特征参数分别为加速比例、减速比例、怠速比例、匀速比例,P(0-10), P(10-20), P(20-30), P(30-40), P(40-50), P(>50)。
采用马尔科夫方法的工况合成阶段,是一个典型的使用静态蒙特卡洛模拟法解决问题的过程,具体过程为:设当前状态为i, 下一状态为j,则其状态转移概率矩阵如表 9所示。
| j | 1 | 2 | 3 | 4 | 5 | 6 |
| Pij | Pi1 | Pi2 | Pi3 | Pi4 | Pi5 | Pi6 |
由状态转移矩阵的性质可知其每一行的概率之和为1,即式(8),其中Pij为当前状态为i下一状态为j的概率。
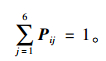
|
(8) |
而利用MATLAB产生的[0, 1]之间符合均匀分布的随机数x,若此随机数符合:
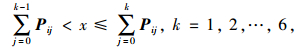
|
(9) |
则下一状态就为k,在k所属的状态类别中找到起始速度与上一片段结尾速度接近的片段进行合成,若其速度差值在合理范围内,该片段就可确定为下一片段。合成完毕后将k赋值于i,重复之前的步骤进行合成,直至达到理想的工况长度。
由于此方法合成过程保留了很大的行驶过程的随机性,故而一次合成不能完全代表最终工况。因此通过此方法,进行多个备选工况的构建。备选工况构建完成后,进行备选工况与总体试验数据之间的对比,并最终依据备选工况与总体试验数据间的相关系数
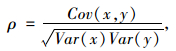
|
(10) |
进行选取,选取相关系数最大的备选工况作为最工况。
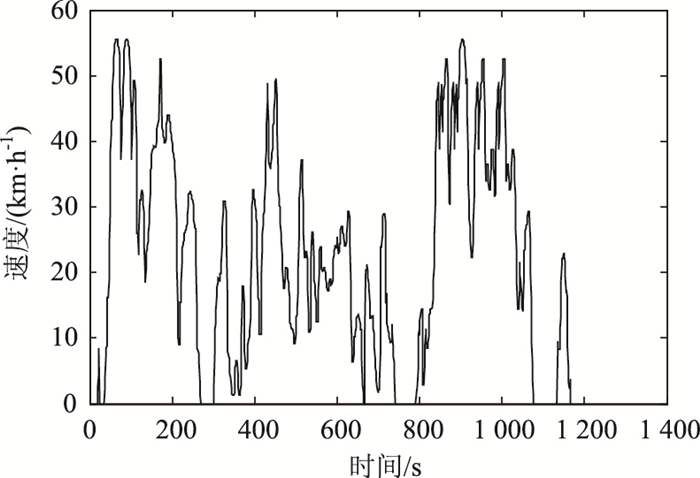
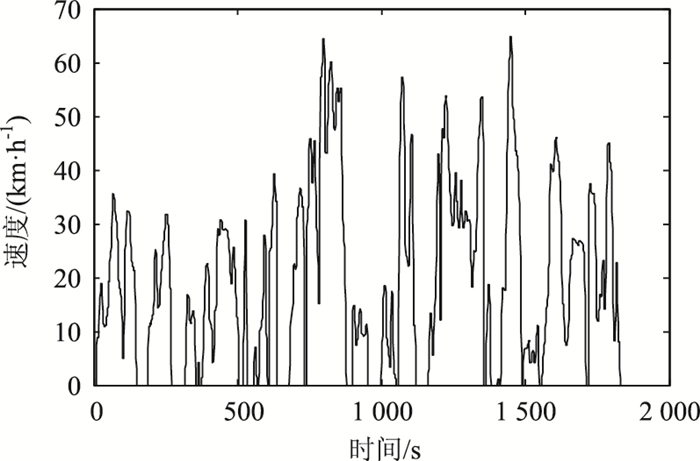
4 工况对比利用本研究方法合成的最终工况如图 11,其时间长度约1 200 s。为验证本研究方法所合成的工况的准确性,还利用短行程法、V-A矩阵法、定步长截取法进行了工况的合成,用以进行对比分析,其工况分别为图 12、图 13、图 14。

|
| 图 11 马尔科夫合成工况 Fig. 11 Markov synthesis driving cycle |
| |
|
| 图 12 短行程工况 Fig. 12 Short trip driving cycle |
| |
|
| 图 13 V-A矩阵工况 Fig. 13 V-A matrix driving cycle |
| |

|
| 图 14 定步长截取工况 Fig. 14 Driving cycle by constant step cutting |
| |
通过对比分析这4种工况与原始数据之间的总体特征参数,如表 12,与标准工况的对比情况如表 13。对比情况如图 15。4种工况与原始数据之间的误差率情况如表 10。
| 参数/% | FTP | ECE | UDDS | 本研究所建 |
| 总距离/km | 17.67 | 0.99 | 11.99 | 6.61 |
| 平均车速/(km·h-1) | 25.82 | 18.26 | 31.51 | 20.12 |
| 总时间/s | 2 477 | 195 | 1 369 | 1 182 |
| 最高车速/(km·h-1) | 91.25 | 50 | 91.25 | 62.29 |
| P(0-10)/% | 46.05 | 53.06 | 29.85 | 34.35 |
| P(10-20)/% | 10.69 | 25 | 15.26 | 17.43 |
| P(20-30)/% | 24.86 | 15.31 | 37.45 | 20.64 |
| P(30-40)/% | 9.44 | 6.63 | 9.34 | 14.13 |
| P(40-50)/% | 2.82 | 0 | 2.55 | 9.39 |
| P(> 50)/% | 6.13 | 0 | 5.55 | 4.06 |

|
| 图 15 特征参数对比 Fig. 15 Comparison of characteristic parameters |
| |
| 参数/% | V-A | 短行程 | 定步长 | 本研究所建 |
| 平均车速 | 1.25 | 18.23 | 7.16 | -5.27 |
| 加速比例 | 4.39 | 1.44 | 9.67 | 5.70 |
| 减速比例 | 5.13 | 8.12 | 2.72 | 9.39 |
| 匀速比例 | 4.07 | 6.20 | 3.00 | 6.60 |
| 怠速比例 | 4.46 | 10.71 | 25.51 | 0.92 |
| P(0-10) | 9.59 | 1.03 | 17.53 | 6.75 |
| P(10-20) | 6.54 | 3.31 | 8.50 | 9.37 |
| P(20-30) | 15.84 | 3.19 | 44.39 | 5.35 |
| P(30-40) | 12.48 | 36.00 | 31.08 | 4.50 |
| P(40-50) | 31.41 | 37.97 | 0.66 | 9.53 |
| P(> 50) | 1.25 | 18.23 | 7.16 | 5.27 |
| 平均误差 | 9.52 | 12.62 | 15.02 | 6.34 |
由上述图表可见西安市行驶工况在低速区间的运行时间最长,其平均速度较低,仅为20.027 2 km/h,低于10 km/h的运行概率达到34.03%,且其行驶过程不平稳,加速减速情况较多,最高车速在70 km/h左右。
通过对本研究所用马尔科夫-蒙特卡洛模拟法合成的工况及其与短行程法、V-A矩阵法、定步长截取法以及试验数据的对比如表 10和表 11所示,可以发现本研究所采用的方法平均误差率只有6.34%,而采用短行程法、V-A矩阵法、定步长截取法的平均误差率分别为12.62%,9.52%,15.02%,可见本研究所用方法虽合成过程较其他方法复杂,但其精度更高,与其他工况对比如表 12所示,所建立的工况更符合地区的实际情况,能够反映地区的实际交通环境,西安市的城市交通行驶工况与其他标准工况具有很大的差异,其平均车速低,加减速频繁,最高车速仅为62.29 km/h,结合第三节对比分析可知,本研究所建行驶工况与西安市地区实际最为符合。
| 特征参数 | V-A矩阵 | 短行程 | 定步长截取 | 本研究所建 | 原始数据 |
| 平均车速 | 19.456 5 | 21.884 6 | 21.325 1 | 20.094 7 | 20.027 2 |
| 加速比例 | 22.064 4 | 25.763 8 | 20.231 2 | 20.643 0 | 21.791 8 |
| 减速比例 | 22.009 8 | 21.387 3 | 23.121 4 | 19.881 6 | 21.083 3 |
| 匀速比例 | 36.319 0 | 35.177 5 | 37.241 9 | 41.878 2 | 38.284 7 |
| 怠速比例 | 19.606 8 | 17.671 3 | 19.405 5 | 17.597 3 | 18.840 1 |
| P(0-10) | 35.554 3 | 30.388 1 | 25.350 9 | 34.348 6 | 34.034 8 |
| P(10-20) | 20.480 6 | 18.497 1 | 21.965 3 | 17.428 1 | 18.689 0 |
| P(20-30) | 17.640 6 | 18.249 4 | 20.478 9 | 20.643 0 | 18.874 8 |
| P(30-40) | 12.561 4 | 14.450 9 | 21.552 4 | 14.128 6 | 14.926 5 |
| P(40-50) | 7.864 6 | 12.221 3 | 6.193 2 | 9.390 9 | 8.986 1 |
| P(> 50) | 5.898 4 | 6.193 2 | 4.459 1 | 4.060 9 | 4.488 7 |
5 总结
本研究通过设计行驶工况试验方案,改进行驶工况合成方法,最终合成了基于马尔科夫-蒙特卡洛模拟法的行驶工况。利用蒙特卡洛模拟法解决了传统马尔可夫构建法分类条件单一及小概率事件丢失的问题。最后通过对比该工况与原始数据及其他传统方法合成工况的差异,证明了该方法构建的工况具有更小的误差率,于标准工况对比,更能反映试验地区的交通特征,提高了行驶工况的真实性。
| [1] |
LIU L, HUANG C S, LU B W, et al. Study on the Design Method of Time-variant Driving Cycles for EV Based on Markov Process[C]//2012 Vehicle Power and Propulsion Conference. Seoul: IEEE, 2012: 1277-1281. https://www.researchgate.net/publication/261088665_Study_on_the_design_method_of_time-variant_driving_cycles_for_EV_based_on_Markov_Process
|
| [2] |
BAI Z L. The Specification of Model, Statistical Tests and New Progresses of Panel Data Analysis[J]. Statistics & Information Forum, 2010(10): 1-12. |
| [3] |
姜平.城市混合道路行驶工况的构建研究[D].合肥: 合肥工业大学, 2011 JIANG Ping. Investigation of Driving Cycle Construction for Urban Mixed Roads[D]. Hefei: Hefei University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10359-1011124246.htm |
| [4] |
石琴, 仇多洋, 周洁瑜. 基于组合聚类法的行驶工况构建与精度分析[J]. 汽车工程, 2012, 34(2): 164-169. SHI Qin, QIU Duo-yang, ZHOU Jie-yu. Driving Cycle Construction and Accuracy Analysis Based on Combined Clustering Technique[J]. Automotive Engineering, 2012, 34(2): 164-169. |
| [5] |
XING J, HAN X, YE H, et al. Driving Cycle Recognition for Hybrid Electric Vehicle[C]//2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific). Beijing: IEEE, 2014: 1-6. http://www.researchgate.net/publication/289064780_Driving_cycle_recognition_for_hybrid_electric_vehicle
|
| [6] |
HUNG W T, TONG H Y, LEE C P, et al. Development of a Practical Driving Cycle Construction Methodology:A Case Study in Hong Kong[J]. Transportation Research Part D:Transport and Environment, 2007, 12(2): 115-128. |
| [7] |
NESAMANI K S, SUBRAMANLAN K P. Development of a Driving Cycle for Intra-city Buses in Chennai India[J]. Atmospheric Environment, 2011, 45(31): 5469-5476. |
| [8] |
李鹏祥. 随机抽样中必要样本容量的确定[J]. 赤峰学院学报:自然科学版, 2009, 25(9): 18-19. LI Peng-xiang. Determination of Necessary Sample Size in Random Sampling[J]. Journal of Chifeng University:Natural Science Edition, 2009, 25(9): 18-19. |
| [9] |
郑庆玉. 参数估计与检验中样本容量的确定[J]. 临沂师范学院学报, 2001(6): 3-4. ZHENG Qing-yu. The Establishment of Sample Content in Parameter's Test And Estimate[J]. Journal of Linyi Teachers' College, 2001(6): 3-4. |
| [10] |
孙树荣.限额设计在高校建设中的应用研究及评价[D].淮南: 安徽理工大学, 2015. SUN Shu-rong. Research and Evaluation of Quota Design in College Construction[D]. Huainan: Anhui University of Science and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10361-1015581816.htm |
| [11] |
郑殿宇, 吴晓刚, 陈汉, 等. 哈尔滨城区乘用车行驶工况的构建[J]. 公路交通科技, 2017, 34(4): 101-107. ZHENG Dian-yu, WU Xiao-gang, CHEN Han, et al. Construction of Driving Conditions of Harbin Urban Passenger Cars[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 101-107. |
| [12] |
KOPPELMAN M. An Introduction to Data Mining[J]. Journal of American Association of Variable Star Observers, 2010, 38(2): 235. |
| [13] |
蔺宏良.西安市交通环境轿车行驶工况与燃料消耗研究[D].西安: 长安大学, 2013. LIN Hong-liang. Investigation of Driving Cycle and Fuel Consumption of Sedan in Xi'an Urban Traffic Environment[D]. Xi'an: Chang'an University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014032442.htm |
| [14] |
张鹏.基于城市道路汽车行驶工况的能量利用评价方法研究[D].哈尔滨: 东北林业大学, 2015. ZHANG Peng. Evaluation Methodology of Energy Utilization Based on Automobile Running Condition of City Road[D]. Harbin: Northeast Forestry University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10225-1015655875.htm |
| [15] |
姜平, 石琴, 陈无畏. 基于马尔科夫的城市道路行驶工况构建方法[J]. 农业机械学报, 2009, 40(11): 26-30. JIANG Ping, SHI Qin, CHEN Wu-wei. Driving Cycle Construction Methodology of City Road Based on Markov Process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(11): 26-30. |
| [16] |
邵伟.蒙特卡洛方法及其在一些统计模型中的应用[D].济南: 山东大学, 2012. SHAO Wei. Monte Carlo Method and Its Application in Some Statistical Models[D]. Jinan: Shandong University, 2012. http://d.wanfangdata.com.cn/Thesis/Y2263245 |
| [17] |
ZHAO X, MA J, WANG S, et al. Developing an Electric Vehicle Urban Driving Cycle to Study Differences in Energy Consumption[J]. Environmental Science and Pollution Research, 2018(5), 26(14): 13839-13853. http://link.springer.com/article/10.1007%2Fs11356-018-3541-6
|
 2019, Vol. 36
2019, Vol. 36
