扩展功能
文章信息
- 孙蕾, 林歆悠
- SUN Lei, LIN Xin-you
- 基于SOC参考斜率优化的PHEV能量管理控制策略
- Energy Management Control Strategy for PHEV Based on Optimal Reference SOC Gradient
- 公路交通科技, 2019, 36(11): 134-141
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 134-141
- 10.3969/j.issn.1002-0268.2019.11.018
-
文章历史
- 收稿日期: 2018-05-04
2. 福州大学 机械工程及自动化学院, 福建 福州 350002
2. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350002, China
插电式混合动力汽车(Plug-in Hybrid Electric Vehicle,PHEV)是混合动力向纯电动汽车的过渡车型。相比传统的混动汽车(Hybrid Electric Vehicle,HEV),PHEV拥有更佳的燃油经济性潜能[1],而且不存在纯电动汽车带来的“里程焦虑”。
PHEV通常匹配大容量的动力电池,且可以通过电网直接给电池充电以提升燃油经济性,但是PHEV的能量控制策略因此变的更加复杂[2]。这种复杂程度体现在两个方面,一方面PHEV对电池使用程度不同,HEV的电池荷电状态(State of Charge, SOC)始终保持在常数附近[3],而PHEV的SOC则通常是有较大的电池充放电窗口(通常0.3~0.9);另一方面,PHEV在两次充电的里程间隔,将会在很大程度上影响能量控制策略,当目标行驶里程小于纯电动续航里程时,应尽可能多的使用电池电量,而当目标行驶里程大于纯电动续航里程时则需要合理的分配各个时刻的电池使用[4-5]。由此,PHEV的控制目标可总结为,在尽量使用从电网获得电能的前提下,如何分配发动机和电机的功率,使得整车获得最佳的燃油经济性。车辆的初始SOC和总行驶里程是影响PHEV能量分配的重要参数[6-8]。文献[9]通过遗传算法(Genetic algorithm,GA)考察多组初始SOC和总行驶里程下的最优等效系数,并将其制作成MAP用于实时的控制,该策略相比为优化的策略燃油经济性提升20.8%。但其通过MAP获取的最优等效系数在一次行驶过程中为常数,这使得其在部分条件下无法获取最优的控制。文献[10]将当前电池的可用电量除以剩余里程作为设计参数,并以此建立基于规则的能量控制策略,且成功运用于一款量产车。该策略相比于CD-CS策略提升8.2%的燃油经济性。但该策略仅从全局SOC控制的角度对电量进行整体的调控,而缺少对放电局部过程的能量最优分配,使得其燃油经济性还有提升空间, 基于SOC开展能量管理策略成为研究的新趋势[11-13]。
离线最优算法可获取全局的最优解,如动态规划(Dynamics Programming, DP)通过将某一循环工况能量分配问题分解为有限个子问题,通过确定每个子问题的能量分配进而确定整车的控制策略。DP需要整个行驶工况的数据和较大的计算量,因此DP不能运用于实际汽车的优化。但DP由于可以获得全局最优的燃油经济性,通常作为其他控制策略控制结果的参考和参数提取的来源[14]。文献[15]采用DP对一款ISG型速度耦合混合动力汽车的控制策略进行了优化,并基于DP规划的结果提取设计参数建立相应模糊控制策略,获得较好燃油经济型提升。
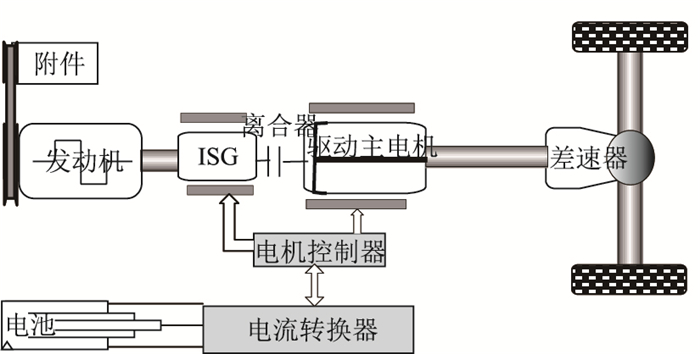
鉴于此,为综合考虑SOC和总行驶里程的影响且从全局和局部的角度综合考虑电量的使用,以文献[16]中的插电混联混合动力系统为例,具体如图 1所示。在已知总行驶里程的情况下,首先定义SOC斜率,并使用DP获取中国城市典型循环工况下的SOC斜率;进一步通过SOC标准斜率修正DP下的SOC斜率作为SOC参考斜率,并将其转化为参考SOC;最后基于ECMS控制策略通过SOC惩罚函数修正成等效系数,使实际的SOC能跟随参考SOC,提升燃油经济性。
|
| 图 1 混联式混合动力系统 Fig. 1 Powertrain of series-parallel hybrid |
| |
1 基于DP的SOC参考斜率获取 1.1 动态规划下SOC斜率求解
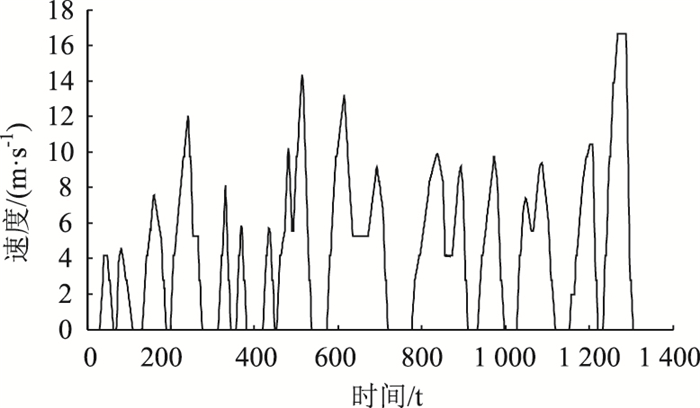
以中国城市典型工况为例,图 2为中国城市典型公交循环工况图。在该工况下,将整车需求转矩分配的最优控制问题离散成和时间相关的多阶段决策序列,以油耗最低,利用离散动态规DP算法,通过逆向求得其全局最优控制解集,再正向求解获取控制过程的状态变化。定义SOC斜率如下:
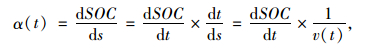
|
(1) |
|
| 图 2 中国城市典型循环的工况 Fig. 2 Chinese typical city bus driving cycle |
| |
式中, v(t)为当前整车行驶速度;则SOC斜率α(t)可以理解为当前时刻,单位里程消耗的SOC。
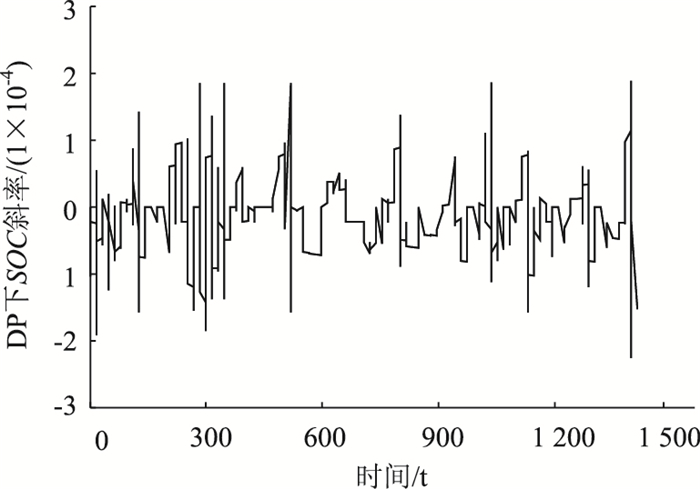
选定状态变量为电池SOC,控制变量为电机的输出转矩与整车需求转矩之比u。参考文献[15],采用DP在初始SOC为0.4,单个中国城市典型公交循环工况下,总行驶里程为5.8 km时,动态规划下求解的SOC斜率α的分布如图 3所示。
|
| 图 3 动态规划下的SOC斜率分布 Fig. 3 SOC slope distribution under DP |
| |
1.2 SOC参考斜率的获取
动态规划全局优化的结果可以为其他控制策略提供设计基准[15-16]。但由于1.1节中DP仅获取在特定的初始电池荷电状态和特定总行驶里程下的SOC斜率α。为使得1.1节中DP优化后SOC斜率α可以适用于不同的初始SOC和不同的总行驶里程,需要对SOC斜率α进行修正。
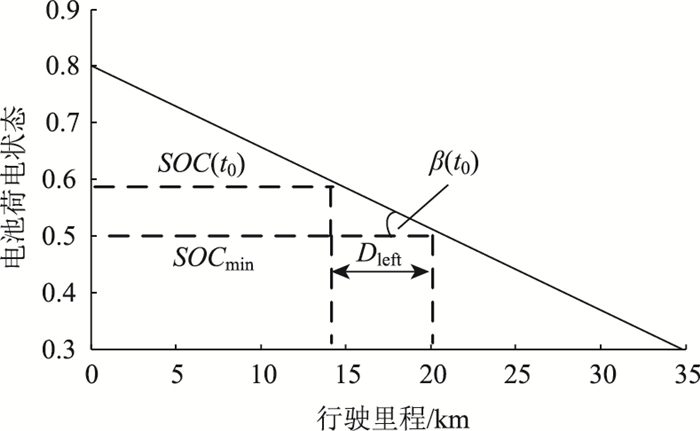
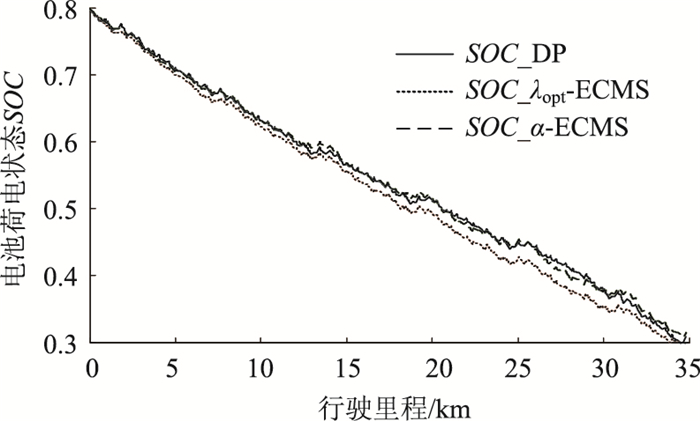
综合考虑SOC和总行驶里程的影响,根据文中SOCmin为保护电池的SOC下限值,Dtotal为预先已经获取的总行驶里程,D(t)为当前已经行驶的里程。当初始电池荷电状态为SOC(t0),剩余行驶里程为Dleft时,如图 4所示。β(t0)为如图直线的斜率绝对值,β(t0)可以理解为一次行驶过程中,单位行驶里程电池可提供消耗的SOC。文献[17],定义标准斜率β(t)如下:
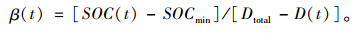
|
(2) |
|
| 图 4 标准斜率的定义 Fig. 4 Definition of standard gradient |
| |
对于插电式混合动力汽车,若两次行驶里程的距离小于纯电动行驶里程,那么控制策略应该选择尽量消耗从电网获得的电量以获得最高的燃油经济性。显然电池SOC和行驶工况都将直接影响纯电动行驶里程,本研究忽略行驶工况影响,在中国城市典型公交循环工况下,仿真获得常用SOC下电动行驶里程,如表 1所示。
| SOC | 纯电动行驶里程DAER | 全局参考斜率βAER |
| 0.5 | 4.889 1 | 0.049 0 |
| 0.6 | 7.002 5 | 0.042 8 |
| 0.7 | 9.732 6 | 0.041 1 |
| 0.8 | 11.858 | 0.044 6 |
结合式(2),计算纯电动行驶的标准斜率:
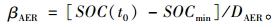
|
(3) |
各个SOC下的βAER如表 1所示。为便于处理,取各个SOC下的标准斜率平均值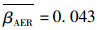
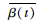
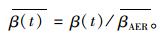
|
(4) |
显然当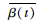
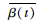
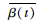
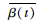
如图 5所示,当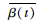
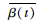
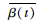
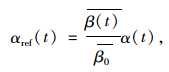
|
(5) |
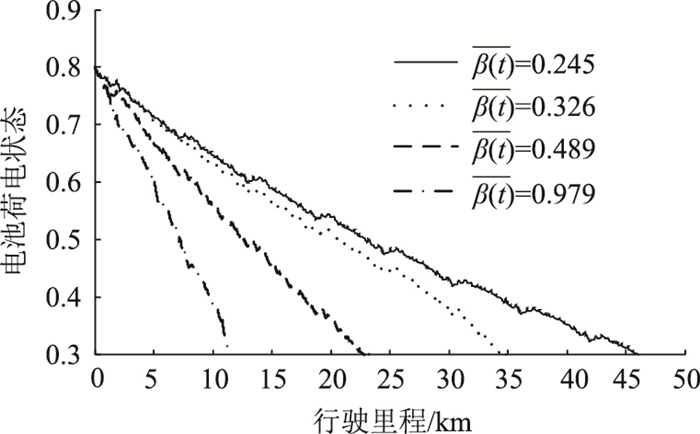
|
| 图 5 动态规划下不同行驶里程的SOC轨迹 Fig. 5 SOC trajectories of different trip distances under DP |
| |
其中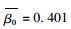
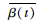
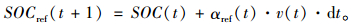
|
(6) |
在获取参考SOC后,本研究采用ECMS策略通过分配发动机功率和电机的功率使实际的SOC跟随参考SOC。
ECMS的目标函数定义如下:
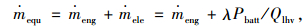
|
(7) |
式中, ṁequ为单位时间等效燃油消耗量; ṁeqg为单位时间发动机燃油量; ṁele为单位时间电池等效燃油消耗量; λ为等效系数;Pbatt为电池功率;Qlhv为燃油低热值。
通过加入SOC惩罚函数,参考文献[18]定义如下价值函数:
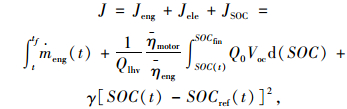
|
(8) |
式中,JSOC为因实际SOC不能跟随参考SOC带来的惩罚函数; ηmotor为电机的平均效率;ηeng为发动机的平均效率γ为惩罚系数; SOCref(t)为根据上一时刻预测获得的当前时刻的参考SOC;J为总价值函数;Jeng为发动机的价值函数;Jele为电池价值函数;Q0为电池初始容量;Voc为电池电压。
结合公式(30),拉格朗日乘子表示为:
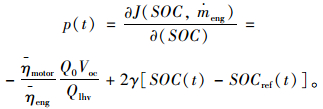
|
(9) |
又由等效系数和拉格朗日乘子的关系有:
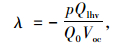
|
(10) |
结合式(9),(10)有:
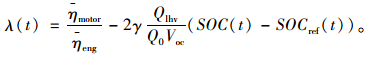
|
(11) |
将等效系数的确定过程修改为比例积分环节:
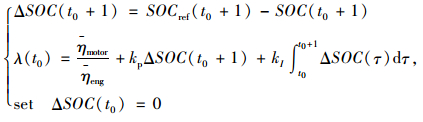
|
(12) |
式中kp为调节系数。
在确定当前时刻等效系数λ(t),控制策略优化问题可以描述为,当等效系数为λ(t),求解最佳的控制:
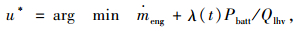
|
(13) |
式中,u*为最佳控制量,即arg min获得最小油耗下的控制变量。
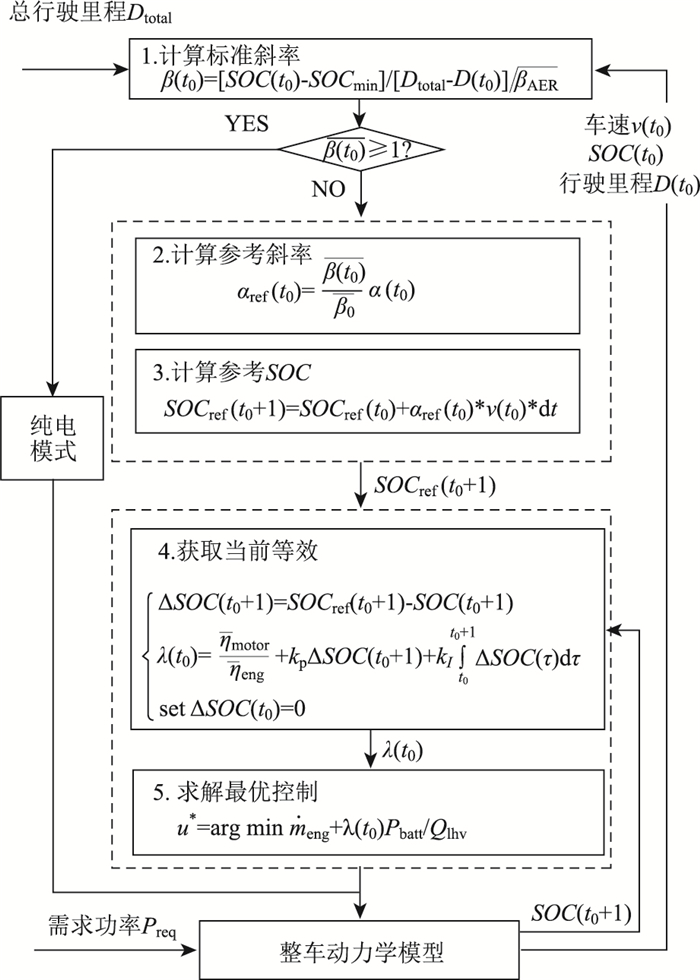
至此,建立基于SOC参考斜率优化的ECMS控制策略,从t0时刻起的过程如图 6可分为3个步骤:
|
| 图 6 基于SOC参考斜率优化的ECMS策略流程图 Fig. 6 Flowchart of ECMS based on optimal reference SOC gradient |
| |
(1) 工况开始时t0时刻,给定总行驶里程Dtotal,以及初始电池荷电状态SOC(t0),根据当前已经行驶的里程D(t0),计算当前时刻标准斜率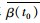
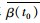
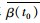
(2) 在t0+1时刻获取SOC(t0+1),通过式(12)对t0+1时刻的等效系数λ(t0+1)进行修正,并将其作为t0+1时刻的等效系数。
(3) 用当前时间替换t0,重复步骤(1),(2)。
3 仿真实验及结果分析为验证所制定基于SOC参考斜率优化的策略(以下简称为α-ECMS)对PHEV在不同初始电池荷电状态SOC(t0)以及不同行驶里程Dtotal燃油经济性的优越性进行验证。
选中国城市典型公交循环工况进行仿真试验,运行Dtotal等于34.8 km,以SOC(t0)为0.8时(即标准斜率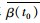
|
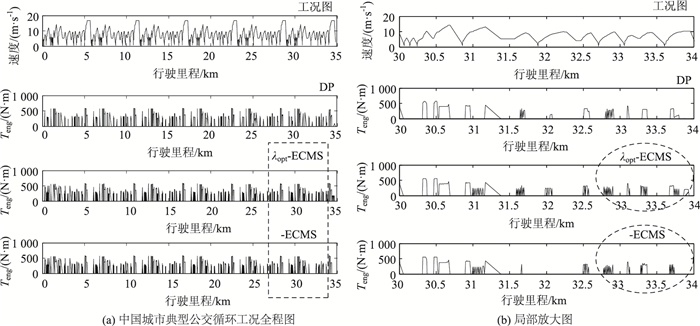
| 图 7 DP, α-ECMS和λopt-ECMS的发动机扭矩 Fig. 7 Engine torques under DP, α-ECMS and λopt-ECMS |
| |
|
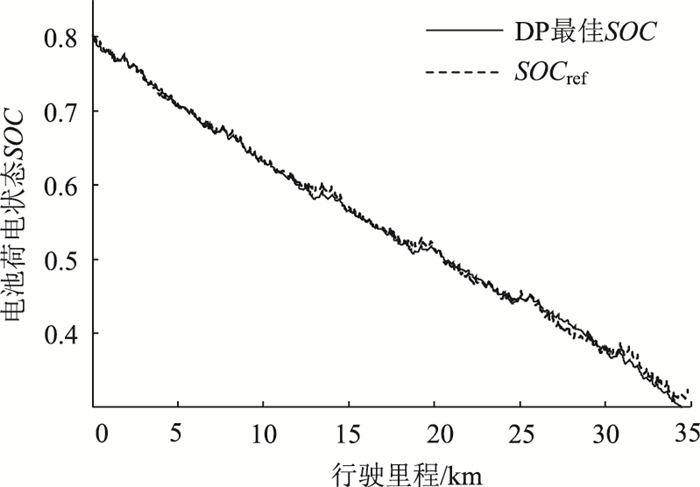
图 8 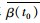 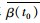 |
| |
|
图 9 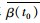 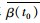 |
| |
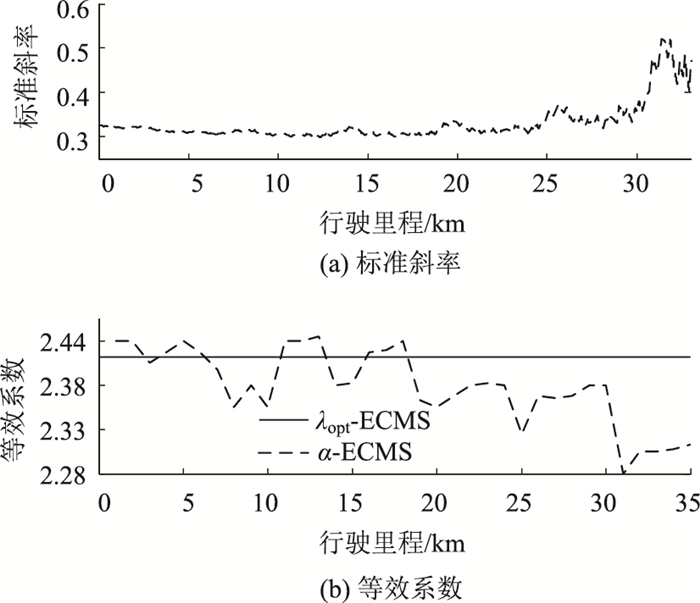
|
图 10 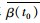 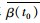 |
| |
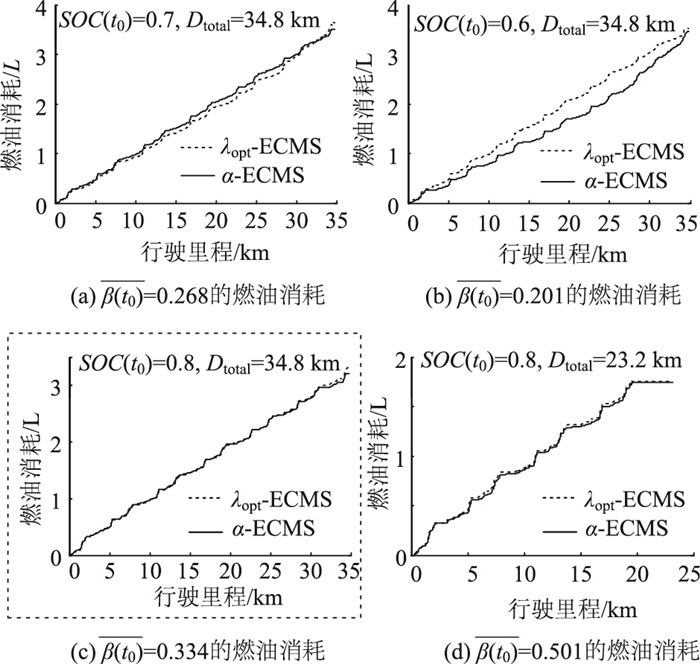
|
| 图 11 不同标准斜率下的λopt-ECMS与α-ECMS油耗结果 Fig. 11 Fuel consumptions of λopt-ECMS and α-ECMS under different standard gradients |
| |
图 8为该工况下DP轨迹和SOCref(t)的运行轨迹,图中SOCref(t)在DP的轨迹下上下波动,但基本与DP的轨迹贴合。图 9为该工况下λopt-ECMS,DP和α-ECMS策略的SOC轨迹。对于λopt-ECMS的SOC轨迹,在0~10 km期间,其SOC轨迹与DP的SOC轨迹十分接近,而在之后与DP规划的轨迹差值逐渐增大。其原因是对于λopt-ECMS控制策略,等效系数始终为常数,使得该策略无法在所有时刻都获取最佳的经济性。
如图 10所示,α-ECMS在整个行驶工况下当标准斜率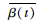
对比λopt-ECMS和α-ECMS的油耗曲线如图 11所示,选取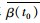
为验证提出的α-ECMS可以适应不同的行驶里程Dtotal和不同初始电池荷电状态SOC(t0)。通过仿真多组不同SOC(t0)和Dtotal获得的油耗结果如表 2所示,括号中则表示在该条件相对于动态规划燃油消耗还尚存的燃油提升空间。观察表 2,相比于λopt-ECMS策略,α-ECMS在不同的SOC(t0)和Dtotal下均获得一定的燃油经济性提升。具体而言,还是以斜率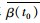
| SOC(t0)=0.8 Dtotal=34.8 km ( 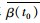 =0.334) =0.334) |
SOC(t0)=0.8 Dtotal=23.2 km ( 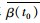 =0.501) =0.501) |
SOC(t0)=0.6 Dtotal=34.8 km ( 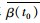 =0.201) =0.201) |
|
| λopt-ECMS | 9.456 L(5.8%) | 7.762 L(8.0%) | 10.48 L(7.3%) |
| α-ECMS | 9.179 L(2.7%) | 7.560 L(5.1%) | 10.06 L(3.0%) |
| DP | 8.940 L | 7.191 L | 9.771 L |
4 结论
(1) 以一款插电混联式混合动力系统为研究对象,通过DP提取SOC斜率,并使用标准斜率进行修正获取参考斜率,再获取参考SOC,通过对参考SOC的跟随,提出基于SOC参考斜率优化的等效燃油消耗最小控制策略。
(2) 仿真结果表明,本研究提出策略作用下的SOC与DP的最佳SOC几乎吻合;在燃油经济性方面,以斜率 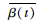
(3) 本研究提出的α-ECMS控制策略可以基于SOC斜率,并根据SOC标准斜率对等效系数进行动态调整,有效提升PHEV在不同Dtotal和SOC(t0)下的燃油经济性。
| [1] |
舒红, 彭大, 袁月会, 等. 插电式并联混合动力汽车动力传动系统与控制参数匹配设计[J]. 汽车工程学报, 2012, 2(2): 105-112. SHU Hong, PENG Da, YUAN Yue-hui, et al. Matching Design of Power train and Control Parameters for a Plug-in Parallel Hybrid Electric Vehicle[J]. Chinese Journal of Automotive Engineering, 2012, 2(2): 105-112. |
| [2] |
程飞, 赵韩, 尹安东, 等. 插电式并联混合动力汽车模糊控制策略设计与仿真[J]. 合肥工业大学学报:自然科学版, 2015, 38(9): 1159-1164. CHENG Fei, ZHAO Han, YI An-dong, et al. Design and Simulation of Fuzzy Control Strategy of Plug-in Parallel Hybrid Electric Vehicle[J]. Journal of Hefei University of Technology:Natural Science Edition, 2015, 38(9): 1159-1164. |
| [3] |
LIN X Y, ZHAI L Q, LIN H B. Investigation of Real-time Adaptive Energy Management Strategy for a Series-Parallel Hybrid Electric Bus[J]. International Journal of Electric and Hybrid Vehicles, 2016, 8(3): 195-212. |
| [4] |
LIN X Y, FENG Q G, MO L P, et al. Optimal Adaptation Equivalent Factor of Energy Management Strategy for Plug-in CVT HEV[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2019, 233(4): 877-889. |
| [5] |
林歆悠, 夏玉田, 李雪凡, 等. 燃料电池汽车行驶里程自适应ECMS策略[J]. 汽车工程, 2019, 41(7): 750-756. LIN Xin-you, XIA Yu-tian, LI Xue-fan, et al. Equivalent Consumption Minimization Strategy Adaptive to Various Driving Ranges for Fuel Cell Vehicles[J]. Automotive Engineering, 2019, 41(7): 750-756. |
| [6] |
倪成群, 赵强, 张幽彤, 等. 插电式混合动力客车电能消耗阶段控制策略的研究[J]. 汽车工程, 2014, 36(1): 12-16, 27. NI Cheng-qun, ZHAO Qiang, ZHANG You-tong, et al. A Study on the Control Strategy for PHEB in Energy Depletion Mode[J]. Automotive Engineering, 2014, 36(1): 12-16, 27. |
| [7] |
MANZIE C, DEWANGAN P, CORDE G, et al. State of Charge Management for Plug in Hybrid Electric Vehicles with Uncertain Distance to Recharge[C]//2013 9th Asian Control Conference. Istanbul: IEEE, 2013: 1-6. http://www.researchgate.net/publication/261350737_State_of_charge_management_for_plug_in_hybrid_electric_vehicles_with_uncertain_distance_to_recharge
|
| [8] |
HOU C, XU L, WANG H, et al. Energy Management of Plug-in Hybrid Electric Vehicles with Unknown Trip Length[J]. Journal of the Franklin Institute, 2015, 352(2): 500-518. |
| [9] |
YU H, KUANG M, MCGEE R. Trip Oriented Energy Management Control Strategy for Plug-in Hybrid Electric Vehicles[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference. Orlando: IEEE, 2011. http://www.researchgate.net/profile/Ming_Kuang4/publication/228438133_Trip-Oriented_Energy_Management_Control_Strategy_for_Plug-In_Hybrid_Electric_Vehicles/links/56215e6308ae70315b58cd76/Trip-Oriented-Energy-Management-Control-Strategy-for-Plug-In-Hybrid-
|
| [10] |
LIN Xin-you, FENG Qi-gao, ZHANG Shao-bo. Global Optimal Discrete Equivalent Factor of Equivalent Fuel Consumption Minimization Strategy Based Energy Management Strategy for a Series-parallel Plug-in Hybrid Electric Vehicle[J]. Journal of Mechanical Engineering, 2016, 52(20): 102-110. |
| [11] |
HEPPELER G, SONNTAG M, WOHLHAUPTER U, et al. Predictive Planning of Optimal Velocity and State of Charge Trajectories for Hybrid Electric Vehicles[J]. Control Engineering Practice, 2017, 61: 229-243. |
| [12] |
MANZIE C, DEWANGAN P, CORDE G, et al. State of Charge Management for Plug-in Hybrid Vehicles with Uncertain Trip Information[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(9): 1-7. |
| [13] |
CORDINER S, GALEOTTI M, MULONE V, et al. Trip-based SOC Management for a Plug-in Hybrid Electric Vehicle[J]. Applied Energy, 2016, 164: 891-905. |
| [14] |
LARSSON V, JOHANNESSON L, EGARDT B. Analytic Solutions to the Dynamic Programming Sub-problem in Hybrid Vehicle Energy Management[J]. IEEE Transactions on Vehicular Technology, 2015, 64(4): 1458-1467. |
| [15] |
杨亚联, 叶盼, 胡晓松, 等. 基于DP优化的ISG型速度耦合混合动力汽车模糊控制策略的研究[J]. 汽车工程, 2016, 38(6): 674-679. YANG Ya-lian, YE Pan, HU Xiao-song, et al. A Research on the Fuzzy Control Strategy for a Speed-coupling ISG HEV Based on Dynamic Programming Optimization[J]. Automotive Engineering, 2016, 38(6): 674-679. |
| [16] |
林歆悠, 薛瑞, 孙冬野. SPHEB基于动态规划的规则控制策略研究[J]. 系统仿真学报, 2013, 25(5): 1077-1082. LIN Xin-you, XUE Rui, SUN Dong-ye. Rule Based Strategy Derived from Dynamic Programming for Novel Series-parallel Hybrid Electric City Bus[J]. Journal of System Simulation, 2013, 25(5): 1077-1082. |
| [17] |
KUM D. Modeling and Optimal Control of Parallel HEVs and Plug-in HEVs for Multiple Objectives[D]. Ann Arbor: University of Michigan, 2010.
|
| [18] |
FENG T, LIN Y, GU Q, et al. A Supervisory Control Strategy for Plug-in Hybrid Electric Vehicles Based on Energy Demand Prediction and Route Preview[J]. IEEE Transactions on Vehicular Technology, 2015, 64(5): 1691-1700. |
 2019, Vol. 36
2019, Vol. 36
