扩展功能
文章信息
- 张建莉, 陈榕峰, 姚岢
- ZHANG Jian-li, CHEN Rong-feng, YAO Ke
- 公路路面不平整度对汽车振动的影响分析
- Analysis on Influence of Road Pavement Roughness on Vehicle Vibration
- 公路交通科技, 2019, 36(11): 129-133
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 129-133
- 10.3969/j.issn.1002-0268.2019.11.017
-
文章历史
- 收稿日期: 2019-01-10
2. 广东省交通运输规划研究中心, 广东 广州 510101
2. Guangdong Provincial Transport Planning & Research Center, Guangzhou Guangdong 510101, China
车辆与路面相互作用的动力学已成为近来研究热点。影响轮式车辆振动的原因既多且复杂,而公路路面不平整是引起车辆振动的主要因素[1]。路面不平使车辆在行驶中产生振动,对行驶车辆的平顺性(即乘员由于汽车振动引起疲劳感和舒适感,或者载运货物的损伤程度)以及行驶系统(包括悬架、轮胎、车体等)的可靠度和寿命耐久性会产生很大影响。王秉纲[2-7]等对路面功率谱进行了研究,进而模拟路面不平整度。由于路面不平整是平稳而均匀的Gauss随机场,在路面不平整的激励下,车辆的振动也表现出随机的特性。不平整路面激励下的车辆随机振动响应已引发学者的高度兴趣并开展了研究工作,但研究多限于较为简单的两自由度1/4车辆模型[8-10], 或需采用较为复杂的自编程序进行模拟仿真[11-12]。本研究基于国家标准GB/T 7031—2005[13]确定的路面不平度功率谱密度公式,运用傅氏逆变换模拟公路路面不平整度,再将路面不平整数值作为车轮竖向激励输入四自由度车辆振动模型, 通过分析车辆行驶在不平整路面上的振动响应,进而获得车体振动加速度均方差随车速及路面等级变化的规律曲线。
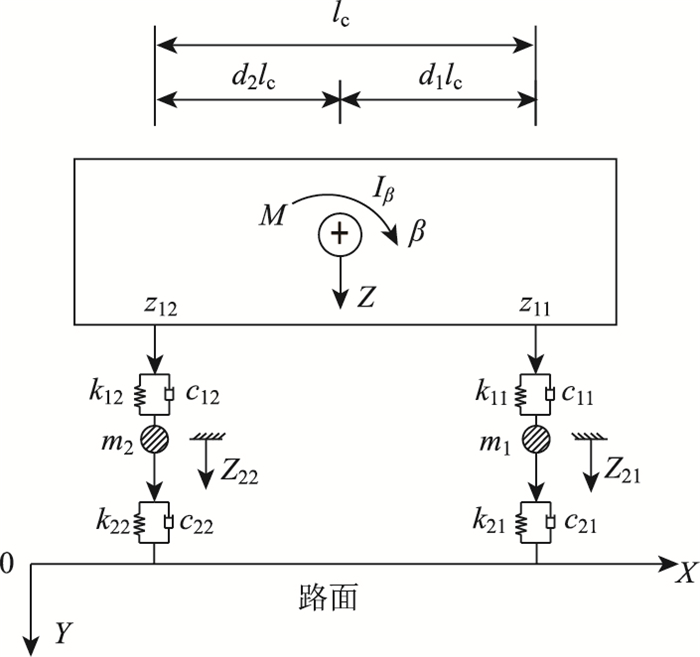
1 车辆振动问题的求解图 1为考虑计算结果与实际情况较为吻合的1/2车辆模型,将其简化为四自由度的质量-阻尼-弹簧系统。
|
| 图 1 四自由度车辆振动模型 Fig. 1 Four-DOF vehicle vibration model |
| |
图 1中,M为车体的质量,车体具有两个方向的自由度,也就是质心的竖直方向位移z和绕车体横轴转动(即车体的俯仰)的转角β;m1和m2分别为车辆前后轴的簧下质量;k11和k12分别为车辆前轴和后轴悬架弹簧的刚度;c11和c12分别为车辆前轴和后轴悬架弹簧的阻尼;k21和k22分别为车辆前轮和后轮胎的刚度;c21和c22分别为车辆前轮和后轮胎的阻尼;lc为车辆前后轴的轴距;Iβ为车体绕横轴的转动惯量;d1和d2为车辆质心与前后轴距离的比例常数;z11和z12分别为前后轴位置车体竖直方向的位移;z21和z22分别为车辆前后车轮竖直方向的位移。
根据车辆模型的几何关系可得:
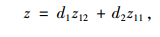
|
(1) |

|
(2) |
由广义虚功原理[14](即动力学总势能不变值原理):
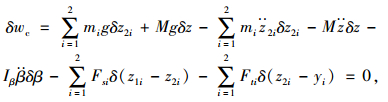
|
(3) |
可得微分方程组:
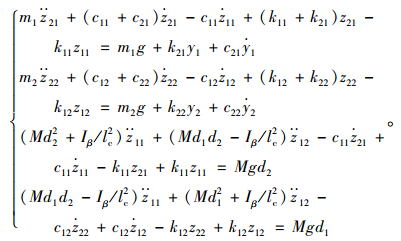
|
(4) |
将微分方程组进一步整理、矩阵化:
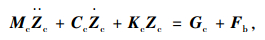
|
(5) |
式中,wc为系统虚功;Fsi,Fti分别为车辆悬架弹簧的恢复力、轮胎弹簧的恢复力;δ为变分符号;Zc为车辆竖向位移矩阵;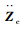
研究认为,路面不平整是平稳而均匀的Gauss随机场,具有均值为零和各态历经的特性,该特性通常可以利用功率谱来仿真模拟。国外从20世纪中叶开始对路面不平整功率谱进行研究,如国际标准化协会制定的ISO SCI/WG4标准、M.米奇克公式等。我国汽车工程研究人员参照国外研究成果,结合国内实际情况,制定了我国的国标GB/T 7031—2005,提出了较为符合我国实际的模拟公路路面不平整的功率谱密度公式[13]:
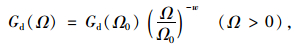
|
(6) |
式中,Ω为每单位长度中的波数;Ω0为标准波数(取Ω0=0.1 m-1);Gd(Ω0)为标准波数对应的谱密度数值,即路面平度系数;Gd(Ω)为位移功率谱密度;w为路面功率谱密度的频率结构, 取w=2。GB/T7031—2005规定的各等级路面平度系数平均值如表 1所示。
| 路面等级 | Gd(Ω0)几何均值 |
| A | 16 |
| B | 64 |
| C | 256 |
| D | 1 024 |
| E | 4 096 |
| F | 16 384 |
2.2 路面不平度与行车速度的关系分析
汽车振动系统输入信息的另外一个重要因素是车速。车速v与空间谱密度的关系是Gd(f)=Gd(Ω)/v。因此,地面作用于轮胎的激励时间频率f与汽车振动时需要的空间频率Ω的关系为:f=vΩ[15]。由此,根据特定的车速和时间频率可以确定汽车振动所在空间频率的区间。
研究认为,只要地面作用于轮胎的激励时间频率f的区间能够覆盖汽车振动固有频率,即可保证研究结论符合实际情况。通常情况下,汽车车体的固有频率为1~2 Hz,车轮部分的固有频率为10~15 Hz[15]。因此设时间频率范围f=0.4~25 Hz,即可将汽车振动固有频率的区间涵盖在内。若取常用车速30~150 km/h(8.33~41.67 m/s),则只需取空间频率Ω的下限为0.01 m-1、上限为3.0 m-1的区间内仿真路面不平度,并将模拟所获得的路面不平度数值作为激励,输入到汽车振动模型中来研究车辆振动情况即可。
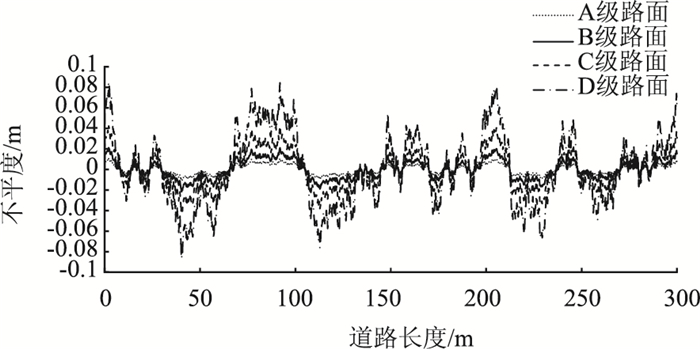
2.3 路面不平度的模拟路面平度系数取国标GB/T7031—2005规定平均值,道路长度L=300 m,可模拟出各级路面不平整度序列数值。图 2为A~D级路面不平度序列数值在道路长度方向形成的变化曲线。
|
| 图 2 A~D级路面的不平度曲线 Fig. 2 Curves of roughness of grades A-D road pavement |
| |
3 算例及结果分析
车辆振动微分方程为高阶微分方程组,通常采用逐步积分法进行数值求解。其中,Wilson-θ法[16]是一种修正线性加速度逐步积分数值求解法,具有无条件稳定的特性。本研究基于Wilson-θ法,运用MATLAB强大的数值求解功能编制了求解程序,将道路长度L=300 m路面不平度值作为激励,输入到车辆振动系统微分方程中,对不同等级的路面、不同行驶速度的车辆所产生的振动响应进行求解。
采用文献[17]中的车辆数据:M=38 500 kg;Iβ=2.446×106 kg·m2;lc=8.4 m;d1=d2=0.5;m1=m2=4 330 kg;k11=k12=2.535×106 N/m;k21=k22=4.28×106 N/m;c11=c12=1.96×105 kg/s;c21=c22=9.8×104 kg/s。
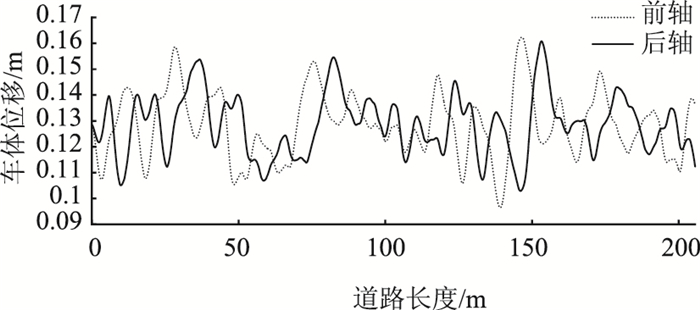
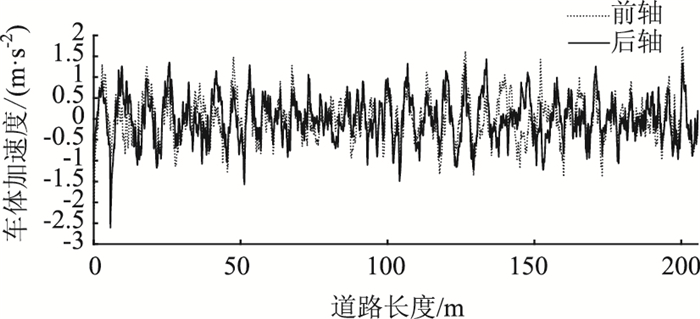
限于篇幅,本研究仅示出以60 km/h速度行驶在B级路面上的车辆前轴、后轴位置处,车体的垂向位移变化曲线(图 3)和垂向加速度变化曲线(图 4)。
|
| 图 3 车体振动位移曲线 Fig. 3 Curves of vehicle vibration displacement |
| |
|
| 图 4 车体振动加速度曲线 Fig. 4 Curves of vehicle vibration acceleration |
| |
由于车辆振动是平稳各态历经的随机过程,其车体振动的位移和加速度都是围绕均值为零的随机振动的离散数据系列。为了描述车体随机振动在均值附近的振动程度,本研究引入车体加速度均方差来反映车体振动的情况[18],即可定义车体振动强度σ。
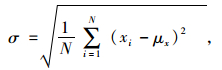
|
(7) |
式中,xi为车辆前后轴位置车体的加速度值;μx为车体振动加速度均值;σ为车体加速度均方差,表示车体振动强度。
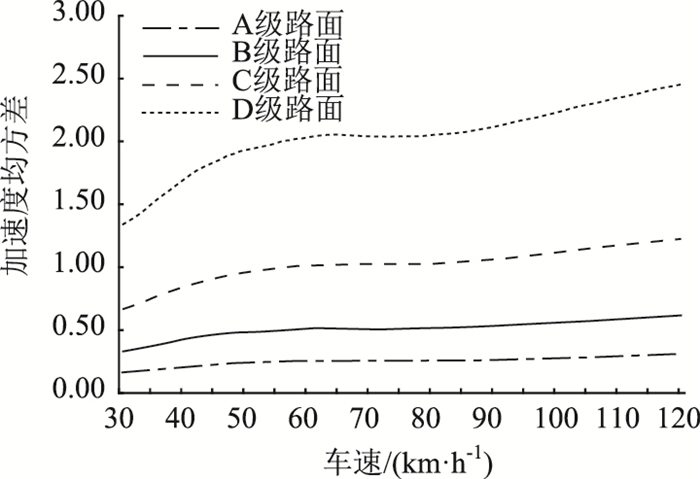
A~D级路面上车速为30~120 km/h时,车体振动强度(σ)的变化曲线如图 5和图 6所示。
|
| 图 5 车辆速度与车体加速度均方差的关系 Fig. 5 Relationship between vehicle velocity and vehicle acceleration mean square error |
| |
|
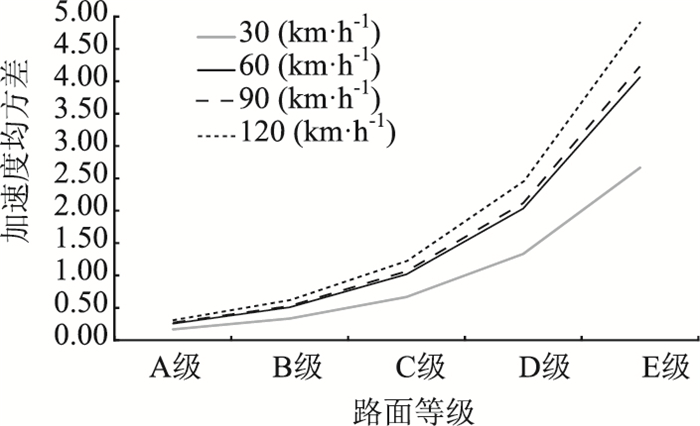
| 图 6 路面不平度与车体加速度均方差的关系 Fig. 6 Relationship between pavement roughness and vehicle acceleration mean square error |
| |
由图 5可知,各等级路面上行驶车辆的车体振动强度均随车速增加而呈增大趋势,其中在货车常行驶的60~80 km/h区间有一个几乎不再增大的平缓区间。以B级路面为例,车体振动强度从3 km/h的0.333 1增大至60 km/h的0.508 2,增大了74.2%;但车速从60 km/h增大至80 km/h时,车体振动强度仅增大至0.511 7,仅增大0.69%;随后当车速继续增大至120 km/h时,车体振动强度随之增大至0.612 8,增大了19.8%。
由图 6可知,在相同车速下,随着车体振动强度路面状况变差呈二次抛物线形态的增大趋势。以车速为60 km/h为例,车体振动强度从A级路面的0.254 1增大到E级路面的4.065 8,增大了15倍,路面状况是影响车体振动的最显著因素。
4 结论车辆振动是一个复杂的问题,建立车辆振动模型准确模拟车体振动较为困难。本研究建立了四自由度车辆振动模型,并运用GB/T7031—2005提出的公路路面功率谱密度公式模拟路面不平整度,对以不同速度在不同等级公路路面上行驶的车辆车体振动进行了模拟分析,获得了较好的分析结果。主要结论如下:
(1) 影响车体振动最重要、最显著的因素是公路的路面状况。在相同的车速情况下,车体振动强度随着公路路面等级降低,显现出几何级增大的形态,道路路面等级越低,车体振动强度增加的幅度越明显。
(2) 影响车体振动强度的另一个的重要因素是车速。在本研究引用的车辆参数条件下,当路面等级相同时,车体振动强度随车速增大而增大,呈“前急中平后缓”的趋势,其中在货车常用的60~80 km/h区间,存在一个车速增大但车体振动强度不再增大的平缓区间。
(3) 考虑随机性路面不平整度影响下,建立数值模型模拟的研究方法还可用于提高车辆行驶舒适性和稳定性、降低对运输货物损伤为目标的车辆设计参数优化设计等。
| [1] |
葛剑敏, 郑联珠. 路面特性对车辆振动影响规律研究[J]. 中国公路学报, 2004, 17(3): 117-121. GE Jian-min, ZHENG Lian-zhu. Effects of Terrain Characteristic on Vehicle Vibration[J]. China Journal of Highway and Transport, 2004, 17(3): 117-121. |
| [2] |
杜峰, 葛晓成, 陈翔, 等. 路面功率谱密度换算及不平度建模理论研究[J]. 振动、测试与诊断, 2015, 35(5): 981-986, 998. DU Feng, GE Xiao-cheng, CHEN Xiang, et al. Conversion of Spatial Power Spectral Density and Study on Road Irregularity Modeling Theory[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 981-986, 998. |
| [3] |
许海亮, 何兆才, 何炼. 车路耦合条件下沥青混凝土路面变形特性时域分析[J]. 公路交通科技, 2017, 34(12): 16-22. XU Hai-liang, HE Zhao-cai, HE Lian. Analysis on Asphalt Concrete Pavement Deformation Characteristics Time-domain Considering Vehicle-pavement Coupling Effect[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 16-22. |
| [4] |
王新明, 王秉纲. 高速公路路面功率谱[J]. 交通运输工程学报, 2003, 3(2): 53-56. WANG Xin-ming, WANG Bing-gang. Expressway Pavement Power Spectral Density[J]. Journal of Traffic and Transportation Engineering, 2003, 3(2): 53-56. |
| [5] |
刘云, 钱振东. 路面平整度及车辆振动模型的研究综述[J]. 公路交通科技, 2008, 25(1): 51-57. LIU Yun, QIAN Zhen-dong. Review of Road Roughness and Vehicle Vibration Model[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 51-57. |
| [6] |
刘献栋, 邓志党, 高峰. 基于逆变换的路面不平度仿真研究[J]. 中国公路学报, 2005, 18(1): 122-126. LIU Xian-dong, DENG Zhi-dang, GAO Feng. Study of Simulation of Road Roughness Based on Inverse Transform[J]. China Journal of Highway and Transport, 2005, 18(1): 122-126. |
| [7] |
刘献栋, 邓志党, 高峰. 公路路面不平度的数值模拟方法研究[J]. 北京航空航天大学学报, 2003, 29(9): 843-846. LIU Xian-dong, DENG Zhi-dang, GAO Feng. Research on the Method of Simulating Road Roughness Numerically[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(9): 843-846. |
| [8] |
许海亮, 袁勇, 屈铁军, 等. 考虑路面不平整度因素的车路耦合振动模型的建立[J]. 振动与冲击, 2014, 33(19): 152-156. XU Hai-liang, YUAN Yong, QU Tie-jun, et al. Dynamic Model for a Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Vibration and Shock, 2014, 33(19): 152-156. |
| [9] |
许海亮, 何炼, 何兆才, 等. 考虑路面不平整度因素的车路耦合系统非线性数值模型[J]. 公路交通科技, 2017, 34(8): 23-28. XU Hai-liang, HE Lian, HE Zhao-cai, et al. A Nonlinear Numerical Model of Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 23-28. |
| [10] |
赵旗, 王培德, 罗兰, 等. 路面激励Simulink模型的建立及其应用[J]. 科学技术与工程, 2018, 18(1): 128-132. ZHAO Qi, WANG Pei-de, LUO Lan, et al. Establishment of Simulink Model for Road Excitation and Its Application[J]. Science Technology and Engineering, 2018, 18(1): 128-132. |
| [11] |
邓涛, 潭海鑫, 李志飞, 等. 随机路面激励下车辆垂向振动微分几何解耦控制[J]. 噪声与振动控制, 2017, 37(6): 1-6, 11. DENG Tao, TAN Hai-xin, LI Zhi-fei, et al. Differential Geometry Decoupling Control of Vehicle's Vertical Vibration under Random Road Excitations[J]. Noise and Vibration Control, 2017, 37(6): 1-6, 11. |
| [12] |
荣吉利, 郑育龙, 刘琥, 等. 某大型运输车的时域平顺性仿真分析[J]. 北京理工大学学报, 2017, 37(2): 146-150, 156. RONG Ji-li, ZHENG Yu-long, LIU Hu, et al. Time Domain Method in Large Freight Vehicle Ride Comfort Analysis[J]. Transactions of Beijing Institute of Technology, 2017, 37(2): 146-150, 156. |
| [13] |
GB/T 7031-2005, 机械振动道路路面谱测量数据报告[S]. GB/T7031-2005, Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data[S]. |
| [14] |
曾庆元. 弹性系统动力学总势能不变值原理[J]. 华中理工大学学报, 2000, 28(1): 1-3, 14. ZENG Qing-yuan. The Principle of Total Potential Energy with Stationary Value in Elastic System Dynamics[J]. Journal of Huazhong University of Science and Technology, 2000, 28(1): 1-3, 14. |
| [15] |
余志生. 汽车理论[M]. 北京: 机械工业出版社, 2002: 173-176. YU Zhi-sheng. Automobile Theory[M]. Beijing: China Machine Press, 2002: 173-176. |
| [16] |
夏禾. 车辆与结构动力相互作用[M]. 北京: 科学出版社, 2002: 59-62. XIA He. Dynamical Interaction between Vehicle and Structure[M]. Beijing: Science Press, 2002: 59-62. |
| [17] |
沈火明, 肖新标. 求解车桥耦合振动问题的一种数值方法[J]. 西南交通大学学报, 2003, 38(6): 658-662. SHEN Huo-ming, XIAO Xin-biao. Numerical Method for Vehicle-Bridge Coupled Vibrations[J]. Journal of Southwest Jiaotong University, 2003, 38(6): 658-662. |
| [18] |
周长城, 周金宝. 汽车振动分析与测试[M]. 北京: 北京大学出版社, 2011: 195-199. ZHOU Chang-cheng, ZHOU Jin-bao. Analysis and Testing on Vehicle Vibration[M]. Beijing: Peking University Press, 2011: 195-199. |
 2019, Vol. 36
2019, Vol. 36
