扩展功能
文章信息
- 吴微, 张宏立
- WU Wei, ZHANG Hong-li
- 基于投影寻踪与模糊聚类的车辆工况构建
- Construction of Driving Cycle Based on Projection Pursuit and Fuzzy Clustering
- 公路交通科技, 2019, 36(11): 119-128
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 119-128
- 10.3969/j.issn.1002-0268.2019.11.016
-
文章历史
- 收稿日期: 2018-03-20
车辆行驶工况是一种表征了车辆行驶速度与时间关系的曲线,其研究对于车辆油耗以及污染物排放研究等具有重要的参考价值[1]。目前,全球化的工况标准主要有美国(FTP75)、日本(JAPAN10-1)、欧洲(NEDC)三大体系,其中美国的FTP75工况是一种瞬态工况,而欧洲NEDC主要是模态工况,这二者目前使用最广泛[2]。目前我国自主工况还在研究阶段,主要还是以欧洲工况作为参考,但我国城市交通状况与欧州存在明显差异,各城市间也不尽相同,因此采用某一统一工况并不能反映城市实际行驶工况[3]。随着国内经济发展,目前家庭轻型车的保有量正在呈快速增长的趋势,这对城市的交通、环境等提出了不小的挑战,因此研究城市轻型车行驶工况具有实际意义。
最早的工况研究起源于欧美等发达国家,随着汽车工业的发展,目前见于文献的工况构建方法种类繁多。构建汽车行驶工况的传统方法有聚类分析[4-5]、主成分分析[6]等。随着研究的深入,也有不少学者提出以马尔科夫分析方法[7]、模糊神经网络[8]等改进方法进行工况分析。2013年,Fotouhi等[9]采集了德黑兰车辆行驶数据,并采用K均值聚类法建立了城市行驶工况,并与其他标准工况相比研究其异同;2009年,S H Kamble等[10]以短行程片段出发利用主成分分析构建了异构的浦那城市行驶工况,并与现有标准工况作对比;2010年,石琴等[7]将采用状态转移算法与相似性检验实现工况的选择,并将工况与马尔科夫过程相联系;2011年,田毅等[8]提出模糊神经网络算法判别工况的思想,并实现了混合动力车节能减排的目标。
但以上方法仍有一定的不足,如常用K均值聚类,虽然算法简单快速,但容易出现局部最优的情况,受初始值影响大,其精度往往不令人满意。而基于马尔科夫方法的工况构建方法其计算量大,且目前来看其工况构建结果与实际情况符合性较差。运用神经网构建行驶工况受训练数据影响,其精度与数据量存在一定关系,而大量数据计算大大增加计算时间,且其参数设置受经验调试的影响。考虑到交通混合的异质性,必须找到一种更为合理的城市工况构建方法,构建更贴近各城市实际的轻型车行驶工况。
针对以上提出的传统工况构建方法的缺点,本研究提出一种基于投影寻踪与模糊聚类优化算法的城市工况构建方法,依托于中国新能源汽车产品检测工况研究和开发项目,测量采集乌鲁木齐12个月中10辆轻型车实测行驶数据。对数据样本按运动学片段理论划分为若干片段,获得各行驶片段中重要的特征参数;再利用投影寻踪的方法对特征值进行约简,对约简的各片段样本进行模糊聚类;最后根据聚类结果构建出乌鲁木齐实际行驶工况。将本研究提出的投影寻踪与模糊聚类工况构建方法与主元分析K聚类方法所得结果,与实测数据结果相比较发现,该新方法拟合的工况精度更高,更能综合反映城市交通真实状况。
1 算法基础 1.1 投影寻踪模型投影寻踪模型是20世纪70年代出现的一种降维统计方法[11],通过投影的方式将高维数据降维到低维投影空间并保留其高维结构特征,随后通过对投影的分析达到反应高维数据结构特征的目的。
设X为高维n×p数据矩阵,其中n和p分别表示样本个数和维数。投影方向用k×p矩阵A表示,其中矩阵秩k<p,矩阵Z表示p维数据在k维空间上的线性投影,其可表示为:
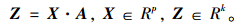
|
(1) |
对于投影寻踪,其降维过程最重要的是寻找最优投影指标。投影指标是衡量投影好坏的量化指标。设X是p维随机变量,服从于分布F,A为服从于FA分布的k×p满秩矩阵。投影指标在投影方向A上的定义是在k维函数集合上的实值函数Q,表示为Q(FA)。准确地说,投影寻踪方法就是要寻找一个使其投影指标达到极值的A或a。
选择最优投影指标的一个标准是高维数据降维后其损失最小,使降维后数据最大程度地反映原高维数据的结构与特征。因此,投影指标的选择直接关系到投影寻踪结果的好坏。目前主要的投影指标主要有Friedman-Tukey投影指标、Friedman投影指标、Hall投影指标。本研究主要使用Friedman-Tukey投影指标[12],其利用样本整体离散度局部密度的乘积构建而成,其表示为:
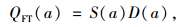
|
(2) |
式中,QFT(a)为投影指标函数;S(a)为样本整体离散度;D(a)为样本的局部密度。根据实际问题的不同,对于投影指标的要求也会产生区别,可根据需要对投影指标进行不同的设计构造。投影寻踪算法的具体步骤如下:
(1) 样本评价指标集的归一化处理。将指标集无量纲化并统一其变化范围,如式(3)所示:
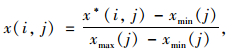
|
(3) |
式中,xmax(j)和xmin(j)分别为第j个指标值的最大值和最小值;x*(i,j)为第i个样本第j个指标值; n,p分别为样本的个数和指标的数目。
(2) 投影指标的计算。假设某一高维数据其最优投影方向为a=(a1,a2,…,ap),投影寻踪就是将x(i,j)投影于a得到其投影值z(i)。
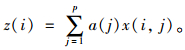
|
(4) |
(3) 构造投影指标函数并优化。根据上文的叙述,选择Friedman-Tukey投影指标并采用惩罚函数法将其转化为一个无约束优化问题。
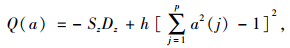
|
(5) |

|
(6) |

|
(7) |
式中,E(z)为投影值平均值;R为局部密度的窗口半径,取全部样本投影特征值方差的10%;r(i,j)为样本间距离;u(t)为单位阶跃函数。
在处理多变量寻优的问题时,全局搜索能力弱、提前收敛等缺点是传统寻优算法不可避免的缺陷。针对本研究数据存在多参量的特点,为求解多参数优化问题,本文采用协同粒子群算法。
1.2 协同粒子群算法粒子群算法(PSO)是于20世纪提出的一种寻优算法,主要通过模仿飞禽觅食过程实现寻优[13]。该算法假设每个物体都是空间中一个粒子(无质量与体积),想要找到觅食的最优位置就需要动态调整每个粒子的速度与方向,而速度与方向的调整通过对粒子之间的经验综合分析得到[14]。
种群规模为n的粒子群在D维空间寻优,各粒子位置变化基于个体和种群历史最优位置点进行。设第i个粒子的速度和位置分别表示为:
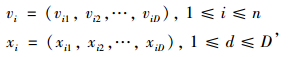
|
(8) |
式中,vi和xi分别代表种群中各粒子的速度和位置,利用惯性权重ω对算法性能进行调整,调整后速度和位置更新公式为:
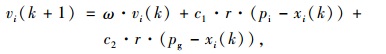
|
(9) |
式中,pi和pg分别为个体历史最优位置与全局最优位置;c1和c2为权重,r是0~1之间随机常数;ω为惯性权重,作为权重影响调整程度。设适应度函数极小值时为最优解,迭代规则可表示为:
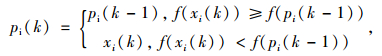
|
(10) |
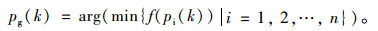
|
(11) |
考虑到本研究运动学片段特征值数目多,使用粒子群算法寻优多参数结果往往不够精确。因此,本研究提出协同优化算法(CEA),解决粒子群算法忽略参数内在联系的问题。CEA是一种新型算法框架[15]。它把复杂问题分解为简单子问题,利用分而治之的方法实现各子问题的求解。各优化过程独立、互不干扰地运行,只有在计算适应度值时才将各结果放到一起进行综合评价。算法流程图如图 1所示。

|
| 图 1 合作协同粒子算法流程图 Fig. 1 Flowchart of cooperative particle algorithm |
| |
2 工况构建方法 2.1 数据预处理
本研究的样本来源于乌鲁木齐市2辆正常运营的出租车与8辆私家车12个月正常道路行驶采集的数据,表 1列举了所选车辆代表性性能。考虑到城市交通情况,轻型车行驶状况差距不大,选用的这10台车基本可以覆盖轻型车实际行驶状况。通过标准OBD接口将各种行驶数据采集到车载终端,最终获得了7 081 534条有效数据,剔除信号偏差和不合理数据点分割整合后提取了10 880个有效短行程片段,组成驾驶循环数据库,并具有大样本的特点[16],保证了本研究结果具有一般性。利用GPS数据绘制了所选车辆行驶路线的覆盖图,其结果如图 2所示。从图中可以看出,所选车辆基本覆盖了整个乌鲁木齐的主要城区道路网络,保证所构建工况具有普遍适用性。
| 车辆编号 | 排量/t | 最大功率/kW | 最大扭矩/(N·m-1) | 百公里加速时间/s |
| 私家车1 | 1.6 | 86 | 153 | 11.4 |
| 私家车2 | 2.0 | 155 | 280 | 6.9 |
| 私家车3 | 1.4 | 96 | 225 | 9.1 |
| 私家车4 | 1.5 | 92 | 170 | 8.4 |
| 私家车5 | 1.6 | 94 | 156 | 9.6 |
| 私家车6 | 1.6 | 81 | 155 | 12.5 |
| 私家车7 | 1.6 | 81 | 155 | 12.3 |
| 私家车8 | 1.8 | 132 | 300 | 8.3 |
| 出租车1 | 1.6 | 94 | 156 | 10.4 |
| 出租车2 | 1.6 | 94 | 156 | 10.4 |

|
| 图 2 轻型车行驶路线覆盖图 Fig. 2 Coverage map of light vehicle routes |
| |
根据车辆实际行驶频繁起停的特点,采用运动学片段划分的方法,将车辆行驶数据划分成各个短行程,方便数据处理。车辆从一个怠速到下一个怠速的行驶过程称为一个短行程,短行程由怠速段和运行段组成,如图 3所示。车辆行驶的总行程可视为各短行程的组合[16]。在每个短行程中定义4种状态:

|
| 图 3 运动学片段定义 Fig. 3 Definition of kinematic fragment |
| |
(1) 怠速状态:车辆行驶中加速度|a|≤0.15 m/s2并且速度v=0的状态;
(2) 加速状态:车辆行驶中加速度a≥0.15 m/s2并且速度v≠0的状态;
(3) 减速状态:车辆行驶中加速度a≤-0.15 m/s2并且速度v≠0的状态;
(4) 匀速状态:车辆行驶中加速度|a|≤0.15 m/s2并且速度v≠0的状态。
根据传统特征参数定义,拟采用运行时间、运行速度、最大速度、最大加速度、加速度的标准偏差等15个特征值作为片段特征参数,如表 2所示。同时,定义了12个用于统计分布的片段特征值,如表 3所示。
| 序号 | 特征值 | 意义 | 单位 |
| 1 | T | 运行时间 | s |
| 2 | Ta | 加速时间 | s |
| 3 | Td | 减速时间 | s |
| 4 | Tc | 匀速时间 | s |
| 5 | Ti | 怠速时间 | s |
| 6 | S | 运行距离 | m |
| 7 | Vmax | 最大速度 | km/h |
| 8 | Vm | 平均速度 | km/h |
| 9 | Vmr | 运行速度 | km/h |
| 10 | Vsd | 速度标准偏差 | km/h |
| 11 | amax | 最大加速度 | m/s2 |
| 12 | aa | 加速段的平均加速度 | m/s2 |
| 13 | amin | 最大减速度 | m/s2 |
| 14 | ad | 减速段的平均减速度 | m/s2 |
| 15 | asd | 加速度标准偏差 | m/s2 |
| 序号 | 特征值 | 意义 | 单位 |
| 1 | P0~10 | 0~10 km/h的速度比例 | % |
| 2 | P10~20 | 10~20 km/h的速度比例 | % |
| 3 | P20~30 | 20~30 km/h的速度比例 | % |
| 4 | P30~40 | 30~40 km/h的速度比例 | % |
| 5 | P40~50 | 40~50 km/h的速度比例 | % |
| 6 | P50~60 | 50~60 km/h的速度比例 | % |
| 7 | P60~70 | 60~70 km/h的速度比例 | % |
| 8 | P> 70 | > 70 km/h的速度比例 | % |
| 9 | Pa | 加速时间比例 | % |
| 10 | Pd | 减速时间比例 | % |
| 11 | Pc | 匀速时间比例 | % |
| 12 | Pi | 怠速时间比例 | % |
2.2 算法的构建
工况各特征参数之间存在一定的相关性,为了方便地进行研究,可以运用投影寻踪方法进行特征值约简,利用新的投影值代替原来样本特征值的特性,从而可以对新的投影值方便、准确、快速地进行聚类。具体过程如下:
(1) 运动学片段样本特征参数的归一化处理。为消除工况样本的量纲和统一各片段特征值的变化范围,采用公式(3)进行正向归一化处理:设工况样本分割后的矩阵为X=[x1,x2,x3,…,xp]n×p,其中n=1,2,…,10 880为样本分割片段数,p=1,2,…,15为片段特征参数。
(2) 构造投影指标函数并优化。根据上节的叙述,选择Friedman投影指标并采用惩罚函数法将其转化为一个无约束优化问题,具体公式见公式(5)至(7)。R的取值采用全部样本投影特征值方差的10%。
(3) 通过优化粒子群算法计算投影指标函数。通过协同粒子群计算投影指标函数,当其函数值趋近于0,表示找到样本特征参数的最优投影向量a。
(4) 片段样本特征参数投影值的计算。将原工况样本投影于a得到其投影值,按公式(4)可以得到原工况样本的投影值z(i),将原工况样本的多特征参数约简成为一维参数。
(5) 进行模糊聚类。通过计算工况样本投影值z(i)的隶属度矩阵,确定每个样本所属的交通状况。传统方法常使用K均值聚类具有不准确性,因此将软聚类方法引入工况构建方法中,以提高聚类的准确性。经过约简的样本特征值使模糊聚类更为快捷、准确。
3 结果分析 3.1 两种工况构建方法构建结果与对比本研究提出采用协同粒子群优化的投影寻踪约简运动学片段特征值,然后对降维样本进行模糊聚类,最后挑选各类中合适片段构建工况;而常用的工况构建方法主要使用主成分分析与K均值聚类的方法对运动学片段特征值进行降维,并对降维后的主成分进行聚类,根据聚类结果构建行驶工况[17-18]。下面介绍以上两种方法构建工况的结果并进行对比。
对本研究提出的优化粒子群的投影寻踪算法进行计算,大约33次迭代后达到收敛。经过计算可以得到各片段特征参数的最优投影向量分别为a*=(0.293 9,0.707 3,0.432 8,0.530 6,0.305 6,0.202 9,0.819 2,0.779 3,0.997 9,0.938 1,0.794 3,0.498 1,-0.418 9,-0.107 1,1)。根据公式(4)将最优投影向量与原样本矩阵相乘后可得各运动学片段的投影值。
随后,对片段投影值进行模糊聚类分析,为了获得更为准确的聚类结果,尝试将投影值分为2类、3类和4类。为了获得最好的聚类结果,本研究采用silhouette方程对聚类结果进行评价,silhouette方程所得到的轮廓值描述了相邻类别之间的点的距离情况,其方程如下式所示:
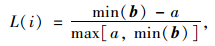
|
(12) |
式中,a为相同类里不同运动学片段之间的平均距离;b为不同类里不同运动学片段之间的平均距离,为矢量;L(i)值域区间为[-1,1],表明不同运动学片段的类别属性。当L(i)的值越接近于1,表示该运动学片段与其他类的距离越远,聚类效果越明显,一般轮廓值大于0.6表明聚类结果有效;当L(i)的值为0,表明无法分辨该运动学片段属于哪个特定类别;当L(i)的值小于0,表明该运动学片段很可能被分入错误的类别。不同片段在不同聚类数目下的轮廓值如图 4所示。
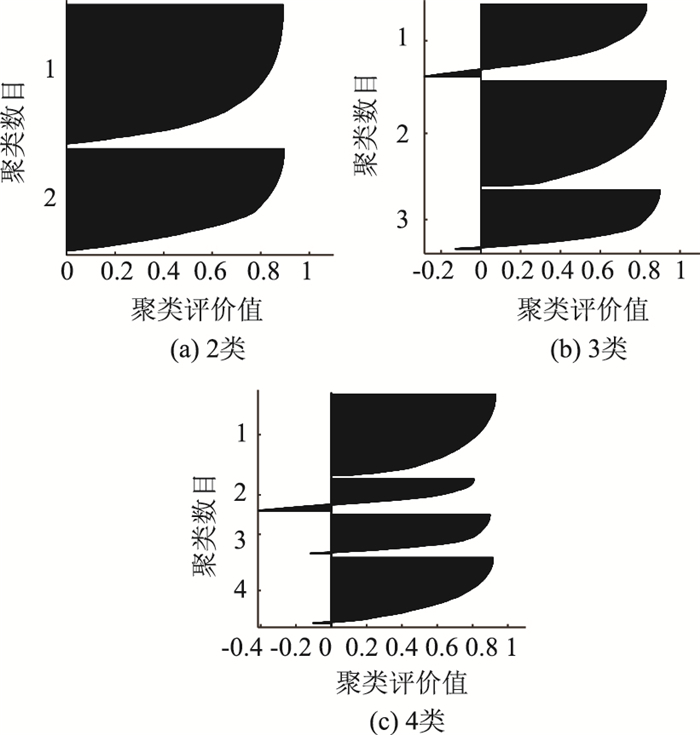
|
| 图 4 不同聚类数目的评价值 Fig. 4 Evaluation values of different clustering numbers |
| |
从图中我们可以看出,当聚类数目为2时,所有的片段轮廓值都大于0,且绝大部分片段轮廓值都在0.6以上;当聚类数目为3时,少部分片段的轮廓值出现了负数;当聚类数目为4时,轮廓值出现负数的片段数目开始增多;当聚类数目多于2时,部分运动学片段被错误地分类。因此,基于以上的论述选择聚类数目2为最佳分类数目。
对于常用的工况构建方法,使用上文分割的运动学片段进行主成分分析,主成分分布如表 4所示。由表可知,前5个主成分累积贡献率已经超过90%,已经可以代表原高维数据间的信息,因此选用前5个主成分进行分析。表 5展示了前5个主成分所对对应的特征参数。
| 主成分序号 | 主成分方差 | 贡献率/% | 累计贡献率/% |
| 1 | 6.831 0 | 45.54 | 45.54 |
| 2 | 3.524 7 | 23.50 | 69.04 |
| 3 | 1.387 1 | 9.25 | 78.29 |
| 4 | 1.042 1 | 6.95 | 85.23 |
| 5 | 0.736 8 | 4.91 | 90.14 |
| 6 | 0.430 8 | 2.87 | 93.02 |
| 7 | 0.319 3 | 2.13 | 95.14 |
| 8 | 0.265 0 | 1.77 | 96.91 |
| 9 | 0.188 6 | 1.26 | 98.17 |
| 10 | 0.117 4 | 0.78 | 98.95 |
| 11 | 0.077 5 | 0.52 | 99.47 |
| 12 | 0.045 6 | 0.30 | 99.77 |
| 13 | 0.021 2 | 0.14 | 99.91 |
| 14 | 0.013 0 | 0.09 | 100.00 |
| 15 | 0.000 0 | 0.00 | 100.00 |
| 主成分 | 特征值 |
| 第1主成分 | 运行时间、加速时间、减速时间、怠速时间、运行距离、最大速度、平均速度、运行速度、速度标准差、最小加速度 |
| 第2主成分 | 加速段平均加速度、减速段平均减速度、加速度标准差 |
| 第3主成分 | 匀速时间 |
| 第4主成分 | 一般相关 |
| 第5主成分 | 最大加速度 |
利用K均值聚类方法对各主成分得分的片段样本进行聚类分析。根据上文的讨论,采用silhouette方程评价不同聚类数目下的聚类结果,如图 5所示。比较可得,K均值聚类方法选择聚类数目为3时,聚类错误片段明显少于聚类数目为2或4时的错误片段,且聚类数目为4时明显存在一类数目过少,综上选择聚类数目为3。通过图 4和图 5对比可看出图 5中的错误片段数量要明显多,可以推断,使用本研究提出的PPFCM方法从聚类效果上要优于常用的PCAKM方法。
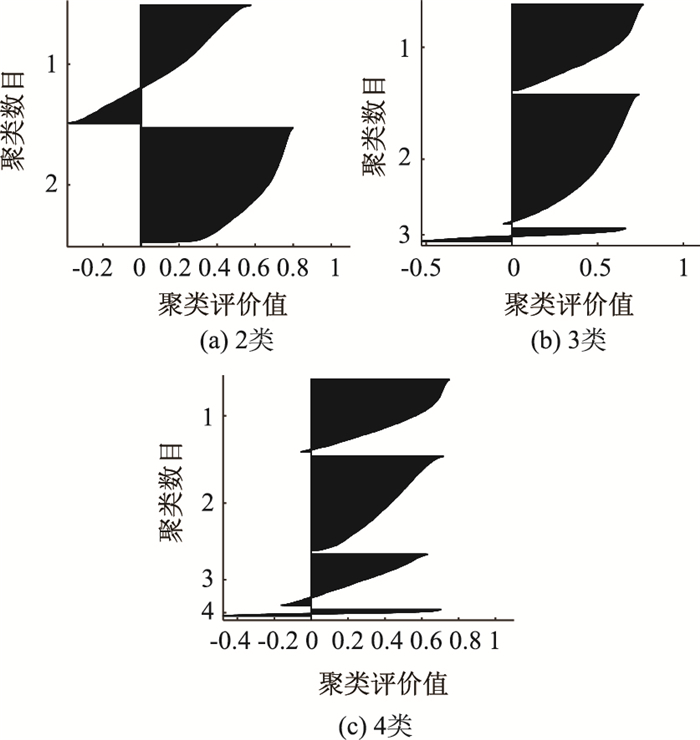
|
| 图 5 不同聚类数目的评价值 Fig. 5 Evaluation values of different clustering numbers |
| |
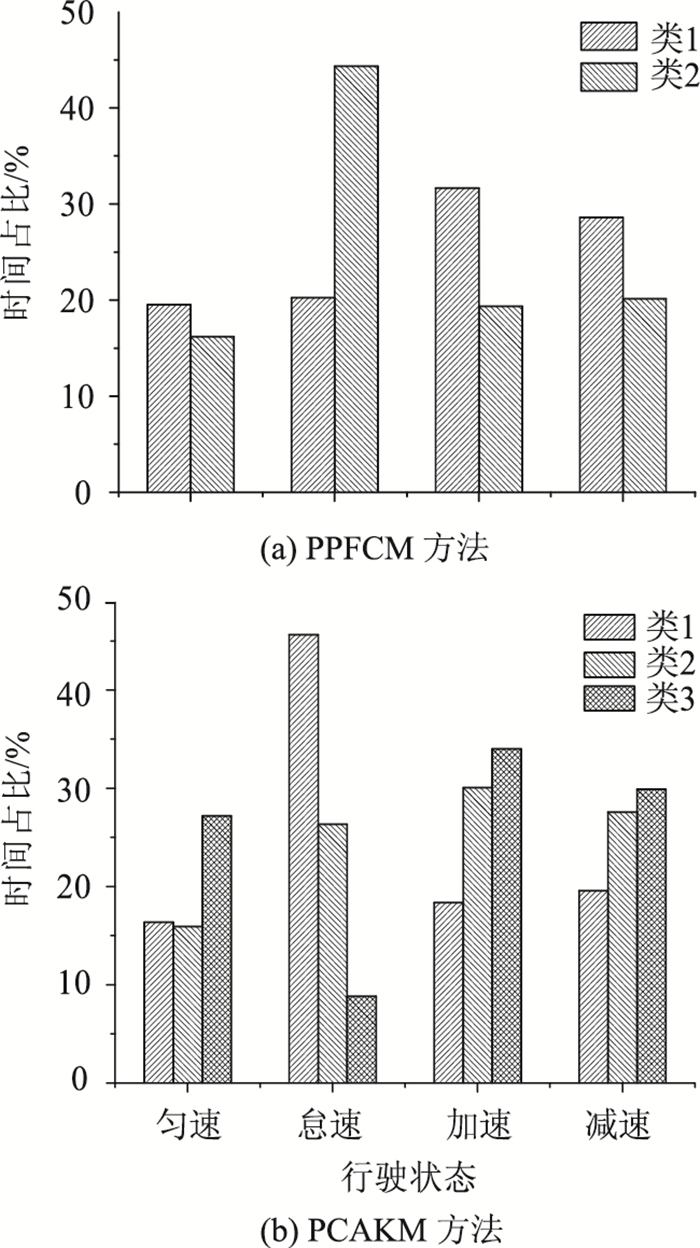
两种工况构建方法聚类结果中各类样本数量情况如表 6所示,比较可知PPFCM方法分类后每类中片段数更为均衡,错误分类数更少。根据两种方法聚类结果统计怠速、匀速、加速和减速4种状态的时间比例,如图 6所示。从图 6(a)中可以看出,本研究提出PPFCM中第1类的怠速比例明显较低,且运行状态比例较高,其平均速度为31.84 km/h,表明第1类为顺畅的交通状况;第2类的怠速比例达到44.33%,而匀速状态比例仅为16.18%,其平均速度为7.16 km/h,表明第2类为拥堵交通状况。由图 6(b)可知,常用PCAKM方法中第1类的怠速比最高,达到45.65%,其他状态时间分布均匀,其平均速度为9.58 km/h;第2类的4种时间状态比例较为均匀,其平均速度为25.81 km/h;第3类的怠速比例最低,且匀速比例最高,其平均速度为65.49 km/h。结合国内外经验,可以定义第1类为低速状态,第2类为中速状态,第3类为高速状态。
| 分类数目 | PPFCM | PCAKM | |||||
| 2类 | 3类 | 4类 | 2类 | 3类 | 4类 | ||
| 类1片段数量 | 6 301 | 3 325 | 4 057 | 5 524 | 4 080 | 3 526 | |
| 类2片段数量 | 4 579 | 4 835 | 1 587 | 5 356 | 6 192 | 4 573 | |
| 类3片段数量 | 2 720 | 1 939 | — | 608 | 2 418 | ||
| 类4片段数量 | — | — | 3 297 | — | — | 300 | |
|
| 图 6 不同类别下4种驾驶状态时间占比的对比 Fig. 6 Comparison of time percentages in 4 driving states under different clusters |
| |
通过两种方法聚类结果的对比可以明显看出,两种方法聚类结果有较大区别。本研究方法聚类结果将样本分为了顺畅与拥堵两种交通状况,而常用的方法将样本分为低速、中速、高速3种状态,从聚类结果评价来看本研究提出的方法要优于常用工况构建方法。
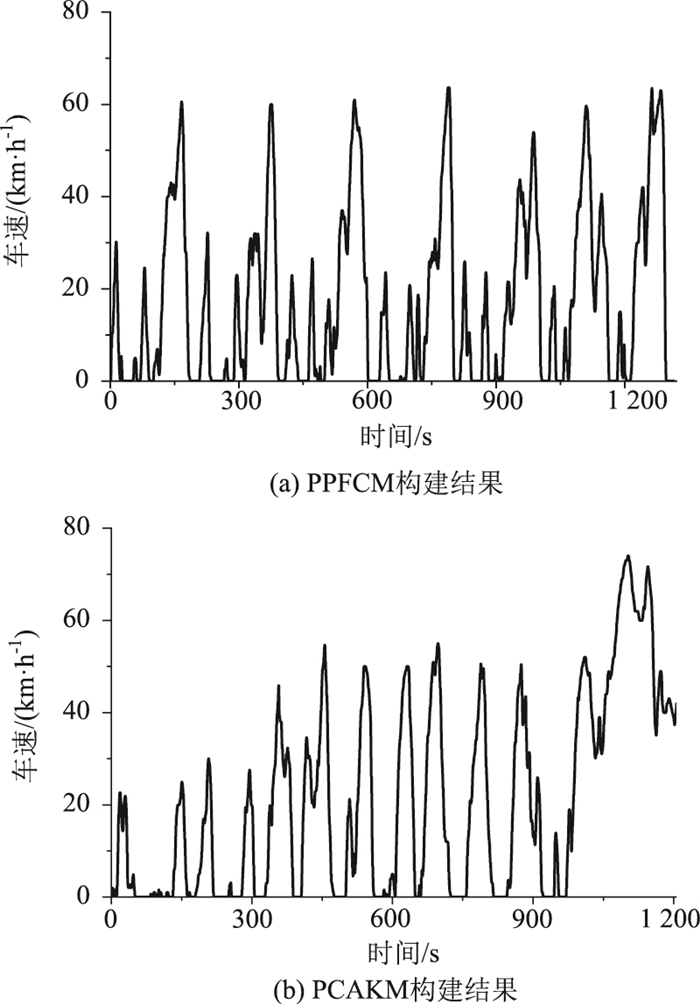
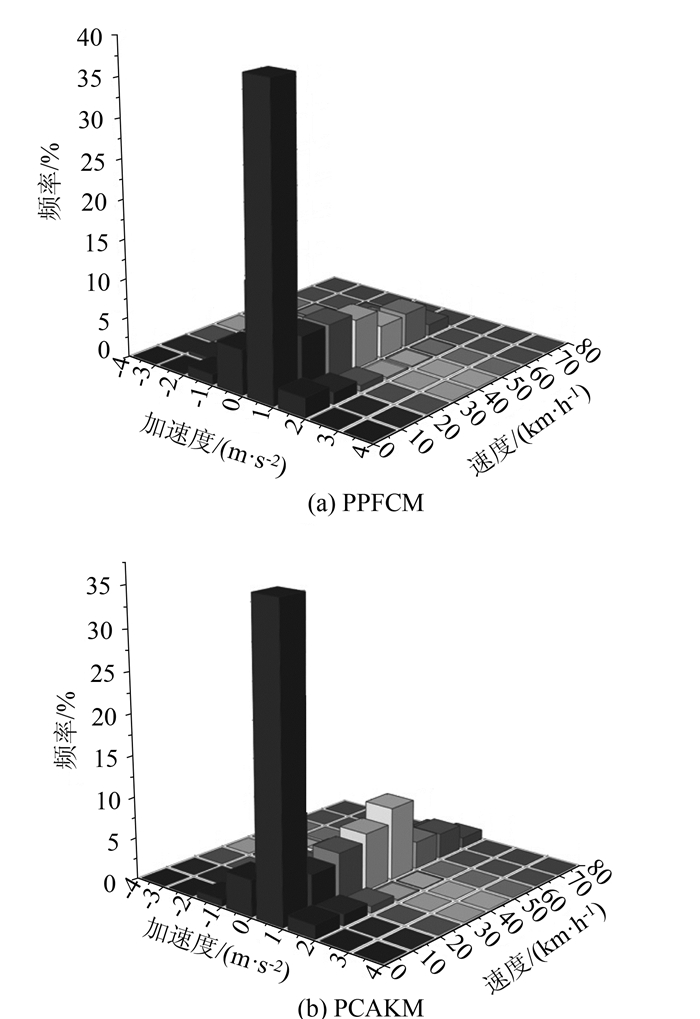
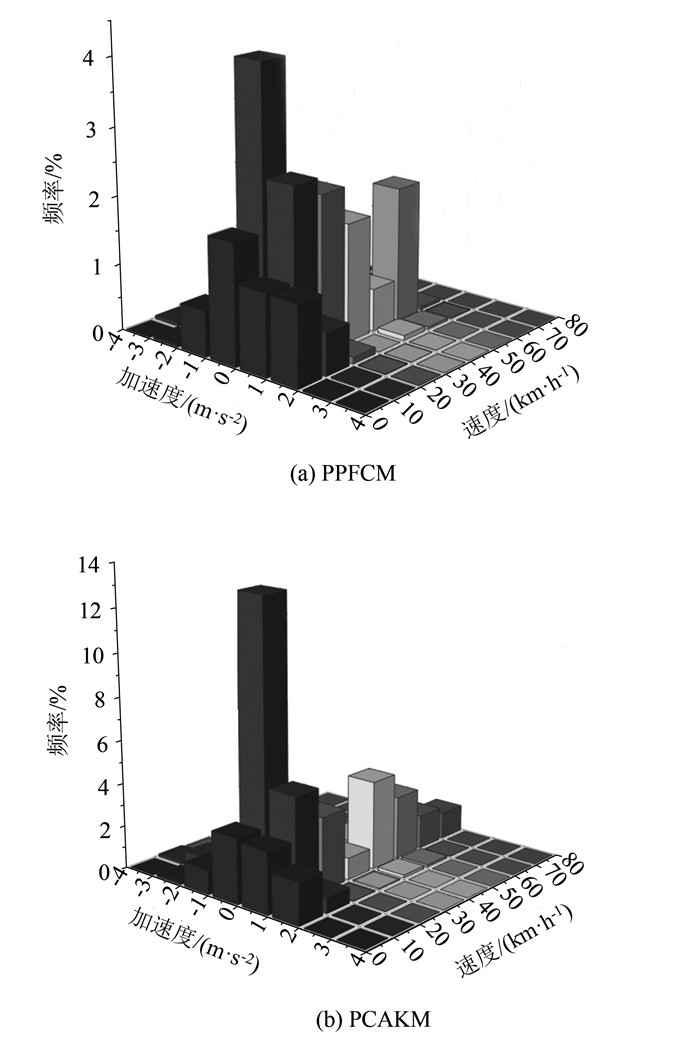
最后,根据两种方法聚类结果构建工况。计算每类各数据片段与该类平均特征值的相关系数,相关系数越接近1,表明该片段代表此类数据的能力越强,因此选取各类中相关系数较大的片段分别代表两类工况,根据国内外工况构建经验,选取各类片段组成一个1 200 s左右的工况。构建中的各类片段选取是通过该类片段在总样本中占比确定的,其计算公式如式(13)所示,其中ti为第i类在拟合工况中的持续时间;td为最终代表性工况的持续时间;tall为所有工况块数据的总持续时间;ti,j为第i类中工况块j的时间。本研究选取7个顺畅片段和11个拥堵片段构成的乌鲁木齐市轻型车典型工况如图 7(a)所示,并通过统计方法获得了工况中速度-加速度频率分布情况,如图 8(a)所示。对于原始方法聚类结果,分别选取了5个低速片段、8个中速片段和1个高速片段构成乌鲁木齐市典型工况如图 7(b)所示,同样采用通过统计方法获得了工况中速度-加速度频率分布情况,如图 8(b)所示。
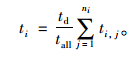
|
(13) |
|
| 图 7 乌鲁木齐市轻型车道路行驶工况 Fig. 7 Road driving cycle of light vehicles in Urumqi |
| |
|
| 图 8 工况速度-加速度频率分布 Fig. 8 Velocity-acceleration frequency distribution of driving cycle |
| |
3.2 工况构建结果评估与对比
对目标行驶工况的评估有多种方法,一些学者采用最小绩效值(PV)来评估最终的工况。本研究采用加速时间占比、怠速时间占比、匀速时间占比、平均速度、平均加速度和加速度标准差这6个特征参数以及速度-加速度频率分布差值(SAFD)对构建的工况进行评估。整体样本与两种方法构建工况之间SAFD的差别如图 9所示,从图 9(a)中可知整体样本与PPFCM方法构建工况的SAFD不大,基本都在4%以内;而图 9(b)可看出PCAKM方法构建工况的SAFD在某些点较大,超过了10%,且整体误差要大于本文提出方法的SAFD。整体样本与两种方法构建工况的评估参数如表 7所示。由表可知,基于本研究提出的PPFCM方法所构建的工况与原始样本的行驶状况较为符合,其误差基本在8%以内;而基于原始PCAKM方法构建的工况与原始样本的行驶状况之间的误差明显更大,且平均速度与加速度标准差两项误差分别达到了21.87%和12.69%。主要是因为PCA降维较投影寻踪会损失更多的原样本信息。同时,由于原始方法分类时高速状态有部分样本被错误地分类,因此导致其构建工况平均速度偏高。
|
| 图 9 整体样本与构建工况SAFD Fig. 9 SAFDs of overall sample and constructed driving cycles |
| |
| 特征参数 | 整体样本 | PPFCM | 误差 | PCAKM | 误差 |
| Pa/% | 27.99 | 28.67 | 2.43 | 30.24 | 8.04 |
| Pc/% | 16.32 | 16.65 | 2.02 | 16.90 | 3.55 |
| Pi/% | 28.60 | 28.21 | 1.36 | 27.75 | 2.97 |
| Vm/(km·h-1) | 15.93 | 17.32 | 8.73 | 19.40 | 21.78 |
| aa/(m·s-2) | 0.624 7 | 0.647 1 | 3.59 | 0.589 0 | 5.71 |
| asd/(m·s2) | 0.642 4 | 0.673 4 | 4.83 | 0.560 9 | 12.69 |
乌鲁木齐轻型车道路行驶工况(UQDC)与其他主要标准工况的对比如表 8所示,从中不难发现乌鲁木齐轻型车工况与现有标准工况的差异较为明显。首先UQDC的平均速度方面要明显低于其他工况,其次UQDC的匀速时间比例较低,其他运行状态的时间比例相近,这一点与其他工况也不相符。结合乌鲁木齐的路况可以推断乌鲁木齐交通状况为较拥堵并且停车较多,导致频繁的怠速和加减速,匀速运行时间较少。与其他城市相比,最慢的平均车速和最低的匀速时间比例可能会使乌鲁木齐的燃油消耗、排放和交通拥挤问题更加严重。
| 行驶工况 | T/s | Pa/% | Pi/% | Pc/% | Vm/ (km·h-1) |
aa/ (m·s-2) |
| UQDC | 1 315 | 28.7 | 28.2 | 16.7 | 17.32 | 0.63 |
| WHTC | 1 800 | 28.7 | 17.1 | 21.5 | 20.22 | 0.74 |
| UDDS | 1 369 | 29.4 | 17.8 | 27.3 | 31.5 | 0.50 |
| NEDC | 1 184 | 22.9 | 23.9 | 37.4 | 33.21 | 0.54 |
| FTP-75 | 1 875 | 39.3 | 18.1 | 7.7 | 34.10 | 0.17 |
| J10-15 | 660 | 26.1 | 32.6 | 19.5 | 22.68 | 0.54 |
4 结论
本研究提出了一种基于投影寻踪与模糊聚类优化算法的城市工况构建新方法。利用投影寻踪理论将高维的工况样本数据投影到低维空间,其中投影目标函数采用改进的协同粒子群算法进行优化,再基于运动学片段理论,对投影寻踪简约特征值后的进行模糊聚类,进而构建出工况情况,最后以乌鲁木齐12个月实测轻型车行驶数据为样本,构建出乌鲁木齐市轻型车行驶工况,并与原始的PCA与Kmeans聚类方法构建的工况进行对比。试验结果表明,投影寻踪方法可以很好地解决样本数据的高维性分析问题;改进的协同粒子群算法可以大大提高多参数耦合优化效果,得到更为精确的降维效果;基于投影寻踪和模糊聚类的构建算法与传统PCA与Kmeans聚类方法相比,与原始样本情况更为贴近,表明本文提出的新方法具有优越性;同时,对本方法构建的工况与原始样本数据进行综合评估,评估结果显示本方法构建的乌鲁木齐轻型车工况与原始样本误差在合理范围内,表明该方法构建的工况具有准确性。
| [1] |
石琴, 仇多洋, 周洁瑜. 基于组合聚类法的行驶工况构建与精度分析[J]. 汽车工程, 2012, 34(2): 164-169. SHI Qin, QIU Duo-yang, ZHOU Jie-yu. Driving Cycle Construction and Accuracy Analysis Based on Combined Clustering Technique[J]. Automotive Engineering, 2012, 34(2): 164-169. |
| [2] |
HE H, GUO J, ZHOU N, et al. Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles[J]. Energies, 2017, 10(11): 1796. |
| [3] |
高建平, 孙中博, 丁伟, 等. 车辆行驶工况的开发和精度研究[J]. 浙江大学学报:工学版, 2017, 51(10): 2046-2054. GAO Jian-ping, SUN Zhong-bo, DING Wei, et al. Development of Vehicle Driving Cycle and Accuracy of Research[J]. Journal of Zhejiang University:Engineering Science Edition, 2017, 51(10): 2046-2054. |
| [4] |
郑殿宇, 吴晓刚, 陈汉, 等. 哈尔滨城区乘用车行驶工况的构建[J]. 公路交通科技, 2017, 34(4): 101-107. ZHENG Dian-yu, WU Xiao-gang, CHEN Han, et al. Construction of Driving Conditions of Harbin Urban Passenger Cars[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 101-107. |
| [5] |
石琴, 马洪龙, 丁建勋, 等. 改进的FCM聚类法及其在行驶工况构建中的应用[J]. 中国机械工程, 2014, 25(10): 1381-1387. SHI Qin, MA Hong-long, DING Jian-xun, et al. An Improved FCM Clustering Algorithm and Its Applications of Vehicle Driving Cycle Construction[J]. China Mechanical Engineering, 2014, 25(10): 1381-1387. |
| [6] |
秦大同, 詹森, 漆正刚, 等. 基于K-均值聚类算法的行驶工况构建方法[J]. 吉林大学学报:工学版, 2016, 46(2): 383-389. QIN Da-tong, ZHAN Sen, QI Zheng-gang, et al. Driving Cycle Construction Using K-means Clustering Method[J]. Journal of Jilin University, 2016, 46(2): 383-389. |
| [7] |
姜平, 石琴, 陈无畏. 聚类和马尔科夫方法结合的城市汽车行驶工况构建[J]. 中国机械工程, 2010, 21(23): 2893-2897. JIANG Ping, SHI Qin, CHEN Wu-wei. Driving Cycle Construction Method of City Motors Based on Clustering Method and Markov Process[J]. China Mechanical Engineering, 2010, 21(23): 2893-2897. |
| [8] |
田毅, 张欣, 张良, 等. 神经网络工况识别的混合动力电动汽车模糊控制策略[J]. 控制理论与应用, 2011, 28(3): 363-369. TIAN Yi, ZHANG Xin, ZHANG Liang, et al. Fuzzy Control Strategy for Hybrid Electric Vehicle Based on Neural Network Identification of Driving Conditions[J]. Control Theory and Application, 2011, 28(3): 363-369. |
| [9] |
MONTAZERI-GH M, FOTOUHI A. Tehran Driving Cycle Development Using the k-means Clustering Method[J]. Scientia Iranica, 2013, 20(2): 286-293. |
| [10] |
KAMBLE S H, MATHEW T V, SHARMA G K. Development of Real-World Driving Cycle:Case Study of Pune,India[J]. Transportation Research Part D:Transport & Environment, 2009, 14(2): 132-140. |
| [11] |
ZHANG H, WANG C, FAN W. A Projection Pursuit Dynamic Cluster Model based on a Memetic Algorithm[J]. Tsinghua Science and Technology, 2015, 20(6): 661-671. |
| [12] |
FRIEDMAN J H, TUKEY J W. A Projection Pursuit Algorithm for Exploratory Data Analysis[J]. IEEE Transactions on Computers, 2006, 23(9): 881-890. |
| [13] |
齐琳, 姚俭, 王心月. 基于改进粒子群算法的电动汽车充电站布局优化[J]. 公路交通科技, 2017, 34(6): 136-143. QI Lin, YAO Jian, WANG Xin-yue. Optimizing Layout of Electric Vehicle Charging Station Based on Improved Particle Swarm Optimization Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 136-143. |
| [14] |
KENNEDY J,EBERHART R. Particle Swarm Optimization[C]//Proceedings of IEEE 1995 International Conference on Neural Networks. Washington,D. C.: IEEE,2002: 1942-1948.
|
| [15] |
王凌, 沈婧楠, 王圣尧, 等. 协同进化算法研究进展[J]. 控制与决策, 2015, 30(2): 193-202. WANG Ling, SHEN Jing-nan, WANG Sheng-yao, et al. Advances in Co-evolutionary Algorithms[J]. Control & Decision, 2015, 30(2): 193-202. |
| [16] |
HUANG D, XIE H, MA H, et al. Driving Cycle Prediction Model Based on Bus Route Features[J]. Transportation Research Part D:Transport & Environment, 2017, 54: 99-113. |
| [17] |
罗孝羚, 蒋阳升. 基于K-means聚类的城郊公交网络设计[J]. 公路交通科技, 2018, 35(5): 115-120,134. LUO Xiao-ling, JIANG Yang-sheng. Design of Transit Network between Urban Area and Suburb Based on K-means Clustering[J]. Journal of Highway and Transportation Research and Development, 2018, 35(5): 115-120,134. |
| [18] |
刘应吉, 夏鸿文, 姚羽, 等. 组合主成分分析和模糊c均值聚类的车辆行驶工况制定方法[J]. 公路交通科技, 2018, 35(3): 79-85. LIU Ying-ji, XIA Hong-wen, YAO Yu, et al. A Method of Vehicle Driving Cycle Development Based on Combined Principal Component Analysis and Fuzzy C Means Clustering[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 79-85. |
 2019, Vol. 36
2019, Vol. 36
