扩展功能
文章信息
- 李磊
- LI Lei
- 基于ANSYS的子午线轮胎力学特性研究
- Analysis on Mechanical Characteristics of Radial Tire Based on ANSYS
- 公路交通科技, 2019, 36(11): 111-118, 141
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 111-118, 141
- 10.3969/j.issn.1002-0268.2019.11.015
-
文章历史
- 收稿日期: 2018-03-09
轮胎作为汽车重要的接地部件,传递着汽车和地面间的作用力和力矩[1-2],决定着汽车的安全[3]。近年来,随着汽车行驶速度的提高,对轮胎结构设计提出了更高要求[4]。建立准确的轮胎力学模型对于开展整车动力学分析是汽车行业亟待解决的关键难题[1, 5-6]。
危银涛等[4]对轮胎动态模型的研究现状进行了综述,同时指出轮胎力学的研究对于开展车辆-轮胎-道路系统的定量分析具有非常重要的意义。Pacejka等[7]采用魔术公式研究了简化轮胎模型在纵/横向运动下的瞬态响应特性。郑香美等[8]基于Matlab/simulink仿真环境并运用“魔术公式”分析了轮胎在纯制动、纯转弯和制动、转弯等工况下轮胎的力学特性。Sakai[9]采用试验手段结合理论推导方式建立了轮胎的六分力模型。Fujioka等[10]基于一维离散刷子模型研究了大外倾角情况下轮胎绕垂直轴线的力矩特性。Wei等[11]和Oertel等[12]基于有限单元法建立起了轮胎的多柔性体模型。但基于“魔术公式”的经验模型对环境试验要求较多,试验成本高[13],而理论模型又因对轮胎结构简化过多,较难真实反映轮胎的力学特性。因此,基于有限单元法建立的多柔体模型不仅在结构上更接近真实轮胎,而且仿真所获得的力学特性与理论和试验结果[6, 11-12]也更为接近[14-16]。
此外,在轮胎力学特性分析时,轮胎与地面间相互作用的处理也是一个关键问题。文献中关于模拟轮胎与地面接触的力学模型有点接触模型[17],滚子包络模型[18],固定印迹模型[18],径向弹簧模型[19],环模型[20],有限元接触模型[21-24]。其中,基于有限元的接触模型在模拟轮胎力学特性时具有较高的精度[1, 5]。
以上文献研究表明,基于有限单元法构建的多柔体轮胎-地面接触有限元模型是较为精确、经济且高效的分析手段,所获取的信息量也较传统的试验研究多。此外,文献中也较少涉及轮胎局部结构尺寸如帘线直径、帘线间距、帘线夹角以及胎压对其力学特性的影响规律。基于此,本研究主要借助于ANSYS建立了一种考虑轮胎局部细节特征(胎冠、胎侧、胎体、三角胶以及帘线等)的多柔性体有限元模型,并借助ANSYS中的接触单元,真实地反映了轮胎与地面的相互作用过程,进一步分析了帘线直径、帘线间距、钢丝帘线夹角以及胎压对轮胎径向和横向力学特性的影响规律。
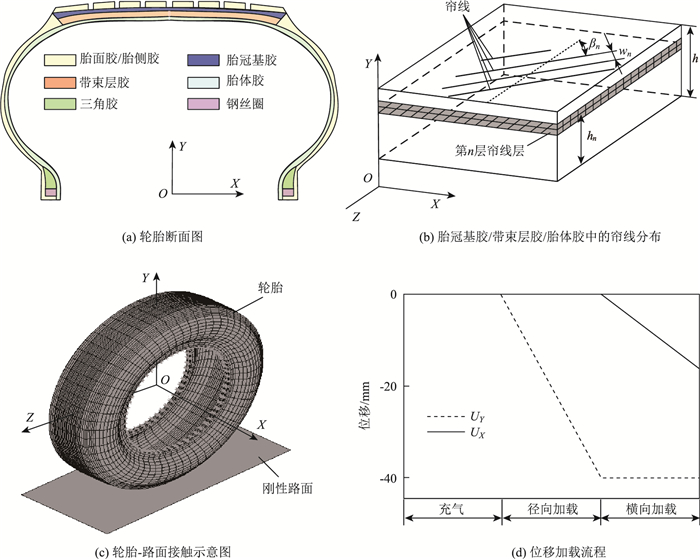
1 轮胎-路面接触有限元模型 1.1 有限元建模轮胎结构断面如图 1(a)所示,主要由胎面胶、胎侧胶、胎冠基胶、带束层胶,胎体胶、三角胶和钢丝圈等构成。首先通过Mesh200四边形分网单元对该轮胎断面进行面网格剖分,再通过扫略操作形成三维轮胎实体有限元模型,实体单元选择为Solid185。此外,各橡胶中还分布着一定数量的帘线骨架材料,在分析过程中,主要通过帘线层数n,无量纲帘线层高度ln (hn/h, hn为第n个基层的高度,h为基层所处的橡胶层厚度),帘线夹角β,帘线间距w进行定义,有限元建模中通过加强纤维单元Reinf265来进行模拟,且纤维属性定义为各项同性的层状结构(见图 2(b))。轮胎相关材料参数设置详见表 1。对于轮胎与路面接触部分,通过在轮胎和路面间建立面面接触的方式进行考虑,其中轮胎考虑为柔性体,采用Conta174单元进行网格划分,路面假定为刚性体,采用Targe170单元进行模拟,接触算法为增广的拉格朗日乘子法;对于轮胎-轮缘接触部分,以点面接触的方式建立相应的接触对,目标节点位于轮心O处,采用Targe170单元进行网格划分,接触节点为轮胎内缘面,采用Conta174单元分网,接触算法为基于刚性约束的多点约束算法(MPC)。此外,考虑到胎面和路面间摩擦因素的影响,设置摩擦系数μ=0.9。轮胎-路面接触的三维有限元模型如图 1(c)所示。
|
| 图 1 轮胎及刚性路面结构 Fig. 1 Structure of tire and rigid pavement |
| |
|
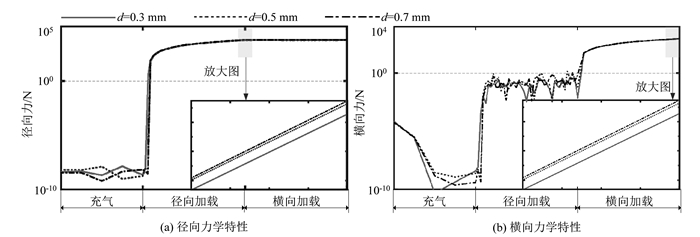
| 图 2 帘线直径对轮胎径向/横向力学特性的影响规律 Fig. 2 Influence rule of cord diameter on radial/transverse mechanical behaviors of tire |
| |
| 轮胎部位 | Yeoh材料常数 | 弹性模量 E/GPa |
泊松比 ν |
||
| C10 | C20 | C30 | |||
| 胎面胶 | 0.701 6 | -0.268 3 | 0.091 5 | — | — |
| 胎侧胶 | 0.519 1 | -0.169 2 | 0.051 2 | — | — |
| 胎体胶 | 0.850 5 | -0.207 2 | 0.077 5 | — | — |
| 三角胶 | 3.944 2 | -8.155 3 | 12.259 7 | — | |
| 胎冠基胶 | 1.388 1 | -0.506 0 | 0.202 4 | — | — |
| 带束层胶 | 1.234 4 | -0.457 9 | 0.182 7 | — | — |
| 钢丝帘线 | — | — | — | 120 | 0.3 |
| 聚酯帘线 | — | — | — | 9.5 | 0.3 |
| 胎体帘线 | — | — | — | 7.55 | 0.3 |
| 钢丝圈 | — | — | — | 2.06 | 0.27 |
1.2 轮胎加载过程模拟
考虑到轮胎加载过程中几何非线性、材料非线性和接触非线性的影响,同时也为了保证结果收敛性以及数值准确性,拟采用位移加载方式并结合ANSYS中的多载荷步分析技术,将轮胎加载过程划分为充气—径向加载—横向加载3个典型的阶段(见图 1(d)),而刚性路面采用全约束进行处理。对于图 1(d)中的充气阶段,气压是通过施加在胎体内表面上的压力来进行考虑,气压施加过程采用阶跃加载,共分5步进行;对于图 1(d)中的径向加载(Y向加载)阶段,通过在轮缘上(位于图 1(c)中的坐标原点O)施加Y向位移,载荷施加方式为斜坡加载,位移变化范围为(0, 40] mm,共分80步进行;对于图 1(d)中的横向加载(X向加载)阶段,在载荷步2的基础上,保持径向(Y向)位移为-40 mm,同时在横向(X向)施加变化范围为(0, 16] mm的位移载荷,仍采用斜坡加载方式,共分100步进行。此外,在充气阶段为了避免轮胎和刚性路面间因接触作用而引入对轮缘胎面处的附加载荷作用,设刚性路面与轮胎胎面间存在一定的间隙(3 mm)。
2 轮胎径向/横向力学特性分析以型号为185/60 R14 82H子午线轮胎的带束层-帘线复合结构为研究对象(见图 1),讨论带束层帘线直径d、帘线间距w、帘线夹角β和胎压p对轮胎力学特性的影响,相关工况参数设置详见表 2。带束层中的帘线考虑为2层结构,而其他橡胶层中的帘线均为单层,且无量纲帘线层位置均设置为0.5,帘线直径和帘线间距统一设置为1 mm,胎体层中帘线夹角为90°,冠带基胶中的帘线夹角设为0°。
| 工况 | p/MPa | 钢丝帘线 | |||
| βn(n=1, 2)/(°) | wn(n=1, 2)/mm | dn(n=1, 2)/mm | hn(n=1, 2) | ||
| 1 | 0.2 | β1=40, β2=-40 | w1=w2=2 | d1=d2=0.3 d1=d2=0.5 d1=d2=0.7 |
h1=0.25 h2=0.75 |
| 2 | 0.2 | β1=40, β2=-40 | w1=w2=1; w1=w2=2; w1=w2=3; |
d1=d2=0.5 | h1=0.25 h2=0.75 |
| 3 | 0.2 | β1=10, β2=-10 β1=40, β2=-40 β1=70, β2=-70 |
w1=w2=2 | d1=d2=0.5 | h1=0.25 h2=0.75 |
| 4 | p=0.18; p=0.22; p=0.26; |
β1=40, β2=-40 | w1=w2=2 | d1=d2=0.5 | h1=0.25 h2=0.75 |
值得说明的是,在计算轮胎径向和横向静刚度时,分别采用如下导出公式进行计算:
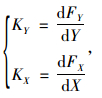
|
(1) |
式中,FX和FY分别为提取轮心O处的横向力和径向力分量;KX和KY分别为关于轮胎的横向刚度和径向刚度。
2.1 帘线直径d的影响图 2给出了帘线直径d对轮胎横向和径向力学特性的影响规律。在充气阶段,轮胎径向力FY和横向力FX几乎为0。图 2(a)表明,在径向加载阶段,径向力先存在一个陡增的趋势,随后呈现出非线性增加的趋势,出现这种现象的原因主要是由于轮胎与路面经历了从未接触到接触的跳变阶段;在横向加载阶段,轮胎的径向力FX几乎为一定值。图 2(b)表明,在径向加载阶段,横向力FX也存在突然增大的现象,且围绕某一均值上下波动。之所以在径向加载下出现横向力FX的作用,这主要是由于带束层帘线采用双层布置且存在帘线夹角βn(n=1, 2),导致轮胎结构关于YOZ平面存在非对称性。因此,当轮胎与路面发生接触作用时,轮胎因横向变形产生的力作用效果并不能完全抵消,其会对轮胎施加一定的横向力作用;在横向加载阶段,轮胎所承受的横向力随着横向位移的增加而呈现出非线性增大的趋势。帘线直径d对轮胎横向和径向力存在轻微的影响;随着帘线直径d的增加,轮胎径向力FY和横向力FX均呈增加趋势。
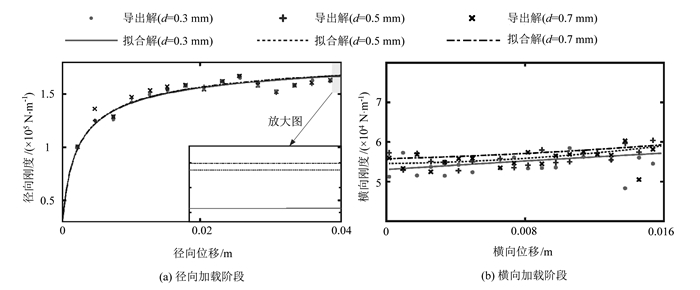
图 3分别给出了轮胎在径向和横向加载阶段时(见图 1(d))的径向和横向刚度随加载位移的变化规律。从图 3可以看出,尽管随帘线直径d的增加,轮胎的径/横向刚度呈现出增大的趋势,但总体来讲,帘线直径d对轮胎径/横向刚度的影响较小。值得说明的是,图 3中的导出解是基于公式(1)通过差分计算得到。考虑到导出解数据的波动性,本研究基于最小二乘法原理对导出解进行了数据拟合,其中径向刚度的拟合函数采用幂级数模型KY=aYb+c,而横向刚度的拟合函数则采用二次多项式KX=dX2+eX+f。此外,图 3中的径/横向刚度导出解是以5为间隔对导出解进行取点描图所得。
|
| 图 3 帘线直径对轮胎径向/横向刚度特性的影响规律 Fig. 3 Influence rule of cord diameter on radial/transverse stiffness characteristics of tire |
| |
2.2 帘线间距w的影响
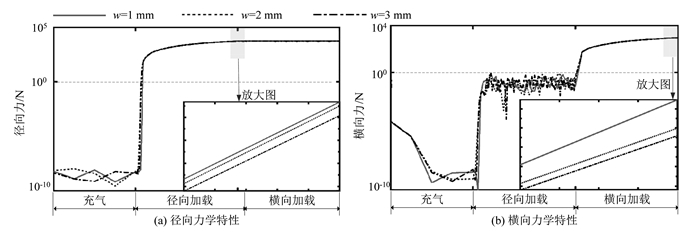
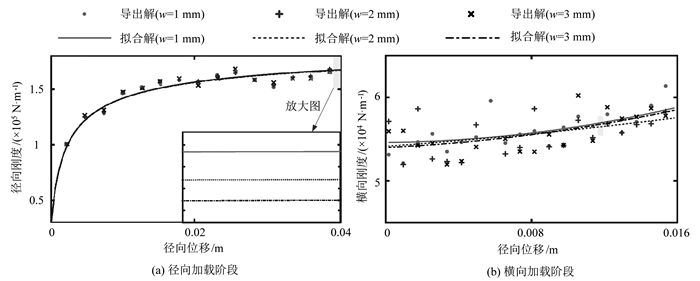
帘线间距w对轮胎横向和径向力学特性的影响如图 4所示。从图 4(b)中可以看出,在径向加载阶段,横向力FX的波动程度较大(相对于图 2(b)而言)。随着帘线间距w的增大,轮胎径向力FY和横向力FX均呈现出减小的趋势。这主要是由于帘线间距的增加,导致帘线层中起骨架作用的钢丝帘线数减少,从而导致轮胎径向刚度的降低(如图 5(a)所示),在相同形变下承受的载荷降低,但轮胎横向刚度受帘线间距的影响比较复杂(见图 5(b))。总体来讲,帘线间距对轮胎径/横向刚度特性的影响较小。
|
| 图 4 帘线间距对轮胎径向/横向力学特性的影响规律 Fig. 4 Influence rule of cord space on radial/transverse mechanical behaviors of tire |
| |
|
| 图 5 帘线间距对轮胎径向/横向刚度特性的影响规律 Fig. 5 Influence rule of cord distance on radial/transverse stiffness characteristics of tire |
| |
2.3 帘线夹角βn的影响
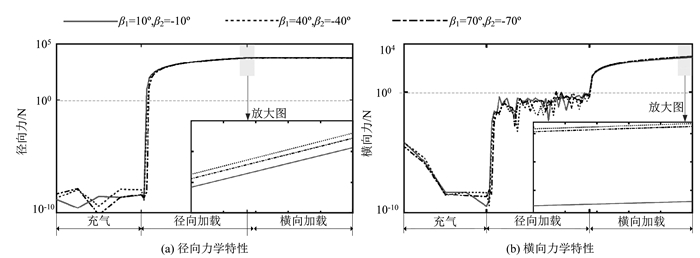
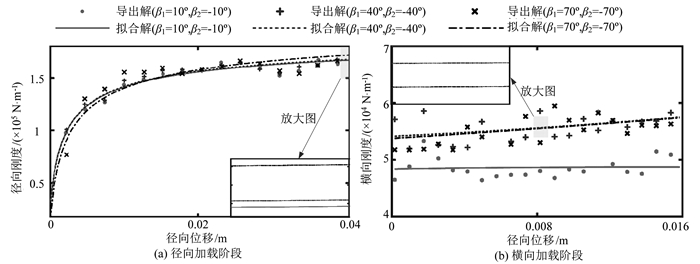
帘线夹角βn对轮胎横向和径向力学特性的影响如图 6所示。从图 6可以看出,随着帘线夹角βn (n=1, 2)的增加,在径向加载阶段,径向力FY呈现出先增加后减少的趋势(如图 6(a)所示);在横向加载阶段,横向力FX同样呈现出先增大后减小的趋势(如图 6(b)所示)。该现象表明,轮胎会存在一个最优帘线夹角βn,使得径向力FY和横向力FX均达到最大值,从而提高轮胎的承载能力。图 7的径/横向刚度曲线同样反映出了类似的变化规律。值得指出的是,相对于径向刚度,帘线夹角βn对横向刚度的影响尤为明显,且当横向交角超过一定值时(本研究中为40°),横向刚度趋于稳定(见图 7(b))。
|
| 图 6 帘线夹角对轮胎径向/横向力学特性的影响规律 Fig. 6 Influence rule of cord angle on radial/transverse mechanical behaviors of tire |
| |
|
| 图 7 帘线夹角对轮胎径向/横向刚度特性的影响规律 Fig. 7 Influence rule of cord angle on radial/transverse stiffness characteristics of tire |
| |
2.4 胎压p的影响
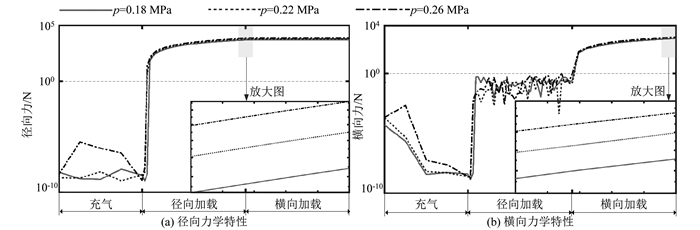
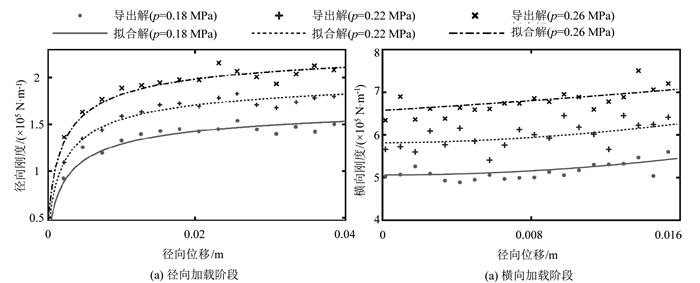
图 8给出了胎压p对轮胎横向和径向力学特性的影响规律。图 8(a)表明,在径向加载阶段,径向力FY随着胎压p的增加而增大;图 8(b)表明,在横向加载阶段,横向力FX随着胎压p的增加而增大。这表明适当提高轮胎的胎压值会提高轮胎的承载能力,但是过大的胎压值可能会因轮胎的结构强度不够而产生破坏作用。因此,应在保证轮胎结构强度的前提下,尽可能地提高轮胎的胎压值。图 9表明胎压对轮胎的径/横向刚度影响较大,且随着胎压的增加,轮胎的径/横向刚度呈现出增大的趋势。
|
| 图 8 胎压对轮胎径向/横向力学特性的影响规律 Fig. 8 Influence rule of tire pressure on radial/transverse mechanical behaviors of tire |
| |
|
| 图 9 胎压对轮胎径向/横向刚度特性的影响规律 Fig. 9 Influence rule of tire pressure on radial/transverse stiffness characteristics of tire |
| |
3 结论
本研究基于ANSYS建立了一种子午线轮胎(185/60 R14 82H)与刚性路面接触的有限元模型,考虑材料非线性和接触非线性的影响,分析讨论了轮胎带束层帘线直径d、帘线间距w、帘线夹角βn和胎压p对轮胎横向和径向力学特性的影响,主要研究结论如下:
(1) 帘线直径或胎压的增加会使轮胎的径向和横向受载呈现出增大的趋势;帘线间距的增加则会使轮胎的径向和横向受载呈现出下降的趋势;帘线夹角的增加会使轮胎的径向和横向受载呈现出先增大后减小的趋势,因此,会存在一个合理的帘线夹角值,使得轮胎的径向和横向受载均达到或接近最大值,从而提高轮胎的承载能力。
(2) 随着胎压的增加,轮胎的径/横向刚度均呈现出明显增大的趋势,而帘线夹角则对横向刚度的影响最为明显,且在一定的交角范围内,轮胎的横向刚度随交角的增加而增大。此外,在本研究中,帘线直径和帘线间距对径/横向刚度的影响较小。
(3) 带束层中帘线层数和帘线夹角的引入会导致轮胎结构上存在一定的非对称性,从而导致在径向受载过程中,轮胎因发生非对称的横向变形而造成相应的横向载荷作用。
| [1] |
管迪华, 范成建. 用于不平路面车辆动力学仿真的轮胎模型综述[J]. 汽车工程, 2004, 26(2): 162-167. GUAN Di-hua, FAN Cheng-jian. A Review of Tire Models for Vehicle Dynamics Simulation on Uneven Road[J]. Automotive Engineering, 2004, 26(2): 162-167. |
| [2] |
危银涛, 沈筱亮. 轮胎稳态运动学与六分力预报Ⅰ:理论与方法[J]. 机械工程学报, 2012, 48(15): 65-74. WEI Yin-tao, SHEN Xiao-liang. Theory and Method of Tire Rolling Kinematics and Prediction of Tire Forces and Moments[J]. Journal of Mechanical Engineering, 2012, 48(15): 65-74. |
| [3] |
何仁, 胡青训, 薛翔. 汽车轮胎气压监测系统发展综述[J]. 中国安全科学学报, 2005, 15(10): 105-109. HE Ren, HU Qing-xun, XUE Xiang. Review on Development of Tire Pressure Monitoring System[J]. China Safety Science Journal, 2005, 15(10): 105-109. |
| [4] |
危银涛, 冯希金, 冯启章, 等. 轮胎动态模型研究的进展[J]. 汽车安全与节能学报, 2014, 5(4): 311-323. WEI Yin-tao, FENG Xi-jin, FENG Qi-zhang, et al. State of the Art for Tire Dynamical Model Research[J]. Journal of Automotive Safety and Energy, 2014, 5(4): 311-323. |
| [5] |
葛剑敏, 刘春辉, 郑联珠. 软(硬)路面行驶车辆轮胎模型分析[J]. 轮胎工业, 2001, 21(2): 73-80. GE Jian-min, LIU Chun-hui, ZHENG Lian-zhu. Analysis of Vehicle Tire on Soft (or Hard) Road[J]. Tire Industry, 2001, 21(2): 73-80. |
| [6] |
ORENGO F, RAY M H, PLAXICO C A. Modeling Tire Blow-out in Roadside Hardware Simulations Using LS-DYNA[C]//2003 ASME International Mechanical Engineering Congress and Exposition. Washington, D.C.: American Society of Mechanical Engineers, 2012: 71-80.
|
| [7] |
PACEJKA H B, BESSELINK I J M. Magic Formula Tyre Model with Transient Properties[J]. Vehicle System Dynamics, 1997, 27(S1): 234-249. |
| [8] |
郑香美, 高兴旺, 赵志忠. 基于"魔术公式"的轮胎动力学仿真分析[J]. 机械与电子, 2012(9): 16-20. ZHENG Xiang-mei, GAO Xing-wang, ZHAO Zhi-zhong. Simulation Analysis of Tire Dynamic Based on "Magic Formula"[J]. Mechanical and Electronic, 2012(9): 16-20. |
| [9] |
SAKAI H. Theoretical and Experimental Studies on the Dynamic Properties of Tyres Part 1:Review of Theories of Rubber Friction[J]. International Journal of Vehicle Design, 1981, 2(1): 78-110. |
| [10] |
FUJIOKA T, GODA K. Discrete Brush Tire Model for Calculating Tire Forces with Large Camber Angle[J]. Vehicle System Dynamics, 1996, 25(S1): 200-216. |
| [11] |
WEI Y, OERTEL C, SHEN X. Tyre Rolling Kinematics and Prediction of Tyre Forces and Moments:Part Ⅱ-Simulation and Experiment[J]. Vehicle System Dynamics, 2012, 50(11): 1689-1706. |
| [12] |
OERTEL C, WEI Y. Tyre Rolling Kinematics and Prediction of Tyre Forces and Moments:Part Ⅰ-Theory and Method[J]. Vehicle System Dynamics, 2012, 50(11): 1673-1687. |
| [13] |
郭孔辉. UniTire统一轮胎模型[J]. 机械工程学报, 2016, 52(12): 90-99. GUO Kong-hui. UniTire:Unified Tire Model[J]. Journal of Mechanical Engineering, 2016, 52(12): 90-99. |
| [14] |
朱文华. 用显式有限元程序分析轮胎转向模拟[J]. 轮胎工业, 1999, 19(4): 215-219. ZHU Wen-hua. Tire Steering Simulation Using Explicit Finite Element Program[J]. Tire Industry, 1999, 19(4): 215-219. |
| [15] |
张红军, 薛隆泉.基于ANSYS的汽车轮胎有限元分析研究[D].西安: 西安理工大学, 2005. ZHANG Hong-jun, XUE Long-quan. FE Analysis and Research of Motor Type Based on ANSYS Software[D]. Xi'an: Xi'an University of Technology, 2005. http://d.wanfangdata.com.cn/Thesis/W029783 |
| [16] |
冯希金, 郑小刚, 危银涛, 等. 轮胎振动特性的有限元分析及关键影响因素研究[J]. 轮胎工业, 2013, 33(1): 12-20. FENG Xi-jin, ZHENG Xiao-gang, WEI Yin-tao, et al. Finite Element Analysis on Tire Vibration and Study on Its Key Influencing Factors[J]. Tire Industry, 2013, 33(1): 12-20. |
| [17] |
POTTS G R. Application of Holography to the Study of Tire Vibration[J]. Tire Science and Technology, 1973, 1(3): 255-266. |
| [18] |
CAPTAIN K M, BOGHANI A B, WORMLEY D N. Analytical Tire Models for Dynamic Vehicle Simulation[J]. Vehicle System Dynamics, 1979, 8(1): 1-32. |
| [19] |
BADALAMENTI J M, DOYLE G R. Radial-interradial Spring Tire Models[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110(1): 70-75. |
| [20] |
HUANG S C, SU C K. In-plane Dynamics of Tires on the Road Based on an Experimentally Verified Rolling Ring Model[J]. Vehicle System Dynamics, 1992, 21(1): 247-267. |
| [21] |
NOOR A K, TANNER J A. Computational Modeling of Tires[J]. Molecular and Cellular Biology, 1995, 33(1): 159-169. |
| [22] |
路永婕, 杨绍普, 李韶华. 载重子午轮胎与路面相互作用的分析[J]. 公路交通科技, 2009, 26(12): 12-16. LU Yong-jie, YANG Shao-pu, LI Shao-hua. Analysis of Interaction between Truck Radial-ply Tire of Heavy Duty Vehicle and Road Surface[J]. Journal of Highway and Transportation Research and Development, 2009, 26(12): 12-16. |
| [23] |
宋勇, 梁彦龙, 马学军, 等. 汽车轮胎与路面接触应力分布特点及力学模型[J]. 公路交通科技, 2014, 31(10): 112-118. SONG Yong, LIANG Yan-Long, MA Xue-jun, et al. Distribution Characteristics of Contact Stress between Vehicle Tire and Road Surface and Mechanical Model[J]. Journal of Highway and Transportation Research and Development, 2014, 31(10): 112-118. |
| [24] |
黄晓明, 代琦, 平克磊. 轮胎胎面与柔性路面摩擦接触的数值分析[J]. 公路交通科技, 2008, 25(1): 16-20. HUANG Xiao-ming, DAI Qi, PING Ke-lei. Numeric Analysis of Friction Contact between Tread and Flexible Pavement[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 16-20. |
 2019, Vol. 36
2019, Vol. 36
